Проверка гипотезы о виде распределения
реклама

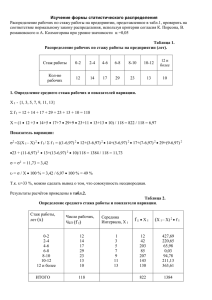
ПРОВЕРКА ГИПОТЕЗЫ О ВИДЕ РАСПРЕДЕЛЕНИЯ Критерии согласия При получении той или иной выборки встречаются случаи, когда закон распределения заранее не известен, но есть основания предположить, что он имеет определенный вид (назовем его вид А). В таких случаях исследователь формулирует нулевую гипотезу следующим образом: H0 – генеральная совокупность распределена по закону А. Критерий согласия – это критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Простая гипотеза прямо указывает некий закон вероятностей, по которому возникли выборочные значения. Сложная гипотеза указывает семейство распределений. С помощью критерия согласия мы проверяем, согласуются эмпирические данные с нашим гипотетическим предположением относительно теоретической функции распределения или нет. Рассмотрим критерии согласия Пирсона («хи-квадрат») и критерий согласия Колмогорова. Критерий согласия Хи-квадрат Пирсона Пусть дан ряд из n измерений. Важно установить, можно ли описать эти n значений с помощью принятой теоретической модели. Наиболее часто используют модель нормального (Гауссова) распределения или распределения Пуассона. Для проверки выдвигают нулевую гипотезу – H0: «между эмпирическим распределением и теоретической моделью нет никакого различия». 148 Из n значений (n>50) оценивают среднее x и стандартное отклонение s, а затем разбивают n значений на m n классов. Для каждого полученного класса определяют абсолютную частоту h попавших в него значений и сопоставляют ее с теоретической частотой ht. Из эмпирических и теоретических частот составляют выражение m ( h h )2 χ 2 i ti . hti i 1 Найденное выражение будет следовать хи-квадрат распределению с m – k степенями свободы. Где m – количество классов, а k представляет число параметров, необходимых для описания выборки. Для нормального распределения k = 3 (среднее, стандартное отклонение и объем выборки), для распределения Пуассона k = 2 (среднее и объем выборки). Исходя из уровня значимости α и числа степеней свободы находим критическую точку. 2 , то Если при проверке получается, что χ 2 χ кр проверяемая гипотеза отбрасывается; между эмпирическим и теоретическим распределением существует значимое различие. 2 Различие не значимо, если χ 2 χ кр . Условием использования критерия “хи-квадрат” является достаточно большое число измерений (n>50). Критерий согласия Колмогорова – Смирнова Критерий нормальности Колмогорова – Смирнова обладает достаточной чувствительностью даже при малом числе значений. Его можно применять также для проверки соответствия любому распределению (например, равномерному). Однако следует иметь в виду, что функция распределения, установленная гипотезой, должна быть непрерывной. Для проверки нормируют значения xi по формуле 149 ui x i x s и отыскивают значения гауссова интеграла, соответствующие ui. Затем находят разности d i Y i Y u i и сравнивают максимальную из них с критическим значением dкрит из таблицы. Процентные точки (α=0,05) для проверки на нормальность по Колмогорову и Смирнову. n d n d n d 3 0.376 9 0.274 15 0.219 4 0.375 10 0.261 16 0.213 5 0.343 11 0.251 17 0.207 6 0.323 12 0.242 18 0.202 7 0.304 13 0.234 19 0.197 8 0.288 14 0.226 20 0.192 е мр и П В результате 8-ми титрований получились значения объема V(мл): 20,23 20,12 20,21 20,17 20,13 20,07 20,24 20,19 Надо проверить, следуют ли они Гауссовому распределению. Решение. Воспользуемся критерием согласия Колмогорова. Вычислим точечные оценки для математического ожидания и среднеквадратического отклонения x 20,17 и s 0,06 . Ранжируем данные и записываем их в порядке возрастания. Составим таблицу. V (мл) 1 20,07 20,12 20,13 20,17 20,19 20,21 20,23 Частота Абсол ютная. 2 1 1 1 1 1 1 1 Относит ельная. 3 0,125 0,125 0,125 0,125 0,125 0,125 0,125 Кумулят ивная Yi 4 0,125 0,250 0,375 0,500 0,625 0,750 0,875 ui Y(ui) |di| 5 -1,667 -0,833 -0,677 0 0,333 0,667 1,000 6 0,048 0,203 0,252 0,5 0,629 0,748 0,841 7 0,077 0,047 0,123 0,000 0,004 0,002 0,016 150 20,24 1 0,125 1,000 1,167 0,867 0,133 Максимальное значение статистики Колмогорова max(|d|)=0,133. Сравним полученное максимальное значение с табличным d(α = 0,05, n = 8) = 0,288. Получили dmax<d, следовательно, нет оснований отбрасывать гипотезу о нормальном распределении. 151