Вариант 12 с решениями

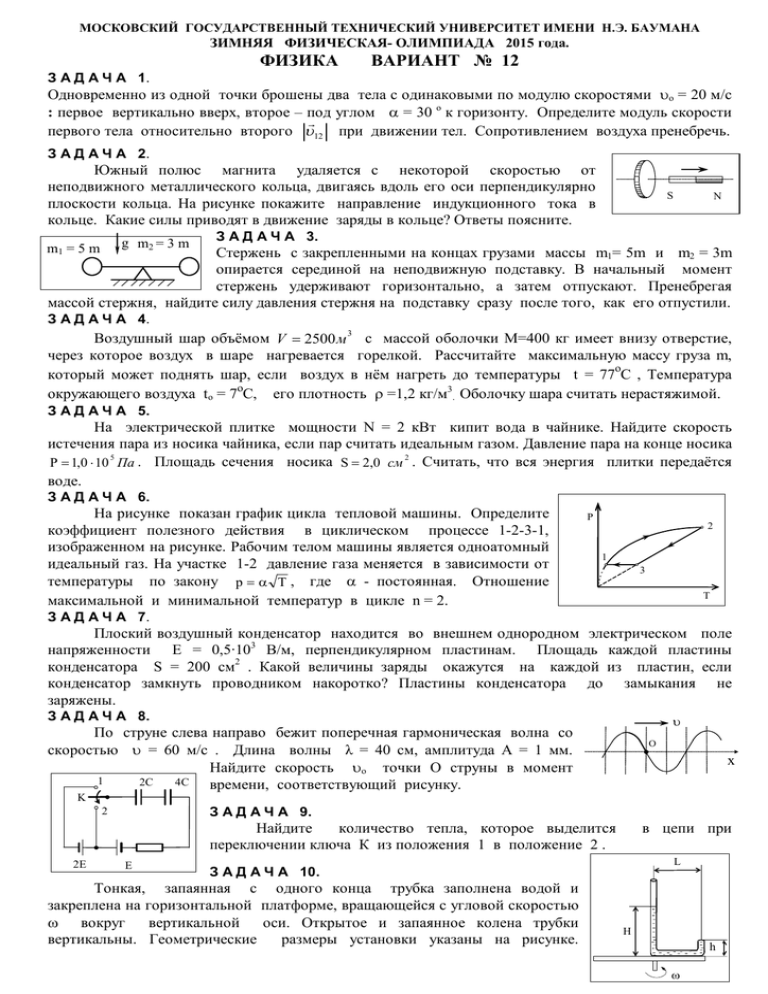
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Н.Э. БАУМАНА
ЗИМНЯЯ ФИЗИЧЕСКАЯ- ОЛИМПИАДА 2015 года.
ФИЗИКА
ВАРИАНТ № 12
З А Д А Ч А 1.
Одновременно из одной точки брошены два тела с одинаковыми по модулю скоростями o = 20 м/c
: первое вертикально вверх, второе – под углом  = 30 о к горизонту. Определите модуль скорости

первого тела относительно второго 12 при движении тел. Сопротивлением воздуха пренебречь.
З А Д А Ч А 2.
Южный полюс магнита удаляется с некоторой скоростью от
неподвижного металлического кольца, двигаясь вдоль его оси перпендикулярно
плоскости кольца. На рисунке покажите направление индукционного тока в
кольце. Какие силы приводят в движение заряды в кольце? Ответы поясните.
g m2 = 3 m
m1 = 5 m
S
N
З А Д А Ч А 3.
Стержень с закрепленными на концах грузами массы m1= 5m и m2 = 3m
опирается серединой на неподвижную подставку. В начальный момент
стержень удерживают горизонтально, а затем отпускают. Пренебрегая
массой стержня, найдите силу давления cтержня на подставку сразу после того, как его отпустили.
З А Д А Ч А 4.
Воздушный шар объёмом V  2500м 3 с массой оболочки М=400 кг имеет внизу отверстие,
через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза m,
который может поднять шар, если воздух в нём нагреть до температуры t = 77оС , Температура
окружающего воздуха to = 7оС, его плотность  =1,2 кг/м3. Оболочку шара считать нерастяжимой.
З А Д А Ч А 5.
На электрической плитке мощности N = 2 кВт кипит вода в чайнике. Найдите скорость
истечения пара из носика чайника, если пар считать идеальным газом. Давление пара на конце носика
5
2
Р  1,0  10 Па . Площадь сечения носика S  2,0 см . Считать, что вся энергия плитки передаётся
воде.
З А Д А Ч А 6.
На рисунке показан график цикла тепловой машины. Определите
коэффициент полезного действия в циклическом процессе 1-2-3-1,
изображенном на рисунке. Рабочим телом машины является одноатомный
идеальный газ. На участке 1-2 давление газа меняется в зависимости от
температуры по закону p   T , где  - постоянная. Отношение
максимальной и минимальной температур в цикле n = 2.
P
2
1
3
T
З А Д А Ч А 7.
Плоский воздушный конденсатор находится во внешнем однородном электрическом поле
напряженности Е = 0,5∙103 В/м, перпендикулярном пластинам. Площадь каждой пластины
конденсатора S = 200 см2 . Какой величины заряды окажутся на каждой из пластин, если
конденсатор замкнуть проводником накоротко? Пластины конденсатора до замыкания не
заряжены.
З А Д А Ч А 8.

По струне слева направо бежит поперечная гармоническая волна со
скоростью  = 60 м/с . Длина волны λ = 40 см, амплитуда А = 1 мм.
Найдите скорость o точки О струны в момент
1
2C
4C
времени, соответствующий рисунку.
О
x
K
З А Д А Ч А 9.
2
Найдите
количество тепла, которое выделится
переключении ключа К из положения 1 в положение 2 .
2E
E
в цепи при
L
З А Д А Ч А 10.
Тонкая, запаянная с одного конца трубка заполнена водой и
закреплена на горизонтальной платформе, вращающейся с угловой скоростью
 вокруг
вертикальной
оси. Открытое и запаянное колена трубки
вертикальны. Геометрические
размеры установки указаны на рисунке.
H
h

Атмосферное давление Ро , плотность воды . Найдите давление воды у запаянного конца трубки.
Силами поверхностного натяжения пренебречь.
121
ЗИМНЯЯ ФИЗИЧЕСКАЯ ОЛИМПИАДА 2015 г..
I ТУР
РЕШЕНИЕ ВАРИАНТА № 12
З А Д А Ч А 1. (8 баллов)

Ответ: . : 12  vo 2(1  sin  )  20 м/c


1   2  20 м / с



1   01  gt 



 2   02  gt 

V12

V 01




12  1   2   01   02
60о
о
 = 30

V02
По теореме косинусов:

1
2
12   21   2  21 2 cos 60 o  2 2  2 2  cos 60 o   2(1  cos 60 o )  20 2   20 м / с ,
2

o
12  20 2(1  sin 30 )  20 м/c .
З А Д А Ч А 2. (8 баллов)
Ответ:
.
S
N
З А Д А Ч А 3. (10 баллов)
Ответ: R 
4m1 m2
g  7,5mg
m1  m 2

g
R
N1
N2
m2
m1

a1
.

F1

F2

a2
m1 = 5 m
g
m2 = 3 m
g
На
рисунке
показаны
силы,
действующие на стержень, и на каждое
m2 g
m1 g
из прикрепленных к нему
тел
в
интересующий нас момент времени. Стержень невесомый, поэтому суммарный момент сил,


действующих на него, должен быть равен нулю. Следовательно, F1  F2  F .
По третьему закону Ньютона силы, действующие на шарики со стороны стержня, тоже равны
между собой по модулю:






N 1  F1 , N 2  F2 следовательно, N 1  N 2  N . Т.е. F = N.
Так как стержень опирается на подставку своей серединой, то ускорения шариков равны между


собой по величине. a 1  a 2  a .
Запишем уравнения движения тел с массами m1, m2 в проекции на ось x.:
m1a  m1 g  N (1)
- m 2 a  m2 g  N (2)
Решая систему уравнений (1), (2), находим
4m1m 2
2m1 m 2
m  m2
g  4,8mg
. N
g
а 1
g ; R
m1  m 2
m1  m 2
m1  m2
  
Второй закон Ньютона, примененный к стержню, даёт: R  F1  F2 . Учитывая, что . F = N, m1=5m,
4m1m2
453
g
 7,5 mg
m2 = 3m,
получаем R  2N 
m1  m 2
53
12-2
З А Д А Ч А 4. (10 баллов)
Ответ: m  200 кг
.
Шар поднимает груз при условии: ( M  m ) g  m ВШ g   Vg , где M – масса оболочки шара, m – масса
груза,
m ВШ - масса воздуха в шаре,  V  m В АТ - масса такого же по объёму воздуха вне шара.( в атмосфере)
M  m  mВ
Сокращая уравнение на g, имеем
АТ
 m ВШ . При нагревании воздуха в шаре его давление p
и его объём V не меняются. Следовательно, согласно уравнению Менделеева - Клапейрона,
m
m ВШ
RT Ш  В АТ RT АТ , где


 - средняя молярная масса воздуха, T Ш  его температура внутри шара
T
T
m ВШ  m В АТ АТ   V АТ , где  - плотность окружающего воздуха.
TШ
TШ
pV 
и T АТ  вне шара. Отсюда :
 T 
 T 
 m ВШ   V  1  АТ  ; M  m   V  1  АТ  . Следовательно,
TШ 
TШ 


 T 
280 

m  200 ( кг ) /
m   V  1  АТ   M  1, 2  2500  1 
  400  200 ( кг ) .
TШ 
350 


mВ
АТ
З А Д А Ч А 5. (10 баллов)
Ответ:  
NRT
 7 ,6 м / с .
r p S
Массовый расход пара, выходящего из носика чайника в 1 секунду ,
N
 m  S 
(1). С другой стороны ,
m 
(2) , где N – мощность плитки; r – удельная
r
теплота испарения воды.
m
m
p
Из уравнения Менделеева – Клапейрона
pV  RT следует, что плотность пара  


V
RT
(3)
NRT
Из уравнений (1) , (3) получаем  
 7 ,6 м / с .
r p S
З А Д А Ч А 6. (10 баллов)
Ответ:  
A полезн
1

 U 1- 2  A 1  2 4
n 1
 0 ,043 .
n 1
1) Перестроим график, заданный
в условии задачи из координат
РТ в координаты РV: процесс 2P2
3 – изохора; 3-1 – изобара. Для
1
1
процесса
1-2
по
условию
P1
3
3
P2
P   T , отсюда T  2 (1).

T
V1
V2 V
Подставив (1) в уравнение
2
P2
V
состояния идеального газа , получим PV  R 2 , откуда P 
(2),
R

т.е. P
линейно зависит от V. С учетом полученной зависимости строим график цикла в PV
координатах.
P
P
2
2
1
P V
A полезная
 2
КПД цикла :  
Q подведенно е
Q 1 2
(3)
12-3
1
1
R
R
R 2
2
Aполезн  ( P2  P1 )(V2 - V1 )  ( P2  P1 )( P2  P1 ) 2  2 ( P2  P1 )  2  T2  T1
2
2

2
2
2
R

T2  T1
2



2


(4)
(5)
Q1- 2  U1- 2  A1- 2
3
U 1- 2  R(T2 - T1 )
2
2
2
P1  R
1
1
R
R
R  P2
2
2
  (T2  T1 )
A1 2  (P2  P1 )(V2 - V1 )  ( P2  P1 )(P2  P1 ) 2 
( P2  P ) 

2
2
2
2   2  2  2

2
3
R
Q1- 2  R(T2 - T1 )  ( T2  T1 )  2 R (T2  T1 )
(6)
2
2
Подставим (4) и (6) в (3), найдем КПД цикла
T2
2
R
1
2
T 2  T1
A полезн
1 T 2  T1
1 T 2  T1
1 T1
1 n 1
2
 





 U 1- 2  A1 2
2 R (T 2  T1 )
4 (T 2  T1 )
4 T 2  T1
4 T2
4 n 1
1
T1


1
4
n 1 1

n 1 4



2  1 0, 414

 0,043
2  1 9,657
З А Д А Ч А 7. (10 баллов)
Ответ: q  CU   o SE  8,85 10
11
Кл .
Так как пластины замкнуты, то они имеют один и тот же потенциал, т.е. поле внутри
конденсатора равно нулю. Это значит, что на пластинах появились заряды, создавшие поле,
напряженность которого равна по модулю и противоположна по направлению напряженности
3
внешнего поля. Зная напряженность поля
E  0,5  10 B / м , и площадь каждой пластины
конденсатора S  200 cм 2 , вычислим заряд:
S
11
12
2
3
q  CU   o Ed   o SE  8,85  10  2,0  10  0,5  10  8,85  10 Кл
d
Заряд на одной пластине равен +q, на другой  q.
З А Д А Ч А 8. (10 баллов)
v
2Av
 0,94 м/c

О
Частицы струны
совершают гармонические колебания
x(t)  Acos(t  ) , где   2
v
2v
Т.к:   , где v- скорость волны, то  
.


Частица, находящаяся в точке О, проходит положение равновесия. В этот момент она имеет
2Av
наибольшую скорость vo  A 
 0,94 м / .с .

.
Ответ: v0 
12-4
З А Д А Ч А 9. (12 баллов)
8
3
2
Ответ: Q  qE  CE .
При переключении ключа через источник тока Е протечет некоторый заряд q. Работа батареи
равна Eq. Эта работа может частично пойти на увеличение энергии, запасенной в батарее
конденсаторов, частично на выделение тепла в цепи. Как видно из рисунка, заряд и ,
следовательно, энергия, запасенная в батарее конденсаторов, не изменяются при переключении
ключа. Меняются лишь знаки зарядов на обкладках. Следовательно, при переключении ключа К
через источник тока протекает заряд
1
4
8
q  2C БAT E , где C БAT  C т.е. q  CE
3
3
8
2
и в цепи выделилось количество тепла Q  qE  CE
3
2C
4C
K
2
2E
E
З А Д А Ч А 10. (12 баллов)
 2 L2
2
Обозначим p1, - давление воды в месте изгиба трубки на оси вращения, p 2- в месте изгиба трубки,
расположенном на расстоянии L от оси вращения, и p3 - у запаянного конца. Тогда p1  p o  gH .
Центр масс воды в горизонтальном колене находится на расстоянии L/2 от оси вращения и имеет
2  L
L
ускорение
а
. Масса воды в горизонтальном колене
L/2
2
po
m  LS , где S – площадь поперечного сечения трубки.
По
второму закону Ньютона
ma  p 2 S  p1 S
или
p3
2
H
 L
SL 
 ( p 2  p1 ) S .
h
2
2 2
2 2
p1
 L
 L
p2

Отсюда p 2  p1  
 po  gH  
2
2
2 2
 L
 2 L2
Тогда
p3  p2  gh  po  gH  
 gh  po  g ( H  h)  
Ответ: p3  p o  g ( H  h) 
2
2
p 3  p o  g ( H  h ) 
2
 L
.
2
2