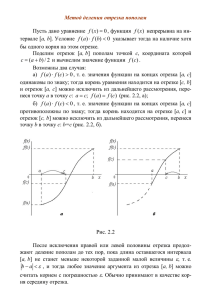
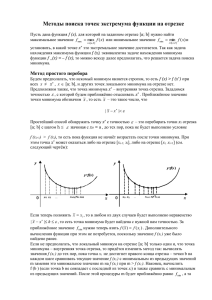
12.6.8. МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ

ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
12.6.8. МЕТОД ДЕЛЕНИЯ
ОТРЕЗКА ПОПОЛАМ
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №1
Убедившись в унимодальности функции f ( x ) = x − 2 x + e
2
−x
на отрезке
[ 1;1,5 ], найти методом деления отрезка пополам поиска точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №2
Убедившись в унимодальности функции f ( x ) = x − 2 x + e
2
−x
на отрезке
π
[ 0; ], найти методом деления отрезка пополам точку минимума x∗ функции f ( x )
4
на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним запасным знаком.
Вариант №3
Убедившись в унимодальности функции f ( x ) =
1 + x 2 + e − 2 x на отрезке
[ 0;1 ], найти методом деления отрезка пополам точку минимума x∗ функции f ( x )
на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним запасным знаком.
Вариант №4
Убедившись в унимодальности функции
f ( x ) = x 4 + 4 x 2 − 32 x + 1 на
отрезке [ 1,5;2 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
запасным знаком.
ε = 0 ,05 . Вычисления вести с одним
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №5
x2
x7
3
Убедившись в унимодальности функции f ( x ) =
−x +
− x на отрезке
2
7
[ 1;1,5 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №6
Убедившись в унимодальности функции f ( x ) = x − 3 sin x на отрезке
3
[ 0 ,5;1 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №7
5
Убедившись в унимодальности функции f ( x ) = 5 x − 8 x 4 − 20 x на отрезке
2
[ 3;3 ,5 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №8
x3
Убедившись в унимодальности функции f ( x ) =
− 5 x + x ln x на отрезке
3
[ 1,5;2 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №9
Убедившись в унимодальности функции f ( x ) = x sin x + 2 cos x на отрезке
[ − 5;−4 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №10
Убедившись в унимодальности функции f ( x ) = x + 8 x − 6 x − 72 x + 90
4
3
2
на отрезке [ 1,5;2 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №11
Убедившись в унимодальности функции
f ( x ) = x 6 + 3 x 2 + 6 x − 1 на
отрезке [ − 1;0 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №12
x2
Убедившись в унимодальности функции f ( x ) = 10 x ln x −
на отрезке
2
[ 0 ,5;1 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №13
Убедившись в унимодальности функции f ( x ) = x + 2 ( x lg
2
x
− 2 ) на отрезке
e
[ 1,5;2 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №14
Убедившись в унимодальности функции f ( x ) = 3 x − 10 x + 21x + 12 x
4
3
2
на отрезке [ 0 ;0 ,5 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №15
Убедившись в унимодальности функции
2x
− 2 x 2 на отрезке
f (x ) =
ln 2
[ 3 ,5;4 ,5 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №16
x3
Убедившись в унимодальности функции f ( x ) = e −
+ 2 x на отрезке
3
x
[ − 1,5;1 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №17
Убедившись в унимодальности функции
f ( x ) = x 4 + 2 x 2 + 4 x + 1 на
отрезке [ − 1;0 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №18
Убедившись в унимодальности функции f ( x ) = x − 5 x + 10 x − 5 x на
5
3
2
отрезке [ − 3;−2 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №19
Убедившись в унимодальности функции f ( x ) = x + 3 x(ln x − 1) на отрезке
2
[ 0 ,5;1 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №20
Убедившись в унимодальности функции f ( x ) = x − 2 x − 2 cos x на отрезке
2
[ 0 ,5;1 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №21
Убедившись в унимодальности функции f ( x ) = ( x + 1) − 2 x
4
2
на отрезке
[ − 3;−2 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №22
4
Убедившись в унимодальности функции f ( x ) = 3(5 − x )3 + 2 x на отрезке
2
[ 1,5;2 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №23
Убедившись в унимодальности функции f ( x ) = − x + 3(1 + x ) [ ln(1 + x ) − 1 ]
3
на отрезке [ − 0 ,5;0 ,5 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №24
Убедившись в унимодальности функции f ( x ) = x − 3 x + x ln x на отрезке
2
[ 1;2 ], найти методом деления отрезка пополам точку минимума x∗ функции f ( x )
на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним запасным знаком.
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №25
Убедившись в унимодальности функции
f ( x ) = ln( 1 + x 2 ) − sin x на
отрезке [ 0 ; π ], найти методом деления отрезка пополам точку минимума x∗
4
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №26
Убедившись в унимодальности функции
x4
f (x ) =
+ x 2 − 8 x + 12 на
4
отрезке [ 0 ;2 ], найти методом деления отрезка пополам точку минимума x∗
функции f ( x ) на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним
запасным знаком.
Вариант №27
x2
Убедившись в унимодальности функции f ( x ) =
− sin x на отрезке [ 0;1 ],
2
найти методом деления отрезка пополам точку минимума x∗ функции f ( x ) на этом
отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним запасным знаком.
Вариант №28
Убедившись в унимодальности функции f ( x ) = x + e
4
−x
на отрезке [ 0 ;1 ],
найти методом деления отрезка пополам точку минимума x∗ функции f ( x ) на этом
отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним запасным знаком.
ИрГУПС
Кафедра «Высшая математика»
12.6.8. Метод деления отрезка пополам
_____________________________________________________________________________________
Вариант №29
Убедившись в унимодальности функции f ( x ) = e +
x
1
на отрезке [ 0 ,1;1,2 ],
x
найти методом деления отрезка пополам точку минимума x∗ функции f ( x ) на этом
отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним запасным знаком.
Вариант №30
Убедившись в унимодальности функции f ( x ) = x + 4 x − 1 на отрезке
3
2
[ 0 ,2;1,2 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №31
Убедившись в унимодальности функции f ( x ) = x − 2 x + e
2
−x
на отрезке
[ 1;1,5 ], найти методом деления отрезка пополам точку минимума x∗ функции
f ( x ) на этом отрезке с точностью ε = 0 ,05 . Вычисления вести с одним запасным
знаком.
Вариант №32
Убедившись в унимодальности функции f ( x ) = x − 2 x + e
2
−x
на отрезке
π
[ 0; ], найти методом деления отрезка пополам точку минимума x∗ функции f ( x )
4
на этом отрезке с точностью
ε = 0 ,05 . Вычисления вести с одним запасным знаком.