Будагян И.Ф. Наносекундные технологии и метаматериалы

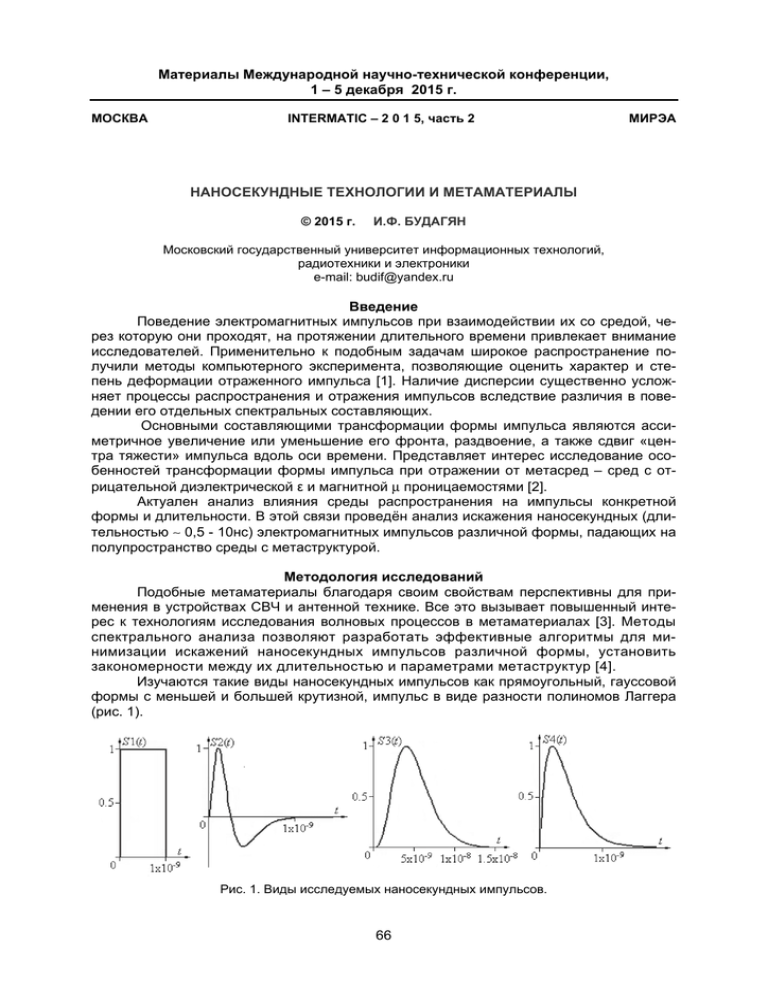
Материалы Международной научно-технической конференции,
1 – 5 декабря 2015 г.
МОСКВА
INTERMATIC – 2 0 1 5, часть 2
МИРЭА
НАНОСЕКУНДНЫЕ ТЕХНОЛОГИИ И МЕТАМАТЕРИАЛЫ
© 2015 г.
И.Ф. БУДАГЯН
Московский государственный университет информационных технологий,
радиотехники и электроники
e-mail: [email protected]
Введение
Поведение электромагнитных импульсов при взаимодействии их со средой, через которую они проходят, на протяжении длительного времени привлекает внимание
исследователей. Применительно к подобным задачам широкое распространение получили методы компьютерного эксперимента, позволяющие оценить характер и степень деформации отраженного импульса [1]. Наличие дисперсии существенно усложняет процессы распространения и отражения импульсов вследствие различия в поведении его отдельных спектральных составляющих.
Основными составляющими трансформации формы импульса являются ассиметричное увеличение или уменьшение его фронта, раздвоение, а также сдвиг «центра тяжести» импульса вдоль оси времени. Представляет интерес исследование особенностей трансформации формы импульса при отражении от метасред – сред с отрицательной диэлектрической ε и магнитной μ проницаемостями [2].
Актуален анализ влияния среды распространения на импульсы конкретной
формы и длительности. В этой связи проведён анализ искажения наносекундных (длительностью ∼ 0,5 - 10нс) электромагнитных импульсов различной формы, падающих на
полупространство среды с метаструктурой.
Методология исследований
Подобные метаматериалы благодаря своим свойствам перспективны для применения в устройствах СВЧ и антенной технике. Все это вызывает повышенный интерес к технологиям исследования волновых процессов в метаматериалах [3]. Методы
спектрального анализа позволяют разработать эффективные алгоритмы для минимизации искажений наносекундных импульсов различной формы, установить
закономерности между их длительностью и параметрами метаструктур [4].
Изучаются такие виды наносекундных импульсов как прямоугольный, гауссовой
формы с меньшей и большей крутизной, импульс в виде разности полиномов Лаггера
(рис. 1).
Рис. 1. Виды исследуемых наносекундных импульсов.
66
Исследуется процесс отражения этих импульсов от ε-негативных метаматериалов (плазменных слоев и слоев композитного метаматериала), μ-негативных метаматериалов при изменении топологических параметров метаструктуры и бинегативных
метаматериалов при достаточно больших углах падения. На границу раздела с исследуемой средой падает из вакуума наносекундный импульс S(t) единичной амплитуды,
эффективной длительностью T. Предполагается, что волна распространяется вдоль
оси z. При горизонтальной поляризации волны вектор напряженности электрического
поля ориентирован вдоль границы раздела – оси y, а магнитного поля – вдоль оси
x.Учитывается, что частотные составляющие, лежащие в диапазоне -ωкр<ω<ωкр, полностью отражаются от ε- или μ-негативныхсред и не распространяются внутри них.
При этом можно, используя обратное преобразование Фурье и учитывая коэффициент отражения, найти отраженное поле соответственно от полупространства или
от слоя метасреды на расстоянии z[5]:
E pп.отр
, d (t , z )
= E y0
ωкр
 S (ω) R (ω)exp[ j (ωt − kz )]dω
− ωкр
S(ω) – спектральная плотность падающего импульса, и предполагается,
что R (ω) = exp[jβ(ω)].
Для наибольшего отражения от данных сред необходимо, чтобы их критические
частоты ωкр были соизмеримы или больше граничной частоты ωгр, где под ±ωгрпонимаются граничные частоты, внутри диапазона которых сосредоточено 99% энергии спектра импульса. При ωкр=ωгр отраженный импульс по форме должен быть похож на падающий импульс, так как гармоники с частотами, лежащими в пределах |ω|<ωкр, полностью отражаются и несут основную энергию импульса.
Процесс вычислений сводится к следующему:задается интервал по оси времени, выбирается тип падающего импульса и по соответствующей формуле вычисляется
его форма; для вычисления спектра падающего импульса S(ω) используется быстрое
преобразование Фурье;коэффициенты отражения вычисляются для полубесконечной
среды и для слоя конечной толщины при нормальном и наклонном падении волны на
слой (характерные графики при нормальном падении представлены на рис. 2); с учетом R(ω) вычисляется дискретный спектр отраженного сигналаSR(ω) = R(ω)· S(ω).
Обратное преобразование Фурье позволяет перейти от спектральной плотности к отраженному сигналу S(t). Особенности при отражении импульсов от
слоя метаматериала связаны с необходимостью учитывать знаки диэлектрической и магнитной проницаемостей при
нахождении коэффициентов преломления и импедансов сред.
Рис. 2. Частотные зависимости модулей
коэффициентов отражения для плазмы.
Результаты моделирования
Ниже приводятся результаты численных экспериментов в среде MathCAD (на
основе составленной программы для моделирования), проводимых на математических
моделях с учетом реальной дисперсии при отражении наносекундных импульсов.
1. Отражение от ε-негативных метаматериалов:
ε(ω) = 1 − ω2p ω2
-
плазменных слоев полубесконечной и конечной толщины без потерь, полубесконечных
слоев композитного метаматериала c плазменной частотой ω2p = 2πc 2 ( a 2 ln a 2πr ) в
виде набора тонких металлических проводников радиуса r с межпроводным расстоянием a, погруженных в поддерживающий диэлектрик. Рассматривалась нормированная
к длительности импульса толщина слоя N = d/cT.
Изменение формы прямоугольного импульса, импульса в виде разности полиномов Лаггера и гауссова импульса с большей крутизной при отражении от слоя плазмы полубесконечной (пунктирная) и конечной (сплошная кривая) толщины для различной нормированной к длительности импульса толщине слоя N представлено на рис. 3.
Отражённое поле от полубесконечного композитного метаматериала находится
67
с учетом того, что частотные составляющие, лежащие в диапазоне |ω|<ωр, отражаются
полностью и не распространяются внутри этих сред. В случае полубесконечных слоев
композитного метаматериала наименьшие искажения формы падающего импульса показал при отражении импульс в виде разности полиномов Лаггера, так же, как и для
плазменных слоев. Отражённые гауссовы импульсытеряют форму на конце при всех
длительностях. При меньшей длительности форма импульса лучше сохраняется на
более высоких плазменных частотах, с увеличением длительности оптимальная частота уменьшается. Наилучшей картины можно добиться путём подбора оптимального
соотношения параметров длительности импульса и плазменной частоты.
N=0,007
N=0,025
N=0,025
Рис. 3. Динамика изменения отраженных импульсов от плазмы.
2. Отражение от μ-негативных метаматериалов: μ(ω) = 1 − ω2pm ω2 - полубесконечных слоев без потерь и с потерями (рис. 4) композитного метаматериала в
−1
πr 2 
3l
2σ  ,
виде двойного кольцевого резонатора с μ эф = 1 −
+ j
1− 2 3 2

2 
a  π r ω μ 0ε0ε
μ 0 rω 
включая конечные слои метаматериала, при изменении топологических параметров
метаструктуры – внутреннего радиуса r меньшего из колеци зазора l между разрезными кольцами в поперечном сечении (рис. 5). Наблюдается небольшое изменение формы импульсов при резком падении амплитуды в случае полубесконечных слоев с потерями (рис. 4, слева). При уменьшении параметра r наблюдается значительное
уменьшение амплитуды для всех типов отраженных импульсов с учетом потерь,тогда
как без потерь – изменений нет.
Рис. 4. Формы импульса в виде разности полиномов Лаггера, отраженного от
полубесконечного слоя(r=2мм,l=0,05мм).
Рис. 5. Формы отраженных прямоугольного и гауссовых импульсов меньшей и большей крутизны при
изменении зазора l в 10 раз (пунктирная кривая).
Уменьшение параметра l в 10 раз приводит к небольшому изменению формы
отраженного импульса прямоугольной формы (при падении амплитуды больше чем в 2
раза с учетом потерь); в случае без потерь амплитуда отраженного импульса гауссовой формы с меньшей крутизной не изменяется, а с большей крутизной уменьшается
на 15%, тогда как с учетом потерь у импульсов обеих форм амплитуда падает∼ на 6070% (рис. 5). Амплитуда импульса в виде разности полиномов Лаггера снижается примерно на 50%.
68
3. Отражение от бинегативных метаматериалов (DNG) с диэлектрической и магнитной проницаемостями близкими к -1. Угол θ=0 характеризует угол полного
преломления волны, когда отраженная волна отсутствует. Поэтому для моделирования выбираются достаточно большие углы падения (порядка 75 град).
Рис. 6. Формы гауссова импульса,
отраженного от слоя конечной толщины при изменении его толщины и
длительности импульса:N=0,1; T=10-8
(слева) и N=5; T=0,5⋅10-9 (справа).
Рис. 7. Динамика изменения форм прямоугольного
импульса, импульса в виде разности полиномов
Лаггера и гауссова импульса меньшей крутизны,
отраженных от DNG слоя конечной толщины для
параметра метаслоя N = 0,1 и длительности импульса T=10-8.
Выводы
Проведенныйанализ полученных результатов показал эффективность алгоритма: выявлены закономерности между соотношением длительности импульса, плазменной частотой и размерами метаструктуры. Оценено влияние размеров ее элементов без и с учетом потерь. Показано, что наименее подвержен искажению по форме
импульс в виде разности полиномов Лаггера, при малых значениях плазменных частот
и малой длительности он теряет амплитуду, но сохраняет форму, гауссов импульс не
теряет амплитуду, но искажается по форме, так же, как и прямоугольный. При меньшей
длительности форма импульса лучше сохраняется на более высоких плазменных частотах, с увеличением длительности оптимальная частота уменьшается.
Качественных различий при отражении импульсов разной длительности нет.
Чуть лучше других сохраняет форму при отражении импульс, представленный в виде
разности полиномов Лаггера, и заметно хуже других - прямоугольный сигнал. Характер
отражения для различных поляризаций примерно одинаков, однако отраженные сигналы отличаются знаком, и амплитуда отраженного сигнала при горизонтальной поляризации больше (с увеличением угла это отличие сглаживается), отраженный сигнал
перевернут относительно падающего импульса, а при вертикальной они совпадают.
При угле падения 88 градусов можно получить степень отражения вплоть до 0,8 по амплитуде. Форма отраженного импульса наиболее хорошо сохраняется, когда нормированная на скорость света толщина слоя d/c=NT составляет 2,5…5*10-9.
СПИСОК ЛИТЕРАТУРЫ
1. Будагян И.Ф., Илюшечкин М.Н. Компьютерное моделирование процессово тражения наносекундных сигналов // T-Comm. 2011. №8. С. 22-27.
2. Costas M. Soukoulis, Martin Wegener. Past achievements and future challenges in the
development of three-dimensional photonic metamaterials. Reviews // NaturePhotonics.
2011.No.5. P. 523–530.
3. Вендик И.Б., Вендик О.Г. Метаматериалы и их применение в технике сверхвысоких
частот (Обзор) // Журнал технической физики. 2013. Т.83, вып.1. С.3-28.
4. Будагян И.Ф. Методология исследований процессов отражения наносекундных импульсов от метаматериалов // Инновационные научные исследования в гуманитарных, естественных, технических и общественных науках. Методология, теория,
практика. 4 – 5 декабря 2014 года, г. Санкт- Петербург. − СПб: Изд-во «КультИнформПресс». 2014. С. 28-32.
5. Будагян И.Ф., Илюшечкин М.Н., Щучкин Г.Г.Анализ формы наносекундных сигналов. Излучение и распространение: LAPLAMBERT Academic Publishing GmbH&Co.
KG. 2012. 132 С.
69