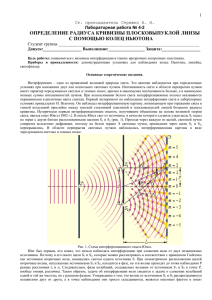
Определение длины волны света при помощи

Министерство образования и науки Российской Федерации
Уральский федеральный университет
имени первого Президента России Б.Н. Ельцина
Определение длины волны света
при помощи колец Ньютона
Методические указания к лабораторной работе 26 по физике
для студентов всех форм обучения всех специальностей
Екатеринбург
УрФУ
2010
Составители Т.И. Папушина, А.В. Михельсон
Научный редактор проф., д-р физ.-мат. наук А.А. Повзнер
Определение длины волны света при помощи колец Ньютона: методические
указания к лабораторной работе №26 по курсу «Физика» / Т.И. Папушина,
А.В.Михельсон / Екатеринбург: УрФУ, 2010. 20 с.
Методические указания предназначены для выполнения лабораторной
работы. Теоретическая часть содержит общие условия интерференции света.
Экспериментальная
часть
включает
описание
лабораторной
установки,
конкретных задач, методик измерений и обработки результатов. Приведена
форма отчета.
Подготовлено кафедрой физики
© УрФУ, 2010
2
Целью
работы
является
определение
длины
волны
света
интерференционным методом. При этом используется один из способов
наблюдения полос равной толщины, в котором интерференционная картина
называется кольцами Ньтона.
1. Условия образования интерференционной картины
Свет является электромагнитным излучением, которое представляет
собой единое электрическое и магнитное поля, распространяющиеся в
пространстве.
Световая волна обладает всеми свойствами электромагнитных волн и для
неё наблюдаются такие явления как интерференция, дифракция и поляризация.
Интенсивность света I в любой точке пропорциональна квадрату

амплитуды световой волны, т.е. пропорциональна квадрату напряженности Е
электрического
поля.
Для
произвольной
точки
Р
пространства,
где
перекрываются две световые волны, согласно принципу суперпозиции:

 
Е Р  Е1  Е2 ,
(1.1)
 
где Е1 , Е2 – напряженности электрических полей световых волн в точке Р.
Результирующая интенсивность равна:
I p  I1  I 2  2 I1I 2 cos  ,
(1.2)
где  = 2 – 1 – разность фаз налагающихся световых волн.
Если источники световых волн независимы, то среднее по времени
значение косинуса разности фаз cos   0 и
IP = I1 + I2.
(1.3)
Если разность фаз световых волн не изменяется в течение некоторого
времени, большего чем время, необходимое для регистрации картины
( cos   0 ), то равенство (1.3) не выполняется. Суммарная интенсивность
результирующей волны (а значит, и освещенность, например, экрана, на
3
котором
наблюдается
результат
сложения
волн)
не
равна
сумме
интенсивностей, создаваемых каждым источником световых волн (возникает
интерференция).
Иными
словами,
для
возникновения
интерференции
необходимо, чтобы разность фаз  сохраняла свое значение за время
усреднения. Это возможно только при одинаковой частоте складываемых
колебаний. Волны, для которых разность фаз за время наблюдения остается
неизменной, называют когерентными.
Таким
образом,
явление
интерференции
перераспределении энергии колебаний в
заключается
в
пространстве. В результате
интенсивность света в определенных точках пространства увеличивается, а в
других уменьшается по сравнению с (1.3). Интерференция, возникающая при
наложении двух когерентных волн, называется двухлучевой, при наложении
многих волн – многолучевой.
Излучение
любого
реального
источника
не
является
строго
монохроматическим, так как представляет собой совокупность излучений
отдельных атомов. Испускание света отдельными атомами происходит
хаотически. Каждое такое испускание можно представить как участок волны.
Часть
такой
характеристик,
волны,
сохраняющая
называется
примерное
цугом.
Длина
постоянство
цуга
называется
волновых
длиной
когерентности Lког, а время испускания цуга τког – временем когерентности.
Очевидна связь этих величин
Lког  ског ,
(1.4)
где с – скорость света в вакууме.
Для
получения
когерентных
световых
волн
и
наблюдения
их
интерференции с помощью обычных (не лазерных) источников излучения
применяют метод разделения волны, излучаемой одним источником света, на
две или большее число волн, которые после прохождения различных путей
накладываются друг на друга. Результат интерференции таких волн зависит от
разности фаз, приобретаемой когерентными волнами при прохождении
4
различных расстояний (или различных сред) от источника до экрана (точки
наблюдения). Однако для получения интерференционной картины достаточно
хорошей четкости необходимо выполнение некоторых условий, связанных с
определенными свойствами световых волн. Эти условия определим на примере
двухлучевой интерференции.
2. Двухлучевая интерференция
Рассмотрим
возникающую
интерференцию,
при
наложении
двух

когерентных волн, для которых вектор Е
колеблется в одном и том же направлении.
S1 и S 2 – источники этих волн (рис. 1).
Пусть первая волна распространяется в
Рис. 1
среде с показателем преломления n1 , а
Рис.1
вторая
-
в
среде
с
показателем
преломления n2 . Из теории колебаний известно, что в тех точках
пространства, где разность фаз
удовлетворяет
условию
 2  1   21 складываемых колебаний
 m  0,1,2... ,
 21  2 m
будет
наблюдаться
максимальное усиление колебаний. Если же 21  2m  1 , то колебания будут
в наибольшей степени ослабляться. Разность фаз складываемых колебаний в
точке A (рис. 1.1) равна
 21  t  k 2 r2   t  k1r1   k1r1  k 2 r2 .
Учитывая, что k 
2 2n

, разность фаз можно выразить как

0
 21 
где
2
r1n1  r2 n2   2 12 ,
0
0
12  r1n1  r2 n2  .
5
(2.1)
(2.2)
( – длина волны в данной среде, 0 – длина волны в вакууме, n1 и n2 –
абсолютные показатели преломления сред).
Скалярная величина 12 называется оптической разностью хода волн 1 и 2.
При n = 1 0 =  и тогда условия усиления и ослабления света могут быть
определены через оптическую разность хода двух когерентных волн:
1) условие усиления 12  m , m  0,1,2... .
(2.3)
Интерференционный максимум будет наблюдаться, если на разности хода двух
лучей укладывается целое число волн
1

2) условие ослабления 12   m   , m  0,1,2... ,
2

(2.4)
Интерференционный минимум наблюдается, если на разности хода двух лучей
укладывается полуцелое число волн.
3. Интерференция света при отражении
от клинообразной пластинки
Интерференционная картина, которая получается при освещении тонкой
клинообразной пластинки пучком параллельных лучей, называется полосами
равной толщины.
Рис. 2
Ход световых лучей для этого случая показан на рис. 2. Падающая на
поверхность световая волна 00’ частично отражается (1), частично проходит
6
внутрь клина и отражается от его нижней поверхности (2). При небольшом
угле  оптическую разность хода волн 2 и 1 можно с достаточной степенью
точности вычислить по формуле (1.21)
 21  2dn cos  

,
2
(3.1)
где d – толщина клина в месте падения луча; n – показатель преломления
вещества клина;  – угол преломления света в клине;  – длина световой
волны, падающей на клин. Световые волны 1 и 2, отраженные от внешней и
внутренней поверхностей клина, когерентны и дают интерференционную
картину, локализованную вблизи поверхности клина. Интерференционная
картина представляет собой систему светлых и темных полос, которые можно
наблюдать либо непосредственно, либо с помощью микроскопа.
Каждая из полос образуется за счет отражения от мест пластинки,
имеющих одинаковую оптическую толщину, т.е. одинаковое произведение nd.
Поэтому в данном случае интерференционные полосы называются полосами
равной толщины.
4. Кольца Ньютона
Кольца Ньютона являются частным случаем полос равной толщины. Они
получаются следующим образом. Плосковыпуклая линза с большим радиусом
кривизны помещается на толстую плоскопараллельную стеклянную пластину
(рис. 3). Тонкая кольцеобразная прослойка воздуха между линзой и пластиной
является "клином" с малым переменным преломляющим углом. Поэтому при
освещении линзы параллельным пучком света, направленным перпендикулярно
к ее плоской поверхности, в воздушном клине появляется интерференционная
картина в виде чередующихся темных и светлых концентрических колец, так
как места с одинаковой толщиной воздушного слоя образуют окружности с
центром в точке соприкосновения линзы и пластины. Поскольку угол
воздушного "клина" мал (на рис. 3 этот угол сильно преувеличен), о
оптическую разность хода волн 2 и 1 при их почти нормальном падении на
7
"клин" можно с достаточной степенью точности найти по формуле (3.1) при
cosβ = 1 и п = 1.
 21  2d 

.
2
(4.1)
Используя условия усиления (2.3) и ослабления (2.4) света, можно получить
условия максимумов и минимумов для интерференционных колец (рис. 3).
Светлые кольца будут соответствовать условию
2d 

 m ,
2
m  1,2,... ,
( 4.2)
а темные
2d 
 
1
  m   ,
2 
2
m  0,1,2... .
(4.3)
В условиях (4.2) и (4.3) m обозначает номер кольца. Ближайшее к центру
кольцо соответствует m = 1, следующее m = 2 и т.д. При этом нумерация для
темных и светлых колец ведется раздельно. В центре образуется темное пятно,
соответствующее m = 0.
5. Вывод расчетной формулы
Hа рис. 3: О – центр сферы радиуса R, часть которой образует выпуклую
поверхность линзы; d – толщина воздушного слоя в том месте, где находится
кольцо с номером m. Радиус этого кольца обозначим rm . Очевидно, что
R  d 2  rm2
или
 R2
R 2  2 Rd  d 2  rm2  R 2 ,
8
(5.1)
(5.2)
Рис.3
Так как толщина d слоя мала по сравнению с rm и R, то квадратом этой
величины можно пренебречь и последнюю формулу записать в виде
2d 
rm2
.
R
(5.3)
Подставив значение величины 2d в (4.2) и (4.3), получим для светлых
колец
9
rm2 
2m  1R ,
2
(5.4)
для темных колец
rm2  mR .
(5.5)
Из этих формул видно, что, измерив, радиус rm какого-либо светлого или
темного кольца с номером m, можно вычислить длину волны света  .
Для большей точности в определении искомых величин преобразуем
формулы (5.4) и (5.5) так, чтобы они были связаны с разностью диаметров
колец, которые могут быть легко измерены. Пусть нам известны диаметры
каких-либо колец с номерами k и l (l>k). Тогда формула (5.4) для светлых колец
дает
Dl2

 2l  1R ,
4
2
Dk2

 2k  1R ,
4
2
(5.6)
где Dl и Dk – диаметры колец.
Вычитая из первого уравнения второе, получим
Dl2  Dk2
 l  k   R .
4
(5.7)
Точно такое же равенство получится и для темных колец из формулы
(5.5). Для величины  из (5.7) получаем основную расчетную формулу
Dl2  Dk2

.
4 Rl  k 
(5.8)
6. Установка для наблюдения колец Ньютона
Прибор для наблюдения колец Ньютона смонтирован на базе
микроскопа-компаратора типа МИР-12. Он состоит из массивного основания,
на котором крепится стол 1, имеющий форму прямоугольной рамы. К
основанию рамы прикреплен дугообразный кронштейн 2 с установленным
измерительным устройством и микроскопом.
10
Рис. 4
Оптическая система, с помощью которой получается интерференционная
картина, представляет собой массивную линзу с большим (30...60 см) радиусом
кривизны и плоскопараллельную стеклянную пластину, которые укреплены в
металлической
обойме
3.
Обойма
может
перемещаться
вдоль
стола
компаратора. Она закрепляется в нужном положении посредством винтов 4.
Источником света служит лампа накаливания со светофильтром или светодиод
5, укрепленные на оправе объектива микроскопа.
В поле зрения окуляра одновременно наблюдаются кольца Ньютона и
визирная линия, по которой производится отсчет положения колец. Вначале
вращением оправы 6 окуляра добиваются четкого изображения визирной
линии. Затем вращением пояска 7 объектива микроскопа производится
фокусировка на резкость изображения колец.
Измерительное устройство состоит из микрометрического винта с
барабаном, вращением которого обеспечивается перемещение микроскопа в
горизонтальном направлении. Отсчет положения концов диаметров колец
производится по миллиметровой шкале 9 и шкале барабана 8, позволяющей
отсчитывать десятые и сотые доли миллиметра.
11
7. Порядок измерений
Прибор подготовлен к работе и не требует дополнительной юстировки.
После включения источника света в поле зрения видны кольца Ньютона.
Кольца имеют некоторую толщину (размыты). Для измерения диаметров колец
визирную линию устанавливают на середине темных колец слева и справа от
центра.
Сначала вращением рукоятки барабана перемещают микроскоп так, чтобы
визирная линия располагалась на середине десятого темного кольца справа от
центрального пятна. Сделав отсчет по шкалам линейки и барабана, перемещают
визир на середины девятого, восьмого (и так далее) темных колец.
После прохождения через центральное
темное пятно продолжают
измерения, последовательно записывая возрастающие номера
колец и
соответствующие показания. Для устранения ошибок, возникающих из-за
люфта микрометрического винта, визир должен подводиться к кольцам всегда
с одной стороны.
Очевидно, разность отсчетов для одного и того же кольца, сделанных
справа и слева от центрального пятна, дает величину его диаметра. Всего
рекомендуется измерить диаметры десяти колец и представить результаты в
виде таблицы.
Таблица 1
Результаты измерения диаметров колец Ньютона
Кольцо
Положение середины кольца
Диаметр кольца
D = Xп – Хл
1
2
Направление
Направление
.
отсчета
отсчета
.
10
12

Расчет длины волны
По результатам измерений, представленных в табл. 1, вычисляют среднее
значение

длины волны. Для этого формулу (5.8) преобразуют к виду
 
A
R
,
(7.1)
n
 Ai
A 
где
l 1
n
,
Dl2  Dk2  Dl  Dk  Dl  Dk 
Ai 

4 l  k 
4 l  k 
(7.2)
Значения Dl , Dk и A заносят в табл. 2.
Таблица 2
l-k
Dl ,
Dk ,
мм
мм
Dl  Dk , Dl  Dk ,
мм
мм
A 
A,
i
мм2
A
мм2
, A 
i
A
,
м4
6–1
7–2
…
10 – 5
A 
n
2
  Ai 
мм2
A 
мм4
i 1
При составлении табл. 2 значения (l – k) следует брать не менее четырех. При
этом необходимо использовать диаметры всех десяти колец. Из данных табл. 2
определяется средняя длина волны света (4.11) и доверительная граница  A
случайной погрешности A по формулам:
 A  t p ,n S
n
S
A

A
,
(7.3)
2
 Ai  A 
i 1
nn  1
13
,
(7.4)
2
где n – число комбинаций колец, внесенных в табл. 2; t p ,n – коэффициент
Стьюдента
для данного n и доверительной вероятности P.
Расчет всех
параметров  A , S  A ,   может быть проведен на ЭВМ по заранее разработанной
программе.
Систематической
погрешностью
в
определении
A
пренебрегаем
вследствие ее малости, следовательно,
A  A .
(7.5)
Доверительная граница абсолютной погрешности
 0
результата
измерения длины волны λ определяется по формуле
    λ ,
2
(7.6)
2
   
  A   R  .
  А    R 
где
(7.7)
Величина  R задается в таблице, прилагаемой к установке. Окончательный
результат записывается в виде
P  0,95 .
       ,
(7.8)
8. Графический метод обработки данных для определения длины
волны 
Формулу (5.8) для определения длины волны можно переписать в виде
D 12  D k2  4 R  l  k  .
(8.1)
Если ввести обозначения: y  D12  Dk2 ,
x  l  k , то эта формула примет вид
y  ax .
(8.2)
Графиком,
соответствующим
формуле
(8.2),
является
прямая.
Для
построения этого графика значения l  k , D1 , Dk заносятся в табл. 3, причем
для расчета всех значений х номер k берется равным 1, а l – принимает значения
последовательно от 2 до 10.
14
Таблица 3
x  l  k Dl , мм Dk , мм

Dl  Dk , мм Dl  Dk , мм

y  Dl2  Dk2 , мм2
1=2-1
2=3-1
…
9=10-1
Угол наклона зависимости y  f  x  позволяет оценить длину волны

 y2  y1 
4 R  x2  x1 
.
(8.3)
Первые точки на графике y = f(x) могут не попасть на прямую, так как первые
кольца Ньютона несколько искажены. При проведении прямой эти точки
можно не учитывать.
Рис.5
15
Контрольные вопросы
1. Сформулируйте цель лабораторной работы.
2. В чем заключается явление интерференции света?
3. Какие волны называются когерентными?
4. Запишите общее условие ослабления и усиления света при двухлучевой
интерференции.
5. Объясните возникновение интерференционной картины при отражении от
клинообразной пластинки. Изобразите ход лучей.
6. Выведите расчетную формулу для определения длины световой волны с
помощью колец Ньютона.
7. Как производится измерение диаметров колец Ньютона?
Литература
1.Иродов И.В.Волновые процессы. Основные законы: Учеб.
пособие для вузов.– М.: Лаборатория Базовых знаний, 2001. 256
2.Трофимова Т.И. Курс физики: Учеб. пособие для вузов. 3-е изд., испр. Высш.
шк., 1994. 316-331.
3. Лабораторные занятия по физике/ под ред. Л.Л. Гольдина. М.:
Наука, 1983.434 .
16
ПРИЛОЖЕНИЕ
ФОРМА ОТЧЕТА
Титульный лист
УРФУ
Отчет по лабораторной работе 26
Определение длины волны света при помощи колец Ньютона
Студент_______________________
Группа _______________________
Дата _________________________
На внутренних страницах: (поля – слева, 3см)
1.
Основная расчетная формула
Dl2  Dk2

,
4 Rl  k 
где  –
Dl и Dk –
R–
2. Номер установки.
3. Источник света .
4. Приборы и их характеристики
Наименовани Назначение Постоянная
№ п/п
е прибора и
прибора
Предел
Цена
характеристика измерений деления
его тип
шкалы
17
5. Ход лучей при отражении света от клинообразной пластинки (рис.2) .
6. Схема получения колец Ньютона (рис.3).
7. Результаты измерений диаметра колец
Таблица 1
Кольцо
Положение середины кольца
Диаметр кольца
D = Xп – Хл
1
2
Направление
Направление
.
отсчета
отсчета
.
10
8. Расчет Аi
Dl2  Dk2  Dl  Dk  Dl  Dk 
Ai 

4 l  k 
4 l  k 
Таблица 2
l-k
Dl ,
Dk ,
мм
мм
Dl  Dk , Dl  Dk ,
мм
мм
A,
мм2
A 
i
A
мм2
6–1
7–2
…
10 – 5
A 
n
  Ai 
мм2
2
A 
i 1
9. Расчет длины волны
 
 
A

R
м.
10. Расчет погрешности измерений
18
мм4
, A 
i
A
м4
,
2
 A  t p ,n S
A
n
S

A
мм2;
=
2
 Ai  A 
i 1
nn  1
мм2.
,=
A  A .
   λ
2
,
2
   
  A   R  .
  А    R 
где
11. Окончательный результат в виде
       , =
м.
11. Расчет значений x и y.
x  l  k Dl , мм Dk , мм
Таблица 3
Dl  Dk , мм Dl  Dk , мм
1=2-1
2=3-1
…
9=10-1
12. График зависимости y = f(x).
13. Расчет длины волны 

 y2  y1 
4 R  x2  x1 
м.

14. Выводы.
19


y  Dl2  Dk2 , мм2
Учебное издание
Определение длины волны света
при помощи колец Ньютона
Составители Михельсон Анна Вильгельмовна
Папушина Татьяна Ивановна
Компьютерная верстка Анохиной Н.Н.
Подписано в печать
10.10.2010 г.
Формат 6084 1/16
Бумага типографская
Плоская печать
Усл.печ.л. 1,1.
Уч.-изд. л. 1,0. Тираж
Заказ.
Редакционно-издательский отдел УрФУ
620002, Екатеринбург, ул. Мира, 19
[email protected]
Ризография НИЧ УрФУ
620002, Екатеринбург, ул. Мира, 19
20