Заряженная частица влетает в однородное магнитное поле под

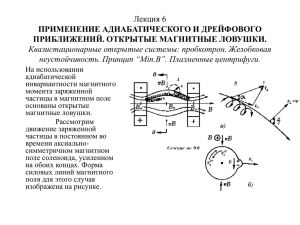
Заряженная частица влетает в однородное магнитное поле под
углом ° к линиям индукции и движется по спирали. Определить
радиус спирали, если за один ее оборот частица смещается вдоль
линий индукции на 110 мм.
Расстояние, которое проходит заряженная частица за один оборот
вдоль силовой линии магнитного поля, ― это шаг спирали :
‖ ,
где T ― период обращения; ‖ ― модуль составляющей скорости
частицы вдоль направления силовых линий.
Вдоль силовой линии поля частица движется со скоростью, модуль
которой определяется формулой
‖ cos ,
где ― модуль скорости частицы, 30° ― угол между векторами
скорости и индукции магнитного поля.
Период обращения частицы ― это время одного оборота заряженной
частицы в магнитном поле:
2
,
⏊
где ⏊ ― модуль составляющей скорости частицы вдоль направления,
перпендикулярного направлению силовых линий, ― радиус
окружности.
На рисунке показаны направления скорости
частицы, силовых линий магнитного поля и
разложение вектора скорости на составляющие:
‖ ⏊ .
Модуль составляющей скорости на направление,
перпендикулярное силовым линиям магнитного
поля, определяется формулой:
⏊ sin .
Подстановка ⏊ в выражение для периода обращения частицы дает:
2
.
sin Запишем формулу для шага спирали с учетом явного вида входящих в
нее величин:
‖ за время T ―
2 cos 2α.
sin Отсюда следует выражение для расчета искомой величины ― радиуса
спирали, по которой движется частица в магнитном поле:
.
2α
Произведем вычисление:
110 ∙ 10 √3
∙
# 10,1 ∙ 10 10,1мм.
2 ∙ 3,14 ∙ √3 √3
Таким образом, заряженная частица движется по окружности, радиус
которой приблизительно равен 10 мм.