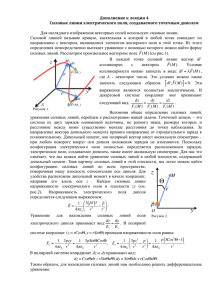
Электрический диполь и его поле
реклама

Электрический диполь и его поле Совокупность равных по величине и противоположных по знаку двух точечных зарядов –q и +q, находящихся на расстоянии l друг от друга, называется электрическим диполем. l € +q p = ql −q Если длина l мала по сравнению с расстоянием от диполя до точки наблюдения, то диполь называется точечным. € Потенциал поля диполя P r− Θ −q l r+ +q q "1 1% q r− − r+ ϕP = − = = $ ' 4πε 0 # r+ r− & 4πε 0 r+r− " l cosΘ % 2 2 r+ = r− − l r+ = r− − 2r−l cosΘ + l ≈ r− $1− ' r # & − q l cosΘ q (lr ) r− − r+ = l cosΘ ϕ P = = 4πε 0 r 2 4πε 0 r 3 1 ( pr ) ϕP = 4πε 0 r 3 Напряженность поля диполя E(r ) = −gradϕ (r ) % " " p r 3 p r) 1 ∂ ( ) 1 px % ( E x (r ) = − $ 3 '= $ 5 x− 3 ' 4πε 0 ∂ x # r & 4πε 0 # r r & " 3 p r) py % 1 ( E y (r ) = $ 5 y− 3 ' 4πε 0 # r r & " 3 p r) pz % 1 ( E z (r ) = $ 5 z− 3 ' 4πε 0 # r r & % " 1 3 ( pr ) r p E(r ) = − 3' $ 5 4πε 0 # r r & r p 1 " 3 pr 2 p % 1 2p E = $ 5 − 3'= 4πε0 # r r & 4πε0 r 3 r⊥p E = 1 p 4πε0 r 3 Силовые линии поля диполя z p € dy dz = E y Ez r Θ y O z € € € € € € € p 1 " 3pz 2 p % Ez = $ 5 − 3' 4πε 0 # r r & dy dz = 1 3pzy 1 " 3pz 2 p % − 3' $ 5 5 4πε 0 r 4πε 0 # r r & 1 3pzy Ey = 4πε 0 r 5 y = r sin Θ z = r cosΘ r = Const sin 2 Θ y Сила, действующая на диполь во внешнем поле O r− € −q l r+ +q F = q E(r+ ) − E(r− ) E(r+ ) = E(r− + l ) E x (r− + l ) = E x (x− + lx , y− + ly , z− + lz ) = ( ) ∂ Ex ∂ Ex ∂ Ex ≈ E x (x−, y−, z− ) + lx + ly + lz ∂x ∂y ∂z E(r+ ) = E(r− ) + l ∇ E ∂E F = q l ∇ E = ( p∇) E ≡ p ∂l ( ) € ( ) Момент сил, действующих на диполь +q € F− € −q € € € € r− r+ l O F+ € M = !"r+ F+ #$ + !"r− F− #$ = = q !"r+ E+ #$ − !"r− E− #$ = q !"r+ − r−, E #$ = = q !"l , E #$ = !" p, E #$ ( )