3-13 И.М. Лагун Моделирование температурных полей в

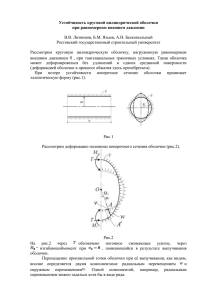
УДК 621.1:536.24
МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНЫХ ПОЛЕЙ
В ЦИЛИНДРИЧЕСКИХ ОБОЛОЧКАХ
И.М. Лагун
Тульский государственный университет
Показана
возможность
электрического
моделирования
процессов
распространения тепла в цилиндрических оболочках на RC-сеточных моделях,
разработанных для декартовой системы координат. Получены новые соотношения
электротепловой аналогии. Решена задача определения температурного поля в
цилиндрической оболочке, подвергающейся нестационарному нагреву.
Ключевые слова
Электромоделирование, электротепловая аналогия, RC – сеточные модели,
нестационарный теплообмен.
Условные обозначения
Ai и Bi - обобщенные параметры; а – коэффициент температуропроводности,
м2/с; C - относительная теплоемкость; c – удельная теплоемкость, Дж/(кг.К); C Э электроемкость ячейки, Ф; K i - масштабные коэффициенты; Ka - коэффициент
нестационарности теплообмена; L – длина оболочки, м; R - относительная плотность;
R X и RZ - электрические сопротивления ячейки, Ом; RT , Z - относительные
цилиндрические координаты тепловой задачи; rX и rZ - относительные электрические
сопротивления ячейки; r, z - координаты цилиндрической системы координат, м; T –
температура, К; t – относительное время теплового процесса; t Э - относительное время
электрического процесса; u – напряжение, В; U - относительное напряжение; X Э , Z Э относительные декартовы координаты; xЭ , z Э - координаты электрической модели
(ячеек);
- коэффициент теплоотдачи, Вт/(м2.К); a - относительный коэффициент
теплоотдачи; a с - стационарное значение коэффициента теплоотдачи, соответствующее
установившимся параметрам газового потока, Вт/(м2.К); q
- относительная
температура;
- относительный коэффициент теплопроводности; - коэффициент
теплопроводности, Вт/(м.К);
- плотность, кг/м3 ; t - время, с; t Э - время
электрического процесса, с.
Индексом «1» обозначены опорные значения переменных, индексами «г» и «в»,
а также «0» и «L» – параметры, относящиеся к внутренней и наружной, а также
торцевым поверхностям цилиндрической оболочки соответственно.
Введение
Известны различные способы расчета температурных полей элементов
конструкции энергетических устройств [1, 2]. Выбор способа расчета определяется, в
основном, особенностями поставленной задачи и требованиями, предъявляемыми к
точности результатов.
Решалась задача определения температурного поля в цилиндрической оболочке
с переменным подводом тепла со стороны внутренней поверхности оболочки,
наружная и торцевые поверхности охлаждались свободной конвекцией.
Теплоносителем являлся газ, с высокой температурой и скоростью движения. К
особенностям решаемой задачи относятся переменные условия теплообмена на
внутренней нагреваемой поверхности оболочки, а также высокие значения тепловых
потоков, поступающих в тело оболочки. Следует отметить, что из-за короткого
времени нагрева в оболочке отсутствовали фазовые превращения, то есть источники и
стоки тепла. Кроме того, из-за малой разностенности оболочки тангенциальная
составляющая теплового потока была мала, и задача рассматривалась как
осесимметричная.
1. Постановка задачи
С учетом вышеизложенных особенностей физическая модель тепловой задачи
представляла собой уравнение теплопроводности с граничными условиями третьего
рода, причем коэффициент теплоотдачи на нагреваемой поверхности оболочки, а также
температура горячего газа являлись функциями времени, то есть:
2
T
t
T
a
r
2
2
2
1 T
r r
T
rГ
z
r
rВ ,
0
z
L,
t
0;
r
rГ ,
0
z
L,
t
0;
l
T
r
a Г t TГ (t ) T
l
T
r
a В TВ T
0
r
rВ ,
0
z
L,
t
0;
l
T
z
a 0 T0 T
0
rГ
r
rВ ,
z
0,
t
0;
l
T
z
a L TL T
0
rГ
r
rВ ,
z
L,
t
0;
T
0
f r, z
rГ
r
rВ ,
0
z
L,
t
0.
Вследствие изменения характера течения горячего газа, а также малого времени
нагревания оболочки коэффициент теплоотдачи на нагреваемой поверхности изменялся
весьма существенно. Причем его изменение в различных рассматриваемых случаях
описывалось либо зависимостью вида [5]:
aГ
m
a с 1 (Ka 1)(1 t ) ,
либо полиномом третьей степени,
экспериментальными данными.
что
удовлетворительно
согласовалось
с
В качестве метода расчета был выбран метод электромоделирования на
специализированных RC – сеточных моделях прямой аналогии.
2. Электромоделирование
Известно [3,4], что для пространственных задач имеется возможность
приближенного моделирования процессов, записанных в цилиндрической системе
координат, на моделях, построенных для прямоугольной системы координат. Однако,
указанные пределы могут быть расширены, если в уравнении теплопроводности
перейти к новым переменным. Рассмотрим математические модели теплового и
электрического процессов.
2.1. Электрический процесс в RC-сеточной модели. Рассмотрим электрическую
модель, состоящую из последовательно соединенных RC-ячеек, принципиальная схема
которых представлена на рис.1.
Если к модели из таких ячеек
подсоединить граничные сопротивления
по координатным осям, то электрический
процесс в такой модели можно описать
следующим образом:
u
tЭ
CЭ
u
xЭ
xЭ
RX
uГ
RГ
1
RX
u
xЭ
u
0,
1
RZ
zЭ
u
,
zЭ
Рис. 1. Электрическая схема RC-ячейки.
u
xЭ
RX
uВ
RВ
u
zЭ
RZ
R0
u
0,
u0 u
0,
RZ
u
zЭ
RL
uL u
u
0,
f 1 xЭ , z .
Вводя линейные преобразования для всех переменных величин:
u
u1U ,
xЭ
x1Э X Э ,
zЭ
z1Э Z Э ,
tЭ
СЭ
t 1Э tЭ ,
c1Э cЭ ,
RГ
RГ1 rГ ,
RВ
RВ1 rВ ,
R 0 R 01r0 ,
RL
RL1 rL ,
RX
R X 1rX ,
RZ
RZ1rZ ,
получим обобщенное уравнение для переходного электрического процесса:
cЭ
U
tЭ
B1
XЭ
1
rX
U
XЭ
B2
ZЭ
1
rZ
U
ZЭ
с граничными условиями:
U
XЭ
B3
U
ZЭ
B5
rX
UГ
rГ
rZ
r0
U
U0 U
0,
0,
U
XЭ
B4
U
ZЭ
B6
rX
rB
rZ
rL
UВ U
0,
UL U
0,
где
t Э1
B1
2
cЭ1 xЭ1
RX 1
RX1
B4
R В1
,
B2
xЭ1 ,
B5
t Э1
2
cЭ1 z Э1
RZ1
R Z1
R 01
B3
,
zЭ1 ,
B6
R X1
R Г1
R Z1
R L1
xЭ1 ,
zЭ1 .
2.2. Тепловой процесс в цилиндрической оболочке. Основой физической модели
процесса передачи тепла в оболочке служит уравнение теплопроводности, записанное в
цилиндрической системе координат:
T
1
r lr
r r
r
T
t
cr
z
lz
T
.
z
Очевидно, что из-за различной структуры уравнений, описывающих тепловой и
электрический процессы, прямое моделирование весьма ограничено. Но если перейти к
2
переменным r и z , то физическая модель процесса теплопередачи будет:
2
T
t
cr
4
r
2
l rr 2
T
r
z
lz
T
,
z
2
причем условия на границах оболочки:
2rlr
lz
T
z
T
r
2
a Г TГ T
a 0 T0 T
0,
0,
2rlr
lz
T
r
2
a В TВ T
T
a L TL T
z
0,
0.
Переходя к обобщенным переменным, будем иметь математическую модель:
q
t
CR
A1
RT2
q
RT2
R
A2
2
RT
Z
Z
q
Z
с граничными условиями:
q
A3
RТ2
q
Z
A5
aГ
qГ
RТ R
a0
q0 q
q
q
0;
RТ2
q
Z
0;
Z
aВ
qВ q
RТ R
A4
A6
aL
qL q
0;
0,
Z
где обобщенные параметры, выполняющие роль критериев подобия:
A1
A4
4l r1t 1
c1 r1 r12
;
A2
a В1r1
;
2 l r1
A5
l z1t 1
c1 r1 z12
;
a 01 z1
;
l z1
A3
a Г 1r1
;
2l r1
A6
a L1 z1
.
l z1
Таким образом:
– структура математических моделей теплового и электрического процессов
становится одинаковой, что дает возможность моделирования тепловых задач,
записанных в цилиндрической системе координат, на прямоугольных RC-сетках;
– сравнительный анализ математических моделей этих процессов позволяет
установить, наряду с известными соотношениями подобия, новые соотношения
электротепловой аналогии, которые расширяют возможности использования RCсеточных моделей. Некоторые соотношения
электротепловой аналогии
представлены в таблице.
Таблица электротепловой аналогии.
Параметры
теплового
процесса
сr
T
t
r
Параметры
электрического
процесса
СЭ
u
tЭ
xЭ
2
z
2
r lr
lz
aГ
rlr
aВ
rl r
a0
aL
zЭ
1
RX
1
RZ
RX
RГ
RX
RВ
1
R0
1
RL
– для получения количественных соотношений, необходимых для проектирования
электрической модели, достаточно приравнять обобщенные параметры процессов:
Ai
Bi , где i = 1, …6.
3. Практическая реализация метода электрического моделирования
Математическое моделирование тепловой задачи осуществлялось на модели,
блок-схема которой представлена на рис.2.
Рис.2. Блок-схема электромодели.
ЭМ – RC-сеточная электрическая модель; БПГУ – блок переменных граничных
условий; БПЭМ – блок питания электромодели; БКП - блок катодных повторителей;
ИУ – измерительное устройство; БПКП и БПИУ - блоки питания катодных
повторителей и измерительного устройства.
Электрическая схема интегрирующего контура ЭМ представляет собой цепочку
последовательно соединенных электрических ячеек, состоящих из постоянных
емкостей CЭ = 40 мкФ и переменных сопротивлений.
Для задания переменных граничных условий третьего рода служит блок
переменных граничных условий БПГУ, где осуществляется ступенчатая
аппроксимация напряжения uГ и граничного сопротивления RГ. Блок состоит из
наборных полей напряжения и граничного сопротивления, а также из программного
коммутационного устройства, предназначенного для развертки во времени
аппроксимирующих функций.
Ниже приведенные расчетные зависимости получаются приравниванием
соответствующих отношений подобия в математических моделях, описывающих
тепловой и электрический процессы.
RX 1
R В1
Kr
K r2
,
4Kt ar1cЭ1
2lr1 R X 1
K r a В1
r1
,
xЭ1
RZ1
R 01
,
Kz
z1
,
z Э1
Kt
K z2
,
Kt a z1cЭ1
l z1 RZ 1
a 01K z
t1
,
t Э1
R Г1
R L1
,
a r1
lr1
,
c1 r 1
2l r1R X 1
K r a Г1
l z1 RZ 1
a L1 K z
,
,
a z1
l z1
.
c1 r 1
С помощью RC-сеточной модели была решена задача определения
температурного поля осесимметричной цилиндрической стенки с постоянными
теплофизическими параметрами, поэтому вышеприведенные зависимости, полученные
для нелинейного случая, имели несколько более простой вид. Причем некоторые
расчетные величины, такие, например, как масштабы координат K r и K z ; масштаб
времени K t ; электрическая емкость ячейки C Э ; размерные коэффициенты a r1 , a Г 1
выбирались произвольно, что создавало дополнительные удобства с точки зрения
обеспечения моделирующей установки и расчета ее элементов.
Результаты проведенного электрического моделирования показали хорошее
согласование с экспериментальными и расчетными данными, полученными численным
моделированием методом конечных разностей.
Выводы
На основе анализа математических моделей нестационарного теплового и
электрического процесса показана возможность электромоделирования
дифференциальных уравнений различной структуры, что расширяет возможности
применения RC-сеточных моделей.
Наряду с известными, получены новые соотношения электротепловой аналогии,
а также основные уравнения проектирования и расчетные соотношения для
электрического моделирования пространственно-временных тепловых процессов при
переменных параметрах теплообмена.
Методом электромоделирования определено нестационарное температурное
поле цилиндрической оболочки.
Литература
1. Лыков А.В. Тепломассообмен. М.: Энергия, 1978. 480с.
2. Зарубин В.С. Инженерные методы решения задач теплопроводности. М.:
Энергоатомиздат, 1983. 328с.
3. Кузьмин М.П. Электрическое моделирование нестационарных процессов
теплообмена. М.: Энергия, 1974. 416 с.
4. Кузьмин М.П., Лагун И.М. Нестационарный тепловой режим элементов
конструкции двигателей летательных аппаратов. М.: Машиностроение, 1988.
240 с.
5. Лагун И.М. Тепловой режим конструкции при нестационарном теплообмене//
Известия РАН. Энергетика. 1997. № 2. С. 125-129.