Моделирование деформирование твердых гранулирован

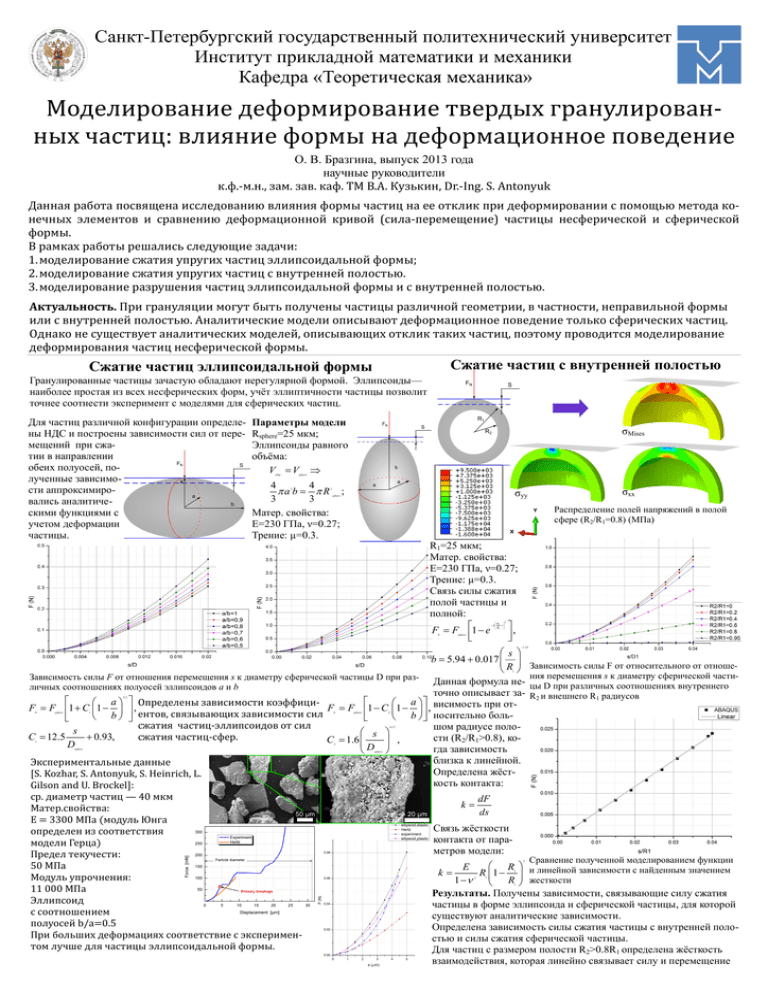
Санкт-Петербургский государственный политехнический университет
Институт прикладной математики и механики
Кафедра «Теоретическая механика»
Моделирование деформирование твердых гранулированных частиц: влияние формы на деформационное поведение
О. В. Бразгина, выпуск 2013 года
научные руководители
к.ф.-м.н., зам. зав. каф. ТМ В.А. Кузькин, Dr.-Ing. S. Antonyuk
Данная работа посвящена исследованию влияния формы частиц на ее отклик при деформировании с помощью метода конечных элементов и сравнению деформационнои кривои (сила-перемещение) частицы несферическои и сферическои
формы.
В рамках работы решались следующие задачи:
1. моделирование сжатия упругих частиц эллипсоидальнои формы;
2. моделирование сжатия упругих частиц с внутреннеи полостью.
3. моделирование разрушения частиц эллипсоидальнои формы и с внутреннеи полостью.
Актуальность. При грануляции могут быть получены частицы различнои геометрии, в частности, неправильнои формы
или с внутреннеи полостью. Аналитические модели описывают деформационное поведение только сферических частиц.
Однако не существует аналитических моделеи, описывающих отклик таких частиц, поэтому проводится моделирование
деформирования частиц несферическои формы.
Сжатие частиц с внутренней полостью
Сжатие частиц эллипсоидальной формы
Гранулированные частицы зачастую обладают нерегулярной формой. Эллипсоиды—
наиболее простая из всех несферических форм, учѐт эллиптичности частицы позволит
точнее соотнести эксперимент с моделями для сферических частиц.
Для частиц различной конфигурации определены НДС и построены зависимости сил от перемещений при сжатии в направлении
обеих полуосей, полученные зависимости аппроксимировались аналитическими функциями с
учетом деформации
частицы.
Параметры модели
Rsphere=25 мкм;
Эллипсоиды равного
объѐма:
V V 
ellip .
σMises
sphere
4
4
a b  R ;
3
3
Матер. свойства:
E=230 ГПа, ν=0.27;
Трение: µ=0.3.
2
σyy
3
sphere
σxx
Распределение полей напряжений в полой
сфере (R2/R1=0.8) (МПа)
R1=25 мкм;
Матер. свойства:
E=230 ГПа, ν=0.27;
Трение: µ=0.3.
Связь силы сжатия
полой частицы и
полной:
,
F  F 1  e


R

 b 2 1
 R1 
N
2
sphere
1.25
 s 
b  5.94  0.017  
 R  Зависимость силы F от относительного от отношения перемещения s к диаметру сферической частиЗависимость силы F от отношения перемещения s к диаметру сферической частицы D при разДанная формула не- цы D при различных соотношениях внутреннего
личных соотношениях полуосей эллипсоидов a и b
точно описывает за- R2 и внешнего R1 радиусов


 a   Определены зависимости коэффици a   висимость при отF  F 1  С 1    ,
F  F 1  C 1    ,
 b   ентов, связывающих зависимости сил
 b   носительно боль

сжатия частиц-эллипсоидов от сил
шом радиусе полоs
 s 
C  12.5
 0.93,
сжатия частиц-сфер.
сти (R2/R1>0.8), коC

1.6
,


D
гда зависимость
D 
близка к линейной.
Экспериментальные данные
Определена жѐст[S. Kozhar, S. Antonyuk, S. Heinrich, L.
кость контакта:
Gilson and U. Brockel]:
ср. диаметр частиц — 40 мкм
dF
k
Матер.свойства:
ds
E = 3300 МПа (модуль Юнга
Связь жѐсткости
определен из соответствия
контакта от парамодели Герца)
метров модели:
Предел текучести:
Сравнение полученной моделированием функции
50 МПа
 R  и линейной зависимости с найденным значением
E
k
R 1  
Модуль упрочнения:
1 
R  жесткости

11 000 МПа
Результаты. Получены зависимости, связывающие силу сжатия
Эллипсоид
частицы в форме эллипсоида и сферической частицы, для которой
с соотношением
существуют аналитические зависимости.
полуосей b/a=0.5
Определена зависимость силы сжатия частицы с внутренней полоПри больших деформациях соответствие с эксперименстью и силы сжатия сферической частицы.
том лучше для частицы эллипсоидальной формы.
Для частиц с размером полости R2>0.8R1 определена жѐсткость
взаимодействия, которая линейно связывает силу и перемещение
1
3/2
N
sphere
1
N
sphere
2
0.17
1
2
sphere
sphere
2
2
2
1
1