Íå óäàëîñü âûâåñòè ðèñóíîê!
реклама
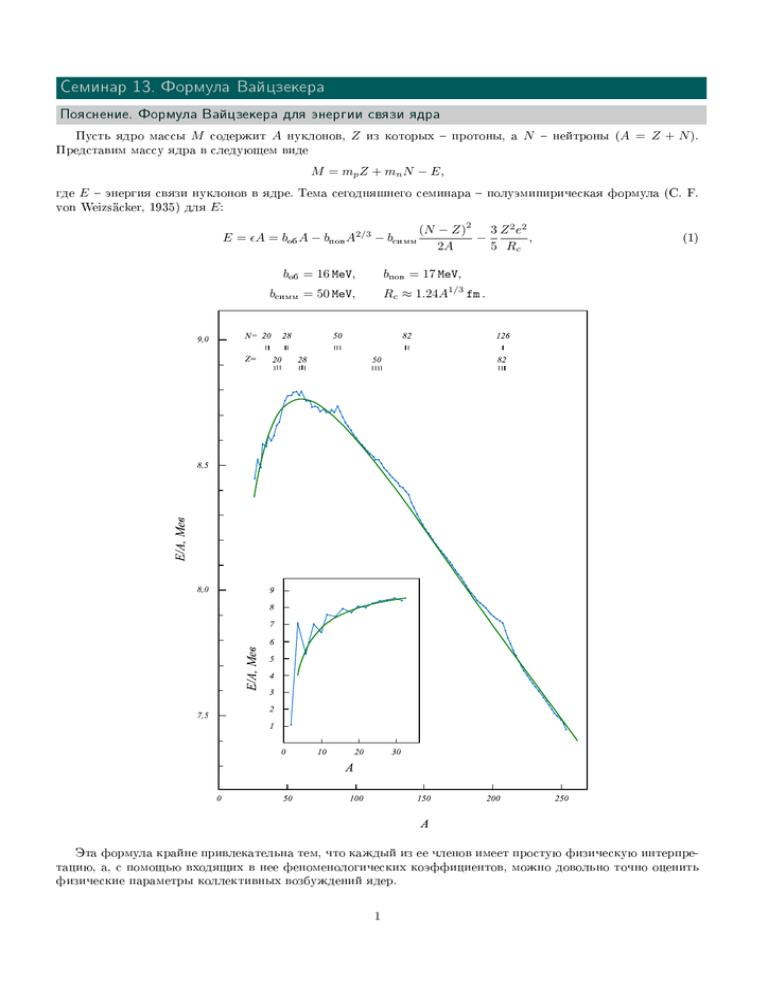
Ñåìèíàð 13. Ôîðìóëà Âàéöçåêåðà Ïîÿñíåíèå. Ôîðìóëà Âàéöçåêåðà äëÿ ýíåðãèè ñâÿçè ÿäðà Ïóñòü ÿäðî ìàññû M ñîäåðæèò A íóêëîíîâ, Z èç êîòîðûõ ïðîòîíû, à N íåéòðîíû (A = Z + N ). Ïðåäñòàâèì ìàññó ÿäðà â ñëåäóþùåì âèäå M = mp Z + mn N − E, ãäå E ýíåðãèÿ ñâÿçè íóêëîíîâ â ÿäðå. Òåìà ñåãîäíÿøíåãî ñåìèíàðà ïîëóýìèïèðè÷åñêàÿ ôîðìóëà (C. F. von Weizs acker, 1935) äëÿ E : 2 E = ²A = bîá A − bïîâ A2/3 − bñèìì bîá = 16 MeV, 3 Z 2 e2 (N − Z) − , 2A 5 Rc (1) bïîâ = 17 MeV, Rc ≈ 1.24A1/3 fm . bñèìì = 50 MeV, Ýòà ôîðìóëà êðàéíå ïðèâëåêàòåëüíà òåì, ÷òî êàæäûé èç åå ÷ëåíîâ èìååò ïðîñòóþ ôèçè÷åñêóþ èíòåðïðåòàöèþ, à, ñ ïîìîùüþ âõîäÿùèõ â íåå ôåíîìåíîëîãè÷åñêèõ êîýôôèöèåíòîâ, ìîæíî äîâîëüíî òî÷íî îöåíèòü ôèçè÷åñêèå ïàðàìåòðû êîëëåêòèâíûõ âîçáóæäåíèé ÿäåð. 1 Íà ðèñóíêå (1.1) ñèíèìè òî÷êàìè èçîáðàæåíû ýêñïåðèìåíòàëüíûå äàííûå ïî ýíåðãèè ñâÿçè íà îäèí íóêëîí, çåëåíîé êðèâîé ðåçóëüòàò ðàñ÷åòà ïî ôîðìóëå (1) . Âèäíî, ÷òî ñîãëàñèå áëèçêî ê èäåàëüíîìó, îäíàêî íà ôîíå ãëàäêîé êðèâîé îò÷åòëèâî âèäíû íåêîòîðûå ïðèïóïèíû. ×èñëà ïðîòîíîâ è íåéòðîíîâ, ïðè êîòîðûõ îáðàçóþòñÿ ïðèïóïèíû, íàçûâàþòñÿ ìàãè÷åñêèìè, î íèõ â ñëåäóþùåì ñåìèíàðå. Çàäà÷à 13.1. Êóëîíîâñêàÿ ýíåðãèÿ ÿäåð Âû÷èñëèòü ýíåðãèþ êóëîíîâñêîãî âçàèìîäåéñòâèÿ çàðÿäîâ â ðàâíîìåðíî çàðÿæåííîì øàðå ñ ïîëíûì çàðÿäîì Z . Ðåøåíèå EColomb 1 = 2 Z Z ρ (r) ρ (r0 ) 3 3 0 d r d r = ρ20 |r − r0 | 14 3 3 2 2 3 2 2 πr dV = ρ Ω = e Z . r3 5R 0 5R Îòâåò EColomb = 3 2 2 e Z . 5R Çàäà÷à 13.2. Àñèììåòðèÿ ïðîòîíîâ è íåéòðîíîâ Âû÷èñëèòü âêëàä â ýíåðãèþ àñèììåòðèè (÷ëåí ïðîïîðöèîíàëüíûé bñèìì ) âîçíèêàþùèé îò íåñèììåòðè÷íîãî ðàñïðåäåëåíèÿ êèíåòè÷åñêîé ýíåðãèè ìåæäó ïðîòîíàìè è íåéòðîíàìè â ìîäåëè âûðîæäåííîãî ôåðìè-ãàçà. Ðåøåíèå µ pF = } 3π 2 Z Ω ¶1/3 µ =} 3Z 3Z 2 Ep = EF (p) = } 5 5 µ 9π 4r03 9πZ 4r03 A ¶1/3 , ¶2/3 µ ¶2/3 Z 1 , A 2m µ µ ¶5/3 ¶5/3 2/3 (Z − N ) (Z − N ) }2 3 (9π) }2 A 1 + A 1 − + , 2mr02 A 40 2mr02 A µ ¶ 2/3 10 (Z − N )2 3 (9π) }2 3 2 (Z − N )2 2A + ≈ = A (E ) + (E ) . F F Z=N Z=N 40 2mr02 9 A 5 3 2A 2/3 Ep + En = 3 (9π) 40 Îòâåò δbñèìì ≈ 25 MeV. Åñòü åùå äîïîëíèòåëüíàÿ ýíåðãèÿ ñâÿçè îáóñëîâëåííàÿ íàëè÷èåì òîæäåñòâåííûõ ÷àñòèö ∆, (Z, N ) − (even, even), 0 − odd, δE = −∆, (Z, N ) − (odd, odd). Ñëåäóÿ íàèâíîé ìîäåëè ôåðìè-ãàçà, ∆ ìîæíî îöåíèòü êàê ðàññòîÿíèå ìåæäó îäíî÷àñòè÷íûìè óðîâíÿìè âáëèçè ïîâåðõíîñòè ôåðìè ¯ d² ¯¯ 2 ²F , ∆∼ = dn ¯²=²F 3 A îäíàêî ýêñïåðèìåíòàëüíûå çíà÷åíèÿ îêàçûâàþòñÿ çíà÷èòåëüíî áîëüøå ∆ ≈ 12 A−1/2 MeV. Òàêîé ïðîáåë â ñïåêòðå îäíî÷àñòè÷íûõ âîçáóæäåíèé óêàçûâàåò íà ñèëüíûå ïàðíûå êîððåëÿöèè ñïàðèâàíèå òîæäåñòâåííûõ ÷àñòèö âáëèçè ïîâåðõíîñòè ôåðìè. Çàäà÷à 13.3. Ïàðàìåòðû êðèâîé Âàéöçåêåðà. Äàâàéòå èññëåäóåì ïàðàìåòðû ôóíêöèè Âàéöçåêåðà íà ïëîñêîñòè ïåðåìåííûõ Z , N . 2 1. Ìàêñèìóì ýíåðãèè ñâÿçè íà îäèí íóêëîí ïðèõîäèòñÿ íà æåëåçî F e26 56 (ñì. ðèñóíîê (1.1) ): bïîâ A−4/3 2 e2 −1/3 ∂² = − A ⇒ ∂A 3 5 4r0 10 bïîâ r0 A= ≈ 50 3 e2 2. Ñåðåäèíà äîëèíû β -ñòàáèëüíîñòè " à !# µ ¶ 2 ∂M ∂ 1 (2N − A) 3 (A − N )2 e2 2/3 = mp (A − N ) + mn N − bîá A − bïîâ A − bñèìì − =0 ∂N A=const ∂N 2 A 5 r0 A1/3 ⇒ mn − mp = −2bñèìì (N − Z) = (N − Z) 3 e2 + (A − (N − Z)) ⇒ A 5 r0 A1/3 e2 3 5 r0 A1/3 A − (mn − mp ) ¡ ¢. 2bñèìì /A + 3e2 / 5r0 A1/3 Ýòà ôîðìóëà ïðåäñêàçûâàåò çàìåòíîå îòêëîíåíèå îò ïðÿìîé N = Z äëÿ áîëüøèõ A. 3. Ýíåðãèÿ îòäåëåíèÿ íåéòðîíà: 2 1 (N − Z) 3 Z 2 e2 E = bîá A − bïîâ A2/3 − bñèìì − 2 A 5 Rc µ ¶ ∂E 2bïîâ A−1/3 bñèìì 1 Z 2 e2 =0 ≈ bîá − − (N − Z) + ∂N Z=const 3 2A2 5 r0 A2/3 µ ¶ e2 bñèìì 2bïîâ A−1/3 bñèìì 2 Z + Z + b − − =0 îá A2 3 2A 5r0 A2/3 Ïàðàìåòðè÷åñêè çàäàííàÿ êðèâàÿ (A − Zmax (A) , Zmax (A)) íà ïëîñêîñòè (N, Z) îãðàíè÷èâàåò âîçìîæíûé èçáûòîê íåéòðîíîâ íàä ïðîòîíàìè. ßäðà ëåæàùèå íèæå ýòîé êðèâîé íåñòàáèëüíû ïî îòíîøåíèþ ê íåéòðîííîìó "èñïàðåíèþ ò.å. îòäåëåíèþ åäèíè÷íîãî íåéòðîíà. Çàäà÷à 13.4. Äåëåíèå ÿäåð. Ýíåðãåòè÷åñêîå óñëîâèå. Ïóñòü ÿäðî ñîäåðæèò A íóêëîíîâ. Îíî ìîæåò ðàçäåëèòüñÿ íà äâà ÿäðà ñ êîëè÷åñòâîì íóêëîíîâ xA è (1 − x) A, ñîîòâåòñòâåííî, åñëè óðàâíåíèå E (A) = E (xA) + E ((1 − x) A) èìååò ðåøåíèå ïðè 0 < x < 1, ãäå E (A) åñòü ýíåðãèÿ ñâÿçè (1) . Îöåíèòü çíà÷åíèå A ïðè êîòîðîì ïîÿâëÿåòñÿ ïåðâîå ðåøåíèå ýòîãî óðàâíåíèÿ. 3 Ðåøåíèå ³ ´ ´ 3 A5/3 e2 ³ −bïîâ A2/3 1 − 2 · 2−2/3 − 1 − 2 · 2−5/3 = 0 ⇒ 20 r0 ³ ´· ´¸ 3 e2 −2/3 ³ 1/3 2/3 1/3 A 2 − 1 bïîâ − A2 2 + 1 = 0, 20 r0 ¶−1 µ 3 e2 b ¡ ïîâ ¢ = A ≈ 70. −2/3 20 r0 2 21/3 + 1 Îòâåò A ≈ 70. Çàäà÷à 13.5. Äåëåíèå ÿäåð. Íåñòàáèëüíîñòü êîëåáàíèé. Ðàññìîòðèì êîëåáàíèÿ ïîâåðõíîñòè ñôåðè÷åñêîãî ÿäðà â ìîäåëè æèäêîé êàïëè.  ýòîé ìîäåëè ïîëüçóþòñÿ ñëåäóþùèì ïðèáëèæåíèåì äëÿ ïëîòíîñòü ÿäåðíîé ìàòåðèè ρ (r) = ρ0 θ (|r| − R (t, n)) , n= r/ |r| . Èçìåíåíèå ñî âðåìåíåì ðàäèóñà â íàïðàâëåíèè n îò öåíòðà ÿäðà ìîæíî ïàðàìåòðèçîâàòü ñ ïîìîùüþ íàáîðà íåçîâèñèìûõ ïàðàìåòðîâ αλ,µ àìïëèòóä íîðìàëüíûõ êîëåáàíèé: X ? R (t, n) = R0 1 + αλ,µ (t) Yλ,µ (n) . λ,µ Îêàçûâàåòñÿ, ÷òî ýíåðãèþ ÿäðà ñâÿçàííóþ ñ êîëåáàíèÿìè ïîâåðõíîñòè ìîæíî ïðåäñòàâèòü â âèäå ñóììû ýíåðãèé íåçàâèñèìûõ ìîä êîëåáàíèé (ôîíîíîâ): X E = E0 + H (α̇λ,µ , αλ,µ ) , λ,µ H (α̇λ,µ , αλ,µ ) = 2 Dλ α̇λ,µ 2 + 2 Cλ αλ,µ . 2 Ïðè ýòîì àìïëèòóäû αλ,µ áóäóò óäîâëåòâîðÿòü îáû÷íûì óðàâíåíèÿì äëÿ ìàÿòíèêà: α̈λ,µ = − Cλ 2 αλ,µ = −ωλ,µ αλ,µ . Dλ Îöåíèòü âåëè÷èíû Dλ , Cλ è ω , à òàêæå ïîêàçàòü, ÷òî ñóùåñòâóåò ïðåäåëüíîå ÷èñëî ïðîòîíîâ Zcrit. ïî îòíîøåíèþ â ïîëíîìó ÷èñëó íóêëîíîâ, òàêîå ÷òî, äëÿ ÿäåð ó êîòîðûõ µ 2¶ µ 2¶ Z Z > = const A A crit. 2 êîëåáàíèÿ ôîðìû ñòàíîâÿòñÿ íåñòàáèëüíûìè, ò.å. ωλ,µ ñòàíîâèòñÿ îòðèöàòåëüíûì, ÷òî ïðèâîäèò èëè ê äåôîðìàöèè ÿäåð èëè ê èõ äåëåíèþ. Ðåøåíèå Z v2 dV ∼ AmR2 α̇2 , 2 mA5/3 r02 mr2 Ep ∼ bïîâ A2/3 α2 ⇒ ω 2 ∼ ∼ A 0, 2/3 bïîâ bïîâ A Z 2 2 Z e 1 ρ (r1 ) ρ (r2 ) dV1 dV2 ∼ −α2 Ec = . 2 |r1 − r2 | r0 A1/3 ¯ ¯ µ 2¶ 2 2 ¯ Ec ¯ 10 bïîâ r0 17 ¯ ¯∼ Z e >1⇒ Z = ≈ 14 ≈ 49. ¯ Ep ¯ bïîâ Ar0 A crit. 3 e2 5 Ekin = ρ 4 Îòâåò mr02 , bïîâ 10 bïîâ r0 = ≈ 49. 3 e2 ω2 ∼ A µ Z2 A ¶ crit. 5





