Лекция 18 Метод потенциальных функций

Лекция 18
Лекция 18
Метод потенциальных функций
Метод потенциальных функций в настоящее время считается одним из наиболее
разработанных и математически обоснованных методов постановки диагнозов.
U ( x)
+Q
x1
−Q
−Q
x3
x2
x
x4 −Q
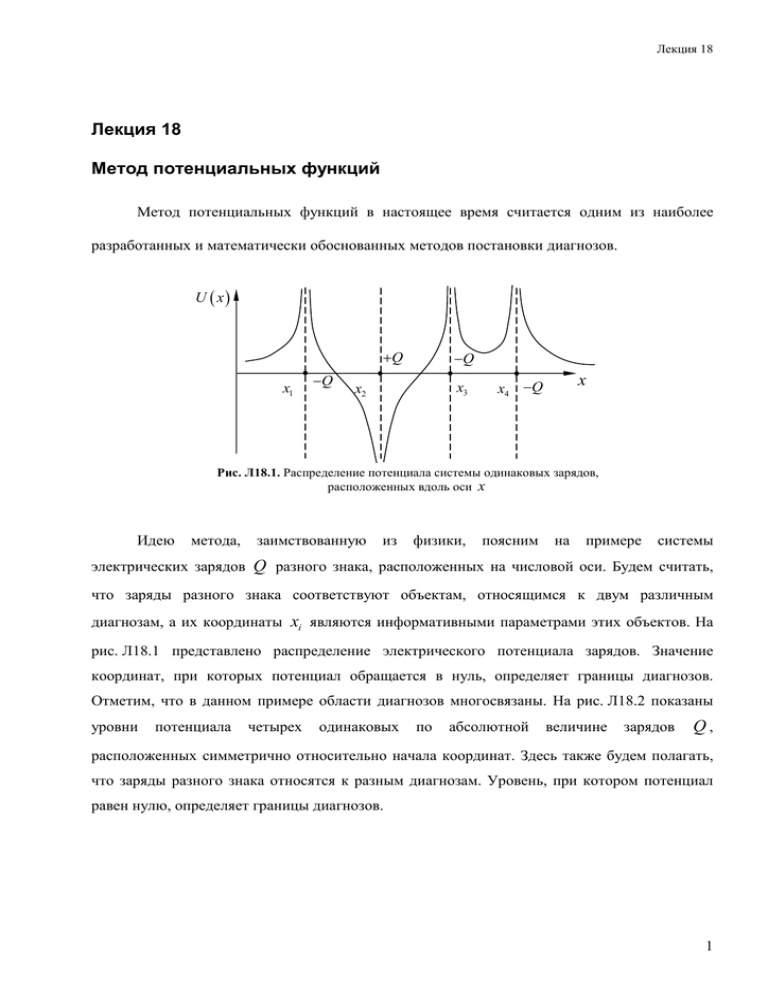
Рис. Л18.1. Распределение потенциала системы одинаковых зарядов,
расположенных вдоль оси x
Идею
метода,
заимствованную
из
физики,
поясним
на
примере
системы
электрических зарядов Q разного знака, расположенных на числовой оси. Будем считать,
что заряды разного знака соответствуют объектам, относящимся к двум различным
диагнозам, а их координаты xi являются информативными параметрами этих объектов. На
рис. Л18.1 представлено распределение электрического потенциала зарядов. Значение
координат, при которых потенциал обращается в нуль, определяет границы диагнозов.
Отметим, что в данном примере области диагнозов многосвязаны. На рис. Л18.2 показаны
уровни
потенциала
четырех
одинаковых
по
абсолютной
величине
зарядов
Q,
расположенных симметрично относительно начала координат. Здесь также будем полагать,
что заряды разного знака относятся к разным диагнозам. Уровень, при котором потенциал
равен нулю, определяет границы диагнозов.
1
Лекция 18
−Q
Q
Q
−Q
Рис. Л18.2. Уровни потенциала двух пар одинаковых по величине зарядов Q = 1 ,
расположенных симметрично относительно начала координат
Как видно из этих примеров, потенциал системы зарядов обладает свойствами разделяющих,
а потенциал отдельных отрицательных зарядов  свойствами дискриминантных функций.
Как известно, потенциал в точке x поля электрического заряда Q , расположенного в точке
x 0 , определяется функцией
U ( x, x 0 ) = −Q x − x 0 .
Эта функция зависит только от расстояния ρ ( x, x 0 ) = x − x0 между точками x и x 0 и,
следовательно, симметрична относительно перестановки векторов x и x 0 . Кроме того, она
монотонно стремится к нулю при ρ ( x, x 0 ) → ∞ . В технической диагностике функции,
обладающие указанными свойствами, называются потенциальными функциями. Однако в
отличие от электростатики эти функции выбирают ограниченными, имеющими максимум
при ρ( x, y ) = 0, например:
K (x, y ) = exp {− a ρm (x, y )} ;
K (x, y ) = 1/(1 + a ρm (x, y )), a, m > 0 ,
(Л18.1)
причем в качестве расстояния между векторами параметров x и y может использоваться
обобщенное расстояние порядка q
1/ q
 n
q
ρ(x, y ) = ∑ ( xi − yi ) 
 i =1

, q = 1, 2, ... .
2
Лекция 18
C помощью потенциальных функций можно построить дискриминантные функции
состояний объекта, если их области диагнозов не пересекаются.
Пусть, например, в j -м приближении известны дискриминантные функции всех
состояний
f j( k ) (x) (k = 0, 1, ..., N ) и предъявляется объект обучающей выборки с
вектором x j +1 ∈ D p . Корректировка дискриминантных функций проводится согласно
следующему правилу:
— дискриминантные функции не меняются, если
f j( p ) ( x j +1 ) > f j( k ) (x j +1 ), k = 0, 1, ..., N ; p ≠ k ;
— если для некоторых k = n1 , n2 , ..., nm f j
( p)
(x k +1 ) < f j( k ) (x k +1 ), то полагается
f j(+p1) (x) = f j( p ) (x) + c j K (x, x k +1 );
f j(+k1) (x) = f j( k ) (x) − c j K (x, x j +1 ), (k = n1 , n2 , ..., nm ) ,
(Л18.2)
где c j  положительные постоянные. Корректировка прекращается, если для всех объектов
обучающей выборки справедливо соотношение (Л15.1), см. лекцию 15. Отметим, что в
первом приближении в качестве дискриминантных функций состояний могут быть выбраны
функции
f1( k ) (x) = K (x, m ( k ) ); k = 0, 1, ..., N ,
где m
(k )
 средний вектор области диагноза Di, см. лекцию 13.
При
дихотомии
потенциальные
функции
могут
быть
использованы
для
непосредственного построения разделяющей функции. Выберем в первом приближении
разделяющую функцию состояний в виде
(
f1 ( x ) = K x, m (
0)
) − K ( x, m( ) ) ,
1
(Л18.3)
или же
 K (x, x1 ), если x1 ∈ D0 ;
f1 (x) = 
− K (x, x1 ), если x1 ∈ D1 ,
где
x1  вектор, характеризующий первый объект обучающей выборки. После
предъявления объекта с вектором x 2 проводится корректировка по правилу
3
Лекция 18
 f1 (x) + c2 K (x, x 2 ), если x 2 ∈ D0 и f1 (x 2 ) < 0;

f 2 (x) =  f1 (x) − c2 K (x, x 2 ), если x 2 ∈ D1 и f1 (x 2 ) > 0;
 f (x), в остальных случаях,
 1
(Л18.4)
где c2  положительный корректирующий коэффициент. Далее процесс корректировки
продолжается по правилу (Л18.4) до тех пор, пока не будут выполнены неравенства
f ( xi ) > 0 , при xi ∈ D0 ,
f ( x j ) < 0 , при x j ∈ D1 .
(Л18.5)
Задача. Л18.1. С помощью потенциальных функций построить разделяющую
функцию диагнозов D0 и D1 , обучающие выборки которых представлены векторами,
указанными в задаче Л17.1 лекции 17, а также во втором и пятом столбцах табл. Л18.1.
В
качестве
потенциальной
функции
возьмем одну из
функций,
заданных
соотношением (Л18.1)
(
)
K ( x, y ) = 1 1 + ( x − y ) ,
2
а разделяющую функцию в первом приближении выберем в соответствии с выражением
(Л18.2). Для этого рассчитаем средние векторы областей диагнозов
D0 и D1 :
m ( ) = ( 4,7; 4,6 ) и m ( ) = ( 4,7; 8,7 ) , тогда
0
1
{
(
f1 ( x ) = 1 1 + x − m (
0)
)}
2
{
(
−1 1 + x − m( )
1
) }.
2
Определяем ее значения для векторов обучающей выборки, относящихся к диагнозам D0 и
D1 , (третий и шестой столбцы табл. Л18.1). Для первого вектора области D1 x11 = ( 2; 6 )
f1 ( x11 ) > 0 . Проводим корректировку по правилу (Л18.4). Поскольку значение f1 ( x11 )
незначительно отличается от нуля, зададим небольшое значение корректирующего
коэффициента — c2 = 0,1, тогда во втором приближении разделяющая функция согласно
(Л18.4) будет определяться соотношением
{
(
f 2 ( x ) = 1 1 + x − m(
0)
)}
2
{
(
−1 1 + x − m( )
1
) } − 0,1 {1 + ( x − x ) } .
2
2
11
(Л18.6)
4
Лекция 18
Расчет значений этой функции для векторов обучающей выборки (четвертый и седьмой
столбцы табл. Л18.1) показывает, что соблюдаются неравенства (Л18.5). Таким образом,
функция (Л18.6) является разделяющей функцией состояний D0 и D1 .
Таблица Л18.1. Значения функций f1(x) и f2(x) для векторов обучающей выборки
n
xi 0 ∈ D0
f1 ( xi 0 )
f 2 ( xi 0 )
xi1 ∈ D1
f1 ( xi1 )
f 2 ( xi1 )
1
2
3
4
5
6
7
(3; 4)
(4; 3)
(4; 6)
(5; 4)
(5; 5)
(5; 6)
(7; 4)
0,20
0,22
0,18
0,65
0,73
0,21
0,12
0,18
0,21
0,16
0,64
0,72
0,20
0,11
(2; 6)
(2; 9)
(4; 9)
(4; 11)
(6; 10)
(7; 9)
(8; 7)
0,03
−0,08
−0,59
−0,12
−0,20
−0,12
−0,01
−0,07
−0,09
−0,59
−0,13
−0,12
−0,12
−0,01
На рис. Л18.3 показаны образы обучающих выборок областей D0 и D1 , их средние
значения и разделяющая функция областей диагнозов, рассчитанная с помощью
потенциальных функций (6).
x2
12
D1
10
8
f2 ( x )
6
4
D0
2
x1
0
2
4
6
8
10
12
Рис. Л18.3. Образы обучающих выборок областей диагнозов
D0 и D1 , их
средние значения и разделяющая функция, рассчитанная с помощью
потенциальных функций
На примере этой задачи видно, что применение потенциальных функций приводит к
более простому и сравнительно быстрому решению задачи разделения областей диагнозов,
чем применение методов разделения в диагностическом пространстве, использованных в
предыдущих задачах и примерах.
Рассмотренные методы не исчерпывают перечень существующих непараметрических
методов принятия решений, однако они сравнительно часто применяются при обработке
диагностической информации. Основное внимание уделено изложению сути каждого из
5
Лекция 18
рассмотренных
методов.
рассмотренных
задачах
математические
Размерность
и примерах
тонкости
непараметрических
вычислений,
методов,
и
пространства
информативных
параметров
в
невелика. Это позволяет, не отвлекаясь на
понять
привести
принципы,
наглядную
заложенные
графическую
в
основы
интерпретацию
полученных решений. Уяснив сущность изложенных методов, можно без труда перейти к
решению практических задач, в которых требуется анализ диагностических параметров в
пространстве существенно большей размерности.
6