УДК 536.71 КАЧЕСТВЕННЫЙ И КОЛИЧЕСТВЕННЫЙ АНАЛИЗ
реклама

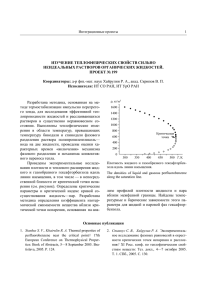
УДК 536.71 КАЧЕСТВЕННЫЙ И КОЛИЧЕСТВЕННЫЙ АНАЛИЗ РАЗЛИЧНЫХ МОДЕЛЕЙ ОПИСАНИЯ ЛИНИЙ ФАЗОВОГО РАВНОВЕСИЯ ВЕЩЕСТВ Полторацкий М.И Университет ИТМО, Санкт-Петербург. e-mail: [email protected] Научный руководитель: профессор Рыков В.А., Университет ИТМО Краткое вступление, постановка проблемы. В последнее время в мире идет активное применение в промышленности технологий сверхкритических флюидов (СКФ-технологии), основанных на использовании особых свойств веществ в сверхкритических состояниях. СКФ являются не только хорошими растворителями, но и обладают высоким коэффициентом диффузии, т.е. они легко проникают в глубинные слои различных твердых веществ и материалов. Вследствие выше изложенного, они нашли широкое применение в химической и фармацевтической промышленности. Сейчас 90% всех СКФ – технологий ориентированы на сверхкритический СО2. Но помимо диоксида углерода начинают постепенно использоваться и другие вещества. Для успешного решения задачи развития СКФ технологий необходимо иметь характеристики веществ, потенциал использования которых в качестве флюидов еще не раскрыт. Для расчета теплофизических характеристик необходимо привлекать методы, позволяющие описать линию фазового равновесия веществ в диапазоне от тройной точки до критической. При построении уравнений состояния, учитывающих особенности поведения вещества в окрестности критической точки, необходимо описывать линию насыщения с учетом правила криволинейного диаметра. В настоящее время широкое распространение получили две модели. Первая модель, известная как модель Вегнера, учитывает особенности поведения вещества в окрестности критической точки с учетом правила криволинейного диаметра. Для описания линии насыщения в области сильно развитых флуктуаций в соотношение входит множитель 𝜏 (1−𝛼) , где α - критический индекс изохорной теплоемкости. Вторая модель, известная как модель Янга-Янга, воспроизводит правило криволинейного диаметра в соответствии с зависимостью, в которую входит множитель 𝜏 2𝛽 , где β - критический индекс кривой сосуществования. Однако, до сих пор не решен вопрос, насколько правомерно использовать ту или иную модель при построении системы уравнений, описывающих линию фазового равновесия в интервале от тройной точки до критической. Рассмотрению этого вопроса посвящена выполненная мною работа. Базовые положения исследования. Для решения этого вопроса была рассчитана линия фазового равновесия хорошо изученных веществ: СО2 и хладагента R23 в соответствии с обоими методиками, а результаты сравнены с табличными значениями. Для описания паровой ветви линии насыщения используется уравнение КлапейронаКлаузиуса. В это уравнение входит производная от давления по температуре на линии упругости и "кажущаяся" теплота парообразования. Из уравнения для паровой ветви находится параметр x0 - значение "масштабной" переменной х на линии насыщения в критической области, общий для паровой и жидкостной ветви. Затем, используя это параметр, строится уравнение жидкостной ветви линии насыщения. Для решения этой задачи написана программа на языке Fortran с использованием процедуры SVD. Основной результат. Расчеты позволили по обоим моделям построить системы взаимосогласованных уравнений линии фазового равновесия (линия упругости, паровая ветвь и жидкостная ветвь), 2 описывающие линию фазового равновесия от тройной точки до критической с погрешностью экспериментальных данных, и удовлетворяющих первой и второй модели в критической области. Затем был проведен анализ результатов, заключавшийся в сравнении полученных значений с ранее установленными точными значениями для СО2 и R23. Расчеты позволили сделать вывод, что обе модели можно использовать для построения широкодиапазонных уравнений состояния. Однако, расчетная схема системы уравнений, построенных по модели Янга-Янга проще в реализации. Литература. 1. Кудрявцева И.В, Камоцкий В.И, Рыков С.В, Рыков В.А. Расчет линии фазового равновесия диоксида углерода //научный журнал НИУ ИТМО, 2013. - №4. 2. Кудрявцева И.В, Рыков А.В, Рыков В.А. Модифицированное уравнение линии насыщения, удовлетворяющее требованиям масштабной теории // научный журнал НИУ ИТМО, 2014. - №3. 3. Рыков А.В, Кудрявцева И.В, Рыков С.В. Уравнение линии насыщения, удовлетворяющее модифицированному правилу криволинейного диаметра // научный журнал НИУ ИТМО, 2014. - №3. Аспирант НИУ ИТМО ИХиБТ Полторацкий М.И. Научный руководитель, проф. кафедры ИиПМ-2 ИХиБТ Рыков В.А. Заведующий кафедрой ИиПМ-2, проф. ИХиБТ Рыков В.А.