Общие вопросы взаимодействия эластичного колеса с

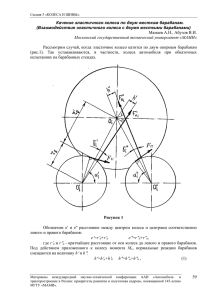
Секция 5 «КОЛЕСА И ШИНЫ».
Общие вопросы взаимодействия эластичного колеса с
жесткой опорной поверхностью
Мамаев А.Н., Вирабов Р.В., Балабина Т.А.
Московский государственный технический университет «МАМИ»
Принятые допущения и условности
Так как пара «эластичное колесо - опорная поверхность» относится к
фрикционным парам, то при решении поставленных задач воспользуемся следующими
допущениями и условностями, применяемыми в теории фрикционных передач:
1. Основание, по которому перекатывается колесо, считаем абсолютно жестким.
2. Форму пятна контакта цилиндрического колеса с жестким основанием
принимаем близкой к прямоугольной с размерами 2 a и 2 b в продольном (по
направлению скорости) и поперечном направлениях (рис.1, б).
3. Предполагаем, что при прижатии эластичного колеса к жесткому основанию
распределение нормальных давлений в продольном направлении контакта близко к
параболическому закону (рис.2), т.е.:
(1)
q n = q n0 ( a 2 − x 2 ) ,
где
3 Fz
,
(2)
8 a 3 bs
Fz - нормальная нагрузка на колесе; s - коэффициент насыщенности рисунка
беговой дорожки колеса, равный отношению площади выступов к контурной площади
пятна контакта.
Реальный закон изменения нормальных давлений по площадке контакта
катящегося колеса зависит от конструкции эластичного колеса, его упругих
характеристик, условий качения. У пневматических шин низкого и среднего давления он
более близок к трапецеидальному закону, высокого - к параболическому. Большой класс
колесных машин - машины напольного транспорта (погрузчики, штабелеры, робокары и
т.п.), оборудуются массивными резиновыми шинами, для которых отсутствуют
экспериментальные данные о распределении нормальных давлений по площадке контакта.
В связи с этим на стенде ИДШ-1 в НИИ шинной промышленности автором были
выполнены соответствующие экспериментальные исследования ведомых колес с
цилиндрической и тороидальной формой беговых дорожек и с разной толщиной
резинового слоя /1,2/.
Приведенные на рис. 3 и 4 некоторые экспериментальные результаты показывают,
что у рассматриваемых шин распределение нормальных давлений занимает
промежуточное положение между параболическим и эллиптическим законами, причем
при наличии тороидальной беговой дорожки приближается к параболическому закону в
крайних продольных сечениях и к эллиптическому - в средних. По краям пятна контакта
(на входе и выходе из него), как показывают экспериментальные данные, эпюра
нормальных давлений меняет знак кривизны. Наличие касательной силы в контакте
искажает симметричность эпюры нормальных давлений.
q n0 =
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
71
Секция 5 «КОЛЕСА И ШИНЫ».
Рисунок 1
Рисунок 2
В данной работе принят параболический закон распределения нормальных
давлений по площадке контакта, позволяющий получать непрерывные по длине пятна
контакта функции интересующих параметров и более полно отражающий физическую
картину явлений в контакте колеса с основанием (что показано в докторской диссертации
Р.В.Вирабова).
Аналогичный закон использовался в ряде решений прикладных задач, связанных с
качением упругих тел /3,4,5,6 и др./.Правомерность использования данного закона будет
показана также ниже.
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
72
Секция 5 «КОЛЕСА И ШИНЫ».
Рисунок 3
Рисунок 4
5. Тангенциальные напряжения (или удельные касательные силы) qt, возникающие
на поверхности колеса в зоне контакта при реализации касательной силы, принимаем
пропорциональными смещениям U точек поверхности колеса:
qt = λU
(3)
где
qr
λ = k 3д
(4)
а
- коэффициент тангенциальной жесткости, зависящий, как показано в /3/, от
упругих свойств материала шины и ее нормальной деформации (для параболического
закона распределения нормальных давлений к = 1,5, для эллиптического - к = 1,08);
rд - динамический радиус колеса, который примерно равен его статическому
F
радиусу; q = z - погонная нормальная нагрузка.
2b
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
73
Секция 5 «КОЛЕСА И ШИНЫ».
Тангенциальным смещением называем измеренную по касательной к поверхности
колеса величину смещения точки его поверхности относительно радиального луча, на
котором находилась эта точка в недеформируемом состоянии колеса.
6. Рассматриваем тангенциальные смещения, возникающие с момента входа точки
поверхности колеса в контакт с основанием до момента ее выхода из контакта.
7. Исходя из закона сухого трения Амонтона, тангенциальные напряжения на
участке скольжения в зоне контакта принимаем равными величине q tck = μq n , где μ коэффициент трения скольжения..
8. Рассматриваем качение колеса с малой скоростью, что позволяет все упругие
процессы, происходящие при качении, считать квазистатическими.
9. Рассматриваем установившиеся процессы.
10. Геометрическую неоднородность и дисбаланс колеса, а также влияние
микропрофиля опорной поверхности не учитываем.
Основные зависимости, определяющие силовые и кинематические характеристики
эластичного цилиндрического колеса при прямолинейном качении по жесткому
основанию
Качение ведомого и тормозного колес осуществляется, как известно, под
действием продольной силы Fx, приложеной к оси колеса параллельно плоскости
основания в направлении движения.
При качении ведомого колеса, нагруженного только нормальной нагрузкой,
вследствии несовершенной упругости материала имеют место потери на внутреннее
трение в материале колеса (гистерезис), которые обуславливают возникновение момента
сопротивления Мf и появление силы сопротивления качению Ff - продольной касательной
силы, действующей в контакте колеса с основанием в направлении, противоположном
движению колеса. Подобная сила сопротивления качению возникает и у тормозного
колеса, нагруженного, в сравнении с ведомым колесом, дополнительным тормозным
моментом Мт (рис. 5). Наличие этой силы приводит к потере угловой скорости колеса и к
проскальзыванию элементов его беговой дорожки относительно основания в зоне
контакта. Относительная потеря угловой скорости в этом случае может быть представлена
как отношение абсолютной потери угловой скорости колеса под действием касательной
силы к угловой скорости ω0 при свободном качении, определяемой из условия равенства
нулю действующей в контакте касательной силы:
ξвм = (ω0 – ω) / ω0
При качении ведущего колеса, движение которого происходит под действием
крутящего момента Мк (рис.6), в контакте возникает ведущая (тяговая) сила, направленная
по ходу колеса. Наличие этой силы вызывает проскальзывание элементов беговой
дорожки колеса в зоне контакта с основанием и к потере линейной скорости оси колеса,
которую будем оценивать величиной относительной потери скорости
ξвщ = (V0 – V) / V0 ,
c
где V0 = ωr k – скорость оси колеса при его свободном качении, при котором в
контакте с основанием отсутствует касательная сила; V = ωrk – cкорость оси колеса при
наличии силы в контакте.
Отношение V/ω = rk , являющееся с позиций теории механизмов и машин
кинематической передаточной функцией (аналогом линейной скорости), называют
радиусом качения. В соответствии с этим rck - радиус свободного качения колеса при
отсутствии в контакте продольной касательной силы. Для ведущего колеса rck = V0 / ω,
для тормозного и ведомого - rck = V / ω0 .
Механизм возникновения скольжения элементов поверхности колеса относительно
основания подробно рассмотрен Вирабовым Р.В /3/. С использование схемы обращенного
Материалы международной научно-технической конференции ААИ «Автомобиле- и
74
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
Секция 5 «КОЛЕСА И ШИНЫ».
механизма «упругое колесо – жесткое основание», на основе теории предварительного
смещения в /3/ показано, что при установившемся качении вступающие в зону контакта
элементы поверхности колеса, не будучи ещё “подготовленными” к восприятию
касательой силы и в то же время прижатые к основанию нормальной силой, начинают
движение без скольжения, получая при этом тангенциальные смещения (направленные
противоположно качению для тормозного и ведомого колес, и по направлению качения –
для ведущего колеса). По мере перемещения сцепленных элементов колеса и основания в
обращенном механизме в зоне контакта их тангенциальные смещения нарастают,
следовательно, нарастает и действующая между сцепленными элементами касательная
сила трения. В том месте контакта, где возросшая сила трения достигает предельной по
сцеплению, происходит срыв и на всей части контакта, расположенной за точкой срыва,
вне зависимости от того, находится ли она в зоне убывающих или возрастающих
нормальных давлений, происходит скольжение.
Рисунок 5
Рисунок 6
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
75
Секция 5 «КОЛЕСА И ШИНЫ».
С увеличением потери скорости колеса и соответствующим увеличением
действующей в контакте касательной силы, увеличивается зона скольжения, а также
мощность потерь на трение в контакте, характеризующая интенсивность износа беговой
дорожки и частично – сопротивление качению колеса.
Тангенциальные смещения точек беговой дорожки в зоне контакта в соответствии
с /3/ могут быть представлены в виде суммы двух слагаемых, одно из которых
обусловлено реализацией касательной силы в контакте, а второе - геометрией колеса (его
круговой формы в поперечном к оси сечении).
В работе /7/ показано, что пренебрежение смещениями, обусловленными
геометрией колеса, не приводит к существенной погрешности в определении
кинематических параметров колеса в функции реализуемой касательной силы. В связи с
этим в дальнейшем будем учитывать только тангенциальные смещения точек беговой
дорожки колеса, обусловленные реализацией касательной силы, которые на участке
сцепления могут быть представлены выражением Ux = ξx(a-x), общим и для ведущего и
для тормозного режимов качения /8, 9/. Здесь
rc
ξx = k − 1
(5)
rk
- относительная потеря скорости; rk и rkc - радиус качения и радиус свободного качения
колеса.
Исходя из пропорциональности тангенциальных напряжений (удельных
касательных сил) тангенциальным смещениям можем написать, что тангенциальные
напряжения, обусловленные реализацией касательной силы в контакте, равны:
(6)
qtx = λxUx = λxξx(a-x)
При достижении продольными тангенциальными напряжениями предельной по
сцеплению величины q t x = μq n происходит срыв и начинается скольжение. Координата xг
(рис.2) участков сцепления и скольжения найдется из последнего равенства, если
подставить в него выражения (6) и (2):
x Г = −a ±
λx ξx
μq n
(7)
0
Здесь и далее верхний знак относится к ведущему режиму качения, нижний - к
тормозному.
Продольная касательная сила в контакте может быть найдена, как:
xГ
xГ
⎡+ a
⎤
⎡+ a
⎤
(8)
Fx = 2b ⎢ ∫ q t x dx ± ∫ μq n dx ⎥ = 2b⎢ ∫ λ x ξx ( a − x )dx ± ∫ μq n dx ⎥
⎢⎣ x Г
⎥⎦
⎢⎣ x Г
⎥⎦
−a
−a
После подстановки вышеприведенных зависимостей и преобразований
полученного уравнения, имеем:
μq n0
⎡λ ξ
⎤
Fx = 2b⎢ x x ( a − x Г ) 2 ±
( 2a 3 + 3a 2 x Г − x Г3 )⎥
(9)
3
⎣ 2
⎦
Подводимая к колесу мощность при равномерном движении расходуется, кроме
совершения полезной работы, на преодоление сопротивления качению, обусловленного
гистерезисом в материале шины и потерями на трение скольжения в контакте колеса с
опорной поверхностью. Уравнение мощностного баланса имеет вид:
(10)
Р = РГ + Ртр +Рп
где РГ и Ртр - потери мощности на гистерезис и трение в контакте; Р - подводимая к
колесу мощность (для ведущего колеса Р = Мкω, где Мк - подводимый к колесу движущий
момент, для ведомого колеса Р = FxV); Рп - отводимая от колеса полезная мощность.
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
76
Секция 5 «КОЛЕСА И ШИНЫ».
Потери мощности на трение в контакте, имеющие место на участке скольжения,
расположенном со стороны выхода из контакта, могут быть представлены в виде:
xГ
Ртр = 2b ∫ μq n Vck dx ,
(11)
−a
где Vск - скорость скольжения элементов беговой дорожки колеса относительно
опорной поверхности.
На участке сцепления скорость Vсц тангенциальной деформации беговой дорожки
колеса, т.е. скорость, с которой точка колеса, находящаяся в контакте с опорной
поверхностью, опережает или отстает от того положения, в котором она находилась бы
при отсутствии тангенциального смещения, обусловленного реализацией касательной
силы, равна величине:
dU x dU x dx
Vсц =
=
= −ξx V
(12)
dt
dx dt
По достижении тангенциальными напряжениями величины, предельной по
сцеплению, т.е. qtx = μqn, начинается скольжение элементов беговой дорожки колеса
относительно основания. При этом скорость изменения тангенциального смещения,
равная скорости скольжения беговой дорожки колеса, будет иная, чем на участке
сцепления, поскольку тангенциальное смещение будет ограничиваться величиной
нормальных напряжений, и скорость Vqn изменения тангенциальных смещений,
обусловленная изменением нормальных напряжений, ограничивает (уменьшает) ту
скорость тангенциального смещения, с которой рассматриваемая точка беговой дорожки
«подошла бы» к началу участка скольжения. На участке скольжения при -а<хГ<0 падение
qn уменьшает величину тангенциальных смещений, что возможно лишь в случае, когда
скорость Vqn и Vсц противоположны, т.е.:
(13)
Vck = −ξxV − Vqn
Если скольжение распространяется и на часть переднего участка площади
контакта, т.е. 0<хГ<а, то последнее равенство справедливо и для участка 0<х<хГ, на
котором нормальные давления возрастают.
Тангенциальные напряжения на участке скольжения можно представить в виде
μq n = λxU xck , где U xck - тангенциальное смещение элементов беговой дорожки колеса на
участке скольжения. Из последнего выражения следует, что U xck = μq n / λx .
Скорость изменения тангенциальной деформации на участке скольжения,
обусловленная изменением нормальных напряжений, может быть выражена в виде:
μq
d( n )
ck
ck
λx
dU x
dU x dx
Vqn =
=
=V
(14)
dt
dx dt
dx
Таким образом, скорость скольжения будет равна:
μq ⎤
⎡
d( n )⎥
⎢
λx
⎥
(15)
Vck = −V ⎢ξx +
dx ⎥
⎢
⎥
⎢
⎦
⎣
Для ведущего колеса:
μq ⎤
⎡
d( n )⎥
⎢
λx
⎥
Vck = V ⎢ξx +
dx ⎥
⎢
⎢
⎥
⎣
⎦
Материалы международной научно-технической конференции ААИ «Автомобиле- и
77
Vck = Vсц − Vqn
или
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
Секция 5 «КОЛЕСА И ШИНЫ».
и выражение для потери мощности на трение в контакте примет следующий вид:
μq n ⎤ ⎫
⎧
⎡
d
(
)
⎪xГ
⎢
λ x ⎥ ⎪⎪
⎪
⎥ dx ⎬ =
Рт р = 2b⎨ ∫ μq nV ⎢ξx +
dx
⎢
⎥ ⎪
⎪− a
(16)
⎢
⎥ ⎪
⎪⎩
⎣
⎦ ⎭
xГ
xГ
μq
μq ⎪⎫
⎪⎧
= 2b⎨μVξx ∫ q n dx + λ x V ∫ n d ( n )⎬
λx
λx ⎪⎭
⎪⎩
−a
−a
Применительно к параболическому закону (1) распределения нормальных
давлений для границы участков сцепления и скольжения имеем μq n( x = x Г ) = λx ξx ( a − x Г ) .
Принимая это во внимание, после преобразований (16) с учетом (1), получим:
2
Рт р = μq n0 b( 2a 3 + 3ax Г 2 − x Г3 )ξx V + bλx ( a − x Г ) 2 ξх 2V
3
или, вынося общий множитель 2bξxV,
⎡ μq n0
⎤
1
Ртр = 2bξx V ⎢
( 2a 3 + 3a 2 x Г − х Г3 ) + λx ξx ( a − x Г 2 ⎥
(17)
2
⎣ 3
⎦
Сравнивая последнее уравнение с (8), нетрудно заметить, что выражение в
квадратных скобках, стоящее в (17), есть погонная касательная сила Fx/2b. Тогда:
Ртр Fx ξx V
(18)
=
2b
2b
Аналогичным образом можно показать, что формула (18) является справедливой и
для тормозного режима качения, если считать Fx и ξх отрицательными.
Таким образом, потеря мощности на трение в контакте эластичного колеса с
жестким основанием, обусловленная реализацией в контакте касательной силы,
определяется уравнением:
Ртр = FxξxV,
(19)
в котором величины Fx и ξx подставляются со своими знаками (Fx и ξx
положительны для ведущего режима качения и отрицательны для ведомого и тормозного).
Полученное выражение совпадает с аналогичной зависимостью, выведенной
Вирабовым Р.В. /7/.
Из выражения (7) следует, что:
λxξx = μ q n0 (a+xГ)
(20)
Подставляя это равенство в уравнение (8), после преобразований и решения
полученного уравнения относительно хГ, получаем:
х Г = a (1 − 2 ⋅ 3 1 m Fx / μFz ) ,
(21)
После подстановки полученного для хГ выражения в формулу (20), с учетом того,
что ξ х = rkc / rk − 1, после преобразований приходим к зависимости, позволяющей
рассчитывать радиус качения колеса во всем диапазоне изменения касательной силы от
нуля до предельной по сцеплению:
⎡ 2μq n0 a
F ⎤
rk = rk / ⎢1 ±
(22)
(1 ± 3 1 m x )⎥
λx
μFz ⎦
⎣
При действии небольших касательных сил, раскладывая сначала подкоренное
выражение, а затем преобразованный знаменатель в степенные ряды, и отбрасывая при
этом члены второго и более высоких порядков малости, приходим к выражению:
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
78
Секция 5 «КОЛЕСА И ШИНЫ».
rk = r −
c
k
2q n0 rkc a
F ,
(23)
3λx Fz x
в котором Fx подставляется со своим знаком («плюс» - для ведущего режима
качения и «минус» - для ведомого).
Так как мощность потерь на трение в контакте определяется зависимостью (19), то,
выражая входящую в нее ξх через полученное для радиуса качения выражение (22), будем
иметь:
2μq n0 a
F
Рт р =
(1 − 3 1 m x )Fx V
(24)
λx
μFz
или (при относительно небольших касательных силах):
γ
aFx2V
2 aq n0 2
Рт р =
= Fc Fx2V
(24,а)
Fx V ≈
3 λx Fz
2krд sFz rk
Сравнивая формулу Е.А.Чудакова
rk = rkc ± γ F F ,
(25)
определяющую зависимость радиуса качения эластичного колеса от продольной
касательной силы, с зависимостью (23), можно отметить, что они имеют одинаковую
структуру. Приравнивая правые части равенств (25) и (23), можно получить формулу,
позволяющую рассчитывать коэффициент тангенциальной эластичности, входящий в
формулу Е.А.Чудакова:
2q n0 rkc a
γF =
(26)
3λx Fz
или, подставляя выражения (2) и (4):
arkc
a
≈
(26,а)
γF =
2krд Fz s 2kFz s
Из совместного решения уравнений мощностного баланса и силового равновесия
колеса связь между приложенным к колесу моментом и реализуемой в контакте
касательной силой может быть представлена в виде М = Fx rkc . Это позволяет установить
связь между коэффициентами γF и γМ тангенциальной эластичности в формуле
Е.А.Чудакова:
rk = rkc − γ M M = rkc − γ F Fx
Отсюда
γ
a
(26,б)
γ M = Fc =
2krд Fz s
rk
Входящие в последние формулы величины а и rд = r-W0 могут быть определены
экспериментально или теоретически. В частности, для определения прогиба W0
пневматических шин могут быть использованы зависимости, представленные в /10, 11/;
для массивных резиновых шин - формулы, приведенные в /12, 13/.
Полуширина площадки контакта жесткого плоского основания и колеса с
пневматической или сплошной резиновой шиной меньше величины a = r 2 − rд2 ,
определяемой из чисто геометрических соображений (рис.1).
Анализ большого количества экспериментальных значений полуширины площадки
контакта автомобильных шин с жестким плоским основанием показывает, что с
точностью до 1...3% величина a может быть рассчитана по формуле:
a = 0,85 W0 ( 2r − W0 ) ≈ 0,85 2rW0
(27)
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
79
Секция 5 «КОЛЕСА И ШИНЫ».
К практически таким же результатам пришел В.С.Никитин /14/, получивший
экспериментально, что для тракторных шин:
a = ( 0, 76...0,84) W0 ( 2r − W0 )
Полученные выше простые выражения (26,а,б) позволяют рассчитать γМ и γF c
достаточно высокой точностью.
Для подтверждения этого в таблице 1 приводятся расчетные значения γМ для ряда
шин и величины, полученные на основании большой серии экспериментов, выполненных
под руководством В.А.Петрушова /11/.
Таблица 1.
Параметр
мм/даНнм
γ
γ
эксп.
М
теор.
М
Шина
И-П184
0,05
0,053
ОИ-25
0,067
0,0636
И-247
0,031
0,034
Сравнение теоретических и экспериментальных результатов показывает их
относительно небольшое расхождение, что подтверждает правомерность принятых
допущений, а также используемой методики исследования.
При определении потерь мощности на гистерезис в материале шины будем
учитывать лишь вертикальную деформацию шины на площадке контакта под действием
нормальной нагрузки (поскольку деформация колеса в тангенциальном направлении
намного меньше), что позволяет пренебречь потерями мощности на гистерезис в
тангенциальном направлении (хотя практически их определение не представляет особых
трудностей):
a
dW
Р Г = 2 bβ Г ∫ q n
dx
dt
0
где βГ - коэффициент гистерезисных потерь, dW/dt - скорость деформирования
шины в нормальном направлении:
dW
dW dW dx dW
=
=
V=
ωr
dx
dt
dt dx dx
Из геометрических соображений (рис.2.2) приближенно можно принять, что:
a2 x2 a2 − x2
x2
(28)
W=
−
=
= W0 (1 − 2 ) ,
2r 2r
2r
a
где W0 = a2/2r - максимальный прогиб колеса (в среднем сечении).
С учетом (28) скорость деформирования шины в нормальном направлении будет равна
dW
x
=− V
dt
r .
как:
Тогда потери мощности на гистерезис составят величину:
a
3
x
РГ = βГ 2bV ∫ q n0 ( a 2 − x 2 ) dx = βГ aωFz
r
16
0
При найденном значении РГ момент от гистерезиса в материале шины найдется
МГ =
РГ
ω
=
3
β aF
16 Г z
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
80
Секция 5 «КОЛЕСА И ШИНЫ».
Зная момент от гистерезиса, можем найти также плечо сдвига нормальной реакции
основания, обусловленное гистерезисом:
M
3
b0 = Г = βГ а
16
Fz
bГ = f 0 rkc ,
Приравнивая к этому выражению аналогичное выражение
выведенное Р.В.Вирабовым /3,7/ для того же плеча,
3
b0 = βГ a = f 0 rkc
(28,а)
16
получим формулу
3 a
f0 =
β ,
16 rkc Г
позволяющую расчетным путем определять коэффициент сопротивления качению
ведомого колеса по его параметрам а и βГ, получаемым при статическом прижатии колеса
к основанию.
Коэффициент гистерезисных потерь можно найти, воспользовавшись, например,
методикой, изложенной в работе /15/.
Как уже отмечалось, при решении задач, связанных с качением эластичных колес
(например, нахождение тангенциальных напряжений в контакте, касательной силы,
мощности потерь на трение и других), реальный закон изменения нормальных давлений
на площадке контакта заменяют обычно упрощенным, чаще всего параболическим,
эллиптическим, трапецеидальным или законом постоянных (равных) давлений.
Для сравнения расчетных величин тангенциальной силы и мощности потерь на
трение в контакте при разных принимаемых законах изменения нормальных давлений qn
используем выражения (8) и (19).
1. Параболический закон изменения нормальных давлений (рис.7,а):
F
1,5qr
0,75q
q n = q n0 ( a 2 − x 2 );
q n0 =
λx = 3 д
; q= z ;
3
2b
a
а
хГ = −а +
λх ξх
μq n
0
2
Fx = λxξx ( a − x Г ) 2 b ± μq n0 b( 2a 3 + 3a 2 x Г − х Г3 )
3
2. Эллиптический закон изменения нормальных давлений (рис.7,б):
q n = q n0 1 − x 2 / a 2 ; q n0 = 2q / πa; λx = 1,08qrд / a 3
[
][
х Г = − а 1 − (λx ξx a ) 2 / ( μq n0 ) 2 / 1 + (λx ξx a ) 2 / ( μq n0 ) 2
[
]
]
Fx = λx ξx b( a − x Г ) 2 ± μq n0 b x Г a 2 − x Г2 + a 2 (π / 2 + arcsin x Г / a ) / a
3. Трапецеидальный закон изменения нормальных давлений (рис. 7,в):
r
a+x
q
a−x
q nлев. = q 2
q nс р. =
; q nп р ав. = q 2
λx = q д3
2 ;
2 ;
a+c
a −c
a −c
а
Здесь 2с - ширина верхнего основания трапеции нормальных давлений.
В отличие от двух первых законов, нормальные давления изменяются по ломанной
линии. В связи с этим для случая, когда предельные тангенциальные напряжения на
участке сцепления не превышают величины μq nс р. , т.е. не выходят за пределы левой
боковой стороны, что соответствует Fx≤0,556μFz , имеем:
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
81
Секция 5 «КОЛЕСА И ШИНЫ».
⎡
⎤
2 μq
х Г = a ⎢1 −
⎥;
2
2
⎣ μq ± ( a − c )λx ξx ⎦
Fx =
± 4 μqλx ξx a 2 b
μq ± ( a 2 − c 2 )λx ξx
При Fx≥0,556μFz
⎡
⎤
μFz
a
Fx = μFz ⎢ 0,5 +
m
2 ⎥
a + c 4λx ξx ( a + c ) b ⎦
2λx ξx ( a + c )b
⎣
4. Закон постоянных нормальных давлений (рис.7,г):
F
qn = z ;
λx = 0,8qrд / a 3
4ab
Аналогично предыдущему случаю имеем:
При Fx≤0,5μFz
х Г = − а;
Fx = 4λx ξx a 2 b
При Fx≥0,5μFz
μFz
μFz
хГ = a m
;
Fx = μFz (1 m
)
4λx ξx ab
16λx ξx a 2 b
хГ = a m
μFz
;
Рисунок 7
На рис.8 представлены графические зависимости касательных сил от величины
относительной потери скорости, а на рис.9 - зависимость относительной мощности потерь
на трение в контакте Ртр/V от реализуемой продольной силы. Сравнение кривых приводит
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
82
Секция 5 «КОЛЕСА И ШИНЫ».
к выводу о том, что для первых трех законов разница в определении Fx невелика. Закон
постоянных давлений дает наибольшее отклонение от средних значений.
Поскольку мощность потерь на трение в контакте колеса с дорогой
пропорциональна касательной силе и выражается зависимостью Ртр=FxξxV, то,
следовательно, соотношение мощностей трения в контакте для рассматриваемых законов
распределения нормальных давлений будут аналогичны приведенным соотношениям
касательных сил.
При реализации касательных сил, близких к предельным по сцеплению (т.е. когда
Fx→μFz) различие упрощенных законов qn, положенных в основу данного расчета, вносит
определенные расхождения: для параболического закона изменения нормальных давлений
касательная сила достигает предельной по сцеплению величины Fx=μFz при
относительной потере скорости ξхпред.=μа/rд, для трапецеидального закона - при
ξхпред.=μа/rд(1-(с/а)2). Для закона постоянных давлений ξпред. =∞, что предполагает
мгновенное увеличение тангенциальных напряжений qtx до величины μqn на входе в
контакт. Однако, как показывает опыт, уже при ξх = 0,1...0,2 начинается скольжение всех
точек поверхности колеса в зоне контакта. Поэтому с этой точки зрения наиболее близкие
к реальности результаты должны давать параболический и трапецеидальный законы,
которым и следует отдать предпочтение.
Рисунок 7
Рисунок 8
Отметим, что с математической точки зрения, параболический закон нормальных
давлений позволяет получить непрерывные функции Fx=f(x); xГ=f(x), в то время как
трапецеидальный закон предполагает излом функции в точке х=-с (рис.7,в), что
вынуждает при определении Fx, хГ, Ртр и других величин рассматривать отдельно два
участка: -с≥х≥-а и +а≥х≥-с. Вместе с тем зависимости, получаемые с использованием
трапецеидального закона, могут быть более простые. Еще более упрощается для
трапецеидального закона определение Fx, Ртр и иных параметров, если принять на участке
-с≥хГ≥-а (что соответствует Fx≤0,556μFn), как это сделано в /353/, хГ≈-(а+с)/2≈-0,9a (при
с=0,8а):
Fx=3,8λxξxa2b;
Ртр=3,8λxVa2bξx2
Можно отметить также, что в приближенных расчетах, особенно при небольших
касательных силах, вполне применим и самый простой закон распределения нормальных
давлений - закон постоянных нормальных давлений, который, хотя и является чрезмерно
упрощенным с присущим ему указанным недостатком, позволяет по очень простым
зависимостям определять Fx и Ртр (впрочем, эти зависимости почти такие же, как и
полученные для трапецеидального закона при введении упрощения хГ≈-0,9а).
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
83
Секция 5 «КОЛЕСА И ШИНЫ».
Эллиптический закон распределения нормальных давлений не может быть
рекомендован для использования как вследствие отмеченного ранее свойственного ему
недостатка, так и в силу того, что приводит к усложненным зависимостям (в частности,
при решении двух- и трехмерных задач - к эллиптическим интегралам).
Выше уже отмечалось, что реальное распределение нормальных давлений в
контакте реальных колес с жесткой опорной поверхностью для массивных шин и шин
высокого давления занимает промежуточное положение между эллиптическим и
параболическим законами: более близко к эллиптическому в средней части пятна контакта
и к параболическому на краях пятна контакта. В связи с этим для этих шин в расчеты
целесообразно вводить коэффициент тангенциальной жесткости λх, величина которого
имеет среднее значение между величинами, относящимися к эллиптическому и
параболическому законам qn, т.е. принять λх=1,3 /16/.
Литература
1. Ермилов В.Н., Мамаев А.Н. Экспериментальное исследование напряжений в контакте
массивной резиновой шины и жесткого основания при прямолинейном качении колеса. Произв. шин, резинотехнических и асбестотехнических изделий, 1982, №6, с.31-33.
2. Ermilow V.N., Mamajev A.N. Experimental study of the contact stresses between a solid
rubber tyre and a rigid surface during rolling of the wheel in a straight line/ - International
Polymer Science and Technology, 1983, vol.10, ¹ 7, p.78-79.
3. Вирабов Р.В. О реализации касательной силы в зоне контакта упругих тел при качении.
- Машиностроение, 1967. - № 2.
4. Lorenz R. Schiene und Rad. VDJ-Z, 2, №6, 1928.
5. Freudenstein G. Luftreifen bei Schrag und Kurvenlauf (Experimentalle und theoretische
Untersuchung an LKW-Reifen). Deutdche Kraftfahrtforschung, 1961, H. 152.
6. Fiala E. Seitenkrafte am rollenden Luftreifen. VDJ-Z, 1954, Bd. 96, ¹29, S. 973...79. Пер.
ЦПБ №17347, М., 1956.
7. Вирабов Р.В. Качение упругого колеса по жесткому основанию. - Изв. ВУЗов,
Машиностроение, 1967. - № 4. - с.78-85.
8. Вирабов Р.В., Мамаев А.Н. Определение мощности потерь на трение в контакте
фрикционной пары - колесо с пневматической шиной-жесткое основание. Межвуз.сб.научных трудов «Бесступенчато-регулируемые передачи», Ярославль, 1978,
с.61-67.
9. Вирабов Р.В., Мамаев А.Н. Анализ кинематических и силовых соотношений при
качении колеса по жесткому основанию. - Механика машин, М., Наука, 1980, вып.57,
с.101-105.
10. Евграфов В.Н. Исследование влияния рабочих качеств колесного движителя на
некоторые технические показатели автопоезда. - Автореферат диссертации на соискание
уч.ст. к.т.н., М., МАМИ, 1979.
11. Евграфов В.Н., Московкин В.В., Петрушов В.А., Стригин И.А. Геометрические и
кинематические параметры колеса и его сопротивление качению. - Автомоб.промыш.,
1982, №8, с.16-17.
12. Мамаев А.Н. Влияние конструктивных параметров эластичных колес на величину их
прогиба и размеры площадки контакта с жестким основанием. - Межвуз.сб. научных
трудов «Безопасность и надежность автомобиля». - М., МАМИ, 1982, с.203-211.
13. Мамаев А.Н., Алепин Е.А. Определение размеров площадки контакта и прогиба колеса
с резиновой шиной при статическом прижатии колеса к жесткому основанию. Сб.научных трудов «Машиноведение», Челябинск, 1980, №251, с.82-85.
14. Никитин В.С. Влияние нагрузочных режимов колес на тяговые показатели и износ
шин трактора колеса. - Автореферат диссертации на соискание ученой степени к.т.н., М.,
МГМИ, 1989.
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
84
Секция 5 «КОЛЕСА И ШИНЫ».
15. Мамаев А.Н. Об определении коэффициента гистерезисных потерь высокоэластичных
тел качения. – М., НИИНавтопром, 1982, №779, ап-Д82.
16. Мамаев А.Н. Определение коэффициента тангенциальной эластичности колеса с
тороидальной формой беговой дорожки. - Изв. ВУЗов, Машиностроение, 1982, N 10.
Материалы международной научно-технической конференции ААИ «Автомобиле- и
тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию
МГТУ «МАМИ».
85