дополнительная диссоциация и ориентация
реклама

ÒÅÎÐÅÒÈ×ÅÑÊÈÅ ÎÑÍÎÂÛ
ÕÈÌÈ×ÅÑÊÎÉ ÒÅÕÍÎËÎÃÈÈ
ÒÅÊÑÒÈËÜÍÛÕ ÌÀÒÅÐÈÀËÎÂ,
ÊÎÆ, ÌÅÕÀ
ÓÄÊ 541.124.7
ÄÎÏÎËÍÈÒÅËÜÍÀß ÄÈÑÑÎÖÈÀÖÈß È ÎÐÈÅÍÒÀÖÈß
ÍÈÇÊÎÌÎËÅÊÓËßÐÍÛÕ ÑÎÅÄÈÍÅÍÈÉ Â ÏÐÈÑÓÒÑÒÂÈÈ
ÏÎËÈÌÅÐÎÂ È ÒÂÅÐÄÛÕ ÏÎÂÅÐÕÍÎÑÒÅÉ
Ý.Ô.Âàéíøòåéí
Ìåòîäàìè òåðìîäèíàìèêè ïîêàçàíà âîçìîæíîñòü îðèåíòàöèè íèçêîìîëåêóëÿðíûõ ñîåäèíåíèé è
äîïîëíèòåëüíîé äèññîöèàöèè àññîöèèðîâàííûõ æèäêîñòåé. Ðàññìîòðåíà âîçìîæíîñòü èñïîëüçîâàíèÿ äàííûõ ïðîöåññîâ â òåêñòèëüíîé ïðîìûøëåííîñòè.
Ðàíåå áûëî òåîðåòè÷åñêè îáîñíîâàíî è ýêñïåðèìåíòàëüíî ïîêàçàíî [1], ÷òî àññîöèèðîâàííûå íèçêîìîëåêóëÿðíûå ñîåäèíåíèÿ (ÍÌÑ) äèññîöèèðóþò â ïðèñóòñòâèè ïîëèìåðîâ è ïîâåðõíîñòåé ðàçäåëà ôàç. Ïîñêîëüêó àññîöèèðîâàííûå ÍÌÑ, òàêèå, êàê âîäà, ïåðåêèñü âîäîðîäà, ïðèìåíÿþòñÿ âî
ìíîãèõ ïðîöåññàõ îáðàáîòêè è ïðè èñïîëüçîâàíèè
òåêñòèëüíûõ ìàòåðèàëîâ, íàïðèìåð, ïðè ñòèðêå
òêàíåé, òî ïîíèìàíèå äàííîãî ïðîöåññà ìîæåò ïðèâåñòè ê óâåëè÷åíèþ ýôôåêòèâíîñòè òåõíîëîãè÷åñêèõ ïðîöåññîâ.
Îñíîâíîé ôèçèêî-õèìè÷åñêîé ïðè÷èíîé âîçíèêíîâåíèÿ äîïîëíèòåëüíîé äèññîöèàöèè ÿâëÿåòñÿ ðàçëè÷èå èçáûòî÷íûõ êîìáèíàòîðíûõ ýíòðîïèé
ñìåøåíèÿ ìîëåêóë ðàçëè÷íûõ ðàçìåðîâ (àòåðìàëüíûå ðàñòâîðû) äëÿ ðàñòâîðîâ öåïåé â àññîöèèðîâàííîì è íåàññîöèèðîâàííîì ðàñòâîðèòåëå. Íàïîìíèì, ÷òî äàííàÿ ñîñòàâëÿþùàÿ èçìåíåíèÿ ñâîáîäíîé ýíåðãèè îáðàçîâàíèÿ ðàñòâîðà ÿâëÿåòñÿ
îäíîé èç ãëàâíûõ [2].
Èçëîæåííûé âûøå âûâîä ìîæíî ïîëó÷èòü, èñïîëüçóÿ ëþáóþ èç ñóùåñòâóþùèõ òåîðèé ðàñòâîðîâ öåïíûõ ìîëåêóë (ñì., íàïðèìåð, ðàáîòû [3-5]).
 ïðèáëèæåíèè Ôëîðè-Õàããèíñà [6, 7] èçáûòî÷íàÿ ñâîáîäíàÿ ýíåðãèÿ ñìåøåíèÿ GÈ äëÿ àòåðìàëüíîãî ðàñòâîðà ìîæåò áûòü çàïèñàíà â âèäå (1):
GÈ=-RTS
xilnfi/xi
i
(1),
ãäå: fi=rixi/ Srixi - îáúåìíàÿ äîëÿ i-òîãî êîìïîíåíi
5 - 2020
òà, õi - åãî ìîëüíàÿ äîëÿ, ri - ÷èñëî ìåñò â êâàçèðåøåòêå, çàíèìàåìûõ i ìîëåêóëîé, ïðè óñëîâèè, ÷òî
íàèìåíüøàÿ ìîëåêóëà (îáû÷íî ðàñòâîðèòåëü) çàíèìàåò â íåé îäíî ìåñòî.
Äëÿ ðàñòâîðîâ öåïíûõ ìîëåêóë (ïîëèìåðîâ) â
íåàññîöèèðîâàííîé æèäêîñòè èçáûòî÷íàÿ ñâîáîäíàÿ ýíåðãèÿ ñìåøåíèÿ ìîëåêóë ðàçëè÷íûõ ðàçìåðîâ (GÈÍ ) ìîæåò áûòü âûðàæåíà óðàâíåíèåì (2), à â
à
àññîöèèðîâàííîé æèäêîñòè (GÈ ) - (3):
GÈÍ =-RT
N1
r (N +N )
N2 r2(N1+N2)
ln 1 1 2 +
ln
(2),
N1+N2 r1N1+r2N2 N1+N2 r1N1+r2N2
N
mr1( n1 + N2)
N1/n
N2
GÈ =-RT
ln
+
x
N1
N1
N1
mr
+r
N
+N
+N
1 n
2 2
2
n
2
n
N1
r2( n + N2)
x ln
N
mr1 1 +r2N2
n
à
(3),
ãäå: n - ÷èñëî ìîëåêóë ðàñòâîðèòåëÿ â àññîöèàòå;
m - õàðàêòåðèçóåò óâåëè÷åíèå ÷èñëà ìåñò,
çàíÿòûõ öåïíîé ìîëåêóëîé â íåàññîöèèðîâàííîì ðàñòâîðèòåëå ïî ñðàâíåíèþ ñ ÷èñëîì ìåñò â êâàçèðåøåòêå ïðè àññîöèàöèè ðàñòâîðèòåëÿ;
N1 è N2 - êîíöåíòðàöèè ìîëåêóë íåàññîöèèðîâàííîãî ðàñòâîðèòåëÿ
34
ÒÅÊÑÒÈËÜÍÀß ÕÈÌÈß, 1998, ¹ 1 (13)
è ïîëèìåðà, ñîîòâåòñòâåííî;
r1 è r2 - ÷èñëî ìåñò â êâàçèðåøåòêå, çàíèìàåìûõ, ñîîòâåòñòâåííî, ìîëåêóëàìè ðàñòâîðèòåëÿ è ïîëèìåðà.
à
Òàê êàê 1<m<n, òî DG = GÈÍ - GÈ <0
{
G=RT
D
+ ln 1+
N 1N 2
N
(N1+N2)( n1+N2)
N1(1-1/n)
- ln 1+
N1
n +N2
ln
r1 N1/n
ln m +
r2 N 1
+N
2
n
N1r1(1-m/n)
N
mr1 1 +r2N2
n
}
(4).
Êàê âèäíî èç óðàâíåíèÿ (4), ýòà ñîñòàâëÿþùàÿ
èçìåíåíèÿ ñâîáîäíîé ýíåðãèè ìîæåò èìåòü äîñòàòî÷íî áîëüøîå çíà÷åíèå (ïî àáñîëþòíîé âåëè÷èíå)
è, êàê óêàçûâàëîñü âûøå, âíîñèò ñóùåñòâåííûé
âêëàä â îáùóþ ñâîáîäíóþ ýíåðãèþ îáðàçîâàíèÿ
ðàñòâîðà, ÷òî è ñïîñîáñòâóåò äîïîëíèòåëüíîé äèññîöèàöèè ÍÌÑ â ïðèñóòñòâèè öåïíûõ ìîëåêóë.
Óðàâíåíèå (4) öåëåñîîáðàçíî èñïîëüçîâàòü òîëüêî
ïðè îòíîñèòåëüíî íåáîëüøèõ ìîëåêóëÿðíûõ ìàññàõ (Ì) öåïåé. Ïðè áîëüøèõ Ì, à ñëåäîâàòåëüíî, è
áîëüøèõ r2 âñåìè ñëàãàåìûìè â ñêîáêàõ, êðîìå
ïåðâîãî, ìîæíî ïðåíåáðå÷ü.
Ïðè êîëè÷åñòâåííîé îöåíêå êîíñòàíòû ðàâíîâåñèÿ äèññîöèàöèè ÍÌÑ (Ê) íóæíî ó÷èòûâàòü è
âêëàä äðóãèõ ñîñòàâëÿþùèõ ñâîáîäíîé ýíåðãèè
îáðàçîâàíèÿ ðàñòâîðà. Íàïðèìåð, ñâîáîäíàÿ ýíåðãèÿ èäåàëüíîãî ñìåøåíèÿ áóäåò âîçðàñòàòü ïðè
óâåëè÷åíèè ÷èñëà ìîëåêóë â ñèñòåìå, ÷òî òàêæå
ñïîñîáñòâóåò äèññîöèàöèè. Ïðè óâåëè÷åíèè ÷èñëà
ìîëåêóë, îáóñëîâëåííîì äîïîëíèòåëüíîé äèññîöèàöèåé, â îáùåì ñëó÷àå âîçðàñòàåò îáúåì ðàñòâîðà
(â ðàçáàâëåííûõ ðàñòâîðàõ ñîñòàâëÿþùåé èçìåíåíèÿ ñâîáîäíîé ýíåðãèè, ñâÿçàííîé ñ èçìåíåíèåì
îáúåìà ñèñòåìû, ìîæíî ïðåíåáðå÷ü), ÷òî òàêæå
ïðèâîäèò ê óâåëè÷åíèþ ýíòðîïèè, à ñëåäîâàòåëüíî, ñïîñîáñòâóåò äèññîöèàöèè. Íåêîòîðîå, îòíîñèòåëüíî ìàëîå çíà÷åíèå ýíòðîïèè, îáóñëîâëåííîå
êîìáèíàòîðèêîé ðàñïîëîæåíèÿ àññîöèèðîâàííûõ
è íåàññîöèèðîâàííûõ ìîëåêóë âîêðóã öåïè (íà
ïîâåðõíîñòè ðàçäåëà ôàç), óìåíüøàåò äîïîëíèòåëüíóþ äèññîöèàöèþ ÍÌÑ.
Î÷åâèäíî, ÷òî ïðè óâåëè÷åíèè ÷èñëà êîìïîíåíòîâ ðàñòâîðà âûâîä î âîçìîæíîñòè äîïîëíèòåëüíîé
äèññîöèàöèè îñòàíåòñÿ íåèçìåííûì, õîòÿ êîëè÷åñòâåííûå õàðàêòåðèñòèêè ìîãóò ñóùåñòâåííî èçìåíèòüñÿ.
Åñòåñòâåííî, Ê áóäåò çàâèñåòü è îò ðàçëè÷èÿ âî
âçàèìîäåéñòâèè àññîöèèðîâàííûõ è íåàññîöèèðîâàííûõ ìîëåêóë ðàñòâîðèòåëÿ ìåæäó ñîáîé è ñ öåïíûìè ìîëåêóëàìè.  áîëüøèíñòâå ñëó÷àåâ íåàññîöèèðîâàííûå ìîëåêóëû îáëàäàþò áîëåå ñèëüíûì
âçàèìîäåéñòâèåì, ÷òî â ñîîòâåòñòâèè ñ áîëåå òî÷íîé òåðìîäèíàìè÷åñêîé ìîäåëüþ È.Ïðèãîæèíà
[5], ó÷èòûâàþùåé è èçáûòî÷íóþ ýíòðîïèþ ñìåøåíèÿ ïî Ï.Ôëîðè, äîëæíî âåñòè íå òîëüêî ê óâåëè-
÷åíèþ äèññîöèàöèè, íî è ê îðèåíòàöèè ìîëåêóë
ðàñòâîðèòåëÿ âáëèçè öåïíûõ ìîëåêóë ïðè àññèìåòðè÷íûõ ìîëåêóëàõ è áîëåå ïëîòíîé óïàêîâêå âîêðóã öåïè ñôåðè÷åñêèõ ìîëåêóë.
Ïðè íåñèììåòðè÷íîñòè íåàññîöèèðîâàííûõ
ìîëåêóë ðàñòâîðèòåëÿ íàèáîëüøåå ðàçëè÷èå â ñîîòíîøåíèè ìåæäó ðàçìåðàìè öåïè è ðàñòâîðèòåëÿ áóäåò ïðè ñðàâíåíèè êîíòóðíîé äëèíû öåïè ñ
ìèíèìàëüíûì ðàçìåðîì ðàñòâîðèòåëÿ. Ïîýòîìó
ìàêñèìàëüíàÿ èçáûòî÷íàÿ ýíòðîïèÿ ñìåøåíèÿ
ìîëåêóë ðàçëè÷íûõ ðàçìåðîâ ïðîÿâèòñÿ â ñëó÷àå
ðàñïîëîæåíèÿ ìîëåêóë ðàñòâîðèòåëÿ âîêðóã öåïíûõ ìîëåêóë íàèáîëåå óçêèì ñå÷åíèåì. Åñëè ìîëåêóëû ðàñòâîðèòåëÿ èìåþò òðè ðàçëè÷íûõ ðàçìåðà, òî îíè áóäóò ïîâåðíóòû îïðåäåëåííûì îáðàçîì
îòíîñèòåëüíî îñè öåïè. Íàèáîëåå âåðîÿòíîå ðàñïîëîæåíèå ìîëåêóë ðàñòâîðèòåëÿ âîêðóã öåïè ðåàëèçóåòñÿ òîãäà, êîãäà öåïü îêðóæàåò ìàêñèìàëüíî âîçìîæíîå êîëè÷åñòâî ìîëåêóë ðàñòâîðèòåëÿ.
Åñòåñòâåííî, ðå÷ü èäåò î ðàçìåðàõ ñå÷åíèÿ ìîëåêóë, êîòîðûå ìîãóò êîíòàêòèðîâàòü ñ öåïüþ. Ïðè
îöåíêå îðèåíòàöèè ìîëåêóë ðàñòâîðèòåëÿ íåîáõîäèìî ó÷èòûâàòü, ÷òî ïðè îðèåíòàöèè òåðÿåòñÿ
÷àñòü ýíòðîïèè, îáóñëîâëåííàÿ ïîòåðåé ÷èñëà ñîñòîÿíèé, ñâÿçàííûõ ñ ðàçëè÷íûì ðàñïîëîæåíèåì
ìîëåêóë ðàñòâîðèòåëÿ â ïðîñòðàíñòâå. Îäíàêî ýòà
ñîñòàâëÿþùàÿ îáû÷íî çíà÷èòåëüíî ìåíüøå, ÷åì
èçáûòî÷íàÿ êîìáèíàòîðíàÿ ýíòðîïèÿ â ñëó÷àå îðèåíòèðîâàííûõ ìîëåêóë. Îáîñíîâàíèå âîçìîæíîñòè îðèåíòàöèè ÍÌÑ ìîæíî ïîëó÷èòü, èñïîëüçóÿ
âûøåïðèâåäåííûå óðàâíåíèÿ, àíàëîãè÷íî äîêàçàòåëüñòâó âîçìîæíîñòè äîïîëíèòåëüíîé äèññîöèàöèè.
Ïðè êîëè÷åñòâåííîé îöåíêå îðèåíòàöèè, êàê
îáû÷íî, íåîáõîäèìî ó÷èòûâàòü âñå ñîñòàâëÿþùèå
ñâîáîäíîé ýíåðãèè îáðàçîâàíèÿ. Íàïðèìåð, âçàèìîäåéñòâèå ìåæäó ìîëåêóëàìè ðàñòâîðèòåëÿ,
îêðóæàþùèìè öåïü, ìîæåò èçìåíèòü íàèáîëåå âåðîÿòíóþ îðèåíòàöèþ, õàðàêòåðíóþ äëÿ ÷èñòî ýíòðîïèéíîãî ðàññìîòðåíèÿ.
Ïðè êîíòàêòå íèçêîìîëåêóëÿðíûõ æèäêîñòåé
ñ ïîâåðõíîñòüþ ðàçäåëà ôàç òàêæå äîëæíû íàáëþäàòüñÿ êàê äîïîëíèòåëüíàÿ äèññîöèàöèÿ àññîöèèðîâàííûõ ñîåäèíåíèé, òàê è îðèåíòàöèÿ íåàññîöèèðîâàííûõ ìîëåêóë, òàê êàê ñîõðàíÿþòñÿ ïðè÷èíû âîçíèêíîâåíèÿ äàííûõ ïðîöåññîâ. Ðàñ÷åò èçáûòî÷íîé ýíòðîïèè ðàñïîëîæåíèÿ ìîëåêóë íà ïîâåðõíîñòè, â îòëè÷èå îò èçáûòî÷íîé ýíòðîïèè ñìåøåíèÿ ìîëåêóë ðàçëè÷íûõ ðàçìåðîâ â ðàñòâîðàõ,
ïðîâîäèòñÿ â äâóõ, à íå â òðåõ èçìåðåíèÿõ. ßñíî,
÷òî ïðè êîëè÷åñòâåííîé îöåíêå íàáëþäàåìûõ ïðîöåññîâ íóæíî ó÷èòûâàòü âñå ñîñòàâëÿþùèå ñâîáîäíîé ýíåðãèè, âëèÿþùèå íà ýòè ïðîöåññû.
Ðàññìîòðèì âëèÿíèå äëèíû öåïè è äðóãèõ ïàðàìåòðîâ íà ïðîöåññû äîïîëíèòåëüíîé äèññîöèàöèè è îðèåíòàöèè.
Ïðè èçìåíåíèè ìîëåêóëÿðíîé ìàññû öåïè ïðè
ïîñòîÿííîì êîëè÷åñòâå èñõîäíûõ ìîëåêóë (â ïåðåñ÷åòå íà íåàññîöèèðîâàííûå ìîëåêóëû) è ïîñòî-
ÒÅÊÑÒÈËÜÍÀß ÕÈÌÈß, 1998, ¹ 1 (13)
35
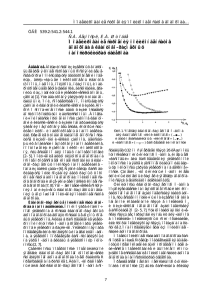
g¥
1,0
0,8
0,6
1
0,4
2
3
4
0,2
0
10
20
30
40
50
r2/r1
Ðèñ. 1. Çàâèñèìîñòü ïðåäåëüíîãî êîýôôèöèåíòà àêòèâíîñòè (g¥ ) ðàñòâîðèòåëÿ îò ñîîòíîøåíèÿ ðàçìåðîâ öåïè è ðàñòâîðèòåëÿ â ïðèáëèæåíèè Ï.Ôëîðè (1) è
Ãóããåíãåéìà (2-4) ïðè z = 4, r1= 1(2), r1 = 2(3) è r1 = 6(4)
[8]
ÿííûõ âíåøíèõ óñëîâèÿõ âîçðàñòàåò (ïî àáñîëþòíîé âåëè÷èíå) èçáûòî÷íàÿ ñâîáîäíàÿ ýíåðãèÿ ñìåøåíèÿ ìîëåêóë ðàçëè÷íûõ ðàçìåðîâ, à ñëåäîâàòåëüíî, äîëæíà óâåëè÷èâàòüñÿ äîïîëíèòåëüíàÿ
äèññîöèàöèÿ è îðèåíòàöèÿ ìîëåêóë ÍÌÑ. Íà ðèñ. 1
ïðåäñòàâëåíà çàâèñèìîñòü ïðåäåëüíîãî êîýôôèöèåíòà àêòèâíîñòè ðàñòâîðèòåëÿ (g¥ ) îò ñîîòíîøåíèÿ
r1/r2, âçÿòàÿ èç ðàáîòû [8]. ßñíî, ÷òî óâåëè÷åíèÿ
ñòåïåíè äèññîöèàöèè íå áóäåò íàáëþäàòüñÿ äî òåõ
ïîð, ïîêà íå áóäåò äîñòèãíóòî çíà÷åíèå èçáûòî÷íîé ñâîáîäíîé ýíåðãèè, äîñòàòî÷íîå äëÿ äîïîëíèòåëüíîãî ðàçðûâà àññîöèèðîâàííûõ ìîëåêóë. Ñëåäîâàòåëüíî, âîçíèêíîâåíèå äîïîëíèòåëüíîé
äèññîöèàöèè â çàâèñèìîñòè îò ìîëåêóëÿðíîé ìàññû åñòü ïðîöåññ äèñêðåòíûé, ò.å. ïðè çàäàííîì
ñòðîåíèè öåïåé è ÍÌÑ è ïîñòîÿííûõ âíåøíèõ
óñëîâèÿõ äîïîëíèòåëüíàÿ äèññîöèàöèÿ è îðèåíòàöèÿ íàáëþäàþòñÿ, íà÷èíàÿ ñ îïðåäåëåííîé äëèíû
(ìîëåêóëÿðíîé ìàññû (Ì)) öåïè. Ïðè äàëüíåéøåì
óâåëè÷åíèè Ì ýòè ïðîöåññû íåïðåðûâíî âîçðàñòàþò, ñòðåìÿñü ê ïðåäåëó ïðè Ì® ¥.
Äëÿ ïðîöåññîâ íà ïîâåðõíîñòè ðàçäåëà ôàç çàâèñèìîñòè îò ðàçìåðîâ ýòîé ïîâåðõíîñòè è îò äëèíû öåïè êà÷åñòâåííî îäèíàêîâû, ïðè÷åì êîëè÷åñòâåííî çàâèñèìîñòè îò ðàçëè÷íûõ êîîðäèíàò ïîâåðõíîñòè (äâóìåðíîå ïðîñòðàíñòâî) ìîãóò ðàçëè÷àòüñÿ.
Ïîñêîëüêó îò ïîïåðå÷íîãî ñå÷åíèÿ öåïè çàâèñèò
êîëè÷åñòâî îêðóæàþùèõ åå ìîëåêóë ÍÌÑ è âçàèìîäåéñòâèå öåïü - ÍÌÑ, òî, âåðîÿòíî, ïðîöåññû äîïîëíèòåëüíîé äèññîöèàöèè è îðèåíòàöèè çàâèñÿò è
îò äèàìåòðà âîëîêíà. Ýòà çàâèñèìîñòü ïðåäñòàâëÿåò ñîáîé ïëàâíóþ êðèâóþ, ñòðåìÿùóþñÿ ê ïàðàìåòðàì, õàðàêòåðíûì äëÿ ïëîñêîé ãðàíèöû ðàçäåëà
ôàç. Ïî-âèäèìîìó, ïðîöåññû äîïîëíèòåëüíîé äèññîöèàöèè è îðèåíòàöèè äîëæíû ïðîÿâëÿòüñÿ è ïðè
íàáóõàíèè òðåõìåðíîé ñèñòåìû.
Èñõîäÿ èç âûøåèçëîæåííîãî, ìîæíî ïðåäïîëàãàòü, ÷òî äàííûå ïðîöåññû çàâèñÿò íå òîëüêî îò
êîîðäèíàò (ðàçìåðîâ) n-ìåðíîãî (n = 1, 2, 3) ïðîñòðàíñòâà, íî è îò èõ ôîðìû (n = 1 - ïîëèìåð (öåïü),
n = 2 - ïîâåðõíîñòü, n = 3 - ñåòêà).
Ñ ðîñòîì òåìïåðàòóðû â ïðåäïîëîæåíèè î ïîñòîÿíñòâå äðóãèõ ïàðàìåòðîâ ñèñòåìû ñîñòàâëÿþùèå ñâîáîäíîé ýíåðãèè, îáóñëîâëåííûå êîìáèíàòîðíûìè ÷ëåíàìè (ñâîáîäíûå ýíåðãèè èäåàëüíîãî
ñìåøåíèÿ è ñìåøåíèÿ ìîëåêóë ðàçëè÷íûõ ðàçìåðîâ), äîëæíû ëèíåéíî âîçðàñòàòü (ïî àáñîëþòíîé
âåëè÷èíå).  ðåàëüíûõ óñëîâèÿõ ïðè ïîâûøåíèè
òåìïåðàòóðû óìåíüøàþòñÿ ýíåðãèè âçàèìîäåéñòâèÿ àññîöèàò - àññîöèàò è öåïü - ÍÌÑ. Ýòî äîëæíî ïðèâåñòè ê áîëåå ÷åì ëèíåéíîìó âîçðàñòàíèþ
ñòåïåíè äîïîëíèòåëüíîé äèññîöèàöèè. Î÷åâèäíî,
÷òî ñóùåñòâóþò ìèíèìàëüíàÿ òåìïåðàòóðà, âûøå
êîòîðîé ÍÌÑ ïîëíîñòüþ äèññîöèèðîâàíî, è ìàêñèìàëüíàÿ òåìïåðàòóðà, íèæå êîòîðîé äîïîëíèòåëüíàÿ äèññîöèàöèÿ ÍÌÑ íå íàáëþäàåòñÿ. Ñëåäîâàòåëüíî, çàâèñèìîñòü ñòåïåíè äèññîöèàöèè àññîöèèðîâàííîãî ðàñòâîðèòåëÿ (a) îò òåìïåðàòóðû â
ïðèñóòñòâèè öåïíûõ ìîëåêóë èëè ïîâåðõíîñòè
ðàçäåëà ôàç èìååò S-îáðàçíûé âèä (ðèñ. 2).
Òàê êàê îáû÷íî îáðàáîòêà òåêñòèëüíûõ ìàòåðèàëîâ âåäåòñÿ â ïðèñóòñòâèè ðàñòâîðèòåëÿ, òî íåîáõîäèìî ó÷èòûâàòü, ÷òî êîíöåíòðàöèè âåùåñòâ â
îáúåìå è âáëèçè ïîâåðõíîñòè ðàçäåëà ôàç è/èëè
öåïíûõ ìîëåêóë ìîãóò ðàçëè÷àòüñÿ. Ïðèìåð îöåíêè êîíöåíòðàöèè ÍÌÑ è åãî àññîöèèðîâàííîé ôîðìû â îáúåìå è âáëèçè öåïè ïî ýêñïåðèìåíòàëüíûì
äàííûì ïðèâåäåí â ðàáîòå [1]. Âñëåäñòâèå òîãî, ÷òî
äîïîëíèòåëüíàÿ äèññîöèàöèÿ è îðèåíòàöèÿ îáóñëîâëåíà òîëüêî ÍÌÑ, íàõîäÿùèìèñÿ âáëèçè öåïè
èëè ïîâåðõíîñòè ðàçäåëà ôàç, òî ÷åì âûøå âçàèìîäåéñòâèå àññîöèàòà ñ öåïüþ, òåì ìåíüøå âûðàæåíû äàííûå ïðîöåññû. Ñ ðîñòîì êîíöåíòðàöèè
ÍÌÑ êîëè÷åñòâî ìîëåêóë, îêðóæàþùèõ öåïü, óâåëè÷èâàåòñÿ, è â ïðåäåëå öåïè îêðóæàþòñÿ òîëüêî
ÍÌÑ.
a
1
T
Ðèñ. 2. Çàâèñèìîñòü ñòåïåíè äèññîöèàöèè ÍÌÑ â
ïðèñóòñòâèè öåïíûõ ìîëåêóë îò òåìïåðàòóðû
36
ÒÅÊÑÒÈËÜÍÀß ÕÈÌÈß, 1998, ¹ 1 (13)
×åì ñèëüíåå âçàèìîäåéñòâèå ìåæäó ìîëåêóëàìè â àññîöèàòå, òåì ñëàáåå ïðè ïðî÷èõ ðàâíûõ
óñëîâèÿõ âûðàæåíà äîïîëíèòåëüíàÿ äèññîöèàöèÿ.
Î÷åâèäíî, ÷òî óìåíüøåíèå ñâîáîäíîé ýíåðãèè
îáðàçîâàíèÿ ñèñòåìû çà ñ÷åò äîïîëíèòåëüíîé äèññîöèàöèè è îðèåíòàöèè ÍÌÑ ïðèâîäèò ê åå ñòàáèëèçàöèè, à ñëåäîâàòåëüíî, è ê ñòàáèëèçàöèè îòäåëüíûõ êîìïîíåíòîâ ñèñòåìû.
Èñïîëüçîâàíèå äàííûõ ÿâëåíèé â òåêñòèëüíîé
õèìèè áûëî íà÷àòî ñ ïðîöåññà áåëåíèÿ õëîï÷àòîáóìàæíûõ òêàíåé [9]. Ïðåäâàðèòåëüíî áûë ðåøåí
âîïðîñ î ñòàáèëèçàöèè ïåðîêñèäà âîäîðîäà äîáàâêàìè ïîëèýòèëåíãëèêîëÿ. Â ðåçóëüòàòå ïðåäëîæåí
è ðåàëèçîâàí íà ïðàêòèêå áåññèëèêàòíûé ìåòîä ïåðåêèñíîãî áåëåíèÿ òåêñòèëüíûõ ìàòåðèàëîâ, èíòåíñèôèöèðóþùèé ïðîöåññ â 1,5-2 ðàçà è óëó÷øàþùèé ïîêàçàòåëè êà÷åñòâà òåêñòèëüíûõ ìàòåðèà-
ëîâ (êàïèëëÿðíîñòü, ñòåïåíü áåëèçíû) [10].
Ñóùåñòâåííàÿ ñòàáèëèçàöèÿ ïåðîêñèäà âîäîðîäà áûëà äîñòèãíóòà ïðè äîáàâêàõ ëèíåéíûõ (ïîëèýòèëåíãëèêîëü, ïîëèâèíèëîâûé ñïèðò) è òðåõìåðíûõ (êàòèîíèòû ÊÓ-2õ8, ÊÁ-4Ï2) ïîëèìåðîâ [11].
Ê ñîæàëåíèþ, äðóãèå íàïðàâëåíèÿ èñïîëüçîâàíèÿ
îïèñàííûõ ïðîöåññîâ â òåêñòèëüíîé õèìèè àâòîðó íåèçâåñòíû, õîòÿ î÷åâèäíî, ÷òî îíè èìåþò áîëåå øèðîêîå çíà÷åíèå. Íàïðèìåð, äàííûå ïðîöåññû íåîáõîäèìî ó÷èòûâàòü ïðè àíàëèçå ïðîïóñêàíèÿ âëàãè ÷åðåç òêàíè.
Åñòåñòâåííî, ýòè ïðîöåññû äîëæíû ó÷èòûâàòüñÿ è áûòü èñïîëüçîâàíû è â äðóãèõ ïðîöåññàõ, íàïðèìåð, â êàòàëèçå [12], ìåìáðàííûõ òåõíîëîãèÿõ, êîòîðûå òàê èëè èíà÷å ñâÿçàíû ñ ïðîèçâîäñòâîì, ïåðåðàáîòêîé è èñïîëüçîâàíèåì òåêñòèëüíûõ èçäåëèé.
ËÈÒÅÐÀÒÓÐÀ
1. Âàéíøòåéí Ý.Ô., Ñòîâáóí Å.Â. Î âîçìîæíîñòè äîïîëíèòåëüíîé äèññîöèàöèè ìîëåêóë íèçêîìîëåêóëÿðíûõ ñîåäèíåíèé â ïðèñóòñòâèè öåïíûõ ìîëåêóë / Â ñá. «Ñâîéñòâà
âåùåñòâ è ñòðîåíèå ìîëåêóë», Êàëèíèí, Êàëèíèíñêèé ãîñ.óíèâåðñèòåò, 1984, ñ. 55-59.
2. Vainstein E.F. Polymer Yearbook, 1991, ¹ 8, p. 85-113.
3. Guggenheim E.M. Mixtures, Oxford, Clarendon Press, 1952, p. 272.
4. Staverman A.I. Rec.Trav. Chim Phys-Pays. Bas., 1950, ¹ 69, p. 163.
5. Prigogine I. The Molecular Theory of solution, Amsterdam, North Holland Publ. Co.,
1957, p. 448.
6. Flory P.I. J. Chem. Phys., 1942, v. 19, p. 51.
7. Huggins M.L., Ann. N.Y.Acad. Sci, 1942, v.43, Art.I, p. 1.
8. Ìîðà÷åâñêèé À.Ã., Ñìèðíîâà È.À., Áàëàøîâà È.Ì. è äð. Òåðìîäèíàìèêà ðàçáàâëåííûõ ðàñòâîðîâ íåýëåêòðîëèòîâ, Ë., Õèìèÿ, 1982, 240 ñ.
9. Ïàâëîâà Â.Â., Ïàâëîâ Í.Í., Àðòåìîâ À.Â., Âàéíøòåéí Ý.Ô. Âëèÿíèå äîáàâîê ïîëèýòèëåíîêñèäà íà ïðîöåññ áåëåíèÿ õëîï÷àòîáóìàæíûõ òêàíåé / Íàó÷íî-òåõí. êîíô. «Ïóòè
ðàçâèòèÿ íàó÷íî-òåõíè÷åñêîãî ïðîãðåññà â òåêñòèëüíîé ïðîìûøëåííîñòè». Òåç. äîêë.,
Òáèëèñè, 1986, ñ. 152-155.
10. Ïàâëîâà Â.Â., Ïàâëîâ Í.Í., Àðòåìîâ À.Â. Ïîâûøåíèå êà÷åñòâà è ýêîíîìè÷íîñòè
ïðîöåññà ïåðåêèñíîé îòáåëêè õëîï÷àòîáóìàæíûõ òêàíåé / Íàó÷íî-òåõí. êîíô. «Íîâûå
òåõíè÷åñêèå è òåõíîëîãè÷åñêèå ðàçðàáîòêè è èõ âíåäðåíèå â òåêñòèëüíîé è ëåãêîé ïðîìûøëåííîñòè». Òåç.äîêë., Èâàíîâî, 1989, ñ. 141.
11. Ãàðèíà Î.Â., Ãàëàøèíà Â.Ì., Êëþåâ Ì.Â. Ñòàáèëèçàöèÿ âîäíûõ ðàñòâîðîâ ïåðîêñèäà âîäîðîäà â ïðèñóòñòâèè ïîëèìåðîâ / II Êîíãðåññ õèìèêîâ-òåêñòèëüùèêîâ è êîëîðèñòîâ. Òåç.äîêë., Èâàíîâî, 1996, ñ. 29.
12. Ïîìîãàéëî À.Ä., Âàéíøòåéí Ý.Ô. Óñïåõè è ïðîáëåìû â ñîçäàíèè ìåòàëëîïîëèìåðíûõ êàòàëèçàòîðîâ /  ñá. «Êîìïëåêñíûå ìåòàëëîîðãàíè÷åñêèå êàòàëèçàòîðû ïîëèìåðèçàöèè îëåôèíîâ». Âûï. XI, ×åðíîãîëîâêà, 1991, ñ. 9-32.
Èíñòèòóò áèîõèìè÷åñêîé ôèçèêè
èì. Í.Ì.Ýìàíóýëÿ ÐÀÍ,
ã. Ìîñêâà
Ïîëó÷åíî 17.01.98 ã.