Belyavskiy S.S._2013 T2 349-350

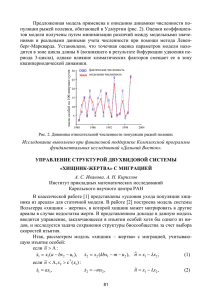
1. Н ормативны й докум ент систем ы технической защ иты информации.
К ритерии оценки защ ищ енности информации в ком пью терны х систем ах от
несанкционированного доступа: НД ТЗИ 2 .5 -0 04 -19 99. — К іів: ДСТСЗІ СБ
У краш и, 1999. — 45 с.
2. А удит и информационная безопасность / А .П . Ф исун, А .Н . Касилов,
Ю .А . Глоба [и др.]. — М .: П риоритет-издат, 2005. — 272 с.
3. М енедж мент інф ормаційноі безпеки в галузі зв ’ язку: навч. посіб. /
Т.М . Тардаскіна, В.Г. К ононович. — Одеса: ОНАЗ ім. О.С. П опова, 2010. —
268 с.
С.С. Белявский, канд. физ.-мат. наук, доцент
БГЭУ (Минск)
НЕКОТОРЫЕ ЗАДАЧИ О РАЦИОНАЛЬНОМ
ИСПОЛЬЗОВАНИИ РЫБНЫХ РЕСУРСОВ
Рассмотрим задачу о рациональном использовании рыбных ресур­
сов в двух постановках — дискретной и непрерывной.
Будем предполагать, как и в [1], что в отсутствие лова плотность по­
пуляции рыб определяется уравнением Nt+1 = f(Nt), где / — некоторая
заданная функция. Если щ — количество выловленной рыбы в l-м году
(/ = 0 , 1, 2 , ...), то численность рыбы в (/ + 1)-м году определится следу­
ющим образом:
м м = т , ) - и,
( 1)
Пусть в начальный период популяция составляет N q —А. Требуется
разработать план вылова на Т лет таким образом, чтобы в конечный пе­
риод рыбные ресурсы составляли В единиц и суммарная прибыль от
улова за этот период была максимальной.
Решение этой проблемы может быть сведено к задаче оптимально­
го управления с закрепленными концами. Требуется найти сеточные
функции Nf и uty t —0, 1, 2, ..., Т -1 , удовлетворяющие уравнению (1) и
граничным условиям
N0 =A,
NT = В,
и доставляющие максимум функционала
Т-1
->■т а х t=о
При этом предполагается, что Nf > 0, 0 < uf < Nf, t = 0 ,1 , 2, ..., Т -1 .
На функцию g(ii), которая описывает зависимость прибыли от улова,
налагаются условия: §'(и) > 0 , g"(u) < 0 .
Используя дискретный принцип максимума [2], получено решение
задачи в двух частных случаях, когда функция f(N t) линейная и квад­
ратичная.
Теперь рассмотрим задачу о рациональном использовании рыбных ре­
сурсов в непрерывном случае. Предполагается, что в одной среде обитания
имеются два вида популяций — хищники и жертвы. В отсутствие лова
плотность популяции рыб определяется отношением «хищник—жертва»
(модель Вольтера—Лотка) (см., например, [3]). Если лов жертв ведется
с интенсивностью и, а хищников — с интенсивностью v, то процесс изме­
нения популяции хищников и жертв может быть записан в виде
(2)
где Ni жN 2 — число жертв и хищников соответственно.
Для системы (2) ставится задача об оптимальном управлении с за­
крепленными концами
iVi(O) = A ,, N ^ T ) = А т, N 2( 0) = В 0, N 2(T) = В т,
(3)
т
max.
(4)
0
Последний интеграл задает суммарную прибыль, полученную от до­
бычи рыбы за промежуток времени [О, Т\.
Для задачи (2)—(4) построена компьютерная модель в системе
MatLab.
Литература
1. Мюррей, Дж. Математическая биология: в 2 т. / Дж. Мюррей. —
М., 2009. — Т. 1. — 774 с.
2. Ногин, В Д . Введение в оптимальное управление / В.Д. Ногин. —
СПб.: ЮТ АС, 2008.
3. Волыперра, В. Математическая теория борьбы за существова­
ние / В. Вольтерра. — М.: Наука, 1976.
А.О. Брилеве кий, магистр экон. наук
БГЭУ (Минск)
ИНТЕРАКТИВНЫЙ МОДУЛЯТОР МАРШРУТОВ
Крупные компании с большим ассортиментом продукции, огром­
ным числом клиентов, производственных предприятий и складов, с
350
.
.
БДЭУ Беларускі дзяржаўны эканамічны ўніверсітэт. Бібліятэка.
БГЭУ Белорусский государственный экономический университет. Библиотека.
BSEU Belarus State Economic University. Library.
http://www.bseu.by
[email protected]