1. Состав и размер ядра. NZ диаграмма атомных ядер. Черными

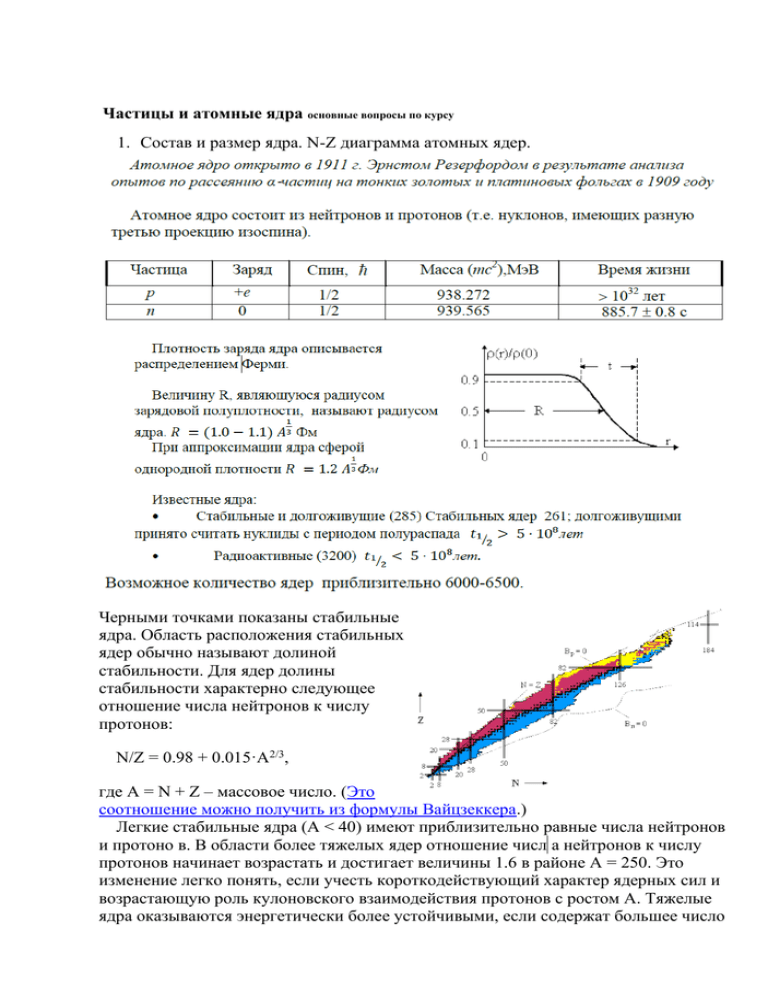
Частицы и атомные ядра основные вопросы по курсу
1. Состав и размер ядра. N-Z диаграмма атомных ядер.
Черными точками показаны стабильные
ядра. Область расположения стабильных
ядер обычно называют долиной
стабильности. Для ядер долины
стабильности характерно следующее
отношение числа нейтронов к числу
протонов:
N/Z = 0.98 + 0.015·A2/3,
где A = N + Z – массовое число. (Это
соотношение можно получить из формулы Вайцзеккера.)
Легкие стабильные ядра (А < 40) имеют приблизительно равные числа нейтронов
и протоно в. В области более тяжелых ядер отношение числ а нейтронов к числу
протонов начинает возрастать и достигает величины 1.6 в районе А = 250. Это
изменение легко понять, если учесть короткодействующий характер ядерных сил и
возрастающую роль кулоновского взаимодействия протонов с ростом А. Тяжелые
ядра оказываются энергетически более устойчивыми, если содержат большее число
нейтронов N по сравнению с числом протонов Z. Наиболее тяжелыми стабильными
ядрами являются изотопы свинца (Z = 82) и висмут (Z = 83). С левой стороны от
стабильных ядер находятся ядра, перегруженные протонами (протоноизбыточные
ядра), справа - ядра, перегруженные нейтронами (нейтроноизбыточные ядра).
Ядра, сильно перегруженные нейтронами или протонами, обычно
называют экзотическими ядрами. Более темным цветом на рис.1.1 выделены
атомные ядра, обнаруженные в настоящее время.
Пунктирная линия очерчивает область возможного существования атомных ядер.
Связанное состояние ядра определяется как состояние, стабильное относительно
испускания нейтронов или протонов, т.е. считается, что атомное ядро существует,
если оно не испускает нуклоны из основного состояния. Линия Bp = 0 (Bp - энергия
отделения протона) ограничивает область существования атомных ядер слева
(proton drip-line). Линия Bn = 0 (Bn - энергия отделения нейтрона) - справа (neutron
drip-line). Вне этих границ атомные ядра существовать не могут, так как они
распадаются за характерное ядерное время (~ 10-23 c) с испусканием одного или
нескольких нуклонов. Если среднее время жизни ядра τ < 10-22 с, обычно считается,
что ядра не существуют. Характерные времена жизни для радиоактивных ядер
τ > 10-14 c
2. Масса и энергия связи ядра. Формула Вайцзеккера.
Пятый член учитывает эффект спаривания нуклонов одного типа, находящихся на
одном энергетическом уровне. С точки зрения эффекта существуют три типа ядер:
четно-четные (все нуклоны спарены, энергия эффекта максимальна, α=+34МэВ)
нечетно-нечетные (по одному нуклону каждого типа не спарены, энергия эффекта
наименьшая) α=-34МэВ)
чётно-нечетные и нечётно-чётные (промежуточный случай, по договоренности
Е=0. α=0)
3. Радиоактивный распад ядер. Законы радиоактивного распада ядра.
Способность ядер самопроизвольно распадаться, испуская частицы, называется
радиоактивностью. Процесс распада - по своей природе процесс статистический.
Виды распада:
альфа-распад - распад атомных ядер, сопровождающийся испусканием альфачастиц (ядер 4He).
бета-распад - спонтанное превращение ядра (A,Z) в ядро-изобар (A,Z+1) в
результате испускания лептонов (электрон и антинейтрино, позитрон и нейтрино), либо
поглощения электрона с испусканием нейтрино (е-захват).
гамма-распад- испускание гамма квантов при переходе ядра из возбуждённого
состояния в основное, и др.
спонтанное деление- самопроизвольное деление ядер на осколки.
К более редким видам радиоактивного распада относятся процессы испускания ядром
двух электронов, одного или двух протонов, а также кластеров – лёгких ядер
от 12C до 32S.
4. Альфа-распад. Кулоновский и центробежный барьеры.
При взаимодействии с ядрами частиц с орбитальным моментом l ≠ 0 возникает
центробежный барьер. Высота центробежного барьера
где - приведенная постоянная Планка,
частицы, R - радиус ядра.
и m- приведенная и обычная массы
Для заряженных частиц наряду с центробежным
потенциалом необходимо учитывать также
кулоновский потенциал. Высота кулоновского
потенциала на границе ядра
где Z, z - атомные номера взаимодействующих
частицы и ядра, R -радиус ядра, е - заряд
электрона. Для протонов за исключением совсем
легких ядер Bk > Bц(l = 1). Учитывая, что R = r0A1/3
1.3 Фм и e2 1.4 Мэв·Фм, можно переписать
(5.3) в виде
МэВ
5.Бета-распад. Экспериментальное обнаружение (анти)нейтрино.
β-распад, также как и α-распад, происходит между дискретными состояниями
начального (A,Z) и конечного (A,Z±1) ядер. Поэтому долгое время после открытия
явления β-распада было непонятно, почему спектры электронов и позитронов,
вылетающих из ядра при β-распаде были непрерывными, а не дискретными, как
спектры α-частиц.
На рис. показаны спектры электронов и антинейтрино, образующихся при β-распаде изотопа40K.
Рис. 3.1. Спектры электронов и антинейтрино, образующихся при β--распаде
изотопа 40K,
40
K → 40Ca + e- + e.
Считалось даже, что в β-распаде не выполняется закон сохранения энергии.
Объяснение непрерывного характера β-спектра было дано В. Паули, который
высказал гипотезу, что при β-распаде вместе с электроном рождается ещё одна
частица с маленькой массой, т.е. β-распад − трехчастичный процесс. В конечном
состоянии образуется ядро (A,Z±1), электрон и лёгкая нейтральная частица –
нейтрино (антинейтрино). Т.к. масса ядра (A,Z±1) гораздо больше масс электрона и
нейтрино, энергия β-распада уносится лёгкими частицами. Распределение энергии
β-распада Qβ между электроном и этой нейтральной частицей приводит к
непрерывному β-спектру электрона.
Из закона сохранения энергии следует, что спектр антинейтрино зеркально
симметричен спектру электронов.
Nν(E) = Ne(Qβ – E),
где Nν(E) − число антинейтрино с энергией Е, Ne(Qβ – E) − число электронов с
энергией (Qβ – E), Qβ− энергия β-распада, равная суммарной энергии, уносимой
электроном и антинейтрино (энергия ядра отдачи 40Ca не учитывается).
Наряду с законами сохранения энергии, импульса, момента количества движения
в процессе β-распада выполняются законы сохранения барионного B и электронного
лептонного Le квантовых чисел.



Электроны, нейтрино имеют B = 0, Le = +1.
Позитроны, антинейтрино имеют B = 0, Le = −1.
Каждый нуклон, входящий в состав ядра, имеет B = +1, Le = 0.
Поэтому появление электрона при β--распаде всегда сопровождается
образованием антинейтрино. При β+-распаде образуются позитрон и нейтрино.
При е-захвате из ядра вылетают нейтрино. Так как е-захват – двухчастичный
процесс, спектры нейтрино и ядра отдачи являются дискретными. Наблюдение
дискретного спектра ядер отдачи, образующихся при е-захвате, было первым
подтверждением правильности гипотезы Паули.
β-радиоактивные ядра имеются во всей области значений массового числа A,
начиная от единицы (свободный нейтрон) и кончая массовыми числами самых
тяжелых ядер.
За счет того, что интенсивность слабых взаимодействий, ответственных за βраспад, на много порядков меньше ядерных, периоды полураспада β-радиоактивных
ядер в среднем имеют порядок минут и часов. Для того чтобы выполнялись законы
сохранения энергии и углового момента при распаде нуклона внутри ядра, оно
должно перестраиваться. Поэтому период, а также другие характеристики β-распада
в сильной степени зависят от того, насколько сложна эта перестройка. В результате
периоды β-распада варьируются почти в столь же широких пределах, как и периоды
α-распада. Они лежат в интервале T1/2(β) = 10-6 с – 1017 лет.
6. Гамма-переходы в ядрах. Электрические и магнитные гамма-переходы.
Изменения состояний атомных ядер,
сопровождающиеся испусканием или
поглощениемγ-квантов, называют γпереходами. Примерные границы периодов
полураспада для γ-переходов от 10-19 с до
1010 лет. Энергии γ-переходов изменяются
от нескольких кэВ до нескольких МэВ
Законы сохранения энергии E, момента
количества движения (спина) J и четности P
приγ-переходах в атомных ядрах требуют
выполнения следующих соотношений:
Ei = Ef + Eγ + TR, i = f + , Pi = PfP,
где Ei, Ef, i, f, Pi, Pf − энергии, спины и четности начального и конечного
состояний ядер, Eγ, , P − энергия, спин и четность фотона, TR − кинетическая
энергия ядра отдачи:
где E0 = Ei - Ef − энергия γ-перехода, MR − масса ядра отдачи.
Полный момент количества движения фотона J называется мультипольностью.
Значение спина фотона Jmin = 1. Поэтому, полный момент J уносимый фотоном
может принимать целочисленные значения 1, 2, ... (кроме нуля).
Различают электрические (EJ) и магнитные (MJ) переходы. Е1 − электрический
дипольный переход, М1 − магнитный дипольный переход, Е2 − электрический
квадрупольный переход и т.д.
В зависимости от чётности при определенном значении полного момента J γкванты различают по типу на магнитные и электрические:
P = (-1)J+1 – магнитные γ-кванты (МJ);
P = (-1)J – электрические γ-кванты (ЕJ).
Названия «магнитный» и «электрический» происходят от типа систем зарядов и
токов, излучающих соответствующие γ-кванты. Так, при колебании электрического
диполя испускаемое электромагнитное излучение с квантовой точки зрения состоит
из E1 γ-квантов. Колеблющийся магнитный диполь испускает M1 γ-кванты и т. д.
Правила отбора по чётности для γ-переходов имеют вид:
Pi ·Pf = (-1)J для EJ γ-квантов;
Pi ·Pf = (-1)J+1 для MJ γ-квантов.
В случае γ-переходов большой диапазон периодов полураспада объясняется
сильной зависимостью вероятности γ-перехода от энергии и мультипольности
переходов. Период полураспада T1/2γ-переходов зависит от мультипольности
перехода J и длины волны излучения .
Для электрических переходов EJ ,
для магнитных переходов MJ ,
где R − радиус ядра.
7. Дейтрон - связанное состояние нейтрона и протона.
Дейтрон (2Н) - это связанная система протон-нейтрон. Дейтрон стабилен и не
имеет возбуждённых состояний. Характеристики дейтрона приведены в таблице.
Спин дейтрона определяется векторной суммой спина протона sp, спина нейтрона
sn и их относительного орбитального момента L
(2H) =
p
+
n
+
.
Так как чётность дейтрона P = +1, а чётности протона и нейтрона положительны, L
может принимать только значения L = 0 и 2. Возможные ориентации спинов и
орбитальных моментов дейтрона показаны на рис. 1.
Дейтроны постоянно образуются в природе при захвате тепловых нейтронов
свободными протонами в водородсодержащих средах:
Однако бо́льшая часть всех дейтронов во Вселенной образовалась (в основном по
этой же реакции) во время первичного нуклеосинтеза в первые несколько минут
после Большого Взрыва.
В дейтроне действуют тензорные силы. Они зависят от величины проекций спинов
s1 и s2, нуклонов на направление единичного вектора , направленного от одного
нуклона дейтрона к другому. Положительный квадрупольный момент дейтрона
(вытянутый эллипсоид) соответствует притяжению нуклонов, сплюснутый
эллипсоид - отталкиванию.
8. Свойства нуклон-нуклонного взаимодействия.
Обменный характер нуклон-нуклонного взаимодействия проявляется при рассеянии
нейтронов высоких энергий (несколько сот МэВ) на протонах.
Свойства ядерных сил
1. Малый радиус действия ядерных сил (a ~ 1 Фм).
2. Большая величина ядерного потенциала V ~ 50 МэВ.
3. Зависимость ядерных сил от спинов взаимодействующих частиц.
4. Тензорный характер взаимодействия нуклонов.
5. Ядерные силы зависят от взаимной ориентации спинового и орбитального
моментов нуклона (спин-орбитальные силы).
6. Ядерное взаимодействие обладает свойством насыщения.
Свойство насыщения - каждый нуклон взаимодействует с ограниченным
числом нуклонов.
7. Зарядовая независимость ядерных сил.
8. Обменный характер ядерного взаимодействия.
9. Притяжение между нуклонами на больших растояниях (r > 1 Фм) сменяется
отталкиванием на малых (r < 0.5 Фм).
Нуклон-нуклонный потенциал имеет вид (без обменных членов)
Рис. 4. Нуклон-нуклонный
потенциал
V = V1(r) + V2(r)(
1 2)
+ V3(r)(
1
)(
2
) + V4(r)(
). (6)
Первое слагаемое описывает зависимость ядерного взаимодействия от расстояния
между нуклонами Второе слагаемое описывает зависимость ядерного
взаимодействия от спинов нуклонов Третье слагаемое описывает тензорный
характер ядерных сил. Четвертое слагаемое описывает зависимость ядерных сил от
взаимной ориентации спинового и орбитального моментов нуклона. Кроме того в
полное выражение для нуклон-нуклонного потенциала необходимо добавить еще 4
аналогичных члена, учитывающих обмен протона и нейтрона.
9. Мезонная теория ядерных сил.
Согласно модели Юкавы, механизм ядерного взаимодействия заключается в обмене
виртуальным мезоном между нуклонами. За время ядерного взаимодействия t
вблизи нуклона образуется виртуальный мезон с массой m. Используя соотношение
неопределенности
(1)
Δt·ΔE > ,
можно оценить величину массы виртуального мезона
(2)
m = ΔE/c2 = /c2Δt.
За время взаимодействия виртуальный мезон отойдет от нуклона на расстояние
(3)
a = cΔt = c /ΔE = /mc.
a - радиус ядерного взаимодействия.
Время ядерного взаимодействия Δt и массу мезона m можно оценить, используя
(3) и (2) Δt = a/c = 1.4·10-13/3·1010 ~ 0.5·10-23 c,
mc2 = /Δt = 6.6·10-22/0.5·10-23 ~ 130 МэВ.
Экспериментально измеренные массы -мезонов близки к этой оценке.
Потенциал ядерного взаимодействия при r > 1 Фм (потенциал Юкавы) имеет вид
(4)
V(r) = -(gяд/r)exp(-r mc/ ),
где gяд - константа ядерного взаимодействия (аналог элементарного заряда e в
электромагнитном взаимодействии). Константа ядерного взаимодействия (константа
связи)
g2яд/ c ~ 10.
За взаимодействие между нуклонами на малых
расстояниях ответственны также и более
тяжелые мезоны η (549 МэВ)(a ~ 0.36 Фм),
ρ (770 МэВ) и ω (782 МэВ) (a ~ 0.25 Фм); ρ и ω
мезоны определяют отталкивающий характер
нуклон-нуклонного потенциала на малых
расстояниях (r < 0.3 Фм).
Нуклон-нуклонный потенциал
На кварковом уровне описание p-n
взаимодействия с обменом π-мезоном показано на рисунке ниже.
p-n взаимодействие с обменом
Частица
Кварковый
состав
-мезоном
Масса,
Mc2
(МэВ)
Время жизни
(сек)
Спин-четность,
изоспин
JP(I)
Основные моды
распада
π+,π-
u ,d
139.57
2.6·10-8
0-(1)
ν μ+, μ-
π0
u -d
134.98
8.4·10-17
0-(1)
2γ
10. Ядерные реакции. Законы сохранения, кинематика.
Я́ дерная реа́кция — это процесс взаимодействия атомного ядра с другим ядром или
элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением
большого количества энергии.
1.
2.
3.
4.
5.
Закон сохранения электрического заряда.
Закон сохранения числа нуклонов.
Закон сохранения энергии.
Закон сохранения импульса.
Закон сохранения момента количества движения.
Эти пять законов сохранения выполняются во всех типах реакций, идущих под
действием ядерных электромагнитных и слабых взаимодействий. В реакциях
идущих в результате ядерных и электромагнитных взаимодействий выполняются
также:


Закон сохранения пространственной четности.
В сильных и электромагнитных взаимодействиях пространственная четность
P сохраняется. В слабых взаимодействиях пространственная четность не
сохраняется. Закон сохранения четности - мультипликативный закон. Для
ядерной реакции a + A b + B можно записать
,
В реакциях идущих в результате ядерных взаимодействий выполняется:

Закон сохранения изотопического спина и его проекции.
Если процесс происходит в результате сильного взаимодействия, то
суммарный изоспин и его проекция Iz сохраняются. В электромагнитных
процессах сохраняется только проекция изоспина. В слабых взаимодействиях
изоспин и его проекция не сохраняются. Для электромагнитных дипольных
переходов выполняется правило отбора I = 0, 1. Закон сохранения
изотопического спина - аддитивный закон.
Для реакции a + A b + B, идущей через сильное взаимодействие
a
+
A
=
b
+
B,
11. Механизмы ядерных реакций. Прямые реакции. Составное ядро.
12. Деление ядер.
Деление атомных ядер было открыто при бомбардировке нейтронами ядер урана.
Расчитывали получить трансурановые элементы, однако Ган иШтрассман после
тщательного химического анализа образующихся элементов обнаружили среди них
атомы среднего веса. Мейтнер и Фриш предположили, что ядра урана после захвата
нейтрона делятся на два примерно равных по массе осколка.
Наибольшую устойчивость имеют ядра с А = 40-120, т.е. находящиеся в середине
периодической таблицы. Энергетически выгодными являются процессы соединения
(синтеза) легких ядер и деления тяжелых ядер. В обоих случаях конечные ядра
располагаются в той области значений А, где удельная энергия связи большее, чем
удельная энергия связи начальных ядер.
Оценка энергии, освобождающейся при делении, может быть получена
непосредственно изформулы Вайцзеккера. При делении ядра на два осколка
изменяются поверхностная энергия Еп = а2А2/3 и кулоновская энергия Eк = aзZ2/A1/3,
причем поверхностная энергия увеличивается, а кулоновская энергия уменьшается.
Деление возможно в том случае, когда энергия, высвобождающаяся при делении
Е > 0.
Здесь A1 = 2A2, Z1 = 2Z2, индех 1 – делящееся ядро, 2 – осколки деления. Отсюда
получим, что деление энергетически выгодно, когда Z2/A > 17. Величина Z2/A
называется параметром делимости. Энергия Е, освобождающаяся при делении,
растет с увеличением Z2/A.
В процессе деления ядро изменяет форму последовательно проходит через следующие стадии
(рис.2): шар, эллипсоид, гантель, два грушевидных
Рис.2. Изменение формы
осколка, два сферических осколка. Как меняется
ядра в процессе деления
потенциальная энергия ядра на различных стадиях
деления? После того как деление произошло, и осколки
находятся друг от друга на расстоянии, много большем их радиуса, потенциальную
энергию осколков, определяемую кулоновским взаимодействием между ними,
можно считать равной нулю.
Вследствие эволюции формы ядра изменение его потенциальной энергии
определяется изменением суммы поверхностной и кулоновской энергий Е'п + Е'к.
Предполагается, что объем ядра в процессе деформации остается неизменным.
Поверхностная энергия Е'п при этом возрастает, так как увеличивается площадь
поверхности ядра. Кулоновская энергия Е'к уменьшается, так как увеличивается
среднее расстояние между нуклонами. В случае малых эллипсоидальных
деформаций рост поверхностной энергии происходит быстрее, чем уменьшение
кулоновской энергии.
В области тяжелых ядер сумма поверхностной и кулоновской энергий
увеличивается с увеличением деформации. При малых эллипсоидальных
деформациях рост поверхностной энергии препятствует дальнейшему изменению
формы ядра, а, следовательно, и делению. Наличие потенциального барьера
препятствует мгновенному самопроизвольному делению ядер. Для того чтобы ядро
мгновенно разделилось, ему необходимо сообщить энергию Q, превышающую
высоту барьера деления Н.
Высота барьера Н тем больше, чем меньше отношение кулоновской и
поверхностной энергии Ек/Еп в начальном ядре. Это отношение, в свою очередь,
увеличивается с увеличением параметра делимости Z2/А Чем тяжелее ядро, тем
меньше высота барьера Н, так как параметр делимости увеличивается с ростом
массового числа:
Ек/Еп = (a3Z2)/(a2A) ~ A.
Более тяжелым ядрам, как правило, нужно сообщить меньшую энергию, чтобы
вызвать деление. Из формулы Вайцзеккера следует, что высота барьера деления
обращается в нуль при Z2/A > 49. Т.е. согласно капельной модели в природе должны
отсутствовать ядра с Z2/А > 49, так как они практически мгновенно (за характерное
ядерное время порядка 10-22 с) самопроизвольно делятся. Существование атомных
ядер с Z2/А > 49 ("остров стабильности") объясняется оболочечной структурой
атомных ядер. Зависимость формы, высоты потенциального барьера H и энергии
деления E от величины параметра делимости Z2/А показана на рис. 3.
Рис.3. Зависимость формы, высоты потенциального барьера H и энергии
деления E от величины параметра делимости Z2/А
Самопроизвольное деление ядер с Z2/А < 49, для которых высота барьера Н не
равна нулю, с точки зрения классической физики невозможно. С точки зрения
квантовой механики такое деление возможно в результате прохождения осколков
через потенциальный барьер и носит названиеспонтанного деления. Вероятность
спонтанного деления растет с увеличением параметра делимости Z2/А, т.е. с
уменьшением высоты барьера деления. Вынужденное деление ядер с Z2/А < 49
может быть вызвано любыми частицами: фотонами, нейтронами, протонами,
дейтронами, -частицами и т.д., если энергия, которую они вносят в ядро достаточна
для преодоления барьера деления.
Массы осколков, образующихся при
делении тепловыми нейтронами не
равны. Ядро стремится разделиться
таким образом, чтобы основная часть
нуклонов осколка образовала
устойчивый магический остов. На рис. 4
приведено распределение по массам при
делении 235U. Наиболее вероятная
комбинация массовых чисел - 95 и 139.
Отношение числа нейтронов к числу
протонов в ядре 235U равно 1.55, в то
время как у стабильных элементов,
Рис.4. Массовое распределение осколков
имеющих массу, близкую к массе
осколков деления, это отношение 1.25- деления 235U тепловыми нейтронами
1.45. Следовательно, осколки деления
сильно перегружены нейтронами и неустойчивы к β--распаду - радиоактивны.
В результате деления высвобождается энергия ~200 МэВ. Около 80% ее
приходится на энергию осколков. За один акт деления образуется более
двух мгновенных нейтронов деления со средней энергией ~2 МэВ.
13. Модель ядерных оболочек.
14. Одночастичные и коллективные возбуждения ядер.
15. Фундаментальные частицы Стандартной модели
Стандартная модель - современная теория сильного и электрослабого взаимодействий
фундаментальных фермионов (лептонов и кварков), основанная на инвариантности уравнений
движения к произвольным изменениям координат пространства-времени.
В основе Стандартной модели лежат две теории:
1. Теория (или модель) электрослабого взаимодействия (ЭСМ), описывающая
электромагнитные и слабые взаимодействия лептонов и кварков.
2. Квантовая хромодинамика (КХД), описывающая цветное взаимодействие кварков.
Фундаментальными частицами Стандартной модели являются 6 лептонов (e-, μ-, τ-, νe, νμ, ντ)
и 6 кварков (u, d, c, s, t, b), объединенных в три поколения. Каждый из 6 типов кварков может
находиться в трёх цветовых состояниях (например: красный, зеленый, синий). Кварки и
лептоны являются фермионами и имеют спин J = 1/2. 12-ти фундаментальным фермионам
соответствуют 12 антифермионов.
Таблица 1
Фундаментальные фермионы
Поколения
Взаимодействия
1
лептоны
кварки
2
3
Заряд
Q/e
е
0
e
-1
u
c
t
+2/3
d
s
b
-1/3
Взаимодействия фундаментальных фермионов осуществляются за счет
обмена переносчиками взаимодействия - фундаментальными (или
калибровочными) бозонами. Взаимодействие частиц, имеющих электрический
заряд, происходит посредством обмена квантами электромагнитного поля фотонами. Фотон электрически нейтрален. Сильное взаимодействие
осуществляется за счет обмена глюонами (g) - электрически нейтральными
безмассовыми переносчиками сильного взаимодействия. Глюоны переносят
цветовой заряд. В слабом взаимодействии принимают участие все лептоны и
все кварки. Переносчиками слабого взаимодействия являются массивные W- и
Z-бозоны. Существуют положительные W+-бозоны и отрицательные W-бозоны, являющиеся античастицами по отношению друг к другу. Z-бозон
электрически нейтрален.
Таблица 2. Фундаментальные взаимодействия
Квант Радиус, Константа взаимодействия
Пример
Взаимодействие
поля
см
(порядок величины)
проявления
-13
сильное
глюон
10
1
ядро, адроны
-2
электромагнитное γ-квант
∞
10
атом
±
-16
-6
слабое
W ,Z
10
10
β-распад
16. Законы сохранения в физике частиц
17. Частицы и античастицы.
Антивещество состоит из античастиц – антипротонов , антинейтронов и
антиэлектронов - позитронов е+. Частицы и античастицы равноправны. Выбор того,
какие частицы считать частицами, а какие античастицами, условен и определяется
соображениями удобства. В наблюдаемой части Вселенной вещество состоит из
отрицательно заряженных электронов, положительно заряженных протонов и
нейтронов.
При столкновении электрона и позитрона они исчезают (аннигилируют),
превращаясь в гамма-кванты. При аннигиляции сильновзаимодействующих частиц,
например, протона и антипротона, образуется несколько мезонов π+, π-, π0, K+, K-, K0.
18. Резонансные частицы.
Резонансы - коротко живущие возбужденные состояния адронов, распадающиеся в
результате сильного взаимодействия.
Характерное время жизни резонанса 10-22 - 10-24 с. Впервые резонансы наблюдались
в сечении взаимодействияπ-мезонов с нуклонами.
Масса резонансной частицы m определяется из релятивистского инварианта
mc2 = (E2 - c2p2)1/2,
где E и p - полная энергия и полный импульс π-мезона и нуклона.
Нуклонные резонансы
Δ(1232) имеют спин, четность JP = 3/2+, изоспин I = 3/2. Δ+ и Δ0 можно
рассматривать как возбужденные состояния протона и нейтрона соответственно. По
сравнению с нуклонами, у которых два одинаковых кварка имеют параллельные
спины, а третий кварк имеет антипараллельный спин, у этих резонансов спины всех
кварков параллельны, что дает спин 3/2. У нуклонных резонансов N(1440) JP = 1/2+,
изоспин I = 1/2. Низкорасположенные нуклонные резонансы в основном
распадаются по каналу (n или p) + π. Время жизни резонанса τ определяется из
ширины его распада Г, используя соотношение неопределенности Гτ~ħ. Резонансы
наблюдаются и во взаимодействии π-мезонов с другими адронами.
В таблице приведены основные характеристики Δ(1232) и N(1440) резонансов
Частица
Масса, Mc2
(МэВ)
Ширина
Г, МэВ
Спинчетность, Основные моды
изоспин
распада
P
J (I)
Δ++, Δ+, Δ0, Δ-
1230-1234 (~1232)
115-125
3/2+(3/2)
(n или p) + π
N+, N0, N-
1430-1470 (~1440)
250-450
1/2+(1/2)
n(p)+π(2π), Δπ
Частицы ρ0, ω0, φ0 являются мезонными резонансами, которые обладают
квантовыми числами фотона (JP = 1-), поэтому их можно интерпретировать как
проявление процессов, показанных на рис. 4, 5, 6. Эти мезонные резонансы можно
наблюдать на e+e- -коллайдерах.
Рис. 4.
Масса ρ -мезона 770 МэВ. Ширина распада Г = 151 МэВ.
0
Рис. 5.
Масса ω0-мезона 782 МэВ. Ширина распада Г = 8.4 МэВ.
Рис. 6.
Масса φ0-мезона 1020 МэВ. Ширина распада Г = 4.4 МэВ.
19. Электромагнитные взаимодействия. Структура нуклона.
Электромагнитное взаимодействие
Квантовая электродинамика описывает взаимодействие электронов, мюонов, таулептонов и фотонов - частиц нечувствительных к сильному взаимодействию.
На рис. 1 изображен узел, описывающий электромагнитное
взаимодействие. Константой связи является gэл.
gэл = (e2/ c)1/2 = (1/137)1/2 0.1,
где e - заряд электрона, - приведенная постоянная Планка, c - Рис.1. Узел
скорость света. Этот узел универсален, т.е. не зависит от того, электромагнитного
взаимодействия
как ориентированы его линии относительно оси времени.
На рис. 2 показаны реальные процессы квантовой
электродинамики. Приводятся основныедиаграммы Фейнмана низшего порядка
1. Рассеяние электрона на электроне
Рис. 2.
2. Образование электрон-позитронной пары в кулоновском поле ядра
Рис. 3.
3. Процесс двух и трехфотонной аннигиляции электрона и позитрона
Рис. 4. Основные диаграммы Фейнмана
низшего порядка двух и трехфотонной
аннигиляции
Число узлов на диаграмме Фейнмана называется порядком диаграммы. Сечение
процесса, содержащего диаграмму порядка N пропорционально g2N. Таким образом,
сечение трехфотонной аннигиляции будет подавлено по сравнению с двухфотонной
в 100 раз.
На рис.5-6 показаны диаграммы двухфотонной аннигиляции более высокого
порядка, чем второй.
Рис. 5. Диаграмма четвертого
порядка
Рис. 6. Диаграмма шестого
порядка
Эти процессы будут подавлены еще более сильно по сравнению с двух и
трехфотонной аннигиляцией, приведенной на рис. 4, что определяется числом
вершин на соответствующих диаграммах Фейнмана.
4. Рождение μ+μ- и τ+τ- в процессе e+e--аннигиляции
Рис. 7.
Такие процессы наблюдаются в экспериментах на встречных пучках на электронпозитронных коллайдерах. Пороги реакций
e+e- μ+μ- и e+e- τ+τдолжны превышать энергии покоя соответственно мюона (106 МэВ) и тау-лептона
(1784 МэВ), т.е. энергия каждого из встречных пучков должна быть
[m(μ) - m(e)]c2 и [m(τ) - m(e)]c2.
Структура нуклона.
Результаты исследований показали, что нуклон это частица, состоящая из трех
валентных кварков, виртуальных морских кварков-антикварков и глюонов.
1. Внутри нуклона обнаружены точечные объекты – партоны, в которых
сосредоточена вся масса (внутренняя энергия) нуклона. Размер партонов < 10–
17
см.
2. Заряженные партоны имеют все характеристики кварков – их спин 1/2, а
заряды в единицах елибо +2/3, либо –1/3.
3. Нейтральные партоны, отождествляемые с глюонами, несут около половины
внутреннего импульса (энергии) нуклона.
4. Валентные кварки окружены испускаемыми и поглощаемыми ими
виртуальными глюонами, реализующими межкварковое сильное
взаимодействие. Глюоны рождают виртуальные кварк-антикварковые пары,
аннигилирующие затем вновь в глюоны. Эти виртуальные пары образуют
множество морских кварков.
Уменьшение длины волны виртуального фотона.
Знание внутренней структуры нуклонов даёт информацию о природе сильных
взаимодействий, за счет которых протоны и нейтроны образуют атомные ядра. При
больших значениях длины волн виртуального фотона нуклон выглядит как некий
кор, окруженных облаком виртуальных π-мезонов, Виртуальные π-мезоны
реализуют взаимодействие между нуклонами в атомном ядре. При уменьшении
длины волны, когда она становится сравнимой с разменом нуклона, проявляется
кварковая структура нуклона. Протон состоит из двух u-кварков и одного d-кварка.
Нейтрон состоит из одного u-кварков и двух d-кварков. При ещё большем
уменьшении длины волны виртуального фотона видно, что на самом деле
валентные кварки являются сложными образованиями большого числа кваркантикварковых пар связанных глюонами. Как формируется трехкварковая структура
нуклона из моря виртуальных кварк-антикварковых пар является одной из
фундаментальных проблем современной физики
Данные о структуре нуклона свидетельствуют о том, что нуклон имеет сложную
внутреннюю структуру. По современным представлениям он состоит из кварков,
взаимодействующих посредством обмена квантами сильного
взаимодействия − глюонами.
20. Изоспин. Изоспиновые мультиплеты.
Изоспин I − одна из квантовых характеристик (квантовых чисел) адронов,
описывающая их симметрию относительно сильных взаимодействий. Зарядовая
независимость ядерных сил привела к сохраняющемуся квантовому числу −
изоспину. Ядерное взаимодействие нейтрона и протона в одинаковых квантовых
состояниях одинаково и не зависит от заряда нуклона. Поэтому нейтрон и протон
рассматривают как два состояния одной частицы - нуклона - с одним и тем же
значением изоспина I = 1/2, но с разными значениями проекции изоспина
(обозначают обычно I3 или Iz).
Протон | I = 1/2, I3 = +1/2>.
Нейтрон | I = 1/2, I3 = −1/2>.
Вектор изоспина ведёт себя так же, как вектор обычного спина, но в фиктивном
зарядовом (изоспиновом) пространстве. Атомное ядро, содержащее A нуклонов (Z
протонов и N нейтронов) имеет значение проекции изоспина I3 равное сумме
проекций изоспинов всех нуклонов
I3 = (Z − N)/2.
Полный изоспин ядра, состоящего из A нуклонов, равен векторной сумме
изоспинов всех его нуклонов
Максимально возможное значение изоспина ядра I = A/2. Оно достигается в том
случае, когда изоспины всех нуклонов параллельны друг другу. Так как длина
вектора не может быть меньше длины любой его проекции, для изоспина ядра I
возможны следующие значения
(N − Z)/2 < I < (N + Z)/2.
Из зарядовой независимости ядерного взаимодействия следует, что при повороте
вектора изоспина в изоспиновом пространстве это взаимодействие не изменяется, т.
е. система нуклонов инвариантна относительно поворотов в изопространстве.
Третья проекция изоспина связана с измеряемой величиной – электрическим
зарядом. Заряд нуклона qN
qN = e(1/2 + I3).
Изоспиновая симметрия имеет кварковую природу. Изоспиновым квантовым
числом I = 1/2 характеризуются два самых легких кварка − u и d. Входя в состав
сильновзаимодействующих частиц (протонов, нейтронов, пионов и других адронов),
они определяют величину их квантового числа − изоспина.
Изоспиновый мультиплет − система частиц, имеющих одинаковые значения
изоспина I и различные значения проекции изоспина Iz.
Поскольку частицы в мультиплете отличаются проекцией I3 изоспина, то число n
частиц в мультиплете определяется величиной изоспина I и связано с ним
очевидным соотношением n = 2I + 1. Кваркам u и d приписывается изоспин I = 1/2 с
проекциями I3 на ось квантования в изоспиновом пространстве, равными
соответственно +1/2 (изоспин направлен вверх) и –1/2 (изоспин направлен вниз):
p ≡ uud (I = 1/2, I3 = +1/2,
n ≡ udd (I = 1/2, I3 = –1/2).
21. Странность. Рождение и распад странных частиц.
Странность, s
Квантовое число s может принимать значения -3, -2, -1, 0, 1, 2, 3 и определяется
кварковым составом адронов. Частицы, в сос тав которых входит странный кварк,
называются странными частицами. Сохранение странности в сильных
и электромагнитных взаимодействиях проявляется в особенности их рождения
и распада. Странные частицы в сильных и электромагнитных взаимодействиях как
прави ло рождаются парами. Характерное время жизни странных частиц10—10 с. Это
объясняется тем, что в слабых распадах странность может не сохраняться. Барионы
L, S, X, W со странностью, отличной от нуля, называются гиперонами.
В сильных и электромагнитных взаимодействиях странность сохраняется
В слабых взаимодействиях странность не изменяется или изменяется на единицу
Рождение странных частиц (как их стали называть) было обусловлено сильным
взаимодействием (т.е. происходило с большой вероятностью), их распады не имели
характерного для сильного взаимодействия времени жизни, хотя они и распадались на
сильновзаимодействующие частицы (например , ). Вместо величин порядка с, как следовало
ожидать для частиц, распадающихся за счёт сильного взаимодействия, их время жизни
оказалось в пределах от до с, что характерно для слабого взаимодействия.
Для объяснения особенностей распада странных частиц предполагается, что странность
сохраняется в сильном взаимодействии и не сохраняется в слабом взаимодействии.
Следовательно, хотя закон сохранения запрещает распад странных частиц на более лёгкие,
нестранные частицы, за счёт сильного взаимодействия, такие распады происходят и за счёт
слабого взаимодействия. Но слабые распады происходят гораздо медленнее, что соответствует
большим временам жизни.
Сохранение странности оказалось первым примером «частично сохраняющейся
величины», странность сохраняется в сильном и не сохраняется в слабом взаимодействии.
22. Сильные взаимодействия. Кварки. Глюоны. Цвет.
23. Кварковая структура адронов. Барионы. Мезоны.
24. Слабые взаимодействия. Промежуточные бозоны.
25. Слабые распады лептонов и кварков.
26. Пространственная инверсия. Р-четность.
27. Зарядовое сопряжение. Зарядовая четность. СР-инверсия.
28. Обращение времени. СРТ-теорема.
29. Фундаментальные взаимодействия. Объединение взаимодействий. Проблема
нестабильности протона.
30. Нуклеосинтез во Вселенной. Ядерные реакции в звездах.
31. Космические лучи. Состав и происхождение.