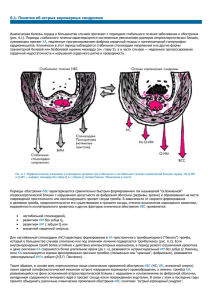
моделирования кровотока в сонной артерии в области

ОРИГИНАЛЬНЫЕ СТАТЬИ
УДК 616.133-004.6-005+004.94
© Коллектив авторов, 2014.
МОДЕЛИРОВАНИЯ КРОВОТОКА В СОННОЙ АРТЕРИИ
В ОБЛАСТИ АТЕРОСКЛЕРОТИЧЕСКОЙ БЛЯШКИ В ДВУМЕРНОЙ
И ТРЕХМЕРНОЙ ПОСТАНОВКЕ
М.А. Белоцерковская, Ю.В. Родин, В.Ю. Михайличенко, Р.Ю. Юсупов
ГУ «Институт неотложной и восстановительной хирургии им. В.К. Гусака НАМН Украины» (директор – академик
НАМН Гринь В.К.), г. Донецк.
BLOOD-GROOVE MODELLING IN THE CAROTID IN FIELD OF THE ATHEROSCLEROTIC PLAQUE IN
TWO-DIMENSIONAL AND THREE-DIMENSIONAL STATEMENT
M.A. Belotserkovskaya, Yu.V. Rodin, V.Yu. Mikhaylichenko, R.Yu. Yusupov
SUMMARY
We have attempted a comparison of the results of two-dimensional and three-dimensional mathematical
modeling of hydrodynamic and cavitation effects on the atherosclerotic plaque. The blood flow was considered
as an incompressible fluid. To determine the hydrodynamic features of the flow in the vessels with stenosis, we
solved the complete system of Navier-Stokes equations supplemented by the continuity equation. Similar results
were obtained: an increase in pressure on the windward side and a decrease – on the leeward, increasing
locally the Reynolds number and causing appearance of a turbulent wave behind the plaque that promotes the
destruction of its surface. This allows using two-dimensional modeling for the primary analysis, and threedimensional – to identify additional patterns.
МОДЕЛЮВАННЯ КРОВОТОКУ У СОННІЙ АРТЕРІЇ В ОБЛАСТІ АТЕРОСКЛЕРОТИЧНОЇ БЛЯШКИ У
ДВОВИМІРНІЙ І ТРИВИМІРНІЙ ПОСТАНОВЦІ
М.А. Білоцерковська, Ю.В. Родін, В.Ю. Михайліченко, Р.Ю. Юсупов
РЕЗЮМЕ
Була зроблена спроба порівняння результатів двовимірного і тривимірного математичного моделювання
гідродинамічних і кавітаційних впливів на атеросклеротичну бляшку. Кров’яний потік вважався нестисливою
рідиною. Для визначення гідродинамічних особливостей перебігу в судинах зі стенозом вирішувалася повна
система рівнянь Нав’є-Стокса, доповнена рівнянням нерозривності. Були отримані подібні результати:
збільшення тиску з вітряного боку і зменшення – з підвітряного, зростання місцевого числа Рейнольдса і
виникнення турбулентного сліду за бляшкою, що сприяє руйнуванню її поверхні, що дозволяє використовувати
двовимірне моделювання для первинного аналізу, а тривимірне – для виявлення додаткових закономірностей.
Ключевые слова: атеросклеротическая бляшка, стеноз, математическая модель, кавитация,
гидродинамика.
Атеросклероз – это хроническое заболевание,
основные проявления которого связаны с образованием в стенке артерий специфических для данной
патологии атероматозных бляшек, вызывающих нарушение кровотока в органах и тканях [1]. Атеросклеротическое поражение магистральных артерий
головного мозга является причиной 20-30% инсультов [7, 8]. Патогенетическое значение атеросклеротической бляшки сонной артерии в развитии инсульта связано с двумя основными механизмами: прогрессирующим снижением перфузионного давления,
вследствие нарастания стеноза артерии, и артериоартериальной микроэмболии ветвей мозговых артерий атероматозным материалом, кристаллами солей
кальция, микротромбами с поверхности бляшки.
В связи с этим профилактика и лечение атеросклероза имеют колоссальное практическое значение.
Чрезвычайно важной и актуальной остаётся пробле-
ма исследования поведения потоков крови в сосудах человека при наличии разнообразных патологий, которые нарушают кровоснабжение мозга [6].
Цель исследования - сравнить результаты моделирования кровотока в сонной артерии в области атеросклеротической бляшки в двумерной и трехмерной постановке и оценить механизмы деструктивного воздействия на атеросклеротическую бляшку.
МАТЕРИАЛЫ И МЕТОДЫ
Кровь считалась ньютоновской жидкостью с
плотностью 1060 кг/м3 и динамической вязкостью
4Ч10-3 ПаЧс. [4]. Данные допущения не являются
строго соответствующими физиологическим условиям, но для крупных кровеносных сосудов результаты расчётов качественно соответствуют особенностям течений в живом организме.
Для моделирования нестационарного ламинарного течения использовалось решение полной сис13
2014, том 17, №2 (66)
ТА В Р И Ч Е С К И Й М Е Д И К О - Б И ОЛ О Г И Ч Е С К И Й В Е С Т Н И К
темы уравнений Навье-Стокса, полученное с помощью неявной разно стной схемы в пакете
OpenFoam. Для определения гидродинамических
особенностей течения в сосудах со стенозом решалась полная система уравнений Навье-Стокса,
дополненная уравнением неразрывности. Расчеты
проведены для области, имитирующей сосуд с анастомозом 30%. Расчетная области двумерной и
трехмерной моделей приведены на рисунках 1 и 2
соответственно.
Рис.1. Схема расчетной области для двумерной постановки.
Рис.2. Схема расчетной области для трёхмерной постановки.
Геометрия расчётной области, построение сетки и обработка результатов проводились с помощью
свободно распространяемых Linux-ориентирован-
ных пакетов Salome Meca и ParaView. Система расчётных уравнений для двумерной постановки имеет
вид:
u
u
u
P
1  2u
 2u
 u
 w
 

(

)
2
t
x
z
x
R e x
z 2
(1)
w
w
w
P
1  2w  2w
u
 w
 

(

)
t
x
z
z
R e x 2
z 2
(2)
u
u

 0
x
z
(3)
U D

Для трёхмерной модели система расчётных уравнений усложняется:
Система содержит следующий безразмерный параметр:
Re 
– число Рейнольдса.
u
u
u
u
P 1  2 u  2 u  2 u
u
v
w


(


)
t
y
z
z
x Re x 2 y 2 z 2
(4)
v
v
v
v
P 1  2 v  2 v  2 v
u v w  

(


)
t
x
z
z
y Re x 2 y 2 z 2
(5)
w
w
w
w
P 1  2 w  2 w  2 w
u
v
w


(


)
t
y
z
z
z Re x 2 y 2 z 2
(6)
 u v w


0
x  y  z
(7)
ного поля скоростей выбран профиль Пуазейля. На
продольный градиент давления налагалась синусо-
В качестве начальных данных задается исходное поле скоростей и давления. В качестве началь14
ОРИГИНАЛЬНЫЕ СТАТЬИ
чётного алгоритма для более высоких чисел Рейнольдса и Пекле. Для проверки устойчивости полученной системы уравнений применялись методы
дифференциальных приближений и фон Неймана
[2,3,5], в котором решение уравнений представляется рядом Фурье с конечным числом членов и устойчивость определяется тем, что каждое отдельное
колебание затухает.
идальная волна возмущений. Для удовлетворения
граничных условий на препятствии применим описанный в работе [9] метод фиктивных областей с
продолжением по младшим коэффициентам в расширенной области:
Re 
U D

Для численного решения сформулированной задачи в качестве основы был взят метод расщепления. В настоящей работе для аппроксимации конвективных членов использованы разности против потока, что приводит к повышению устойчивости рас-
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Как видно на рисунках 3 и 4, анализ поставленной задачи в двумерной и трехмерной постановке дал
сходные результаты.
Рис 3. Распределение поля давления в области атеросклеротической бляшки в двумерной
модели.
Наличие анастомоза вносит существенную неоднородность в распределение поля давления, которая возникает вследствие значительного увеличения
скорости. На наветренной стороне наблюдается увеличение гидродинамического давления по сравнению с основным потоком, а на подветренной стороне возникает зона с отрицательным давлением на
поверхности бляшки. Возникающее локальное отрицательное давление служит источником дополнительных напряжений на поверхности и в совокупности с неоднофазностью потока крови может привести к возникновению неразвитой кавитации.
По расчётным данным был вычислен коэффи  48.5 , что говорит об
циент кавитации
отсутствии развитого кавитационного обтекания, но
не исключает возникновения кавитационных явлений в моменты времени, соответствующие макси-
мальному увеличению скорости.
Также увеличение скорости и, как следствие,
образование области с пониженным давлением приводит к турбулизации потока, ввиду чего возникают
значительные касательные напряжения на подветренной стороне бляшки (турбулентные напряжения больше ламинарных примерно на два порядка). Это может привести к срыву верхнего плотного слоя бляшки и её дальнейшему разрушению. Возникающие в
турбулентном следе пульсации давления способствуют разрушению поверхности бляшки и могут служить дополнительным катализатором возникновения
кавитационных явлений. Увеличение касательных
напряжений при турбулизации потока приводит к
разрушению макромолекул, в обычном случае стабилизирующих поток и способствует возникновению
дополнительной неустойчивости.
Рис 4. Распределение давления в области атеросклеротичекой бляшки в трехмерной модели.
15
2014, том 17, №2 (66)
ТА В Р И Ч Е С К И Й М Е Д И К О - Б И ОЛ О Г И Ч Е С К И Й В Е С Т Н И К
Таким образом, двумерная постановка может использоваться для решения задачи в первом приближении, в то время как трёхмерное моделирование
требует больших вычислительных затрат.
Полученные распределения гидродинамических
характеристик потока в пространственной области
позволяют точнее оценить механизмы деструктивного воздействия на бляшку:
а) в трёхмерной области с пониженным давлением может возникать явление кавитации, при котором паровые пузырьки переносятся в область с большим давлением вниз по потоку (на задней стенке) и
схлопываются, что приводит к изъязвлению бляшки;
б) возникновение турбулентного пятна на границе трёхмерной вихревой области приводит к тому,
что касательные напряжения могут увеличиваться на
два порядка.
2. Математическое моделирование гидродинамических и кавитационных воздействий на атеросклеротическую бляшку как обоснование к оперативному лечению при малых степенях стеноза / Ю.В.
Родин, А.А. Штутин, Ю.А. Скобцов, В.С. Оверко //
Матер. междунар. конф. «Актуальные вопросы диагностики и лечения сосудисто-мозговой недостаточности и распространённого атеросклероза», г. Киев
– 2003. - С. 18-21.
3. Математическое моделирование энергетических воздействий на атеросклеротическую бляшку в
зависимости от угла атаки / В.К. Гусак, Н.В. Финошин, Ю.В. Родин и др. // Вестник неотложной и восстановительной медицины. - 2001.-.№ 2-3.-C. -139.
4. Механика кровообращения / К. Каро, Т. Педли, Р. Шротер, У. Сид: Мир, 1981. - 624 с.
5. Ричардсон Э. Динамика реальных жидкостей.
М.: Мир - 1965. - 328 с.
6. Скобцов Ю.А., Родин Ю.В., Оверко В.С. Моделирование и визуализация поведения потоков крови при патологических процессах. – Донецк: Издатель Заславский А.Ю., 2008. – 212 с.
7. Epidemiologнa de los subtipos de ictus en
pacientes hospitalizados atendidos por neurуlogos:
resultados del registro EPICES (I) / S. Arias-Rivas, J.
Vivancos-Mora, J. Castillo at al. // Rev. Neurol. - 2012 .
– Vol.54.-№1. – P.385-393.
8. Risk factors, outcome, and treatment in sub-types
of ischemic stroke: the German stroke data bank / A.J.
Grau, C .Weimar, F. Buggle at al. // Stroke.- 2001. -32. –
P. 2559-2566.
9. Rockman Caron B. Focused screening for occult
carotid artery disease: Patients with known heart disease
are at high risk / Rockman Caron B., Jacobowitz Glenn
R., Gagne Paul et al. // JVS.-2004.-V.39.-N.1.-P.44-50.
ВЫВОДЫ
1. Результаты моделирования кровотока в сонной артерии в области атеросклеротической бляшки
в двумерной и трёхмерной постановке сходны, что
позволяет использовать двумерное моделирование
для первичного анализа, а трёхмерное – для выявления дополнительных закономерностей.
2. Увеличение скорости в области сужения приводит к увеличению давления на наветренной стороне и уменьшение – на подветренной, возрастанию
местного числа Рейнольдса и возникновению турбулентного следа за бляшкой, что способствует разрушению ее поверхности.
ЛИТЕРАТУРА
1. Аронов Д.М. Некоторые аспекты патогенеза
атеросклероза / Д.М. Аронов, В.П. Лупанов // Атеросклероз и дислипидемии . – 2011. - № 1. - С.48-56.
16