В.И. Черноштан, Э.Е. Благов. Рациональное профилирование

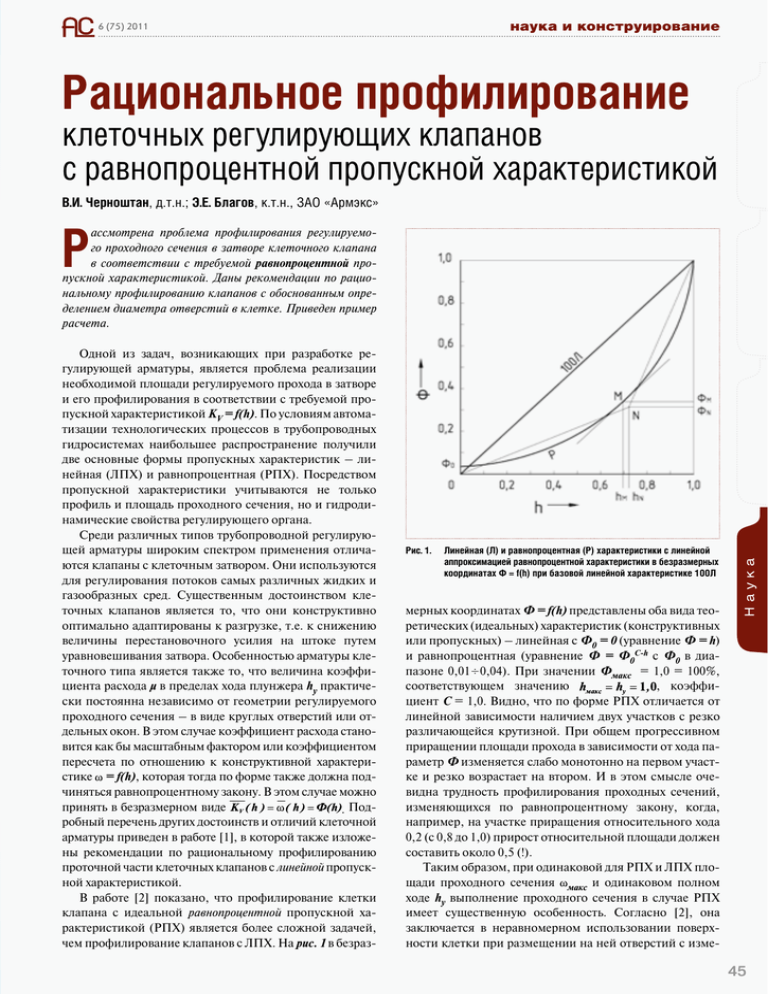
6 (75) 2011
наука и конструирование
Рациональное профилирование
клеточных регулирующих клапанов
с равнопроцентной пропускной характеристикой
В.И. Черноштан, д.т.н.; Э.Е. Благов, к.т.н., ЗАО «Армэкс»
Р
Одной из задач, возникающих при разработке регулирующей арматуры, является проблема реализации
необходимой площади регулируемого прохода в затворе
и его профилирования в соответствии с требуемой пропускной характеристикой KV = f(h). По условиям автоматизации технологических процессов в трубопроводных
гидросистемах наибольшее распространение получили
две основные формы пропускных характеристик – линейная (ЛПХ) и равнопроцентная (РПХ). Посредством
пропускной характеристики учитываются не только
профиль и площадь проходного сечения, но и гидродинамические свойства регулирующего органа.
Среди различных типов трубопроводной регулирующей арматуры широким спектром применения отличаются клапаны с клеточным затвором. Они используются
для регулирования потоков самых различных жидких и
газообразных сред. Существенным достоинством клеточных клапанов является то, что они конструктивно
оптимально адаптированы к разгрузке, т.е. к снижению
величины перестановочного усилия на штоке путем
уравновешивания затвора. Особенностью арматуры клеточного типа является также то, что величина коэффициента расхода μ в пределах хода плунжера hу практически постоянна независимо от геометрии регулируемого
проходного сечения – в виде круглых отверстий или отдельных окон. В этом случае коэффициент расхода становится как бы масштабным фактором или коэффициентом
пересчета по отношению к конструктивной характеристике = f(h), которая тогда по форме также должна подчиняться равнопроцентному закону. В этом случае можно
принять в безразмерном виде
. Подробный перечень других достоинств и отличий клеточной
арматуры приведен в работе [1], в которой также изложены рекомендации по рациональному профилированию
проточной части клеточных клапанов с линейной пропускной характеристикой.
В работе [2] показано, что профилирование клетки
клапана с идеальной равнопроцентной пропускной характеристикой (РПХ) является более сложной задачей,
чем профилирование клапанов с ЛПХ. На рис. 1 в безраз-
Рис. 1. Линейная (Л) и равнопроцентная (Р) характеристики с линейной
аппроксимацией равнопроцентной характеристики в безразмерных
координатах Ф = f(h) при базовой линейной характеристике 100Л
мерных координатах Ф = f(h) представлены оба вида теоретических (идеальных) характеристик (конструктивных
или пропускных) – линейная с Ф0 = 0 (уравнение Ф = h)
и равнопроцентная (уравнение Ф = Ф0С-h с Ф0 в диапазоне 0,010,04). При значении Фмакс = 1,0 = 100%,
соответствующем значению
, коэффициент С = 1,0. Видно, что по форме РПХ отличается от
линейной зависимости наличием двух участков с резко
различающейся крутизной. При общем прогрессивном
приращении площади прохода в зависимости от хода параметр Ф изменяется слабо монотонно на первом участке и резко возрастает на втором. И в этом смысле очевидна трудность профилирования проходных сечений,
изменяющихся по равнопроцентному закону, когда,
например, на участке приращения относительного хода
0,2 (с 0,8 до 1,0) прирост относительной площади должен
составить около 0,5 (!).
Таким образом, при одинаковой для РПХ и ЛПХ площади проходного сечения макс и одинаковом полном
ходе hу выполнение проходного сечения в случае РПХ
имеет существенную особенность. Согласно [2], она
заключается в неравномерном использовании поверхности клетки при размещении на ней отверстий с изме-
Наука
ассмотрена проблема профилирования регулируемого проходного сечения в затворе клеточного клапана
в соответствии с требуемой равнопроцентной пропускной характеристикой. Даны рекомендации по рациональному профилированию клапанов с обоснованным определением диаметра отверстий в клетке. Приведен пример
расчета.
45
наука и конструирование
6 (75) 2011
нением площади прохода по равнопроцентному закону,
что иногда не позволяет обеспечить значения пропускной способности, выполнимые при ЛПХ.
Практика показывает, что профилирование регулируемого прохода в соответствии с равнопроцентным
законом является довольно трудоемким этапом расчета РО, что заставляет изготовителя использовать упрощающие приемы, которые, в конечном счете, нередко
оказываются малоэффективными. Так, согласно работе
[3] для выполнения профилированного прохода в виде
набора круглых отверстий рекомендуется равнопроцентную зависимость заменить параболической. При
этом число отверстий и их диаметры на каждом уровне
различаются, возрастая от уровня к уровню по ходу подвижного элемента затвора. Реализация РПХ с набором
отверстий произвольно выбранного диаметра или разных диаметров исключает унификацию ряда KVу с наиболее рациональными размерами отверстий. Техникоэкономические недостатки такого подхода, включая его
нетехнологичность, очевидны.
Оставляя пока в стороне проблему реализации необходимой площади регулируемого прохода, которая будет
рассмотрена ниже, остановимся на одном из возможных
способов рационального решения проблемы профилирования клетки клапана с РПХ. Он заключается в выполнении регулируемого прохода в виде набора одинаковых отверстий не более двух диаметров в соответствии
с двумя участками на равнопроцентной зависимости.
В этой связи в настоящей работе предлагается другой
упрощенный подход, заключающийся в линеаризации
характеристики путем замены участков равнопроцентной кривой линейными участками.
В качестве основного условия выполнения аппроксимации примем принцип эквивалентности безразмерных
площадей двух участков под идеальной РПХ и двух соответствующих участков с линейным ограничением и точкой перелома N с координатами ФN, hN (см. рис. 1). Согласно [2] для значений Ф  1,0 (Ф = 1,0; 0,8; 0,63 и т.д.
вплоть до Ф = ФМ) точки касания касательных, параллельных ЛХ, располагаются на ординате Фм, значение
которой, как это будет показано ниже, для конкретного
значения Ф0 является величиной постоянной. В общем
случае ординаты ФM и ФN показаны несовпадающими
по величине (см. рис. 1), что соответствует результатам
анализа, приведенным в настоящей статье.
Две фигуры в виде треугольника и трапеции будут
иметь общую ординату ФN при относительном ходе hN.
Для указанного случая аппроксимации определим безразмерные значения площадей участков под РПХ. Зависимость для определения площади под первым участком
идеальной кривой имеет вид:
S1 =
=
(1)
Для аппроксимирующего треугольника его площадь
определяется как:
(2)
S1 = ФN·hN/2.
Равенство уравнений (1) и (2) дает первую корреляцию величин ФN и hN :
46
(3)
Выражение для определения площади под вторым
участком кривой соответственно принимает вид:
S2 =
=
(4)
Эквивалентная площадь трапеции определяется как:
S2 = (1 + ФN)·(1 – hN)/2 (5)
После приравнивания полученных выражений для S1
и S2 и сложения левых и правых частей равенств получаем вторую корреляцию величин ФN и hN :
ФN = hN – 1 +
.
(6)
Таким образом, зная значения суммарной площади
прохода в клетке  и хода плунжера hу, можно определить распределение площадей по участкам: 1 = ·ФN
при ходе от 0 до h1 = hN ·hу и 2 = (1 – ФN) при ходе от
h1 до hу.
Рис. 2. Схема расположения отверстий в клетке при линеаризованной
равнопроцентной характеристике
Примем для одного наклонного ряда (набора) отверстий их распределение, показанное на рис. 2. Здесь d –
диаметр отверстий; n – число отверстий в наклонном
ряду; а –величина мостика (перемычки) между отверстиями по внутреннему диаметру клетки;  – перекрыша (перекрытие смежных отверстий по вертикали); s –
площадь сегмента, соответствующая перекрыше, равной
стрелке сегмента; tг – шаг рядов отверстий по горизонтали на внутренней (вн) или наружной (н) поверхности
клетки. Число наклонных рядов m равно числу отверстий на одном уровне и выражается четными числами,
например, 2, 4, 6 и т.д. (принцип парности для клетки).
Проведем анализ геометрических соотношений для
аппроксимирующей линейной зависимости на первом
участке с отверстиями диаметра d1 . Из рис. 2 следует, что
h1 = n1 (d1 – 1), откуда:
n1 = h1/(d1 – 1). (7)
наука и конструирование
6 (75) 2011
Очевидным является также соотношение:
р1 = n1·· /4 – s1, которое дает выражение для
определения величины диаметра d1:
(8)
и с учетом (7) – вспомогательную зависимость:
h1 = 4·(p1 + s1)·(d1 – 1)/· . (9)
Величина площади одного наклонного ряда отверстий p1 зависит от принятого четного числа рядов
m1 = 2, 4 и т.д. Рассмотрим два крайних случая. При величине перекрыши 1 = 0, т.е. при s1 = 0, зависимости (7)
и (9) преобразуются к виду:
n1 = h1/d1
(10)
d1 = 4·p1/·h1
(11)
При величине перекрыши 1 = d1/2 после несложных
алгебраических преобразований зависимости для d1 и n1
приобретают следующий вид:
n1 =2·h1/d1
(12)
d1 = 2·(h1 –
)
(13)
После анализа результатов расчета и выбора значения m1, определяющего величину p1, находят среднее
значение числа отверстий n1ср и округляют его до целого
числа n1. По формуле (7) определяют значение разности
(d1 – 1) = h1/n1. Для установления величины d1 используется метод последовательных приближений, для чего
по формуле (8) при s1 = 0 предварительно оценивают d1,
затем 1 и соответственно s1, после чего последовательность расчета повторяется уже с учетом s1. Можно ограничиться двумя приближениями при сходимости значений
d1 менее 5%. При расчете и выборе величины диаметра
отверстий ряда d1 и их числа n1 следует помнить о необходимости выполнении условий n1  2 и 0 < 1 < d1/2.
Перейдем к анализу геометрических соотношений
для аппроксимирующей линейной зависимости на втором (крутом) участке с отверстиями диаметра d2. Принимаем, как в работе [1], что значение максимального
хода плунжера hу соответствует положению центров
последнего (верхнего) ряда отверстий. Отрезок хода
на втором участке определяется как h2 = hу·(1 – hN).
В свою очередь, из рис. 2 следует, что величина части
хода h2 обусловлена следующими составляющими:
h2 = (n2 – 1)·(d2 – 2) + d2/2. Полученная зависимость
дает общее выражение для определения числа отверстий
на втором участке:
n2 = (h2 + 0,5·d2 – 2)/(d2 – 2). Наука
(14)
Применительно к рис. 2 напишем очевидное выражение:
p2 = [(n2 – 0,5)·· d22/4] + s1, (15)
которое дает зависимость для определения диаметра
отверстий d2 при назначенном их числе n2:
d2 = 2·
(16)
47
наука и конструирование
6 (75) 2011
При необходимости можно определить величину
перекрыши из соотношения для хода h2, приведенного
выше:
(17)
Совместное решение уравнений (14) и (15) дает следующее полезное выражение:
h2 =
(18)
При величине перекрыши 2 = 0, т.е. при s2 = 0, зависимости (14) и (18) преобразуются к виду:
n2 = (h2/d2) + 0,5
(19)
d2 = 4·(p2 – s1)/·h2. (20)
При величине перекрыши 2 = d2/2 после несложных
преобразований зависимости (14) и (18) приобретают
следующий вид:
n2 = 2·h2/d2. (21)
d2 = 2·[h2 –
]
(22)
Расчет и выбор величины диаметра отверстий d2 и их
числа n2 производится в последовательности, изложенной для первого участка. Однако при этом отпадает необходимость в итерациях, так как значение d2 однозначно определяется по формуле (16). Обязателен контроль
условий n2  2 (это число включает отверстия самого
верхнего уровня с половинным диаметром) и 2 < d2/2.
Таким образом, исходя из необходимой величины площади регулируемого прохода в клетке, соответственно двум линейным участкам, аппроксимирующим
равнопроцентную кривую, можно установить всего два
рациональных значения диаметра отверстий d1, d2 при
числе их в одном наклонном ряду n1, n2. С целью дальнейшей рационализации профилирования и изготовления клетки рекомендуется провести анализ величин d1 и
d2 с тем, чтобы попытаться выбрать только одно значение d, которое удовлетворяет обоим диапазонам диаметров отверстий. Технико-экономические преимущества
такого решения очевидны.
Ниже приводятся расчетные соотношения, облегчающие разбивку отверстий на внешней боковой поверхности клетки через разбивку на внутренней. Шаги
отверстий по горизонтали на внутренней и наружной
поверхности клетки связаны соотношением
tг.н = tг.вн + 2··/m, (23)
где  – толщина стенки клетки. Согласно рис. 2 величина угла наклона ряда отверстий к горизонтали на
внутренней поверхности клетки определяется из соотношения:
,
(24)
где t0 = d + a – величина шага между отверстиями в
ряду на внутренней поверхности клетки. Во избежание
подрезки отверстий (их пересечения при сверлении)
значение а должно быть не менее 1,52,0 мм. Величина
проекции шага отверстий по горизонтали на внутренней
48
поверхности клетки определяется как tвн = (d + a)·cos вн.
С проекцией шага по наружной поверхности она связана
соотношением tн = tвн·(Dкл.н /Dкл ). Тогда выражение для
угла наклона ряда на наружной поверхности примет вид:
н = arctg[(d – )/tн ]. (25)
В свою очередь, шаг между отверстиями по наружной
поверхности определяется из соотношения t0н = tн /cos н
и соответственно величина перемычки ан = t0н – d.
Проблема реализуемости равнопроцентных пропускных характеристик частично нашла отражение в
ГОСТ 23866-87 [4], который, начиная только с DN  50,
для одного и того же типоразмера клапана в зависимости от формы пропускной характеристики регламентирует различающиеся значения условной пропускной способности KVу: более высокое – для клапана с
ЛПХ и более низкое (на одну ступень KVу) – для клапана с РПХ. Другими словами, для номинальных значений KVу (Р) = 0,80·KVу (Л) или KVу (Л)/KVу (Р) = 1,25,
где 1,25 – среднее значение знаменателя соотношения
ряда R10 [5].
С целью проверки корректности указанного выше регламента проведем дополнительный анализ характеристик, для чего обратимся к рис.1. Положение граничной
точки М определяется как координаты точки касания
прямой, параллельной базовой ЛХ с угловым коэффициентом к = 1. Уравнение касательной к точке М имеет
вид:
Ф – ФМ = (dФ/dh)·(h – hМ ).
(26)
С одной стороны, угловой коэффициент касательной
к = (dФ/dh)М = 1,0; с другой:
dФ/dh = Ф0С-h·lnФ0·(-1) = -Ф0С-h·lnФ0 . (27)
Здесь значение коэффициента С  1,0 (С = 1,0 при
Фмакс = 1,0). Согласно [2] коэффициент С рассчитывают
по формуле:
С = 1 + (lg Фст /lg Ф0 ), (28)
где Фст – стандартные значения Ф при h = 1,0 в соответствии со ступенями
=1,0; 0,8; 0,63; 0,5 и т.д. Величина С  1,0 является постоянной для каждой кривой Р.
С учетом соотношения
и уравнения (27)
получены выражение для определения координаты hM
(29)
и простая зависимость для определения ординаты ФM,
величина которой для конкретного значения Ф0 является величиной постоянной:
(30)
Ниже в таблице 1 приведены значения ФM и hM
для аргументов Ф0 = 0,010,04. Здесь же Ф – доля
неиспользуемой площади в пределах единичной величины, соответствующей характеристике 100 Л;  –
доля использованной площади в тех же пределах; D –
дефицит площади по сравнению с величиной Фст.
Обратная величина 1/ показывает, во сколько раз
единичная площадь превосходит долю использованной площади .
В соответствии с принятым принципом линеаризации РХ приближенно принимается, что ФN  ФМ. В этой
связи необходимо оценить и сравнить фактические значения указанных величин. Для расчета можно использовать метод итераций, для чего, задавая значения hN,
по формулам корреляции (3) и (6) определяют значения
ФN. Искомый результат соответствует их сходимости.
Расчеты выполнены для С = 1 с внесением результатов в
таблице 1. Оценена степень расхождения значений Фм
значений ФN и ФМ по отношению к ФМ при Ф0 = idem.
Таблица 1
Ф0
0,01
0,02
0,03
0,04
l lnФ0 l
4,605
3,912
3,506
3,219
ln l lnФ0 l
1,527
1,364
1,254
1,169
1,0
Фст
1,0
1,0
1,0
1,0
hM = ФМ (Л)
0,668
0,651
0,642
0,637
ФM (Р)
0,217
0,255
0,285
0,311
Ф = ФМ (Л) – ФM (Р)
0,451
0,396
0,358
0,326
 = 1 – Ф
0,549
0,604
0,642
0,674
D =  – 1,0
- 0,451
- 0,396
- 0,358
- 0,326
1/
1,821
1,655
1,557
1,484
(1/)/1,252
1,165
1,059
0,996
0,950
hN
0,743
0,725
0,720
0,718
ФN
0,173
0,226
0,273
0,3145
Фм, %
+ 20,3
+ 11,4
+ 4,2
- 1,1
С
0,80
Фст
С
1,0485
1,057
1,064
1,069
hM = ФМ (Л)
0,717
0,708
0,707
0,706
ФM (Р)
0,217
0,255
0,285
0,311
Ф = ФМ (Л) – ФM (Р)
0,500
0,453
0,422
0,395
 = 1 – Ф
0,500
0,547
0,578
0,605
D =  – 0,80
- 0,300
- 0,253
- 0,222
- 0,195
0,63
Фст
С
1,100
1,118
1,132
1,1435
hM = ФМ (Л)
0,768
0,769
0,775
0,780
ФM (Р)
0,217
0,255
0,285
0,311
Ф = ФМ (Л) – ФM (Р)
0,551
0,514
0,490
0,469
 = 1 – Ф
0,449
0,486
0,510
0,531
D =  – 0,63
- 0,181
- 0,144
- 0,120
- 0,099
С
1,1505
1,177
1,198
1,215
hM = ФМ (Л)
0,819
0,828
0,841
0,852
ФM (Р)
0,217
0,255
0,285
0,311
Ф = ФМ (Л) – ФM (Р)
0,602
0,573
0,556
0,541
 = 1 – Ф
0,398
0,427
0,444
0,459
D =  – 0,63
- 0,102
- 0,073
0,056
- 0,041
0,50
Фст
Поскольку случай Ф0 = 0,01 применяется достаточно
редко, можно считать выявленное расхождение ФN и ФМ
практически допустимым для принятия равенства ФN и
ФМ. Обращает на себя внимание, что в промежутке между Ф0 = 0,03 и Ф0 = 0,04 меняется знак погрешности Фм.
Это позволяет предположить, что имеется только одна
точка для РХ, в которой значения ФN и ФМ полностью
совпадают, т.е. Фм = 0.1 Для определения характеристик
этой точки задают значения Ф0 между 0,03 и 0,04 с вычислением ФМ по формуле (30). Полагая, что ФN = ФМ,
находят значение hN по видоизменённой формуле (6) и
затем значение ФN – по формуле (3). Результаты вычисления этой точки, соответствующей Ф0 = 0,037, приведены в таблице 2.
Если согласно таблице 1 принять
= 1,0,
то полученные значения  в зависимости от
Ф0 = 0,010,04 дадут соответственно следующие исполнения с фактическими значениями
= , а
именно 0,549; 0,604; 0,642 и 0,674. Другими словами, фактическое различие между значениями KVу (Л)
и KVу (Р) составляет не 1,25, а 1/ = 1,821,48, т.е.
в среднем не на одну, а на две ступени по Kvу и даже
больше (ср. 1,252 = 1,56). Рассчитанные значения упомянутых величин приведены в той же таблице. Числовые значения в нижней графе таблицы показывают,
насколько фактическое значение KVу (Л) отличается от
сниженного на две ступени значения KVу (Р), соответствующего коэффициенту 1,56. Значение коэффициента больше единицы, вычисляемое как (1/)/1,252,
означает, что различие касается уже третьей ступени.
Для численного примера анализа используем координаты точки М (0,642; 0,285), соответствующие значению Ф0 = 0,03 (для удобства сравнения с данными [2]).
В этой точке дефект площади достигает величины
Ф = 0,358, т.е. в пределах квадрата площадь, соответствующая РПХ, составит лишь  = 0,642 от площади,
соответствующей ЛПХ. Фактическое различие между
номинальными значениями KVу (Л) и KVу (Р) составит
1/ = 1,558 = 1,252, т.е. на две ступени ниже. В указанном диапазоне значений Ф0 вроде бы необходимо
снизить значения KV на две ступени, что уже на одну
ступень больше регламента.
Однако на этом проблему нельзя считать закрытой. Дело в том, что графический вид характеристик
(см. рис.1) еще не дает представления о том, как они могут быть воплощены в виде проходного сечения определенной площади и конфигурации (одного окна или нескольких окон и отверстий) и насколько выдерживается
при этом равнопроцентный закон изменения площади.
По результатам расчета, приведенным в таблице 1,
построены интегральные проходные сечения для ряда
стандартных значений Фст, а также для значения Фм
Наука
наука и конструирование
6 (75) 2011
1 Данное утверждение может быть строго доказано методами
функционального анализа, но это явно выходит за рамки настоящей статьи (прим. ред.).
Таблица 2
Ф0
I lnФ0 I
ln I lnФ0 I
Фст
С
hM
ФM
hN
ФN
Фм, %
0,037
3,297
1,193
1,0
1,00
0,638
0,303
0,719
0,303
0
49
наука и конструирование
Рис. 3. Профили безразмерных проходных сечений в функции b = f(h)
для равнопроцентных характеристик в диапазоне Ф = 1,00,285
при базовой линейной характеристике 100Л и Ф0 = 0,03
(рис. 3). В пределах единичной площади относительная
величина площади, соответствующая РПХ, составит
лишь часть  от площади, соответствующей ЛПХ, т.е.
KVу (Р)= ·KVу (Л). Таким образом, согласно рис. 2 особенность профилирования на основе РПХ заключается
в недоиспользовании части площади при ходе от 0 до hМ
и дефиците ее в пределах хода от hМ до 1,0. Согласно [2]
было выявлено, что, например, для Ф0 = 0,03 при ЛПХ
в пределах площади, принимаемой за 100%, может быть
размещено лишь 64,2% площади при РПХ. При этом ее
размещение подчиняется двум закономерностям: равнопроцентной – на участке хода от 0 до hМ = 0,642 и линейной – на участке от 0,642 до 1,0, совпадающей с отрезком касательной к равнопроцентной характеристике
в точке М. Для одного и того же клапана комбинированная характеристика будет иметь место для значения пропускной способности KVу (Л) = 100% с возможностью
реализации KVу (Р) = 64,2%, т.е. для клапана с DN = idem
50
6 (75) 2011
площадь проходного сечения, изменяющаяся по равнопроцентному закону во всем диапазоне хода, не может быть осуществлена вплоть до граничного значения
Фгр = ФМ = 28,5 %. При этом полезно иметь в виду следующее. Хотя могут быть реализованы все три величины
Ф = 100, 80, 63%, – по пропускной способности или по
максимальной площади, – снижение величины площади (100%  80%  63%) свидетельствует о возрастающей
гарантии размещения необходимой площади прохода в
виде отверстий.
Таким образом, наглядно показано, что в чистом виде
реализовать равнопроцентную характеристику возможно только, начиная с величины пропускной способности
ФМ и меньше. Снижение KV на одну ступень, как рекомендует ГОСТ 23866-87 [4], и даже на две, как показано в
настоящей работе, проблемы не решает.
Как вывод приходится констатировать: все, что выдается за реализованные в арматуре равнопроцентные
пропускные характеристики, большей частью ничего
общего с ними не имеет. Другим словами, изготовители
регулирующей арматуры, пытаясь обеспечить требуемую пропускную способность с равнопроцентной зависимостью изменения KV от хода, прибегают к подгонке
профилируемого проходного сечения путем принудительного размещения требуемой площади, даже если это
ведет к отходу от требуемой формы регулировочной характеристики, т.е. к ее фальсификации и искажению.
Иначе ничем иным нельзя объяснить все чаще появляющиеся в каталогах регулирующей арматуры оговорки,
что арматура поставляется с модифицированными (!)
равнопроцентными характеристиками. Однако, что это
такое и чем они отличаются от идеальных РХ, не поясняется. Из рис. 4 и 3 видно, что наибольшая степень искажения РХ получается в случае профилирования при
условии KVу (Р) = KVу (Л) = 100% (показано пунктиром).
В этой связи встает вопрос, как сказывается невыполнение требования обеспечения формы РХ в регулирующей арматуре на качестве управления технологическими
процессами, и тут свое слово должны сказать разработчики и эксплуатационники АСУ ТП.
Рис. 4. Равнопроцентные (Р) и комбинированные характеристики Ф = f(h)
при базовой линейной характеристике 100Л и Ф0 = 0,03
Профилирование при возможности реализации только комбинированной характеристики, которую, повидимому, можно было бы назвать равнопроцентной модифицированной (РмХ), будет иметь свои особенности,
которые следует также проанализировать. С этой целью
рассмотрим рис. 5. Как уже было установлено, изменение
площади на втором участке выше ординаты ФМ подчиняется линейному закону, при котором величина  < ФСТ .
Оно представляет собой касательную, параллельную
базовой ЛХ, в точке М любой РХ со значением ФСТ в
диапазоне от 1,0 до ФМ. В данном случае ФСТ = 0,63.
Криволинейную часть на первом (начальном) участке
предлагается заменить линейной зависимостью на основе упомянутого принципа эквивалентности площадей
под ними с пересечением прямых в точке K.
Рис. 5. Линейная (100 Л), равнопроцентная (63 Р) и комбинированная
характеристики с линейной аппроксимацией криволинейного
участка в безразмерных координатах Ф = f(h)
Касательная отсекает на осях абсцисс и ординат соответственно отрезки h0 и . При этом h0 < hK < hM.
Уравнение касательной представим в виде Ф = h – h0 =
= h – (1 – ) = h –Ф. Для точки К оно примет вид:
ФК = hК –Ф (31)
С другой стороны, для участка кривой и заменяющей
ее прямой будет справедливо равенство:
, (32)
из которого следует корреляция величин ФК и hК:
.
(33)
Равенство уравнений (31) и (33) относительно ФК
дает следующее соотношение, решаемое итеративно:
.
(34)
Распределение площадей по участкам и порядок профилирования с определением рационального диаметра
и числа отверстий производится в соответствии с рекомендациями, изложенными выше.
Пример расчета. Рассчитать геометрические параметры профилирования клеточного клапана DN 50 с РПХ.
Исходные данные: номинальный ход hу = 25 мм; внутренний диаметр клетки Dкл.вн = 50 мм; толщина стенки
 = 10 мм, т.е. наружный диаметр клетки Dкл.н = 70 мм;
диаметр седла Dс = 45 мм.
Решение. Площадь прохода в седле с = 15,9 см2. Оценим согласно таблице в работе [1] предельные максимальные значения площади регулируемого проходного
сечения пр.lim = 12,7 см2 и пропускной способности
KVlim (100Л) = 35,3 м3/ч. Согласно таблице 1 может быть
реализована только модифицированная (комбинированная) характеристика с коэффициентом использования площади  = 0,642. Таким образом, допустимое
стандартное значение пропускной способности для
РмПХ будет на две ступени ниже, т.е. будет составлять
ФСТ = 0,63 от KVlim (Л), т.е. KVмакс = 0,63·35,3 = 22,24 м3/ч
(или KVу = 20). Для принятого расчетного значения коэффициента расхода μ = 0,55 суммарная площадь прохода в клетке составит  (Р) = 8,02 см2. При Ф0 = 0,03,
С = 1,0 и Ф = 1 –  = 0,358 находим по формуле (34)
методом итераций значение hК = 0,535 и затем из соотношения (31) значение ФК = 0,177.
А. Первый участок (пологий). Значения хода и площади, приходящиеся на первый участок: h1 = hК·hу =
= 0,535·25 = 13,4 мм; 1 = ФК· = 0,177·8,02 =1,42 см2 =
= 142 мм2. Для числа рядов отверстий m = 6; 4; 2 получим
соответственно значения площади наклонного ряда отверстий р1 =23,7; 35,5; 71,0 мм2. Для двух крайних случаев 1 = 0 и 1 =d1/2 по формулам (11, 10) и (13, 12) находим значения диаметра d1 и числа отверстий n1:
при m1 = 6: d1 = 2,251,15 мм и n1 = 6,023,3;
при m1 = 4: d1 = 3,371,74 мм и n1 =4,015,4;
при m1 = 2: d1 = 6,753,61 мм и n1 = 2,07,4.
Из результатов расчета видно, что при m1 = 6 значения
d1 < 3 мм неприемлемы, а при m1 = 4 при наличии перекрыши величина d1 > 3 мм недостаточна. Остается вариант
с числом рядов противолежащих отверстий m1 = 2. Оцениваем среднее значение числа отверстий n1ср = 4,7 и принимаем округленное целое число отверстий в наклонном
ряду n1 = 4. Можно также принять n1 = 5, но при этом следует помнить, что значение диаметра отверстия уменьшается. Согласно соотношению (7) d1 – 1 = 13,4/4 = 3,35 мм.
При s1 = 0 по формуле (8) оцениваем значение
d1 = 4,755 мм с последующим округлением его до
d1 = 4,8 мм. Находим 1 = 1,45 мм, = 1,45/2,4 = 0,6042,
s1 = 4,61 мм2. Рассчитываем второе приближение по формуле (8) и получаем d1 = 4,907 мм  4,9 мм, 1 = 1,55 мм,
= 1,55/2,45 = 0,63265, s1 = 5,12 мм2. Выполняем контрольный расчет по исходной зависимости для формулы (8): р1 = 4·0,785·4,92 – 5,12 = 70,3 мм2. Расхождение
значений р1 (требуемого 71 мм2 и реализуемого 70,3 мм2)
лежит в пределах допустимой погрешности расчета. Таким образом, достаточно двух приближений. Условия
n1 = 4 > 2 и 1 = 1,55 < 2,45 мм выполнены.
Определим для первого участка геометрические
параметры расположения отверстий (см. рис. 2). Величины шага по горизонтали соответственно на внутренней и наружной поверхностях клетки будут равны
Наука
наука и конструирование
6 (75) 2011
51
наука и конструирование
6 (75) 2011
tг.вн = ·Dкл/m1 = ·50/2 = 78,5 мм и tг.н = ·Dкл.н/m1 =
= ·70/2 = 109,9 мм  110 мм. Также tг.н = tг.вн + 2··/m1 =
= 78,5 + 2··10/2 = 109,9 мм. Для величины перемычки
между отверстиями в ряду а = 2 мм угол наклона ряда составит:
,
где t0.вн = d1 + a = 4,9 + 2 = 6,9 мм. Проекция шага отверстий в ряду по внутренней поверхности клетки
tвн = t0.вн·cos вн = 6,9·0,874 = 6,03 мм. Та же величина проекции по наружной поверхности клетки tн = tвн·(Dкл.н /Dкл ) =
= 6,03·(70/50) = 8,44 мм. Угол наклона ряда на наружной
поверхности клетки составит:
.
Шаг отверстий в ряду по наружной поверхности будет равен t0.н = tн /cos н = 8,44/0,9379 = 9,08 мм. Размер перемычки (мостика) между отверстиями составит
ан = t0.н – d1 = 9,08 – 4,9 = 4,18 мм.
Б. Второй участок (крутой). Значения хода и площади, приходящиеся на второй участок: h2 = (1 – hК )·hу =
= 0,465·25 = 11,6 мм; 2 = (1 – ФК)· = (1 – 0,177)·8,02 =
= 6,60 см2 = 660 мм2.
Принимаем число рядов m2 = 4; 6; 8; 10 и соответственно определим значения площади одного наклонного ряда отверстий р2 = 2/m2 = 165; 110; 82,5; 66 мм2.
Для двух крайних случаев 2 = 0 и 2 =d2/2 по формулам
(20, 19) и (22, 21) находим значения диаметра d2 и числа
отверстий n2:
при m2 =4: d2 = 17,611,8 мм и n2 = 1,161,97;
при m2 = 6: d2 = 11,56,74 мм и n2 =1,503,44;
при m2 = 8: d2 = 8,54,73 мм и n2 = 2,236,39;
при m2 = 10: d2 = 6,73,63 мм и n2 = 2,617,95.
Видно, что значения d2 и n2 становятся приемлемыми, начиная с m2  6. Принимаем число рядов m2 = 10,
при котором площадь одного наклонного ряда отверстий составит р2 = 66 мм2. Оцениваем среднее число
отверстий n2ср =4,3 и принимаем n2 =4. По формуле (16)
с учетом s1 = 5,12 мм2 однозначно определяем значение
диаметра отверстий на втором участке d2 = 4,70 мм.
В этом случае значение перекрыши, рассчитываемое
по формуле (17), составит 2 = 1,62 < 2,35 мм.
Определим для второго участка геометрические параметры расположения отверстий (см. рис. 2). Величины
шага по горизонтали соответственно на внутренней и наружной поверхностях клетки будут равны tг.вн = ·Dкл /m2 =
= ·50/10 = 15,7 мм и tг.н = ·Dкл.н /m2 = ·70/10 =
= 21,98 мм  22 мм. Также tг.н = tг.вн + 2··/m2 = 15,7 +
+ 2··10/10 = 21,98 мм. Для величины перемычки между
отверстиями в ряду а = 2 мм угол наклона ряда составит:
,
где t0.вн = d + a = 4,7 + 2 = 6,7 мм. Проекция шага
отверстий в ряду по внутренней поверхности клетки
tвн = t0.вн·cos вн = 6,7·0,888 = 5,95 мм. Та же величина проекции по наружной поверхности клетки tн = tвн·(Dкл.н/Dкл) =
= 5,95·(70/50) = 8,33 мм. Угол наклона ряда на наружной
поверхности клетки составит:
.
Шаг отверстий в ряду по наружной поверхности будет
равен t0.н = tн /cos н = 8,33/0,9379 = 8,88 мм. Размер перемычки (мостика) между отверстиями составит ан = t0.н – d =
= 8,88 – 4,7 = 4,18 мм.
Для удобства разметки и изготовления клетки допускается округлять до целого числа расчетные значения шага
t0.н, например, с 9,08 мм до 9,0 мм и с 8,88 мм до 9,0 мм с
последующим уточнением зависимых величин. Расчет показывает также, что при дополнительном анализе вполне
реально профилирование клетки на основе одного, одинакового для обоих участков размера диаметра отверстия.
список литературы
1. Черноштан В.И., Благов Э.Е. Рациональное профилирование проточной части клеточных регулирующих клапанов с линейной пропускной характеристикой //Электрические станции.
2010. № 3. С.34-41.
2. Черноштан В.И., Благов Э.Е. Особенности профилирования регулирующих органов с требуемой пропускной характеристикой //Электрические станции. 2010. № 6 . С.32-36.
3. Клеточные регулирующие клапаны. // Обзорная информация.
Серия ХМ-10 «Промышленная трубопроводная арматура» /Г.С. Белозерская, Ю.Я. Казинер. – М.: ЦИНТИхимнефтемаш. 1979. – 33с.
4. ГОСТ 23866-87. Клапаны регулирующие односедельные,
двухседельные и клеточные. Основные параметры.
5. ГОСТ 8032-84. Предпочтительные числа и ряды пред­
почтительных чисел.
Если я сталкивался с новым наблюдением,
или мыслью, которая противоречила моим общим выводам,
я обязательно и не откладывая делал короткую запись о них,
ибо как я убедился на опыте, такого рода факты или
мысли обычно ускользают из памяти гораздо скорее, чем
благоприятные для тебя.
Чарльз Дарвин
52