Формирование УУД при решении задач на

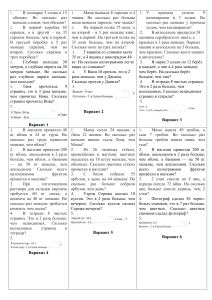
Источник: Непрерывное постдипломное образование специалистов
начальной школы как условие реализации Федерального
государственного образовательного стандарта начального общего
образования
Материалы межрегиональной научно-практической конференции
с международным участием 23 марта 2011 года
Под редакцией С.А. Усковой
Санкт-Петербург
ФОРМИРОВАНИЕ УУД ПРИ РЕШЕНИИ ЗАДАЧ
НА I СТУПЕНИ ОБУЧЕНИЯ
А.В. Ефимова,
Санкт-Петербург
С задачами житейскими, производственными, научными каждый человек
сталкивается ежедневно, совершая любую работу, занимаясь любым делом.
Задача – это: «1. То, что требует исполнения, разрешения. 2. Упражнение,
которое выполняется посредством умозаключения, вычисления. 3. Сложный
вопрос, проблема, требующие исследования и разрешения» [1]. Решение
задач формирует у детей практические умения и вычислительные навыки,
необходимые каждому человеку в повседневной жизни. Поэтому научиться
решать всевозможные задачи важно для достижения успеха в различных
сферах деятельности.
В школьном курсе математики решаются математические и сводимые к
ним задачи. С точки зрения методики преподавания математики: задача – это
задание на нахождение какого-то результата, когда сами действия по
нахождению результата не указаны в условии, но в условии содержится часть
необходимых для выполнения задания сведений. В курсе математики
начальных классов текстовые задачи являются объектом изучения, усвоения,
формирования умений и навыков, а также средством формирования
математических понятий. Задачи связывают теорию и практику обучения,
способствуют развитию логического мышления и пространственного
воображения,
вырабатыванию
практических
навыков
применения
математических знаний, развитию эвристического и творческого начал.
Каждая конкретная учебная математическая задача предназначается для
достижения комплекса педагогических, дидактических, учебных целей.
Образовательное значение математических задач заключается в
приобретении математических знаний, повышении математического
образования, овладении методом решения задач определенного типа.
Практическое значение задач обусловлено тем, что ученик обучается
применять имеющиеся математические знания к решению проблем в
повседневной деятельности. Воспитательное значение задач заключается в еѐ
фабуле, текстовом содержании, в котором отражается достижения в области
науки, техники, промышленности, культуры.
Рассмотрим на примере решения задач формирование регулятивных
УУД. Можно выделить следующие компоненты, способствующие
формированию УУД: «1 этап – анализ задачи; 2 этап – схематическая запись
задачи; 3 этап – поиск способа решения задачи; 4 этап – осуществление
решения задачи; 5 этап – проверка решения задачи; 6 этап – исследование
задачи; 7 этап – формулирование ответа задачи; 8 этап – анализ решения
задачи» [2].
При анализе задачи в начальной школе, ее надо внимательно изучить,
выяснить условие и вопросы, исходя из которых, будет проводиться
решение. Результаты предварительного анализа надо представить в виде
схематической записи условия. Далее с помощью анализа и схематической
записи необходимо найти способ решения конкретной задачи. «Решить
математическую задачу – это значит найти такую последовательность общих
положений математики …, применяя которые к условиям задачи …,
получаем то, что требуется в задаче – ее ответ» [2]. Но нахождение ответа
любыми способами не является полноценным решением задачи. После
изложения хода решения, необходимо провести проверку решения,
соотнести с вопросом задачи, а также рассмотреть возможность других более
рациональных способов решения. Психологи установили, что поиск
нескольких способов одной и той же задачи, выбор среди них наиболее
рационального приносит учащимся больше пользы, чем решение группы
однотипных задач. «Предполагается, что результатом формирования
познавательных УУД будут являться умения: произвольно и осознанно
владеть общим приемом решения задач; использовать знаковосимволические средства, в том числе модели и схемы для решения учебных
задач; ориентироваться на разнообразие способов решения задач» [3].
За время обучения в школе каждый учащийся решает большое
количество задач. При этом все ученики решают одни и те же задачи, но с
разным конечным результатом. Многие ученики вникают в процесс анализа,
поиска решения задачи, стараются освоить приемы и методы решения задач.
С другой стороны решение математических задач вызывает и большие
затруднения у некоторых учащихся. Причина неудач заключается в том, что
они не понимают самой сущности задач и их решения, не владеют общими
приемами поиска плана решения, не умеют проанализировать исходные
данные конкретной задачи, установить связь между величинами, входящими
в составную задачу, составить план решения; выполнить проверку
полученных результатов. Происходит это потому, что основное внимание
направлено на достижение единственной цели – нахождение ответа на
вопрос задачи. Это приводит к тому, что группа таких учащихся решают
задания по образцу, не осознавая свою деятельность, ориентируясь на поиск
похожих или знакомых задач.
Для того чтобы научиться решать текстовые задачи, надо выяснить, что
они представляют, как они устроены, как производится решение задачи, у
учащихся необходимо выработать навыки решения текстовых задач через
систематическую работу по овладению алгоритмами и приемами поиска
решения задачи.
В работе с учащимися я использую методику решения задач блоками.
Ученики получают вариант, состоящий из задач по различным темам.
Каждому учащемуся необходимо самостоятельно найти решение задач, не
пользуясь способом «Делай по образцу». Проверка работы учителем
сводится не к оцениванию решения задач по критериям «Верно» или
«Неверно», а к анализу хода решения и полученного результата. При
неправильно выполненном решении дается пояснение учителя, в чем
допущена ошибка: в вычислениях или в выборе способа решения. После
этого учащиеся имеют возможность возвратиться к данным задачам для
достижения правильного результата. Такая форма работа дает хорошие
результаты, потому что у каждого учащегося появляется уверенность в своих
силах в удачном усвоении материала. Ниже приведены типовые карточки с
задачами, которые целесообразно использовать на уроках при обобщении
темы, при итоговом повторении.
1 класс.
1. В пакет положили 4 груши и 5 яблок. Сколько всего фруктов в пакете?
2. На крыше сидели 7 птиц, 3 улетели. Сколько птиц осталось на крыше?
3. В одном букете 7 тюльпанов, а во втором – на 2 меньше. Сколько
тюльпанов во втором букете?
4. Высота берѐзы 8 м, а липы – 4 м. На сколько метров берѐза выше липы?
2 класс.
1. В магазин привезли 12 ящиков яблок, а груш на 3 ящика меньше. Сколько
всего ящиков фруктов привезли в магазин?
2. Утром в магазине было 42 кг моркови. После дневной продажи осталось 28
кг. Сколько килограммов моркови продали за день?
3. В классе 17 девочек и 12 мальчиков. На сколько девочек больше, чем
мальчиков?
4. С одной яблони собрали 15 кг яблок, с другой – 17 кг. Из 20 кг яблок мама
сварила повидло. Сколько килограммов яблок осталось?
3 класс.
1. На клумбе посадили 4 ряда красных роз по 8 штук в каждом и белые розы.
Сколько было белых роз, если всего посадили 40 кустов?
2. На 6 юбок пошло 12 м ткани. Сколько нужно ткани, чтобы сшить 14
платьев, если на платье расходуется на 2 м ткани больше, чем на юбку?
3. В хранилище привезли 8 машин с картофелем и 3 машины с капустой.
Сколько тонн капусты привезли, если всего было 55 т овощей?
4. Пол в кухне прямоугольной формы надо выложить плитками площадью 2
дм 2. Сколько понадобится плиток, если длина кухни 40 дм, а ширина – на 10
дм меньше
4 класс.
1. Из двух городов выехали одновременно навстречу друг другу два
автомобиля. Один ехал со скоростью 60 км/ч и проехал до встречи 240 км, а
другой двигался со скоростью 57 км/ч. Какое расстояние между городами?
2. Две электрички движутся в противоположных направлениях, скорость
одной из них – 52 км/ч, а другой – 54 км/ч. Сейчас между ними 18 км. Какое
расстояние будет между ними через 2 ч?
3. В первом куске 5 м ткани, во втором – 8 м. Первый кусок на 156 рублей
дешевле, чем второй. Сколько стоил каждый кусок ткани?
4. В магазин привезли 950 буханок хлеба, 3/5 которого составлял чѐрный
хлеб. Сколько буханок белого хлеба привезли в магазин?
Овладение общим приемом решения задач позволит учащимся
самостоятельно анализировать и решать задачи различных типов в начальной
и средней школе. Использование задач, имеющих различные варианты
решения, заданий на построение и конструирование геометрических фигур,
преобразования величин, задач, составленных по заданному решению,
способствует развитию дивергентного мышления. Это послужит важнейшим
условием успеха «в творческой деятельности: в исследовательском и
научном поиске, создании произведений искусства, руководящей работе,
предпринимательстве и вообще, в жизни человека».
Список литературы
8. Ожегов С.И., Шведова Н.Ю. Толковый словарь русского языка. – М., 1992.
9. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. – М.:
Просвещение, 1989.
165
3. Федеральный государственный образовательный стандарт начального
общего образования и его реализация средствами УМК «Школа России»:
пособие для учителя. – М.: Просвещение, 2010