Основные этапы решения задачи на ЭВМ
реклама
Тема 1.2 Основные структуры алгоритмов
Основные структуры алгоритмов (ОСА) – это определенный набор блоков и стандартных
способов их соединения для выполнения типичных последовательностей действий.
ОСА используются при структурном подходе к разработке алгоритмов и программ,
предполагающем использование нескольких основных структур, комбинация которых дает все
многообразие алгоритмов и программ.
К основным алгоритмическим структурам относятся линейные, разветвляющиеся и
циклические структуры.
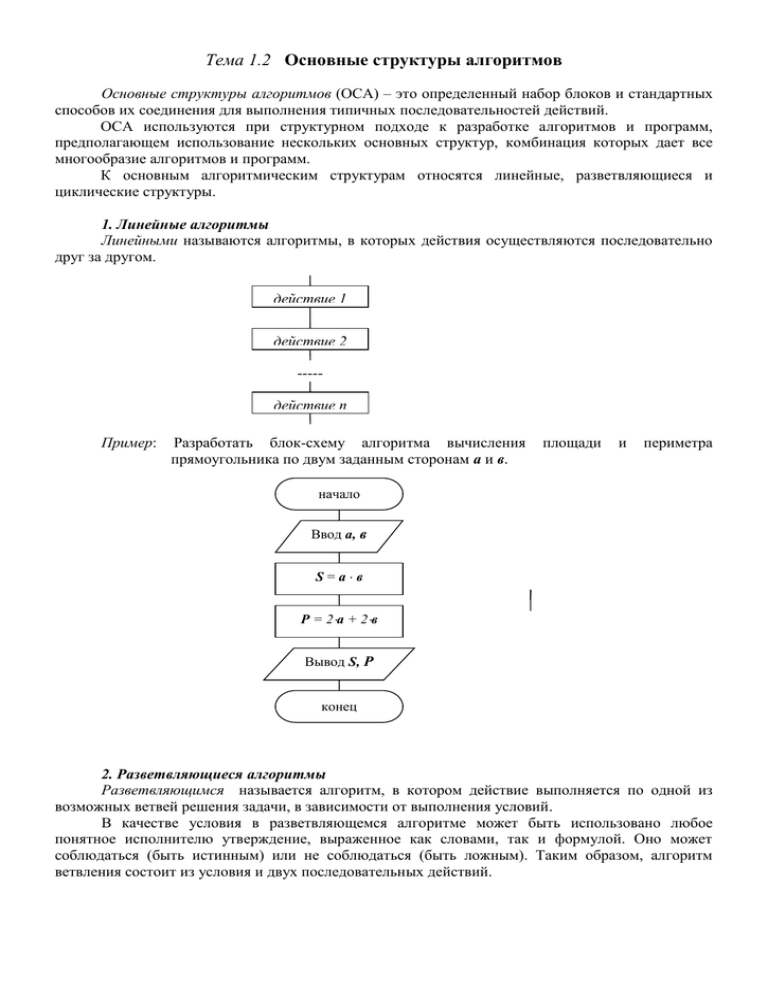
1. Линейные алгоритмы
Линейными называются алгоритмы, в которых действия осуществляются последовательно
друг за другом.
действие 1
действие 2
----действие n
Пример:
Разработать блок-схему алгоритма вычисления
прямоугольника по двум заданным сторонам а и в.
площади
и
периметра
начало
Ввод а, в
S=ав
P = 2а + 2в
Вывод S, P
конец
2. Разветвляющиеся алгоритмы
Разветвляющимся называется алгоритм, в котором действие выполняется по одной из
возможных ветвей решения задачи, в зависимости от выполнения условий.
В качестве условия в разветвляющемся алгоритме может быть использовано любое
понятное исполнителю утверждение, выраженное как словами, так и формулой. Оно может
соблюдаться (быть истинным) или не соблюдаться (быть ложным). Таким образом, алгоритм
ветвления состоит из условия и двух последовательных действий.
да
нет
нет
условие
условие
да
действие 1
действие 2
действие 1
или
Пример: Разработать блок-схему алгоритма вычисления Z , если даны два действительных
числа x и y .
Z =
{
X–Y,
если X >Y
Y - X + 1, если X<=Y
начало
Ввод X, Y
да
нет
X >Y
Z = Y – X +1
Z=X-Y
Вывод Z
конец
3. Циклические алгоритмы
Циклическим называется алгоритм, в котором некоторая часть операций выполняется
многократно.
Цикл - последовательность действий, выполняющихся многократно, каждый раз при новых
значениях параметра.
Для организации цикла необходимо:
1) задать перед циклом начальное значение переменной, изменяющейся в цикле;
2) изменять переменную перед каждым новым повторением цикла;
3) проверять условие окончания или повторения цикла;
4) управлять циклом, т.е. переходить к его началу, если он незакончен, или выходить из
него по окончании.
Последние три функции выполняются многократно.
Переменная, изменяющаяся в цикле, называется параметром.
В цикл входят в качестве базовых следующие структуры: блок проверки условия и блок,
называемый телом цикла.
В зависимости от способа организации числа повторений различают 3 типа циклов:
цикл с предварительным условием (цикл-ПОКА);
цикл с последующим условием (цикл-ДО);
цикл с параметром (цикл со счетчиком).
Цикл с предварительным условием имеет следующий вид:
нет
Если условие истинно, то
тело цикла выполняется и
управление передается снова
на вычисление условия, если
же условие ложно, то тело
цикла не выполняется и
происходит выход из цикла.
условие
да
Тело
цикла
Выход из цикла
Цикл с последующим условием имеет следующий вид:
Тело
цикла
нет
Если условие ложно, то
вновь
выполняются
операторы тела цикла, если
же условие истинно, то цикл
заканчивается.
условие
да
Выход из цикла
Цикл с параметром имеет следующий вид:
параметры
i := iн; iк; Δi
Тело
цикла
Выход из цикла
Циклические
алгоритмы,
в
которых тело цикла выполняется
заданное число раз, реализуются с
помощью цикла с параметром.
В этом случае предусматривается
повторное выполнение тела цикла с
одновременным изменением по
правилу арифметической прогрессии
значения, присваиваемого параметру
цикла.
При вычислении конечной суммы в циклическом алгоритме предварительно необходимо
начальную сумму приравнять нулю (S = 0), а при вычислении конечного произведения –
начальное произведение приравнять единице (P = 1).
Пример: Разработать блок-схему алгоритма вычисления факториала (F)
натурального
числа N. Факториал числа (!) – это произведение всех натуральных чисел от 1 до N.
N! = 1*2*3*…* N , (0! =1)
начало
начало
Ввод N
Ввод N
F=1
F=1
i=1
i=1
начало
i≤N
нет
Ввод N
F=1
i =1; N;1
F=F*i
да
i = i +1
F=F*i
i = i +1
F=F*i
нет
i≥N
да
Вывод F
Вывод F
конец
конец
а) цикл с предварительным условием
б) цикл с последующим условием
Вывод F
конец
в) цикл с параметром



