Примеры решения задач ()

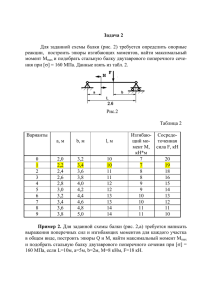
Указания к выполнению контрольной работы № 3
Пример решения задачи № 7
Для стального стержня (рис. 3.16) круглого поперечного сечения,
находящегося под действием осевых сил F1 и F2 и F3, требуется:
1) построить в масштабе эпюры продольных сил N;
2) из условия прочности определить размеры поперечных сечений
стержня;
3) построить эпюры перемещений в масштабе. Собственным весом
стержня пренебречь.
Дано:
2
1) модуль упругости для стали принять равным Е = 2´105 Н/мм ;
2) допускаемое напряжение [
=160 Н/мм2;
3) l1 = 100 мм; l2 = 300 мм; l3 = 200 мм;
4) F1 = 20 кН; F2 = 5 кН; F3 = 30 кН.
Решение. 1. Построение эпюры продольной силы N. Разбиваем
стержень на участки. Началом и концом участка являются точки
приложения внешних сил и опорных реакций. Для того чтобы не определять
опорные реакции из уравнений равновесия, будем рассматривать
отсеченные участки со свободного конца (рис. 3.16).
Согласно определению величина продольной силы численно равна
алгебраической сумме проекций всех сил, действующих на оставшуюся часть
стержня, на ось стержня.
Участок I, 0 £ z1 ³100 мм.
N1 = F1 = 20 кН.
Участок II, 0 £ z2 ³ 300 мм.
N 2 = F1 + F2 = 20 + 5 = 25 кНм ;
Участок III, 0 £ z3 ³ 200 мм.
N 3 = F1 + F2 - F3 = 20 + 5 - 30 = - 5 кН .
По полученным данным строим эпюру N (рис. 3.17, а), предварительно
выбрав масштабный коэффициент.
III
A3
II
I
A2
F3
A1
F2
B
A
z1
z2
z3
l1
l2
l3
D
C
F1
I
N
F1
z1
II
F2
N
z2
III
N
F3
F1
l1
F2
l2
z3
F1
l1
Рис. 3.16
2. Подбор размеров поперечного сечения. Из условия прочности
определим площади и размеры поперечных сечений стержня.
Для первого участка
sI =
N1
= [s ];
A1
A1 =
N 1 20000
=
= 125 мм 2 .
[s ] 160
Площадь и диаметр круглого поперечного сечения определяем по
формуле
p d 12
A1 =
,
4
отсюда
III
4 × 125
= 5, 42 мм .
3,14
4 A1
=
p
d1 =
A3
II
F3
A1
F2
B
A
l1
l2
25
20
25
F1
D
C
z2
z3
l3
а
I
A2
z1
20
Эпюра N, кH
0
0
5
5
f
f
f
б
0,16
в
0,08
Эпюра D , мм
0
0
0,16
Рис. 3.17
Для второго участка
s II =
N
25000
N2
= 156 , 25 мм 2 .
= [s ]; A 2 = 2 =
[s ] 160
A2
4 A1
=
p
d2 =
4 × 156 , 25
= 5,84 мм .
3,14
Для третьего участка
s III =
N
5000
N3
= 31 , 25 мм 2 .
= [s ]; A3 = 3 =
[s ] 160
A3
d3 =
4 A3
4 × 31,25
=
= 3,4 мм.
p
3,14
Конструируем стержень (рис. 3.17, б).
3. Построение эпюры перемещений. Для построения эпюры
перемещений используем формулу закона Гука.
При построении эпюры Dl учтем, что в точке А ( жесткая заделка)
перемещение сечения стержня отсутствует. С этой точки и начинаем
отсчитывать ординаты перемещений.
D А = 0;
D В = D А + D l АВ
(
)
N 3 l3
- 5 × 10 3 × 200
=0+
=
= - 0 ,16 мм ;
EA 3
2 × 10 5 × 31 , 25
N 2l2
25 ×10 3 × 300
D С = -0,16 +
= -0,16 +
= -0,16 + 0,24 = 0,08 мм ;
EA2
2 ×10 5 × 156 ,25
D D = D С + D lСD
N 1l1
20 × 10 3 × 100
= 0,08 +
= 0,08 +
= 0,16 мм .
EA1
2 × 10 5 × 125
Строим эпюру перемещений в масштабе (рис. 3.17, в).
Проверяем стержень по условию жесткости:
D D £ [D ],
где [D] = 0,01 мм, принимается конструктивно.
(2.31)
D D = 0,16 мм > [D ] = 0,01мм.
Вывод: условие жесткости не выполняется. Для уменьшения
деформаций необходимо увеличить размеры поперечных сечений стержня.
Пример решения задачи № 8
Для стального стержня круглого поперечного сечения (рис. 3.18, a),
находящегося под действием осевой силы F и нагретого до температуры Dt,
требуется:
1) построить эпюру продольных сил;
2) построить эпюру напряжений;
3) проверить стержень по условию прочности.
Дано:
1) допускаемое напряжение [s] = 160 МПа = 160 Н/мм2;
2) модуль упругости стали Е = 2 105 Н/мм2;
3) коэффициент температурного расширения a = 125×10-7;
4) F = 80 кН; l1 = 100 мм; l2 = 100 мм; l3 = 200 мм;
5) А1 = 400 мм2; А2 = 600 мм2; Dt = 100 °C; D = 0,01 мм.
Решение. 1. Определяем перемещение сечения «а-а» для того, чтобы
убедиться, закроется ли зазор D:
D а - а = D l F + D lt ,
где
DlF =
(2.32)
Fl 1 – удлинение стержня от действия осевой силы F;
EA 1
D l t = a D t (l1 + l 2 + l 3 ) – удлинение от температурного расширения.
Тогда
Dа - а =
=
80 × 10 3 ×100
5
2 ×10 × 400
Fl1
+ a D t (l1 + l 2 + l3 ) =
EA1
+ 125 × 10 - 7 ×100 × 400 = 0,6 мм > D = 0,1 мм .
Зазор закрывается, и в точке Д возникает опорная реакция RД.
I
А1
RA
а
II
А2
RД
F
Д
С
В
А
D
Z2
Z1
l3
l2
l1
Эпюра N, кН
б
40
Эпюра
40
120
, МПа
120
в
100
100
200
200
300
300
Рис. 3.18
2. Определяем степень статической неопределимости системы по
формуле
C = S - n = 2 - 1 = 1,
где S – число неизвестных усилий; n – число всех возможных уравнений
статики.
Система один раз статически неопределима, поэтому кроме уравнения
равновесия составляют дополнительное уравнение совместности деформаций
D а -а = D ;
R (l1 + l 2 ) R Д l 3
Fl 1
= D;
+ a D t (l1 + l 2 + l 3 ) - Д
EA 1
EA 2
EA 2
-
R Д (l1 + l 2 )
EA1
-
-
R Д l3
EA2
200 R Д
2 × 105 × 400
-
æ Fl
ö
= D - çç 1 + a Dt (l1 + l 2 + l3 )÷÷;
è EA1
ø
-
200 R Д
2 × 105 × 400
200 R Д
2 × 105 × 600
-
= 0,1 - 0,6;
200 R Д
2 × 105 × 600
= -0,5 ;
R Д = 120 кН.
3. Из уравнения равновесия åFz = RA + F - RД = 0 находим
RA = R Д - F = 120 - 80 = 40 кН.
4. Определяем продольную силу N.
Участок I, 0 £ z1 £ (l1+l2):
N1 = -RA = -40 кН.
Участок II, 0 £ z2 £ l3:
N 2 = - R Д = -120 кН.
Строим эпюру продольной силы N в выбранном масштабе (рис. 3.18, б).
5. Определяем нормальные напряжения s.
Участок АВ:
N1 - 40 ×103
s=
=
= -100 МПа .
A1
400
Участок ВС:
N 2 - 120 × 103
s=
=
= -300 МПа .
A2
400
Участок СД:
N 2 - 120 × 103
s=
=
= -200 МПа.
A2
600
Строим эпюру нормальных напряжений s в масштабе (рис. 3.18, в).
6. Проверяем стержень по условию прочности s max £ [s ]. Опасным
является участок ВС, так как
s max = - 300 МПа > [s ] = 160 МПа .
Следовательно, условие прочности не выполняется и необходимо увеличить
площадь поперечного сечения стержня.
Пример решения задачи № 9
I. Для балки, работающей на изгиб (рис. 3.19, а), требуется:
1. построить эпюры внутренних силовых факторов – поперечной силы
Q и изгибающего момента М;
2. подобрать размеры поперечного сечения стальной балки для случаев:
двутавровой; прямоугольного поперечного сечения со сторонами h –
большая, b – меньшая (h/b = 2); круглого поперечного сечения;
3. вычислить нормальные напряжения в характерных точках сечения;
4. проверить балку двутаврового сечения на прочность по касательным
напряжениям.
Рис. 3.19
Дано:
1) допускаемые напряжения для стали: [s] = 180 МПа; [t] = 110 МПа;
2) F = 40 кН; q = 18 кН/м; М = 20 кНм;
3) l1 = 0,5 м; l2 = 1,2 м; l3 =0,8 м.
Решение. 1. Для балок с жестким защемлением нет необходимости
первоначально определять опорные реакции, так как все участки можно
рассматривать со свободного конца балки.
Для определения поперечной силы Q и изгибающего момента М
воспользуемся методом сечений (рис. 3.20).
Рис. 3.20
Участок I, 0 £ z1£ 0,5 м:
Q = q z1 ; Qz = 0 = 0 ; Qz =0,5 = q × 0,5 = 18× 0,5 = 9 кН;
z1
z12
М = -q × z1× = -q ; M z =0 = 0 ;
2
2
M z = 0, 5
q × 0,52
18 × 0,52
=== -2,25 кНм.
2
2
d 2М
< 0, то кривая момента расположена выпуклостью вверх.
Так как
d z2
Участок II, 0 £ z2£ 1,2 м:
Q = q × l1 = 18 × 0,5 = 9 кН;
ö
æl
M = - q l1 ç 1 + z 2 ÷ ;
ø
è2
M z =0 = -
q × 0,5 2
= -2,25 кНм.
2
æl
ö
æ 0,5
ö
M z =1, 2 = q l1 ç 1 + 1,2 ÷ = -18 × 0,5 ç
+ 1,2 ÷ = -13,05 кНм .
è 2
ø
è2
ø
Участок III, 0 £ z3£ 0,8 м:
Q = q l1 - F = 18 × 0,5 - 40 = -31 кН;
æl
ö
M = - q l1 ç 1 + l2 + z3 ÷ + F z3 - M ;
è2
ø
æl
ö
æ 0,5
ö
M z = 0 = -q l1 ç 1 + l 2 ÷ - M = -18 × 0,5ç
+ 1, 2 ÷ - 20 = -33,05 кНм;
è 2
ø
è2
ø
æl
ö
M z = 0,8 = -q l1 ç 1 + l 2 + 0,8 ÷ + F × 0,8 - M =
è2
ø
æ 0,5
ö
= -18 × 0,5 ç
+ 1,2 + 0,8 ÷ + 40 × 0,8 - 20 = -8,25 кНм.
è 2
ø
Строим эпюры поперечной силы Q и изгибающего момента M в
выбранном масштабе (рис. 3.21). Для контроля правильности построения
эпюр воспользуемся дифференциальными зависимостями.
2. Подберем размеры поперечного сечения балки различных
профилей.
Используя условие прочности при изгибе, определим величину
момента сопротивления сечения Wx:
Wx =
M max
;
[s]
M max = - 33,05 кНм ;
33,05 × 103
Wx =
= 0,206 × 10-3 м3 = 206 см3.
6
160 × 10
Рис. 3.21
Двутавровое поперечное сечение. Из таблиц сортамента прокатной
стали (ГОСТ 8509-72) определяем номер двутавра – № 20а; Wx = 197 см3;
площадь поперечного сечения А = 28,3 см2.
Так как момент сопротивления принятого двутавра меньше, чем
расчетный, то необходимо определить перенапряжение, которое не должно
превышать 5 %.
s max =
M max
33,05
=
= 168 МПа ;
Wx
197 × 10 -6
168 - 160
× 100 % = 5 % , что допустимо.
160
Прямоугольное поперечное сечение, h = 2b:
2b 3
bh 2 2b 3
Wx =
=
;
; 206 =
6
3
3
b=3
3 × 206 3
= 309 = 6,76 см;
2
h = 2b = 2 × 6,76 = 13,52 см;
A = bh = 6,76 × 13,52 = 91,40 см 2 .
Круглое поперечное сечение:
Wx = 0,1 d 3 ; 206 = 0,1 d 3 ; d = 3
206 3
= 2060 = 12,72 см;
0,1
pd 2
A=
= 127 см 2 .
4
Наиболее рациональным является двутавровое сечение, так как имеет
меньшую площадь поперечного сечения по сравнению с остальными типами
сечений.
My
.
3. Нормальные напряжения вычисляем по формуле Навье s =
Ix
В опасном сечении |Mmax| = 33,05 кНм, Q = -31 кН.
Данные для двутавра № 20а: h = 200 мм; b = 110 мм; d = 5,2 мм; t = 8,3 мм;
A = 28,3 см2; Ix = 1970 см4; Sx = 111 см3.
Обозначим характерные точки по высоте сечения (рис. 3.22).
Точка 1:
y1 =
s (1) =
h 200
=
= 100 мм = 0,1 м ;
2
2
М max y1 33,05 × 0,1
=
= 168 ×103 кН/м 2 = 168 МПа.
8
Ix
1970 ×10
Так как изгибающий момент отрицательный, то точки 1 и 2 лежат в
растянутой зоне и напряжение в этих точках имеет положительный знак.
Рис. 3.22
Точка 2:
y2 =
s( 2 ) =
200
h
-t =
- 8,3 = 91,7 мм = 0,0917 м;
2
2
М max y2 33,05 × 0,0917
3
2
=
×
= 154 МПа .
=
154
10
кН/м
Ix
1970 ×10-8
Точка 3
s (3 ) = 0 , так как у3 = 0. Ось, проходящая через точку 3, называется
нейтральной линией.
Точки 4 и 5. В этих точках значения нормальных напряжений те же,
что и в точках 2 и 1, только отрицательные, так как точки 4 и 5 лежат в
сжатой зоне.
s (4 ) = -154 МПа ;
s (5 ) = -168 МПа .
4. Касательные напряжения t вычисляем по формуле
t=
Q Sx
.
b Ix
В точках 1 и 5 t = 0.
В точках 2 и 4 t изменяются скачкообразно, за счет изменения ширины
волокна, проходящего через точку 2. График в этих точках носит несколько
условный характер, так как резкое изменение ширины сечения вызывает
местное распределение напряжений. Знак касательных напряжений тот же,
что и поперечной силы Q.
Точки 2, 4. Вычисляем статический момент площади поперечного
сечения
S*x = A*x y*c ,
где A*x - отсеченная часть площади поперечного сечения; y*c - координата
центра тяжести отсеченной площади.
æh t ö
æ 0,2 0,0083 ö
-6 3
S *x = b t ç - ÷ = 0,11 × 0,0083 ç
÷ = 87 ,5 × 10 м .
2 ø
è2 2ø
è 2
При b = 110 мм
t' =
Qmax S *x - 31 × 87,5 × 10 -6
= 1,250 × 103 кН/м 2 = 1,25 МПа.
=
8
Ix b
1970 × 10 × 0,11
При b = t = 8,3 мм
Qmax S *x
- 31 × 87,5 × 10-6
t' ' =
=
= -16,6 × 103 кН/м 2 = -16,6 МПа.
8
I xb
1970 × 10 × 0,0083
*
3
Точка 3. S x = 111 см - берется из справочника.
t=
- 31 ×111 × 10 -6
1970 × 10
-8
× 0,0083
= -21 × 103 кН/м 2 = -21 МПа.
Строим эпюры напряжений (рис. 3.22).
Максимальное касательное напряжение имеет место на нейтральной
линии, т. е. tmax = 21 МПа.
Допускаемое касательное напряжение по 3-й теории прочности
принимаем равным [t] = 0,6[s], т. е. [t] = 96 МПа.
Следовательно, для балки двутаврового сечения
t max = 21 МПа < 96 МПа = [t ].
Условие прочности выполняется.
II. Для балки, работающей на изгиб (рис. 3.19, б), требуется:
1. определить опорные реакции;
2. построить эпюры внутренних силовых факторов – поперечной силы
Q и изгибающего момента М;
3. подобрать размеры двутаврового поперечного сечения стальной
балки.
4. построить эпюру прогибов балки и проверить балку по условию
жесткости.
Дано:
1. допускаемые напряжения для стали: [s] = 180 МПа; [t] = 110 МПа;
2. F = 40 кН; q = 18 кН/м; М = 20 кНм;
3. l1 = 0,5 м; l2 = 1,2 м; l3 =0,8 м.
Решение: 1. Определяем опорные реакции, используя вторую форму
условий равновесия:
SFz = 0; H A = 0;
Sm A = 0; - F1 l 1 - M + F 2 (l 1 + l 2 ) + R В (l 1 + l 2 + l 3 ) = 0;
RВ =
F1l1 + M - F2 (l1 + l 2 ) 40 × 0,5 + 20 - 30 × 1,7
= -4,4 кН;
=
(l1 + l 2 + l3 )
2,5
Sm В = 0; - M - F2 l3 + F1 (l 2 + l3 ) - R A (l1 + l 2 + l3 ) = 0;
RA =
- M - F2l3 + F1 (l 2 + l3 ) - 20 - 30 × 0,8 + 40 × 2
= 14,4 кН.
=
(l1 + l 2 + l3 )
2,5
Для проверки правильности определения опорных реакций составим
уравнение SFy = 0.
SFy = 0; R A - F1 + F2 + RВ = 14,4 - 40 + 30 - 4,4 = 0.
Следовательно, опорные реакции определены правильно.
2. Для определения поперечной силы Q и изгибающего момента М
воспользуемся методом сечений.
Участок 1, 0 £ z1£ l1:
Q = R A = 14,4 кН;
M = R A z1 ; M z1 =0 = 0; M z1 =l1 = R Al1 = 14,4 × 0,5 = 7,2 кНм.
Участок 2, 0 £ z2 £ l2:
Q = R A - F1 = 14,4 - 40 = -25,6 кН;
M = R A (l1 + z 2 ) - F1 z 2 ; M z2 = 0 = R Al1 = 7,2 кНм;
M z2 =l2 = R A (l1 + l2 ) - F1l2 = 14,4 ×1,7 - 40 ×1,2 = -23,52 кНм.
Участок 3, 0 £ z3 £ l3:
Q = - RВ = -(-4,4) = 4,4 кН;
M = RВ z3 ; M z3 = 0 = 0; M z3 =l3 = RВ l3 = -4,4 × 0,8 = -3,52 кНм.
Строим эпюры поперечной силы Q и изгибающего момента М в
масштабе (рис. 3.23).
y
A
1
RA
F1
2
RB
3
HA
z
B
z1
z2
z3
F2
l1
а
M
l2
Эпюра Q, кН
14,4
14,4
l3
4,4
4,4
0
0
25,6
25,6
б Эпюра М, кНм 7,2
0
0
3,52
23,52
RA
в
F1
M
RB
0
l1
l2
F2
l3
z
1,9
г Эпюра y, мм
0,65
0
0
Рис. 3.23
3. Подбираем двутавровое поперечное сечение из условия прочности
при изгибе.
M
Wx = max ; M max = -23,52 кНм .
[s]
Wx =
23,52
= 0,147 × 10-3 м3 = 147 см3 .
3
160 × 10
Из таблиц сортамента прокатной стали выбираем двутавр № 18, для
которого Wx = 143 см3 ; I x = 1290 см 3 ; А = 23,4 см 2 . Так как у выбранного
момента сопротивления момент инерции меньше расчетного, то необходимо
вычислить напряжение при Wx = 143 см3 и сравнить с допускаемым
напряжением. Перенапряжение допускается до 5 %.
M max
23,52
=
= 164,5 кНм , перенапряжение составило 2,8 %,
Wx
143 ×10 -6
что допустимо.
s max =
4. Вычисляем прогибы балки у и углы поворота q
точках балки.
Допускаемые значения прогибов принять:
[ y ]=
в характерных
1
×l - для двухопорных,
1000
где l – длина пролета.
Запишем универсальное дифференциальное уравнение изогнутой оси
балки (3.36). Начало координат выбираем на левом конце балки
(рис. 3.23, в). Уравнение изгибающего момента составляем для крайнего
правого сечения, используя специальные приемы (см. п. 3.1.2).
E I y '' = R А z - F1 ( z - l1 ) + F2 ( z - l1 - l2 ) + M ( z - l1 - l2 ) 0 ;
'
EI y =
EI y =
RА z 2
2
RА z3
6
F ( z - l1 )
F ( z - l1 - l2 )
- 1
+ 2
+ M ( z - l1 - l2 ) + C ;
2
2
2
2
F ( z - l1 ) F2 ( z - l1 - l2 ) M ( z - l1 - l2 )
- 1
+
+
+ C z + D.
6
24
2
3
3
2
Для определения прогибов y используется третье уравнение.
Произвольные постоянные определяем из условий закрепления балки:
1) z = 0; y = 0. Подставляем эти значения в третье уравнение и
получаем D = 0;
2) z = (l1 + l2 + l3) = 3 м; y = 0. Подставляем в третье уравнение:
0=
14,4 × 2,53 40 × 23 30 × 0 ,83 20 × 0,82
+
+ С × 2 ,5 ;
6
6
6
2
С = 2,75 кНм 2 .
Далее определяем прогибы в характерных точках, используя третье
уравнение:
а) z = l1 = 0,5 м :
R A l13
14, 4 × 0,5 3
EIy =
+ Cl1 =
+ 2,75 × 0,5 = 1,675 кНм 3 ;
6
6
1,675
y=
8
2 ×10 × 1290 ×10
-8
= 6,5 ×10 - 4 м = 0,65 мм.
б) z = (l1 + l2 ) = 1,7 м :
R A × 1,7 3 F1 (1,7 - 0,5) 3
EIy =
+ C × 1,7 =
6
6
=
14,4 ×1,7 3 40 ×1,2 3
+ 2,75 × 1,7 = 4,945 кНм 2 .
6
6
y=
4,945
= 1,9 × 10 -3 м = 1,9 мм .
8
-8
2 × 10 × 1290 ×10
Строим эпюру y в масштабе (рис. 3.23, г). Если изгибающий момент M
на участке больше нуля (M > 0), то кривая y выпуклостью вниз. Если M < 0,
то кривая у выпуклостью вверх.
5. Проверяем балку по условию жесткости:
y max £ [ y ];
[ y ] = 0,001l = 0,001 × 2,5 = 2,5 × 10 -3 м .
у max = 1,9 ×10-3 м < [ y ] = 2,5 ×10 -3 м .
Вывод: условие жесткости выполняется.
Пример решения задачи № 10
Для вала, работающего на кручение (рис. 3.24), требуется:
1) построить эпюру крутящих моментов Mz;
2) из условия прочности вычислить диаметр опасного сечения вала;
3) определить касательные напряжения на всех участках вала и
построить эпюру напряжений;
4) построить эпюру углов закручивания j.
Дано:
1) допускаемое касательное напряжение [t] = 50 МПа;
2) длины участков l1 = 0,6 м; l2 = 0,6 м; l3 = 0,5 м;
3) крутящие моменты Т1 = 10 кНм; Т2 =20 кНм.
Решение. 1. Разбиваем вал на участки, начиная с незакрепленного
конца. Границами участков являются сечения с сосредоточенными
крутящими моментами.
Для нахождения крутящих моментов применим метод сечений на
каждом из участков. В пределах каждого участка проводим нормальное
сечение на расстоянии z от границы с предыдущим. Мысленно отбрасываем
левую часть вала, оставшуюся уравновешиваем.
Участок1, 0 £ z1 £ l1 :
M z = Т1 = 10 кНм.
Участок 2, 0 £ z 2 £ l2 :
M z = Т1 - Т 2 = 10 - 20 = -10 кНм .
Участок 3, 0 £ z 3 £ l 3 :
M z = Т1 - Т 2 - Т1 = 10 - 20 - 10 = -20 кНм .
Строим эпюру крутящих моментов Мz (рис. 3.24, a).
2. Определяем диаметр вала в опасном сечении из условия прочности
при кручении.
Опасное сечение находится там, где действует наибольший крутящий
момент M zmax = - 20 кНм .
d =
3
Mz
=
0 , 2 [t ]
3
20 × 10 6
= 126 мм .
0 , 2 × 50
A
T1
T2
T1
B
C
D
z3
z1
z2
l3
l2
l1
10
Эпюра MZ , кНм
10
а
10
20
20
Эпюра , МПа
10
25
25
б
25
50
25
50
Эпюра
в
, рад.
0,005
0,005
0,008
Рис. 3.24
3. Определяем касательные напряжения на каждом участке:
10 ×10 6
Mz
Мz
t(1) =
=
=
= 25 МПа ;
W р 0,2 d 3 0,2 ×126 3
t (2 ) =
- 10 ×10 6
Mz
Mz
= -25 МПа ;
=
=
W р 0,2 d 3 0,2 ×126 3
Mz
Mz
- 20 × 10 6
t (3) =
=
=
= -50 МПа.
W р 0,2 d 3 0,2 × 126 3
Строим эпюру касательных напряжений t (рис. 3.24, б).
4. Определяем углы закручивания сечений вала. При этом рассматриваем вал с закрепленного конца. Проставляем характерные точки границ
участков А, В, С, Д.
В точке А угол поворота равен нулю;
jА = 0.
В точке В
j В = j А + Dj АВ
M z l3
- 20 × 10 6 × 0,5 × 103
= jА +
=0+
= -0,005 рад.
G Ip
8 × 10 4 × 0,1 × 126 4
В точке С
jС = j В + Dj ВС
М z I2
- 10 ×106 × 0,6 × 103
= jВ +
= -0,005 +
= -0,008 рад.
G Ip
8 ×104 × 0,1× 1264
В точке Д
j Д = jС + DjСД = jС +
М z I1
10 × 10 6 × 0,6 × 10 3
= -0,008 +
= -0,005 рад.
4
4
G Ip
8 × 10 × 0,1 × 126
Строим эпюру углов закручивания j (рис. 3.24, в).
5. Проверяем вал по условию жесткости qmax £ [q]:
q max =
Mz
max
G Ip
=
20 × 10 6
= 1 × 10 - 5 рад/м.
4
4
8 × 10 × 0,1 × 126
Допускаемый
угол
поворота
принимается
конструктивно.
В машиностроении в большинстве случаев принимается [q] = 0,01 рад на
один метр длины вала:
qmax = 1×10-5 p [q] = 0,01.
Вывод: условие жесткости выполняется.