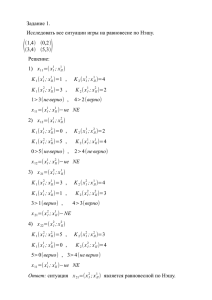Семинар _3

Семинары по теории игр, 2011 год
Семинар №3. Равновесие по Нэшу в смешанных стратегиях. Парето
оптимальные точки.
Словарь
Смешанная стратегия – случайный эксперимент, в результате которого
выбирается одна из чистых стратегий.
№1.
(a) Рассмотрим модель дуополии Курно. Две фирмы производят одинаковый
однородный продукт
в количествах q1 и q2. Обратный спрос на продукцию фирм:
P(Q ) = a − bQ = a − b(q1 + q 2 ) . Предельные издержки фирм MC1 = c , MC 2 = 2c .
Найдите точку равновесия по Нэшу.
(b) Найдите равновесие в случае, если количество фирм равно N, а предельные
издержки фирм равны MC i = c ∀ i = 1,..., N .
№2.
Игрок А выбирает число x ∈ R , а игрок В (одновременно с А) число y ∈ R .
Выигрыши
игроков
равны
соответственно
U A ( x, y ) = − x 2 + 6 xy
и
U B ( x, y ) = −2 y 2 + xy − 8 y . Найдите равновесие Нэша.
№3.
t1
В игре
l1
l2
t2
t3
( 2;8) (1; 6 ) ( 9; 20 )
( 7; 7 ) ( 6;8 ) ( 2; 6 )
а) Какая стратегия является наилучшим ответом второго игрока на стратегию l2
б) Какая стратегия является наилучшим ответом второго игрока на стратегию
1
2
l1 + l2
3
3
в) Найдите все смешанные стратегии (смешиваются t2 и t3 ), которые строго
доминируют чистую стратегию t1
г) Найдите равновесия по Нэшу в смешанных стратегиях.
д) Найдите Парето оптимальные точки.
1
Семинары по теории игр, 2011 год
№4.
d
a
а) b
c
e
(3; 2) (2; 2)
f
(7;1)
(0;1) (3;3) ( −3; 2) ;
(1; 4) (2; 2) (0; 0)
d
e
a (0; 2) (2;1)
f
(−2;1)
б) b (0;1) (3;3) (−3; 4) ;
c (1;0) (2; 2) (0;0)
d
a (2; 2)
в) b
(0;1)
e
f
(3; 2)
(7;1)
(3;3)
(−3;1) ;
c (0; 4) (−1; 2)
(0;0)
а) Вычеркнув строго доминируемые стратегии сведите данные игры к размеру
(2 × 2)
Подсказка: при вычеркивании можно использовать смешанные стратегии!
б) Найдите равновесия по Нэшу в смешанных стратегиях;
в)
Найдите
Парето-оптимальные
точки
в
чистых
стратегиях
2
Семинары по теории игр, 2011 год
Задача №5.
Найти все равновесия по Нэшу в смешанных стратегиях в биматричной игре:
c
d
e
a
3;5
-1;1
7;5
b
-1;-1
3;5
1;1
Задача №6.
Два игрока одновременно называют натуральное число от 1 до 5. Первый игрок
получает выигрыш, равный квадрату разности чисел. Второй игрок получает выигрыш
равный наименьшему числу.
Найдите равновесия по Нэшу в чистых стратегиях и Парето-оптимальные точки.
3