ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ПОЛУМАРКОВСКИХ

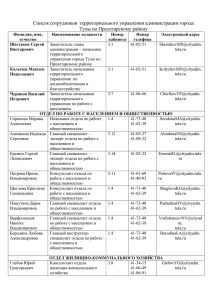
Известия ТулГУ. Технические науки. 2013. Вып. 4
Ларкин Евгений Васильевич, д-р техн. наук, проф., зав.
[email protected], Россия, Тула, Тульский государственный университет
кафедрой,
INDUSTRIAL ROBOT WITH INFORMATION CONTROL SYSTEM
T.A. Akimenko, A.A. Arshakyan, S.A. Budkov, E.V. Larkin
Considered an industrial robot with a management information system, which can be
used in various industries, such as electrical engineering, robotics for processing and assembly.
Key words: robot control system, the signal data communication module, an industrial robot.
Akimenko Tatiana Alekseevna, candidate
[email protected], Russia, Tula, Tula State University,
of
technical
science,
docent,
Arshakyan Alexander Agabekovich, candidate of technical science, postgraduate,
[email protected], Russia, Tula, Tula State University,
Budkov Sergey Anatolievich, postgraduate, [email protected], Russia, Tula, Tula
State University,
Larkin Evgenii Vasilevich, doctor of technical science, professor, head of the Department, [email protected], Russia, Tula, Tula State University
УДК 519.217.2
ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ПОЛУМАРКОВСКИХ
ПРОЦЕССОВ ОБРАБОТКИ ИНФОРМАЦИИ
СПЕЦИАЛИЗИРОВАННОЙ ЭВМ
А.Н. Ивутин
Предложены аналитические математические зависимости для оценки времени блуждания по циклическому стохастическому полумарковскому процессу в модели
обработки данных специализированной ЭВМ.
Ключевые слова: цифровая система, алгоритм, полумарковский процесс, сеть
Петри-Маркова, время выполнения.
Вычислительные
системы
с
параллелизмом
качественно
отличаются от фон-неймановских в плане диапазона времени выполнения
алгоритмов. Интуитивно можно предположить, что указанный параметр
может быть варьирован от величины, получающейся в случае, если все
операторы алгоритма последовательно интерпретируются одним
138
Управление, вычислительная техника и информационные технологии
процессором, а остальные компоненты системы в это время простаивают
(верхний предел), до величины, получающейся если все компоненты
начинают и заканчивают интерпретацию своих частей алгоритма
одновременно и при решении задачи исключены случаи их простоя
(нижний предел). Указанное обстоятельство плюс тот факт, что любой
алгоритм может быть разделен на одновременно выполняемые фрагменты
неоднозначно, порождают предпосылки для оптимизации временной
сложности алгоритмов, реализуемых в параллельных системах.
В [1] на основании исследования процесса выполнения команды
процессором фон-неймановской ЭВМ было показано, что для внешнего
наблюдателя количество машинных тактов, затрачиваемое процессором на
ее выполнение, является случайной величиной, распределение которой
зависит как от особенностей аппаратных средств, так и от распределения
обрабатываемых командой данных. Кроме того, в [2] был исследован
характер переходов между операторами алгоритма для внешнего
наблюдателя и показана его квазистохастичность.
Из квазистохастичности переходов и случайности времени
выполнения операторов исследуемых алгоритмов можно заключить, что
естественной моделью для описания интерпретации последовательности
команд процессорами ЭВМ фон-неймановского типа является
полумарковский процесс [3], определенный пятеркой
M = [ A, Z , p, f (t ), q] ,
где A = {a1( a ) ,K, a j ( a ) } - конечное непустое множество состояний,
совпадающее
с
множеством
операторов
алгоритма;
Z = { a1( a ) , a j ( a )  ,K,  ak ( a ) , a1( a ) } — конечное непустое множество переходов
между состояниями, совпадающее с множеством переходов алгоритма;
p =  pi ( a ), j ( a ) 
—
вложенная
цепь
Маркова;
J ( a ) × J (a ) -мерная
f (t ) =  f1( a ), j ( a ) (t )  — J ( a ) × J (a ) -мерная матрица плотностей распределения
времени пребывания процесса в состояниях; q =  qi ( a )  — J (a ) -мерный
вектор
начального
распределения
вероятностей.
Начальными
(поглощающими) состояниями полумарковского процесса являются
состояния, совпадающие с подмножеством B( E ) начальных (конечных)
операторов алгоритма.
При моделировании алгоритмов параллельных систем необходимо
учитывать следующие их особенности:
определенная и специфицированная для каждой параллельной
системы стратегия использования ресурсов для обработки информации;
динамический
характер
высвобождения/задействования
вычислительных ресурсов в процессе решения конкретных задач;
необходимость обмена данными (промежуточными результатами)
139
Известия ТулГУ. Технические науки. 2013. Вып. 4
между вычислительными модулями и связанная с этим явлением необходимостью синхронизации функционирования процессоров;
наличие эффекта "соревнования" между параллельно функционирующими компонентами (чем оправдывается термин concurrency, применяемый в зарубежной литературе).
Получение оценок времени выполнения алгоритма является одной
из важнейших задач эффективного распараллеливания и оптимального
распределения потоков управления в многопроцессорных конфигурациях.
Традиционно именно время выполнения является основным, хотя и не
единственным, индексом производительности. При этом, как показано
в [1], измерения производительности на реальных системах для случая
немонопольного использования ресурсов не могут считаться надежными в
силу того, что подобные измерения очень чувствительны к рабочей
нагрузке на систему в момент измерения.
Процесс решения задачи специализированной ЭВМ может быть
представлен как блуждание по полумарковской цепи, при котором ЭВМ
пребывает в состоянии ai (a ) в течение случайного времени, а затем с вероятностью pi ( a ), j ( a ) переключается в состояние a j (a ) . Время, в течение которого ЭВМ пребывает в состоянии ai (a ) , определено с точностью до плотности распределения f i ( a ), j ( a ) (t ) .
Состояния, в которые последовательно попадает процесс при блужданиях, будем называть траекторией решения. Очевидно, что для каждого
конкретного набора обрабатываемых данных D = (d1(i), ..., dn(i), ..., dN(i))
траектория решения строго детерминирована. Для внешнего же по отношению к информационно-измерительной системе, наблюдателя каждый
конкретный вектор обрабатываемых данных является случайным и поэтому траектория решения для него также является случайной.
В соответствии с методологией, приведенной в [4, 5, 6], одним из
способов оценки временных интервалов в полумарковском процессе является выделение траекторий с заранее заданными свойствами на графе состояний G = (A, Z) (для алгоритма обработки прерываний — Gint = (U, W))
и определение плотности распределения времени перемещения по выделенным траекториям.
Выделим в полумарковском процессе М = (G, H(t)) множество траекторий решения {G1 , ..., G n , ..., G N } ⊂ G таких, что
Gn = ( An , Z n ) =
= [{a0n( n ) , ..., ain( n ) , ..., a Jn ( n ) }, {(a0n( n ) , a1n( n ) ), ..., (ain( n ) , ain( n )+1 ), ..., (a Jn ( n )−1 , a Jn ( n ) )}] ,
где n = 1, 2, ..., N .
На состояния ain( n ) траекторий не накладывается никаких ограниче140
Управление, вычислительная техника и информационные технологии
ний кроме ain( n) ∈ An ⊂ A , в том смысле, что для любого состояния
ai (a) ∈ A
возможна
ситуация,
когда
a i ( a ) = a in( n ) ∈ An ⊂ A
и
a i ( a ) = a mj ( m ) ∈ Am ⊂ A (рис. 1).
a10(1)
a11(1)
...
a1i(1)
...
a1J(1)
ani(n)
...
anJ(n)
aNi(N)
...
aNJ(N)
. . .
an0(n)
...
an1(n)
. . .
aN0(N)
...
aN1(N)
Рис. 1. Выделенные траектории в полумарковском процессе
Пусть в выделенной траектории Gn = [ An , Z n ] процесс начинается в
состоянии a 0n( n ) ∈ An и заканчивается в состоянии a Jn ( n ) ∈ An , причем плотность распределения времени пребывания в состоянии a in( n ) ∈ An с последующим переключением в состояние a in( n ) +1 ∈ An равна f i (nn ),i ( n )+1 (t ) , а вероятность перехода из состояния a in( n ) ∈ An в состояние a in( n ) +1 ∈ An равна
pin( n ),i ( n )+1 . Тогда взвешенная плотность распределения времени достижения
подмножества состояний {a1J (1) , ..., a Jn ( n ) , ..., a JN( N ) ,} из подмножества состояний {a1J (1) , ..., a Jn ( n ) , ..., a JN( N ) ,}
{G1 , ..., G n , ..., G N } ⊂ G
по
одной
из
выделенных
траекторий
N
h (t ) = ∑ h0n( n ),1( n ) (t ) * ... * hin( n ),i ( n )+1 (t ) * ... * hJn( n )−1, J ( n ) (t ) ;
n
n =1
плотность распределения времени достижения подмножества состояний
{a1J (1) , ..., a Jn ( n ) , ..., a JN( N ) ,}
из
подмножества
состояний
{a1J (1) , ..., a Jn ( n ) , ..., a JN( N ) ,}
по
одной
из
выделенных
траекторий
{G1 , ..., G n , ..., G N } ⊂ G
N
f n (t ) =
∑ f 0n( n ),1( n) (t ) * ... * f i (nn),i ( n)+1 (t ) * ... * f Jn( n )−1, J ( n) (t )
n =1
N
J ( n ) −1
∑ ∏p
n =1 i ( n ) = 0 ( n )
141
n
i ( n ),i ( n ) +1
J ( n ) −1
∏p
i ( n )=0 ( n )
n
i ( n ),i ( n ) +1
;
(1)
Известия ТулГУ. Технические науки. 2013. Вып. 4
вероятность
достижения
{a1J (1) , ..., a Jn ( n) , ..., a JN( N ) , }
из
{a1J (1) , ..., a Jn ( n) , ..., a JN( N ) , }
по
{G1 , ..., G n , ..., G N } ⊂ G
n
подмножества
состояний
одной
J ( n ) −1
N
∏
p = ∑
состояний
n =1i ( n ) =0( n )
из
подмножества
выделенных
траекторий
pin( n),i ( n) +1 .
(2)
Зависимости (1) и (2) являются достаточно общими и из них могут
быть получены все возможные частные случаи определения плотностей
распределения временных интервалов в алгоритмах исследуемого класса.
Из (1) могут быть получены выражения для определения числовых
характеристик плотности распределения f n (t ) по числовым характеристикам плотностей f in( n),i ( n)+1 (t ) и вероятностям pin( n),i ( n) +1 :
N
∞
T n = ∫ tf n (t )dt =
J ( n ) −1
∑ ∏p
n =1 i ( n ) = 0 ( n )
N
J ( n ) −1
n
i ( n ),i ( n ) +1
n
i ( n ),i ( n ) +1
i ( n )=0 ( n )
J ( n ) −1
∑ ∏p
0
∑T
n =1 i ( n ) =0 ( n )
;
(3)
n
i ( n ),i ( n ) +1
∞
D n = ∫ (t − Ti (nn ),i ( n )+1 ) 2 f n (t )dt =
0
2
 J ( n )−1 n
  J ( n )−1 n
 J ( n )−1 n
 
 ∏ pi ( n ),i ( n )+1   ∑ Di ( n ),i ( n )+1 + ∑ Ti ( n ),i ( n )+1  
∑
n =1  i ( n ) =0 ( n )
 i ( n ) =0 ( n )
 
 i ( n )=0 ( n )
N
=
N
J ( n ) −1
∑ ∏p
n =1 i ( n ) = 0 ( n )
− (T n ) ;
2
(4)
n
i ( n ),i ( n ) +1
 J ( n )−1 n

T = min  ∑ Ti ( n ),i ( n )+1min  ;
(5)
n
i ( n )=0 ( n )

 J ( n )−1

n
Tmax
= max  ∑ Ti (nn ),i ( n )+1max  .
(6)
n
( n ) = 0 ( n )

Таким образом, для модели обработки данных специализированной
ЭВМ, представленной в виде полумарковского процесса, состояниями которого являются операторы алгоритмов обработки данных, получены аналитические математические зависимости для оценки времени блуждания
по циклическому стохастическому полумарковскому процессу.
n
min
Список литературы
1. D. E. Morgan and J. A. Campbell. 1973. An answer to a user's plea?
In Proceedings of the 1973 ACM SIGME symposium (SIGME '73). ACM, New
142
Управление, вычислительная техника и информационные технологии
York: NY; USA. P. 112-120.
2. Thomas E. Bell. 1974. Computer performance variability. In Proceedings of the May 6-10, 1974, national computer conference and exposition
(AFIPS '74). ACM. New York: NY. USA. P. 761-766.
3. Феррари Д. Оценка производительности вычислительных систем.
М.: Мир, 1981.
4. Игнатьев В.М., Ларкин Е.В. Анализ производительности ЭВМ:
учеб. пособие. Тула: ТГТУ, 1994. 104 с.
5. Игнатьев В.М., Ларкин Е.В. Временные характеристики алгоритмов в системах с прерываниями // Проектирование ЭВМ. Рязань, РГРТА,
1994. С. 29-40.
6. Игнатьев В.М., Ларкин Е.В. Сети Петри-Маркова. Тула: ТулГУ,
1997. 163 с.
Ивутин Алексей Николаевич, канд. техн. наук, доц., [email protected],
Россия, Тула, Тульский государственный университет
TIME CHARACTERISTICS OF SEMI-MARKOV PROCESSES OF INFORMATION
PROCESSING BY SPECIALIZED COMPUTER
A.N. Ivutin
The analytical mathematical relationships for estimate the time wandering to the
cyclic semi-Markov stochastic process in the data processing model by specialized computer
are proposed.
Key words: digital system, algorithm, semi-Markov process, Petri-Markov net, execution time
Ivutin Alexey Nicolaevich, candidate of technical
[email protected], Russia, Tula, Tula State University
143
science,
docent,