Термодинамические циклы

Министерство образования Российской Федерации
ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ АРХИТЕКТУРНО-СТРОНТЕЛЬНАЯ
АКАДЕМИЯ
Кафедра "Промышленная теплоэнергетика"
УЧЕБНОЕ ПОСОБИЕ
Термодинамические циклы
тепловых двигателей
(поршневые ДВС)
по выполнению курсовых работ и домашних заданий
по термодинамике с применением ЭВМ для студентов
всех форм обучения специальности - промышленная
теплоэнергетика (100700)
Тюмень 2003
2
Учебное пособие "Термодинамические циклы тепловых двигателей" к
курсовой работе "Расчет термодинамических циклов тепловых двигателей с
применением ЭВМ".
Составители: Моисеев Б.В., Яблонский Ю.П.
Пособие содержит методические указания и примеры расчета
термодинамических циклов поршневых ДВС с применением ЭВМ.
Тюмень: ТюмГАСА, 2003 г. стр. 34
Рецензент: к.т.н., доцент
В.Л. Ли
Учебно-методический материал обсужден и утвержден на заседании
кафедры ПТ
протокол № ___ от "___" ___________ 2003 г.
Зав. кафедрой ПТ
д.т.н., профессор
Учебно-методический материал утвержден УМС академии:
Протокол № ___ от "___" ___________ 2003 г.
Тираж 100 экземпляров
Степанов О.А.
3
ВВЕДЕНИЕ
В предлагаемом методическом пособии приведены примеры расчѐта
термодинамических циклов поршневых двигателей внутреннего сгорания (ДВС),
рекомендуемых в качестве домашнего задания для студентов. Домашнее задание
по термодинамическим циклам тепловых двигателей достаточно полно отражает
основные части курса технической термодинамики и для его выполнения
студентам следует освоить следующие разделы.
- идеальный газ и смеси идеальных газов
- теплоѐмкость;
-
первое начало термодинамики;
термодинамические процессы изменения состояния:
круговые процессы:
второе начало термодинамики;
-
термодинамические циклы тепловых двигателей (поршневых двигателей
внутреннего сгорания).
Выполнение домашнего
задания
позволит
закрепить теоретический
материал, получаемый на лекциях и в результате самостоятельной проработки
части курса, применить его к решению практической задачи - исследованию
термодинамических циклов тепловых двигателей.
Для расчѐта термодинамических циклов ДВС предложена программа на
ЭВМ.
Этой программой студенты могут воспользоваться в дисплейном классе.
Применение ЭВМ позволит студентам избавиться от ручного счѐта и больше
времени уделить анализу эффективности термодинамических циклов тепловых
двигателей.
4
ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ ДОМАШНЕГО ЗАДАНИЯ ПО
ТЕРМОДИНАМИЧЕСКИМ ЦИКЛАМ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ.
До начала выполнения расчѐтов по домашнему заданию студенту надо
уяснить цель и смысл задания [3] и усвоить материал, излагаемый на лекциях и в
учебниках [1, 2, 3, 8].
Bсе
вычисления
должны
быть
изложены
подробно. Формулы
записываются в общем виде, затем подставляются числовые значения величин (в
системе СИ) и только после этого приводится результат расчѐта. Необходимый
графический материал - термодинамические циклы в различных координатах следует изображать на миллиметровке в формате А4.
Домашнее задание оформляется на отдельных листах и сдаѐтся на проверку
в виде сшитой тетради из листов стандартного размера.
Студенты, которые правильно сделали и оформили задание, допускаются к
займите. При защите они должны свободно отвечать на вопросы, связанные с
теоретическими основами, методикой расчѐта задания.
Для подготовки к защите домашнего задания рекомендуется ответить на
вопросы, предлагаемые в конце пособия.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В понятие расчѐта газового цикла входит:
- расчѐт газовой смеси: определения массового состава
mi ,
кажущейся
молекулярной массы смеси  см , характеристической газовой постоянной смеси
Rсм;
- определения параметров состояния Р, V, Т в характерных точках цикла;
см
cm
- расчѐт средних массовых теплоѐмкостей смеси С рм
и Сvm
, для каждого про-
цесса:
- определение для каждого процесса, входящего в цикл, функций состояния;
изменения внутренней энергии  U, изменения энтальпии  h, изменения
энтропии  S и функций процесса: количество подведѐнного (отведѐнного)
тепла q, термодинамической L и потенциальной W работ.
5
- определение работы цикла Lц и термического коэффициента полезного действия
t ;
- построения цикла в P-V и T-S координатах.
Методические указания иллюстрируются примером расчѐта газового цикла.
Все расчѐты ведутся в удельных величинах, отнесѐнных к 1 кг рабочего тела
(газовой смеси), которое считается идеальным газом.
Самостоятельная работа студента (СРС) при выполнении домашнего
задания преследует цель научиться правильно использовать системы единиц
измерения и умело применять для расчѐта цикла теоретический материал.
1.1 Основные понятия и расчѐтные соотношения
При проведении расчѐтов термодинамических циклов тепловых двигателей
принято считать, что рабочим телом в них является идеальный газ. Это позволяет
использовать закономерности для идеальных газовых смесей, что хотя и снижает
точность расчѐта, но позволяет значительно облегчить вычисления и не
отражается на особенностях протекания термодинамических циклов. Поэтому
воспользуемся уравнением состояния идеального газа.
Рv  RT
где Р - абсолютное давление, Па; v - удельный объѐм, м3 /кг; Т - абсолютная
температура, К; R - характеристическая газовая постоянная, Дж/(кг. К),
RR 
(1)
R - универсальная газовая постоянная, 8314 Дж/ (кмоль. К),  - молекулярная
масса газа, кг/кмоль.
1.2 Газовые смеси
Рабочим телом большинства тепловых машин является смесь газов. Состав
газовой смеси определяется количеством (Мi, Vi) каждого из газов - компонентов,
входящих в смесь, и задаѐтся массовыми mi, или объѐмными ri долями.
Для смеси идеальных газов, если смесь задана массовыми концентрациями,
молекулярная масса смеси:
i  1
n
 m
i 1
i
i 
(2)
6
где тi= Gi /G; G - масса смеси, кг;
 i , Gi - массовой концентрация,
mi,
молекулярная масса (кг/кмоль) и масса (кг) i - го компонента.
Тогда газовая постоянная смеси газов:
n
Rсм   mi Ri
Rсм  R  см или
(3)
i 1
Формулы для расчѐта газовых смесей приведены в табл. 1.
Таблица 1
Задание состава
смеси
Перевод из одного
состава в другой
Массовые доли
mi 
Mi
M см
mi
ri

mi

mi 
1
mi
 см 
i
Объѐмные доли
V
ri  i
Vсм
Кажущаяся
молекулярная
масса смеси
Газовая
постоянная смеси
Rсм   mi Ri
i
i
ri  i
 ri  i
 cм   ri  i
Rсм 
8314
 ri  i
1.3 Теплоёмкость
Теплоѐмкость газа зависит от температуры. По этому признаку различают
среднюю и истинную теплоѐмкости. Если q - количество теплоты, подведѐнного
(отведѐнного) к единице количества вещества при изменении его температуры от
t1 до t2, то величина Сm  q t 2  t1  - средняя теплоѐмкость в пределах температур
от t1 до t2. Предел этого отношения, когда разность температур стремится к нулю,
см
называют истиной теплоемкостью С рм
и Сvмсм .
Для газов важное значение имеют теплоѐмкости в процессах изобарном
(Срm) и изохорном (Сvm),которые связаны между собой законом Майера
С pm- С vm = R.
Для вычисления средних теплоѐмкостей в диапазоне температур от t1 до t2
пользуются формулой:
t
Сm 2 
t1
Cm
t2
0
t 2  Cm
t 2  t1
t1
1
t1
;
(4)
7
где С m
t
- средняя теплоѐмкость газа в интервале температур от 0 °С до t °С, она
0
может быть мольной, объѐмной или массовой как при постоянном давлении, так и
при постоянном объѐме.
Средняя массовая теплоѐмкость смеси определяется:
Сmcm   mi Cmi
(5)
где С mi - средняя массовая теплоѐмкость i - го компонента.
1.4 Показатель адиабаты
Идеальных газов
k  С рт Ст
(6)
Значения молекулярных масс и характеристических газовых постоянных
(  i , Ri,) компонентов смеси выбираются из табл.3. Значения изобарных
теплоѐмкостей Сpmi следует выбирать по таблицам при заданной температуре [3],
или из таблиц в приложениях.
1.5 Первое начало термодинамики
Аналитическое выражение первого начала термодинамики для конечного
изменения состояния 1кг газа имеет вид:
q12  u  l12 ;
(7)
q12  h  w12 ;
(8)
2
Количества тепла q1-2 термодинамическая работа l1 2   Pd потенциальная
1
P2
работа W12   VdP являются функциями процесса. Внутренняя энергия U,
P1
энтальпии h являются функциями состояния, то есть изменение этих величин не
зависит от пути процесса и определяется по следующим формулам:
U  Cvm t 2  t1  ;
(9)
h  C pm t 2  t1  .
(10)
1.6 Термодинамические процессы
Основными процессами, которые изучаются в термодинамике, являются
изохорным (V = idem), изометрический (Т = idem) и адиабатный (PVk = idem).
Связь между параметрами в процессах и формулы расчета функций состояния и
8
процесса приведены в табл.2. Перечисленные процессы - частные случаи
обобщѐнного процесса, который называется политропным и описывается
уравнением PVn = idem, где n - показатель политропы, который может принимать
любые значения от - ∞ до + ∞.
1.7 Второе начало термодинамики
Определяет направление, в котором протекают процессы, устанавливает
условия преобразования тепловой энергии в механическую и для обратимых
процессов имеет вид:
dS 
q
;
(11)
q  TdS .
(12)
T
В технической термодинамике приходится иметь дело не с абсолютным
значением энтропии, а с еѐ изменением S  
q
T
.
1.8 Круговой процесс (цикл).
Совокупность термодинамических процессов, в результате осуществления
которых рабочего тело возвращается в исходное состояние. Степень
совершенства работы цикла характеризуется термическим КПД:
t 
lц
q1

q1  q 2
q1
 1
q2
q1
.
(13)
Первое начало термодинамики для цикла имеет вид:
 q   dU   l   dh   W .
(14)
Внутренняя энергия, энтальпия, энтропия являются функциями состояния,
поэтому в круговых процессах изменения этих величин равно нулю.
Следовательно, выражение (14) примет вид:
lц   q   l   W ,
lц   qi   li  Wi
где lц - работа цикла, Дж/кг;
q i - количество подведѐнной (отведѐнной) теплоты;
l i - термодинамическая работа;
Wi - потенциальная работа;
U i - изменение внутренней энергии;
hi - изменение энтальпии;
q1 - количество подводимой теплоты, Дж/кг;
q2 , - количество отводимой теплоты, Дж/кг;
(15)
(16)
9
Связь между
параметрами
Термодинамическая
работа
Потенциальная работа
Теплоѐмкость
процесса
Количество
теплоты
Таблица 2
Адиабатный
2
3
4
5
6
PVn = idem
P=idem
V=idem
PV=idem
РVk=idem
n0
n=±∞
n=1
Показатель
политропы
Уравнение
процесса
Наименование
процесса
1
Связь между параметрами в процессах
Политропный
Изобарный
Изохорный
Изотермический
n
W
l
P2  V1 
 
P1  V2 
n
T2  V1 
 
T1  V2 
n 1
n 1
T2  P2  n
 
T1  P1 
P V  P2V2
l1 2  1 1
n 1
R T1  T2 
l1 2 
n 1
P1  P2
V1  V2
Т1  Т 2
T2 V2

T1 V1
T2 P2

T1 P1
Р2 V1

Р1 V2
l1 2  RT2  T1 
nP1V1  P2V2 
n 1
nR T1  T2 

n 1
W1 2 
W1 2
С n  C vm
W12  0
q12  h  W12
q12  C n T2  T1 
l1 2 
l12  RT ln
P1
P2
l1 2
Срт
Сvm

q1 2  U  l1 2
q12  h  W12
q1 2  l1 2 
Т1
q12  Cvm T2 
W1 2
T1
q1 2  TS
k 1
k
k P1V1  P2 
k 1
kRT1  T2 

k 1
W1 2 
W1 2
k 1
P1V1  P2V2
k 1
RT1  T2 

k 1
V2
V1
W1 2  l1 2
q1 2  C pm Т 2 
C vm
T2  P2 
 
T1  P1 
W1 2  RT2  T1 
nk
n 1
q12  U  l12
W1 2  V P1  Р2 
C pm
T2  V1 
 
T1  V2 
l12  RT ln
l1 2  0
l1 2  PV2  V1 
nk
0
q1 2  0
10
1
2
3
S  C pm ln
Изменения
энтропии
R ln
4
6
T2

T1
V2
V1
R 

S   C pm 

n 1

T
ln 2
T1
S  C n ln
5
S  C pm  ln
T2
T1
S  C vm 
ln
T2
T1
S  R ln
V2
V1
P
S  R ln 1
P2
S = 0
T2
T1
1.9 Термодинамические циклы поршневых
двигателей внутреннего сгорания
В предварительных исследованиях термодинамических циклов поршневых
ДВС рассматривают идеализированные циклы. В них процессы сжатия и
расширения рабочего тела принимаются адиабатными, а рабочим телом является
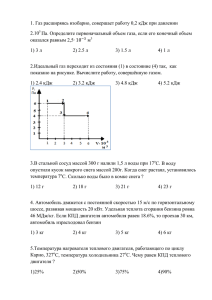
идеальный газ. Различают циклы с изохорным подводом тепла - цикл Отто (рис.
1а), изобарным подводом - цикл Дизеля (рис. 1б) и со смешанным подводом тепла
- цикл Сабатэ - Тринклера (рис. 1 в).
Основными характеристиками термодинамических циклов поршневых ДВС
являются:  - степень сжатия,   1  2 ;  - степень повышения давления в
процессе подвода тепла при   idem,   P3 P2 ;
Рис 1. Термодинамические циклы поршневых ДВС:
а) Отто, б) Дизеля, в) Сабатэ - Тринклера
11
 - степень предварительного расширения в процессе подвода тепла при
Р = idem,    3  2 (для цикла Дизеля),    4  3 (для цикла Сабатэ -Тринклера).
Термический КПД цикла со смешанным подводом тепла определяется по
формуле:
tC T  1 
 k  1
 1  k 1
  1  k   1
(17)
Анализ формулы (36) свидетельствует, что термодинамический КПД
возрастает с повышением степени сжатия  , показателя адиабаты К, степени
повышения давления  и с уменьшением степени предварительного расширения
.
При одинаковых исходных значениях рабочего тела и степени сжатия
tO > tC T > tD
(18)
Но правомерней сравнивать значения термодинамических КПД в условиях
одинаковых максимальных параметров Ртах и Ттах - В этом случае
tD > tC T > tD
(19)
Термический КПД циклов ДВС может достигать 60 – 65%.
В реальных двигателях внутреннего сгорания, вследствие не обратимых
потерь работы, действительный КПД меньше термического и в среднем
составляет 30-40% для дизелей и 20- 30 % для карбюраторных двигателей.
Варианты заданий для выполнения расчетов студентами приведены в
приложении 4,5.
12
2. ПРИМЕР РАСЧЁТА ТЕРМОДИНАМИЧЕСКОГО ЦИКЛА
ПОРШНЕВОГО ДВИГАТЕЛЯ ВНУТРЕННЕГО СГОРАНИЯ
Рассчитать термодинамический цикл поршневого ДВС (рис.2.), если рабочим
телом является смесь идеальных газов следующего состава:
кислород О2  тО  0,113 ;
азот N 2  mN  0,730 ;
углекислый газ СО2  тСО  0,100 ;
водяные пары Н 2О  тН О  0,057 ;
2
2
2
2
Р
3
4
n
2
PV = idem
5
4
1
n
PV
1
= idem
V
Рис.2. Термодинамический цикл
ДВС со смешанным подводом тепла.
Температура и давление рабочего
тела в начале такта сжатия равны
соответственно t1 = 600 C и
Р1 = 0,105 Мпа. Показатель политроны в процессе сжатия (1 - 2)
n1 = 1,39, а в процессе расширения
(4 - 5) n2=1,36. Кроме того заданы
степень сжатия   V1 V2  15 ,
степень повышения давления
  Р3 Р2  1,4 и степень
предварительного
расширения   V4 V3  2
Определить:
Значение функций состояния в характерных точках цикла Р, v, t, и, h, s.
Изменение функций состояния Δи, Δh, Δs, термодинамическую l и
потенциальную w работы и теплообмен q во всех процессах цикла.
Работу цикла lц, его термический КПД  t , и КПД цикла Карно tk осуществляемой
в том же интервале температур. Изобразить цикл в координатах P-v и T-s.
Как измениться термический КПД цикла и его термодинамическое
совершенство, если политропный процесс расширения (4-5) заменить на
изотермический?
1. Определяем характеристики рабочего тела.
Средняя молекулярная масса смеси.
По таблице, приложения 3, определяем молекулярные массы компонентов
газовой смеси [кг/кмоль].
 О  32 ;  N  28 ;  СО  44 ;  Н О  18 .
2
2
2
2
13
Тогда
т 
 0,113 0,73 0,1 0,057 
1 



  28,54 кг/моль.
32
28 44
18 

 mi  i
1
n
i 1
Газовая постоянная смеси:
R  R m 
8314
 291,3
28,54
Дж/(кг К)
Средняя удельная изобарная теплоѐмкость смеси.
Интерполируем табличные данные по изобарным теплоѐмкостям идеальных
газов (приложение 1) и при температуре рабочего тела в начале такта сжатия
t1=600 имеем (в Кдж/(кг.К)):
С рт О2  = 0,926; С рт N2  = 1,046; C pm CO2  = 0,844; C pm H 2O  = 1,920.
4
С рт   mi Cipm =0,113·0,926+0,73·1,046+0,1·0,844+0,057·1,920 = 1,063 кДж1{кг - К).
i 1
Средняя удельная изохорная теплоѐмкость смеси
Сvm= Cpm – R = 1,063 – 0,291 =0,772 кДж/(кг·К).
Показатель адиабаты смеси идеальных газов
k  C pm C vm 
1,063
 1,377 .
0,772
2. Определяем термодинамические параметры состояния в характерных точках
цикла (рис.2).
Точка 1
Т1 = t1+273 = 60 + 273= 333 K;
v1 
RT1 291,3  333
3

 0,924 м /кг.
6
P1
0,105  10
Точка 2
Параметры в точке определим, зная степень сжатия s и уравнение политропного
процесса 1-2
0,924
3
 0,062 м /кг;
15
тогда Р2  Р1 v1 v2 n1  0,105 151,39  4,53 Мпа;
v2  v1  
Р1v1n1  P2 v2n1 ,
Р2 v2 4,53  10 6  0,062
Т2 

 964,2 К;
R
291,3
0
t 2  T2  273  964,2  273  691,2 С.
14
Точка 3
Так как процесс 2-3 изохорный:
3
v3  v2  0,062 м /кг;
Р3  Р2  1,4  4,53  6,34 Мпа;
Р3 v3 6,34  10 6  0,062

 1349,4 К;
R
291,3
0
t3  T3  273  1349,4  273  1076,4 С.
Т3 
Точка 4
Процесс 3-4 изобарный, поэтому
Р4  Р3  6,34 Мпа;
v4  v3  2  0,062  0,124 м /кг;
3
P4 v4 6,34  10 6  0,124

 2698,8 К;
R
291,3
0
t 4  T4  273  2698,8  273  2425,28 С.
T4 
Точка 5
Учитывая, что процесс 4-5 политропный, а процесс 5-1 изохорный, имеем
3
v5  v1  0,924 м /кг;
Р4 v4n  P5 v5n ;
2
2
1, 36
 0,124 
n
Р5  Р4 v 4 v5  2  6,34
  0,413 Мпа;
 0,924 
Рv
0,413  10 5  0,924
Т5  5 5 
 1310 К;
R
291,3
0
t5  T5  273  1037 С.
Полученный данные заносим в табл.3.
3. Определяем функции состоянии в характерных точках цикла.
1) Внутренняя энергия
иj = Cvm Tj;
где j - индекс точки цикла
u1 = 0,772 × 333 = 257,1 кДж/кг;
u2 = 0,772 × 964,2 = 744,4 кДж/кг;
u3 = 0,772 × 1349,4 = 1041,7 кДж/кг;
u4 = 0,772 × 2698,8 = 2083,5 кДж/кг;
u5 = 0,772 × 1310 = 1011,3 кДж/кг.
2) Энтальпия
hj = Cpm Tj
h1 = 1,063 × 333= 354,0 кДж/кг;
h2 = 1,063 × 964,2 = 1025,0 кДж/кг;
h3 = 1,063 × 1349,4 = 1434,4 кДж/кг;
h4 = 1,063 × 2698,8 = 2868,8 кДж/кг;
h5 = 1,063 × 1310 = 1392,5 кДж/кг.
15
3) Энтропия
sj = Cmp ln (Tj /TO) + R ln (PO /Рj);
где ТО = 273,15 К;
PО = 0,101·106 Па.
Так как приняли, что теплоѐмкость рабочего тела не зависит от температуры,
т. е.
Срт = Стр и Сvm = Cmv, тогда
s 1  1,063 ln
333
273,15
 0,291 ln
0,101
0,105
 0,200 кДж/(кг · К);
s 2  1,063 ln
964,2
0,101
 0,291 ln
 0,235 кДж/(кг · К);
273,15
4,53
s 3  1,063 ln
1349,4
0,101
 0,291 ln
 0,494 кДж/(кг · К);
273,15
6,34
s 4  1,063 ln
2698,8
0,101
 0,291 ln
 1,231 кДж/(кг · К);
273,15
6,34
s 5  1,063 ln
1310
0,101
 0,291 ln
 1,257 кДж/(кг · К).
273,15
0,413
Найденные значения функций состояния заносятся в табл.3.
Таблица 3
Значение параметров и функций состояния в характерных точках цикла
Номер
Р,
v,
t,
T,
u,
h,
s,
3
0
точки
МПа
м /кг
C
K
кДж/кг кДж/кг кДж/(кг К)
1
0,105
0,924
60
333,0
257,1
354,0
0,200
2
точки
3
то
4
5
4. Изменение
4,53
4,53
6,34
0,062
0,062
691
1076,4
964,2
1349,4
744,4
1041,7
1025,0
1434,4
0,235
0,494
6,34
0,413
0,124
0,924
2425,8
1037,0
2698,8
1310,0
2083,5
1011,3
2868,8
1392,5
1.231
1,257
функций
состояния
в
каждом
процессе
цикла ∆и, ∆h, ∆s
определяется как разность значений этих функций в конечной (j) и начальных
точках процесса (i) ∆Zi-j = Zj - Zi.
Результаты этих вычислений помещены в таблицу 4.
5. Находим термодинамическую l, потенциальную w работы и теплообмен q во
всех процессах цикла.
16
Процесс 1-2 - политропное сжатие
l12 
6
P1v1
1   12   0,105  10  0,924 1  2,896   471,7 кДж/кг.
n1  1
1,39  1
Характеристика сжатия
 12 
Т 2 964,2

 2,896 .
Т1
333
w12  n1l12  1,39 471,7   655,7 кДж/кг.
q1 2 
k  n1
k 1
l1 2 
1,377  1,39
 471,7   16,3 кДж/кг.
1,377  1
Процесс 2-3 — изохорный подвод тепла
l2-3 = 0;
w2-3 = - v(Р3 – Р2) = 0,062(6,34 · 106 – 4,53 · 106) = - 112,2 кДж/кг;
q2-3 = Δu2-3 = 297,3 кДж/кг.
Процесс 3-4 - изобарный подвод тепла
w3-4 = 0;
l3-4 = P3(v4 – v3) = 6,34 · 106(0,124 – 0,062) = 393,1 кДж/кг;
q3-4 = Δh3-4 = 1434,4 кДж/кг.
Процесс 4-5 - политропное расширение
l 4 5 
6
P4 v 4
1   45   6,34  10  0,124 1  0,485  1124  50,7 кДж/кг.
n2  1
1,36
Характеристика расширения
 4 5  Т 5 Т 4 
1310
 0,485 .
2698,8
w45  n2l45  1,36 1124,7  1529,6 кДж/кг.
q 4 5 
k  n2
1,377  1,36
l 4 5 
1124,7  50,7 кДж/кг.
k 1
1,377  1
Процесс 5-1 — изохорный отвод тепла
l51  0 ;


w51  v5 P1  P5   0,924 0,105  10 6  0,413  10 6  284,6 кДж/кг
Результаты вычисления заносим в табл.4.
17
Таблица 4
Изменение функций процесса и состояния в процессах цикла
Процесс
1-2
2-3
3-4
4-5
5-1
Σ
и , кДж/кг
h , кДж/кг
487,3
297,3
1041,8
-1072,2
-754,2
0
671,0
409,4
1434,4
-1476,3
-1038,5
0
l, , кДж/кг
w, кДж/кг
q, кДж/кг
s, кДж/кг
-471,7
0
393,1
1124,7
0
1046,1
-655,7
-112,2
0
1529,6
284,6
1046,3
16,3
297,3
1434,4
50,7
-754,2
1044,5
0,035
0,259
0,737
0,026
-1,057
0
Проверка полученных результатов по первому началу термодинамики для
каждого процесса и цикла в целом
qi  j  u i  j  li  j  hi  j  wi  j
 q   l   w
показывает, что относительная погрешность расчѐтов, наличие которой связано с
проводимыми округлениями, мала, что допустимо для приближѐнных
термодинамических расчѐтов.
6. Определяем работу цикла lц, термический КПД цикла ηt и КПД цикла Карно ηtк
lц  l12  l23  l34  l45  l51  -471,7+0+393,1+1124,7+0=1046,1 кДж/кг;
 t  lц / q1 
где су, - количество подведенного тепла Ч\ = ^-2 + ^2-3 + ^-4 + ^1-5 =
16,3+297,3+1434,3+50,7 = 1798,7 кДж/кг;
0,88 или 88%. 2698,8
7. Изобразим цикл поршневого ДВС в координатах P-v и Г-^(рис.3 а, б). Для этого
определяем координаты промежуточных точек в процессах цикла. а. Расчѐт
промежуточных точек для построения цикла в P-v координатах.
б)
Рис.3. термодинамический цикл поршневого ДВС со смешанным подводом тепла.
Промежуточная точка х в процессе политропного сжатия 1-2 Выбираем 1\ = 2
МПа(^ < Р, < Р^), тогда по уравнению политропы
/^"i _ p,,"i I i^i —-f-i i'->.
-0^4^05
Промежуточная точка в процессе политропного расширения 4-5 Принимаем Г, = 3 МПа (^ > 1\.
> Р,) и учитывая, что Г^'"^ = 1\.\^ , получим
^
у \ 1 II,
=(Ш4^
^=^
=0,215м7к1-.
б. Расчѐт промежуточных точек для построения
цикла в Т-^-координатах.
Промежуточная точка z в процессе 1-2. Принимаем Т. = 600 К (Г, < Т. < Г,). Тогда т^ =Т_П\ =
( Г. 1 1\ )<"-"'"",
18
( ^г^n'\'^"•''^~^
P. = Р^Т./Т^" *""" = 0,105^^
= 0,858 МПа,
{333)
x = С In ^+7? In ^-= 1,063 In -^^ +0,291 In ^^ = 0.215 кДж/(кг К). '
0,858
' To
Г.
273,15
Промежуточная точка i в процессе изохорного подвода тепла 2-3 Принимаем 7; 1 150 К (Г) < Т, < J}). Так как v, = ^ = 0.062 м^ /кг,
„ RT, 291,3-1150 _,,^ Р = —'- = —----— ^ ^,4 МПа,
' v,
0,062
л = С In ^'- + ^ In -^ = 1 063 In -li^- +0 291 In ^^ = 0,370 кДж/(кг • К). ' "" 7„
273,15
5,4
7^
Промежуточная точка j в процессе изобарного подвода тепла 3-4
(7" =Р,= 6,34 МПа)
Принимаем 7\. = 2000 К (7^ < ^ < 7^ ).
л' - С In -'- + R In ^ = 1,063 In -^^L + 0,291 In ^^- = 0,91 I кДж/(кг K). ' "'" 7„
273,15
6,34
7^
Промежуточная точка m в процессе 4-5 Принимаем 7„, - 2000 К (7, > Т, > 7,),
т
-'."L-(plp'\"'-^"--^ 4-iii
^
V ill I •' 4 )
'
^-1
(т V' ^"
^ =^^
'" \rJ
Г 2000 V^'-^
= 2,04 МПа,
=6.34-^"-
12698.8,1
v Г li/"'l^ln^-1.06^1n^^ l 0.:^>l!n ^'"'-1.241 кЛж^кг K).
""
'/„
/',
273.15
2,04
Промежуточная точка п в процессе изохорного отвода тепла 5-1 Принимаем 7„ - 800 К (7, >
Т, > 7,) и учитываем, что v„ - v, = 0,924 м' /KI.
^^=^^= 0,252.10-Па.
1'„
0,924
.s' =(' In ^-+R In ^-1,063 In -°^+0,291 In ^^L= 0,877 кДж/(кг К).
' 7,
P,
273,15
0,252
8. Проведѐм расчѐт термодинамического цикла поршневого ДВС с изотермическим расширением в
гак ie раооче! о хода 4-5.
При данном изменении в цикле определяем термодинамические параметры состояния в точке 5\
Т,. = 7, = 2698,8 К:
^ = ^ = 0,924 м' / KI :
/. = ^ = -^-0.85 МПа.
v-,
0 924
19
Термодинамическая работа / и теплообмен q. Процесс 4-5'
/^
/^/1
/, -. - q,.. = R1\ In ^ = 0,291 • 2698.S In ''^ = 1578.1 кДж/кг. '
0.85
'
' !\.
Процесс 5'-l /._, = 0;
q^ = Д»,._1 = C„,„(/i - /„) = 0,772(60 - 2425,8) = 1826,4 кДж/кг.
Работа цикла /'„ =S/=-471,7+ 393,1 +1578.1 - 1499,5 кДж/кг.
Трепло подведѐнное к рабочему телу q'i = 16,3 + 297,3 +1434,4 +1578.1 3326.1 кДж/кг.
Термический КПД цикла
/' 1499 5
/p = -^ = --— = 0,45 пли 45%. ' q', 3326,1
Коэффициент полезного действия цикла Карно остался неизменным, так как не
изменились минимальная 7^ и максимальная 7'^ температуры цикла.
9. Замена политропического процесса расширения с показателем политропы и, > 1 на
изотермический приводит к снижению термического коэффициента полезного действия. Кроме
того, снижается и термодинамическое совершенство цикла, так как в первом случае работа
цикла /, составляет 66% от теоретически возможной работы цикла 1ц.,. = q^^ , а во втором
случае этот показатель, называемый коэффициентом заполнения, снижается до 51%.
3. Расчёт цикла на ЭВМ
3.1 Краткое описание расчетных программ
Предлагаемые программы предназначены для расчѐта двух термодинамических циклов
поршневых двигателей внутреннего сгорания.
Программы расчѐта термодинамических циклов поршневых ДВС написаны на языке
Бейсик с использованием программы Microsoft QuickBASIC V4.5 и позволяют определять
термодинамические параметры (давление P, объѐм V, температуру Т)и изменение функций
состояния (энтальпииЛН, энтропии A.S', внутренней энергии д^') и процессов (работу /,
потенциальную работу W, количество теплоты q) для процессов и оценить эффективность
цикла (термический коэффициент полезного действия //,). В программе не включены расчѐты
газовой смеси: удельных теплоѐмкостей, показателя адиабаты идеальных газов: которые
производятся предварительно исполнителем до выхода на ЭВМ. Однако предусмотрены
расчѐты программами молекулярной массы смеси и газовой постоянной.
В программах предусмотрено проведение расчѐтов для циклов с переменными исходными
данными, что позволяет ш-юпести анплиз •-x!)(hcь:тин^^oc'ти
20
цикла, выявить факторы, влияющие на термический коэффициент полезного действия.
В программах не предусмотрено проведение расчѐтов промежуточных точек процессов с
целью построения термодинамических циклов поршневых ДВС в координатах P-V и T-S.
Подобные расчѐты проводятся самим исполнителем. Такое сочетание машинных и ручных
расчѐтов позволит студентам лучше изучить вопросы, связанные с расчѐтом
термодинамических циклов поршневых ДВС.
Последовательность расчѐтов циклов на ЭВМ строго совпадает с примерами расчѐтов
циклов поршневых ДВС, результаты проведѐнных расчѐтов на ЭВМ практически совпадают с
ручным расчѐтом. 3.2 Обращение к программам
Программы расчѐта термодинамических циклов поршневых ДВС записаны на диске в
исполняемых скомпилированных файлах с расширением .ехе.
Для проведения расчётов необходимо
1. из среды DOS - набрать А:\*.ехе, где вместо символа «*» набрать имя требуемой
программы и нажать клавишу HNTER.
2. Из оболочки типа "Norton Commander" - навести клавишами управления курсором либо
мышью на нужный файл и нажать клавишу ENTER или на левую кнопку мыши.
Программы записаны на диске под именами:
•для расчѐта параметров термодинамического цикла поршневых ДВС с изохорным
подводом тепла «Pvt_V_id.ехе»;
•для расчѐта термодинамического цикла поршневых ДВС с изорным подводом тепла —
«V idem.ехе»;
•для расчѐта параметров термодинамического цикла поршневых ДВС со смешанным
подводом тепла-«Pvt_sm.ехе»;
•для расчѐта термодинамического цикла поршневых ДВС со смешанным
подводом тепла - «Smesh.ехе».
В процессе работы можно в любой момент прекратить работу программ нажатием клавиш
Ctrl + Pause/Break. 3.3 Исходные данные для расчёта
Т - абсолютная температура рабочего тела в начале такта сжатия, К; Р - давление рабочего тела
в начале такта сжатия, МПа; К^К^ -показатель адиабат в процессах сжатия и расширения
рабочего тела;
£- степень сжатия в ДВС;
/1- степень повышения давления в процессах подвода при V^idem; р'- степень
предварительного расширения в процессе подвода тепла при P=idem;
i\.r^i\ -доли газовых компонентов в смеси; ^.//,,/л -молярные
массы компонентов смеси;
21
С"" - удельные средние изобарные теплоѐмкости смеси газов в процессах,
кДж/кг К.
3.4 Соответствие обозначений методики и программ расчёта на ЭВМ. Соответствие
обозначений методики и программ расчѐта на ЭВМ приведено в табл.5. Таблица 5
Обозначение величин в методике расчёта.
Обозначение величин в программах
Р
Р
V
V
Т
Т
AIJ
U
АН
н
AS
S
1
L
W
W
q
0
£ = V, /V,
F
^=P,/P,
Е
^=V.^/V,3,
RO
R
R
C;:"
С
^C!U
С1
K\
N
K,
NI
1~i
К
r(i)
Z(i)
R(i)
X(i)
m,
Mcom(i)
3.5. Расчетная часть
Пример расчета. 1 кг. рабочей смеси совершает цикл со смешанным подводом тепла.
Исходные данные:
r -0.15; r -0.3; r =0.5. H^
02
возд
Р1=102254Па; Ti=304,21K; Ki=1.359; K2=1.298.
£=^=\~7.5- l=^=l.S•,p=^=}.5.
^
^
^ Определить:
1. Параметры P V Т в характерных точках цикла;
2. Средние массовые теплоемкости в процессах цикла;
22
3. Термодинамическую работу 1, потенциальную работу W, теплоту q, изменение внутренней
энергии ли,энтальпии Ai, энтропии AS в процессах цикла, работу цикла 1ц, термический
КПД цикла п\.
4. Построить цикл в координатах P-V и T-S.
Решение:
1 . Расчет газовой постоянной и параметров в характерных точках. Включаем компьютер. После
появления на мониторе панелей программы Norton Commander нажимаем Alt+FI, выбираем
диск А, клавишами управления курсором или мышью наводим на файл "PVT_SM",после
чего нажимаем клавишу ENTER или левую кнопку мыши. На экране появляются следующие
надписи: Программа расчета параметров цикла ДВС со смешанным подводом
тепла
Введите исходные данные Т в 1 точке цикла, К?
С клавиатуры последовательно набираем данные, следуя запросам:
304.21
Р в 1 точке цикла, Ра? 102254 Степень
сжатия? 17.5
Соотношение давлений в процессе подвода тепла? 1.8 Соотношение
объемов в процессе подвода тепла? 1.5 Показатель адиабаты в
процессе сжатия? 1.359 Показатель адиабаты в процессе
расширения? 1.298 Количество компонентов смеси? 3 Доля 1
компонента? 0.15
Молекулярная масса 1 компонента, кг/моль^ 2.016 Доля 2
компонента? 0.35
Молекулярная масса 2 компонента, кг/моль? 32 Доля 3
компонента? 0.5
Молекулярная масса 3 компонента, кг/моль? 28.96 Результаты
Pi= 102254
V^,9519715
T1=304,21 ?2=4999988
V2^5,4398837E0,2
T2= 850,0101 Рз=8999978
Уз=5,4398837Е-0,2
T3= 1530,018
?4=8999978
^8,597555-0,2
J4= 2295,027 Ps=370974,9
Vs=,9519715
Т5=1103,666
Переписываем данные в таблицу (см. таблицу 6), попутно вычисляя температуру в"С, отнимая
от абсолютной 273,15:
23
Таблица 6
Точка
1
2
3
4
5
Р,Па
V, м"/кг
102254
0,9519715
4999998
0,054398837
8999978
0,054398837
8999978
0,0859755
370974,9
0,9519715
Т, К
t,"C
304,21
31,06
850,0101
576,8601
1530,018
1256,868
2295,027
2021,877
1103,666
830,516
2. Расчет средних массовых теплоемкостей в процессах цикла А. Средние массовые
теплоемкости компонентов смеси определяются методом линейной интерполяции по
приложению 1 и 2, обязательно проверяя расчет по закону Майера. Например, для кислорода
в интервале температур от О "С до 31,06 "С:
31.06
ртО"^ О
С
^-0.260^ 32
31.06
vmO-) О
кг К
=R
С
(ъ
R
R(h
^ъ 0,917-0,657=0,260
После проверки данные сводят в таблицу (см. таблицу 7)
Таблица 7
Диапазон
температур
Теплоемкости, кДж/кгК
С ""0.
С ""0,
С ""возд.
С "^
С "•"0.
С ""возд.
0-31.06
0-576.8601
14.244
14.534
0.917
0.990
1.004
1.047
10.120
10.409
0.657
0.730
0.717
0.760
0-1256.868
0-2021,877
14.985
15.554
1.055
1.106
1.113
1.168
10.860
11.636
0.795
0.846
0.826
0.881
0-830.516
14.661
1.019
1.074
10.537
0.759
0.787
Б. Средние массовые теплоемкости смеси от О "С до температур точек цикла определяются по
формуле (3). Расчет обязательно проверяется по закону Майера. Данные заносятся в таблицу 8:
Таблица 8
0 "С - t "С
0-31,06
0-576,8601
0-1256,868
0-2021,877
0-830,516
cm . кДж ^Р"^
кгК
1.112
1.171
1.240
1.301
1.200
cm. хДж ^"^
кгК
0.795
0.853
0.923
0.984
0.882
В. Средние массовые теплоемкости смеси в процессах цикла расчитываются по формуле (2).
Проверив расчет по закону Майера, заполняем таблицу 9.
24
Таблица 9
Процесс
1-2
Диапазоны
температур
cm . кДж ^Р^'
кгК
2-3
3-4
4-5
5-1
31,06-576,8601 576,86011256,868
1256,8682021,877
2021,877830,516
830,516-31,06
1,174
1,300
1,390
1,367
1,203
cm. кДж ^^'' кгК 0,856
0,982
1,072
1,049
0,886
3. Расчет функций состояния и процессов.
Запускаем программу "Smesh". В соответствии с запросами программы вводим
исходные данные (указанные в пункте 1), газовую постоянную и средние
массовые теплоемкости смеси в процессах цикла (таблица 9): Программа
расчета цикла ДВС со смешанным подводом тепла Введите исходные данные
Т в 1 точке цикла, К? 304.21 Р в 1 точке цикла, Ра? 102254 Степень сжатия?
17.5
Соотношение давлений в процессе подвода тепла? 1.8
Соотношение объемов в процессе подвода тепла? 1.5
Показатель адиабаты в процессе сжатия? 1.359 Показатель
адиабаты в процессе расширения? 1.298 Изобарная
теплоемкость в процессе 1-2, кДж/кгК? 1.174 Изобарная
теплоемкость в процессе 2-3, кДж/кгК? 1.3 Изобарная
теплоемкость в процессе 3-4, кДж/кгК? 1.39 Изобарная
теплоемкость в процессе 4-5, кДж/кгК? 1.367 Изобарная
теплоемкость в процессе 5-1, кДж/кгК? 1.203
Процесс 1-2
Процесс 5-1 W=-255,8147 H=-961,7457
КПД цикла 0,5917761
L=-486,4855
U=466,6591
L=0
U=667,0878
L=244,7921
U=819,3426
L=
1279,257
U=-1248,546
L=0
U=-706,7192
Термический
W=-661,1339 H^640,7693 Процесс 23 W=217,5929 H=884,0104
Процесс 3-4 \N=0 H=1063,363
Процесс 4-5 W-1660,476 H=1628,59
25
Q=0 S-0
Q=667,0878 S=0
Q=1064.117 S=0
Q=0 S=0
Q=-706,7192 S=0
Работа цикла 1024,485
26
Данные переписываем в таблицу 10
Таблица 10
процессы
1, кДж/кг
W, кДж/кг
Ди, кДж/кг
Ai, кДж/кг
AS. кДж/кг
q, кДж/кг
1-2
-486.4855
-661.1339
466.6591
640.7693
0
0
2-3
0
217.5929
667.0878
884.0104
0
667.0878
^-4
^447^1
О
81^3^46
1063 363
0
1 064 1 1 7
4-^
5-1
12/^.25/
0
166U.4 /6
-255.8147
-1248.546
-706.7192
-1628.59
-961.7457
0
0
0
-706.7192
4. Построение цикла в P-V и T-S координатах При построении цикла в координатах P-V сначала
строятся характерные точки цикла (1,2,3,4^) по известным значениям давления и удельного
объема. Затем процессы, изображаемые прямыми линиями - изохорный 2-3 и 5-1, изобарный
3-4. Для построения криволинейных адиабатных процессов 1-2 и 4-5 необходимо
определить 2-3 промежуточные точки между характерными по уравнениям процесса (см.
таблица 2).
При построении цикла в координатах T-S сначала также строятся характерные точки
цикла по значениям Т и Д8. Так как абсолютное значение энтропии неизвестно ни для одной
из точек , то она выбирается произвольно, затем строятся процессы, изображаемые прямыми
линиями- адиабатные. При построении промежуточных точек криволинейных процессов
температуры этих точек задаются, а изменение энтропии определяются по формулам
(таблица 2).
Таким образом, используя данные расчета характерных и промежуточных точек,
термодинамический цикл изображается в масштабе в P-V и T-S координатах в
миллиметровой бумаге.
27
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое круговой процесс, термодинамический цикл?
2. Что называется тепловым двигателем, холодильной машиной?
3. Как графически, в P-V координатах, определишь работу, затраченную на сжатие рабочего
тела и работу цикла теплового двигателя?
4. Как графически, в T-S координатах, определить количество тепла, подведенного к рабочему
телу, полезно используемого в термодинамическом цикле теплового двигателя?
5. Напишите выражение первого начала термодинамики для цикла.
6. Как определяется коэффициент полезного действия теплового двигателя,
термодинамического цикла теплового двигателя?
7. Изобразите цикл Карно в P-V и T-S координатах.
8. Как определяется КПД цикла Карно?
9. Почему не применяется цикл Карно для реальных поршневых двигателей внутреннего
сгорания, газотурбинных установок, паросиловых установок?
10. Как увеличить КПД термодинамического цикла тепловых двигателей? 1 1. Изобразите
циклы поршневых ДВС с адиабатными процессами сжатия и расширения рабочего тела и
изохорным, изобарным и смешанным подводом тепла в P-V и T-S координатах.
12.Сравните КПД термодинамических циклов Отто, Дизеля и Сабатэ-Тринклера при
одинаковых значениях степени сжатия, максимальной температуры.
13. От каких параметров зависит термический КПД цикла Отто, Дизеля и Саба-тэ-Тринклера?
14. Изобразите термодинамические циклы Брайтона и Гемфри для ГТУ в P-V и T-S
координатах.
15. Сравните КПД термодинамических циклов Брайтона и Гемфри.
16.От каких параметров зависит термический КПД цикла Брайтона?
17. Что дает регенерация тепла в ГТУ?
18. Из каких агрегатов состоит ГТУ? Какое их назначение, и какие термодинамические
процессы в них осуществляются?
19. Изобразите цикл ГТУ (поршневого ДВС) в T-S координатах с необратимыми потерями в
процессах сжатия и расширения рабочего тела.
20.Как в P-V и T-S координатах будут изображаться политропные процессы сжатия и
расширения рабочего тела с показателем, отличным от показателя
адиабаты ( ^k)?
28
ЛИТЕРАТУРА
1. Кириллин В.А., Сычев В.В., Шейндлин А.Е. « Техническая термодинамика» - М.:
Энергоиздат, 1983.
2. Техническая термодинамика (под ред. д.т.н.,проф.,Крутова В.И.).-М.: Высшая школа, 1981.439 с.
3. Иванов И.А., Крамской В.Ф., Моисеев Б.В., Степанов О.А. Теплоэнергетика при
эксплуатации транспортных средств в нефтегазодобывающих районах Западной Сибири. М.: Недра, 1997.- 269 с.
4. Сборник задач по технической термодинамике и теплопередаче (под ред. Юдаева Н.Б.).- М.:
Высшая школа. 1964.- 372 с.
5. Рабинович О.М. Сбооник задач по технической теомодинамике. М.. 1969.
кс.-М.: Энергия. 1971. 352 с.
7. Андрианова Т.Н., Дзампов Б.В., Зубарев B.I 1., Ремизов С'.А. «Сборник задач по технической
термодинамике».- М.Энергоиздат, 1981 .- 240 с.
8. Теплотехника (под ред. д.т.н.,проф., Луканина В.Н.).- М.: Высшая школа. 1999.-671 с.
29
Приложение 3
Газ
HZ
02
воздух
N2
CO
R, Дж/кгК
// ЛО^кг/моль
р, кг/м^
4124
2.016
0.090
259.8
32
1.429
287
28.96
1.293
296.8
28.016
1.251
296.8
28.01
1.250
Характеристики некоторых газов
Приложение 4
состав рабочей сшеси в объемных долях
^^^^Газ № 02
^^\ •"смеси \
1
0,25
N2
H2
CO
H20
Воздух
0,35
-
0 25 \J,L.J 0,15
-
-
i
0,15
0,50
0,10
0,25
-
-
"t
4
0,60
0,80
0,20
-
0,20
0,10
-
0,10
-
-
5
6
0,35
0,50
-
0,15
0,20
—^—-
0,30
-
0,50
-
7
8
-
0,50
-
0,10
-
•
0,50
0,20
0,20
0,20
0,20
0,10
9
-
-
-
-
0,30
0,30
0,40
10
11
0,30
-
0,20
-
0,70
-
-
0,30
0,10
0,40
12
13
0,40
0,20
0,20
-
0,20
-
0,40
-
0,20
0,40
-
14
15
0,30
0,30
0,25
0,10
0,30
0,25
-
-
0,50
-
16
17
0,60
0,40
-
0,10
-
0,40
0,20
0,10
-
0,20
-
18
-
0,35
0,05
0,20
-
-
0,40
19
20
0,30
-
-
0,20
0,20
0,30
0,40
0,30
0,10
-
0,20
21
22
0,35
0,10
0,35
0,10
-
0,40
-
-
0,30
0,40
23
-
-
0,20
0,30
0,20
0,30
-
24
0,25
0,25
-
0,25
-
-
0,25
25
26
0,15
0,20
-
0,30
-
-
0,30
0,20
0,40
0,20
0,25
27
28
0,35
-
0,35
0,10
-
0,45
0,05
0,20
0,25
0,25
-
29
30
0,40
-
0,40
-
0,35
0,10
0,20
0,10
0,35
-
0,10
002
30
Приложение 5
Варианты заданий
^ 4 —\ ё q=Q ^\ /^^\
^
£-=V2/Vi /l^Pz/Pl ^V4/V3 5 3 2
1
£-=V,/V2 S q=Q X =Рз/Р2 ^ P=\ ^^^4 ^^^1
^ (D £
Sди
^и
го
P
1
su
иS
UЙ
Ю
c3
нu
оо
^
^ и & >^
^ a n "L>
С s OJ ^
^
(U ^ [< м г^ >s
^ m ^ S Й> ^ ^ ^
l~'[ ^ ^ ю ^ 0
F^
^ (U S
SКЯ
^Я
!Г)
/1
^ я &< ^ ь и s и д с ^ ^ is S g> и S
и о, (ц с S ^ и я ^ ^ ^ ^ i) ^ ^ ю U я
<и Н ^
&ч
^о
ии
^U
оu
^
1
2
"t
4
1.5
1,4
1,3
1.3
1.5
1.7
1,6
1,6
1,7
1.7
5
9
14
17
21
Ti=350
350
300
350
300
-
V-0,35
0,3
0,35
0,3
0,35
21
22
23
24
25
9
8
8,2
7,5
8,5
3,4
3,4
3,4
3.4
3,7
Т2=750
750
800
820
T i-3 50
-
V4-1.3
1.35
1,25
1.3
1,35
8
19
26
15
8
1,5
1.4
1.5
1,4
1.5
1,8
1.7
1,6
1,8
1,6
5
9
14
17
21
Ь-850
900
820
830
850
P2=5
5,6
5,6
5,6
5,6
-
26
27
28
29
30
7,5
8
8,5
7,5
7,6
3,8
3,8
4
4
4
370
380
Тз=2500
2400
2450
-
1,35
1,35
1,4
1,4
1,4
19
26
8
19
26
T4=2800
2700
2600
2500
2400
T—1800
1600
1700
1750
1650
350
T4=2800
-
V,=0,3
0,3
0.3
0.3
0,3
V.-0,35
0,4
0,3
0.35
0.4
0,35
0,35
31
32
104
105
8,2
8,2
8
8
4
3,9
4
4
2300
Ь=700
Тз=2700
2700
Р2=0,5
-
1,4
Уз=0,32
0,32
15
26
6
7
^
6
7
8
9
10
1
12
13
14
15
16
17
18
19
20
i io
ii
17
16,
5
16
17
16,
5
17,
5
17
16,
5
17
17,
5
18.
1.4 1,8 5
5
18
1.4 1.7 9
18, 1.3 1.7 14
5
5
18
1.3
1.9 17
5
18 1,3 1,9 21
20 1,4 1,6 5
20 1.4 1,5 9
20 1.4 1.4 14
20 1.4 51,4 17
20 1.4 1.4 21
17 1.6 1.7 1
19 1,4 1.9 28
31
Содержание
Введение............................................................3 Требования к выполнению домашнего задания по
термодинамическим циклам тепловых двигателей ...............4 1 . Теоретическая
часть...........................................4 1.1 Основные понятия и расчетные соотношения..........5 1.2
Газовые смеси..................................................5 1 .3 Теплоемкость...................................................6 1
.4 11оказатель адиабаты ..........................................7 1.5 Первое начало
термодинамики..............................7 1 .6 Термодинамические процессы..............................8 1 .7
Второе начало термодинамики..............................8 1 .8 Круговой процесс
(цикл)......................................9
1.9 Термодинамические циклы поршневых двигателей внутреннего
сгорания.........................................! 1
2. Пример расчета поршневого двигателя внутреннего
сгорания..............................................................13
3. Расчет цикла на ЭВМ.........................................20 3.1 Краткое описание расчетных
программ..................20 3.2 Обращение к программам...................................21 3.3 Исходные
данные для расчета.............................21 3.4 Соответствие обозначений методики и программ
расчета на ЭВМ........................................................22 3.5 Расчетная
часть...............................................22 Контрольные вопросы...........................................27
Литература......................................................... 28 Приложения.......................................................29