Численные методы вычисления интегралов
advertisement

Лабораторная работа
Численные методы. Вычисление интегралов.
Теория
x
b
h
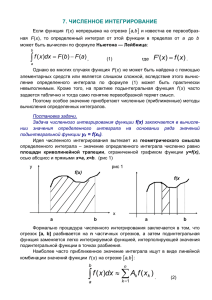
Рис. 2. Равномерная сетка переменной x
Пусть задана функция f(x), определенным интегралом функции f(x) от a до b называется
конечное число, равное пределу lim
Δxi →0
∞
∑ f ( x ) ⋅ Δx
i =1
i
i
, где xi, xi-1 – значения переменной x,
b
лежащие в интервале [a, b], Δxi = xi − xi −1 . Это число обозначается
∫ f ( x)dx .
a
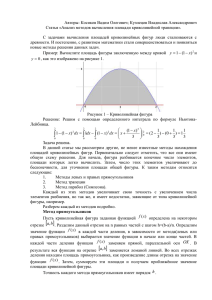
Определенному интегралу можно дать простую геометрическую интерпретацию - он
равен площади криволинейной
трапеции, ограниченной слева,
справа вертикальными прямыми
x=a, x=b, снизу - прямой y=0, а
сверху – кривой y=f(x) (рис. 1). В
соответствии
с
этой
b
интерпретацией иногда говорят,
что определенный интеграл равен
«площади под графиком функции»
a
или
площади
криволинейной
трапеции.
Эта геометрическая интерпретация
лежит в основе численных методов
Рис. 1. Геометрическая интерпретация
вычисления
определенных
интегралов. Из них, наиболее распространенными на практике являются метод
прямоугольников, метод трапеций и метод парабол, так же называемый методом
Симпсона.
Суть всех перечисленных методов состоит в нахождении площади не исходной
криволинейной трапеции, а площади некоторой более простой геометрической фигуры.
Естественно, что найденная площадь не будет совпадать с площадью криволинейной
трапеции – все перечисленные выше методы являются приближенными. Погрешность
вычисления интеграла зависит от того, насколько точно контур предложенной фигуры
повторяет контур исходной криволинейной трапеции.
Рассмотрим методы численного интегрирования подробнее. Для простоты будем иметь
дело с равномерными сетками переменной x (рис. 2).
Равномерная сетка {xi} характеризуется числом точек N и значениями a и b - крайней
левой и правой границей интервала переменной x, и задается следующим образом:
(1)
xi=a+i·h,
b−a
где индекс i пробегает значения от 0 до N-1, шаг сетки h =
.
N −1
y
f(x)
S=f(x)dx
b
x
1
Метод прямоугольников
Заменим фигуру «под графиком функции» на множество прямоугольников, как показано
на рис. 3.
Площадь Sпр построенной таким образом фигуры равна сумме площадей
прямоугольников, имеющих высоту fi и основание h и определяется формулой
f(x)
y
f(x)
y
b
Рис. 3. Метод прямоугольников.
b
x
x
N −1
S пр 2 = h ∑ f i .
(2б)
i =1
либо
N −2
S пр1 = h ∑ f i ,
(2а)
i =0
Метод трапеций
Заменим фигуру «под графиком функции» на множество трапеций, как показано на рис.
4. Площадь Sтр построенной таким образом фигуры равна сумме площадей трапеций,
имеющих длину оснований fi и fi+1 и высоту h.
Заметим, что площадь каждой трапеции есть среднее арифметическое площадей
прямоугольников с высотами fi и fi+1, использованных при построении формул (2а) и (2б).
Таким образом, искомая площадь фигуры равна
y
f(x)
b
Рис. 4. Метод трапеций.
x
2
N −1
N −2
1 ⎛ N −2
⎞ h
(3)
⎜ h ∑ f i + h∑ f i ⎟ = ( f 0 + f N −1 ) + h ∑ f i .
2 ⎝ i =0
i =1
i =1
⎠ 2
Метод парабол (метод Симпсона)
Этот метод основан на замене фигуры «под графиком функции» множеством
криволинейных трапеций (рис. 4). Верхние стороны трапеций представляют собой части
парабол, пересекающих график подынтегральной функции в точках xi. Другими словами,
метод основан на использовании интерполяции параболами таблично заданной функции
f(x) и вычислении интегралов от интерполирующих функций (парабол). Для нахождения
формулы площади параболической трапеции удобно сместить ось Y декартовой системы
S mp =
y
f(x)
2
ax +bx+c
x
Рис. 4. Метод Симпсона. Замена «фигуры под графиком» на
параболические трапеции.
координат так, чтобы она проходила через узел сетки переменной x.
Очевидно, что площадь трапеции (выделенной цветом фигуры) при этом не изменится и
будет определяться выражением
2h
8a 3
s = ∫ (ax 2 + bx + c )dx =
h + 2bh 2 + 2ch
(4)
3
0
коэффициенты a, b и c находятся из системы уравнений
c = f i −1
⎫
⎪
2
(5)
ah + bh + c = f i
⎬,
4ah 2 + 2bh + c = f i +1 ⎪⎭
которая является условием равенства высот параболы в точках xi-1=0, xi=h и xi+1=2h
соответствующим значениям функции fi-1, fi, fi+1. Решение этой системы:
1 f − 2 f i + f i +1
1 3 f − 4 f i + f i +1
,
, c = f i −1 .
(6)
a = ⋅ i −1
b = − ⋅ i −1
2
2
h
2
h
С учетом этого, выражение для площади параболической трапеции принимает вид
h
(7)
s = ( f i −1 + 4 f i + f i +1 )
3
Для численного интегрирования функции по методу Симпсона необходимо найти сумму
площадей трапеций (7).
3
SS =
⎞
h ⎛⎜
f 0 + 4 f1 + f 2 + f 2 + 4 f 3 + f 4 + ... + f N −5 + 4 f N −4 + f N −3 + f N −3 + 4 f N −2 + f N −1 ⎟ =
4244
3 14
4244
3
144424443 14442444
3⎟
3 ⎜ 14
⎝
⎠
h
( f 0 + 4 f1 + 2 f 2 + 4 f 3 + 2 f 4 + ... + 2 f N −5 + 4 f N −4 + 2 f N −3 + 4 f N −2 + f N −1 ) .
3
Объединяя повторяющиеся слагаемые, получаем
N −3
N −3
⎛
⎞
2
2
h⎜
⎟
S S = ⎜ f 0 + 4 ∑ f 2 k +1 + 2 ∑ f 2 k + f N −1 ⎟
3⎜
k =0
k =1
⎟
⎠
⎝
Эта формула называется формулой парабол или формулой Симпсона.
=
(8)
Задание
1
2
Смоделировать таблично-заданную функцию { f i , xi } , используя аналитически
заданную функцию f(x).
Вычислить точное значение интеграла (аналитически)
x N −1
3
Численно
вычислить
интеграл
∫ f ( x )dx ,
используя
формулы
x0
4
прямоугольников, трапеций, парабол.
Сравнить точное значение рассматриваемого интеграла и значения, полученные
численными методами (из п. 3).
Варианты заданий
1.
2.
3.
4.
5.
6.
7.
8.
f ( x ) = x sin( x ) , a=0, b= π
f ( x ) = x cos( x ) , a=0, b= π
f ( x ) = xe − x , a=0, b=1
f ( x ) = sin 2 ( x ) , a=0, b= π
f ( x ) = cos 2 ( x ) , a=0, b= π
f ( x ) = x cos( x 2 ) , a=0, b= π
f ( x ) = x sin( x 2 ) , a=0, b= π
f ( x ) = x 2 e −2 x , a=0, b= π
Порядок выполнения работы
1.
Задать параметры сетки a, b, N; найти h, xi.
2.
Задать аналитически функцию F(x)=f(x).
3.
Вычислить значения функции в точках xi (fi=F(xi)).
4.
Вычислить интеграл по формулам (2, 3, 8) и вывести полученные значения.
5.
Сравнить эти значения с точным интегралом (если это возможно).
4