"Коллоидная химия" по теме "Адсорбция газов и паров"
реклама

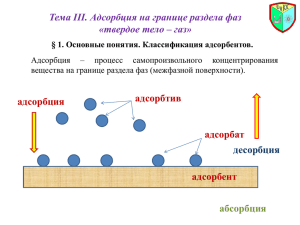
АДСОРБЦИЯ ГАЗОВ И ПАРОВ НА ОДНОРОДНОЙ ТВЕРДОЙ ПОВЕРХНОСТИ Примеры? Области применения? Адсорбция Химическая (хемосорбция) Физическая Признак отличия Физическая адсорбция Хемосорбция Природа действующих сил Ван-дер-ваальсовы Химические Тепловой эффект, кДж/моль 4÷40 40÷400 Обратимость Обратима Необратима Способность молекул адсорбата к перемещению Локализованная, нелокализованная Локализованная Зависимость скорости от температуры W~ T E W ~ exp RT Изменение энергии поверхности Уменьшается Уменьшается Увеличивается Специфичность Неспецифична Специфична Примеры? ТЕОРИИ АДСОРБЦИЯ ГАЗОВ И ПАРОВ НА ТВЕРДОЙ ПОВЕРХНОСТИ a a∞ x kc1/n m p эмпирическое уравнение Бедекера-Фрейндлиха для ориентировочных расчетов a Классические теории адсорбции (1915 г) Ленгмюра Поляни Адсорбция – физический или химический обратимый процесс (трактовка сил межмолекулярного взаимодействия) единая теория? p Теория мономолекулярной адсорбции Ленгмюра • образуется монослой адсорбата a • адсорбция локализована (активные центры) a∞ • поверхность эквипотенциальная • адсорбированные молекулы не взаимодействуют друг с другом • поверхность адсорбента ограничена → насыщение поверхности p • адсорбированные молекулы определенное время удерживаются на поверхности адсорбента, они могут покинуть поверхность и их место займут другие • адсорбция носит квазихимический характер kp a a 1 kp Уравнение Ленгмюра Вывод уравнения? p/a p p 1 a a a k tg 1 ak 1 a p Теория Ленгмюра: Vм (эксп) = (0,03÷0,3) Vм (плотн) активные центры Vм – отличаются для газов близкой природы Vм – отличаются для одного газа при разной Т неоднородность центров Неприменима в большинстве случаев адсорбции газа на тв. поверхности! Применима: • в некоторых случаях обратимой хемосорбции (H ~ 40 кДж/моль) • при низких давлениях паров и температуре выше Tкр • для расчета сложных реальных процессов • для адсорбции молекул из растворов на твердой поверхности Теория полимолекулярной адсорбции Поляни (потенциальная теория Поляни) a конденсация p = ps • • • p • • • • Физические силы взаимодействия На поверхности адсорбента непрерывное силовое поле У поверхности адсорбента – адсорбционный объем, измеряемый экспериментально по а: V a Vм Действие адсорбционных сил уменьшается с расстоянием Полимолекулярная адсорбция Адсорбционный объем не зависит от температуры Адсорбат – в конденсированном состоянии (увеличение плотности без изменения силы взаимодействия) (поры!) Полимолекулярная адсорбция – результат вынужденной конденсации паров под действием поверхностных сил ε – адсорбционный потенциал (дифференциальная молярная работа адсорбции) работа по переносу 1 моль пара работа по сжатию адсорбтива от адсорбтива из достаточно удаленного равновесного давления пара в газовой фазе (р) от поверхности объема в до давления нас. пара в поверхностном слое рs адсорбционный объем при Т=const сорбента (рs) при Т=const RT ln р V a Vм a = f (p) RT ln рs р Майкл Поляни 4=0 (V4) адсорбент 3 (V3) 2 (V2) 1=max (V1) a характеристическая кривая для пары адсорбент/адсорбат T1 f V a T2 p/ps p/ps Fдисп ≠ f (T) V d 0 dT V V Vm a1 Vm a2 1 a1 → V → a2 p1 → ε → p2 T1 T2 2 a2 Vm a1 1 Vm 2 RT1 ln рs p RT2 ln ps p2 1 1 2 Т Т р 1 2 р2 рs 1 2 р s1 Аффинность характеристических кривых (лат. affinus – родственный, соответственный) Для одного адсорбента: i i 0 V 1 0 (стандарт) 2 коэффициент аффинности Vi Теория не дает уравнения изотермы адсорбции, только ТД описание! Широко используется для описания адсорбции на пористых телах! Михаил Дубинин Теория БЭТ (Брунауэра-Эммета-Теллера) (1935–1940 гг) (обобщение теорий Ленгмюра и Поляни) Основные положения теории БЭТ: 1. На поверхности адсорбента имеется определенное число АЦ 2. Взаимодействием молекул в адсорбированных слоях пренебрегают 3. Каждая молекула первого слоя может стать АЦ для адсорбции образования последующих слоев (последовательные комплексы) 4. Во втором и последующих слоях все молекулы имеют такую же сумму статистических состояний, как и в жидкости (жидкость!) a p/ps Уравнение полимолекулярной адсорбции БЭТ К ads Энергия взаимодействия в C Кcond адсорбционном слое! р рs 1 C –1 р рs a 1 – р рs aC aC а∞ – емкость первого адс. монослоя p – равновесное давление пара ps – давление насыщенного пара p/ps – относительное давление p / ps a(1 p / ps ) a p/ps БЭТ → Ленгмюра → Генри p ps p 0 1 ac tg c 1 ac p / ps Теории Ленгмюра и БЭТ неприменимы для описания адсорбции на микропористых телах! Линеаризация уравнения БЭТ возможна при 0,05 p ps 0,3 p ps 0,3 - боковые взаимодействия p ps 0,05 - энергетическая неоднородность поверхности Дает возможность определить удельную поверхность сорбентов (±20%) и распределение пор по размеру S уд a s0 N A Капиллярная конденсация Классификация адсорбентов по размерам пор М. Дубинина Радиус пор, нм Sуд, м2/г Название › 100–200 1,5–100 0,5–1,5 0,5–2 10–500 500–1000 Макропористые адсорбенты Мезопористые адсорбенты Микропористые адсорбенты p 2 Vм ln r p rRT мало влияют на адсорбцию капиллярная конденсация объемное заполнение Адсорбция = адсорбированные + конденсированные молекулы Типичные изотермы адсорбции изотерма Ленгмюра a полимолекулярная адсорбция микропористые тела Sуд? микропоры конденсация мезопористые непористые и макропористые тела высокая однородность поверхности непористые + мезопористые макропоры микропоры p Мезопористые адсорбенты: капиллярноконденсационный гистерезис (неравновесные процессы) Начало появления гистерезиса зависит от природы адсорбента и адсорбата Конические поры: конденсация начинается со дна пор, где кривизна поверхности конденсирующейся жидкости наибольшая. По мере заполнения кривизна уменьшается! гистерезис отсутствует десорбция a адсорбция p/pS a p/pS Цилиндрические поры с одним открытым концом: конденсация начинается со дна пор (небольшая кривизна) и протекает полностью при одном и том же давлении адсорбата гистерезис отсутствует Цилиндрические поры, открытые с одного конца: конденсация начинается на стенках цилиндра десорбция гистерезисное поведение a p/pS rцил = 2rсф pads > pdes a p/pS Кинетические причины гистерезиса?