Фазовые равновесия

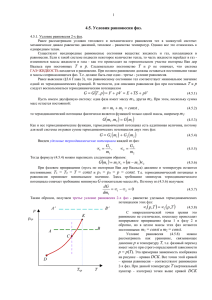
Лекция 7
Фазовые равновесия
План лекции
1.
2.
3.
4.
5.
6.
7.
8.
Фазовые диаграммы однокомпонентной системы.
Линии равновесия двух фаз. Тройная и критическая
точки.
Фазовые переходы 1-го рода.
Формула Клапейрона - Клаузиуса.
Равновесие «жидкость - пар».
Правило фаз Гиббса.
Фазовые диаграммы «жидкость - жидкость».
Фазовые диаграммы «твердое вещество - жидкость».
Фазы вещества
Фазами называют состояния вещества, находящиеся в
равновесии друг с другом, и отличающиеся скачкообразным
изменением хотя бы одного интенсивного свойства.
Сосуществующие пространственные области системы,
отделенные друг от друга межфазной границей, на которой
хотя бы одно интенсивное свойство испытывает скачок,
называют гомогенной частью гетерогенной системы.
Внешняя
граница
системы
Фаза 1
Фаза 2
Фазовые равновесия в однокомпонентной
системе. Диаграмма T - P.
Две фазы в равновесии
Три фазы в равновесии
μ α (T , P) = μβ (T , P)
μ α (T , P) = μβ (T , P) = μ γ (T , P)
Сосуществованию
двух фаз отвечает
линия
Сечение объемной
диаграммы
плоскостью
V = const
Тройная точка нонвариантная
Линия фазового равновесия
может заканчиваться
критической точкой, только
если различия между фазами
носит количественный
характер (жидкость - пар)
Примеры качественного
различия:
1. Две кристаллические
модификации вещества
2. Кристалл - пар
Диаграмма P - V
Сосуществованию
двух фаз отвечает
целая область
диаграммы
Сечение объемной
диаграммы
плоскостью
T = const
Правило рычага:
фаза 1 l (AA 2 )
=
фаза 2 l (AA1 )
Количество
вещества в фазе
обратно
пропорционально
длине отрезка от
фигуративной
точки до линии
равновесия фаз.
Диаграмма P - V с тройной точкой
Равновесию трех фаз (тройная точка на диаграмме T,P)
соответствует линия А1А2А3
Диаграмма P - V с критической точкой
В критической точке
нарушается одно из
термодинамических
условий устойчивого
равновесия обращается в нуль
производная
⎛ ∂P ⎞
⎜
⎟ =0
⎝ ∂V ⎠T
Фазовые переходы 1-го рода
Обратимый фазовый переход
происходит при постоянном
давлении
P = const
μ
Метастабильные
Состояния
При переходе энергия Гиббса
не меняется
фаза 1
Устойчивые
состояния
ΔGф.п. = ΔH ф.п. − TΔSф.п. = 0
фаза 2
Tф.п.
Qф.п. = H 2 − H1 = ΔH ф.п.
T
ΔSф.п. =
ΔH ф.п.
Tф.п.
=
Qф.п.
Tф.п.
Формула Клапейрона-Клаузиуса
Условие равновесия
При смещении равновесия
μ1 (T , P) = μ 2 (T , P)
dμ1 [T , P (T )] = dμ 2 [T , P(T )]
dP Sm 2 − Sm1 ΔSф.п.
=
=
dT Vm 2 − Vm1 ΔVф.п.
Qф.п.
dP
=
dT TΔVф.п.
⎛ ∂μ1 ⎞ ⎛ ∂μ1 ⎞ dP ⎛ ∂μ 2 ⎞ ⎛ ∂μ 2 ⎞ dP
=⎜
⎟
⎟ +⎜
⎟
⎜
⎟ +⎜
∂T ⎠ P ⎝ ∂P ⎠T dT ⎝ ∂T ⎠ P ⎝ ∂P ⎠T dT
⎝1
424
3 1
424
3
1
424
3 1
424
3
− S1 m
Уравнение
КлапейронаКлаузиуса
V1 m
−S2 m
V2 m
При наличии двух фаз в
равновесии T и P перестают
быть независимыми
переменными
ТД признаки перехода 1-ого рода:
1. Наличие теплового эффекта
2. Скачкообразное изменение многих экстенсивных
свойств (объем, энтропия, энтальпия, и т.п.)
Объемная фазовая диаграмма воды
Физический смысл
имеют только те
точки, которые
соответствуют
уравнению состояния
f(T,P,V) = 0,
т.е. поверхности.
Сечение T-P
фазовой
диаграммы
воды
Равновесие конденсированное вещество пар
Vmпар >> Vmжидк.
Qф.п.
dP
=
dT T (Vmпар − Vmжидк. )
Vmпар =
RT
P
dP Qm P
=
dT RT 2
dP Qm dT ΔH m dT
=
=
2
P
R T
R T2
Интегрирование
lnPатм
6
4
ΔH m
ln P = −
+ const
RT
−ΔSф.п./R
2
0
-2
tgα = −ΔHф.п./R
-4
-6
-8
Фазовые переходы:
1. Испарение
2. Сублимация
α
-10
-12
-14
0,000
0,001
0,002
0,003
0,004
0,005
-1
1/T, K
Число степеней свободы (f)
и правило фаз Гиббса
Предполагаем, что все компоненты подвижные!
f - число интенсивных параметров, которые можно произвольно
менять в гетерогенной системе при условии, что количество фаз
не меняется
Каждый химический потенциал является функцией T,P и K–1
концентрационной переменной
μ11 = μ12 = K = μ1Φ
μ12 = μ 22 = K = μ Φ2
Полное число
переменных в системе
2+Φ(K–1) = 2+ΦK–Φ
LLLLLLL
μ1K = μ 2K = K = μ ΦK
Химический потенциал
каждого компонента в
каждой фазе одинаков
Полное число
уравнений связи
K(Φ–1) = ΦK–K
Температура и давление
одинаковые во всех фазах!
Правило фаз:
f = 2+K–Φ
f = 0: нонвариантное равновесие
Ограниченно растворимые жидкости - 1
Система с нижней
температурой
расслаивания
При температурах ниже Tlc
жидкости смешиваются
неограниченно
Ограниченно растворимые жидкости - 2
Система с двумя
температурами
расслаивания
Жидкости смешиваются
неограниченно при
температурах ниже Tlc и
выше Tuc
N
CH3
N
Никотин
Ограниченно растворимые жидкости - 3
Верхняя
температура
расслаивания
меньше
температуры
кипения
Ограниченно растворимые жидкости - 4
Жидкость
закипает
раньше, чем
достигается
температура
полного
смешения
Фазовая диаграмма «тв. в-во - жидкость»
Линии ликвидуса
Система с
простой
эвтектикой
В твердом
состоянии A и B
нерастворимы друг
в друге
Линия солидуса
Эвтектическая
точка
Фазовая диаграмма «тв. в-во - жидкость»
Система, в
которой
образуется
соединение,
плавящееся
конгруэнтно
(без разложения)