ОПРЕДЕЛЕНИЕ МОЛЕКУЛЯРНОЙ МАССЫ АЗОБЕНЗОЛА Ракитянский Н.А ,Маджигатов Р.В

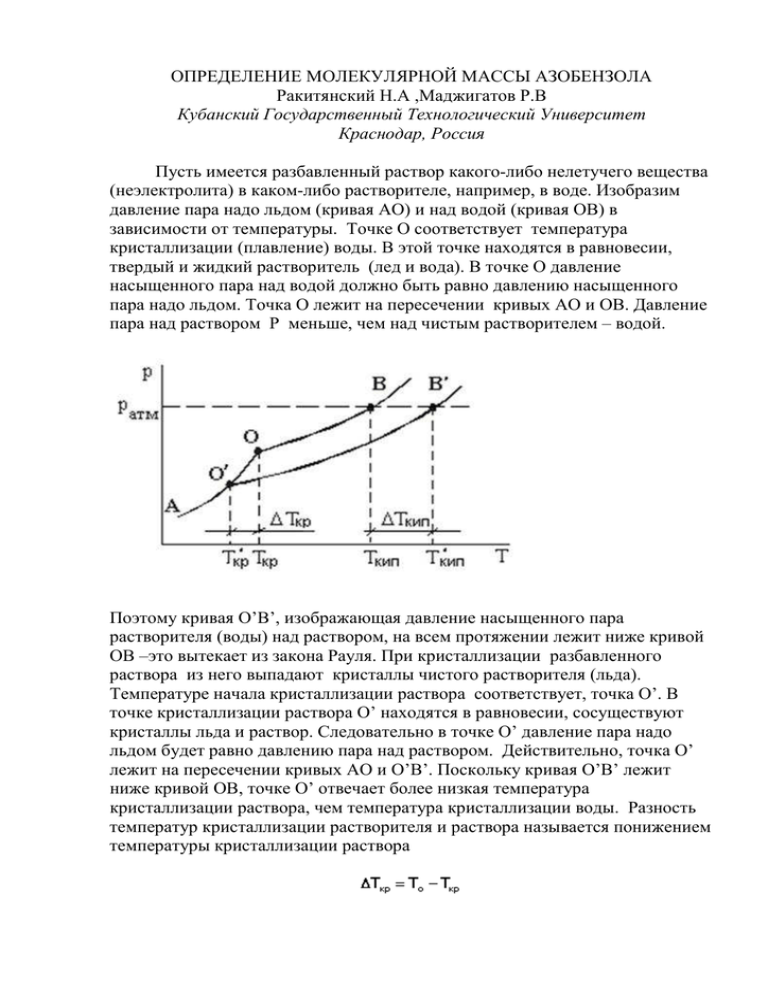
ОПРЕДЕЛЕНИЕ МОЛЕКУЛЯРНОЙ МАССЫ АЗОБЕНЗОЛА
Ракитянский Н.А ,Маджигатов Р.В
Кубанский Государственный Технологический Университет
Краснодар, Россия
Пусть имеется разбавленный раствор какого-либо нелетучего вещества
(неэлектролита) в каком-либо растворителе, например, в воде. Изобразим
давление пара надо льдом (кривая АО) и над водой (кривая ОВ) в
зависимости от температуры. Точке О соответствует температура
кристаллизации (плавление) воды. В этой точке находятся в равновесии,
твердый и жидкий растворитель (лед и вода). В точке О давление
насыщенного пара над водой должно быть равно давлению насыщенного
пара надо льдом. Точка О лежит на пересечении кривых АО и ОВ. Давление
пара над раствором Р меньше, чем над чистым растворителем – водой.
Поэтому кривая О’В’, изображающая давление насыщенного пара
растворителя (воды) над раствором, на всем протяжении лежит ниже кривой
ОВ –это вытекает из закона Рауля. При кристаллизации разбавленного
раствора из него выпадают кристаллы чистого растворителя (льда).
Температуре начала кристаллизации раствора соответствует, точка О’. В
точке кристаллизации раствора О’ находятся в равновесии, сосуществуют
кристаллы льда и раствор. Следовательно в точке О’ давление пара надо
льдом будет равно давлению пара над раствором. Действительно, точка О’
лежит на пересечении кривых АО и О’В’. Поскольку кривая О’В’ лежит
ниже кривой ОВ, точке О’ отвечает более низкая температура
кристаллизации раствора, чем температура кристаллизации воды. Разность
температур кристаллизации растворителя и раствора называется понижением
температуры кристаллизации раствора
Из закона Рауля
Где Nв – мольная доля растворенного вещества следует: чем выше
концентрация этого вещества в растворе Nв, тем больше ∆Р, тем,
следовательно, ниже расположится кривая ОВ и больше будет понижение
температуры кристаллизации раствора ∆t. Понижение температуры
кристаллизации растворов, пропорционально молярной концентрации
mрастворенного вещества, т.е.
∆Ткр=К*М
где К – коэффициент пропорциональности, называемый
криоскопической постоянной, К/моль;
M – моляльная концентрация растворенного вещества, моль/1000г
растворителя.
Физический смысл криоскопической постоянной К следует из
уравнения. Если принять, что молярная концентрация равна единице ( m = 1
моль/1000г растворителей), то: ∆T=К, т.е. криоскопическая константа К –
это величина, показывающая, на сколько градусов раствор, содержащий 1
моль неэлектролита в 1000г данного растворителя, замерзает ниже, чем
чистый растворитель. Поэтому К называют также молярным понижением
температуры кристаллизации ( затвердевания). Если взять раствор,
содержащий 1 моль вещества на 1000г растворителя и определить его ∆Ткр,
то эта величина будет отличаться от К.
Это объясняется тем, что к моляльным растворам законы разбавленных
растворов не применимы. Для определения криоскопической константы
измеряют понижение температуры замерзания ∆Ткр разбавленных
растворов. Затем пересчитывают полученные данные на моляльный раствор.
Таким образом, криоскопическая постоянная К называемая также моляльным
понижением температуры кристаллизации, не является действительным
понижением точки кристаллизации моляльного раствора.
Криоскопическая постоянная может быть вычислена и теоретически по
уравнению
где R – универсальная газовая постоянная, равная 8,31 Дж/(моль . К);
∆Нпл – молярная теплота плавления чистого растворителя в кДж/моль;
Тзам – температура замерзания по шкале Кельвина; М – молярная масса
растворителя.
Из уравнения следует, что криоскопическая постоянная зависит только
от природы растворителя – его температуры кристаллизации(плавления)
Тзам и теплоты плавления ∆Нпл, но не зависит от природы растворенного
вещества, вызывающего понижение температуры кристаллизации раствора.
Если растворенное вещество является электролитом, то под действием
полярных молекул растворителя (воды) оно распадается (диссоциирует на
ионы). Поэтому число частиц в растворе увеличивается. Пусть в растворе
находится n молекул электролита и степень его диссоциации равна α. Тогда
число молекул, распавшихся на ионы, будет nα, а число нераспавшихся
молекул составит n-αn=n(1-α). Если через λ обозначить число ионов, на
которых распадается электролит, то из n молекул растворенного электролита
образуется nαλ ионов. Общее число всех молекул и ионов в растворе равно
n(1-α)+nαλ=n[1+α(λ-1) .
Коэффициент, показывающий во сколько раз, увеличилось число
частиц в растворе в результате диссоциации, называется изотоническим
коэффициентом.
В следствие увеличения числа частиц в растворе, электролита в i раз,
понижение температуры его кристаллизации ∆Ткр будет в i раз больше, чем
раствора неэлектролита той же моляльной концентрации.
Сильные электролиты в растворах диссоциированы полностью. Для
разбавленных растворов иравно числу ионов λ, на которые распадается
электролит.
В более концентрированных растворах сильных электролитов
расстояние между ионами уменьшается и электростатическое
взаимодействие между ними увеличивается. В результате ионы не могут
проявлять себя как вполне свободные частицы. Их становится меньше как бы
меньше, чем в действительности, образуется при полной диссоциации
электролита.
Определение молекулярной массы азобензола
Мы поставили перед собой задачу определить молярную массу
азобензола, проведя все нужные измерения лабораторным методом. Для
этого мы измерили температуру кристаллизации чистого растворителя
(диоксана) и измерили температуру замерзания растворенного азобензола в
этом растворителе
Для чистоты эксперимента мы измерения делали трижды.
Для диоксана:
T1=10,5о
T1=10,4о
T2=10,4о(Чистый растворитель) Т2=10,2о
(Диоксан)
о
о
T3=10,3
Т3=10,2
Tср.=10,4
Тср.=10,2о
∆Тср.=10,4-10,2=0,2
,,,
∆Тср.=
= 0,33
Для азобензола:
Т1=10,6о
Т2=10,5о
Т3=10,5о
Т1=9,9о
Т2=9,1о
Т3=9,9о
Т1ср.=10,4о
Т2ср.=9,9о
∆Т=10,4-9,9=0,5
,
∆Тср.=
= 2,23
Пользуясь законом Рауля, мы вычисляем молекулярную массу азобензола.
∆Тз=К3*m
Табличные значения для диоксана: Кз= 4,71; = 15г.
M=
∗з
=
,∗,
=157г⁄моль
∆Т∗∗ ,∗∗
Вычислим относительную погрешность измерений :
=
(
)
∗ 100% = 7%
Таким образом, мы вычислили молярную массу азобензола ,и погрешность
наших измерений составила 7%.
Вывод: по понижению температуры замерзания раствора, используя закон
Рауля, можно определить молекулярную массу растворенного вещества.