4 урок § 4.1. КПД тепловых двигателей. Цикл Карно Второе

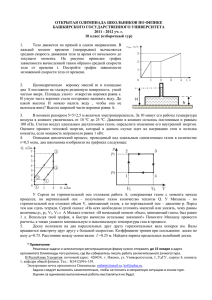
4 урок
§ 4.1. КПД тепловых двигателей. Цикл Карно
Второе начало термодинамики возникло из анализа работы тепловых двигателей
(машин). В формулировке Кельвина оно выглядит следующим образом: невозможен
круговой процесс, единственным результатом которого является превращение теплоты,
полученной от нагревателя, в эквивалентную ей работу.
01.
Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.
Рис. 6.3
Цикл работы теплового двигателя состоит из трех этапов:
• нагреватель передает газу количество теплоты ;
• газ, расширяясь, совершает работу ;
• для возвращения газа в исходное состояние холодильнику передается
теплота .
Из первого начала термодинамики для циклического процесса следует, что
,
где – количество теплоты, полученное газом за цикл, – количество
теплоты, переданное газу от нагревателя, – количество теплоты, отданное газом
холодильнику; поэтому для идеальной тепловой машины является справедливым
равенство
.
02.
Когда дополнительные потери энергии (за счет трения и рассеяния ее в
окружающую среду) отсутствуют, при работе тепловых машин выполняется закон
сохранения энергии:
,
где – теплота, переданная от нагревателя рабочему телу (газу), – работа,
совершенная газом, – теплота, переданная газом холодильнику.
03.
Коэффициент полезного действия тепловой машины вычисляется по одной из
формул:
η
∙ 100%,
η
∙ 100%,
η 1 ∙ 100%,
где – теплота, переданная от нагревателя рабочему телу (газу), – работа,
совершенная газом, – теплота, переданная газом холодильнику.
04.
Наиболее часто в тепловых машинах используется цикл Карно, так как он является
самым экономичным циклом.
Цикл Карно состоит из двух изотерм и двух
адиабат, показанных на рис. 6.4.
• Участок 1-2 соответствует контакту
рабочего
вещества
(газа)
с
нагревателем. При этом нагреватель
передает газу теплоту и происходит
изотермическое расширение газа при
температуре нагревателя . Газ
совершает положительную работу ( 0), его внутренняя энергия не
изменяется (Δ 0).
Рис. 6.4
• Участок 2-3 соответствует адиабатному расширению газа. При этом
теплообмена со внешней средой не происходит, совершаемая
положительная работа приводит к уменьшению внутренней энергии
газа: Δ , газ охлаждается до температуры холодильника .
• Участок 3-4 соответствует контакту рабочего вещества (газа) с
холодильником. При этом холодильнику от газа поступает теплота и
происходит изотермическое сжатие газа при температуре холодильника .
Газ совершает отрицательную работу ( 0), его внутренняя энергия
не изменяется (Δ 0).
• Участок 4-1 соответствует адиабатному сжатию газа. При этом теплообмена
со внешней средой не происходит, совершаемая отрицательная работа приводит к увеличению внутренней энергии газа: , газ
нагревается до температуры нагревателя , то есть возвращается в
исходное состояние.
05.
Коэффициент полезного действия тепловой машины, работающей по циклу
Карно, вычисляется по одной из формул:
η
∙ 100%,
η 1 ∙ 100%,
где – температура нагревателя, – температура холодильника.
§ 4.2. Коэффициент полезного действия произвольного цикла
06.
Круговой процесс (цикл) всегда состоит из нескольких процессов, в том числе и
изопроцессов.
Согласно первому началу термодинамики в каждом из таких процессов газом
может совершаться работа и может изменяться его внутренняя энергия. Теплота,
полученная или отданная газом в каждом процессе, будет различной.
В таблице отражены расчетные формулы, условные обозначения и нулевые
значения для работы, изменения внутренней энергии и теплоты, полученной газом в
некоторых процессах.
Процесс
Работа,
совершенная
газом,
Изменение
внутренней
энергии газа,
Количество теплоты,
полученной газом,
Изотермический
!".
#
0
#
Изохорный
$ !".
0
%
'(Δ
2
%
'(Δ
2
Изобарный
) !".
'(Δ
*Δ+
Адиабатный
/
%
'(Δ
2
%
'(Δ
2
%
*Δ+
2
%
'(Δ
2
,% 2'(Δ
2
,% 2*.+
2
0
В таблице использованы следующие обозначения:
0 – число степеней свободы газа (для одноатомного газа 0 3; для двухатомного газа
0 5; для трех- и многоатомного газа 0 6); ' – количество вещества (газа); Δ – изменение температуры газа в результате процесса, – температура газа в начале
процесса, – температура газа в конце процесса; Δ+ + + – изменение объема газа
в результате процесса, + – объем газа в начале процесса, + – объем газа в конце
процесса; * – давление газа; R 6 8,31 Дж/моль·К – универсальная газовая постоянная.
07.
При решении задач на вычисление коэффициента полезного
произвольного цикла следует использовать следующий алгоритм:
1) построить график кругового процесса в координатах *,+-;
2) выделить участки, соответствующие изопроцессам;
3) заполнить таблицу:
Номер
участка
1 (1-2)
2 (2-3) …
… N (N-1)
Название
процесса
Работа,
совершенная
газом,
Изменение
внутренней
энергии газа,
Количество
теплоты,
полученной газом,
действия
Знак
теплоты
(+ или -)
4) проанализировать, положительным или отрицательным является выражение
для теплоты, полученной/отданной газом, в каждом процессе (в последней
колонке таблицы указать соответствующий знак):
• газ получает теплоту, если 0,
• газ отдает теплоту, если 0;
5) рассчитать работу газа за цикл, суммируя алгебраически работы газа на каждом
из участков (то есть, складывая значения работ из третьей колонки таблицы с
учетом соответствующего знака):
⋯ 9 ;
6) найти теплоту, полученную газом за цикл получ. , суммируя только те значения ,
которые являются положительными;
7) рассчитать коэффициент полезного действия для рассмотренного цикла по
формуле:
?
∙ 100%.
получ.