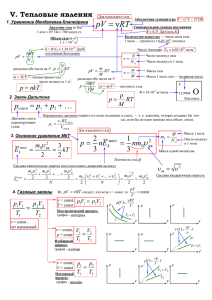
RT pV ν =
реклама
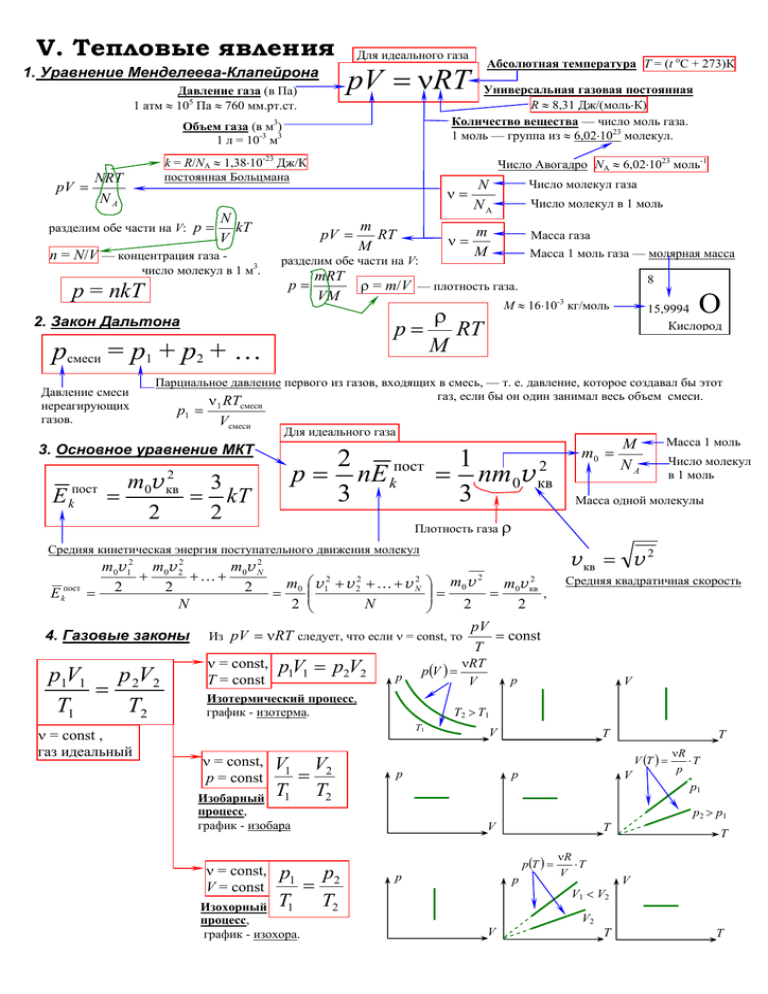
V. Тепловые явления 1. Уравнение Менделеева-Клапейрона Для идеального газа pV = νRT Универсальная газовая постоянная R ≈ 8,31 Дж/(моль⋅К) Количество вещества — число моль газа. 1 моль — группа из ≈ 6,02⋅1023 молекул. Давление газа (в Па) 1 атм ≈ 105 Па ≈ 760 мм.рт.ст. Объем газа (в м3) 1 л = 10-3 м3 pV = k = R/NА ≈ 1,38⋅10-23 Дж/К постоянная Больцмана NRT NA N разделим обе части на V: p = kT V n = N/V — концентрация газа - Число Авогадро NА ≈ 6,02⋅1023 моль-1 pV = 3 число молекул в 1 м . p = nkT mRT VM 2. Закон Дальтона pсмеси = p1 + p2 + … Давление смеси нереагирующих газов. ν= N NA Число молекул газа ν= m M Масса газа Число молекул в 1 моль Масса 1 моль газа — молярная масса 8 ρ = m/V — плотность газа. ρ p = RT M p1 = 1 E m0v 2 Vсмеси Для идеального газа 2 кв = 2 1 пост p = nE k = nm0v кв2 3 3 3 kT 2 4. Газовые законы p1V1 p 2V2 = T1 T2 2 ⎞ m0 v m v2 ⎟⎟ = = 0 кв , 2 2 ⎠ pV Из pV = νRT следует, что если ν = const, то = const T νRT ν = const, p V = p V p (V ) = 1 1 2 2 р р T = const V Изотермический процесс, график - изотерма. V1 V2 = T1 T2 Масса 1 моль Число молекул в 1 моль Масса одной молекулы p1 p2 = T1 T2 Изохорный процесс, график - изохора. v кв = v 2 Средняя квадратичная скорость V V T T V (T ) = р Изобарный процесс, график - изобара ν = const, V = const M NA T2 > T1 T1 ν = const, p = const m0 = Плотность газа ρ m0v 12 m0v 22 m0v N2 + +K+ 2 2 2 2 2 = m0 ⎛⎜ v 1 + v 2 + K + v N = 2 N 2 ⎜⎝ N ν = const , газ идеальный 15,9994 Кислород смеси Средняя кинетическая энергия поступательного движения молекул пост k О М ≈ 16⋅10-3 кг/моль Парциальное давление первого из газов, входящих в смесь, — т. е. давление, которое создавал бы этот газ, если бы он один занимал весь объем смеси. ν RT 3. Основное уравнение МКТ E kпост = m RT M разделим обе части на V: p= Абсолютная температура T = (t oC + 273)К р V T p(T ) = р V p1 p2 > p1 V р νR ⋅T p νR ⋅T V V1 < V2 T V V2 T T Работа газа 5. Первый закон термодинамики Q = ∆U + Aгаза Количество теплоты, полученное (Q > 0) или отданное (Q < 0) системой. (Энергия, полученная или отданная системой в процессе теплопередачи, т. е. при обмене энергиями между молекулами — на микроскопическом уровне.) C= Внутренняя энергия Q ⇒ Q = cm∆T m∆T Удельная теплоемкость вещества Q CM = ⇒ Q = CM ν∆T ν∆T CV = U = Ek тепл = ∆U ∆T Агаза = 0 Потенциальная энергия взаимодействия молекул друг с другом. >> Ep взаим , поэтому i i pV = νRT 2 2 p = const Агаза = p∆V = νR∆T ∆U + A > CV ∆T ∆U = 6. Адиабатический процесс Q = 0 ⇒ Aгаза = − ∆U Агаза = ± Sпод граф. р(V) "+" — если газ расширяется "−" — если газ сжимается р i i ( p2V2 − p1V1 ) = νR∆T 2 2 Для идеального газа Изотермы ηцикла = р 7. КПД циклического процесса (теплового двигателя) Q Aгаза в цикле Qподв − Qотв = = 1 − отв Qподв Qподв Qподв Qполн. за цикл = Qподв + Qотв = ∆Uв цикле + Aгаза в цикле Qотв < 0 ⇒ Qотв = −⏐Qотв⏐ V V Нагреватель Tнаг Qподв ∆U = CV ∆T = cV m∆T = C M V ν∆T Для идеального газа В теплоизолированной системе или при быстрых процессах в любом процессе При адиабатическом расширении (Агаза > 0) газ охлаждается (∆U < 0) р При адиабатическом сжатии (Агаза < 0) газ нагревается (∆U > 0) Адиабата — гипербола, идущая более "круто" чем изотермы (с ростом V убывает T). V ν = const численно i = 3 для одноатомных газов (Не, Ne, 1 Ar, …) i = 5 для двухатомных газов (Н2, N2, О2, воздух, ) i = 6 для многоатомных газов (пары Н2О, …) При p = const: Cp = Кинетическая энергия хаотического (теплового) движения молекул. В идеальном газе Ek тепл Молярная теплоемкость вещества При V = const: V = const Изменение внутренней энергии системы U = Ek тепл + Ep взаим Q ⇒ Q = C∆T ∆T Теплоемкость тела (системы) c= Агаза = − Анад газом ∆Uв цикле = Uкон − Uнач = 0 Qподв −⏐Qотв⏐= Aгаза в цикле − если цикл идет "по часовой стрелке" Агаза в цикле = ± Sвнутри цикла р(V) "+" "−" − если цикл идет "против часовой ηидеал Рабочее вещество (газ) А Qотв Холодильник Tхол Tнаг − Tхол = Tнаг КПД идеальной тепловой машины, работающей по численно стрелки" циклу Карно — максимальный теоретически возможный КПД 6. Насыщенный пар — газ, дальнейшее изотермическое сжатие или изохорное охлаждение которого приводит к превращению части этого при данных Тнагр и Тхол. Идеальная р изотерма рнас р V газа в жидкость (при наличии центров конденсации). газ, находящийся в динамическом равновесии со своей жидкостью, т. е. в состоянии, когда число молекул, переходящих из газа в жидкость равно числу молекул, переходящих обратно за то же время. Реальные изотермы: область I - вода Давление насыщенного пара (а также его плотность) область II - вода в равновесии с насыщенным однозначно определяется температурой и больше ни паром область III - газ от чего не зависит (ни от объема, ни от массы пара). Tкр - критическая температура, при Т > Tкр газ Относительная влажность воздуха никаким сжатием нельзя перевести в жидкость. p пара в воздухе ρ пара в воздухе (×100 %) ϕ= = Условие кипения: pнас = pна пузырек ≈ pатм , p нас. пара при данной Т ρ нас. пара при данной Т V Для воды pнас (100 оС) ≈ 105 Па