/ 10 0, 9 м кг ∙ = ρ
реклама

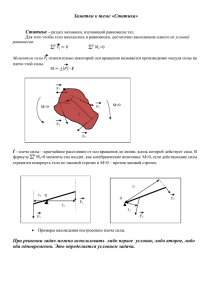
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Н.Э. БАУМАНА ОСЕННЯЯ ФИЗИКОМАТЕМАТИЧЕСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ 2014 2015 г.г. I ТУР ФИЗИКА ВАРИАНТ № 6 З А Д А Ч А 1. После выстрела из пушки снаряд массы m = 10 кг, упал на землю через 10 секунд. Определите модуль изменения импульса снаряда за последние две секунды полёта. Сопротивлением воздуха пренебречь. З А Д А Ч А 2. Однородный тонкий стержень ОВ лежит на двух опорах D и C, D B расстояние между которыми a=0,2 м. Коэффициент трения стержня об C опоры равен = 0,5. Угол наклона стержня к горизонту = 60o, длина O участка СВ = b= 0,42м. Найдите длину стержня L , при которой он будет находиться в равновесии. З А Д А Ч А 3. Два груза массы 2m и m связаны невесомой нерастяжимой нитью, переброшенной через неподвижный блок. В начальный момент груз массы m удерживают, прижимая его к столу. Затем груз отпускают. На какую максимальную высоту поднимется этот груз над столом, если при ударе груза 2m о стол выделяется количество теплоты, равное Q ? Удар абсолютно неупругий. Массой блока и силами трения в блоке пренебречь. g m 2m З А Д А Ч А 4. Тонкий однородный стержень массы m и длины L лежит на дне сосуда с водой. За нить, привязанную к одному концу стержня, его медленно поднимают в вертикальное положение, в котором стержень, опираясь на дно сосуда, выступает над поверхностью воды на 0,4 L. Найдите работу, которую необходимо совершить при таком подъеме стержня. Плотность стержня в три раза больше плотности воды. Силами сопротивления и массой нити пренебречь. З А Д А Ч А 5. Математический маятник с длиной нити L прикреплён к потолку лифта, который движется вниз с ускорением а = g /2, где g – ускорение свободного падения.. Определите период малых колебаний маятника. З А Д А Ч А 6. Где и во сколько раз больше атомов: в стакане воды или в равном по объёму куске меди ? 3 3 Плотность меди Cu 9,0 10 кг / м . З А Д А Ч А 7. В длинной трубе между двумя поршнями массы М каждый находится 2u 6u моль идеального одноатомного газа при температуре То . Масса газа много меньше массы поршней. В остальном пространстве трубы - вакуум. В начальный момент левый поршень имеет скорость 2u, а правый - 6u. Определите максимальную температуру газа при дальнейшем движении поршней. Система теплоизолирована, теплоемкостями поршней и трубы, а также трением пренебречь. З А Д А Ч А 8. 2q 3R Две концентрические металлические сферы радиусами R и 3R жестко R закреплены. Внутренняя сфера соединена с землей, а внешняя сфера заряжена отрицательным зарядом 2q. Какую минимальную скорость должен иметь точечный отрицательный заряд q массы m на бесконечно большом расстоянии от сфер, чтобы двигаясь к их центру, достигнуть точки А, находящейся на расстоянии 4R от центра сфер. Перераспределением зарядов на сферах под действием точечного Е 3Е заряда пренебречь . A З А Д А Ч А 9. 2R R В схеме, приведенной на рисунке, найдите энергию конденсатора. Параметры C элементов схемы, изображенных на рисунке, считать известными. Внутренним сопротивлением источников тока пренебречь. B 2Е З А Д А Ч А 10. 3Е о Проводник АОК, согнутый под углом 60 , расположен в плоскости xy, как показано на рисунке, в постоянном однородном магнитном поле индукции В, перпендикулярной плоскости xy. По проводнику из начала координат О перемещают поступательно вдоль y K A оси y с постоянной скоростью v перемычку MN, параллельную оси x. V B Cопротивление единицы длины перемычки равно . Пренебрегая С сопротивлением проводника и скользящих контактов, а также индуктивностью M 30o 30о N O x контура, найдите полное количество теплоты Q, выделившейся в перемычке, за время её движения до точки С. Длина отрезка ОС равна L . 61 ОСЕННЯЯ ФИЗИКО-МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА 2014-2015 г.г. I ТУР РЕШЕНИЕ ВАРИАНТА № 6 З А Д А Ч А 1. (8 баллов) Ответ:. p mgt 10 9,8 2 196 кг м с З А Д А Ч А 2. (8 баллов) Ответ: tg L 2b a 1 1,7 м . На стержень ОВ действуют: N1 mg - cила тяжести; N1 и N2 – силы нормальной реакции опор D и C ; F ТР 1 и F ТР 2 - силы трения . y F TP 2 Силы трения направлены вдоль F TP 1 B x стержня вверх, так как стержень D C стремится соскользнуть вниз. Стержень будет находиться в равновесии, если будут выполняться два условия: 0 N2 Равенства нулю всех сил, mg действующих на стержень Fi 0 и равенства нулю моментов всех сил, действующих на стержень, относительно оси проходящей, например, через опору С, M C ( Fi ) 0 . Напишем для стержня первое условие равновесия: mg N 1 FТР 1 FТР 2 N 2 0 (1) Направим ось х вдоль стержня, ось y перпендикулярно ей, и спроецируем на них уравнение (1). FТР1 FТР 2 mg sin 0 (2) N 1 N 2 mg cos 0 (3) Принимая во внимание, что FТР N , перепишем уравнения (2) и (3) в виде N 1 N 2 mg sin 0 (4) N 1 N 2 mg cos 0 (5) Напишем для стержня второе условие равновесия относительно оси, проходящей через точку С: M1 M 2 0 (6) , где M 1 mg 1 , M 2 N 1 2 - моменты сил mg и N 1 относительно выбранной оси, где 1 ( L / 2 b ) cos и 2 a - плечи сил mg и N. Подставим выражения для M 1 и M 2 в (6) , получим mg ( L / 2 b) cos N 1a 0 (7). Из уравнение (5) и (7) найдём mg cos ( L / 2 b) mg cos ( L / 2 b a ) N2 , а затем из уравнения (4) выразим длину a a tg . стержня: L 2b a 1 N1 Подставим a = 0,2; b = 0,4; 0,5 ; 60 o ; tg 60 o 3 , найдём 1,73 L 2 0,4 0, 2 1 0,8 0, 2 (1 3,46) 1,7 м 0,5 6-2 З А Д А Ч А 3. (10 баллов) 2Q mg Ответ: H 1) H h1 h2 (1), где h1 высота груза m1 над столом до начала движения; h2 высота подъема груза m2 над столом после удара груза m1 о стол. 2) Используя закон сохранения энергии и уравнение равнопеременного движения, получим Q W К1 m1v 2 (2) , 2 откуда V2 2Q m1 g V2 Q (4) 2 g m1 g 5) Подставляя (3) и (4) в (1) , получим m1 m2 Q 1 1 g (6) (5), где a H m1 m 2 m1 a g Подставляя (6) в (5), найдем Q g a Q g Q m1 m 2 2Q H 1 1 m1 ag m1 g a m1 g m1 m2 (m1 m 2 ) g 3) h1 V2 Q 2 a m1 a 4) h2 (3); Подставим значения m1 = 2 m 2Q 2Q H ( 2m m) g mg m 2= m m2=m =m m1=2m (7) в (7), найдем З А Д А Ч А 4. (10 баллов) Ответ: A1 0,36mgL W KИИ Ai По условию WKИИ 0 , следовательно, A1 A2 A3 0 , где A1-работа внешней силы, A2- работа силы тяжести, Искомая работа A1= A2 A3. A3- работа силы Архимеда. L A2 mg 2 A3 g 0,4V 0,6 L g 0,6V 0,3L (0,4 0,6 0,3 0,6) gVL 0,42 A3 0,42 mgL 0,14mgL 3 A2 mgL 2 m gL . При n = 3 n A1 0,5mgL 0,14mgL (0,5 0,14)mgL 0,36mgL З А Д А Ч А 5. (10 баллов) Ответ: T 2 2L . g a a g ; 2 T 2 g Эфф g a g Подставляя L g ЭФФ , (1) где g g 2 2 g Эфф в (1), получим T 2 2L g L 6-3 З А Д А Ч А 6. (10 баллов) Ответ: Число атомов воды больше числа атомов меди в В стакане воды содержится число молекул N 1 N2 3N1 167 1,2 раза . N 2 140,6 1V NA 1 и 3N 1 атомов, а в куске меди - 2V N A атомов. Подставляя числовые значения, получим : для воды 2 3 3N1 3 10 3 V N A 167 10 V N A . 0,018 3 9,0 10 3 V N A 140,6 10 V N A . Здесь N A число Авогадро, V- объём стакана, 0,064 1 и 2 - плотности воды и меди соответственно. Следовательно, число атомов воды больше числа 3N1 167 атомов меди в 1,2 раза . N 2 140,6 Для меди: N 2 З А Д А Ч А 7. (10 баллов) Ответ: T To 8 Mu 2 3 R . 2u 6u В системе отсчёта, связанной с центром масс поршней, x они движутся навстречу друг другу с равными скоростями ( так как по условию их массы одинаковые. При этом кинетическая энергия поршней, переходит во внутреннюю энергию газа. E кин U o U , где Uo –начальная внутренняя энергия газа U o c v To , , где 1 . U- внутренняя энергия газа при максимальном его сжатии U c v T . M 2u M 6u 4u 2M Скорость левого поршня в системе центра масс 2u С 2u 4u 2u . Скорость центра масс поршней С Скорость правого поршня в системе центра масс 6u С 6u 4u 2u . Используя закон сохранения энергии, запишем Используя закон сохранения энергии, запишем (при 1 ) : 2 8 Mu 2 M 3 3 (2u ) 2 RTo RT , откуда T To . 2 2 2 3 R З А Д А Ч А 8. (10 баллов) Ответ: 2q A 1 q . m 6m o R На заземлённой сфере наводится заряд q x , который находится из условия равенства нулю потенциала внутренней сферы. Согласно принципу суперпозиции , потенциал внутренней сферы равен qx 2q 0, 4 o R 4 o 3R 2q 3R A R 4R q откуда находим искомый заряд q x 2 q. 3 6-4 A Потенциал в точке А 2 q 2q 1 q 3 4 o 4 R 4 o 4 R 12 o R A 1 q . 12 o R 2 2q A m min 1 q A . Откуда q По закону сохранения энергии . m 6m o R 2 З А Д А Ч А 9. (12 баллов) 3Е Ответ: W 2CE 2 . 3E E Ток в цепи I (1) 3R R Закон Ома для правого участка цепи (участок АВ): ( B )C 3 E I A (2) R Из (1) и (2) найдем A - B IR 3 E E 3 E 2 E . Обозначим A B U , тогда энергия конденсатора W CU 2 Е A 2R R С B 2Е 3Е 2 2 CE 2 З А Д А Ч А 10. (12 баллов) 2 Ответ: Q 2 B L 3 1) Длина перемычки 2 y tg ; при y = C max 2L tg . 2 2 2) Сопротивление перемычки R 2y tg ; R max max 2L tg . 2 2 3) ЭДС индукции E B ; E max 2 B Ltg . 2 4) Тепловая мощность, выделившаяся в перемычке 2 2 2 2 2 2 E B B ; R 1 5) Средняя мощность Pcp Pmax 2 P A 2 2 Q Pcp t o M 2 B 2 2 Ltg 2 E max 2 . Pmax Rmax L за время t o , 2 2 2 L B L tg 2 1 Итак , при = 60 , tg tg30 o , 2 3 о V K B С 6) Полное количество теплоты, выделившейся в перемычке, B Ltg y B 2L2 B 2 L2 Q tg 2 3 30o 30о N O x