γ 9,15 6 = α /50 /100 T ≤ Θ ÷Θ ( )0 const Θ = Θ Θ Θ 0 T = Θ

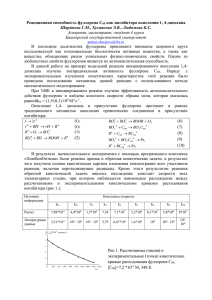
О ТЕМПЕРАТУРЕ ДЕБАЯ ФУЛЛЕРИТА C60
Михальченко В.П.
Институт термоэлектричества НАН и МОН Украины,
58002, Черновцы, Украина, E-mail: [email protected]
Общефизическая значимость температуры Дебая Θc , фигурирующей в его
однопараметрической теории теплоемкости отмечалась известными физиками –
А.Ф.Иоффе, Н.Н.Сиротой и М. Блэкменом еще во второй половине прошлого столетия [13].
Для молекулярного кристалла фуллерита C60 величины Θc определенные различными
авторами из экспериментальных данных теплоемкости C p (T ) и упругих постоянных
Cijkl (T ) оказались крайне разноречивы.
Например, Θc колеблется, от Θ min
= 37 К [4] до Θ max
= 188 К [5]. Аналогичная
c
c
min
ситуация наблюдается и для параметров Грюнайзена: γ Г = 1, 4 до γ Гmax = 9,15 [ 6] .
Столь необычный для твердых тел разброс величин Θc фуллерита C60 (почти в 5 раз)
и γ Г (в 6,5 раз) обусловлен как ограничениями закона T 3 Дебая, так и процедурами учета
вкладов в общую теплоемкость C p и термическое расширение α (T ) трансляционных,
либрационных, вращательных межмолекулярных, а также внутримолекулярных степеней
свободы при различных температурах (о выделении из общей C p (T ) этих вкладов см.
напр.[7]). Не вдаваясь в анализ и подсчет упомянутых степеней свободы, отметим
следующее. Установлено [8], что истинный закон T 3 проявляется в очень узкой области
низких температур T ≤ ( Θc / 50 ÷ Θc /100 ) , но не Θc /12 по Дебаю.
Именно в этой близкой к абсолютному нулю области справедлив закон T 3 для любых
твердых тел независимо от их структуры и типа химической связи. Для фуллерита C60 такая
область экстремально узка: от T ≤ 0,37K до T ≤ 1,88K 1. Ниже будет показано, что никем из
авторов экспериментальных работ по определению Θc фуллерита C60 , за исключением [9],
не достигалась область истинного закона T 3 в которой Θc ( 0 ) = const (достигалась лишь
область имитации – псевдозакона T 3 , в которой Θc зависит от температуры).
Измерения теплоемкостей C p (T ) кристаллических твердых тел представляемых в
виде зависимостей Θc (T ) [3], свидетельствует лишь об отклонении реального объекта от
дебаевской модели и, таким образом, вопрос о величине истинной калориметрической
температуре Дебая Θc ( 0 ) фуллерита C60 остается открытым.
Представляется поэтому актуальным, выполнить расчеты Θc ( 0 ) по упругим
постоянным Cijkl монокристалла фуллерита C60 , которые правомерны лишь с
использованием гармонических величин C% , получаемых путем линейной экстрополяции
ijkl
экспериментальных зависимостей Cijkl (T ) из области высоких температур T > Θc на T = 0
К [10]. Для упругоизотропных кристаллов кубической симметрии величина Θc ( 0 ) может
быть рассчитана с помощью известного соотношения [11]:
1
Согласно [9] для чистого фуллерита C60 истинный закон T 3 начинает проявляться при T < 1K .
3/ 2
3/ 2

 1  
mk B3
1/ 2  1 
Θ =
ρ 
 + 2
 ,
18π 2 h3
 C11 
 C44  
где ρ – плотность, Cij – упругие постоянные в обозначениях В.Фойгта.
−3
c
(1)
Θc ( 0 ) автором настоящего доклада определены величины
монокристаллов фуллерита C60 . Используя экспериментальные
ijkl
зависимости C11 (T ) , C12 (T ) и C44 (T ) в интервале (100-300)К [12], экстраполируя линейно
Cij (T ) из области T ≥ 180 К на T = 0 К, получено: C%11 = 22,50 , C%12 = 13, 60 и C% 44 = 10,55 (в
ед. ГПа с точностью не хуже 1% для диагональных Cij ).
Формула (1) обобщенная автором доклада для упругоанизотропных кристаллов кубической
симметрии путем учета неравенства двух модулей сдвига C44 и ( C11 − C12 ) / 2 преобразуется к
виду:
3/ 2
3/ 2
3/ 2



 1  
mk B3
2
−3
1/ 2  1 
Θc =
ρ 
(2)
 +
 +
 .
18π 2 h3
C
C
C
−
 C11 
12 
 11
 44  
Поскольку степень упругой анизотропии фуллерита C60 (при T = 0К ) А=2
C44 /(C11 − C12 ) = 2,36 заметно превышает А=1 изотропного кристалла, целесообразно
Для
расчета
гармонических C%
рассчитать Θc ( 0 ) и по формулам Беттса [8], учитывающих шесть направлений усреднения
скоростей звука:
h
(3)
Θc−3 (0) = (9 N / 4π V )1/ 3 ρ −1/ 2 J −1/ 3 ,
kB
где J является суммой шести слагаемых, выраженных через комбинации Cijk (формулы
(1.22) и (1.23) в [8], которые здесь не приводятся из-за их громоздкости).
Используя рентгенографическую плотность фуллерита C60 при T ≤ 30 К,
ρ = 1, 735г ⋅ см −3 и V = 416, 7см 3 /моль [7], N = 6, 02 ⋅10−23 (моль)-1 , табличные значения h, h и
k B , молекулярный вес фуллерита mф = 1,95 ⋅10−21 г . и приведены выше C% ij с помощью
формулы (2) рассчитана величина Θc (0) = 70, 24 К.
По формуле (3) получено Θc (0) = 77,12 К, демонстрируя таким образом, влияние упругой
анизотропии на результаты расчета Θc ( 0 ) . Как и следовало ожидать Θc (0) = 77,12 К заметно
превышает Θ c = 66 К определенную в [13] при Т=300К. Более чем вдвое наше значение Θc ( 0 )
превышает ΘCmin ( 0 ) = 37 К, полученное в [4]. Не исключено, что ΘCmin ( 0 ) соответствует
минимуму низкотемпературных зависимостей Θc (T ) , обусловленных псевдозаконом T 3 Дебая.
Существенно
ближе
и
Θc ( 0 ) =77,12К
оказалась
величина
Θc ( 0 ) =74К
мелкодисперсного поликристаллического C60 , полученная из данных C p (T ) в интервале
(1,4 ÷ 20)К2 [14].
Такое же значение Θ c = 74 К получено в [15], использованное в [16] для сравнения с
рассчитанной Θc ( 0 ) на основе закона подобия и равной 40К. Тем не менее, рассчитанная в
[6] с помощью модифицированного потенциала Ми-Леннард-Джонса для разупорядоченной
фазы г.ц.к. фуллерита C60 равна 58,75К, т.е. существенно выше рассчитанной по закону
подобия и более близка к полученной в настоящем докладе.
В поликристаллических прессованных компактах с размерами частиц ≤ 100нм возможно
возрастание Θc , обусловленное лапласовым давлением.
2
Изложенный выше анализ величин Θc (T ) иллюстрируется таблицей, позволяющей
усмотреть тенденцию в приближении к истинной дебаевской величине Θc ( 0 ) .
Величины Θc ( 0 ) фуллерита C60 , полученные разными авторами:
Θc ( 0 ) К
Источник
58,75
[6]
37
[4]
188∗∗
[5]
40
[16]
74
[14]
55, 2∗
[7]
66∗
[13]
80
[9]
74
[15]
50
[17]
100∗
[18]
77,12
наст.докл.
Примечание:
Звездочкой (*) обозначены величины Θc ( 0 ) , полученные из данных Cijkl или скоростей звука при T > 4, 2 К.
(**) – величина Θc ( 0 ) из данных измерений теплоемкости кристаллических экстрактов C60 / C70 в
интервале температур (4 ÷ 10)К.
Поскольку фуллерит в области низких температур (0,1 ÷ 1,8К) находится в состоянии
ориентационного стекла можно тем не менее утверждать, что истинная Θc ( 0 ) не должна
слишком отличаться от полученной нами и равной 77,12К (напомним, что истинный закон
T 3 Дебая справедлив для любых твердых тел независимо от их атомной структуры и типа
химической связи). Действительно, из данных таблицы видно, что наиболее близкое
совпадение с Θc ( 0 ) =77,12К соответствует Θc ( 0 ) =80К [9], полученной в интервале (0,6 ÷
7,6К), т.е. по существу в области (0,4 ÷ 1,8)К истинного закона T 3 Дебая.
Независимое подтверждение близости Θc ( 0 ) =77,12К к истинной дебаевской Θc ( 0 )
показал расчет модуля всестороннего сжатия K% фуллерита C60 с помощью достаточно общего
соотношения [19] для г.ц.к. решеток:
~
9 h
1/ K = ( ) a / mΘC2 .
(4)
2 kB
Подстановкой в (4) численных значений a f = 14,156 A , m f =1,195 ⋅ 10−21 Г и Θc ( 0 ) =
=77,12К, получено K% =17,8 ГПа в хорошем согласии с K% =18,1 ГПа определенным в [20]
гидростатическим методом. Это означает, что близость сравниваемых величин Θc ( 0 )
=77,12К и Θc ( 0 ) =80К [9] не является случайной.
Уместно напомнить, что более утонченная атомистическая теория теплоемкости
твердых тел Борна-Кармана приводит в пределе низких температур к теории Дебая, а в
пределе высоких к теории Эйнштейна [3]. Оказалось, поэтому целесообразно представлять
экспериментальные данные теплоемкостей C p (T ) многих веществ в области T < Θ D /12 в
o
виде температурных зависимостей Θ D = f (T ) : наблюдаемые аномалии Θ D (T ) к тому же
отражают в известной мере характер межатомных (межмолекулярных) сил взаимодействия в
кристаллической решетке. Именно по этой причине (как и около ста лет назад) измерения
C p (T ) в настоящее время интерпретируются экспериментаторами на основе
однопараметрической теории Дебая.
В заключение несколько замечаний общефизического характера. Можно полагать, что
по аналогии с температурой Дебая возникли термины: температура Ферми, температура
Фарадея (при которой твердые электролиты типа AgI переходят в суперионное состояние),
температура Кондо, температура Морина, температура Лэмба-Мёссбауэра … Более того, в
микроскопической теории сверхпроводимости Б.К.Ш. величина Θ D определяет
теоретический предел температуры сверхпроводящего перехода: TC = 0,135Θ D . В недавней
работе [21] показано каким образом точность определения Θ D при расчетах нулевой энергии
существенно влияет на кривую плавления металлического водорода при высоких давлениях,
жидкая фаза которого представляет собой новый класс квантовых жидкостей и новое
состояние материи – сверхпроводящая жидкость, которая не переходит в твердое состояние
при любых давлениях и температурах.
Обратим внимание и на то, что к настоящему времени не проанализираваны и не
объяснены неравенства Θ D > Tплав. некоторых криокристаллов нулевой группы таблицы
Д.И.Менделееева ( Ne, Ar) и применимость для них правила Ф.Линдемана.
И, наконец, о значимости Θ D для физики твердого тела уместно процитировать проф.
Дж.Займана ( [22], стр.137) «…дебаевская температура – это параметр, в которой мы
пытаемся вложить всю динамику решетки данного твердого тела».
ВЫВОДЫ
1. Анализ экспериментальных величин калориметрических температур Дебая Θc ( 0 ) ,
показал, что их разброс (~ в 5 раз) обусловлен псевдозаконом T 3 Дебая.
2. Установлено, что наиболее близкой к истинной дебаевской величине Θc ( 0 )
фуллерита C60 является Θc ( 0 ) =77,12К, вычисленная автором из гармонических упругих
постоянных C% ijkl монокристалла фуллерита C60 в пределе T = 0 К по шестичленным
формулам Беттса.
3. Кратко прокомментирована общефизическая значимость температуры Дебая Θ D
кристаллических твердых тел.
СПИСОК ЛИТЕРАТУРЫ
1. А.Ф.Иоффе, Сборник «Вопросы теории и исследования полупроводников и процессов
полупроводниковой мелаллургии», Изд. АН СССР, 1945г., стр.5.
2. Н.Н.Сирота, ДАН СССР, 115, 901, (1957).
3. M.Blackman, Handb.d. Phys. (S.Flugge ed.) Vol. 7, Teil 1, Springer Verlag, Berlin, 1955,s.325.
4. Б.В.Лебедев ЖФХ, 75, 775, (2001).
5. E. Graivei et al., Solid State Communs, 85,73,(1993).
6. М.Н. Магомедов ФТТ, 47, 758, (2005).
7. И.А.Аксенова и др. ФНТ, 25, 2229, (1996).
8. Дж.Алерс, В кн. Динамика решетки (Физическая акустика под ред. У.Мэзона) Мир.
М.,1968, стр. 13-61.
9. J.R. Olson et al. Science, 259, 1145, (1993).
10. Г.Лейбфрид, В.Людвиг. Теория ангармонических эффектов в кристаллах. И.Л.М. (1993),
231с.
11. H.Hahn, W.Ludvig, Zs.Phys.161, 404 (1963).
12. Н.П.Кобелев и др. ФТТ, 43, 2244(2001).
13. Н.П.Кобелев и др. ФТТ, 40, 173(1988).
14. W.P. Beyermann et al.,Phys.Rev. Letters,68, 2046 (1992).
15. A.Hebard, Ann. Rev. Mater.Sci.23,159(1993).
16. В.Н. Безмельницин и др. УФН, 168,1195(1998).
17. T.Atake et.al.,Phys.Letters, 196, 321 (1992).
18. S.Hoen et.al., Phys.Rev.,46, 12737 (1992).
19. S.S.Mitra, S.K. Joshi, Physica, 27, 376 (1961).
20. M.C. Abramo, Cassato, J.Phys.Chem.Sol., 57,1751 (1966).
21. В.В.Кечин, Письма в ЖЭТФ, 79, 46 (2004).
22. Дж.Рейсленд. Физика фононов, Мир, М. 1975, с.365.