Документ 2018597

1
1. СТАТИСТИЧЕСКИЕ МОДЕЛИ СЛУЧАЙНЫХ ЯВЛЕНИЙ
1.1.
Случайные величины
1.1.1. Функции распределения вероятностей случайных величин
Простейшая модель физического эксперимента – последовательность независимых
опытов (испытаний), когда в результате каждого очередного испытания произойдет, либо
не произойдет некоторое событие. Иначе говоря, в каждом испытании имеет место один
из двух возможных исходов A или A с вероятностью соответственно p и 1 − p . В последовательности n независимых испытаний событие A может произойти k раз с вероятностью
n−k
Pn (k ) = C nk p k (1 − p ) .
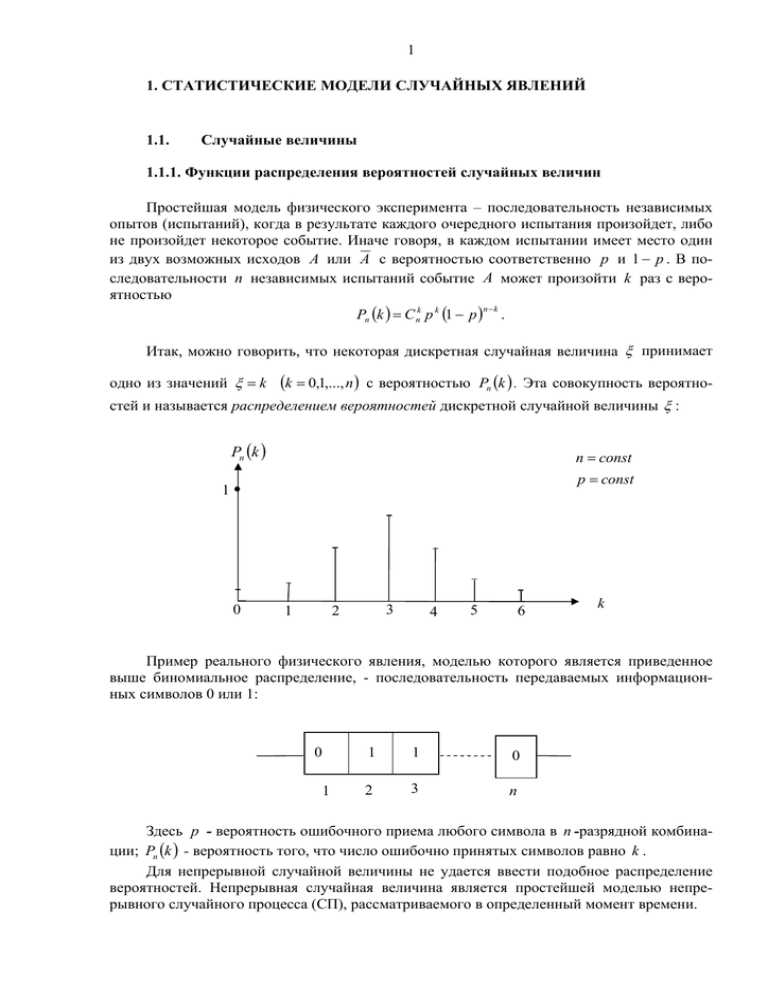
Итак, можно говорить, что некоторая дискретная случайная величина ξ принимает
одно из значений ξ = k
(k = 0,1,..., n )
с вероятностью Pn (k ) . Эта совокупность вероятно-
стей и называется распределением вероятностей дискретной случайной величины ξ :
Pn (k )
n = const
p = const
1
0
1
3
2
4
5
6
k
Пример реального физического явления, моделью которого является приведенное
выше биномиальное распределение, - последовательность передаваемых информационных символов 0 или 1:
0
1
1
1
0
2
3
n
Здесь p - вероятность ошибочного приема любого символа в n -разрядной комбинации; Pn (k ) - вероятность того, что число ошибочно принятых символов равно k .
Для непрерывной случайной величины не удается ввести подобное распределение
вероятностей. Непрерывная случайная величина является простейшей моделью непрерывного случайного процесса (СП), рассматриваемого в определенный момент времени.
2
ξ (t ) случайного процесса ξ (t ) имеет вид:
(i )
Произвольная i -я реализация
ξ (i ) (t )
x1
t
t1
При этом x1 - значение случайной величины ξ1 , являющейся выборочным значением случайного процесса ξ (t ) в момент времени t1 .
Универсальным как для дискретных, так и для непрерывных случайных величин является понятие функции распределения вероятностей (интегральной функции распределения):
Fξ ( x ) = P{ξ ≤ x},
где символ P{A}означает вероятность события A .
Для непрерывной случайной величины функция Fξ (x ) непрерывна:
F ξ (x
1
x
0
Для дискретной случайной величины:
Fξ (x ) =
∑ P{ξ = x }
k
xk ≤ x
Fξ (x )
1
...
xn −1 xn xn+1
...
x
3
Плотность вероятности
случайной величины ξ :
(дифференциальная функция распределения)
Wξ ( x ) =
dFξ ( x )
dx
.
Для непрерывной случайной величины ξ функция Wξ (x ) непрерывна:
Wξ (x )
x
При этом:
x2
P{x1 ⟨ξ ≤ x2 } = ∫ Wξ ( x )dx .
x1
Для дискретной случайной величины :
Wξ ( x ) = ∑ P{ξ = xk }δ ( x − xk ) .
k
Плотность вероятности смешанной случайной величины ξ содержит как непрерывную, так и дискретную части:
Wξ ( x ) = Wξ(н ) ( x ) + Wξ(д ) ( x ) ,
∞
причем:
∫ Wξ (x )dx = 1 .
−∞
Рассмотрим пример: прохождение непрерывного случайного процесса ξ (t ) через
нелинейное безынерционное устройство с характеристикой вида y = f ( x ) :
y
− x0
x0
x
4
Имеем η = f (ξ ) . Эта запись означает, что каждому значению x случайной
величины ξ соответствует определенное значение y случайной величины η , причем в
рассматриваемом примере
⎧ x, x ≤ x 0
⎪
y = f (x ) = ⎨
⎪ x 0 signx, x > x 0 .
⎩
Тогда
Wη ( y ) = Wη(н ) ( y ) + Wη(д ) ( y ) .
При этом, очевидно,
⎧W ( y )
Wη(н ) ( y ) = ⎨ ξ
⎩ 0
y ≤ x0
y > x0 .
В то же время дискретная часть плотности вероятности величины η :
Wnд ( y ) = P{η = − x0 }δ ( y + x0 ) + P{η = x0 }δ ( y − x0 ) =
= P{ξ ≤ − x0 }δ ( y + x0 ) + P{ξ > x0 }δ ( y − x0 ) =
= Fξ (− x0 )δ ( y + x0 ) + [1 − Fξ ( x0 )]δ ( y − x0 ) .
Тогда функция распределения величины η имеет вид:
⎧
⎪
0, y > − x0
⎪
y
⎪⎪
Fη ( y ) = ⎨ Fξ (− x0 ) + ∫ Wξ ( x )dx,
− x0 ≤ y < x0
− x0
⎪
x0
⎪
⎪ Fξ (− x0 ) + 1 − Fξ ( x0 ) + ∫ Wξ ( x )dx = 1, y ≥ x0 .
⎪⎩
− x0
5
Wξ (x)
1 − Fξ ( x 0 )
Fξ (− x0 )
− x0
x
x0
0
f (x )
− x0
x
x0
0
Wη ( y )
1 − Fξ ( x0 )
Fξ (− x0 )
− x0
y
x0
0
Fη ( y )
1
− x0
0
y
x0
На приведенном выше рисунке, составляющие дискретной части плотности вероятности Wη ( y ) , содержащие δ – функции, условно показаны вертикальными стрелками
красного цвета.
1.1.2.
Числовые характеристики случайных величин
Основными числовыми характеристиками случайных величин являются моменты
распределения – начальные и центральные. Начальные моменты k -го порядка (соответственно для непрерывных и дискретных величин):
mk {ξ } =
∞
k
∫ x Wξ (x )dx;
−∞
n
mk {ξ } = ∑ P{ξ = xi }xik .
i =1
6
Аналогично центральные моменты k - го порядка:
M k {ξ } =
∞
k
∫ (xi − m1{ξ })
n
Wξ ( x )dx;
M k {ξ } = ∑ P{ξ = xi }(xi − m1{ξ }) .
k
i =1
−∞
В частности, математическое ожидание и дисперсия случайной величины ξ (соответственно для непрерывной и дискретной величин):
m1 {ξ } =
∞
n
∫ xWξ (x )dx;
m1{ξ } = ∑ P{ξ = xi }xi ;
i =1
−∞
M 2 {ξ } =
∞
n
2
∫ (xi − m1{ξ }) Wξ (x )dx;
M 2 {ξ } = ∑ P{ξ = xi }( xi − m1{ξ }) .
2
i =1
−∞
Для симметричных относительно m1 {ξ } распределений имеем:
M 2i +1 {ξ } = 0
(i = 0,1,2,...) .
Более того, всегда
M 1{ξ } =
∞
∫ [x − m {ξ }] Wξ (x )dx = 0 .
1
−∞
Тогда M 3 {ξ } - «младший» из моментов, характеризующих асимметрию распределения.
Безразмерная величина
γ1 =
M3
M 23
называется коэффициент асимметрии.
Так, для нормального распределения, когда
Wξ ( x ) =
имеем M 3 = 0 и, следовательно,
2
1
e−( x − a )
2π σ
2σ 2
,
γ 1 = 0. В то же время для распределения Релея,
когда
Wξ ( x ) =
x
σ
2
e−x
2
2σ 2
,
γ 1 ≅ 0,63
имеем
Иногда используют численную характеристику «сглаженности» кривой распределения Wξ (x ) около моды (максимального значения):
γ2 =
M4
− 3.
M 22
В частности, для нормального распределения
мя для релеевского распределения γ 2 ≅ 0,23 .
получаем
γ 2 = 0 . В то же вре-
7
Значения γ 1 , γ 2 часто используются, чтобы характеризовать степень отличия
данного распределения от нормального.
1.2. Совокупность случайных величин
1.2.1. Функции распределения вероятностей совокупности случайных величин
Для полного описания случайного процесса, конечно, не достаточно иметь распределение вероятностей его значений лишь в один момент времени. Обычно необходимо
описывать взаимную зависимость значений СП в различные моменты времени t1 , t 2 ,..., как
на приведенном ниже рисунке, где представлена произвольная i -ая реализация случайного процесса ξ (t ) :
ξ (i ) (t )
t3
t2
t
t4
t1
При
этом
можно
говорить
о
совокупности
случайных
величин
ξ1 = ξ (t1 ), ξ 2 = (t 2 ),..., ξ n = ξ (t n ) как более сложной и адекватной модели СП. В этом случае
необходимо перейти к рассмотрению случайного n -мерного вектора ξ
(n )
(n )
(t ),
принимаю-
щего значения x = (x1 ,..., xn ).
Вероятность
⎧n
⎫
(n )
P ⎨∩ξi ≤ xi ⎬ = Fξ x (n )
⎩ i=1
⎭
( )
ξ
(n )
называется n - мерной функцией распределения вероятностей случайного вектора
, или совокупности случайных величин ξ 1 ,..., ξ n .
Очевидно, что
Fξi ( xi ) = Fξ
(n )
(∞,..., ∞, xi , ∞,...∞ ) .
Если
Fξ
(n )
(x ( ) ) = ∏ F (x ),
n
n
i =1
ξi
i
то величины ξ1 ,..., ξ n называются статистически независимыми.
Призводная n - го порядка
Wξ
(n )
(x ) =
(n )
∂ n Fξ
(n )
(x ( ) )
n
∂x1 ,..., ∂xn
8
называется n -мерной плотностью вероятностей случайного вектора ξ (n ) , или
совокупности случайных величин ξ1 ,..., ξ n .
Соответственно
Fξ
(n )
x1
xn
−∞
−∞
(x1 ,..., xn ) = ∫ ... ∫ Wξ (n ) (x1 ,..., xn )
dx1...dxn ,
откуда следует условие нормировки:
Fξ
(n )
∞
∞
−∞
−∞
(∞,.., ∞ ) = ∫ ... ∫ Wξ (n ) (x1 ,..., xn ) dx1...dxn = 1 .
Для статистически независимых величин, очевидно, имеем
Wξ
(n )
n
(x1 ,..., xn ) = ∏Wξ (xi ) .
i
i =1
Далее имеем:
Fξ
(n )
xi
⎛∞
∞
(∞,..., ∞, xi , ∞,..., ∞ ) = ∫ ⎜⎜ ∫ ... ∫ Wξ (n ) (x1 ,..., xn )
⎜ ( кроме x )
−∞ −∞
⎝
Но
i
−∞
⎞
⎟
dx1 ...dxn ⎟dxi .
⎟
⎠
Fξ(n ) (∞,..., ∞, xi , ∞,..., ∞ ) = Fξi ( xi ) .
Следовательно,
⎛∞
⎜
Fξi (xi ) = ∫ ⎜ ∫ ...
−∞⎜ − ∞ ( кроме
⎝
∞
xi
∫ Wξ (x ,..., x )
(n )
1
n
xi ) −∞
⎞
⎟
dx1 ...dxn ⎟dxi .
⎟
⎠
Тогда для любой ξ i :
Wξi ( xi ) =
1.2.2.
∞
∞
( )
∫ ... ∫ Wξ (x ,..., x )dx ...dx
n
1
n
1
n
.
− ∞ ( кроме xi ) −∞
Числовые характеристики совокупности случайных величин
В общем случае вводятся смешанные начальный и центральный моменты совместного распределения совокупности случайных величин:
∞
∞
−∞
−∞
mk1 ...kn {ξ1 ,..., ξ n } = ∫ ... ∫ x1k1 ...xnkn Wξ
∞
∞
−∞
−∞
(n )
(x1 ,..., xn )dx1...dxn
;
M k1 ...kn {ξ1 ,..., ξ n } = ∫ ... ∫ [x1 − m1 {ξ1 }] 1 ...[x n − m1 {ξ n }] n Wξ(n ) ( x1 ,..., x n )dx1 ...dxn .
k
k
Отсюда легко получить любые начальные и центральные моменты для каждой ξ i :
∞
∞
mki {ξ i } = ∫ ... ∫ xikiWξ
−∞
−∞
(n )
∞
(x1 ,..., xn )dx1...dxn = ∫ xik Wξ (xi )dxi ;
i
i
−∞
9
ki
∞
∞
−∞
−∞
M ki {ξ i } = ∫ ... ∫ [xi − m1 {xi }] Wξ
(n )
ki
∞
(x1 ,..., xn )dx1 ...dxn = ∫ [xi − m1 {xi }]
Wξi ( xi )dxi .
−∞
Одна из важнейших характеристик совокупности случайных величин – смешанный
центральный момент вида:
∞
∞
−∞
−∞
M 11 {ξ i , ξ j } = ∫ ... ∫ ( xi − m1{ξ i })(x j − m1 {ξ j })Wξ
(2 )
(x , x )dx dx
i
j
i
j
= K ij
- ковариация случайных величин ξ i и ξ j .
Представим K ij в виде:
∞
∞
( )
∫ ∫ x x Wξ (x , x )dx dx
K ij =
2
i
j
i
j
i
j
− m1{ξi }⋅ m1 {ξ j } = m11 {ξ i , ξ j }− m1{ξ i }⋅ m1 {ξ j }.
−∞ −∞
Безразмерное отношение:
Rij =
K ij
M 2 {ξ i }M 2 {ξ j }
называется коэффициентом корреляции случайных величин ξ i и ξ j .
В частности, для статистически независимых ξ i , ξ j имеем:
∞ ∞
∫ ∫ x x Wξ (x )Wξ (x )dx dx
K ij =
i
j
i
i
j
j
i
j
− m1 {ξ i }⋅ m1 {ξ j } = m1 {ξ i }⋅ m1 {ξ j }− m1 {ξ i }⋅ m1 {ξ j } = 0.
− ∞−∞
Случайные величины, для которых K ij = 0 , называются некоррелированными. Итак,
статистически независимые случайные величины некоррелированны. Обратное в общем
случае неверно.
Рассмотрим физический смысл понятия корреляции случайных величин. Для этого
перейдем от величин ξ i , ξ j к величинам ξ i , ξ j вида:
ξi =
ξ i − m1 {ξ i }
;
M 2 {ξ i }
ξj =
ξ j − m1 {ξ j }
M 2 {ξ j }
,
принимающие значения xi , x j соответственно.
Введем в рассмотрение неотрицательную величину
∫ ∫ (x
)
∞ ∞
L=
2
i
± x j Wξ
(2 )
(x , x )dx dx
i
j
i
j
=
− ∞−∞
∫ (x ) Wξ (x )dx + ∫ (x )
∞
=
i
−∞
∞
2
i
i
i
j
−∞
∞ ∞
2
⎛
⎞
(2 )
Wξ j (x j )dx j ± 2 ∫ ∫ ⎜ xi x j ⎟ Wξ (xi , x j )dxi dx j = 2(1 ± Rij ) ≥ 0.
⎠
− ∞− ∞⎝
2
Заметим, что отсюда, в частности, следует:
10
Rij ≤ 1 .
Далее, пусть Rij = 1. Тогда, используя запись величины L с отрицательным знаком
в подынтегральном выражении, получаем L = 0 . Но это значит, что для всех значений
величин ξ i ,ξ j выполняется xi = x j , т.е. ξ i = ξ j , или
M 2 {ξ i }
(ξ j − m1{ξ j }) + m1{ξi } =
M 2 {ξ j }
ξi =
⎛
⎞
M 2 {ξi }
M 2 {ξ i }
ξ j + ⎜ m1{ξi }−
m1 {ξ j }⎟ ,
⎜
⎟
M 2 {ξ j }
M 2 {ξ j }
⎝
⎠
откуда получаем ξ i = aξ j + b .
Rij = −1 , используя запись L с положительным знаком в по-
Аналогично, для
дынтегральном выражении, получаем ξ i = − ξ j , так что ξ i = − aξ j + c .
Итак, условие Rij = 1 означает линейную зависимость случайных величин ξ i и ξ j .
Рассмотрим в качестве примера двумерное нормальное распределение
Wξ
(2 )
2
⎧⎪
⎡ ( x1 − a1 )2
(
1
x1 − a1 )( x2 − a2 ) (x2 − a2 ) ⎤ ⎫⎪
(x1 , x2 ) =
exp⎨−
− 2r
+
⎥ ⎬,
2 ⎢
2
σ 1σ 2
σ 22 ⎦ ⎪⎭
⎪⎩ 2(1 − r ) ⎣ σ 1
2π 1 − r 2 ⋅ σ 1σ 2
1
где
a1 = m1 {ξ1 };
σ 12 = M 2 {ξ1 };
a 2 = m1 {ξ 2 };
σ 22 = M 2 {ξ 2 } .
Прямым вычислением легко показать:
K12 = rσ 1σ 2 , т.е.
R12 =
rσ 1σ 2
σ 12σ 22
=r.
Для некоррелированных нормальных величин (r = 0 ) имеем:
Wξ
(2 )
(x1 , x2 ) =
⎧ 1 ( x1 − a1 )2 1 ( x2 − a2 )2 ⎫
exp⎨−
−
⎬ = Wξ1 (x1 ) ⋅ Wξ2 ( x2 ).
2
2
2πσ 1σ 2
2
2
σ
σ
1
2
⎩
⎭
1
Отсюда следует важное свойство: некоррелированность нормальных случайных величин означает также и их статистическую независимость.
1.3.
Примеры некоторых часто встречающихся распределений
1.3.1.
Биномиальное распределение.
Вероятность того, что в последовательности из n независимых испытаний некоторое событие произойдет ровно k раз, равна
11
Pn (k ) = C nk p k (1 − p )
n
∑C
Из условий нормировки:
k =0
k
n
n−k
.
n−k
= 1.
p k (1 − p )
m1 {ξ } = np;
Основные моменты:
M 2 {ξ } = np(1 − p ) .
Рассмотрим задачу о случайном блуждании частицы вдоль оси x при возможном
перемещении на каждом шаге на единицу вправо (с вероятностью p) или влево (с вероятностью 1 − p ), причем вероятность каждого очередного перемещения не зависит от того,
что было на любом из предыдущих шагов. Такая модель описывает, например, цифровой
накопитель, на вход которого поступают числа +1 или -1 в случайном порядке.
(
)
Определим вероятность Pn(m ) того, что при нулевом начальном условии P0(0 ) = 1 после приема n импульсов сумма окажется равной величине m :
l прав
l лев
x
-2
-1
0
1
2 . . . . . . . . . m. …….. lправ
Нахождение частицы в точке с координатой x = m является результатом некоторого
числа l прав шагов вправо и l лев = l прав − m шагов влево от нулевого начального положения,
причем l прав + l лев = n .
Тогда имеем:
l прав + l прав − m = n ,
откуда
l прав =
m+n
.
2
Тогда вероятность Pn(m ) совпадает с вероятностью того, что при n испытаниях собыm+n
раз. В остальных испытаниях проистие «сдвиг на шаг вправо» произойдет ровно
2
ходят противоположные события («сдвиг на шаг влево»). Следовательно,
n+ m
⎛m+n⎞
Pn(m ) = Pn ⎜
⎟ = Cn 2 p
2
⎝
⎠
При этом
− n ≤ m ≤ n, т.е.
n+m
2
(1 − p )
n−m
2
.
0≤k ≤n.
При больших n вычисление Pn (k ) затруднительно. Однако рассмотрим значения
Pn (k ) для различных n при p = 0,5 :
12
Pn (k )
Pn (k )
(m = 2k − 1)
n =1
0,5
n=2
0,5
(m = 2k − 2)
0,25
0
1
k
2
0
k
2
Pn (k )
Pn (k )
0,5
0,4
0,5
(m = 2k − 3)
n=3
0,3
0,2
0,2
0,1
0,1
1
2
3
k
4
n=4
0,4
0,3
0
1
0
1
2
3
(m = 2k − 4)
4
k
Pn (k )
0,5
n=5
0,4
(m = 2k − 5)
0,3
0,2
0,1
0
1
2
3
4
5
k
Как видно из рисунков, с ростом n пунктирная кривая, характеризующая распределение вероятностей, стремится к гауссовой. Действительно, можно показать, что при
n >> 1
− ( k − a )2
1
2
P(n ) (k ) ~
e 2σ ,
где
a = np ;
σ 2 = np(1 − p ) , причем
2π σ
наибольшая точность достигается при стремлении значения p к величине 0,5.
В случае же p << 1 , т.е. при описании потока редких событий в последовательности
независимых испытаний, имеет место другое асимптотическое выражение биномиального
a
распределения. Пусть
p= ,
n⟩⟩1,
p⟨⟨1.
n
Тогда
k
⎛a⎞ ⎛ a⎞
Pn (k ) = C ⎜ ⎟ ⎜1 − ⎟
⎝n⎠ ⎝ n⎠
k
n
n−k
;
lim Pn (k ) =
n →∞
a k −a
e - распределение Пуассона.
k!
13
Это распределение представляет и самостоятельный интерес как модель
потока редких событий (поток заряженных частиц, последовательность молниевых разрядов, поток заявок на обслуживание, поток отказов радиоаппаратуры и т.д.).
1.3.2.
Распределение Пуассона
Рассмотрим поток редких событий, происходящих в моменты времени t 0 , t1 ,..., не
связанные жесткой временной сеткой.
τ
t0
t2
t1
t3
t
Будем считать, что выполнены 3 условия :
•
стационарность (вероятность того, что на интервале τ произошло k событий, зависит только от величины интервала и не зависит от расположения этого интервала
на оси времени;
•
отсутствие последействия (вероятность того, что на данном интервале τ
произошло k событий, не зависит от того, сколько событий произошло на любых предыдущих интервалах времени);
•
ординарность (вероятность того, что на достаточно малом промежутке времени Δt произошло 2 и более событий пренебрежительно мала по сравнению с вероятностью одного события).
Тогда вероятность того, что на интервале длительностью τ произошло k событий,
описывается распределением Пуассона:
Pτ (k ) =
(λτ )k e −λτ ,
k!
где λ – среднее число событий в единицу времени.
Покажем справедливость этого выражения для случая k = 0 , т.е. докажем наличие
экспоненциальной зависимости Pτ (k ) от величины λτ :
Pτ (0) = e − λτ .
Для доказательства рассмотрим интервал времени τ + Δτ , где Δτ удовлетворяет
условию ординарности потока. Тогда, с учетом условия отсутствия последействия, имеем:
Pτ + Δτ (0) = Pτ (0) ⋅ PΔτ (0) .
В силу условия ординарности:
PΔτ (0 ) ≅ 1 − PΔτ (1) .
В свою очередь, также в силу условия ординарности, для среднего числа событий на
интервале Δτ имеем:
λ Δτ ≅ 0 ⋅ PΔτ (0) + 1⋅ PΔτ (1),
14
откуда:
PΔτ (1) ≅ λ Δτ .
Итак, примем:
PΔτ (0) = 1 − λ Δτ ,
т.е.
Pτ + Δτ (0) = Pτ (0)(1 − λ Δτ ) .
Тогда:
Pτ + Δτ (0) − Pτ (0)
= −λ Pτ (0) .
Δτ
dPτ (0)
= - λ Pτ (0) .
dτ
При Δτ → 0 имеем:
Интегрируя полученное дифференциальное уравнение методом разделения переменных, имеем:
dPτ (0 )
= - λ dτ ;
Pτ (0 )
ln Pτ (0 ) = - λ τ + C .
Начальное условие:
т.е. C = 0 , так что окончательно:
P0 (0) = 1 ,
Pτ (0) = e − λτ .
Аналогично можно доказать справедливость исходной формулы и при k > 0 .
Моменты распределения Пуассона:
m1 {ξ } = λ ;
1.3.3.
M 2 {ξ } = λ .
Экспоненциальное и связанные с ним распределения
Для описания потока редких событий часто является важным не только определение
вероятности Pτ (k ) наступления k событий за отрезок времени τ , но также и определение
статистических характеристик (функции распределения, плотности вероятностей, моментов распределения) величины временного интервала между соседними событиями. Такой
поток событий является, например, простейшей моделью отказов элементов радиоаппаратуры. Тогда одним из важнейших параметров является вероятность безотказной работы в
течение определенного интервала времени, а также вероятность того, что интервал безотказной работы не окажется меньше заданного значения.
Решение этих задач приводит к экспоненциальному распределению. Мы уже встречались с таким распределением, рассматривая распределение Пуассона Pτ (k ) при k = 0 .
Рассмотрим несколько иную постановку задачи.
Интегральная функция распределения случайной величины τ интервала между соседними событиями, очевидно, равна:
Fτ ( x ) = P{τ ≤ x} = 1 − P{τ > x}.
15
Но вероятность P{τ > x} может быть вычислена как вероятность того, что на
интервале времени x не произошло ни одного события в пуассоновском потоке редких
событий:
(λ τ )k e −λ τ
P{τ ⟩ x} = Pτ (k ) k =0 =
k!
τ =x
Итак,
k =0
= e −λ x .
τ =x
Fτ ( x ) = 1 − e − λx .
При этом λ — средняя частота событий (среднее число событий в единицу времени).
Тогда
1
λ
= τ - средний интервал времени между соседними событиями.
При этом:
Fτ ( x ) = 1 − e
−
x
τ
x ≥ 0.
,
Соответственно, плотность вероятностей величины τ :
x
1 −
Wτ ( x ) = e τ ,
x ≥ 0.
τ
Как и следовало ожидать,
m1 {τ } =
1
τ
∞
∫ xe
−
x
τ
(
τ )2
dx =
τ
0
=τ .
При этом:
M 2 {τ } = m2 {τ } − (m1 {τ }) =
2
1
τ
∞
−
x
2
2
2
∫ x e τ dx − (τ ) = (τ ) .
0
Пример. Пусть среднее время наработки на отказ некоторого радиоэлектронного
устройства составляет τ = 100 дней. Какова вероятность того, что в течение 100 дней не
произойдет ни одного отказа?
Имеем:
100
−
⎛
⎞
P{τ ⟩100} = 1 − Fτ (100) = 1 − ⎜⎜1 − e 100 ⎟⎟ ≅ 0,37 .
⎝
⎠
Дальнейшим обобщением задачи, связанной с потоком случайных событий, является
рассмотрение в качестве случайной величины τ э интервала между некоторым (произвольно взятым) событием и k -ым (k ≥ 1) следующим за ним событием. Функция распределения этой величины называется распределением Эрланга k -го порядка, а соответствующая плотность вероятностей имеет вид:
−
x
x≥0
x k −1e τ
Wτ э ( x )k =
,
k
k ≥1 .
(τ ) (k − 1) !
В частном случае k = 1, естественно, получаем экспоненциальное распределение:
x
1 −
Wτ э ( x )1 = Wτ ( x ) = e τ .
τ
Можно показать:
16
m1 {τ э } = kτ
2
M 2 {τ э } = k (τ )
Обобщением распределения Эрланга является Г-распределение. Пусть
лочисленные k заменены на непрерывную величину α . Тогда имеем:
β α xα −1 − β x
WГ ( x )α , β =
e ,
x≥0 ,
Г (α )
1
τ
= β , а це-
∞
Г (α ) = ∫ e −t t α −1dt - интеграл Эйлера.
где
0
Заметим, что при целочисленных α :
∞
Г (α ) = ∫ e −t t α −1dt = (α − 1) !
0
Можно показать:
m1 {Г } =
1.3.4.
α
;
β
M 2 {Г } =
α
.
β 2
Распределение Рэлея
Среди важных и часто встречающихся на практике распределений, связанных с гауссовским (нормальным), рассмотрим распределение Релея. Впервые оно было введено
лордом Релеем в 1880 году при рассмотрении огибающей суммы большого числа гармонических колебаний различных частот. В дальнейшем выяснилось, что при пристрелке
оружия, если разбросы попаданий в каждом из двух взаимно перпендикулярных направлений независимы и имеют одинаковые нормальные распределения с параметрами
m1 {ξ1 } = m1 {ξ 2 } = 0;
M 2 {ξ1 } = M 2 {ξ 2 } = σ 2 , то значения промаха как отклонения η от
центра мишени в любом направлении будут распределены по закону Релея.
Рассмотрим подробнее задачу нахождения распределения величины η = ξ12 + ξ 22 ,
где ξ1 , ξ 2 - отклонения от центра мишени в двух взаимно перпендикулярных направлениях. Значения величин η , ξ1 , ξ 2 обозначим соответственно y, x1 , x 2 :
ξ2
x2
y
x1
ξ1
Функция
17
Fη ( y ) величины η равна вероятности того, что
распределения
конец вектора с проекциями x1 и x2 не выйдет за пределы окружности радиуса
y = x12 + x22 , или
Fη ( y ) =
( )
∫∫ Wξ (x , x )dx dx
2
1
2
1
,
2
x12 + x22 ≤ y
где
(2 )
Wξ
(x1 , x2 ) =
(
1
2π σ
)
2
e
−
x12 + x22
2σ 2
.
Перейдем к полярным координатам ρ , ϕ заменой переменных:
x1 = ρ cos ϕ
x 2 = ρ sin ϕ
Тогда имеем:
Fη ( y ) =
2π y
1
∫ ∫ 2πσ
2
e
−
ρ2
2σ 2
0 0
∂ ( x1 , x2 )
dρdϕ ,
∂(ρ ,ϕ )
где якобиан преобразования
∂ (x1 , x2 )
∂ (ρ , ϕ )
2π
Итак,
∂x1
∂ρ
=
∂x2
∂ρ
∂x1
cos ϕ
∂ϕ
=
∂x2
sin ϕ
∂ϕ
ρ2
y
y2
− ρ sin ϕ
=ρ
ρ cos ϕ
y2
t
−
−
1
ρ − 2σ
2σ
2σ
Fη ( y ) = ∫ dϕ ∫
e
d
=
e
dt
=
1
−
e
, y ≥ 0.
ρ
2 ∫
2
2
2
πσ
σ
0
0
0
2
2
2
Соответственно,
Wη ( y ) =
y
σ
2
e
−
y2
2σ 2
,
y ≥ 0.
Wη ( y )
σ1
σ 2 > σ1
σ1
σ2
y
18
Модальное значение y = y М определяется из уравнения
1
σ2
e
−
y2
2σ 2
y2
2 y 2 − 2σ 2
−
e
=0,
2σ 4
откуда
yМ = σ
Соответственно
Wη ( y М ) = Wη ( y )max =
1
σ e
.
При этом
m1 {η} = σ
1.3.5.
π
2
,
M 2 {η} =
4 −π 2
σ .
2
Равномерное распределение
Часто рассматривается колебание вида:
S (t ) = A(t )cos(ω 0 t + ϕ (t ) + ψ ) ,
где A(t ) и ϕ (t ) - детерминированные функции, ω0 - заданная частота колебания несущей, а ψ – случайная начальная фаза. Обычно допускаются с равной вероятностью
любые значения начальной фазы в пределах [0,2π ] . В этом случае мы имеем дело с равномерно распределенной случайной величиной ψ . В общем случае равномерного распределения имеем:
⎧ 1
,
a≤ x≤b
⎪
Wξ ( x ) = ⎨ b − a
x < a, x > b.
⎪ 0
⎩
Wξ ( x )
1
b−a
0
a
x
b
Здесь
m1 {ξ } =
a+b
;
2
M 2 {ξ } =
(b − a )2 .
12
19
Функция распределения имеет вид:
⎧ 0
⎪x − a
Fξ ( x ) = ⎨
⎪b − a
⎩ 1
x≤a
a< x≤b .
x>b
Fξ (x )
1
a
0
x
b
Пример 1. Шум квантования δ k = U k − U k(l ) , где U k - истинное выборочное значение
функции U (t ),
U k(l ) — значение ближайшего l -го уровня квантования. Плотность веро-
ятностей значений случайной величины δ k примем
Wδ (x ) =
1
,
Δ
x≤
Δ
.
2
l +1
Uk
l
Uk
Δ
(l )
l −1
tk
Тогда
m1 {δ } = 0 ;
M 2 {δ } =
Δ2
.
12
Пример 2. Распределение начальной фазы ψ .
1
(0 ≤ ϕ ≤ 2π )
,
2π
2π
1
m1 {ψ } =
xdx = π
2π ∫0
(2π )2 − π 2 = π 2
M 2 {ψ } = m2 {ψ } − m12 {ψ } =
3
3
Wψ ( x ) =
20
1.4.
Условные функции распределения и плотности вероятностей
1.4.1.
Условные распределения двух случайных величин
Пусть имеется событие A , появляющееся одновременно с одним из n взаимно несовместимых событий (гипотез) B1 ,..., Bn , составляющих полную группу. Так, например,
событие A заключается в регистрации (в месте приема) некоторого определенного символа y j алфавита, объем которого равен n . При этом событие Bi — передача некоторого
символа yi . Вероятность P( A, Bi ) — вероятность того, что переданным символом является yi , а принятым — некий символ y j (один из возможных передаваемых символов
y1 ,..., y n ). Тогда
n
n
i =1
i =1
P( A) = ∑ P( A, Bi ) = ∑ P( A / Bi )P(Bi ) ,
где
P( A, Bi ) — вероятность одновременного осуществления A и Bi ;
P( A Bi ) — условная вероятность A при условии осуществления Bi ;
P(Bi ) — априорная вероятность Bi .
С другой стороны, очевидно,
P( A Bk )P(Bk ) = P(Bk A)P( A),
Так что апостериорная вероятность события Bk (гипотезы) равна
P ( Bk / A ) =
P( A / Bk )P(Bk )
P( A / Bk )P(Bk )
= n
P ( A)
∑ P( A / Bi )P(Bi )
i =1
- формула Байеса.
Понятие условных вероятностей событий распространяется и на случайные величины. Так, для двух зависимых непрерывных случайных величин ξ и η имеем :
x + Δx y
W ( ) ( x, y )dxdy
∫
∫
P{x < ξ ≤ x + Δx, η ≤ y}
=
.
x < ξ ≤ x + Δx} =
2
P{η ≤ y
x −∞
x + Δx ∞
P{x < ξ ≤ x 1 }
( )
∫ ∫ W (x, y )dxdy
2
x
−∞
Здесь W ( x, y ) - двумерная плотность вероятностей величин ξ и η .
Введем в рассмотрение функцию:
(2 )
Fη ( y x ) = lim P{η ≤ y x < ξ ≤ x + Δx}.
Δx →0
Имеем :
y
Fη ( y x ) = lim
∫ W (x, y )dyΔx
−∞
Δx →0 ∞
( )
∫ W (x, y )dyΔx
−∞
y
(2 )
2
( )
∫ W (x, y )dy
2
==
−∞
∞
( )
∫ W (x, y )dy
2
−∞
=
1
y
W ( ) ( x, y )dy .
∫
Wξ ( x )
2
−∞
Здесь Fη ( y x ) - условная функция распределения величины η , зависящей от величины ξ .
21
∂F ( y x )
, равна, очевидно,
∂y
∂Fη ( y x ) W (2 ) ( x, y )
=
Wη ( y x ) =
∂y
Wξ ( x )
Производная
Здесь Wη ( y x ) - условная плотность вероятности непрерывной случайной величины η , зависящей от ξ .
Аналогично безусловным плотностям выполняется условие нормировки:
∞
∞
Wξ ( x )
1
(
)
W
y
x
dy
W (2 ) ( x, y )dy =
=
= 1.
∫−∞ η
∫
Wξ ( x ) −∞
Wξ ( x )
Легко получить также аналог формулы полной вероятности:
∞
∞
−∞
−∞
Wη ( y ) = ∫ W (2 ) ( x, y )dx = ∫ Wη ( y x )Wξ ( x )dx .
Интегрируя по y, получаем связь Fη ( y x ) и Fη ( y ) :
∞
∞
⎞
⎛y
Fη ( y ) = ∫ Wξ (x )⎜⎜ ∫ Wη ( y x )dy ⎟⎟dx = ∫ Fη ( y x )Wξ (x )dx .
−∞
−∞
⎠
⎝ −∞
Аналогично выражению для Wη ( y x ) , легко получить:
W ( 2 ) ( x, y )
.
Wη ( y )
Тогда получаем для непрерывных случайных величин ξ и η аналог формулы БайеWξ ( x y ) =
са:
Wξ ( x y ) =
Wη ( y x )Wξ ( x )
∞
∫ Wη ( y x )Wξ (x )dx
−∞
Пример. Условная гауссовская (нормальная) плотность вероятностей.
Пусть двумерная плотность вероятностей величин ξ и η подчиняется гауссовскому
(нормальному) распределению (см. 1.2.2.), где a1 ,σ 12 и a 2 ,σ 22 - математическое ожидание
и дисперсия соответственно величин ξ и η . Тогда
1
Wη ( y x ) =
W ( 2 ) ( x, y )
=
Wξ (x )
2π 1 − r 2 σ 1σ 2
×
⎡ ( x − a1 )2 ⎤
1
exp ⎢−
⎥
2σ 12 ⎦
2π σ 1
⎣
⎧⎪
⎡ ( x − a1 )2
(x − a1 )( y − a2 ) + ( y − a2 )2 ⎤ ⎫⎪ =
1
r
2
× exp⎨−
−
⎥⎬
2 ⎢
2
σ 1σ 2
σ 22 ⎦ ⎪⎭
⎪⎩ 2 1 − r ⎣ σ 1
2
2
⎧⎪
⎡ (x − a1 )2
(
x − a1 )( y − a 2 ) ( y − a 2 ) ⎤ ⎫⎪
1
1
2 ( x − a1 )
exp⎨−
=
− 1− r
− 2r
+
⎥⎬ =
2
2 ⎢
σ 1σ 2
σ 12
σ 22 ⎦ ⎪⎭
⎪⎩ 2 1 − r ⎣ σ 1
σ 2 2π 1 − r 2
=
(
)
(
)
1
σ 2 2π (1 − r 2 )
(
)
(
)
2
⎧⎪
⎡ x − a1 y − a 2 ⎤ ⎫⎪
1
r
exp⎨−
−
⎬.
2 ⎢
σ 2 ⎥⎦ ⎪
⎪⎩ 2 1 − r ⎣ σ 1
⎭
(
)
22
Как и следовало ожидать, при r = 0 , когда ξ и η статистически независимы, получаем:
Wη ( y x ) =
1
2π σ 2
e
−
( y − a2 )2
2σ 22
= Wη ( y ).
Интересно отметить, что при r → 1 («полная» статистическая зависимость) имеем:
⎛ y − a 2 x − a1 ⎞
⎟.
Wη ( y x ) → δ ⎜⎜
−
σ 1 ⎟⎠
⎝ σ2
Например, при x = a1 значения η по мере приближения r к значению 1 все более
группируются вокруг y = a 2 :
Wη ( y a1 )
r3 > r2
r2 > r1
r1
y
a1
1.4.2.
a2
Условные числовые характеристики
Рассмотрим условные числовые характеристики зависимых случайных величин.
Условное математическое ожидание:
∞
( )
∫ yW (x, y )dy
2
m1 {η x} =
∞
∫ yWη ( y x )dy =
−∞
−∞
Wξ (x )
.
Условная дисперсия:
∞
M 2 {η x} =
∞
∫ [ y − m {η x}] Wη ( y x )dy =
2
1
( )
∫ [ y − m {η x}] W (x, y )dy
−∞
−∞
Так, для нормальных величин ξ и η имеем:
m1 {η x} =
σ2
r ( x − a1 ) + a 2
σ1
(
2
2
1
M 2 {η x} = σ 22 1 − r 2
)
Wξ (x )
.
23
Очевидно, что при r = 0 условные моменты совпадают с безусловными:
m1 {η x} r =0 = a 2 ;
m1 {η x} →
Однако при r → 1
1.4.3.
M 2 {η x} η =0 = σ 22
σ2
(x − a1 ) + a2 ,
σ1
M 2 {η x} → 0.
Условные распределения совокупности случайных величин
Рассмотрим совокупность случайных величин ξ1 ,..., ξ n , описываемую n -мерной
плотностью вероятностей Wξ(n ) ( x1 ,..., xn ) . Тогда, аналогично случаю двух случайных величин (1.4.1) имеем:
(k )
Wξ
(x1 ,..., xk
xk +1 ,..., xn ) =
Wξ(n ) (x1 ,..., xn )
Wξ(n− k ) (x k +1 ,..., xn )
.
Отсюда, в частности, следует:
Wξ(n ) ( x1 ,..., x n ) = Wξ ( xn xn −1 ,..., x1 ) ⋅ Wξ ( xn −1 ,..., x1 ) =
= Wξ (x n xn −1 ,..., x1 ) ⋅ Wξ ( xn−1 x n− 2 ,..., x1 ) ⋅ Wξ ( xn − 2 ,..., x1 ) =
= Wξ (x n xn −1 ,..., x1 ) ... Wξ ( x2 x1 ) ⋅ Wξ ( x1 ) .