Документ 2002712
реклама

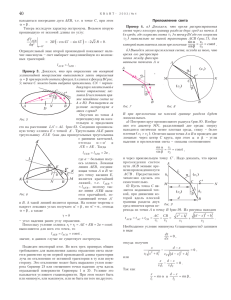
À.Â. Ìîêøèí, Þ.Â. Ìåðêóëîâà Ôëóêòóàöèîííî-øóìîâàÿ ñïåêòðîñêîïèÿ â èññëåäîâàíèè ñèãíàëîâ êîëåáàíèé çåìíîé êîðû ÓÄÊ: 53.01 À.Â. Ìîêøèí, Þ.Â. Ìåðêóëîâà Êàçàíñêèé (Ïðèâîëæñêèé) ôåäåðàëüíûé óíèâåðñèòåò, Êàçàíü, [email protected] ÔËÓÊÒÓÀÖÈÎÍÍÎ-ØÓÌÎÂÀß ÑÏÅÊÒÐÎÑÊÎÏÈß Â ÈÑÑËÅÄÎÂÀÍÈÈ ÑÈÃÍÀËΠÊÎËÅÁÀÍÈÉ ÇÅÌÍÎÉ ÊÎÐÛ Â íàñòîÿùåé ðàáîòå ïðåäëàãàåòñÿ ïîäõîä, ðåàëèçóåìûé â ðàìêàõ ôëóêòóàöèîííî-øóìîâîé ñïåêòðîñêîïèè (Yulmetyev et al., 2005), äëÿ àíàëèçà äàííûõ, õàðàêòåðèçóþùèõ êîëåáàíèÿ çåìíîé êîðû.  êà÷åñòâå êîíêðåòíîãî ïðèìåðà ðàññìàòðèâàþòñÿ äàííûå ïî ñèëüíûì è ñëàáûì çåìëåòðÿñåíèÿì â Òóðöèè (1998 ã. è 1999 ã.) è òåõíîãåííûì âçðûâàì. Îáñóæäàåòñÿ âîçìîæíîñòü ïðåäñêàçàíèÿ çåìëåòðÿñåíèÿ, à òàêæå ñïîñîáíîñòü ïîäõîäà íà îñíîâå ñåéñìè÷åñêèõ äàííûõ âûÿâëÿòü ðàçëè÷èÿ ìåæäó òåõíîãåííûìè âçðûâàìè è çåìëåòðÿñåíèÿìè. Êëþ÷åâûå ñëîâà: òåõíîãåííûå âçðûâû, çåìëåòðÿñåíèÿ, øóìîâûå ïàðàìåòðû, ôóíêöèè ïàìÿòè, âðåìåííàÿ êîððåëÿöèîííàÿ ôóíêöèÿ. 1. Ââåäåíèå Äëÿ êîëè÷åñòâåííîé îöåíêè èçìåíåíèé â äèíàìèêå ÿâëåíèé, õàðàêòåðèçóþùèõñÿ áûñòðûì ÷åðåäîâàíèåì ðàçëè÷íûõ ðåæèìîâ ïîâåäåíèÿ è ïåðåìåæàåìîñòüþ, ÷àñòî èñïîëüçóþòñÿ ìåòîäû, ñâÿçàííûå ñ ëîêàëèçàöèåé ðåãèñòðèðóåìûõ èëè âû÷èñëÿåìûõ ïàðàìåòðîâ (Sornette et al., 1990; 1995; Yulmetyev et al., 2005). Èñïîëüçîâàíèå ëîêàëüíûõ ïàðàìåòðîâ ïîçâîëÿåò èçáåæàòü òðóäíîñòåé, ñâÿçàííûõ ñ íåýðãîäè÷íîñòüþ èññëåäóåìîé ñèñòåìû è äàåò âîçìîæíîñòü èçâëåêàòü äîïîëíèòåëüíóþ öåííóþ èíôîðìàöèþ î ñêðûòûõ ñâîéñòâàõ ðåàëüíûõ ñëîæíûõ ñèñòåì. Ñ ôèçè÷åñêîé òî÷êè çðåíèÿ òàêîé ïîäõîä íàïîìèíàåò èñïîëüçîâàíèå íåëèíåéíûõ óðàâíåíèé îáîáùåííîé ãèäðîäèíàìèêè ñ ëîêàëüíûì ïîâåäåíèåì ãèäðîäèíàìè÷åñêèõ è òåðìîäèíàìè÷åñêèõ ïàðàìåòðîâ è õàðàêòåðèñòèê. Îäíîé èç îñíîâíûõ çàäà÷ â ñåéñìîëîãèè ÿâëÿåòñÿ ïðîãíîçèðîâàíèå íà÷àëà çåìëåòðÿñåíèé. Äðóãàÿ âàæíàÿ çàäà÷à ñâÿçàíà ñ ðàñïîçíàâàíèåì è ðàçäåëåíèåì ñèãíàëîâ ñëàáûõ çåìëåòðÿñåíèé îò ñèãíàëîâ òåõíîãåííûõ ïîäçåìíûõ âçðûâîâ.  íàñòîÿùåé ðàáîòå ìû ïðåäëàãàåì ïîäõîä äëÿ àíàëèçà ñåéñìè÷åñêèõ äàííûõ, ðàçâèâàåìûé â ðàìêàõ ôëóêòóàöèîííî-øóìîâîé ñïåêòðîñêîïèè (Yulmetyev et al., 2001; 2005) ñ èñïîëüçîâàíèåì ëîêàëüíûõ øóìîâûõ ïàðàìåòðîâ. Àíàëèçèðóþòñÿ âðåìåííûå ðÿäû êîëåáàíèé çåìíîé êîðû â ñëó÷àå òðåõ ðàçëè÷íûõ ñëàáûõ çåìëåòðÿñåíèé â Èîðäàíèè 1998 ã. è òðåõ ëîêàëüíûõ ïîäçåìíûõ òåõíîãåííûõ âçðûâîâ. Äëèíà ðåãèñòðàöèè ñîñòàâëÿåò îò 10000 äî 25000 òî÷åê. Øàã äèñêðåòèçàöèè τ = 0,01 ñåê. Êðîìå ýòîãî ðàññìàòðèâàåòñÿ ñèëüíîå çåìëåòðÿñåíèå â Òóðöèè 1998 ã. Äëèíà ðåãèñòðàöèè – 65000 òî÷åê, øàã äèñêðåòèçàöèè τ = 0,02 ñåê. 2. Îñíîâíûå ïîíÿòèÿ ôëóêòóàöèîííî-øóìîâîé ñïåêòðîñêîïèè Ïðåäïîëîæèì, ÷òî äèíàìèêà èññëåäóåìîãî ïðîöåññà õàðàêòåðèçóåòñÿ äèñêðåòíûì ðÿäîì xi íåêîòîðîé õàðàêòåðèñòèêè Õ.  êà÷åñòâå Õ âûáèðàåì àìïëèòóäó êîëåáàíèé çåìíîé êîðû. Äèíàìèêà âåëè÷èíû Õ ïðåäñòàâëÿåòñÿ â âèäå X x T ,x T ,x T 2 ,..., x T k ,..., x T N 1 , (1) ãäå τ – ïîñòîÿííûé âðåìåííîé èíòåðâàë (øàã äèñêðåòèçàöèè), Ò – âðåìÿ íà÷àëà ðåãèñòðàöèè ñèãíàëà, (N-1)τ – äëèòåëüíîñòü ñèãíàëà. Íà îñíîâå (1) îïðåäåëèì ñðåäíåå çíà÷åíèå ⟨x⟩ è ôëóêòóàöèè δõj â âèäå 40 6 (48) 2012 x 1 N N 1 x T j , j 0 (2) xj xT j xT j x. Ôëóêòóàöèè ðàññìàòðèâàåìîé ñëó÷àéíîé âåëè÷èíû áóäóò îáðàçîâûâàòü êîððåëÿöèîííûé âåêòîð ñîñòîÿíèÿ ñèñòåìû, ñîñòîÿùèé èç k êîìïîíåíò Ak0 = Ak0 (0) = (δx(T ), δx(T + τ ),.., δ δx(T + (k − 1)τ )) = (δx0 , δx1 ,..., δx k −1 ). (3) Òîãäà âðåìåííàÿ çàâèñèìîñòü êîððåëÿöèîííîãî âåêòîðà ñîñòîÿíèÿ ìîæåò áûòü ïðåäñòàâëåíà â âèäå äèñêðåòíîãî m-øàãîâîãî ñäâèãà Amm+ k = Amm+ k (t ) = (δx(T + mτ ), δx(T + (m + 1)τ ),..., δx(T + (m + k + 1)τ )) = (δx0 , δx1 ,..., δx m + k −1 ). (4) Âðåìåííàÿ êîððåëÿöèîííàÿ ôóíêöèÿ (ÂÊÔ) âåëè÷èíû áóäåò èìåòü ñëåäóþùèé âèä (Yulmetyev et al., 2000): M 0 (t ) = AN0 −1− m ( 0 ) U ( t = T + mτ , T ) AN0 −1− m ( 0 ) AN0 −1− m ( 0 ) 2 , (5) ãäå óãëîâûå ñêîáêè ïðåäñòàâëÿþò ñîáîé ñêàëÿðíîå ïðîèçâåäåíèå âåêòîðîâ ñîñòîÿíèÿ, à U (t’, t) åñòü îïåðàòîð âðåìåííîé ýâîëþöèè: ANm−1 (T + t ) = U (T + mτ , T )AN0 −1− m (T ) = U (t ,0)AN0 −1−m (0).(6) Ñ äðóãîé ñòîðîíû, ñ ïîìîùüþ òåõíèêè ïðîåêöèîííûõ îïåðàòîðîâ Öâàíöèãà-Ìîðè äëÿ âðåìåííîé êîððåëÿöèîííîé ôóíêöèè Ì0(t) ìîæíî ïîëó÷èòü êîíå÷íî-ðàçíîñòíîå êèíåòè÷åñêîå óðàâíåíèå âèäà m −1 M 0 (t ) = λ1 M 0 (t ) − τΛ 1 ∑ M 1 ( jτ )M 0 (t − jτ ), (7) t j =0 ãäå M1(jτ) – ôóíêöèÿ ïàìÿòè ïåðâîãî ïîðÿäêà, λ1 è Λ1 – øóìîâûå ÷àñòîòíûå ïàðàìåòðû, õàðàêòåðèçóþùèå èññëåäóåìûé ïðîöåññ. Ïðèìåíÿÿ òåõíèêó ïðîåêöèîííûõ îïåðàòîðîâ ê M1(jτ), ïîëó÷àåì öåïî÷êó êîíå÷íî-ðàçíîñòíûõ êèíåòè÷åñêèõ óðàâíåíèé âèäà M i =1 ( t ) = λi M i −1 ( t ) − τ t m −1 − τΛ i ∑ M i ( jτ ) M i −1 ( jτ ) M i −1 ( t − jτ ) i = 1,2,3, j =0 (8) À.Â. Ìîêøèí, Þ.Â. Ìåðêóëîâà ãäå M1(jτ) – ôóíêöèÿ ïàìÿòè i-ãî ïîðÿäêà (Yulmetyev et al., 2000; 2001), λi è Λi – øóìîâûå ïàðàìåòðû i-ãî ïîðÿäêà λn = i Wn −1 2 äóðó (N-M+1) ðàç.  èòîãå ïîëó÷èì òàêîå æå ÷èñëî ëîêàëüíûõ âûáîðîê äëèíû M. ; Λn = i − Wn −1 L Wn Wn −1 2 ; − (9) 2 óäîâëåòâîðÿþùèõ ñâîéñòâó Wn , Wm = δ n , m Wn , δn,m – ñèìâîë Êðîíåêåðà. Íàáîð ôóíêöèé Mi(jτ) è ïàðàìåòðîâ λi è Λi ïîçâîëÿþò âûïîëíÿòü äåòàëüíûé àíàëèç èññëåäóåìîãî ïðîöåññà. Òàê øóìîâûå ïàðàìåòðû λi è Λi õàðàêòåðèçóþò ïîñëåäîâàòåëüíóþ ñìåíó ðàçëè÷íûõ ðåëàêñàöèîííûõ ïðîöåññîâ, ïðîòåêàþùèõ â ñèñòåìå (Sornette et al., 1997; Yulmetyev et al., 2001). Ñ äðóãîé ñòîðîíû, øóìîâûå ïàðàìåòðû ÿâëÿþòñÿ õàðàêòåðèñòè÷åñêèìè ÷àñòîòàìè äèíàìèêè âñåãî ïðîöåññà.  ñëó÷àå, êîãäà èññëåäóåìûé ïðîöåññ ÿâëÿåòñÿ ñòàöèîíàðíûì, ýòè øóìîâûå ïàðàìåòðû ìîãóò áûòü îïðåäåëåíû äëÿ âñåãî èññëåäóåìîãî èíòåðâàëà. Çäåñü ñëåäóåò îòìåòèòü, ÷òî äëèíà èíòåðâàëà äîëæíà áûòü äîñòàòî÷íîé, ÷òîáû ïðîèçâîäèòü õîðîøóþ ñòàòèñòèêó (Sornette et al., 1990).  ñëó÷àå, êîãäà ïðîöåññ ÿâëÿåòñÿ íåñòàöèîíàðíûì è õàðàêòåðèçóåòñÿ ñìåíîé ðàçëè÷íûõ ðåæèìîâ, âîçíèêàåò íåîáõîäèìîñòü â ïðèìåíåíèè ïðîöåäóðû ëîêàëèçàöèè (Yulmetyev et al., 2005). Êëþ÷åâûì ìîìåíòîì ýòîé ïðîöåäóðû ÿâëÿåòñÿ âûáîð ëîêàëüíîãî âðåìåííîãî èíòåðâàëà – òàê íàçûâàåìîãî «îêíà». Äëèíà ýòîãî «îêíà», âî-ïåðâûõ, äîëæíà áûòü äîñòàòî÷íîé äëÿ âûïîëíåíèÿ îïåðàöèè óñðåäíåíèÿ è ñòàòèñòè÷åñêîé îáðàáîòêè è, âî-âòîðûõ, îòíîñèòåëüíî êîðîòêîé, ÷òîáû õàðàêòåðèçîâàòü ïðîöåññû, ëîêàëüíûå âî âðåìåíè. Ïðåäïîëîæèì, ÷òî ëîêàëüíûé âðåìåííîé èíòåðâàë èìååò äëèíó Ì. Íàëîæåíèåì ýòîãî îêíà íà èñõîäíóþ ïîñëåäîâàòåëüíîñòü X âûáåðåì ýëåìåíòû, âõîäÿùèå â íåãî, è ñôîðìèðóåì íîâóþ âûáîð- Ðèñ. 1. Ïðîöåäóðà íàõîæäåíèÿ «ðàáî÷åãî îêíà» îïòèìàëüíîãî ðàçìåðà. a) Êîëåáàíèÿ çåìíîé êîðû äëÿ óñòîé÷èâîãî ñîñòîÿíèÿ Çåìëè; b)d) çíà÷åíèå øóìîâûõ ïàðàìåòðîâ ïðè óâåëè÷åíèè äëèíû âûáîðêè. êó ξ 0 . Ïîñëå ýòîãî âûïîëíèì ñäâèã ðàáî÷åãî îêíà âïðàâî íà îäèí âðåìåííîé øàã t, â ðåçóëüòàòå ÷åãî ïîëó÷èì äðóãóþ ëîêàëüíóþ âûáîðêó äëèíû M. Äëÿ òîãî ÷òîáû îõâàòèòü âñþ ïîñëåäîâàòåëüíîñòü X, íåîáõîäèìî âûïîëíèòü ýòó ïðîöå- − ξ1 =ξ1{ x(T +τ ), x(T + 2τ ), x(T +3τ ),..., x(T + Mτ )} … ãäå Wn – íàáîð äèíàìè÷åñêèõ îðòîãîíàëüíûõ ïåðåìåííûõ, − − ξ0 =ξ0 { x(T ), x(T +τ ), x(T + 2τ ),..., x(T +( M −1)τ )} ∧ ∧ Wn −1 LWn −1 Ôëóêòóàöèîííî-øóìîâàÿ ñïåêòðîñêîïèÿ â èññëåäîâàíèè ñèãíàëîâ êîëåáàíèé çåìíîé êîðû − (10) − ξ N − M = ξ N − M {x(T + ( N − M − 1)τ ), x(T + ( N − M )τ ), x(T + (N − M + 1)τ )..., x(T + ( N − 1)τ )} . Òàêèì îáðàçîì, äèíàìèêà ïðîöåññà áóäåò õàðàêòåðèçîâàòüñÿ íîâîé ïîñëåäîâàòåëüíîñòüþ − − − − − − ξ (t ′) = ξ 0 , ξ 1 , ξ 2 ,..., ξ i ,..., ξ N − M . (11)  ñîîòâåòñòâèè ñ ïîäõîäîì, îïèñàííûì âûøå, ìû ìî− æåì îïðåäåëèòü ÂÊÔ äëÿ êàæäîé ëîêàëüíîé âûáîðêè ξ i ñ ïîìîùüþ óðàâíåíèÿ (5), à ôóíêöèè ïàìÿòè è øóìîâûå ïàðàìåòðû ðàññ÷èòàòü ñ ïîìîùüþ âûðàæåíèé (9).  ðåçóëüòàòå øóìîâûå ïàðàìåòðû λi , Λi ñòàíîâÿòñÿ âåëè÷èíàìè, çàâèñÿùèìè îò âðåìåíè, à èõ âðåìåííûå çàâèñèìîñòè ìîæíî ïðåäñòàâèòü â ñëåäóþùåì âèäå: λi ( t ′ ) = {λi (T + ( M − 1)τ ) , λi (T + M τ ) , } , λi (T + ( M + 1)τ ) ,..., λi (T + ( N − M )τ ) ; Λ i (t ′) = {Λ i (T + (M − 1)τ ), Λ i (T + Mτ ), , Λ i (T + (M + 1)τ ),..., Λ i (T + ( N − M )τ )} . (12) Ïðîöåäóðà ëîêàëèçàöèè ïîçâîëÿåò ïåðåéòè îò ãëîáàëüíûõ ìàêðîõàðàêòåðèñòèê, êîòîðûå äàþò ëèøü íåçíà÷èòåëüíóþ óñðåäíåííóþ èíôîðìàöèþ îáî âñåì èññëåäóåìîì ïðîöåññå â öåëîì, ê ëîêàëüíîìó îïèñàíèþ, ÷òî ïîçâîëÿåò âûïîëíèòü áîëåå äåòàëüíûé àíàëèç ðàçëè÷íûõ äèíàìè÷åñêèõ ñîñòîÿíèé ñèñòåìû. 3. Ïðîöåäóðà îïðåäåëåíèÿ ëîêàëüíûõ øóìîâûõ ïàðàìåòðîâ Êàê ïðàâèëî, ýêñïåðèìåíòàëüíûå ñåéñìè÷åñêèå äàííûå ïðåäñòàâëÿþò ñîáîé äèñêðåòíûé ðÿä, õàðàêòåðèçóþùèé äèíàìèêó êîëåáàíèé çåìíîé êîðû. Ïîýòîìó ïîäõîä, îïèñàííûé âûøå, âïîëíå ìîæåò áûòü èñïîëüçîâàí äëÿ àíàëèçà.  ýòîì ñëó÷àå âðåìåííàÿ çàâèñèìîñòü ëîêàëüíûõ õàðàêòåðèñòèê ìîæåò ñëóæèòü èñòî÷íèêîì äîïîëíèòåëüíîé èíôîðìàöèè ïðè îáðàáîòêå ñèãíàëà, à ëîêàëüíûå øóìîâûå ïàðàìåòðû λi , Λi áóäóò ñîäåðæàòü â ñåáå èíôîðìàöèþ î ïðèñóòñòâèè íåñëó÷àéíîé ñîñòàâëÿþùåé â âûáîðêå (Sornette et al., 1995), èçìåíåíèè õàðàêòåðà êîððåëèðîâàííîãî øóìà è ïîÿâëåíèè äîïîëíèòåëüíîãî ñèãíàëà. Ïîýòîìó èñïîëüçîâàíèå ëîêàëüíûõ øóìîâûõ ïàðàìåòðîâ ôëóêòóàöèîííî-øóìîâîé ñïåêòðîñêîïèè â àíàëèçå ñåéñìè÷åñêèõ äàííûõ ÿâëÿåòñÿ âåñüìà ïîëåçíûì. Ïðîöåäóðà ëîêàëèçàöèè øóìîâûõ ïàðàìåòðîâ λi, Λi ñîñòîèò â ñëåäóþùåì. Ïðåäïîëîæèì, ÷òî èìååòñÿ ìàññèâ äàííûõ X= {x1,x2,x3…XN…,Xp}, è ëîêàëüíàÿ âûáîðêà èìååò äëèíó M, ãäå M<<P. Òîãäà ïðè ïðîõîæäåíèè ïî èñõîäíîìó ìàññèâó X «îêíîì» äëèíû M è âû÷èñëåíèè λi, Λi ìû ïîëó÷àåì ðÿä øóìîâûõ ïàðàìåòðîâ {λi(T+(N-1)τ), λi(T+Nτ), λi(T+(N+1)τ),…, λi(T+(P-1) τ)} è {Λi (T+(N-1) τ), Λi(T+Nτ), 6 (48) 2012 41 À.Â. Ìîêøèí, Þ.Â. Ìåðêóëîâà Ôëóêòóàöèîííî-øóìîâàÿ ñïåêòðîñêîïèÿ â èññëåäîâàíèè ñèãíàëîâ êîëåáàíèé çåìíîé êîðû Λi(T+(N+1)τ),…, Λi (T+(P-1) τ)}. Î÷åâèäíî, ÷òî äëÿ îïðåäåìåòðîâ λi è Λi ñëåäóåò âûïîëíèòü ñëåäóþùèå îïåðàöèè. ëåíèÿ ëîêàëüíûõ ïàðàìåòðîâ λi(t) è Λi(t) íåäîïóñòèìî èñÈç èñõîäíîãî ìàññèâà äàííûõ áåðåòñÿ èíòåðâàë äëèíîþ â ïîëüçîâàíèå ðàáî÷åãî îêíà ñëèøêîì áîëüøîãî ðàçìåðà M ~ 150 òî÷åê, äëÿ êîòîðîãî ñ ïîìîùüþ óðàâíåíèé (9) (1000 è áîëåå òî÷åê).  ýòîì ñëó÷àå òåðÿåòñÿ ñìûñë ïðîöåâû÷èñëÿþòñÿ âñå øóìîâûå ïàðàìåòðû λi è Λi. Çàòåì âûäóðû ëîêàëèçàöèè. Ñ äðóãîé ñòîðîíû, èñïîëüçîâàíèå ñëèøïîëíÿåòñÿ îïåðàöèÿ «ïîøàãîâîãî ñäâèãà âïðàâî» èíòåðêîì êîðîòêîãî îêíà (50 òî÷åê è ìåíüøå) áóäåò ÿâëÿòüñÿ âàëà ôèêñèðîâàííîé äëèíû Ì, äëÿ êîòîðîãî ñíîâà ïðîèçíåêîððåêòíûì, òàê êàê â ýòîì ñëó÷àå íåâîçìîæåí äîñòîâîäèòñÿ âû÷èñëåíèå ïàðàìåòðîâ. Ýòè äåéñòâèÿ âûïîëíÿâåðíûé êîððåëÿöèîííûé àíàëèç èç-çà ïîÿâëåíèÿ áîëüøèõ þòñÿ äî òåõ ïîð, ïîêà ïåðâîíà÷àëüíàÿ âûáîðêà X(t) íå áóïîãðåøíîñòåé.  ðåçóëüòàòå âîçíèêàåò íåîáõîäèìîñòü â äåò ïðîéäåíà.  ðåçóëüòàòå ìû ïîëó÷àåì ñëåäóþùèå çàâèíàõîæäåíèè îïòèìàëüíîãî ðàçìåðà ëîêàëüíîãî èíòåðâàñèìîñòè: {λi(T,T + Mτ), λi(T +τ, T + (M +1) τ),…, λi(T + (N ëà, ò.å. âåëè÷èíû M. M - 1)τ, T + (N - 1) τ)} è {Λi(T, T + Mτ), Λi(T + τ, T + (M + 1) Äëÿ îïðåäåëåíèÿ îïòèìàëüíîãî ðàçìåðà ëîêàëüíîé τ),…, Λi (T + (N - M - 1)τ, T + (N - 1)τ)}. Î÷åâèäíî, ÷òî åñëè âûáîðêè ìû èñïîëüçóåì ïðîöåäóðó, ïðåäëîæåííóþ â ðàâ èññëåäóåìûõ äàííûõ áóäåò èçìåíÿòüñÿ õàðàêòåð øóìà, áîòå (Yulmetyev et al., 2001). Äëÿ ýòîãî ìû èñïîëüçîâàëè ïîÿâëÿòüñÿ è èñ÷åçàòü êàêîé-ëèáî ñèãíàë, òî ýòî íåïîñäàííûå, êîòîðûå ñîîòâåòñòâîâàëè ñïîêîéíîìó ñîñòîÿíèþ ðåäñòâåííî îòðàçèòñÿ íà ïîâåäåíèè ðåëàêñàöèîííûõ õàÇåìëè. Âû÷èñëèòåëüíàÿ ïðîöåäóðà ñîñòîÿëà â ñëåäóþùåì. ðàêòåðèñòèê. Èçíà÷àëüíî áðàëñÿ èíòåðâàë â 40 òî÷åê, äëÿ êîòîðîãî ñ 4. Ðåçóëüòàòû ïîìîùüþ ôîðìóë (9) è (10) âû÷èñëÿëèñü øóìîâûå ïàðàÎïèñàííàÿ âûøå ïðîöåäóðà áûëà èñïîëüçîâàíà äëÿ ìåòðû λ1, Λ1, λ2. Ïîñëå ýòîãî èíòåðâàë óâåëè÷èâàëñÿ íà àíàëèçà äàííûõ ïî çåìëåòðÿñåíèÿì è òåõíîãåííûì âçðûåäèíè÷íûé âðåìåííîé îòðåçîê t, äëÿ êîòîðîãî ñíîâà âûâàì (Yulmetyev et al., 2005; 2001). Ïîëó÷åííûå ðåçóëüòàòû ÷èñëÿëèñü øóìîâûå ïàðàìåòðû. Ýòà ïðîöåäóðà âûïîëíÿïðåäñòàâëåíû íà ðèñóíêàõ 2 è 3. ëàñü äî òåõ ïîð, ïîêà äëèíà ðàáî÷åãî îêíà íå äîñòèãëà 300 Äåòàëüíûé àíàëèç ïîëó÷åííûõ ðåçóëüòàòîâ ïîçâîëÿåò òî÷åê.  ðåçóëüòàòå ìû îáíàðóæèëè, ÷òî ïðè ðàçìåðå â âûÿâèòü ñëåäóþùèå îñîáåííîñòè, êîòîðûå ïðèâåäåì îò150 òî÷åê âñå ïàðàìåòðû íà÷èíàþò ïðèíèìàòü óñòîé÷èäåëüíî äëÿ òåõíîãåííûõ âçðûâîâ è çåìëåòðÿñåíèé: âûå çíà÷åíèÿ (Ðèñ.1). Ýòî îçíà÷àåò, ÷òî ðàçìåð îêíà â 150 (1) Øóìîâûå ïàðàòî÷åê ÿâëÿåòñÿ îïòèìàëüíûì. Êàê âèäíî èç ðèñóíêà 1, ïàìåòðû λ1 è λ2 ïðèíèìàþò ðàìåòðû λ1 è Λ1 ïðè òàêîé äëèíå èíòåðâàëà íà÷èíàþò ïðèîòðèöàòåëüíûå çíà÷åíèÿ íèìàòü ñâîè ìèíèìàëüíûå ïî àáñîëþòíîé âåëè÷èíå çíàâî âñåõ ñëó÷àÿõ. ÷åíèÿ. Êîëåáàíèÿ çíà÷åíèé ïàðàìåòðîâ λ2 è λ3 òàêæå (2) Ïàðàìåòð λ1(t):  óìåíüøàþòñÿ è ïðèíèìàþò óñòîé÷èâûå çíà÷åíèÿ, íà÷èñëó÷àå çåìëåòðÿñåíèÿ íàÿ ñ âûáîðêè äëèíîþ ~150 òî÷åê. àáñîëþòíàÿ âåëè÷èíà ïàÒåñòèðîâàíèå ýòîé ïðîöåäóðû íà äðóãèõ äàííûõ, õàðàêòåðèçóþùèõ ñïîêîéíîå ñîñòîÿíèå Çåìëè, äàåò òàêèå æå ðåçóëüòàòû è îáíàðóæèâàåò ìèíèìàëüíûé ðàçìåð îêíà â 150 òî÷åê. Îòìåòèì, ÷òî ïðè àíàëèçå ñåéñìè÷åñêèõ äàííûõ ñ ïîìîùüþ ëîêàëüíîãî ïîêàçàòåëÿ Õåðñòà, âûïîëíåííûì â ðàáîòå (Yulmetyev et al., 2001), òàêæå áûë îáíàðóæåí ëîêàëüíûé èíòåðâàë â 100120 òî÷åê. Òàêèì îáðàçîì, èìåííî òàêîé ðàçìåð ëîêàëüíîãî îêíà ÿâëÿÐèñ. 3. Çàïèñü êîëåáàíèé çåìíîé êîðû è âðåìåííûå çàâèñèìîñòè ëîåòñÿ îïòèìàëüíûì êàëüíûõ øóìîâûõ ïàðàìåòðîâ â äëÿ íàêîïëåíèÿ ñòàñëó÷àå ñèëüíîãî çåìëåòðÿñåíèÿ. òèñòèêè è áóäåò èñÎáëàñòü I ñîîòâåòñòâóåò äèíàïîëüçîâàòüñÿ íàìè ìèêå äî çåìëåòðÿñåíèÿ («ñîáûäàëåå. òèÿ»), îáëàñòü II – íåïîñðåäñòâåíÄëÿ âû÷èñëå- Ðèñ. 2. Çàïèñü êîëåáàíèé çåìíîé êîðû è âðåìåííûå çàâèñèìîñòè ëîêàëü- íî ïåðåä çåìëåòðÿñåíèåì, îáëàñòü íèÿ âðåìåííîé çà- íûõ øóìîâûõ ïàðàìåòðîâ â ñëó÷àÿõ òåõíîãåííîãî âçðûâà (ðèñ. a,b,c,d) è III – âî âðåìÿ çåìëåòðÿñåíèÿ, îáâèñèìîñòè ïàðà- ñëàáîãî çåìëåòðÿñåíèÿ (ðèñ. e,f,g,h). ëàñòü IV – ïîñëå çåìëåòðÿñåíèÿ. 42 6 (48) 2012 À.Â. Ìîêøèí, Þ.Â. Ìåðêóëîâà ðàìåòðà |λ1| ðåçêî óâåëè÷èâàåòñÿ è çàòåì ìåäëåííî ñïàäàåò ê èñõîäíûì çíà÷åíèÿì. Ïðè ýòîì âðåìÿ âîññòàíîâëåíèÿ èñõîäíîãî ïîâåäåíèÿ ïàðàìåòðà λ1 ïðèìåðíî ñîâïàäàåò ñ äëèòåëüíîñòüþ çåìëåòðÿñåíèÿ. Ïðè òåõíîãåííîì âçðûâå |λ1| òàêæå èñïûòûâàåò ðåçêèé ñêà÷îê. Îäíàêî âðåìÿ âîññòàíîâëåíèÿ èñõîäíîãî ïîâåäåíèÿ â λ1 ìåíüøå äëèòåëüíîñòè êîëåáàíèé, ñâÿçàííûõ ñ òåõíîãåííûì âçðûâîì ïðèìåðíî â 2,5-3 ðàçà. (3) Ïàðàìåòð λ2(t): Ýòîò ïàðàìåòð ðåàãèðóåò íà íà÷àëî «ñîáûòèÿ» ðåçêèì ñêà÷êîì (êàê ïðè çåìëåòðÿñåíèè, òàê è ïðè òåõíîãåííîì âçðûâå). Ïðè ýòîì ñëåäóåò îòìåòèòü: ÷åì áîëüøå ñèëà çåìëåòðÿñåíèÿ èëè òåõíîãåííîãî âçðûâà, òåì áîëüøå âåëè÷èíà ñêà÷êà çíà÷åíèÿ ïàðàìåòðà. (4) Ïàðàìåòð Λ1(t): Ýòîò ïàðàìåòð êîëåáëåòñÿ âáëèçè íóëÿ äî è ïîñëå «ñîáûòèÿ». Ñ íà÷àëîì «ñîáûòèÿ» ïàðàìåòð ðåçêî âîçðàñòàåò, à çàòåì ïëàâíî ñïàäàåò. Îí î÷åíü ÷óâñòâèòåëåí ê èçìåíåíèþ õàðàêòåðà øóìà. Òàê, íàïðèìåð, äëÿ îòäåëüíîãî çåìëåòðÿñåíèÿ ñêà÷îê çíà÷åíèé àìïëèòóäû Λ1(t) ïîÿâëÿåòñÿ ïðèìåðíî çà 4000 òî÷åê äî íà÷àëà çåìëåòðÿñåíèÿ, õîòÿ â èñõîäíûõ äàííûõ òàêîãî èíäèêàòîðà âèçóàëüíî íå íàáëþäàëîñü. Ýòî ìîæåò ñâèäåòåëüñòâîâàòü î âîçìîæíîñòè èñïîëüçîâàíèÿ ïàðàìåòðà â ïðîãíîçèðîâàíèè çåìëåòðÿñåíèé.  ñëó÷àå ñèëüíîãî çåìëåòðÿñåíèÿ âñå ïàðàìåòðû îñòðî ðåàãèðóþò íà ïîÿâëåíèå ñèãíàëà. Ðàññìîòðèì áîëåå äåòàëüíî ïîâåäåíèå ëîêàëüíûõ ïàðàìåòðîâ â äàííîì ñëó÷àå. (5) Ïàðàìåòð λ1(t): Äî íà÷àëà «ñîáûòèÿ» ïàðàìåòð ïðèíèìàåò îòðèöàòåëüíûå çíà÷åíèÿ (îáëàñòü I íà ðèñ. 3). Ñ ïðèáëèæåíèåì «ñîáûòèÿ» àìïëèòóäà êîëåáàíèé óìåíüøàåòñÿ, è äëÿ îáëàñòåé II, III è IV êîëåáàíèÿ ïåðåõîäÿò â íåçíà÷èòåëüíûå ôëóêòóàöèè âáëèçè íóëÿ. (6) Ïàðàìåòð λ2(t): Äî íà÷àëà «ñîáûòèÿ» ýòîò ïàðàìåòð òàêæå ïîêàçûâàåò íàëè÷èå øóìà, ïðèíèìàÿ ëèøü îòðèöàòåëüíûå çíà÷åíèÿ. Îäíàêî ñ ïîÿâëåíèåì ñèãíàëà åãî çíà÷åíèÿ ðåçêî óìåíüøàþòñÿ ïî àáñîëþòíîé âåëè÷èíå è íà÷èíàþò ïðèíèìàòü çíà÷åíèÿ, áëèçêèå ê íóëþ (Ðèñ. 3b). (7) Ïàðàìåòðû Λ1(t) è Λ2(t): Äî íà÷àëà «ñîáûòèÿ» (îáëàñòü I) ïàðàìåòðû êîëåáëþòñÿ, ïðèíèìàÿ ïðåèìóùåñòâåííî ïîëîæèòåëüíûå çíà÷åíèÿ. Ñ íà÷àëîì «ñîáûòèÿ» èõ çíà÷åíèÿ çíà÷èòåëüíî óìåíüøàþòñÿ ïî àáñîëþòíîé âåëè÷èíå, ïðèáëèæàÿñü ê íóëþ.  îáëàñòè II îáà ïàðàìåòðà èçìåíÿþò çíàê ñ ïîëîæèòåëüíîãî íà îòðèöàòåëüíûé.  ìàñøòàáàõ ðèñóíêà 3 c è d äëÿ îáëàñòåé II, III è IV íàáëþäàåòñÿ ëèøü ïðÿìàÿ ëèíèÿ. Òàêèì îáðàçîì, âñå ïàðàìåòðû î÷åíü ÷óâñòâèòåëüíû ê íà÷àëó ñèëüíîãî çåìëåòðÿñåíèÿ. Ðåçêèå èçìåíåíèÿ â èõ ïîâåäåíèè ñòàíîâÿòñÿ çàìåòíûìè çà 10 000 òî÷åê (≈3,3 ìèí) äî íà÷àëà ñèëüíûõ, âûðàæåííûõ êîëåáàíèé. 5. Çàêëþ÷åíèå  äàííîé ðàáîòå ïðåäñòàâëåí ïîäõîä èññëåäîâàíèÿ íåñòàöèîíàðíûõ, íåóñòîé÷èâûõ è íåìàðêîâñêèõ ñëó÷àéíûõ ïðîöåññîâ â äèñêðåòíûõ ñèñòåìàõ íà ïðèìåðå äàííûõ ñåéñìè÷åñêîé àêòèâíîñòè. Ýòîò ïîäõîä ïîçâîëÿåò àíàëèçèðîâàòü êàê áûñòðûå, òàê è ìåäëåííûå ïðîöåññû, à òàêæå ðàçëè÷àòü ïîäîáíûå ïî âèäó ñèãíàëû, èìåþùèå ðàçëè÷íóþ ïðèðîäó. Òåîðåòè÷åñêèé àíàëèç âûïîëíåí ñ ïîìîùüþ ïîäõîäà ôëóêòóàöèîííî-øóìîâîé ñïåêòðîñêîïèè. Ïðèìåíåíèå ïîäõîäà äàåò âîçìîæíîñòü èññëåäîâàòü òàêèå íåñòàöèîíàðíûå, íåóñòîé÷èâûå ïðîöåññû, â êîòîðûõ îäíîâðåìåííî ïðîòåêàþò, ñìåíÿþò äðóã äðóãà è íàêëàäûâàþòñÿ Ôëóêòóàöèîííî-øóìîâàÿ ñïåêòðîñêîïèÿ â èññëåäîâàíèè ñèãíàëîâ êîëåáàíèé çåìíîé êîðû ðàçëè÷íûå ðåæèìû. Ñîîòíîøåíèå ìåæäó âðåìåíàìè ïðîòåêàíèÿ ðåæèìîâ ìîæåò áûòü ñàìîå ðàçíîîáðàçíîå. Òåì íå ìåíåå, àêêóðàòíî âûïîëíåííàÿ ïðîöåäóðà ëîêàëèçàöèè èñïîëüçóåìûõ êðèòåðèåâ è âû÷èñëåíèå èõ äèíàìèêè, êàê ïðàâèëî, ïîçâîëÿåò ðàçäåëèòü âõîäÿùèå øóìû è ñèãíàë, à òàêæå ïðîâåñòè êà÷åñòâåííûé è èíôîðìàòèâíûé àíàëèç. Äðóãèì âàæíûì ïðåèìóùåñòâîì ýòîãî ìåòîäà ÿâëÿåòñÿ òî, ÷òî åãî ìîæíî âûïîëíÿòü â ðåæèìå ðåàëüíîãî âðåìåíè, òî åñòü íåïîñðåäñòâåííî ïî ìåðå íàêîïëåíèÿ ñòàòèñòèêè ìîæíî ïðîâîäèòü îáðàáîòêó è àíàëèç. Ýòî ñâèäåòåëüñòâóåò î åãî ïðàêòè÷åñêîé çíà÷èìîñòè. Ïðåäñòàâëåííûé ïîäõîä ïðèìåíåí íàìè ê àíàëèçó äàííûõ ïî ñèëüíûì è ñëàáûì çåìëåòðÿñåíèÿì, à òàêæå ÿäåðíûì ïîäçåìíûì âçðûâàì. Ïðè àíàëèçå ñèëüíîãî çåìëåòðÿñåíèÿ îêàçàëîñü, ÷òî âñå ïàðàìåòðû ðåçêî èçìåíÿþò õàðàêòåð ïîâåäåíèÿ äî ïîÿâëåíèÿ âèäèìûõ êîëåáàíèé (äî çåìëåòðÿñåíèÿ). Òàê, íàïðèìåð, â ñëó÷àå çåìëåòðÿñåíèÿ, èññëåäóåìîãî â äàííîé ðàáîòå, èçìåíåíèå ïðîèñõîäèò ïðèáëèçèòåëüíî çà 3-3,5 ìèíóòû. Óñòàíîâëåíî, ÷òî àíàëèç øóìîâûõ ïàðàìåòðîâ ïîçâîëÿåò òàêæå ïîëó÷àòü ðàçëè÷èå ìåæäó ñëàáûìè çåìëåòðÿñåíèÿìè è òåõíîãåííûìè âçðûâàìè. Ëèòåðàòóðà Sornette A., Sornette D. Tectonophysics. 179 (1990). 327. Sornette D., Knopoff L. Bull. Seismol. Soc. Am. 87 (1997). 789. Sornette D., Sammis C. J. Phys. I France. 5 (1995). 607. Yulmetyev R., Gafarov F., Hanggi P., Nigmatulin R., Kayumov Sh. Phys. Rev. E. 64 (2001) 066132. Yulmetyev R., Hanggi P., Gafarov F. Phys. Rev. E 62 (2000). 6178. Yulmetyev R.M., Mokshin A.V., Hanggi P. Universal approach to overcoming nonstationarity, unsteadiness and non-Markovity of stochastic processes in complex systems. Physica A. 345 (2005). 303-325.. Yulmetyev R.M., Mokshin A.V., Hanggi P., Shurygin V.Yu. Phys. Rev. E. 64 (2001). 057101. A.V. Mokshin, Y.V. Merkulova. Fluctiation-noise spectroscopy in the study of the fluctuation signals. The approach implemented in the framework of fluctuationnoise spectroscopy (Yulmetyev et al., 2005) is suggested to analyze the data characterizing the earth crust fluctuations. As a particular case the data for strong and weak earthquakes in Turkey (1998 and 1999) and technogenic explosions are considered. The possibility of earthquakes forecast, as well as the ability of the approach to identify differences between technogenic explosions and earthquakes on the basis of seismic data are discussed in this paper. Keywords: technogenic explosions, earthquakes, noise parameters, memory function, time correlation function. 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 Çàâåäóþùèé êàôåäðîé âû÷èñëèòåëüíîé ôèçèêè è ìî123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 äåëèðîâàíèÿ ôèçè÷åñêèõ ïðîöåññîâ, äîöåíò. 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 Àñïèðàíò êàôåäðû âû÷èñëèòåëüíîé ôèçèêè è ìîäåëè123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 ðîâàíèÿ ôèçè÷åñêèõ ïðîöåññîâ. 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 Èíñòèòóò ôèçèêè, Êàçàíñêèé (Ïðèâîëæñêèé) ôåäåðàëü123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 íûé óíèâåðñèòåò. 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 420008 Êàçàíü, Êðåìëåâñêàÿ, 18. Òåë.: (843) 233-77-37. 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 123456789012345678901234567890121234567890123456789012345678901212345678901234 Àíàòîëèé Âàñèëüåâè÷ Ìîêøèí Þëèàíà Âèòàëüåâíà Ìåðêóëîâà 6 (48) 2012 43