ДК районная 14.03 12 отвx

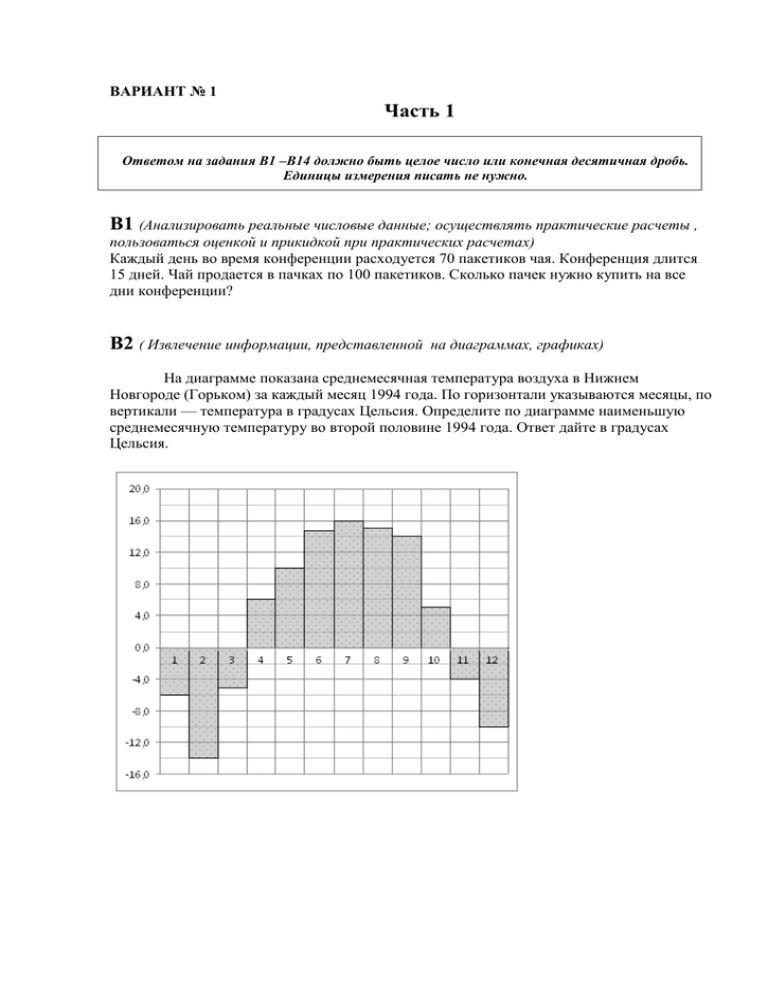
ВАРИАНТ № 1
Часть 1
Ответом на задания В1 –В14 должно быть целое число или конечная десятичная дробь.
Единицы измерения писать не нужно.
В1 (Анализировать реальные числовые данные; осуществлять практические расчеты ,
пользоваться оценкой и прикидкой при практических расчетах)
Каждый день во время конференции расходуется 70 пакетиков чая. Конференция длится
15 дней. Чай продается в пачках по 100 пакетиков. Сколько пачек нужно купить на все
дни конференции?
В2 ( Извлечение информации, представленной
на диаграммах, графиках)
На диаграмме показана среднемесячная температура воздуха в Нижнем
Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по
вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую
среднемесячную температуру во второй половине 1994 года. Ответ дайте в градусах
Цельсия.
В3 (Решение планиметрической задачи на нахождение геометрических величин
(площадь круга, теорема Пифагора)
Найдите (в см2) площадь фигуры, изображенной на клетчатой бумаге с размером клетки
1 см
1 см (см. рис.). В ответе запишите
.
В4 (Умение использовать приобретенные знания и умения в практической деятельности
и повседневной жизни)
В среднем гражданин А. в дневное время расходует 110 кВт ч электроэнергии в месяц, а
в ночное время — 160 кВт ч электроэнергии. Раньше у А. в квартире был установлен
однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,4 руб. за кВт ч.
Год назад А. установил двухтарифный счeтчик, при этом дневной расход электроэнергии
оплачивается по тарифу 2,4 руб. за кВт ч, а ночной расход оплачивается по тарифу
0,7 руб. за кВт ч. В течение 12 месяцев режим потребления и тарифы оплаты
электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы
не поменялся счетчик? Ответ дайте в рублях.
В5
(Решение рационального и логарифмического уравнения)
Решите уравнение
укажите меньший из них.
. Если уравнение имеет более одного корня, в ответе
В6
(Решение планиметрической задачи на нахождение геометрических величин (углов) с
использованием тригонометрических функций)
В треугольнике ABC
, высота AH равна
,
. Найдите
В7 ( Преобразование выражений, включающих операцию логарифмирования)
Вычислите значение выражения:
.
В8 ( Уравнение касательной к графику функции, геометрический смысл производной)
На
рисунке изображен график
— производной функции
, определенной на
интервале
. Найдите количество точек, в которых касательная к графику функции
параллельна прямой
или совпадает с ней.
В9
(Решение простейших стереометрических задач на нахождение геометрических
величин (объемов); использование при решении стереометрических задач
планиметрические факты и методы)
В правильной треугольной пирамиде
. Площадь треугольника
равна 13,
медианы основания пересекаются в точке
. Найдите объем пирамиды.
В10
(Элементы комбинаторики, статистики и теории вероятностей ,поочередный и
одновременный выбор)
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые
три дня по 17 докладов, остальные распределены поровну между четвертым и пятым
днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад
профессора М. окажется запланированным на последний день конференции?
В11
(Решение простейших стереометрических задач на нахождение геометрических
величин ( площадей)
Из единичного куба вырезана правильная четырехугольная призма со стороной основания
0,8 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
В12
(Решение прикладных задач . Применение математических методов для решения
содержательных задач физического характера. Интерпретация результата, учет
реальных ограничений)
Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то
вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся
постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет
выливаться, если сила еe давления на дно будет положительной во всех точках траектории
кроме верхней, где она может быть равной нулю. В верхней точке сила давления,
выраженная в ньютонах, равна
, где m — масса воды в килограммах, v —
скорость движения ведeрка в м/с, L — длина верeвки в метрах, g — ускорение свободного
падения (считайте
м/с ). С какой наименьшей скоростью надо вращать ведeрко,
чтобы вода не выливалась, если длина верeвки равна 160 см? Ответ выразите в м/с.
В13
(Моделирование реальных ситуации на языке алгебры, составление уравнения по
условию задачи; исследование построенной модели с использованием аппарата алгебры)
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров
воды в минуту пропускает первая труба, если резервуар объемом 165 литров она
заполняет на 4 минуты дольше, чем вторая труба?
В14
(Исследование в простейших случаях функции на монотонность, нахождении
наибольшего и наименьшего значения функций)
Найдите наименьшее значение функции
на отрезке
.
Часть 2
Для записи решений и ответов на задания С1- С6 используйте бланк ответов
№2.Запишите сначала номер выполняемого задания , а затем полное обоснованное
решение и ответ.
С1(Решение тригонометрического уравнения, умение отобрать корни ,принадлежащие
отрезку)
Решите уравнение 4cos 2x +4sin² x= cos x. Укажите корни, принадлежащие
отрезку [ -1,5π; π]
С2(Решение стереометрической задачи на нахождение расстояния от точки до
плоскости)
Дан куб АВСДА1В1С1Д1. Длина ребра куба равна 1. Найдите расстояние от середины
отрезка ВС1 до плоскости АВ1Д1.
С3(Решение показательного и логарифмическог нераенств)
4˟−12∙2˟+32≥0
logₓ (x-2) logₓ (x+2)≤0
С4(Решение планиметрической задачи на вписанность окружности в треугольник)
В треугольнике ABC АВ=15, ВС=7, СА=9. Точка D лежит на прямой BC причем
ВД :ДС=5:7. Окружности, вписанные в каждый из треугольников ADC и ADB касаются
стороны AD в точках M и K. Найдите длину отрезка MK.
С5(Решение задания на свойства функций с параметром)
Найти все значения а, при каждом из которых функция
имеет более двух точек экстремума.
С6(Решение задания на целые числа и их свойства)
Перед каждым из чисел 3, 4, 5, . . . 11 и 14, 15, . . . 18 произвольным образом ставят знак
плюс или минус, после чего к каждому из образовавшихся чисел первого набора
прибавляют каждое из образовавшихся чисел второго набора, а затем все 45 полученных
результатов складывают. Какую наименьшую по модулю сумму и какую наибольшую
сумму можно получить в итоге?
ВАРИАНТ №2
Часть 1
Ответом на задания В1 –В14 должно быть целое число или конечная десятичная дробь.
Единицы измерения писать не нужно.
В1
Каждый день во время конференции расходуется 90 пакетиков чая. Конференция
длится 17 дней. Чай продается в пачках по 100 пакетиков. Сколько пачек нужно купить на
все дни конференции?
В2
На диаграмме показана среднемесячная температура воздуха в Минске за каждый
месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в
градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в
первой половине 2003 года. Ответ дайте в градусах Цельсия.
В3
Найдите (в см2) площадь
клетки 1 см
фигуры, изображенной на клетчатой бумаге с размером
1 см (см. рис.). В ответе запишите
.
В4
В среднем гражданин А. в дневное время расходует 110 кВт ч электроэнергии в
месяц, а в ночное время — 160 кВт ч электроэнергии. Раньше у А. в квартире был
установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу
2,5 руб. за кВт ч. Год назад А. установил двухтарифный счeтчик, при этом дневной
расход электроэнергии оплачивается по тарифу 2,5 руб. за кВт ч, а ночной расход
оплачивается по тарифу 0,7 руб. за кВт ч. В течение 12 месяцев режим потребления и
тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот
период, если бы не поменялся счетчик? Ответ дайте в рублях.
В5
Решите уравнение
ответе укажите меньший из них.
. Если уравнение имеет более одного корня, в
В6
В треугольнике ABC
Найдите
.
В7
, высота AH равна √15 ,
Вычислите значение выражения:
В8 На рисунке изображен график
определенной на интервале
графику функции
.
.
— производной функции
,
. Найдите количество точек, в которых касательная к
параллельна прямой
или совпадает с ней.
В9
В правильной треугольной пирамиде
медианы основания пересекаются в
точке . Площадь треугольника
равна 11,
. Найдите объем пирамиды.
В10
Научная конференция проводится в 4 дня. Всего запланировано 50 докладов —
первые два дня по 11 докладов, остальные распределены поровну между третьим и
четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что
доклад профессора М. окажется запланированным на последний день конференции?
В11
Из единичного куба вырезана правильная четырехугольная призма со стороной
основания 0,7 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
В12
Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной
плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на
дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней.
Вода не будет выливаться, если сила еe давления на дно будет положительной во всех
точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила
давления, выраженная в ньютонах, равна
, где m — масса воды в
килограммах, v — скорость движения ведeрка в м/с, L — длина верeвки в метрах, g —
ускорение свободного падения (считайте
м/с ). С какой наименьшей скоростью
надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ
выразите в м/с.
В13
Первая труба пропускает на 3 литра воды в минуту меньше, чем вторая. Сколько
литров воды в минуту пропускает первая труба, если резервуар объемом 238 литров она
заполняет на 3 минуты дольше, чем вторая труба?
В14
Найдите наименьшее значение функции
на отрезке
.
Часть 2
Для записи решений и ответов на задания С1- С6 используйте бланк ответов
№2.Запишите сначала номер выполняемого задания , а затем полное обоснованное
решение и ответ.
С1
Решите уравненение 3cos 2x +sin x= 3cos ² x . Укажите корни, принадлежащие
отрезку [ -π; 1.5π]
С2
Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P
равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка M —
середина бокового ребра пирамиды AP.
С3 Решите систему неравенств :
3∙9˟−28∙3˟+9≤0
logₓ² (x-1)² ≤1
С4
Дан ромб ABCD с диагоналями
и
. Проведена окружность
радиуса
с центром в точке пересечения диагоналей ромба. Прямая, проходящая через
вершину B касается этой окружности и пересекает прямую CD в точке M. Найдите CM.
С5
Найдите все значения а, при каждом из которых множеством решений неравенства
является отрезок.
С6
Каждое из чисел 5, 6, . . ., 9 умножают на каждое из чисел 12, 13, . . ., 17 и перед
каждым произведением произвольным образом ставят знак плюс или минус, после чего
все 30 полученных результатов складывают. Какую наименьшую по модулю сумму и
какую наибольшую сумму можно получить в итоге?
ОТВЕТЫ
Вариант №1
Вариант №2
11
В1
16
-10
В2
16
11
В3
16
3264
В4
3456
6
В5
10
0,75
В6
0,25
7
В7
3
4
В8
4
78
В9
88
0,16
В10
0,28
7,92
В11
7,82
4
В12
2
11
В13
14
-18
В14
-6
π/2+πn,nϵZ; ±arccos1/4+2πn.nϵZ:
−3π/2; −π/2; π/2; ±arccos1/4
С1
√3/3
С2
πn,nϵZ; arcsin⅓+2πn.nϵZ:
π−arcsin⅓+2πn.nϵZ:
−π; 0; π; arcsin⅓; π−arcsin⅓
arcsin(√6/6)
3
С3
(−1;0)U(0;0,5]U(1;2]
43/12 или 13/2
С4
91/17 или 221/7
(−√5;−√3)U(√3;√5)
С5
(−8;−9/4]U(−2;4)
1 и1035
С6
1 и 3045
Критерии оценивания :
За правильно выполненные задания В1-В14 ставится 1 тестовый балл;
За выполнение заданий (в зависимости от полноты решения)
С1-С2 ставится 0, 1 или 2балла ;
С3-С4 ставится 0,1,2 или 3 балла;
С5-С6 ставится 0,1,2 ,3 или 4 балла;
Для получения положительной оценки за работу надо получить 6 баллов; максимальное
количество -32 тестовых балла.