Задание 1 u (рис. 1). В нее бросил
advertisement
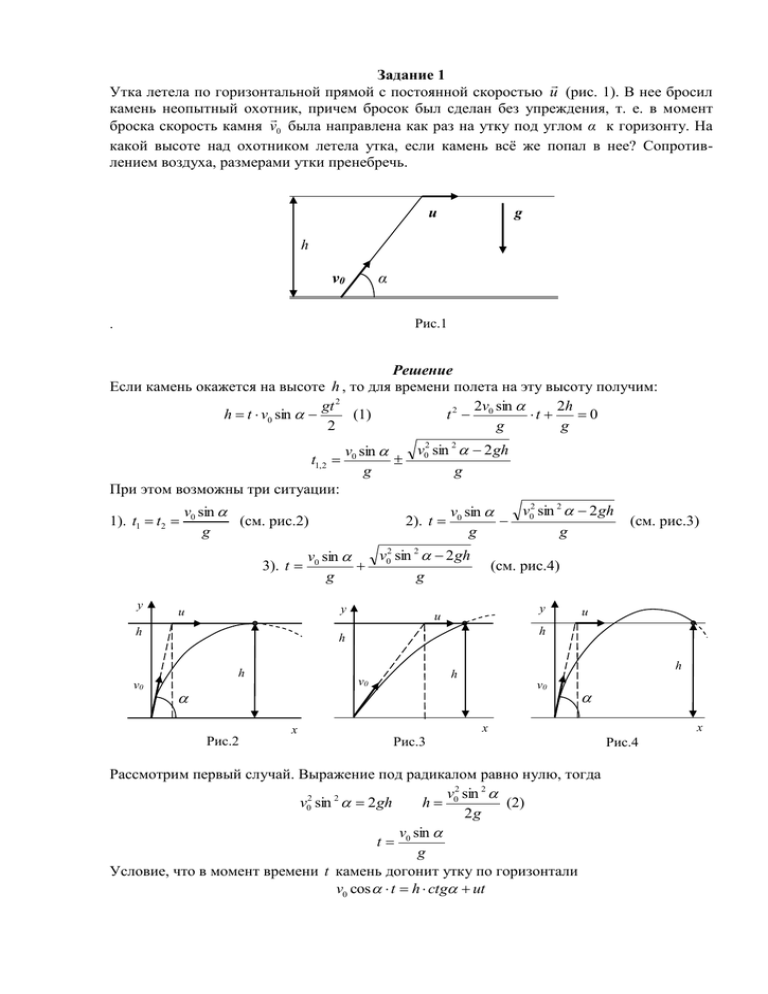
Задание 1 Утка летела по горизонтальной прямой с постоянной скоростью u (рис. 1). В нее бросил камень неопытный охотник, причем бросок был сделан без упреждения, т. е. в момент броска скорость камня v0 была направлена как раз на утку под углом α к горизонту. На какой высоте над охотником летела утка, если камень всё же попал в нее? Сопротивлением воздуха, размерами утки пренебречь. u g h α v0 Рис.1 . Решение Если камень окажется на высоте h , то для времени полета на эту высоту получим: gt 2 2v sin 2h (1) h t v0 sin t2 0 t 0 2 g g v02 sin 2 2 gh v0 sin t1, 2 g g При этом возможны три ситуации: v02 sin 2 2 gh v0 sin 2). t g g v sin 1). t1 t2 0 (см. рис.2) g 3). t y y u h (см. рис.4) y u Рис.2 x h h v0 u h h h v0 v 2 sin 2 2 gh v0 sin 0 g g (см. рис.3) v0 x x Рис.3 Рассмотрим первый случай. Выражение под радикалом равно нулю, тогда v 2 sin 2 (2) v02 sin 2 2 gh h 0 2g v sin t 0 g Условие, что в момент времени t камень догонит утку по горизонтали v0 cos t h ctg ut Рис.4 v0 cos В этом случае будем иметь Рассмотрим второй случай v0 sin v sin h ctg u 0 g g v0 cos 2u v0 cos 2u v0 cos t h ctg ut h ctg t v0 cos u Подставив t в выражение (1), для высоты получим: 2u 2 (3) h tg (v0 cos u ) g В третьем случае v0 cos 2u . Траектория камня будет такой, как показано на рис.4. Выражение для высоты останется таким же (3). При v0 cos 2u формула (3) переходит в формулу (2). Задание 2 Посередине закрытой с торцов трубы длины 2L и сечения S находится поршень (рис. 5). Слева и справа от поршня находятся разные газы при одинаковом давлении р. На какое расстояние сместится поршень, если он становится проницаемым для одного из газов? Сила трения поршня о трубу равна F. Температуру газа считать постоянной. Рис.5 Решение Газ просачивается сквозь поршень, пока его давление (концентрация молекул) по обе стороны поршня не станет одинаковым. p1 nkT Тогда суммарная сила давления на поршень этого газа равна нулю, и ее можно не учитывать при сравнении сил, действующих на поршень. Тем самым задача свелась к совсем простой: с одной стороны на поршень действует сила трения F , с другой сила давления второго газа, который не может просачиваться сквозь поршень. Отсюда следует, что если силы трения не будет, то поршень будет прижат к стенке сосуда, а оба газа будут находиться по другую сторону поршня. 1). Если pS F , то поршень не сдвинется и x 0 2). Пусть поршень сместился на x см. рис.1, тогда второй газ будет находиться в отрезке трубы длиной L x . Так как процесс изотермический, то pL p2 ( L x) где p исходное давление газа, а p2 установившееся давление второго газа. Условие равновесия поршня дает F p2 S 0 отсюда pS x L 1 (1) F Из формулы видно, что при pS 2 F выражение в скобке равно 1 и x L Таким образом, при большом исходном давлении, если pS 2 F получим x L , то есть поршень будет прижат к стенке сосуда, а оба газа будут находиться по другую сторону поршня. При промежуточных значениях p справедливо выражение (1) Задание 3 В двух калориметрах налито по 200 г воды – в одном температура t = +300 С, в другом t = + 400 С. Из «горячего» калориметра зачерпывают 50 г воды, переливают в «холодный» и перемешивают. Затем из «холодного» калориметра переливают 50 г воды в «горячий» и снова перемешивают. Сколько раз нужно перелить такую же порцию воды туда-обратно, чтобы разность температур воды в калориметрах стала меньше 1 °С? Потерями тепла в процессе переливаний и теплоёмкостью калориметров пренебречь Решение Обозначим исходные температуры горячей воды – t h и холодной – t k . Рассчитаем, какая температура t1 установится в «холодном» калориметре после переливания в него горячей воды массой m . Из уравнения теплового баланса имеем: Cm(t1 t k ) Cm(t h t1 ) Здесь т — исходная масса воды, находившейся в каждом из калориметров, С — удельная теплоёмкость воды. Из этого уравнения находим: mt mt h t h t k t1 k m m 1 m 1 где введено обозначение m Далее найдём, какая температура t 2 установится в «горячем» калориметре после переливания в него массы воды m из «холодного» калориметра. Из уравнения теплового баланса имеем: C (m m)(t h t 2 ) Cm(t 2 t1 ) Отсюда: (m m)t h mt1 t k t h t2 m 1 Тогда после одного переливания туда-обратно разность температур в калориметрах составит 1 t2 t1 (th tk ) 1 Ясно, что для того, чтобы получить разность температур в калориметрах (t4 t3 ) после второго переливания туда-обратно, нужно в последней формуле заменить t h на t 2 и t k на t1 : 1 (1 )2 t4 t3 (t2 t1 ) (th tk ) 1 (1 )2 Таким образом, понятно, что при каждом переливании туда-обратно разность температур 1 изменяется в раз. 1 В нашем случае 1 th tk = 10 °С, m = 50 г, m = 200 г, откуда = 0,25 и = 0,6 1 С учётом этого окончательно имеем: разность температур после первого переливания туда-обратно будет равна 10 °С · 0,6 = 6 °С, после второго переливания 10 °С · 0,62 = 3,6 °С, после третьего переливания 10 °С · 0,63 ≈ 2,2 °С, после четвёртого 10 °С · 0,64 ≈ 1,3 °С, после пятого 10 °С · 0,65 ≈ 0,8 °С. Значит, для того, чтобы разность температур воды в калориметрах стала меньше 1 °С, достаточно сделать пять переливаний. Задание 4 В вакуумном диоде, анод и катод которого — параллельные пластины, зависимость тока I от напряжения U дается формулой I = c·U3/2, где c — некоторая постоянная. Во сколько раз увеличится сила давления на анод, возникающая из-за ударов электронов о его поверхность, если напряжение на диоде увеличить в два раза? Начальной скоростью электронов, вылетающих из катода, пренебречь. Решение Рассмотрим небольшой интервал времени t . За это время к аноду подлетят I t n электронов (где е — заряд электрона) e и сообщат ему импульс, равный I t p mvn mv . e Скорость v электрона у анода можно найти из закона сохранения энергии: mv2 eU 2 Согласно второму закону Ньютона F v F a mv Ft p Ft m t m тогда I t Ft mv e 3/ 2 отсюда с учетом связи I cU получаем I 2m 2 F mv c U e e Таким образом, отношение сил 2 F2 U 2 4 F1 U1 Задание 5 Пассажир автобуса, едущего вдоль прямого канала с водой, наблюдает за световым бликом, который отбрасывается спокойной поверхностью воды от фонаря, стоящего на противоположном берегу канала. Найдите скорость движения блика по поверхности воды относительно берегов канала, если высота фонаря над поверхностью воды Н, высота глаз пассажира над поверхностью воды h, скорость автобуса v. Решение Нарисуем вид канала сверху (см. рис. 4) и обозначим на нём положения автобуса, блика и столба буквами А, В и С соответственно. Пусть в момент времени t = 0 автобус находился в начале системы координат XOY — точке O, причём прямая ОС была перпендикулярна берегам канала. Тогда О А = vt. Обозначим также ОС = L, АС = l, АВ = l1, ВС = l2. Рис. 4 Рассмотрим вид сбоку в плоскости АСВ (см. рис. 5) и обозначим местонахождение глаз пассажира А1, а вершину столба С1. Так как при отражении угол А1 ВА равен углу С1 ВС, то треугольники А1 ВА и С1 ВС подобны. Рис. 5 Поэтому BC H AB h Отсюда следует, что BC BC H AC AB BC h H Проведём через точку В на рисунке 4 прямую, параллельную берегам канала; она пересечёт перпендикуляр СО в точке В1. Из подобия треугольников СВВ1 и САО получаем B1C BC H OC AC H h B1C то есть отношение есть постоянная величина. Это означает, что точка B1 не меняет OC своего положения по координате y со временем. Таким образом, блик движется по прямой, проходящей через точку B1 параллельно берегам канала. Найдём его скорость. Длины отрезков В1 В и О А равны ut и vt соответственно. Из подобия треугольников СВВ1 и САО следует отношение: B1 B ut BC H OA vt AC H h из которого получается выражение для скорости блика: H uv H h Задание 6 Два небольших заряженных шарика находятся в невесомости в безвоздушном пространстве на расстоянии l = 30 м друг от друга и очень далеко от других тел. В начальный момент времени их скорости направлены в противоположные стороны перпендикулярно прямой АВ, соединяющей их центры, и равны по величине ν = 4 м/с. Шарики заряжены положительно, и отношение заряда к массе у обоих шариков равно , где ε0 ≈ 8,854*10-12Ф/м – электрическая постоянная, а G ≈ 6,674*10-11м3/(кг·с2) – постоянная тяготения. Какой должна быть величина индукции магнитного поля, перпендикулярного плоскости движения шариков, чтобы они столкнулись при первом же возвращении на прямую АВ? Ответ запишите в ГТл (1ГТл = 109 Тл). Решение Шарики взаимодействуют друг с другом, притягиваясь согласно закону всемирного тяготения и отталкиваясь, будучи заряженными зарядом одного знака, согласно закону Кулона. Записав выражения для этих сил с учетом данных в условии задачи, легко убедиться, что векторная сумма этих сил равна нулю. Значит, на каждый шарик действует нескомпенсированная сила Лоренца. Под действием этой силы каждый шарик будет двигаться по своей окружности, причем радиусы окружностей будут равны, так как радиус R = mv/qB, а m/q и v одинаковы.. Чтобы шарики столкнулись, надо чтобы выполнилось условие R = l/4, тогда B = 4mv/ql./ Подставляя значения, указанные в условии, получим: B = 6,19 ГТл. Задание 7 На лёгкой вертикальной пружине подвешен груз. Летящий вертикально вверх со скоростью 3 м/с комок пластилина такой же массы попадает в груз и прилипает к нему. Найдите максимальную скорость образовавшегося тела при возникших колебаниях, если циклическая частота этих колебаний равна ω=2,5 с−1 . Ускорение свободного падения 10 м/c 2. Решение В положении равновесия груз растягивает пружину на величину x1 = mg/k. После того, как комок пластилина попадет в подвешенный на пружине груз и прилипнет к нему, система тел начнет колебаться около нового положения равновесия x2 = 2mg/k, причем начальная скорость тел, как следует из закона сохранения импульса, будет равна v1 = mv/2mv = v/2 = 1,5 м/с. Максимальную скорость тел найдем из закона сохранения энергии. За нулевой уровень потенциальной энергии тела в поле тяжести Земли возьмем уровень нового положения равновесия. Тогда энергия системы в начальный момент сразу после столкновения равна сумме потенциальной и кинетической энергии тел и потенциальной энергии растянутой пружины: W1 = 2mg (x2 – x1) + 2m(v/2)2 /2 +k(mg/k)2 /2 , а в момент прохождения положения равновесия энергия системы равна сумме кинетической энергии тел и потенциальной энергии растянутой пружины: W2 = 2mUmax2/2 +k4m2g2/2k2. Приравнивая энергии в двух этих положениях найдем максимальную скорость. Umax2 = mg2/2k + v2/4. Заменив в конечном выражении k/2m =w2, как следует из условия, и подставляя заданные значения, получим Umax = 2,5 м/с.


