Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение

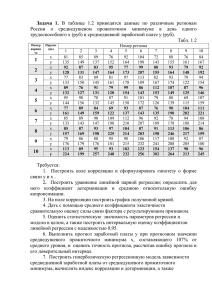
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Московский государственный университет»
(ФГБОУ «МГИУ»)
Кафедра «Математические методы в экономике»
Самостоятельная работа №4
по курсу «Эконометрика»
Москва 2013
Задание на самостоятельную работу № 4
1. Постройте уравнение множественной регрессии методом МНК.
2. Постройте уравнение множественной линейной регрессии для данных,
приведенных в Индивидуальном задании, используя функцию ЛИНЕЙН. Запишите
построенное уравнение.
3. Дайте словесную интерпретацию каждому из коэффициентов регрессии.
4. Рассчитайте прогнозируемое значение результирующего показателя при значениях
факторов, указанных в Индивидуальном задании.
5. Определите стандартную ошибку регрессии и коэффициент детерминации.
Сделайте выводы об адекватности уравнения регрессии эмпирическим данным.
6. Проверьте значимость коэффициента детерминации. Сделайте вывод об
адекватности уравнения регрессии данным генеральной совокупности.
7. Определите стандартные ошибки каждого из коэффициентов регрессии.
8. Проверьте значимость каждого из коэффициентов регрессии любым способом (не
менее 2-х способов).
9. Определите, какой из факторов сильнее влияет на результирующий показатель
(тремя способами).
10. Совпадает ли ваш вывод с результатами, полученными в п.7 и 8?
11. Выполните проверку рассчитанных вами показателей с помощью режима
«Регрессия».
12. Постройте диагностическую диаграмму. Сделайте вывод.
13. Обобщите выводы о качестве построенного уравнения
регрессии: а) о точности прогнозов, сделанных на основе
уравнения регрессии; б) об адекватности уравнения данным
генеральной совокупности; в) о необходимости исключения
факторов из уравнения регрессии; г) о других проблемах и
способах их решения.
14. Если необходимо исключить факторы из уравнения регрессии, запишите вид нового
уравнения, которое вы предлагаете построить.
15. Выполните все задания из индивидуального варианта.
Контрольные вопросы
1.
2.
3.
Запишите теоретическое и эмпирическое уравнение множественной линейной
регрессии.
В чем отличие между ними?
Какое соотношение должно выполняться между количеством переменных в
линейной регресс ионной модели и числом наблюдений? Поясните свой ответ на
примере парной линейной регрессии.
В чем суть МНК? Запишите систему линейных нормальных уравнений для
определения коэффициентов регрессии. Что показывают коэффициенты
множественной регрессии?
4. Какие характеристики используются для оценки точности предсказаний по
уравнению множественной регрессии? Опишите каждую из них.
5. Какие условия относительно генеральной совокупности должны выполняться, чтобы
статистические выводы о качестве уравнения регрессии были обоснованными?
6. Поясните понятия гомоскедастичности и гетероскедастичности.
7. Поясните понятие автокорреляции остатков.
8. Опишите механизм проверки гипотезы о значимости коэффициента детерминации.
Какова цель проверки этой гипотезы? Как она взаимосвязана с проверкой
значимости коэффициентов регрессии?
9. Что показывают стандартные ошибки коэффициентов регрессии? Для чего они
используются? Как можно проверить значимость коэффициентов регрессии?
1 О. Как можно сравнить влияние различных факторов на результирующий показатель?
Приведите формулы расчета соответствующих показателей.
11. Для чего строится диагностическая диаграмма? Как может интерпретироваться ее
структура?
Кроме того,
1.
2.
3.
студент должен
Объяснить значение любого показателя в массиве результатов функции ЛИНЕЙН.
Рассчитать на основании заданной функции множественной регрессии
прогнозируемое значение результирующего показателя, соответствующее заданным
значениям факторов.
Указать в массиве результатов режима «Регрессия» значения известных ему
показателей.
ПРИМЕЧАНИЕ: студент выполняет все пункты общего и индивидуального задания.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Вариант 1. Анализ деятельности ряда нефтяных компаний позволил выявить ряд
факторов,
оказывающих влияние на объем добычи нефти: - объем капиталовложений,
- уровень механизации,
- производительность труда.
Требуется:
1.Построить матрицу парных корреляций и обосновать выбор факторных признаков.
2.Построить модель регрессии со статистически значимыми факторами.
3.Оценить качество построенной модели.
4.Построить прогноз объема добычи нефти, если предположить, что значения
факторных признаков увеличатся относительно средних значений на 1О %.
5.Внести рекомендации по увеличению объема добычи нефти.
у
объем добычи нефти
№ (млн.тонн)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
108.81
81.18
80.75
98.41
88.45
109.19
131.86
141.36
126.46
57.89
55.22
47.76
49.82
112.61
105.69
106.01
147.61
195.09
281.22
244.94
303.92
284.73
326.81
333.29
327.47
442.14
552.59
542.88
533.93
550.38
613.27
773.88
731.07
716.78
598.12
396.22
492.54
366.46
438.12
425.43
434.75
258.53
237.16
233.08
102.73
Х1
Объем капиталоХ2
Х3
вложений
(млн.руб.)
уровень ме- производительность
ханизации
труда
216.89
176.6
136.51
118.78
117.21
159.73
202.82
208.54
350.73
336.05
337.03
354.46
355.86
356.73
345.86
353.57
385.29
429.21
450.7
396.72
425.28
400.39
391.82
377.54
367.66
389.48
394.48
371.88
371.12
401.33
465.31
587.97
503.7
177.15
152.13
95.21
102.04
91.02
129.13
193.13
193.56
177.94
162.2
151.03
147.85
164.2
162.52
147.39
139.14
229.38
363.69
520.39
417.59
502.18
441.04
480.95
504.81
520.14
868.59
1062.6
6
938.69
534.16
431.35
337.74
334.55
304.27
309.64
272.73
249.42
176.35
143.71
123.08
75.93
1684.07
1471.15
958.26
1239.89
968.96
1207.45
1243.55
1294.02
598.85
503.76
501.89
142.3
79.5
74.57
80.57
86.16
63.55
68.85
80.58
83.77
84.44
74.13
65.25
58.59
52.49
53.2
54.63
50.85
49.68
35.96
41.37
43.79
54.74
72.21
96.71
115.4
154.26
234.06
487.61
464.85
386.83
453.46
897.17
991.43
1014.18
1140.9
1
1312.4
1497.9
4
1728.9
7
1571.7
9
986.54
910.15
520.08
871.13
611.08
593.2
658.2
652.34
373.79
315.28
313.65
100.76
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
64.93
77.98
102.57
88.65
77.3
78.53
74.85
66.51
102.98
162.37
137.39
113.77
79.56
89.48
122.62
183.44
238.02
289.63
377
317
258.04
219.33
231.58
268.49
203.41
197.03
150.35
145.25
150.73
144.48
141.06
139.06
138.18
144.12
130.34
126.83
108.61
116.01
135.44
142.88
158.69
168.49
174.8
187.15
168.71
145.7
68.4
59.04
67.43
54.92
45.59
53.95
72.16
90.35
91.05
108.45
106.43
101.8
85.35
94.67
123.47
187.33
242.37
265.27
309.55
314.9
266.77
224.06
268.52
306.8
263.35
264.81
224.12
241.54
277.25
307.8
405.96
408.23
457.67
535.9
474.61
474.3
393.93
403.87
428.61
475.37
476.57
549.98
578.39
581.06
587.67
572.58
77.69
163.82
179.86
143.86
129.32
197.75
192.5
209.06
239.86
393.83
334.33
286.44
233.2
246.16
296.1
459.54
507.68
554.74
697.95
699.97
535.49
452
549.34
629.66
521.35
494.24
322.19
321.44
396.1
366.24
382.02
424.85
432.31
459.61
428.16
441.04
371.08
412.53
534.51
583.03
600.25
612.33
618.54
579.44
527.44
411.14
52
29.25
51.03
41.44
24.38
46.48
58.5
56.22
67.27
143
99.12
93.43
71.43
71.99
93.92
129.99
133.24
153.72
153.71
153.71
133.24
124.62
154.36
154.35
135.51
133.23
86.92
82.05
85.79
77.99
105.61
118.6
120.72
120.16
113.98
118.9
100.08
110.46
154.16
243.8
275.58
309.31
454.09
564.31
567.59
562.65
Вариант 2. По ряду филиалов трастовой фирмы получены данные, характеризующие зави
симость годовых объемов чистой прибыли инвестиционных проектов от следующих
факторов: - объема инвестиций,
- годового оборота проекта,
- срока окупаемости,
- риска потери инвестиций.
Требуется:
1. Построить матрицу парных корреляций и оценить тесноту связи между показателями.
Проверить значимость коэффициентов корреляции.
2. Построить модель множественной линейной регрессии со статистически значимыми
факторами и дать содержательную характеристику коэффициентов регрессии.
3. Оценить статистическую значимость уравнения регрессии.
4. Построить прогноз годового объема чистой прибыли проектов, если предположить,
что значения независимых переменных увеличатся относительно последних значений
на 2 %.
5. Внести предложения по увеличению годового объема чистой прибыли
инвестиционных проектов.
у
объем чистой
прибыли инвестиционного
проекта
(млн.руб.)
№ про-
екта
хз
срок окупаеобъем ин- годовой
мости
вестиций, оборот
(лет)
(млн.руб.) проекта
Х1
Х2
1
2
3
4
5
6
7
8
9
7.80
1.30
0.59
0.83
0.39
0.13
2.60
0.20
2.53
33.00
1.14
1.08
3.00
0.66
0.11
9.10
0.47
6.60
26.00
18.00
1.65
3.90
3.00
0.75
20.40
0.31
14.95
5.50
1.69
2.75
3.85
2.20
2.20
6.50
4.40
3.30
10
11
12
13
14
15
16
17
18
19
20
21
22
0.65
4.88
0.26
4.60
0.11
0.77
0.14
0.26
0.33
0.66
0.98
0.59
0.07
1.54
33.00
1.30
2.40
0.54
0.77
0.50
0.46
1.20
1.80
1.32
1.10
0.16
1.80
26.00
1.20
27.50
1.73
2.52
1.82
1.15
3.30
4.55
4.50
5.20
0.30
6.60
8.80
6.50
0.66
5.50
5.50
5.50
2.60
4.40
2.75
2.20
2.75
3.25
Х4
риск потери
инвестиций
Н
В
Н
Н
Н
Н
Н
Н
В
В
Н
Н
Н
Н
Н
Н
Н
В
Н
Н
В
В
X4 – риск инвестиций (В(высокий) – 1, Н (низкий) – 0)
Вариант 3. В результате анализа уровня потребления продукции по различным
регионам
страны выявлен ряд факторов, оказывающих на него существенное влияние:
- уровень урбанизации,
- относительный образовательный уровень населения,
- относительный возрастной показатель,
- относительная заработная плата,
- географическое положение региона.
В данной задаче У (уровень потребления продукции) - показатель, рассчитанный,
исходя из минимального набора продуктов потребительской корзины. Кроме того, в этот
показатель включается среднестатистическое потребление лекарственных препаратов и
медикаментов. Поэтому единицы измерения этого показателя - условные.
Х1 (уровень урбанизации) - показывает количество городов региона на 100 единиц
населенных пунктов всех видов.
Х2, Х3, Х4 - относительные показатели, рассчитанные по определенным методикам, а
не полученные прямым и измерениями, поэтому единицы измерения - условные.
Х5 (географическое положение района) - характеризует близость региона к
Центральному району ( 1 или О).
Требуется:
1. Построить матрицу парных корреляций и обосновать выбор факторных
признаков.
2. Построить модель множественной линейной регрессии со статистически
значимыми факторами.
3. Построить прогноз уровня потребления продукции, если предположить, что
значения факторных признаков уменьшатся относительно средних значений на 2
%.
4. Внести рекомендации по осуществлению ряда мер, за счет которых может быть
увеличен уровень потребления продукции.
Х2
У
уровень потребления
продукции(усл.ед.)
№ П.П.
относительный
Х1
образовательный
уровень ур- уровень населебанизации
ния,
ХЗ
Х4
Х5
относительный относительная
возрастной по- заработная
географическое
казатель
плата
положение региона
1
2
3
4
5
27.1
24.4
20.8
32.1
28.8
42.2
48.6
42.6
49.1
34.7
11.2
12.6
10.6
11.4
9.3
31.9
23.2
28.7
26.1
30.1
35.2
37.8
32.1
42.3
32.9
1
1
6
34.6
44.5
10.8
28.5
49.6
7
8
9
33.7
34.5
35.7
39.1
40.1
45.9
9.7
10.1
12.2
24.3
28.6
20.4
35.3
45.3
47.1
10
28.7
38.4
11.3
25.3
35.6
11
36.5
46.2
12.8
37.2
43.2
О
1
1
О
О
1
1
О
1
12
13
14
15
34.3
33.6
28.2
24.9
50.1
39.4
31.3
25.8
12.9
10.5
9.2
9.1
38.4
27.2
20.6
29.8
48.4
39.1
30.1
27.8
1
1
1
1
16
26.2
37.4
9.6
30.1
34.6
1
17
26.9
46.1
10.5
25.4
36.2
1
18
19
20
21
22
23.8
32.4
43.4
38.2
34.7
27.2
34.9
48.2
40.2
41.9
8.7
11.2
12.8
11.7
12.3
27.2
21.5
26.7
31.2
27.2
24.7
40.6
44.6
42.1
43.2
1
23
28.3
35.5
10.6
34.8
38.4
О
1
1
1
1
24
25
26
27
28
29
30
34.2
36.1
28.2
38.3
42.1
42.9
45.2
44.7
48.3
39.6
47.2
51.8
52.3
54.5
12.4
12.8
9.6
10.2
10.7
11.1
12.9
32.9
28.6
35.6
42.7
46.4
39.6
42.4
39.1
40.1
37.8
42.6
46.2
48.8
54.3
Вариант 4. В таблице представлены данные о цене технического средства (те),
доходе, возрасте, стаже работы и т.д. 24 сотрудников некоторого предприятия.
№ П.П.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
8.50
16.60
у
Цена ТС
Х1
Доход
Х2
Возраст
36.20
76.90
13.70
12.50
11.30
37.20
19.80
28.20
12.20
46.10
35.50
11.80
21.30
68.90
34.10
78.90
18.60
13.70
54.70
58.30
11.80
9.50
72.00
153.00
28.00
26.00
23.00
76.00
40.00
57.00
24.00
89.00
72.00
24.00
40.00
137.00
70.00
159.00
37.00
28.00
109.00
117.00
23.00
21.00
55.00
56.00
28.00
24.00
25.00
45.00
42.00
35.00
46.00
34.00
55.00
28.00
31.00
42.00
35.00
52.00
21.00
32.00
42.00
40.00
30.00
48.00
17.00
34.00
39.00
42.00
ХЗ
Уровень образ.
0.00
0.00
1.00
1.00
0.00
0.00
1.00
0.00
0.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
0.00
1.00
0.00
0.00
1.00
1.00
0.00
2.00
13.00
Х4
Стаж
Х5
Пол
23.00
35.00
4.00
0.00
5.00
13.00
10.00
1.00
11.00
12.00
2.00
4.00
0.00
3.00
9.00
16.00
0.00
2.00
20.00
19.00
3.00
2.00
0.00
1.00
0.00
1.00
1.00
1.00
1.00
0.00
0.00
1.00
0.00
1.00
0.00
0.00
1.00
1.00
1.00
0.00
0.00
0.00
1.00
1.00
1.00
0.00
Обозначения:
в графе Уровень образования: 1 - высшее и не оконченное высшее, О - среднее, среднее
специальное,
ТС - транспортное средство,
в графе Пол: 1 - мужской, О - женский.
Требуется:
1.Проанализировать тесноту и направление связи между переменными, отобрать факторы
для регрессионного анализа.
1
1
О
О
1
О
1
2.Построить модель множественной регрессии с выбранными факторами. Проверить значимость параметров уравнения.
3.Построить уравнение только со статистически значимыми факторами. Оценить его качество.
4.Оценить степень влияния, включенных в модель факторов на зависимую переменную при
помощи коэффициентов эластичности, бета- и дельта-коэффициентов.
5.Определить точность модели.
Вариант 5. Исследуется взаимосвязь курса доллара США с курсами евро, японской иены и
английского фунта стерлингов. Имеются данные об официальных курсах валют, установленных
Центральным Банком России, за двенадцать дней:
Доллар США
Евро
Японская иена
Английский фунт
(руб./долл.)
(руб./евро)
(руб./l00 иен)
(руб./фунт)
28,12
28,18
28,13
28,08
28,06
28,03
28,02
28,00
27,99
27,93
27,95
27,97
36,13
35,97
35,97
36,00
36,13
36,28
36,34
36,47
36,54
36,50
36,52
36,54
26,97
26,80
26,77
26,63
26,53
26,70
26,67
26,63
26,60
26,50
26,55
26,52
52,63
52,32
52,26
52,28
52,43
52,58
52,90
52,99
52,81
52,89
52,62
52,67
День
1
2
3
4
5
6
7
8
9
10
11
12
1. Построить линейную регрессионную модель курса доллара США, не содержащую
коллинеарных факторов. Оценить параметры модели.
2. Значимо ли статистически уравнение регрессии?
3. Изменение курсов каких валют существенно влияет на изменение курса доллара
США?
4. Спрогнозировать курс доллара, если предполагается, что курсы евро, иены и фунта
составят соответственно: 36,38 руб./евро; 26,65 руб./100 иен и 52,73 руб./фунт.
Вариант 6. По заводу безалкогольных напитков изучается зависимость месячного
объема реализованной продукции от затрат в предыдущем месяце на теле-, радио-,
газетную и наружную рекламу. Имеются данные за двенадцать месяцев:
Месяц
1
2
3
4
5
6
7
8
9
10
11
12
Объемреализации
(тыс. руб.)
15304
17554
16876
16435
15229
16986
17914
16817
16579
15330
16781
17008
Затраты на рекламу (тыс. руб.)
газетную
телерекламу радио рекламу
рекламу
133
35
38
152
40
32
130
48
35
165
40
44
125
42
48
158
37
37
165
50
43
149
37
38
169
33
28
137
31
39
178
42
42
147
49
37
наружную
рекламу
27
29
28
25
18
32
38
29
27
22
18
19
Требуется:
1. Построить линейную регрессионную модель объема реализованной продукции, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Присутствует ли в остатках регрессии авто корреляция первого порядка?
3. Как влияет на изменение объема реализованной продукции изменение затрат на каждый вид
рекламы?
4. Изменение затрат на какой вид рекламы сильнее всего влияет на изменение объема реализованной продукции?
5. Спрогнозировать значение объема реализованной продукции, если прогнозные значения
факторов на 35 % превышают свои средние значения.
ров, включенных в модель регрессии?
Вариант 7. По хлебобулочному предприятию исследуется зависимость месячного объема
реализованной продукции от затрат в предыдущем месяце на теле-, радио-, газетную и наружную
рекламу. Имеются данные за двенадцать месяцев:
Объем реализованЗатраты на рекламу (тыс. руб.)
Месяц
ной продукции
газетную
наружную
телерекла.му
радиорекламу
(тыс.руб.)
рекламу
рекламу
1
14050
240
42
42
34
2
16310
263
47
44
36
3
15632
241
55
45
35
4
15126
276
47
42
32
5
13972
236
49
47
25
6
15753
272
44
45
39
7
16661
276
57
55
45
8
15584
260
46
47
36
9
15326
280
40
35
34
10
14077
248
38
38
29
11
15528
289
49
45
25
12
15755
258
56
52
26
Требуется:
1. Построить линейную регрессионную модель объема реализованной продукции, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Какая доля вариации объема реализованной продукции объясняется вариацией факторов,
включенных в модель регрессии?
3. Присутствует ли в остатках регрессии автокорреляция первого порядка?
4. Приемлема ли точность регрессионной модели?
5. Спрогнозировать значение объема реализованной продукции, если прогнозные
значения факторов на 25 % превышают свои средние значения.
Вариант 8. По четырнадцати страховым компаниям исследуется зависимость месячной
прибыли от численности страховых агентов, затрат на рекламу и расположения офиса
компании
(центральный или периферийный районы города):
№ компаПрибыль
Численность страхоЗатраты на реклаРайон располонии
(тыс. руб.)
вых агентов (чел.)
му (тыс. руб.)
жения
1
726
14
75
периферийный
2
550
8
36
центральный
3
429
4
55
периферийный
4
439
4
45
периферийный
5
646
10
79
периферийный
6
507
10
53
периферийный
7
834
13
69
центральный
8
579
9
47
периферийный
9
701
16
45
центральный
10
532
14
49
периферийный
11
281
7
53
периферийный
12
349
5
45
периферийный
13
625
10
68
периферийный
14
533
11
38
центральный
1.
2.
3.
4.
Требуется:
Построить линейную регрессионную модель прибыли страховой компании, не
содержащую коллинеарных факторов. Оценить параметры модели.
Значимо ли статистически уравнение регрессии?
Существенна ли разница в прибыли компаний, офисы которых расположены в центральном и периферийных районах города?
Спрогнозировать месячную прибыль страховой компании, если прогнозные значения
факторов равны своим средним значениям, а офис расположен: а) в центре города; б)
на окраине.
Вариант 9. Строится модель цены автомобиля на вторичном рынке в зависимости от
пробега, срока эксплуатации и объема двигателя. Имеются данные по пятнадцати
автомобилям одной и той же модели:
Цена автомобиля
Про бег
Срок эксплуатации
Объем двига-
(долл. США)
(тыс. км)
(лет)
теля (л)
12500
13700
9200
11400
15800
12300
16300
10200
11000
130
120
300
180
150
80
170
210
250
12
10
15
13
14
8
10
11
7
2,3
1,9
1,8
2,1
2,6
1,7
2,4
1,9
1,9
№ автомобиля
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12700
15000
10500
17200
16000
17100
150
90
230
120
110
120
9
4
13
8
9
6
1,7
2,2
2,4
2,3
2,5
2,6
Требуется:
1. Построить линейную регрессионную модель цены автомобиля, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Построить модель множественной линейной регрессии со статистически значимыми
факторами
3. Существенно ли влияние пробега, срока эксплуатации и объема двигателя на изменение цены автомобиля?
4. Что сильнее влияет на изменение цены автомобиля - изменение пробега или срока
эксплуатации?
5. Спрогнозировать цену автомобиля с пробегом 150 тыс. км, сроком эксплуатации 10
лет и объемом двигателя 2 л. Пункты 4 и 5 выполнить, используя вторую модель.
Вариант 10. По тринадцати коммерческим банкам имеются данные, характеризующие зависимость годовой прибыли от размера собственного капитала, общей суммы привлеченных средств и
среднегодовых ставок по рублевым депозитам и краткосрочным кредитам:
Прибыль
№ банка
1
2
3
4
5
6
7
8
9
10
11
12
13
(млн. руб.)
115
80
97
92
129
223
251
267
137
163
225
278
367
Собственный
капитал (млн.
руб.)
4428
3756
2970
6231
3960
7354
4662
4760
4569
5274
5418
5359
8254
Привлеченные
средства (млн.
руб.)
3278
5696
2210
5823
4569
2896
3526
2259
4596
3271
4596
3256
5189
Депозитная
ставка (% годовых)
12,5
11,7
11,2
9,7
13,5
10,8
12,1
11,7
13,7
12,5
12,8
11,2
10,4
Кредитная
Ставка (% годовых)
17,7
18,2
19,1
15,2
18,5
18,6
15,7
16,6
17,3
19,3
17,8
14,5
13,7
Требуется:
1. Построить линейную регрессионную модель годовой прибыли банка с полным набором
факторов. Оценить параметры модели.
2. Построить линейную регрессионную модель годовой прибыли банка только с
существенно влияющими на ее изменение факторами. Оценить параметры модели.
3. Значимо ли статистически уравнение регрессии второй модели?
4. Имеют ли остатки второй регрессии одинаковую дисперсию?
5. Используя вторую модель, сравнить силу влияния факторов на годовую прибыль банка.
Вариант 11. По четырнадцати страховым компаниям имеются данные, характеризующие зависимость чистой годовой прибыли от годовых размеров собственных средств, страховых резервов,
страховых премий и страховых выплат (все в тыс. руб.):
№комани
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1.
2.
3.
4.
5.
Годовая
прибыль
92
42
186
48
38
74
48
82
45
46
65
29
34
66
Собственные
средства
3444
2658
9723
4526
5369
2248
5671
4312
2226
3654
2635
2463
3265
7546
Страховые резервы
9563
6354
10245
6398
5692
6359
6892
7256
8256
5982
6359
7532
5632
7625
Страховые
премии
11456
5249
12968
7589
7256
4963
7259
6935
2693
6324
7853
8253
7564
9638
Страховые выплаты
1659
2625
4489
6896
5698
4321
6692
756
5532
3235
5325
6862
6325
4569
Требуется:
Построить линейную регрессионную модель годовой прибыли страховой компании,
не содержащую коллинеарных факторов. Оценить параметры модели.
Значимы ли статистически уравнение регрессии и его коэффициенты?
Имеют ли остатки регрессии одинаковую дисперсию?
Приемлема ли точность регрессионной модели?
Дать экономическую интерпретацию коэффициентам уравнения регрессии.
Вариант 12. По литейному предприятию исследуется влияние объемов производства
алюминия, меди и олова на технологические затраты электроэнергии. Имеются данные за
одиннадцать месяцев:
Затраты электроэнергии
Объем производства (тонн)
Месяц
1
2
3
4
5
6
7
8
9
10
11
1.
2.
3.
4.
(тыс. кВт ·ч)
алюминия
меди
олова
286
374
308
319
616
495
825
253
495
1056
902
68
45
59
62
72
128
78
42
52
96
122
42
32
36
43
59
63
42
34
26
75
56
7
27
14
18
26
48
23
7
27
36
43
Требуется:
Построить линейную регрессионную модель энергозатрат, не содержащую
коллинеарных факторов. Оценить параметры модели.
Проверить статистическую значимость уравнения регрессии и их отдельных
коэффициентов.
Оценить точность модели.
На сколько в среднем изменяются технологические энергозатраты при увеличении
производства каждого из металлов: а) на одну тонну; б) на один процент?
Вариант 13. Исследуется зависимость цены акции компании «Атон» от цен акций смежных
компаний «Бридж», «Вортекс» и «Радон». Имеются данные о результатах биржевых торгов за
пятнадцать дней:
Цена акции (руб.)
День
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
«Атон»
«Бридж»
«Вортекс»
«Радою>
67
63
58
66
63
67
70
63
60
64
56
68
71
62
64
30
27
22
27
18
33
32
24
29
27
32
32
56
40
37
59
55
52
55
78
68
72
75
56
79
62
79
75
72
68
75
68
78
60
72
73
71
78
72
65
82
71
72
78
75
Требуется:
1. Построить трехфакторную и три однофакторные линейные регрессионные модели цены
акции «Атона». Оценить параметры моделей.
2. Проверить статистическую значимость всех уравнений регрессии и их коэффициентов.
3. Используя трехфакторную модель, сравнить силу влияния факторов на изменение цены
акции «Атона».
4. Используя трехфакторную и однофакторные модели, спрогнозировать среднюю цену
акции «Атона», если предполагается, что цены акций «Бриджа», «Вортекса» и «Радона»
составят соответственно 40; 70 и 80 руб. Сравнить результаты расчетов по
трехфакторной и однофакторным моделям.
Вариант 14. По хладокомбинату изучается зависимость месячного объема реализации мороженного от средней цены выпускаемой продукции, затрат на рекламу, среднемесячной температуры воздуха и месячного темпа инфляции. Имеются данные за двенадцать месяцев:
Объем реализации
Цена
Затраты на рекламу
Температура
Темп инфляции
(тыс.руб.)
(руб.)
(тыс. руб.)
воздуха (СС)
(%)
185
162
182
195
226
279
312
286
212
178
182
173
8,3
8,3
8,9
10,6
10,7
10,8
12,2
14,2
14,5
13,7
13,3
12,1
6
7
5
5
7
22
12
17
22
26
8
4
2
4
7
10
13
18
22
24
17
13
8
5
0,3
0,4
0,3
0,2
0,7
0,9
0,9
0,4
0,1
0,1
0,5
0,9
Месяц
1
2
3
4
5
6
7
8
9
10
11
12
Требуется:
1. Построить линейную регресс ионную модель объема реализации мороженного, не содержащую коллинеарных факторов. Оценить параметры модели.
2. Значимо ли статистически уравнение регрессии и его коэффициенты?
3. Присутствует ли в остатках регрессии автокорреляция первого порядка?
4. Приемлема ли точность регрессионной модели?
5. Изменение какого из факторов сильнее всего влияет на изменение объема реализации
мороженного?
Вариант 15
По тринадцати супермаркетам исследуется зависимость квартального торгового
оборота от размера торговых площадей, района расположения (центральный или
периферийные) и формы собственности (муниципальный или частный). Имеются
следующие данные:
№магази
на
магази1
2
3
4
5
6
7
8
9
10
11
12
13
Торговый оборот
(млн. руб.)
59
85
127
178
156
122
89
159
256
156
149
122
178
Торговые площади (м2)
2500
2172
2928
3943
2819
4902
4236
5486
7186
4501
3495
4562
2706
Район расположенuя
периферийный
периферийный
центральный
центральный
центральный
периферийный
центральный
периферийный
центральный
центральный
центральный
периферийный
центральный
Форма собственности
муниципальный
частный
муниципальный
муниципальный
частный
муниципальный
муниципальный
муниципальный
частный
частный
муниципальный
частный
частный
Требуется:
1. Построить линейную регрессионную модель торгового оборота магазина, не
содержащую коллинеарных факторов. Оценить параметры модели.
2. Существенна ли разница в торговом обороте магазинов: а) расположенных в
центральном и периферийных районах города; б) частных и муниципальных?
3. Соответствуют ли остатки регрессии нормальному закону распределения?
4. Спрогнозировать значение торгового оборота муниципального магазина с торговой
площадью 4000 м2, расположенного в центральном районе города
Домашнее задание
Дома выполнить вариант лабораторной работы. Номер варианта выбирается
по своему номеру из учебного журнала группы до № 15. С номера 16
выбирается номер по последней цифре своего порядкового номера в учебном
журнале.