Задания второго тура работы школы «Юный физик» 2012 года.

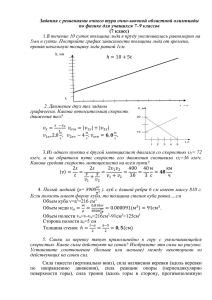
Задания второго тура работы школы «Юный физик» 2012 года.
Задача 1. Пуля попадает в ящик с песком и застревает в нем. На сколько
сожмется пружина жесткостью с, удерживающая ящик, если пуля имеет
массу m и движется со скоростью u, а масса ящика с песком равна М?
Задача 2. Санки массой m и длиной l скользят со скоростью υ0 по гладкому
льду. Неожиданно лед кончается, и санки въезжают на асфальт, где
коэффициент трения равен µ. Известно, что санки заехали на асфальт лишь
частично. Найдите время до полной остановки санок.
Задача 3. На край доски массы М = 3,2 кг, лежащей на гладкой
горизонтальной поверхности, поместили брусок массы m = 1,6 кг (см.
рисунок). Коэффициент трения между бруском и доской k = 0,25. Какая
работа A будет произведена над доской в течении времени, за которое брусок
переместится относительно Земли из начального положения на расстояние,
равное длине доски l = 1 м, если на брусок подействовать вдоль доски
горизонтальной силой F = 2 H.
Задача 4. Цилиндрический сосуд с газом закрыт поршнем массой m и
площадью поперечного сечения S (см. рисунок). В равновесии поршень
находится на высоте l от дна сосуда. В какой – то момент поршень смещают
из положения равновесия вниз на величину h0 и отпускают. Определите
частоту, начальную фазу и амплитуду колебаний. Атмосферное давление pa
известно. Считать, что в процессе колебаний температура газа остается
постоянной.
Задача 5. Поршень массой m находится в равновесии посередине герметично
закрытого цилиндра (см. рисунок). В каждой половине цилиндра находится ν
молей газа при абсолютной температуре T. Поршень выводится из состояния
равновесия. Найдите период τ малых колебаний поршня, считая, что
температура газа при колебаниях остается неизменной. Трением можно
пренебречь.
Задача 6. Влажный воздух, масса которого равна m, занимает объем V при
температуре Т и давлении р. Давление насыщенных паров при этой
температуре равно рн. Определите относительную влажность воздуха.