Лекции - Московский государственный технический университет

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального
образования
——————————————————————————————————————————————
«Московский государственный технический университет имени Н. Э. Баумана»
(МГТУ им. Н.Э.Баумана)
Утверждено
Первым проректором —
проректором по учебной работе
ПЛАНЫ УЧЕБНЫХ ЗАНЯТИЙ СТУДЕНТОВ
второго курса четвертого семестра 2012 /2013 учебного года
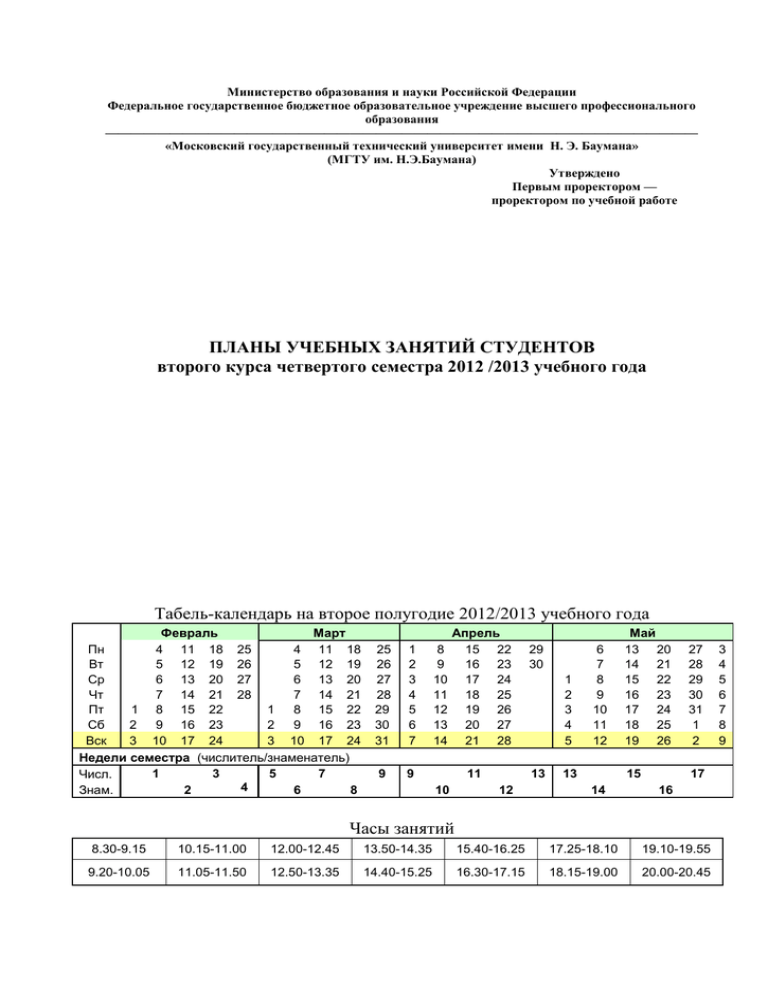
Табель-календарь на второе полугодие 2012/2013 учебного года
Февраль
Март
Пн
4 11 18 25
4 11 18
Вт
5 12 19 26
5 12 19
Ср
6 13 20 27
6 13 20
Чт
7 14 21 28
7 14 21
Пт
1 8 15 22
1 8 15 22
Сб
2 9 16 23
2 9 16 23
Вск
3 10 17 24
3 10 17 24
Недели семестра (числитель/знаменатель)
1
3
5
7
Числ.
4
2
6
8
Знам.
25
26
27
28
29
30
31
1
2
3
4
5
6
7
9
9
8
9
10
11
12
13
14
Апрель
15 22
16 23
17 24
18 25
19 26
20 27
21 28
11
10
29
30
1
2
3
4
5
13
12
6
7
8
9
10
11
12
13
14
Май
13 20
14 21
15 22
16 23
17 24
18 25
19 26
27
28
29
30
31
1
2
15
17
16
Часы занятий
8.30-9.15
10.15-11.00
12.00-12.45
13.50-14.35
15.40-16.25
17.25-18.10
19.10-19.55
9.20-10.05
11.05-11.50
12.50-13.35
14.40-15.25
16.30-17.15
18.15-19.00
20.00-20.45
3
4
5
6
7
8
9
Содержание
Стр.
1. АНГЛИЙСКИЙ ЯЗЫК для студентов факультетов СМ, РК, МТ, Э………………………..………………..4
2. АНГЛИЙСКИЙ ЯЗЫК для студентов факультетов РЛМ, ИУ, ФН, ИБМ……………………….………….8
3. НЕМЕЦКИЙ ЯЗЫК для студентов всех факультетов………………………………………………………12
4. ФРАНЦУЗСКИЙ ЯЗЫК для студентов всех факультетов………………………………………………….13
5. РУССКИЙ ЯЗЫК ДЕЛОВОГО ОБЩЕНИЯ………………………………………………………………….15
6. ФИЗИКА для всех студентов …………………………………………………………………………………18
7. ФИЗИКА для студентов УЦ 1, 2, 4, 8…………………………………………………………………………24
8. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ…………………………………………………………………………..32
9. ТЕОРИЯ ФУНКЦИЙ КОМЛЕКСНОГО ПЕРЕМЕННОГО…………………………………….……………35
10. КОМПЛЕКСНЫЙ АНАЛИЗ…………………………………………………………………….……………38
11. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ И ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА ……………………..41
12. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ОПЕРАЦИОННОЕ
ИСЧИСЛЕНИЕ для СМ3, 4, 6, 12………………………………………………………………………….……..45
13. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ОПЕРАЦИОННОЕ
ИСЧИСЛЕНИЕ для СМ1, 2, 5, 7, 8, 11, РК4……………………………………………………………………..49
14. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ОПЕРАЦИОННОЕ
ИСЧИСЛЕНИЕ для МТ и РК (кроме РК5 и РК6)…………………………………………………….………….54
1 5 . Р ЯД Ы, Т Ф КП И ОП ЕР АЦИ О НН ОЕ И С ЧИ С ЛЕ НИЕ для РК5 и Э5……………………………57
16. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ГАРМОНИЧЕСКИЙ
АНАЛИЗ для студентов факультета Э, обучающихся по программе бакалавра………………….…………..61
17. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО, РЯДЫ ФУРЬЕ И ОПЕРАЦИОННОЕ
ИСЧИСЛЕНИЕ для студентов факультета Э, обучающихся по программе специалиста……………………67
18. ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА для студентов ИУ9………………73
19. КОМПЛЕКСНЫЙ АНАЛИЗ для студентов ИУ9………………………………………………..…………76
20. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА для студентов БМТ 1, 2….……79
21. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА для студентов ИУ1, 2………….85
22. СИСТЕМНЫЙ АНАЛИЗ для студентов ИБМ ………………………………………………………………89
23. ПРИКЛАДНАЯ СТАТИСТИКА для студентов ИБМ4, 5, 6……………………………..………………….93
24. КРАТНЫЕ ИНТЕГРАЛЫ И ТФКП для студентов ИУ3……………………………….……………………96
25. МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ для студентов ИУ3…………..…………100
26. МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ для студентов ИУ7……………………..102
2
27. ДИСКРЕТНАЯ МАТЕМАТИКА для студентов ИУ6………………..……………………………….……….104
28. ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ для студентов ФН2……….….…..110
29. ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ для студентов ФН4………………114
30 АНАЛИТИЧЕСКАЯ ХИМИЯ для бакалавров Э9…………………………………………………...…………117
31. ФИЗИЧЕСКАЯ ХИМИЯ для бакалавров ФН4…………………………………………………………..……121
32. ОРГАНИЧЕСКАЯ ХИМИЯ для бакалавров Э9……………………………………………………………….126
33. НЕОРГАНИЧЕСКАЯ ХИМИЯ для бакалавров Э9……………………………………………………………131
34. ХИМИЯ для специальности ЮР…………………………………………………………….………………….134
35. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов ИУ1……………………………………………….……….139
36 ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов факультетов СМ1, 3, 4, 6, 8, 9, 10, 12, РК4, МТ…..….…147
37. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов ИУ2…………………………………………….…………153
38. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов УЦ1, 2…………………………………….………………160
39. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов ФН2, 4……………………………………………………165
40. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов ПС………………………………….……….…………….173
41. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов УЦ1, 2………………………………...……….…………180
42. ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА для студентов РК5 ……………………..……….………….……183
43. ЭЛЕКТРОТЕХНИКА для студентов СМ7, 11 для бакалавров……………………………….. …….………190
44. ЭЛЕКТРОТЕХНИКА для студентов СМ7, 11 для специалистов……………………………………………197
45. ТЕОРИЯ МЕХАНИЗМОВ И МАШИН для специалистов……………………………………………………205
46. ТЕОРИЯ МЕХАНИЗМОВ И МАШИН для бакалавров………………………………………………………219
47. ФИЗИЧЕСКАЯ КУЛЬТУРА…………………………………………………………………………………….232
3
АНГЛИЙСКИЙ ЯЗЫК
для студентов факультетов СМ, РК, МТ, Э
Практические занятия
МОДУЛЬ 10
2.Контроль лексики урока 10
Аудиторное занятие 1. (ОЛ1)
3.Беседа по теме «Лазеры» упр.1,2 стр.203
1.Сообщение о плане работы в семестре.
4.Упр.21 стр.203-письм. Перевод на время
2.Введение грамматики. Инфинитив, формы
( 20 мин.)
и функции. Упр.1 стр.194.
Домашнее задание.
3.Введение лексики урока 10. Упр.5,6,7 стр.196.
1.Работа с текстом 10В - знать содержание.
4.Работа с текстом 10А 1 ч.- прослушивание,
лексико-грамматический разбор текста.
2.Подготовить вопросы для обсуждения
текста.
5.Каузативные глаголы упр.3.стр.195
Аудиторное занятие 4. (ОЛ1)
Домашнее задание
1.Проверка д.з. Работа с текстом 10В.
1.Текст 10А прочитать и разобрать до конца.
2.Ознакомительное чтение текстов 10С,10D.
2.Отвечать на вопросы упр.8 стр.199
Беседа по содержанию текстов.
3.Упр.9 стр.199.
3.Упр.2,3 стр.211-212 по заданию.
Аудиторное занятие 2. (ОЛ1)
Домашнее задание.
1.Проверка д.з. Работа с текстом 10А.
1.Подготовиться к контрольному мероприятию
2.Повторение конструкции ‘ there + сказуемое’ упр.2
по материалам занятий 1-4.
стр.195
2.Подготовить сообщение по теме «Лазеры.
3.Упр-я на стр.201-202 (выборочно).
Другие новейшие технологии».
Домашнее задание.
3.Упр.5 стр.205.
1.Упр.11,12 стр.200
Аудиторное занятие 5. (ОЛ1)
2.Подготовиться к контролю лексики урока
10.
Рубежный контроль 1
1.Письменная работа по модулю 10 (40 мин.)
Аудиторное занятие 3. (ОЛ1)
2.Мини-конференция по теме урока. «Лазеры».
1.Проверка д.з.
3.Введение грамматики. Сложное
4
3.Ознакомительное чтение доп.текста 11С.
Беседа по тексту.
дополнение. Упр.1стр.214.
Домашнее задание.
1.Упр.3, 4 А стр.215
Домашнее задание.
2.Упражнения и тексты по усмотрению
преподавателя.
Дополнительные тексты на стр.274 (по выбору
студента). Подготовить сообщение по
выбранному тексту.
МОДУЛЬ 11
Аудиторное занятие 6. (ОЛ1)
Аудиторное занятие 9. (ОЛ1)
1.Проверка д.з.
1.Проверка д.з.
2.Введение грамматики. Сложное подлежащее.
2.Подготовка к беседе по теме урока:
«Сверхпроводимость». Упр.1,2 стр. 224-225
3.Упр.2,4 стр.215.
Работа с текстами из раздела дополнительных
заданий стр.230 -231.
4.Введение лексики урока 11. Упр.7,8,9 стр.217
5.Текст 11А 1 ч.- прослушивание, лексикограмматический разбор текста.
Домашнее задание.
1.Подготовиться к контрольному мероприятию по
модулю 11 (по пройденному материалу занятий
6-9).
Домашнее задание.
1.Текст 11А – прочитать, сделать лексикограмматический разбор текста до конца.
2.Подготовить сообщение по теме урока
«Сверхпроводимость» (по материалам
электронных ресурсов).
2.Повторить лексику ур.11
3.Упр.13 стр. 220.
Аудиторное занятие 10. (ОЛ1)
Аудиторное занятие 7. (ОЛ1)
Рубежный контроль 2
1.Проверка д.з. Опрос по тексту 11А. Упр. 10,11,12
стр.220.
1.Письменная работа по модулю 11 (40 мин).
2.Беседа «За круглым столом».
2.Закрепление грамматики.
Тема «Достижения в области
сверхпроводимости».
Упр.13,14 стр.220-221.
Домашнее задание.
Домашнее задание.
1.Ознакомительное чтение доп. текста 11Вответить на вопросы в задании к тексту.
Упражнения и тексты по усмотрению
преподавателя.
2.Упр.22 стр.224 (письменный перевод)
МОДУЛЬ 12
3.Подготовиться к контролю лексики урока 11.
Аудиторное занятие 11. (ОЛ1)
Аудиторное занятие 8. (ОЛ1)
1.Введение грамматики.
1.Проверка д.з.
2.Введение грамматики «Сослагательное
наклонение»
2.Контроль лексики урока 11.
5
Упр.1 стр.233.
Домашнее задание.
3.Введение лексики ур.12 упр.5,6,7 стр.235
1.Подготовиться к контролю лексики урока 12.
4.Текст 12А 1 ч.- прослушивание, лексикограмматический разбор текста.
3.Упр.9, 10 стр.239.
Аудиторное занятие 14. (ОЛ1)
Домашнее задание.
1.Проверка д.з. Контроль лексики урока 12.
1.Текст 12А 2 ч. – прочитать, сделать лексикограмматический разбор текста до конца.
2.Закрепление грамматики. Упр.8 стр.238.
3.Упр.11, 12 стр.240.
2.Подготовить вопросы для
Домашнее задание
обсуждения текста.
1.Подготовиться к контрольному мероприятию по
модулю 12 (по пройденному материалу занятий
11-14).
Аудиторное занятие 12. (ОЛ1)
1.Проверка д.з. Беседа по тексту 12А.
2.Подготовиться к мини конференции по теме
урока. «Исследования космоса в России и за
рубежом».
2.Особенности пассивного залога. Упр. 3 стр.235.
3.Упр.2,4 стр.234-235.
Домашнее задание.
Аудиторное занятие 15. (ОЛ1)
1.Письменная работа по модулю 12.(40 мин.).
1.Ознакомительное чтение текста 12В- знать
2.Мини-конференция по теме урока
содержание. Подготовить вопросы по
«Исследования космоса в России и за рубежом».
содержанию текста.
Домашнее задание.
Текст 12D - знать содержание текста.
2.Составить письменную
Аудиторное занятие 16. (ОЛ1)
1.Проверка д.з. Беседа по тексту 12D.
2.Просмотр и обсуждение видеофильма «МКС».
аннотацию по тексту на стр. 276.
Аудиторное занятие 13. (ОЛ1)
Домашнее задание.
Упражнения и тексты по усмотрению преподавателя.
Аудиторное занятие 17(ОЛ1)
1.Проверка д.з.
2.Ознакомительное чтение текста 12С.
Итоговое занятие.
Самостоятельная подготовка
1.Текущее домашнее задание включает в себя: выполнение грамматических упражнений к каждому
пройденному уроку, перевод предложений с иностранного языка на родной и наоборот, прослушивание
текстов А учебника в лабораториях устной речи или дома, переписав их на электронные носители в
специализированной лаборатории факультета «Лингвистика», ауд. 417л., работу с дополнительными
текстами В и С в каждом уроке учебника.
6
2.Подготовка к тесту 1 по материалу модуля 10 (ОЛ1): упражнения для самостоятельной работы стр.201203.
3.Подготовка к тесту 2 по материалу модуля 11 (ОЛ1): упражнения для самостоятельной работы стр.222224.
4.Подготовка к тесту 3 по материалу модуля 12 (ОЛ1): упражнения для самостоятельной работы стр.240242.
▼Вопросы для подготовки к рубежному контролю / зачёту
1.Условием получения отметки о сдаче 1, 2 и 3 рубежного контроля по модулям семестра является
сдача текущего материала на аудиторных занятиях путем устных ответов, выполнение поурочных
домашних заданий, участие в обсуждении устных тем уроков с получением баллов по балльнорейтинговой системе.
2.Условием получения зачёта является получение студентом от 20 до 33 баллов по 10-му,11-му и
12-му модулям при сумме не ниже 60. При низкой посещаемости занятий студенту могут быть
предложены задания по материалам модулей, к которым относятся пропущенные занятия.
▼Основная и дополнительная литература
Основная литература (ОЛ)
1. Орловская И.В., Самсонова Л.С., Скубриева А.И. Учебник английского языка для технических вузов.
М.: изд-во МГТУ им. Баумана, 2007 – 448 с.
Дополнительная литература (ДЛ))
1. R. Murphy. English Grammar in Use. Cambridge University Press, 2004 – 375 с.
2. Словари:
- Lingvo 8.0- 12.0
- Longman WordWise Dictionary
1.
2.
Рекомендуемые Интернет-сайты:
http://www.englishlearner.com
http://www.breakingnewsenglish.com
3.
http:// www.bbc.com.uk
7
АНГЛИЙСКИЙ ЯЗЫК
для студентов факультетов РЛМ, ИУ, ФН, ИБМ
Практические занятия
МОДУЛЬ 10
2.Контроль лексики урока 10
Аудиторное занятие 1. (ОЛ1)
3.Беседа по теме «Лазеры» упр.1,2 стр.203
1.Сообщение о плане работы в семестре.
4.Упр.21 стр.203-письм. Перевод на время
2.Введение грамматики. Инфинитив, формы
( 20 мин.)
и функции. Упр.1 стр.194.
Домашнее задание.
3.Введение лексики урока 10. Упр.5,6,7 стр.196.
1.Работа с текстом 10В - знать содержание.
4.Работа с текстом 10А 1 ч.- прослушивание,
лексико-грамматический разбор текста.
2.Подготовить вопросы для обсуждения
текста.
5.Каузативные глаголы упр.3.стр.195
Аудиторное занятие 4. (ОЛ1)
Домашнее задание
1.Проверка д.з. Работа с текстом 10В.
1.Текст 10А прочитать и разобрать до конца.
2.Ознакомительное чтение текстов 10С,10D.
2.Отвечать на вопросы упр.8 стр.199
Беседа по содержанию текстов.
3.Упр.9 стр.199.
3.Упр.2,3 стр.211-212 по заданию.
Аудиторное занятие 2. (ОЛ1)
Домашнее задание.
1.Проверка д.з. Работа с текстом 10А.
1.Подготовиться к контрольному мероприятию
2.Повторение конструкции ‘ there + сказуемое’ упр.2
по материалам занятий 1-4.
стр.195
2.Подготовить сообщение по теме «Лазеры.
3.Упр-я на стр.201-202 (выборочно).
Другие новейшие технологии».
Домашнее задание.
3.Упр.5 стр.205.
1.Упр.11,12 стр.200
Аудиторное занятие 5. (ОЛ1)
2.Подготовиться к контролю лексики урока
10.
Рубежный контроль 1
1.Письменная работа по модулю 10 (40 мин.)
Аудиторное занятие 3. (ОЛ1)
2.Мини-конференция по теме урока. «Лазеры».
1.Проверка д.з.
3.Введение грамматики. Сложное
8
3.Ознакомительное чтение доп.текста11С. Беседа
по тексту.
дополнение. Упр.1стр.214.
Домашнее задание.
1.Упр.3, 4 А стр.215
Домашнее задание.
2.Упражнения и тексты по усмотрению
преподавателя.
Дополнительные тексты на стр.274 (по выбору
студента). Подготовить сообщение по
выбранному тексту.
МОДУЛЬ 11
Аудиторное занятие 6. (ОЛ1)
Аудиторное занятие 9. (ОЛ1)
1.Проверка д.з.
1.Проверка д.з.
2.Введение грамматики Сложное подлежащее.
2.Подготовка к беседе по теме урока:
«Сверхпроводимость». Упр.1,2 стр. 224-225
3.Упр.2,4 стр.215.
Работа с текстами из раздела дополнительных
заданий стр.230 -231.
4.Введение лексики урока 11. Упр.7,8,9 стр.217
5.Текст 11А 1 ч.- прослушивание, лексикограмматический разбор текста.
Домашнее задание.
1.Подготовиться к контрольному мероприятию по
модулю 11 (по пройденному материалу занятий
6-9).
Домашнее задание.
1.Текст 11А – прочитать, сделать лексикограмматический разбор текста до конца.
2.Подготовить сообщение по теме урока
«Сверхпроводимость» (по материалам
электронных ресурсов).
2.Повторить лексику ур.11
3.Упр.13 стр. 220.
Аудиторное занятие 10. (ОЛ1)
Аудиторное занятие 7. (ОЛ1)
Рубежный контроль 2
1.Проверка д.з. Опрос по тексту 11А. Упр. 10,11,12
стр.220.
1.Письменная работа по модулю 11( 40 мин).
2.Беседа «За круглым столом».
2.Закрепление грамматики.
Тема «Достижения в области
сверхпроводимости».
Упр.13,14 стр.220-221.
Домашнее задание.
Домашнее задание.
1.Ознакомительное чтение доп. текста 11Вответить на вопросы в задании к тексту.
Упражнения и тексты по усмотрению
преподавателя.
2.Упр.22 стр.224 (письменный перевод)
МОДУЛЬ 12
3.Подготовиться к контролю лексики урока 11.
Аудиторное занятие 11. (ОЛ1)
Аудиторное занятие 8. (ОЛ1)
1.Проверка д.з.
1.Введение грамматики. 2.Введение грамматики
«Сослагательное наклонение»
2.Контроль лексики урока 11.
Упр.1 стр.233.
9
1.Подготовиться к контрольному мероприятию по
модулю 12 (по пройденному материалу занятий
11-14).
3.Введение лексики ур.12 упр.5,6,7 стр.235
4.Текст 12А 1 ч.- прослушивание, лексикограмматический разбор текста.
2.Подготовиться к мини конференции по теме
урока. «Исследования космоса в России и за
рубежом».
Домашнее задание.
1.Текст 12А 2 ч. – прочитать, сделать лексикограмматический разбор текста до конца.
Аудиторное занятие 15. (ОЛ1)
1.Письменная работа по модулю 12.(40 мин.).
2.Подготовить вопросы для
2.Мини-конференция по теме урока
«Исследования космоса в России и за рубежом».
обсуждения текста.
Домашнее задание.
Текст 12D - знать содержание текста.
Аудиторное занятие 12. (ОЛ1)
Аудиторное занятие 16. (ОЛ1)
1.Проверка д.з. Беседа по тексту 12D.
2.Просмотр и обсуждение видеофильма «МКС».
1.Проверка д.з. Беседа по тексту 12А.
2.Особенности пассивного залога. Упр. 3 стр.235.
Домашнее задание.
Упражнения и тексты по усмотрению преподавателя.
Аудиторное занятие 17(ОЛ1)
3.Упр.2,4 стр.234-235.
Домашнее задание.
Итоговое занятие.
1.Ознакомительное чтение текста 12В- знать
содержание. Подготовить вопросы по
содержанию текста.
2.Составить письменную
аннотацию по тексту на стр. 276.
Аудиторное занятие 13. (ОЛ1)
1.Проверка д.з.
2.Ознакомительное чтение текста 12С.
Домашнее задание.
1.Подготовиться к контролю лексики урока 12.
3.Упр.9,10 стр.239.
Аудиторное занятие 14. (ОЛ1)
1.Проверка д.з. Контроль лексики урока 12.
2.Закрепление грамматики. Упр.8 стр.238.
3.Упр.11, 12 стр.240.
Домашнее задание
10
Самостоятельная подготовка
1.Текущее домашнее задание включает в себя: выполнение грамматических упражнений к каждому
пройденному уроку, перевод предложений с иностранного языка на родной и наоборот,
прослушивание текстов А учебника в лабораториях устной речи или дома, переписав их на электронные
носители в специализированной лаборатории факультета «Лингвистика», ауд. 417л., работу с
дополнительными текстами В и С в каждом уроке учебника.
2.Подготовка к тесту 1 по материалу модуля 10 (ОЛ1): упражнения для самостоятельной работы стр.201203.
3.Подготовка к тесту 2 по материалу модуля 11 (ОЛ1): упражнения для самостоятельной работы стр.222224.
4.Подготовка к тесту 3 по материалу модуля 12 (ОЛ1): упражнения для самостоятельной работы стр.240242.
▼Вопросы для подготовки к рубежному контролю / зачёту
1.Условием получения отметки о сдаче 1, 2 и 3 рубежного контроля по модулям семестра
является сдача текущего материала на аудиторных занятиях путем устных ответов, выполнение
поурочных домашних заданий, участие в обсуждении устных тем уроков с получением баллов
по балльно-рейтинговой системе.
2.Условием получения зачёта является получение студентом от 20 до 33 баллов по 10-му,11-му
и 12-му модулям при сумме не ниже 60. При низкой посещаемости занятий студенту могут
быть предложены задания по материалам модулей, к которым относятся пропущенные
занятия.
▼Основная и дополнительная литература
Основная литература (ОЛ)
2. Орловская И.В., Самсонова Л.С., Скубриева А.И. Учебник английского языка для технических вузов.
М.: изд-во МГТУ им. Баумана, 2007 – 448 с.
Дополнительная литература (ДЛ))
1. R. Murphy. English Grammar in Use. Cambridge University Press, 2004 – 375 с.
2. Словари:
- Lingvo 8.0- 12.0
- Longman WordWise Dictionary
Рекомендуемые Интернет-сайты:
4.
5.
http://www.englishlearner.com
http://www.breakingnewsenglish.com
6.
http:// www.bbc.com.uk
11
НЕМЕЦКИЙ ЯЗЫК
для студентов всех факультетов
АУДИТОРНЫЕ ЗАНЯТИЯ
МОДУЛЬ 1: Основы машиностроения. (ОЛ-1)
Занятие 1. Текст 12А, стр.192-193, стр.197 упр.7; стр. 195-196, упр. 2А, В
Занятие 2. Текст 12С; стр.195 упр.1А и 1В; стр.196 упр.3.
Занятие 3. Текст 12В, стр.203 задания 2А и 2В к тексту 12В. Стр.196 упр.4.
Занятие 4. Текст 12D. Введение устных тем: “Лаборатория металловедения”, “Микроскоп”.
Задания к тексту 12D (работа в лингафонном кабинете). Стр.200 упр.13.
Занятие 5. Контрольная работа. (45-50 мин)
Требования к контрольной работе - знание грамматики текстов 12А;12В, 12С и знание активной
лексики (около 40 лексических единиц).
Грамматические темы: обособленные причастные обороты; распространенное определение;
употребление указательного местоимения для замены существительного; разделительный
генетив.
МОДУЛЬ 2: Основы электротехники. Свехпроводимость. (ОЛ-1)
Занятие 6. Текст 13А; стр. 212-213, упр. 1, 2, 3, 4, 5
Занятие 7. Текст 13В; стр.213 упр.6, 8А.
Занятие 8. Текст 13С; стр.213 упр.7, стр.214 упр.9, 10.
Занятие 9. Повторение пройденного лексического и грамматического материала урока 13.
Обмен информацией по самостоятельному внеаудиторному чтению
Занятие 11. Контрольная работа. (45-50 мин), текст 14А - изучающее чтение
Требования к контрольной работе - знание грамматики текстов 13А, 13В, 13С и знание
активной лексики (около 60 лексических единиц).
Грамматические темы: конъюнктив I; конъюнктив II; употребление претеритальных форм;
кондиционалис I.
МОДУЛЬ 3: Экономика производства. (ОЛ-1)
Занятие 11. Тексту 14А; стр.226-227 упр.2, стр.227 упр.3.
Занятие 12. Текст 14С. Стр.230 упр.14 письменный перевод с русского на немецкий язык под
руководством преподавателя.
Занятие 13. Текст 14В, стр.232 задания к тексту 1, 2.
Занятие 14. Текст 14D, стр.234-235, задание к тексту
Занятие 15. Контрольная работа. (45-50 мин), сообщение о работе в лаборатории
“Радиоэлектроника”
Требования к контрольной работе - знание грамматики текстов 14А, 14B, 14С и знание
активной лексики (около 40 лексических единиц).
Грамматические темы: распространенное определение; употребление указательного
местоимения для замены существительного, разделительный генитив, конъюнктив I,
конъюнктив II; употребление претеритальных форм; кондиционалис; конъюнктив в косвенной
речи.
12
Занятие 16-17. Проработка и сдача домашнего чтения “Neue superschwere Elemente”,
“Verzinken auf industriellem Niveau”, “Zink – die “graue Maus“ unter den Metallen “, “Keramik, der
neue Werkstoff im Motorenbau”; стр.269-270 “Teleskop mit 15-m-Spiegel”; стр.277-278
“Grundlagen des Satellitenempfangs”. (ОЛ-1)
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
МОДУЛЬ 1-3:
Текущее домашнее задание включает в себя: выполнение грамматических упражнений к
каждому пройденному уроку, перевод предложений с иностранного языка на родной и
наоборот, проработка текстов А учебника, работу с дополнительными текстами В и С в каждом
уроке учебника.
Подготовка к контрольной работе по материалу модуля (ОЛ-1).
ЗАЧЕТ
Условием получения отметки о сдаче 1, 2 и 3 модуля семестра является сдача текущего
материала на аудиторных занятиях путем устных ответов, выполнение поурочных домашних
заданий, участие в обсуждении устных тем уроков, положительным написанием контрольной
работы с получением баллов по балльно-рейтинговой системе.
ОСНОВНАЯ И ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Основная литература (ОЛ)
1. Богданова Н.Н., Семёнова. Е.Л. Учебник немецкого языка для технических вузов и
университетов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2009
ФРАНЦУЗСКИЙ ЯЗЫК
для студентов всех факультетов
АУДИТОРНЫЕ ЗАНЯТИЯ
МОДУЛЬ 1: Ecologie industrielle : la nature pour patron. (ОЛ-1)
Занятие 1. Текст 4A 1/2 ; упр.1, 2 стр.5, упр.3, 4 стр.6.
Занятие 2. Текст 4А 2/2; упр.5, 6, 7 стр.6-7.
Занятие 3. Текст 4А, подготовка к пересказу, упр. стр.4 стр.14.
Занятие 4. Текст 4А, пересказ, упр. 1, 2, 3 стр.12-13.
Занятие 5. Контрольная работа. (45-50 мин). Обмен информацией на материале текстов
самостоятельного, внеаудиторного чтения.
Требования к контрольной работе - знание грамматики текста 4А и знание активной лексики
(около 40 лексических единиц).
Грамматические темы: le Conditionnel présent, le Conditionnel passé. (Условное наклонение).
МОДУЛЬ 2: Maîtriser sa consommation d’énergie. (ОЛ-1)
Занятие 6. Текст 5А 1/2; упр.1,2,3 стр.19-20.
Занятие 7. Текст 5А 2/2; упр.4,5,6 стр.20-21.
Занятие 8. Текст 5А, подготовка к пересказу, упр.1,2,3 стр.26-27.
Занятие 9. Текст 5А, пересказ, упр.4,5 стр.27.
13
Занятие 11. Контрольная работа. (45-50 мин), обмен информацией на материале текстов
самостоятельного, внеаудиторного чтения
Требования к контрольной работе - знание грамматики текста 5А и знание активной лексики
(около 60 лексических единиц).
Грамматические темы: la Concordance des temps. (Согласование времен).
МОДУЛЬ 3: Que savons-nous de la Lune . (ОЛ-1)
Занятие 11. Текст 6А 1/2; упр.1,2 стр.32.
Занятие 12. Текст 6А 2/2; упр.3,4 стр.33-34.
Занятие 13. Текст 6А, подготовка к пересказу, упр.1,2,3 стр.38.
Занятие 14. Текст 6А , пересказ; упр.4,5 стр.39.
Занятие 15. Контрольная работа. (45-50 мин), обмен информацией на материале текстов
для самостоятельного внеаудиторного чтения.
Требования к контрольной работе - знание грамматики текстов 4А, 5А, 6А и знание активной
лексики (около 40 лексических единиц).
Грамматические темы: условное наклонение, согласование времен, сложное причастие
прошедшего времени, абсолютно-причастная конструкция, отглагольное прилагательное.
Занятие 16-17. Проработка и сдача домашнего чтения текстов 6В, 6С, 6D. (ОЛ-1)
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
МОДУЛЬ 1-3:
Текущее домашнее задание включает в себя: выполнение грамматических упражнений к
каждому пройденному уроку, перевод предложений с иностранного языка на родной и
наоборот, проработка текстов А учебника, работу с дополнительными текстами В, C и D в
каждом уроке учебника.
Подготовка к контрольной работе по материалу модуля (ОЛ-1).
ЗАЧЕТ
Условием получения отметки о сдаче 1, 2 и 3 модуля семестра является сдача текущего
материала на аудиторных занятиях путем устных ответов, выполнение поурочных домашних
заданий, участие в обсуждении устных тем уроков, положительным написанием контрольной
работы с получением баллов по балльно-рейтинговой системе.
ОСНОВНАЯ И ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Основная литература (ОЛ)
С.А.Токарева, М.ФА.Фомина. Французский язык. Методические указания по чтению и
переводу научно-технической литературы для студентов второго курса (IV семестр). Часть
2.- М.: Изд-во МГТУ им.Н.Э.Баумана, 2012.
14
РУССКИЙ ЯЗЫК ДЕЛОВОГО ОБЩЕНИЯ
Дисциплина состоит из 3-х учебных модулей.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Примечание
1.
Упражнения
1-4
4
2.
Домашние задания текущие
1-4
3
3.
Аттестация по модулю
4
1
РК – 1 / 2-я нед.
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
4.
Упражнения
5-12
8
5.
Домашние задания текущие
5-12
7
6.
Аттестация по модулю
12
1
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
7.
Упражнения
13-17
5
8.
Домашние задания текущие
13-16
4
9.
Аттестация по модулю
17
1
Примечание
Модуль 1. Речевая коммуникация и вербальная культура специалиста
Семинары
Занятие 1. Цели и задачи курса как базовой
дисциплины в подготовке специалистов инженерноэкономического профиля. Коммуникативно-речевая
компетенция специалиста. Природа и механизмы
речемыслительной деятельности. Функции языка,
формы и типы речевого общения, русский речевой и
невербальный этикет. Теория речевой коммуникации:
виды речевой деятельности, модели, задачи.
Диагностика стартового уровня культуры речи.
ОЛ-1, 4, 5; ДЛ-6; ЭР-9, 11.
Занятие 2. Культура речи: аспекты и критерии.
Нормативная
база
современного
русского
15
литературного
языка.
Орфоэпические,
морфологические, лексические, синтаксические и
стилистические нормы: анализ трудных случаев
произношения, формообразования, согласования.
Тренировочные упражнения по употреблению
языковых и речевых норм, закреплению навыков
нормативной устной и письменной коммуникации.
ОЛ-1, 4, 5; ДЛ-6; ЭР-9, 11.
Модуль 2. Официально-деловой стиль речи и культура делового общения
Семинары
Занятие 3. Национальный язык и его разновидности.
Функционально-стилевая дифференциация речи.
Стили речи: назначение, сфера употребления,
конструктивные
и
языковые
особенности.
Официально-деловой стиль: сфера функционирования,
подстили, жанры. Письменная деловая коммуникация
и основы документоведения.
ГОСТ на ведение
деловой
документации.
Логические
основы
содержания деловых бумаг. Общие правила
оформления документов, состав реквизитов.
Тренировочные упражнения по закреплению
навыков нормативной деловой коммуникации.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Занятие 4. Документы личного характера:
назначение, сфера употребления. Жанры частных
деловых бумаг: заявление, объяснительная записка,
автобиография, резюме, характеристика, доверенность,
расписка.
Содержательно-композиционные
и
языковые особенности личных документов.
Логико-смысловое редактирование текстов частных
деловых бумаг, их составление в разных жанрах.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Занятие 5. Документы служебного характера:
назначение, сфера употребления. Основные виды и
жанры служебных деловых бумаг: организационнораспорядительные (приказ, распоряжение, устав,
договор) и информационно-справочные (докладная и
служебная записки, акт, протокол, отчет, справка,
деловое письмо). Содержательно-композиционные и
языковые особенности служебных документов.
Логико-смысловое
редактирование
текстов
служебных документов, их составление.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Занятие 6. Устная деловая коммуникация: сферы,
ситуации,
жанры,
конструктивно-языковая
специфика. Деловая беседа, её структурные
особенности, правила подготовки и проведения.
Собеседование как вид деловой беседы. Телефонный
разговор.
Основные
стратегии
и
тактики,
риторические
приемы
гармонизации
устного
делового общения.
Презентации
и
ролевые
(деловые)
игры:
моделирование ситуаций делового общения.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Модуль 3. Культура научной и научно-деловой коммуникации
Семинары
Занятие 7. Научный стиль речи: назначение, сфера
функционирования, конструктивные и лингвистические
особенности, подстили, жанры. Научный текст и его
организация. Первичные и вторичные научные
тексты. Вторичные научные тексты как виды
аналитической обработки информации. План,
тезисы, конспект, аннотация, рецензия, реферат:
структурные и языковые особенности.
Логико-смысловое и языковое редактирование
научного текста, составление разножанровых
вторичных текстов.
ОЛ-3, 4, 5; ДЛ-6; ЭР-9, 11.
Занятие 8. Первичные научные тексты как виды
представления
результатов
исследовательской
деятельности. Структура и композиция научной
работы. Жанры первичных научных текстов. Приемы
цитирования.
Оформление
справочнобиблиографического аппарата научной работы.
Составление
первичных
научных
текстов.
Закрепление навыков оформления текстового
материала работы, ссылок и библиографического
описания информационных источников.
ОЛ-3, 4, 5; ДЛ-6; ЭР-9, 11.
Занятие 9. Зачет по курсу.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала занятий, изучении литературных
(основных и дополнительных) и электронных источников, в выполнении домашних заданий, подготовке к текущим и
рубежным контрольным работам, к ответам на теоретические вопросы и к выполнению практических заданий
зачетной работы по курсу.
16
Контрольные мероприятия и сроки их проведения
1. РК «Диагностический тест по русскому языку и культуре речи».
Срок проведения – 1 / 2-я неделя.
2. Контроль по модулю «Речевая коммуникация и вербальная культура специалиста».
Срок проведения – 3 / 4-я неделя.
3. ДЗ №1 «Культура деловой речи».
Срок выдачи 9 / 10- неделя, срок сдачи – 11/ 12-я неделя.
4. Контроль по модулю «Официально-деловой стиль речи и культура делового общения».
Срок проведения – 12-я неделя.
5. ДЗ №2 «Культура научной речи».
Срок выдачи 13 / 14-я неделя, срок сдачи – 15 / 16-я неделя.
6. Контроль по модулю «Культура научной и научно-деловой коммуникации».
Срок проведения – 16-я неделя.
7. Зачет по курсу.
Срок проведения – 17-я неделя.
Зачет
Условием получения зачета является положительная аттестация по трем модулям курса, суммирующая
результаты текущей успеваемости на аудиторных занятиях, выполнения проверочных и рубежных работ, домашних
заданий, а также оценку личных качеств студента по балльно-рейтинговой системе контроля знаний.
Литература
Основная литература (ОЛ)
1. Жилина О.А., Романова Н.Н. Русский язык и культура речи. Ч. 1. Основы культуры речи: Учебное пособие. – М.:
Изд-во МГТУ им. Н.Э.Баумана, 2008. – 152 с.
2. Жилина О.А., Романова Н.Н. Русский язык и культура речи. Ч. 2. Культура деловой речи: Учебное пособие. – М.:
Изд-во МГТУ им. Н.Э.Баумана, 2007. – 108 с.
3. Жилина О.А., Романова Н.Н. Русский язык и культура речи. Ч. 3. Культура научной речи: Учебное пособие. – М.:
Изд-во МГТУ им. Н.Э.Баумана, 2009. – 75 с.
4. Скорикова Т.П. Практикум по «Русскому языку и культуре речи»: Учебное пособие. – М.: Изд-во МГТУ им.
Н.Э.Баумана, 2013.
5. Романова Н.Н., Скорикова Т.П. Рабочая тетрадь: Учебное пособие. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2013.
Дополнительная литература (ДЛ)
6. Боженкова Р.К. Русский язык и культура речи: Учебник. – М.: Флинта: Наука, 2011. – 608 с.
7. Хазагеров Г.Г., Корнилова Е.Е. Риторика для делового человека: Учебное пособие. – М.: Флинта: Московский
психолого-социальный институт, 2001. – 136 с.
Методические пособия (МЛ)
8. Романова Н.Н. Методические указания к изучению дисциплины «Русский язык и культура речи». Ч. 1. Культура
деловой речи. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 47 с.
Электронные ресурсы (ЭР)
9. Скорикова Т.П. Русский язык и культура речи: методические рекомендации к изучению курса лекций для студентов
МГТУ им. Н.Э. Баумана всех факультетов и специальностей. – ФГУП НТЦ «Информрегистр». Депозитарий
электронных изданий, рег. свид-во № 18802 от 22.03.2010 (электронное издание). – 74 с.
URL:http// fl.bmstu.ru/index.php/component/docman/doc_download/116----.html
10. Яковлева Е.А. Основы деловой коммуникации: Учебное пособие для студентов МГТУ им. Н.Э.Баумана по
дисциплине «Русский язык и культура речи». – ФГБОУ ВПО «Московский государственный технический
университет им. Н.Э.Баумана», 2010 (электронное издание). – 3 п.л.
11. Конспект лекций, справочные материалы // сайт каф. Л-1 факультета «Лингвистика».
17
ФИЗИКА
для всех студентов
▼ Аудиторные занятия
1. Лекции
ящике.
Понятие
о
вырождении
энергетических
уровней.
Одномерный
потенциальный порог и барьер. Туннельный
эффект.
Сканирующий
туннельный
микроскоп. Гармонический осциллятор.
МОДУЛЬ 5:
Элементы квантовой механики.
Лекции 1-2. Квантовые свойства излучения.
Гипотеза Планка, дискретный характер
испускания и поглощения электромагнитного
излучения веществом. Квантовое объяснение
законов теплового излучения. Корпускулярноволновой дуализм света. Фотоны. Фотоэффект
и эффект Комптона.
ОЛ-1 §4.1-4.5. ОЛ-3 §4.6, 4.9, 4.10. ОЛ-4 §26,
27, 29. ДЛ-3 §4.3-4.5. ДЛ-6 §1.11, 1.12. ДЛ-7
§152-154, 156, 158. ДЛ-9 §4.1-4.4.
Лекции 7. Измерение физических величин в
квантовой механике. Основные постулаты
квантовой механики. Операторы координаты,
импульса, момента импульса, потенциальной
и кинетической энергии. Гамильтониан
квантовой системы как оператор полной
энергии. Вероятностный характер результатов
измерений
в
квантовой
механике.
Вычисление средних значений физических
величин в квантовых системах.
ОЛ-1 §1.1-1.5. ОЛ-3 §1.1-1.7,2.2,2.4. ОЛ-4 §1,2.
ОЛ-5 §1-3. ДЛ-3 §1.1-1.5. ДЛ-7 § 80-84, 86-89.
ДЛ-9 §1.1-1.3.
Лекции 3-4. Волновые свойства микрочастиц.
Гипотеза де Бройля. Дифракция микрочастиц.
Принцип неопределенности Гейзенберга.
Задание состояния микрочастицы. Волновая
функция, ее статистический смысл и условия,
которым она должна удовлетворять. Принцип
суперпозиции квантовых состояний. Общее
уравнение
Шредингера.
Уравнение
Шредингера для стационарных состояний.
ОЛ-1 §3.4-3.7. ОЛ-4 §17-19. ДЛ-2 §18, 27. ДЛ-3
§5.1, 5.2. ДЛ-6 §2.1-2.4.
Лекции 8. Квантовая теория атома. Ядерная
модель атома Резерфорда-Бора. Постулаты Н.
Бора. Стационарное уравнение Шредингера
для атома водорода. Волновые функции и
квантовые числа. Спин электрона. Спектр
атома водорода. Правила отбора для
квантовых чисел. Ширина спектральных
линий.
ОЛ-1 §2.1-2.4, 3.1-3.3, 4.1. ОЛ-3 §4.1-4.5, 4.8.
ОЛ-4 §8, 9, 16.ДЛ-2 §28-30. ДЛ-3 §3.1-4.2. ДЛ-6
§1.9, 1.10, 2.5-2.9. ДЛ-7 §140-145, 147, 148. ДЛ9 §2.1-2.3.
Лекции 5-6. Стационарные задачи квантовой
механики. Частица в потенциальной яме с
бесконечно высокими стенками. Частица в
трехмерном прямоугольном потенциальном
ОЛ-1 §5.1-5.4. ОЛ-3 §5.1-5.3. ОЛ-4 §30. ДЛ-3
§6.1. ДЛ-6 §3.1-3.4. ДЛ-8 §2.4.
18
Тему “Механический и магнитный моменты
атома”
студенты
прорабатывают
самостоятельно. При этом рассматривают
следующие вопросы: Опыт Штерна и Герлаха.
Орбитальный, спиновой и полный угловые
моменты. Спин-орбитальное взаимодействие.
Атом во внешнем магнитном поле. Эффект
Зеемана.
Энергия Ферми. Вырожденный электронный
газ, температура вырождения. Распределение
Бозе-Эйнштейна. Фотоны и фононы.
ОЛ-1 §6.2-6.5. ОЛ-3 §7.1, 7.2, 8.1. ДЛ-4 §4.1-4.4.
ДЛ-5 §39.4-39.8. ДЛ-9 §5.1, 5.2.
Тему “Эмиссия электронов из металла”
студенты прорабатывают самостоятельно. При
этом рассматривают следующие вопросы:
Работа выхода электрона из металла.
Термоэлектронная
эмиссия,
формула
Ричардсона-Дэшмана.
Эффект
Шоттки.
Холодная (автоэлектронная) эмиссия.
ОЛ-1 §5.5, 5.6. ОЛ-3 §5.4-5.7. ОЛ-4 §15, 34, 45,
46. ДЛ-3 §6.3, 7.1, 7.2.
Лекция 9. Спонтанное и индуцированное
излучение. Коэффициенты “A” и “B”
Эйнштейна. Активные среды с инверсной
заселенностью
энергетических
уровней.
Оптические
квантовые
генераторы.
Особенности лазерного излучения. Основные
типы лазеров, их применение.
ОЛ-1 §6.6. ОЛ-3 §9.1, 9.2. ОЛ-5 §29. ДЛ-9 §6.16.4.
Лекция 12. Зонная теория твердых тел.
Электроны в периодическом поле кристалла.
Образование
энергетических
зон
для
электронов в кристалле. Зонная структура в
металлах, полупроводниках и диэлектриках.
Проводимость металлов. Сверхпроводимость.
ОЛ-1 §5.7. ОЛ-3 §5.15, 5.16. ДЛ-4 §6.1. ДЛ-5
§38.1, 38.2.
МОДУЛЬ 6:
ОЛ-2 §4.1-4.4. ОЛ-3 §8.2, 8.4, 8.5. ОЛ-4 §65, 66.
ДЛ-5 §40.1-40.3. ДЛ-9 §7.1-7.6.
Квантовая статистика, физика твердого тела,
физика атомного ядра и элементарных
частиц.
Тему “Энергетический спектр электронов в
кристалле”
студенты
прорабатывают
самостоятельно. При этом рассматривают
следующие вопросы: Модель Кронига-Пенни.
Приближение сильной связи. Модель почти
свободных электронов. Динамика электронов
в кристаллической решетке. Эффективная
масса электрона.
Лекция
10. Квантовые системы из
одинаковых
частиц.
Принцип
тождественности одинаковых микрочастиц.
Симметричные
и
антисимметричные
состояния
(волновые
функции)
тождественных микрочастиц. Бозоны и
фермионы. Принцип Паули. Периодическая
система элементов.
ОЛ-2 §4.1. ДЛ-9 §7.1-7.7.
Лекция 13. Собственная и примесная
проводимость полупроводников. Уровень
Ферми
в
чистых
и
примесных
полупроводниках.
Температурная
зависимость проводимости полупроводников.
Фотопроводимость
полупроводников.
Процессы генерации и рекомбинации
ОЛ-1 §6.1. ОЛ-5 §46-47.
Лекция
11.
Квантовые
статистические
распределения.
Плотность
квантовых
состояний. Распределение Ферми-Дирака.
Функция распределения частиц по энергиям.
19
носителей
заряда.
полупроводниках.
Эффект
Холла
в
ОЛ-1 §7.4. ОЛ-3 §11.1, 11.4, 11.8-11.11. ОЛ-6
§104-110. ДЛ-3 §9.1-9.7.
ОЛ-2 §4.4. ОЛ-3 §8.6. ДЛ-4 §40.5, 40.6. ДЛ-8
§8.1-8.4.
Тему “Взаимодействие ядерных излучений с
веществом”
студенты
прорабатывают
самостоятельно. При этом рассматривают
следующие
вопросы:
Детектирование
различных излучений. Понятие о дозиметрии
и защите.
Лекция
14.
Контактные
явления
в
полупроводниках.
Р-n
–
переход.
Распределение электронов и дырок в р-n –
переходе. Ток основных и неосновных
носителей
через
р-n
–
переход.
Вольтамперная
характеристика
р-n
–
перехода. Выпрямляющие свойства р-n –
перехода.
ОЛ-3 §11.2. ОЛ-6 §79-83. ДЛ-5 §41.6.
Лекция 18(резервная). Квантовые объекты
нанотехнологий. Квантовые ямы, квантовые
нити,
квантовые
точки,
углеродные
нанотрубки.
Их
структура,
свойства,
перспективы практического применения.
Сканирующие зондовые микроскопы: СТМ,
АСМ, ОМБП. Принцип работы и разрешающая
способность.
ОЛ-2 §4.5. ОЛ-3 §9.5. ОЛ-4 §69. ДЛ-8 §8.7.
Лекция 15. Структура атомного ядра.
Характеристики ядра: заряд, масса, энергия
связи, спин и магнитный момент. Свойства и
обменный характер ядерных сил. Деление
тяжелых
ядер
и
цепные
реакции.
Термоядерный синтез.
ОЛ-1 Приложение.
ОЛ-1 §7.1. ОЛ-3 §10.1-10.4. ОЛ-6 §87-95, 98.
ДЛ-3 §8.1-8.3.
2. Семинары
МОДУЛЬ 5:
Лекция
16.
Радиоактивность.
Закон
радиоактивного
распада.
Активность.
Естественная
и
искусственная
радиоактивность.
Виды
радиоактивных
излучений.
Эффект
Мессбауэра.
Радиоактивные ряды, закон сложного
распада.
Источники
радиоактивных
излучений. Радиоизотопный анализ.
Занятие 1. Квантовые свойства света.
Ауд.: ОЛ-7 зад. 6.235, 6.240, 5.19, 5.35. МП-3а.
Дома: ОЛ-7 зад. 6.18, 5.34. ОЛ-8. МП-3а.
Занятие 2. Волновые свойства микрочастиц.
Ауд.: ОЛ-7 зад. 5.89, 5.99, 5.100, 5.108.
ОЛ-1 §7.2. ОЛ-3 §6.6, 10.5. ОЛ-6 §71-76. ДЛ-3
§8.4, 8.5.
Дома: ОЛ-7 зад. 5.87, 5.101. ОЛ-8. МП-1. МП-2.
МП-3б.
Лекция 17. Элементарные частицы. Их
основные
характеристики.
Типы
взаимодействий.
Классификация
частиц.
Лептоны и адроны. Кварковая структура
адронов. Симметрия и законы сохранения в
мире элементарных частиц.
Занятие 3. Движение
стационарных полях.
микрочастиц
в
Ауд.: ОЛ-7 зад. 5.131, 5.133, 5.137, 5.157.
Дома: ОЛ-7 зад. 5.125, 5.155. ОЛ-8. МП-1. МП2. МП-3в.
20
Занятие 4. Нахождение средних значений
физических величин.
3. Занятия в физической лаборатории
МОДУЛЬ 5:
Ауд.: ОЛ-7 зад. 5.149а, 5.150, 5.151, 5.152б.
Занятие 1. Лабораторные
квантовой физике.
Дома: ОЛ-7 зад. 5.149б, 5.152а. МП-2. МП-3г,
МП-4.
работы
по
работы
по
работы
по
работы
по
ОЛ-1, 2.
Занятие 5. Электрон в центральносимметричном поле. Квантование момента
импульса и магнитного момента электрона.
Занятие 2. Лабораторные
квантовой физике.
ОЛ-1, 2.
Ауд.: ОЛ-7 зад. 5.144, 5.153. ОЛ-8 зад. 47.9,
47.22, 47.24.
Занятие 3. Лабораторные
квантовой физике.
Дома: ОЛ-8 зад. 47.10, 47.23. МП-3д. ДЛ-10.
ОЛ-1, 2.
Занятие 4. Лабораторные
квантовой физике.
МОДУЛЬ 6:
ОЛ-1, 2.
Занятие 6. Распределение Ферми-Дирака.
Занятие 5. Рубежный контроль модуля 5.
Ауд.: ОЛ-7 зад. 6.274(а,б), 6.275, 6.277, 6.280.
Дома: ОЛ-7 зад. 6.276, 6.278. ОЛ-8. МП-1. МП3е.
МОДУЛЬ 6:
Занятие 7. Электропроводность металлов и
полупроводников.
Занятие 6. Лабораторные работы по
квантовой статистике, физике твердого тела и
ядерной физике.
Ауд.: ОЛ-7 зад. 6.288, 6.289, 6.292, 6.294.
ОЛ-1,2.
Дома: ОЛ-7 зад. 6.290, 6.293.
Занятие 7. Лабораторные работы по
квантовой статистике, физике твердого тела и
ядерной физике.
Занятие 8. Элементы физики атомного ядра и
элементарных частиц.
ОЛ-1,2.
Ауд.: ОЛ-7 зад. 5.250, 5.254, 5.323, 5.322.
Занятие 8. Рубежный контроль модуля 6.
Дома: ОЛ-7 зад. 5.251, 5.326. МП-3ж.
Занятие 5. Итоговое.
21
▼ Самостоятельная подготовка
МОДУЛЬ 5:
Проработка курса лекций, учебников проводится по темам лекций 1 - 10, семинаров 1 - 5 и
занятий в физической лаборатории 1 - 4.
Подготовка к рубежному контролю по темам лекций 1 - 10, материалам семинаров 1 - 5 и
занятий в физической лаборатории 1 - 4.
МОДУЛЬ 6:
Проработка курса лекций, учебников проводится по темам лекций 11 - 18, семинаров 6 - 8 и
занятий в физической лаборатории 6 - 7.
Подготовка к рубежному контролю по темам лекций 11 - 18, материалам семинаров 6 - 8 и
занятий в физической лаборатории 6 - 7.
▼ Домашнее задание
МОДУЛЬ 5:
Домашнее задание включает две задачи по материалам семинаров 1 – 4.
Выдача задач домашнего задания – 1-2 неделя.
Срок выполнения домашнего задания – 1-7 неделя.
МОДУЛЬ 6:
Домашнее задание включает две задачи по материалам семинаров 1 – 3.
22
Выдача задач домашнего задания – 9-10 неделя.
Срок выполнения домашнего задания – 9-16 неделя.
▼ Основная и дополнительная литература
Основная литература (ОЛ)
1. Мартинсон Л.К., Смирнов Е.В. Квантовая физика.– М.: Изд-во МГТУ им. Н.Э. Баумана,
2006, 2009. – 532 с.
2. Винтайкин Б.Е. Физика твердого тела. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006, 2007. –
360 с.
3. Савельев И.В. Курс общей физики. Кн. 5. – М.: Наука. Физматлит. 1998. – 368 с.
4. Матвеев А.Н. Атомная физика. – М.: Высшая школа, 1989. – 439 с.
1. Сивухин Д.В. Общий курс физики. Атомная и ядерная физика. Часть 1. – М.: Наука, 1986.
– 416 с.
2. Сивухин Д.В. Общий курс физики. Атомная и ядерная физика. Часть II. – М.: Наука, 1989.
– 416 c.
3. Иродов И.Е. Задачи по общей физике. – М.: Лаборатория Базовых Знаний, 2001 – 432 с.
4. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Высшая школа, 1988 – 527 с.
Дополнительная литература (ДЛ)
1. Блохинцев Д.И. Основы квантовой механики. – М.: Наука, 1976. – 664 с.
2. Иродов И.Е. Квантовая физика. Основные законы. – М.: Лаборатория Базовых Знаний,
2001. – 272 с.
3. Иродов И.Е. Физика макросистем. Основные законы. – М.: Лаборатория Базовых Знаний,
2001. – 200 с.
4. Калашников Н.П., Смондырев М.А. Основы физики. Т2. – М.: Дрофа, 2004. – 432 с.
5. Толмачев В.В., Федотов А.А., Федотова С.В. Основы квантовой механики: Учебное
пособие. – Москва-Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2005. – 240 с.
6. Шпольский Э.В. Атомная физика. т.1: Введение в атомную физику. – М.: Наука, 1984. – 552
с.
7. Шпольский Э.В. Атомная физика. т.2: Основы квантовой механики и строение электронной
оболочки атома. – М.: Наука, 1984. – 439 с.
8. Толмачев В.В., Скрипник Ф.В. Квазиклассическая и квантовая теория атома водорода. –
Москва-Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2008. – 132 с.
9. Толмачев В.В., Скрипник Ф.В. Физические основы электроники. – Москва-Ижевск: НИЦ
“Регулярная и хаотическая динамика”, Институт компьютерных исследований, 2009. – 464 с.
10. Иродов И.Е. Задачи по квантовой физике. – М.: Лаборатория Базовых Знаний, 2006. – 216
с.
Методические пособия, изданные в МГТУ (МП)
1. Мартинсон Л.К. Методические указания по решению задач по курсу общей физики,
разделы “Элементы квантовой механики”, “Физика твердого тела”. – М.: Изд-во МГТУ им.
Н.Э. Баумана, 1983. – 64 с.
23
2. Мартинсон Л.К., Смирнов Е.В. Методические указания к домашнему заданию по курсу
общей физики, раздел “Элементы квантовой механики” – М.: Изд-во МГТУ им. Н.Э. Баумана,
1999. – 35 с.
3. Мартинсон Л.К., Смирнов Е.В. Методические указания к решению задач по курсу общей
физики:
а) раздел “Квантовая природа излучения. Гипотеза Планка” – М.: Изд-во МГТУ им. Н.Э.
Баумана, 2001. – 24 с.;
б) раздел “Волновые свойства частиц. Гипотеза де Бройля”. – М.: Изд-во МГТУ им. Н.Э.
Баумана, 2002. – 20 с.;
в) раздел “Уравнение Шредингера. Стационарные задачи квантовой механики”. – М.: Издво МГТУ им. Н.Э. Баумана, 2002. – 32 с.;
г) раздел “Измерение физических величин в квантовых системах”. – М.: Изд-во МГТУ им.
Н.Э. Баумана, 2002. – 20 с.;
д) раздел “Квантовые свойства атомов”. – Изд-во МГТУ им. Н.Э. Баумана, 2003. – 36 с.;
е) раздел “Квантовая статистика Ферми-Дирака. Электронный газ”. – Изд-во МГТУ им. Н.Э.
Баумана, 2004. – 28 с.;
ж) раздел “Физика атомного ядра и элементарных частиц”. – Изд-во МГТУ им. Н.Э. Баумана,
2006. – 35 с.;
4. Константинов М.Ю. Методические указания к решению задач по курсу общей физики,
раздел “Принцип суперпозиции в квантовой механике”. – М.: Изд-во МГТУ им. Н.Э.
Баумана, 2009. – 24 с.
ФИЗИКА
для студентов УЦ 1, 2, 4, 8
1. Литература
Основная литература
1. Иродов И.Е. Механика. Основные законы / И.Е.Иродов – 9-е изд. – М.: БИНОМ. Лаборатория знаний,
2007. – 309с.: ил.
2.Савельев И.В. Курс общей физики: В 5-и кн.: Кн.1: Механика: Учеб. пособие для втузов/И.В.Савельев.М.:ООО"Издательство Астрель": ООО"Издательство АСТ", 2003. - 336 с.: ил
3. Иродов И.Е. Волновые процессы. Основные законы / И.Е.Иродов – 4-е изд. – М.: БИНОМ.
Лаборатория знаний, 2007. – 263 с.: ил.
24
4. Савельев И.В. Курс общей физики: В 5-и кн.: Кн.4:Волны. Оптика:
Учеб. пособие для
втузов/И.В.Савельев.-М.:ООО"Издательство Астрель": ООО"Издательство АСТ", 2003. - 256 с.: ил.
5. Глаголев К.В., Морозов А.Н. Физическая термодинамика: Учеб. пособие. – М.: изд-во МГТУ им.
Н.Э.Баумана,2004. – 272 с..: ил.(Физика в техническом университете/Под ред.Л.К.Мартинсона,
А.Н.Морозова).
6. Иродов И.Е. Физика макросистем. Основные законы / И.Е.Иродов – 3-е изд. стереотипное. – М.:
БИНОМ. Лаборатория знаний, 2006. – 207 с.: ил.
7. Савельев И.В. Курс общей физики: В 5-и кн.: Кн.3: Молекулярная физика и термодинамика: Учеб.
пособие для втузов/И.В.Савельев.-М.:ООО"Издательство Астрель": ООО"Издательство АСТ", 2003. – 208
с.: ил.
8. Лукин К.Б. Электронный курс лекций по физике для групп УЦ1, 2, 4, 8. Труды кафедры
"Реабилитация инвалидов" (ГУИМЦ) 2012 г.; 536 стр.; 49,4 МB; выдаётся студентам УЦ1, 2, 4, 8 в
начале каждого семестра на электронном носители информации (компакт-диск, флеш-карта).
Литература к практическим занятиям и по выполнению домашних заданий
9. Иродов И.Е. Задачи по общей физике. Учеб. пособие для вузов/И.Е. Иродов. - 5-е изд.,
испр. - М..: Лаборатория Базовых Знаний, 2003. - 432 с.: ил.
10.Чертов А.Г., Воробьев А.А. Задачник по физике: Учеб. пособие для втузов. - 7-е изд., перераб.
и доп.. - М.: Издательство Физико-математической литературы, 2003. - 640 с. - ISBN 5-94052-032-4
Литература по выполнению лабораторных работ
11. А.И. Савельева, И.Н.Фетисов. Обработка результатов измерений при проведении
физического эксперимента. Методические указания к лабораторной работе М -1 по курсу общей
физики. Под ред. А.Ф.Наумова. -М: Изд-во МГТУ.1990 г.
http://fn.bmstu.ru/1course/labs
12. Н.А.Гладков, М.А.Яковлев. Определение моментов инерции тел. Методические указания к
лабораторным работам М-4, М-5 по курсу общей физики. Под ред. А.И.Савельевой. Рецензент
к.т.н. доц. Л.И.Колобаев. -М: Изд-во МГТУ.1986.-16 с. ил.
http://fn.bmstu.ru/1course/labs
13. Л.С.Ермолаев, А.М.Кириллов, Л.А.Лунёва. Динамика вращательного движения. Методические
указания к лабораторной работе М-6 по курсу общей физики. Рецензент к.т.н., доц В.А.Пылаев. М: Изд-во МГТУ.1990.-24 с. ил.
http://fn.bmstu.ru/1course/labs
14. А.М.Кириллов, Л.Н.Климов, Романов А.С. Механические колебания и волны в газе.
Методические указания к лабораторной работе М-8 по курсу общей физики. Под ред.
Л.К.Мартинсона. -М: Изд-во МГТУ.1992 г.- 20 с., ил.
25
http://fn.bmstu.ru/1course/labs
15. А.М.Кириллов, Л.Н.Климов, А.В.Расторгуева. Изучение механических колебаний и волн.
Методические указания к лабораторным работам М - 9 по курсу общей физики. Рецензент к.т.н.,
доц В.А.Пылаев./Под ред. Л.С.Ермолаева, Л.К.Мартинсона. -М: Изд-во МГТУ.1983.-16 с. ил.
http://fn.bmstu.ru/1course/labs
16. А.Г.Андреев, В.И.Вишняков, Н.А.Гладков, А.М.Кириллов. Определение моментов инерции
тел. Методические указания к лабораторной работе М-10 по курсу общей физики. Под ред.
А.Ф.Наумова. -М: Изд-во МГТУ.2001 г.
http://fn.bmstu.ru/1course/labs
17. С.М.Вишнякова, В.И.Вишняков. Изучение политропических процессов в идеальном газе.
Методические указания к лабораторным работам Т - 3А и Т - 3Б по курсу общей физики. Под
ред. А.Ф.Наумова. -М:Изд-во МГТУ.2002 г. - 20 с., ил.
http://fn.bmstu.ru/1course/labs
2. Лекции
Модуль 1 «Физические основы механики. Колебания и волны. Релятивистская
механика»
Введение. Предмет физики. Физический объект, физическое явление, физический закон. Методы
физических исследований. Физика и современное естествознание. Системы единиц физических
величин. Структура и правила пользования электронным курсом лекций
Лекция 1. Механическое движение, системы отсчета. Кинематика материальной точки и абсолютно
твердого тела: уравнения; траектория; путь и перемещение; мгновенные скорость и ускорение при
прямолинейном и криволинейном движении; центр кривизны; угловая скорость, нормальное и
тангенциальное ускорения при вращательном движении. Классический закон сложения скоростей и
ускорений при поступательном движении подвижной системы отсчёта. Силы, масса в механической
системе. Механическая система и её центр масс. Импульс материальной точки и механической системы.
Динамика поступательного движения материальной точки и механической системы в инерциальных
системах отсчета
Л-1: 1.1 – 1.3; §§ Л-2: §§ 1.1 - 1.5, 2.1 - 2.6.; Л-8.
Лекция 2. Уравнение изменения импульса механической системы. Закон сохранения импульса и
однородность пространства. Момент силы относительно неподвижной точки и оси. Момент инерции
относительно неподвижной оси. Момент импульса материальной точки и механической системы
относительно неподвижной точки и оси. Уравнение моментов импульса механической системы. Закон
сохранения момента импульса механической системы и его связь с изотропностью пространства.
Л-1: §§2.1 – 2.5, 3.1 – 3.4, 5.1 – 5.4; Л-2: §§ 3.10, 3.12, 5.3,5.4; Л-8.
26
Лекция 3. Работа и кинетическая энергия механической системы. Консервативные силы и работа в
потенциальном поле механической системы. Связь между потенциальной энергией и силой в
механической системе. Потенциальная энергия тяготения. Потенциальная энергия упругой деформации.
Уравнение изменения механической энергии. Закон сохранения механической энергии и его связь с
однородностью времени.
Л-1: §§ 4.1 – 4.6; Л-2: §§ 3.1 - 3.7; Л-8.
Лекция 4. Дифференциальное уравнение гармонических колебаний и его решение. Кинематика
гармонических колебаний. Представление гармонических колебаний на векторной диаграмме.
Сложение гармонических колебаний одного направления равных и близких частот. Сложение взаимно
перпендикулярных гармонических колебаний равных и кратных частот.
Л-1: §§ 6.1, 6.2; Л-2: §§ 8.1, 8.4, 8.6- 8.8; Л-8.
Лекция 5. Динамика гармонических колебаний. Энергия и импульс гармонического осциллятора.
Фазовая траектория колебательной системы. Физический маятник. Квазиупругая сила колебательной
системы. Дифференциальное уравнение свободных затухающих колебаний и его решение. Декремент
и логарифмический декремент свободных затухающих колебаний. Добротность колебательной
системы. Дифференциальное уравнение вынужденных колебаний и его решение. Механический
резонанс колебательных процессов.
Л-1: §§ 6.3, 6.4; Л-2: §§ 8.5, 8.9 - 8.11; Л-8.
Лекция 6. Виды механических волн. Основы акустики. Элементы физиологической акустики.
Уравнение синусоидальной бегущей плоской и сферической волн, длина волны, фазовая скорость.
Звуковые волны в газах. Волновое уравнение распространения акустических волн в линейной
однородной изотропной непоглощающей упругой среде: фазовая скорость распространения звука.
Волновое уравнение, фазовая скорость распространения продольных упругих волн в стержнях.
Волновое уравнение, фазовая скорость распространения поперечных волн в гибком шнуре. Давление
звука, интенсивность звуковой волны. Объемная плотность энергии упругих
волн. Вектор Умова вектор плотности потока энергии упругих волн. Когерентные волны в упругой среде. Интерференция
этих волн. Стоячая волна в непоглощающей упругой среде: уравнение смещений частиц упругой среды
относительно положений равновесия; расчёт координат узлов и пучностей; уравнения скорости
смещений и относительной деформации частиц упругой среды относительно положений равновесия.
Л-3: §§ 1.1 - 1.6; Л-4: 1.1-1.10; Л-8.
Лекция 7. Преобразования Галилея. Инвариантность уравнений механики относительно
преобразований Галилея. Специальная теория относительности. Постулаты Эйнштейна.
Преобразования Лоренца. Кинематические следствия из преобразований Лоренца.
Релятивистский закон сложения скоростей. Интервал между двумя событиями в
релятивистской механике.
Л-1: §§ 7.1 -7.5; Л-2: §§ 6.1 - 6.4; Л-8.
Лекция 8. Элементы релятивистской динамики: основное уравнение релятивистской динамики,
кинетическая энергия релятивистской частицы. Взаимосвязь массы и полной энергии релятивистской
частицы. Связь между импульсом и полной энергией релятивистской частицы. Система
27
невзаимодействующих релятивистских частиц: энергия и импульс; столкновение двух релятивистских
частиц; распад релятивистской частицы.
Л-1: §§ 8.1 - 8.5; Л-2: §§ 6.5 - 6.10; Л-8.
Модуль 2 «Физическая термодинамика»
Лекция 9. Статистический и термодинамический методы описания макроскопических тел.
Термодинамические равновесные и неравновесные состояния, обратимые и необратимые
термодинамические процессы. Внутренняя энергия и температура термодинамической системы.
Теплота и работа. Адиабатически изолированная термодинамическая система: опыт Джоуля. Первое
начало термодинамики в дифференциальном и интегральном виде. Работа термодинамической
системы в дифференциальном и интегральном виде. Уравнение Клапейрона – Менделеева состояния
идеального газа и изопроцессы. Идеальный газовый термометр. Основные положения молекулярно –
кинетической теории идеальных газов: зависимость давления от кинетической энергии молекул,
основное уравнение молекулярно – кинетической теории, средняя квадратичная скорость молекул
идеального газа.
Л-5: §§ 1.1 -1.5, 2.1, 2.2; Л-6: §§ 1.1 - 1.5; Л-7: §§ 1.3-1.5, 1.8,1.9; Л-8.
Лекция 10. Равномерное распределение энергии по степеням свободы молекул идеального
газа. Внутренняя энергия идеального газа. Эффективное сечение взаимодействий молекул газа. Длина
свободного пробега и средняя частота соударений молекул газа. Экспериментальное подтверждение
молекулярно – кинетической теории газов: опыты Штерна и Дюнуайе. Теплоемкость идеального газа
при постоянном объеме или давлении. Соотношение Майера. Закон Дюлонга и Пти. Адиабатический
процесс идеального газа: показатель адиабаты, уравнение Пуассона. Политропические процессы:
уравнение, показатель политропы и молярная теплоемкость при изобарическом, изотермическом,
адиабатическом и изохорическом процессе идеального газа.
Л-5: §§ 2.3, 2.4; Л-6: § 1.6; Л-7: §§ 2.2-2.5; Л-8.
Лекция 11. Работа идеального газа в политропическом, изобарическом, адиабатическом
и изотермическом процессах. Газ Ван – дер – Ваальса: уравнение, критические параметры.
Внутренняя энергия газа Ван – дер – Ваальса. Эффект Джоуля – Томсона. Тепловая машина: схема,
термодинамический цикл, КПД. Холодильная машина: схема, термодинамический цикл, холодильный
коэффициент. КПД термодинамического цикла Карно для идеального газа. Теоремы Карно.
Термодинамическая шкала температур. Приведенное количество тепла. Неравенство Клаузиуса для
необратимых тепловых процессов и равенство Клаузиуса для обратимых тепловых процессов.
Л-5: §§ 2.5- 2.7, 3.1 - 3.5; Л-6: § 1.7; Л-7: §§ 1.11-1.13, 3.1,3.2; Л-8.
Лекция 12. Термодинамическая энтропия для обратимого термодинамического процесса. Закон
возрастания энтропии для необратимого термодинамического процесса. Второе начало
термодинамики. Третье начало термодинамики: теорема Нернста. Статистическое обоснование второго
начала термодинамики: формула Больцмана для статистической энтропии. Основное неравенство и
28
основное уравнение термодинамики: зависимость энтропии идеального газа от его объёма и
температуры. Понятие о термодинамических потенциалах: внутренней энергии; энтальпии; свободной
энергии или потенциала Гельмгольца; потенциала Гиббса
Л-5: §§ 3.6 - 3.10; Л-6: §§ 3.1 – 3.6; Л7: §§ 3.3-3.5; Л-8.
Лекция13. Статистическое описание равновесных состояний термодинамических систем: одно -,
дву – и трехмерные функции распределения. Статистическое описание равновесных состояний
термодинамических систем: определение средних значений случайных величин. Распределение
Больцмана для идеального газа в однородном гравитационном поле: зависимость давления,
концентрации и потенциальной энергии молекул от высоты. Распределение Больцмана для частиц,
находящихся в поле центробежных сил. Принцип детального равновесия в системах, находящихся в
состоянии термодинамического равновесия.
Л-5: §§ 5.1, 5.2.; Л-6: §§ 2.1, 2.2; Л-7: §§ 2.8; Л-8.
Лекция14. Распределение Максвелла по абсолютным значениям скоростей: наиболее вероятная
и средняя скорости молекул идеального газа. Функция распределения по значениям кинетической
энергии поступательного движения молекул идеального газа. Экспериментальная проверка
распределения Максвелла по абсолютным значениям скоростей молекул газа (опыт Ламмерта).
Статистическое описание равновесного состояния термодинамических систем с помощью фазового
пространства (каноническое распределение Гиббса). Распределение молекул идеального газа по
координатам и скоростям (распределение Максвелла – Больцмана).
Л-5: §§5.3 - 5.6; Л-6: §§ 2.3, 2.4; Л-7: §§ 2.6,2.7; Л-8.
Лекция15. Случайные отклонения значений параметров в системах, находящихся в состоянии
термодинамического равновесия, от их средних значений (равновесные флуктуации). Явления переноса
в идеальных газах. Термодинамические потоки: определение и классификация. Тепловой поток:
уравнение и коэффициент теплопроводности. Поток импульса: уравнение и коэффициент вязкости.
Диффузионный поток: уравнение и коэффициент диффузии. Эффузия в разреженном идеальном газе.
Условие равновесия для разреженного идеального газа. Физический вакуум. Броуновское движение.
Производство энтропии в необратимых термодинамических процессах.
Л-5: §§ 6.1 - 6.3; Л-6: §§ 6.2, 6.3; Л-7: §§ 7.1- 7.7; Л-8.
Лекция 16. Агрегатные состояния вещества. Условия равновесия фаз: отношение масс вещества,
находящемся в равновесном двухфазном состоянии. Анализ равновесного двухфазного состояния
вещества с помощью термодинамического потенциала Гиббса. Фазовые переходы первого рода в
двухфазной термодинамической системе: уравнение Клапейрона - Клаузиуса. Диаграммы состояний при
фазовых переходах в термодинамической системе. Фазовые переходы второго рода в двухфазной
термодинамической системе. Критические явления при фазовых переходах в термодинамической
системе. Отличительные черты кристаллического состояния твёрдых тел. Классификация кристаллов
твёрдых тел. Физические типы кристаллических решёток твёрдых тел. Дефекты в кристаллах твёрдых
тел. Теплоёмкость кристаллов твёрдых тел.
Л-5: §§ 7.1, 2; 7.4-7.7; Л-6: §§ 5.2, 4; Л-7: §§ 4.1-4.5, 6.1-6.8; Л-8.
Лекция17. Основные представления о строении жидкостей. Поверхностное натяжение и
свободная поверхностная энергия. Равновесие смачивающей и несмачивающей капель жидкости на
29
поверхности твердого тела. Капиллярный эффект. Формула Лапласа для поверхностного натяжения,
дополнительное давление, создаваемое сферической поверхностью жидкости. Анализ равновесного
состояния границы раздела между фазами вещества с помощью термодинамического потенциала
Гельмгольца. Анализ равновесного состояния границы раздела жидкость - газ с помощью
термодинамического потенциала Гельмгольца. Применение термодинамического потенциала
Гельмгольца для определения температурной зависимости коэффициента поверхностного натяжения
жидкости.
Л-5: § 7.3; Л-6: § 5.3; Л-7: §§ 5.1-5.5; Л-8.
3. Практические занятия
Модуль 1 «Физические основы механики. Колебания и волны. Релятивистская
механика»
Занятие 1. Кинематика. Динамика материальной точки и поступательного движения тела.
Законы сохранения импульса и энергии.
Ауд.: Л-10 №№ 1- 15; 1- 58; 1-108; 1-115; 1-131; 1-141; 1 -151; 1-170.
Дома: тематические задачи Л-10 №№1.54, 1.187, 1.190; индивидуально две задачи
Л-10 №№1. 1-1.218.
Занятие 2. Динамика вращательного движения твёрдого тела. Законы сохранения момента
импульса и энергии.
Ауд.: Л-10 №№ 1 -199;1 -220; 1 -248; 1 -271; 1 -305; 1 -322 ; 1 -336; 1 -339.
Дома: тематические задачи Л-10 №№ 1. 219; 1.321; 1.332; индивидуально две задачи
Л-10 №№1. 171 - 1.339.
Занятие 3. Гармонические колебания. Гармонический осциллятор. Свободные затухающие
колебания. Вынужденные колебания.
Ауд.: Л-10 №№ 3. 18; 3. 37; 3. 47; 3. 65; 3. 70; 3. 85; 3. 98; 3. 101.
Дома: тематические задачи Л-10 №№ 3. 34; 3. 89; 3.104; индивидуально две задачи
Л-10 №№3. 1 - 3. 110.
Занятие 4. Плоская бегущая синусоидальная и сферическая волны. Звуковые волны в газах,
продольные и поперечные упругие волны. Когерентные волны. Стоячая волна.
Ауд.: Л-10 №№ 3.187; 3.199; 3.212; 3.214; 3.222; 3. 226; 3. 228; 3. 230.
30
Дома: тематические задачи Л-10 №№ 3.181; 3.195; 3. 225; индивидуально две задачи
Л-10 №№ 3.177 - 3. 231.
Занятие 5. Преобразования Лоренца. Кинематические следствия из преобразований Лоренца.
Релятивистский закон сложения скоростей. Элементы релятивистской динамики.
Ауд.: Л-10 №№ 1.403; 1.413 ;1.416; 1.421; 1.425; 1.428 ;1.438; 1.446 .
Дома: тематические задачи Л-10 №№ 1.405; 1.418; 1.422; индивидуально две задачи
Л-10 №№ 1.396 - 1.445.
Модуль 2 «Физическая термодинамика»
Занятие 6. Первое начало термодинамики. Уравнение состояния идеального газа
изопроцессы. Теплоемкость идеального газа. Адиабатический процесс. Политропические процессы.
и
Газ Ван – дер – Ваальса.
Ауд.: Л-10 №№ 6.9; 6.14; 6.21; 6. 35; 6. 40; 6. 45; 6. 60 ; 6. 61.
.
Дома: тематические задачиЛ-10 №№ 6.20; 6. 41; 6. 62; индивидуально две задачи Л-10
№№ 6. 1 - 6. 60.
Занятие 7. Тепловые и холодильные машины. Термодинамическая энтропия. Распределение
Больцмана и Максвелла для идеального газа.
Ауд.: Л-10 №№ 6.73; 6.90 ; 6.107; 6.116; 6.141; 6.151; 6.172; 6.186.
Дома: Л-10 №№ 6.87; 6. 91; 6.163; индивидуально две задачи
Л-10 №№ 6. 66 - 6. 190.
Занятие 8. Явления переноса. Термодинамические потоки. Агрегатные состояния вещества.
Условия равновесия фаз. Поверхностное натяжение и свободная поверхностная энергия. Формула
Лапласа для поверхностного натяжения. Дополнительное давление, создаваемое поверхностью
жидкости.
Ауд.: Л-10 №№ 6.192; 6.204; 6.219; 6.308; 6.325; 6.332; 6.333; 6. 361.
Дома: Л-10 №№ 6.191; 6.316; 6.354; индивидуально две задачи
Л-10 №№ 6.192 - 6. 227; 6. 295 - 6. 362.
Предлагаемые номера задач надо рассматривать как рекомендуемые.
31
После каждого четырёхчасового семинара группе выдаются условия и ответы трёх тематических
задач, общих для всех студентов этой группы, а также каждому студенту выдаются условия и ответы
двух задач, которые они выполняют индивидуально.
Таким образом, для выполнения задания по прошедшему семинару у каждого студента в
общей тетради к началу следующего семинара должно быть оформлено решение пяти задач:
трёх тематических и двух индивидуальных.
4. Лабораторные работы
Четырехчасовые лабораторные работы выполняются в лабораториях кафедры один раз в две недели
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Дисциплина состоит из 2-х учебных модулей и зачета.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-4
8
Упражнения
1-9
10
Домашние задания текущие
1-9
10
Контроль по модулю №1
10
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
5-14
25
Упражнения
11-15
8
Домашние задания текущие
10-15
10
Контроль по модулю №2
16
4
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
32
Примечание
Модуль 1: Простейшая задача вариационного исчисления и
её некоторые обобщения
Лекции
Лекция 1. Предмет, содержание и особенности
курса. Структура курса, его значение и место в
подготовке инженера. Некоторые классические
задачи вариационного исчисления.
ОЛ-1, п. 1.1; ОЛ-5, часть II, Введение.
Уравнения Эйлера. Частные случаи интегрируемости
уравнения Эйлера в квадратурах. Решение задачи
Бернулли о брахистохроне.
ОЛ-1, п. 2.1; ОЛ-5, гл. 6, §2; МП-1, п. 1.2.
Лекция 4. Постановка вариационных задач с
фиксированными границами. Необходимое условие
экстремума функционалов, зависящих от нескольких
функций и производных высших порядков.
Уравнение
Эйлера-Пуассона.
Уравнение
Остроградского в задаче поиска экстремалей
функционалов от функций многих переменных.
ОЛ-1, пп. 2.2–2.4; ОЛ-5, гл. 6, §§3–5; МП-1, пп. 2.1 –
2.3.
Лекция 2 Функционалы в линейных нормированных
пространствах. Основные определения. Необходимое
условие экстремума функционала в линейном
нормированном пространстве. Основная лемма
вариационного исчисления.
ОЛ-1, пп. 1.2–1.4; ОЛ-5, гл. 6, §§1–2; МП-1, п. 1.1.
Лекция 3. Простейшая задача вариационного
исчисления. Необходимое условие экстремума в
простейшей задаче вариационного исчисления.
Упражнения
Занятие 1. Основные понятия вариационного
исчисления.
Ауд.: ДЛ-2 №№ 28, 36, 33, 36, 40, 50 (1 и 3), 57, 59.
Дома: ДЛ-2 №№ 27, 29, 34, 37, 39, 41, 50 (2 и 4), 58,
60.
ДЛ-2 №№ 71, 74, 76, 78, 83, 85, 87, 88.
Занятие
3-4
Вариационные
задачи
с
фиксированными границами.
Ауд.: ОЛ-4 №№ 16.400, 16. 402, 16.404, 16.406,
16.408, 16.410, 16.412, 16.414, 16.416, 16.418 или
ДЛ-2 №№. 99, 101, 103, 105, 107, 108, 110.
Дома: ОЛ-4 №№ 16.401, 16. 403, 16.405, 16.407,
16.409, 16.411, 16.413, 16.415, 16.417, 16.419 или
ДЛ-2 №№. 100, 102, 104,106, 111.
Занятие 2. Простейшая задача вариационного
исчисления.
Ауд.: ОЛ-4 №№ 16.376, 16.377, 16.379, 16.380, 16.382,
16.386, 16.387, 16.389, 16.391, 16.392 или
ДЛ-2 №№. 72, 73, 75, 77, 79, 81, 82, 84, 86.
Дома: ОЛ-4 №№ 16.375, 16.378, 16. 381, 16.383,
16.384, 16.388, 16.390, 16.393, 16.394, 16.395 или
Занятие 5. Рубежный контроль №1.
Модуль 2: Вариационные задачи с подвижными границами,
на условный экстремум и задача Больца
Лекции
Лекция 1. Постановка вариационных задач с
подвижными границами. Необходимое условие
экстремума в задачах с подвижными границами.
Условие трансверсальности.
ОЛ-1, пп. 3.1–3.2; ОЛ-5, гл. 7, § 1; МП-1, п. 3.1.
ОЛ-1, пп. 4.1–4.2; ОЛ-5, гл. 9, §§ 1,2; МП-1, пп. 4.1–
4.3.
Лекции 4. Изопериметрическая задача. Решение
задачи Дидоны.
ОЛ-1, пп. 4.3, 4.4; ОЛ-5, гл. 9, § 3; МП-1, п. 4.4.
Лекция 2. Экстремали с угловыми точками. Задачи
об отражении и преломлении экстремалей. Условия
отражения и преломления экстремалей. Условие
Вейерштрассе-Эрдмана.
ОЛ-1, п. 3.3; ОЛ-5, гл. 7, § 3; МП-1, п. 3.3.
Лекция 5. Постановка задачи Больца. Необходимое
условие экстремума в элементарной задаче Больца.
ОЛ-1, п. 4.6; МП-1, п. 5.1.
Лекции 6-7. Достаточные условия экстремума
функционала. Вторая вариация функционала.
Достаточные условия сильного и слабого экстремума
в простейшей задаче вариационного исчисления.
Лекции 3. Постановка вариационных задач на
условный
экстремум.
Необходимое
условие
экстремума
в
задачах
с
конечными
и
дифференциальными связями.
33
Инвариантный интеграл Гильберта. Условия Якоби,
Вейерштрасса и Лежандра.
Лекция 11. Прямые методы вариационного
исчисления. Вариационное уравнение. Построение
функционала по вариационному уравнению.
ОЛ-1, пп. 5.1–5.4; ОЛ-5, гл. 8, §§ 1,2; МП-1, п. 1.3.
ОЛ-1, пп. 9.1–9.3; ОЛ-2, § 36; ОЛ-5, гл. 10, §§ 1.
Лекция 8. Принцип Гамильтона. Аэродинамическая
задача Ньютона.
Лекция 12. Метод Ритца, Бубнова-Галеркина,
Канторовича, наименьших квадратов.
ОЛ-1, пп. 12–16; ДЛ-1, пп. 1.3, 1.4, 2.7; ОЛ-2, § 18.
ОЛ-1, пп. 10.1, 10.2; ДЛ-1, пп. 3.3, 3.4, 3.7, 3.8; ОЛ-5,
гл. 10, §§ 3,4.
Лекция 9-10. Вопросы устойчивости конструкций.
Вариационные принципы механики.
Лекция 13. Резерв.
ОЛ-1, пп. 17, 18.
Упражнения
Занятие 1. Вариационные задачи с подвижными
границами.
Ауд.: ОЛ-4 №№ 16.420, 16. 423, 16.424, 16.426,
16.428 или
ДЛ-2 №№ 172, 174, 182.
Дома: ОЛ-4 №№ 16.421, 16.422, 16.425, 16.427,
16.429 или
ДЛ-2 №№ .173, 175, 183.
Дома: ОЛ-4 №№ 16.440, 16.442, 16.443, 16.445.
Занятие 2. Вариационные задачи на условный
экстремум.
Ауд.: ОЛ-4 №№ 16.438, 16.439, 16.441, 16.444.
ДЛ-2 №№ 167, 168, 169,
Занятие 4. Рубежный контроль №2.
Занятие 3. Задача Больца. Достаточные условия
экстремума функционала.
Ауд.: ОЛ-4 №№ 16.430, 16.432, 16.434, 16.436 и
ДЛ-2 №№ 146, 148, 151, 152, 154, 156.
Дома: ОЛ-4 №№ 16.431, 16.433, 16.435, 16.437 и
ДЛ-2 №№ 147, 149, 150, 153, 155, 157.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий,
подготовке к рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Простейшая задача вариационного исчисления и её некоторые обобщения».
Срок выдачи 1 неделя, срок сдачи – 9 неделя
2. Контроль по модулю №1 (РК №1) «Простейшая задача вариационного исчисления и её некоторые
обобщения».
Срок проведения – 10 неделя.
Модуль 2.
1. ДЗ №2 «Вариационные задачи с подвижными границами, на условный экстремум и задача Больца».
Срок выдачи 10 неделя, срок сдачи – 15 неделя.
3. Контроль по модулю №2 (РК №2) «Вариационные задачи с подвижными границами, на условный экстремум
и задача Больца».
Срок проведения – 16 неделя.
Литература
1.
Основная литература (ОЛ)
Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариационное исчисление и оптимальное управление. –
М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. – 488с.
34
2.
3.
4.
5.
1.
2.
3.
4.
Гельфанд И.М., Фомин С.В. Вариационное исчисление. – М.: Физматгиз, 1961. – 228с.
Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. – М.: Наука, 1972. – 592с.
Сборник задач по математике для втузов. Ч.4 / Под редакцией А.В.Ефимова. – М.: Наука, 1990. – 304с.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. Учебник. Изд. 5-е. – М.:
Едиториал УРСС. 2002. – 320с.
Дополнительная литература (ДЛ)
Ванько В.И. Вариационные принципы и задачи математической физики: учеб. пособие / В.И. Ванько – М.:
Изд-во МГТУ им. Н.Э. Баумана, 2010. – 191с.
Краснов М.Л., Киселев А.И., Макаренко Г.И. Вариационное исчисление. Главная редакция физикоматематической литературы изд-ва «Наука», 1973.
Краснов М.Л., Киселев А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И. Вся высшая математика: Учебник.
Т.6. – М.: Едиториал УРСС, 2003. – 256с.
Михлин С.Г. Вариационные методы в математической физике. – М.: Наука, 1970. – 512с.
Методические пособия
1. Герман А.Д., Гришина Г.В. Вариационное исчисление. – М.: Изд-во МГТУ, 1992. 73с.
ТЕОРИЯ ФУНКЦИЙ КОМЛЕКСНОГО ПЕРЕМЕННОГО
Дисциплина состоит из 2-х учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-11
22
Упражнения
1-10
20
Домашние задания текущие
1-10
12
11
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
12-17
12
Упражнения
11-17
14
Домашние задания текущие
11-17
12
17
4
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 1: Теория функций комплексного переменного
35
Лекции
ОЛ3: лекции 4,5, ОЛ1: раздел 5.
Лекция 6 – Последовательности и ряды
комплексных
чисел.
Ряды
Тейлора.
Последовательности и ряды комплексных чисел.
Степенные ряды. Множество точек сходимости
степенного
ряда.
Голоморфность
суммы
степенного
ряда.
Разложение
голоморфной
функции в ряд Тейлора. Неравенства Коши.
Теорема Лиувилля.
ОЛ3: лекция 6, ОЛ1: раздел 6.
Лекция 7 – Ряды Лорана и особые точки.
Разложение голоморфной функции в ряд Лорана.
Сходимость рядов типа Лорана. Неравенства Коши
для коэффициентов ряда Лорана. Изолированные
особые
точки
однозначного
характера
–
определение. Описание устранимых особых точек.
Описание
полюсов.
Теорема
Сохоцкого.
Бесконечность как особая точка.
ОЛ3: лекция 7, ОЛ1: раздел 6, 7.
Лекции 8-9 – Теория вычетов. Вычеты. Теорема
Коши о вычетах. Вычеты в терминах ряда Лорана.
Формулы для вычисления вычетов. Вычет в точке
бесконечность. Теорема о полной сумме вычетов.
Вычет относительно области. Лемма Жордана.
Техника вычисления интегралов при помощи
вычетов.
ОЛ3: лекция 8, ОЛ1: раздел 8.
Лекции 10-11 – Принцип аргумента и его
следствия. Логарифмический вычет. Теорема о
логарифмическом вычете. Принцип аргумента.
Теорема Руше. Принцип максимума модуля.
Принцип
сохранения
области.
Критерии
однолистности и локальной обратимости. Теорема
Гурвица и ее следствия.
ОЛ4: лекции 13,14
Лекция
1
–
Комплексная
плоскость.
Комплексные числа. Комплексная плоскость,
расширенная комплексная плоскость, сфера
Римана, стереографическая проекция. Элементы
топологии комплексной плоскости. Пути и кривые.
Приращение (полярного) аргумента вдоль пути.
Индекс пути относительно точки и его свойства.
ОЛ3: лекция 1.
Лекция 2 – Дифференцируемость функций
комплексного переменного. Вещественная и
комплексная
дифференцируемость
функций
комплексного переменного. Условия Коши-Римана.
Свойства комплексной производной. Производная
по направлению. Голоморфные функции. Понятие
о конформном отображении.
ОЛ3: лекция 2, ОЛ1: раздел 4.
Лекция 3 – Основные элементарные функции
комплексного переменного и их свойства.
Дробно-линейные функции. Показательная и целая
степенная
функции.
Функция
Жуковского.
Тригонометрические функции. Логарифмическая
функция, обратная функция Жуковского, обратные
тригонометрические функции.
ОЛ3: лекция 3, ОЛ1: раздел 3.
Лекции 4-5 – Интегрирование функций
комплексного переменного. Теорема Коши и ее
следствия. Определение и свойства интеграла
вдоль пути. Ориентированная граница жордановой
области в комплексной плоскости. Лемма Гурса.
Теорема Коши для односвязной области.
Комплексная первообразная. Допустимые области
и их ориентированные границы. Интегральная
теорема Коши для допустимых областей.
Интегральная формула Коши. Теорема о среднем.
Формула Коши для производных и бесконечная
дифференцируемость
голоморфных
функций.
Теорема Мореры.
Упражнения
Дома: ДЛ7: 141-161 (неч.).
Занятия 5. Теорема Коши. Интегральная формула
Коши.
Ауд.: ОЛ5: 10.23 (чет.), 10.24, 10.31, 10.39
Дома: ОЛ5: 10.23 (неч.), 10.25, 10.32, 10.42
Занятие 6. Степенные ряды. Ряды Тейлора.
Ауд.: ОЛ5: 11.01 (чет.), 11.02 (чет.), 11.03 (чет.),
11.05, 11.07, 11.10 (чет.), 11.17 (чет.),11.29.
Дома: ОЛ5: 11.01 (неч.), 11.02 (неч.), 11.03 (неч.),
11.04, 11.06, 11.10 (неч.), 11.17 (неч.), 11.30.
Занятие 7. Ряды Лорана и особые точки.
Ауд.: ОЛ5: 19.01, 19.02, 19.07, 19.08, 20.09, 20.16,
20.21 – четные пункты.
Дома: ОЛ5: 19.01, 19.02, 19.07, 19.08, 20.09, 20.16,
20.21 – нечетные пункты.
Занятие 8. Вычеты. Вычисление контурных
интегралов.
Ауд.: ОЛ5: 21.09 (чет.), 21.10 (чет.), 21.11, 22.02
(чет.), 22.12.
Занятие 1. Комплексная плоскость
Ауд.: ОЛ5: 1.04 (чет.), 1.05, 1.06 (чет.), 1.09, 1.13
(чет.), 1.20 (чет.), 1.21 (чет.), 1.30, 1.38.
Дома: ОЛ5: 1.04 (неч.), 1.06 (неч.), 1.07, 1.13 (неч.),
1.20 (неч.), 1.21 (неч.), 1.33, 1.39, 1.68.
Занятие 2. Дифференцируемость функций
комплексного переменного.
Ауд.: ОЛ5: 8.01 (чет.), 8.03, 8.06, 8.08 (чет.), 8.10,
8.11, 8.12, 8.14, 8.30, ДЛ7: 114, 115, 118.
Дома: ОЛ5: 8.08 (неч.), 8.09, 8.15, 8.23, 8.31, ДЛ7:
116, 117.
Занятие 3. Дифференцируемость функций
комплексного переменного. Свойства
элементарных функций комплексного переменного.
Ауд.: ОЛ5: 8.34, 8.39, 8.41 (чет.), 8.51 (чет.), 9.06
(чет.), 9.09 (чет.), 9.10 (чет.), 1.56, 1.59.
Дома : ОЛ5: 33.02, 33.13, 1.58, 1.60, ДЛ7: 73-81.
Занятие 4. Пути и кривые. Интегрирование
функций комплексного переменного.
Ауд.: ДЛ7: 140-160 (чет.).
36
Дома: ОЛ5: 21.09 (неч.), 21.10 (неч.), 21.14, 21.15,
21.16, 22.02 (неч.), 22.13, 22.14.
Занятия 9. Вычисление вещественных интегралов
(в том числе несобственных) методами теории
вычетов.
Ауд.: ОЛ5: 28.01, 28.03 (чет.), 28.04, 28.05 (чет.),
28.08, 28.09 (чет.). 28.15 (чет.).
Дома: ОЛ5: 28.06, 28.07, 28.12, 28.13, 28.14, 28.15
(неч.).
Занятия 10. Рубежный контроль №1
Модуль 2: Конформные отображения и операционное исчисление
Лекции
Лапласа.
Теорема
о
существовании
и
аналитичности изображения, теорема обращения.
Основные свойства преобразования Лапласа.
ДЛ8: §§30-31.
Лекция 4 – Применение операционного
исчисления
к
решению
обыкновенных
дифференциальных уравнений. Теорема о
разложении. Решение ОДУ и систем ОДУ с
использованием преобразования Лапласа.
ДЛ8: §32.
Лекция 5 – Понятие об аналитическом
продолжении. Постановка задачи аналитического
продолжения. Теория Вейрштрасса. Аналитические
функции и их особые точки.
ОЛ3: лекции 10,11.
Лекция 6. Резерв.
Лекция
1
–
Понятие
о
конформных
отображениях.
Понятие
конформного
отображения.
Элементарные
функции
и
осуществляемые ими конформные отображения.
Обратный принцип соответствия границ при
конформном отображении. Лемма Шварца и
вычисление групп конформных автоморфизмов
основных областей.
ОЛ4: лекция 15, ОЛ1: раздел 10.
Лекция 2 – Основные теоремы теории
конформных отображений. Принцип симметрии
Римана-Шварца и его применение. Формулировка и
обсуждение теорема Римана и Каратеодори.
ОЛ4: лекции 17,18.
Лекция 3 – Преобразование Лапласа и его
основные свойства. Определение Преобразования
Упражнения
Ауд.: ОЛ5: 35.22, 35.23, 35.29, 36.06 – четные
пункты.
Дома: ОЛ5: 35.22, 35.23, 35.29, 36.06 – нечетные
пункты.
Занятие 4. Вычисление изображений и оригиналов.
Ауд.: ДЛ7: 524, 526, 529, 540, 546, 555, 560, 564,
566, 569, 573, 576, 580, 583, 613, 625, 627, 635.
Дома: ДЛ7: 528, 536, 542, 547, 563, 565, 570, 579,
620, 633, 634.
Занятие 5. Решение ОДУ и систем ОДУ методами
операционного исчисления.
Ауд.: ДЛ7: 654, 657, 665, 683, 718, 720, 758.
Дома: ДЛ7: 655, 666, 721, 760, 762.
Занятие 6. Рубежный контроль №2.
Занятия 1. Принцип аргумента. Теорема Руше.
Однолистные функции.
Ауд.: ОЛ5: 23.09 (чет.), 23.10, 23.11, 23.18, 32.01
(чет.), 32.02, 32.19
Дома: ОЛ5: 23.09 (неч.), 23.12, 23.13, 23.16, 23.20,
32.01 (неч.), 32.03, 32.09, 32.18
Занятие
2.
Конформные
отображения,
осуществляемые
основными
элементарными
функциями.
Ауд.: ОЛ5: 35.01, 35.04, 35.11, 35.12, 35.13, 35.18,
35.19, 35.20, 35.28 – четные пункты.
Дома: ОЛ5: 35.01, 35.04, 35.11, 35.12, 35.13, 35.18,
35.19, 35.20, 35.28 – нечетные пункты.
Занятие 3. Отыскание конформных отображений
данных областей.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке рекомендованной литературы, материала лекций,
выполнении домашних заданий и в подготовке к контрольным работам.
Контрольные мероприятия и сроки их проведения
Модуль 1
1. Домашнее задание №1. Срок выдачи – 1 неделя, срок сдачи – 9 неделя.
2. Рубежный контроль №1. Срок проведения – 10 неделя.
Модуль 2
1. Домашнее задание №2. Срок выдачи – 9 неделя, срок сдачи – 15 неделя.
2. Контрольная работа. Срок проведения – 12 неделя.
3. Рубежный контроль №2. Срок проведения – 16 неделя.
37
Литература
Основная литература
1. Морозова В.Д. Теория функций комплексного переменного. Выпуск X серии «Математика в техническом
университете». – М.: Издательство МГТУ, 2000. – 519 с.
2. Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. Выпуск XI серии
«Математика в техническом университете». М.: Издательство МГТУ, 1999. – 227 с.
3. Домрин А.В., Сергеев А.Г. Лекции по комплексному анализу. Часть I: Первое полугодие. – М.: МИАН, 2004. – 176 с.
4. Домрин А.В., Сергеев А.Г. Лекции по комплексному анализу. Часть II: Второе полугодие. – М.: МИАН, 2004. – 136 с.
5. Сборник задач по теории аналитических функций. Под ред. М.А. Евграфова. М.: Наука, 1969. – 386 с.
Дополнительная литература
6. Шабат Б.В. Введение в комплексный анализ. Часть I. СПб: Лань, 2004. – 336 с.
7. Краснов М.Л., Киселёв А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление.
Теория устойчивости. М: Наука, 1971. – 256 с.
8. Эйдерман В.Я. Основы теории функций комплексного переменного и операционного исчисления. М.: Физматлит,
2002. – 256 с.
КОМПЛЕКСНЫЙ АНАЛИЗ
Дисциплина состоит из 2-х учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-11
22
Упражнения
1-10
20
Домашние задания текущие
1-10
12
11
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
12-17
12
Упражнения
11-17
14
Домашние задания текущие
11-17
12
17
4
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 1: Теория функций комплексного переменного
Лекции
Лекция
1
Комплексные
расширенная комплексная плоскость, сфера
Римана, стереографическая проекция. Элементы
–
Комплексная
плоскость.
числа. Комплексная плоскость,
38
топологии комплексной плоскости. Пути и кривые.
Приращение (полярного) аргумента вдоль пути.
Индекс пути относительно точки и его свойства.
ОЛ3: лекция 1.
Лекция 2 – Дифференцируемость функций
комплексного переменного. Вещественная и
комплексная
дифференцируемость
функций
комплексного переменного. Условия Коши-Римана.
Свойства комплексной производной. Производная
по направлению. Голоморфные функции. Понятие
о конформном отображении.
ОЛ3: лекция 2, ОЛ1: раздел 4.
Лекция 3 – Основные элементарные функции
комплексного переменного и их свойства.
Дробно-линейные функции. Показательная и целая
степенная
функции.
Функция
Жуковского.
Тригонометрические функции. Логарифмическая
функция, обратная функция Жуковского, обратные
тригонометрические функции.
ОЛ3: лекция 3, ОЛ1: раздел 3.
Лекции 4-5 – Интегрирование функций
комплексного переменного. Теорема Коши и ее
следствия. Определение и свойства интеграла
вдоль пути. Ориентированная граница жордановой
области в комплексной плоскости. Лемма Гурса.
Теорема Коши для односвязной области.
Комплексная первообразная. Допустимые области
и их ориентированные границы. Интегральная
теорема Коши для допустимых областей.
Интегральная формула Коши. Теорема о среднем.
Формула Коши для производных и бесконечная
дифференцируемость
голоморфных
функций.
Теорема Мореры.
ОЛ3: лекции 4,5, ОЛ1: раздел 5.
Лекция 6 – Последовательности и ряды
комплексных
чисел.
Ряды
Тейлора.
Последовательности и ряды комплексных чисел.
Степенные ряды. Множество точек сходимости
степенного
ряда.
Голоморфность
суммы
степенного
ряда.
Разложение
голоморфной
функции в ряд Тейлора. Неравенства Коши.
Теорема Лиувилля.
ОЛ3: лекция 6, ОЛ1: раздел 6.
Лекция 7 – Ряды Лорана и особые точки.
Разложение голоморфной функции в ряд Лорана.
Сходимость рядов типа Лорана. Неравенства Коши
для коэффициентов ряда Лорана. Изолированные
особые
точки
однозначного
характера
–
определение. Описание устранимых особых точек.
Описание
полюсов.
Теорема
Сохоцкого.
Бесконечность как особая точка.
ОЛ3: лекция 7, ОЛ1: раздел 6, 7.
Лекции 8-9 – Теория вычетов. Вычеты. Теорема
Коши о вычетах. Вычеты в терминах ряда Лорана.
Формулы для вычисления вычетов. Вычет в точке
бесконечность. Теорема о полной сумме вычетов.
Вычет относительно области. Лемма Жордана.
Техника вычисления интегралов при помощи
вычетов.
ОЛ3: лекция 8, ОЛ1: раздел 8.
Лекции 10-11 – Принцип аргумента и его
следствия. Логарифмический вычет. Теорема о
логарифмическом вычете. Принцип аргумента.
Теорема Руше. Принцип максимума модуля.
Принцип
сохранения
области.
Критерии
однолистности и локальной обратимости. Теорема
Гурвица и ее следствия.
ОЛ4: лекции 13,14
Упражнения
Дома: ОЛ5: 10.23 (неч.), 10.25, 10.32, 10.42
Занятие 6. Степенные ряды. Ряды Тейлора.
Ауд.: ОЛ5: 11.01 (чет.), 11.02 (чет.), 11.03 (чет.),
11.05, 11.07, 11.10 (чет.), 11.17 (чет.),11.29.
Дома: ОЛ5: 11.01 (неч.), 11.02 (неч.), 11.03 (неч.),
11.04, 11.06, 11.10 (неч.), 11.17 (неч.), 11.30.
Занятие 7. Ряды Лорана и особые точки.
Ауд.: ОЛ5: 19.01, 19.02, 19.07, 19.08, 20.09, 20.16,
20.21 – четные пункты.
Дома: ОЛ5: 19.01, 19.02, 19.07, 19.08, 20.09, 20.16,
20.21 – нечетные пункты.
Занятие 8. Вычеты. Вычисление контурных
интегралов.
Ауд.: ОЛ5: 21.09 (чет.), 21.10 (чет.), 21.11, 22.02
(чет.), 22.12.
Дома: ОЛ5: 21.09 (неч.), 21.10 (неч.), 21.14, 21.15,
21.16, 22.02 (неч.), 22.13, 22.14.
Занятия 9. Вычисление вещественных интегралов
(в том числе несобственных) методами теории
вычетов.
Ауд.: ОЛ5: 28.01, 28.03 (чет.), 28.04, 28.05 (чет.),
28.08, 28.09 (чет.). 28.15 (чет.).
Дома: ОЛ5: 28.06, 28.07, 28.12, 28.13, 28.14, 28.15
(неч.).
Занятие 1. Комплексная плоскость
Ауд.: ОЛ5: 1.04 (чет.), 1.05, 1.06 (чет.), 1.09, 1.13
(чет.), 1.20 (чет.), 1.21 (чет.), 1.30, 1.38.
Дома: ОЛ5: 1.04 (неч.), 1.06 (неч.), 1.07, 1.13 (неч.),
1.20 (неч.), 1.21 (неч.), 1.33, 1.39, 1.68.
Занятие 2. Дифференцируемость функций
комплексного переменного.
Ауд.: ОЛ5: 8.01 (чет.), 8.03, 8.06, 8.08 (чет.), 8.10,
8.11, 8.12, 8.14, 8.30, ДЛ7: 114, 115, 118.
Дома: ОЛ5: 8.08 (неч.), 8.09, 8.15, 8.23, 8.31, ДЛ7:
116, 117.
Занятие 3. Дифференцируемость функций
комплексного переменного. Свойства
элементарных функций комплексного переменного.
Ауд.: ОЛ5: 8.34, 8.39, 8.41 (чет.), 8.51 (чет.), 9.06
(чет.), 9.09 (чет.), 9.10 (чет.), 1.56, 1.59.
Дома : ОЛ5: 33.02, 33.13, 1.58, 1.60, ДЛ7: 73-81.
Занятие 4. Пути и кривые. Интегрирование
функций комплексного переменного.
Ауд.: ДЛ7: 140-160 (чет.).
Дома: ДЛ7: 141-161 (неч.).
Занятия 5. Теорема Коши. Интегральная формула
Коши.
Ауд.: ОЛ5: 10.23 (чет.), 10.24, 10.31, 10.39
- 39 -
Занятия 10. Рубежный контроль №1
Модуль 2: Конформные отображения и операционное исчисление
Лекции
Лапласа.
Теорема
о
существовании
и
аналитичности изображения, теорема обращения.
Основные свойства преобразования Лапласа.
ДЛ8: §§30-31.
Лекция 4 – Применение операционного
исчисления
к
решению
обыкновенных
дифференциальных уравнений. Теорема о
разложении. Решение ОДУ и систем ОДУ с
использованием преобразования Лапласа.
ДЛ8: §32.
Лекция 5 – Понятие об аналитическом
продолжении. Постановка задачи аналитического
продолжения. Теория Вейрштрасса. Аналитические
функции и их особые точки.
ОЛ3: лекции 10,11.
Лекция 6. Резерв.
Лекция
1
–
Понятие
о
конформных
отображениях.
Понятие
конформного
отображения.
Элементарные
функции
и
осуществляемые ими конформные отображения.
Обратный принцип соответствия границ при
конформном отображении. Лемма Шварца и
вычисление групп конформных автоморфизмов
основных областей.
ОЛ4: лекция 15, ОЛ1: раздел 10.
Лекция 2 – Основные теоремы теории
конформных отображений. Принцип симметрии
Римана-Шварца и его применение. Формулировка и
обсуждение теорема Римана и Каратеодори.
ОЛ4: лекции 17,18.
Лекция 3 – Преобразование Лапласа и его
основные свойства. Определение Преобразования
Упражнения
Ауд.: ОЛ5: 35.22, 35.23, 35.29, 36.06 – четные
пункты.
Дома: ОЛ5: 35.22, 35.23, 35.29, 36.06 – нечетные
пункты.
Занятие 4. Вычисление изображений и оригиналов.
Ауд.: ДЛ7: 524, 526, 529, 540, 546, 555, 560, 564,
566, 569, 573, 576, 580, 583, 613, 625, 627, 635.
Дома: ДЛ7: 528, 536, 542, 547, 563, 565, 570, 579,
620, 633, 634.
Занятие 5. Решение ОДУ и систем ОДУ методами
операционного исчисления.
Ауд.: ДЛ7: 654, 657, 665, 683, 718, 720, 758.
Дома: ДЛ7: 655, 666, 721, 760, 762.
Занятие 6. Рубежный контроль №2.
Занятия 1. Принцип аргумента. Теорема Руше.
Однолистные функции.
Ауд.: ОЛ5: 23.09 (чет.), 23.10, 23.11, 23.18, 32.01
(чет.), 32.02, 32.19
Дома: ОЛ5: 23.09 (неч.), 23.12, 23.13, 23.16, 23.20,
32.01 (неч.), 32.03, 32.09, 32.18
Занятие
2.
Конформные
отображения,
осуществляемые
основными
элементарными
функциями.
Ауд.: ОЛ5: 35.01, 35.04, 35.11, 35.12, 35.13, 35.18,
35.19, 35.20, 35.28 – четные пункты.
Дома: ОЛ5: 35.01, 35.04, 35.11, 35.12, 35.13, 35.18,
35.19, 35.20, 35.28 – нечетные пункты.
Занятие 3. Отыскание конформных отображений
данных областей.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке рекомендованной литературы, материала лекций,
выполнении домашних заданий и в подготовке к контрольным работам.
Контрольные мероприятия и сроки их проведения
Модуль 1
3. Домашнее задание №1. Срок выдачи – 1 неделя, срок сдачи – 9 неделя.
4. Рубежный контроль №1. Срок проведения – 10 неделя.
Модуль 2
4. Домашнее задание №2. Срок выдачи – 9 неделя, срок сдачи – 15 неделя.
5. Контрольная работа. Срок проведения – 12 неделя.
6. Рубежный контроль №2. Срок проведения – 16 неделя.
Литература
Основная литература
40
1. Морозова В.Д. Теория функций комплексного переменного. Выпуск X серии «Математика в техническом
университете». – М.: Издательство МГТУ, 2000. – 519 с.
2. Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. Выпуск XI серии
«Математика в техническом университете». М.: Издательство МГТУ, 1999. – 227 с.
3. Домрин А.В., Сергеев А.Г. Лекции по комплексному анализу. Часть I: Первое полугодие. – М.: МИАН, 2004. – 176 с.
4. Домрин А.В., Сергеев А.Г. Лекции по комплексному анализу. Часть II: Второе полугодие. – М.: МИАН, 2004. – 136 с.
5. Сборник задач по теории аналитических функций. Под ред. М.А. Евграфова. М.: Наука, 1969. – 386 с.
Дополнительная литература
6. Шабат Б.В. Введение в комплексный анализ. Часть I. СПб: Лань, 2004. – 336 с.
7. Краснов М.Л., Киселёв А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория
устойчивости. М: Наука, 1971. – 256 с.
8. Эйдерман В.Я. Основы теории функций комплексного переменного и операционного исчисления. М.: Физматлит, 2002.
– 256 с.
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ И ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА
Дисциплина состоит из 2-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-7
14
Упражнения
1-8
16
Домашние задания текущие
1-8
10
Контроль по модулю №1
9
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
8-17
20
Упражнения
9-17
18
Домашние задания текущие
9-17
10
Контрольная работа
13
2
Контроль по модулю №2
17
4
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
41
Примечание
Модуль 1: Кривые и поверхности в пространстве
Лекции
Лекции 1 – 2. Гладкая кривая на плоскости и в
пространстве. Натуральная параметризация кривой.
Кривизна кривой. Репер Френе. Сопровождающий
трехгранник кривой. Формулы Френе. Кручение
кривой. Геометрический смысл кривизны и
кручения. Механический смысл формул Френе.
Вектор Дарбу. Вычисление кривизны и кручения
кривой, отнесенной к произвольному параметру.
Натуральные
уравнения
кривой.
Теорема
существования и единственности кривой с данными
кривизной и кручением.
ОЛ-3; ОЛ-1 гл.1, § 1 – 6; ДЛ-1 гл.4 § 35,36,39 –
41,44; ДЛ-7 гл.2, § 1 – 4, гл.3, § 2 – 5; ДЛ-6 ч.4, гл.1;
МП-1 § 11.
Лекции 3 – 4. Гладкая поверхность в пространстве.
Примеры.
Способы
задания
поверхностей.
Касательная плоскость и нормаль к поверхности.
Касательное пространство. Длина
кривой на
поверхности. Первая
квадратичная
форма
поверхности. Угол между кривыми на поверхности,
площадь поверхности. Внутренняя геометрия
поверхности. Изометричные поверхности. Теорема о
первых квадратичных
формах изометричных
поверхностей.
ОЛ-1 гл.2, § 1 – 3; ОЛ-3 8.1 – 8.3; ДЛ-1 гл.5 § 45 –
47; ДЛ-2 § 6 – 9; ДЛ-7 гл.4, гл.5, § 1, гл.6, § 1 – 3;
ДЛ-6 ч.4, гл.2, § 1 – 5,10,;ДЛ-4 гл.2, § 7; МП-1 § 12.
Лекция 5. Вторая квадратичная форма поверхности,
ее геометрический смысл. Классификация точек
поверхности.
Соприкасающийся
параболоид.
Кривизна кривой на поверхности. Нормальная
кривизна поверхности. Теорема Менье.
ОЛ-1 гл.2, § 4; ОЛ-3 8.4 – 8.6; ДЛ-1 гл.5, § 3, гл.7, §
1; ДЛ-2 § 10 – 11; ДЛ-7 гл.5 § 48 – 50; ДЛ-6 ч.4,
гл.2, § 6 – 7; ДЛ-4 гл.2, § 8; МП-1 § 12.
Лекция 6. Главные направления и главные кривизны
поверхности. Формула Эйлера. Линии кривизны.
Асимптотические линии. Гауссова и средняя
кривизны поверхности. Классификация точек
поверхности по знаку гауссовой кривизны.
Минимальные поверхности.
ОЛ-1 гл.2, § 4; ОЛ-3 8.7; ДЛ-1 гл.5 § 49,50,55 – 60;
ДЛ-2 § 12 – 13; ДЛ-7 гл.7, § 1 – 5; ДЛ-6 ч.4, гл.2, §
8,9; МП-1 § 12.
Лекция 7. Нормальная и геодезическая кривизна
кривой на поверхности. Геодезические линии на
поверхности.
Теорема
о
главной
нормали
геодезической.
Уравнение
геодезических.
Экстремальное свойство геодезических (без док-ва).
Основные уравнения теории поверхностей (обзор).
Деривационные формулы.
Теорема Гаусса.
Формулы
Петерсона-Майнарди-Кодацци
(без
вывода). Теорема Бонне о существовании и
единственности поверхности с заданными первой и
второй квадратичной формами (без доказательства).
ОЛ-1 гл.2, § 3 п.5, § 5, § 6, пп.1,2,5; ДЛ-1 гл.7 § 7690,93 гл.6 § 64,72; ДЛ-2 § 15 – 18; ДЛ-7 гл.7,8, гл.9,
§ 1 – 2,4; ДЛ-6 ч.4, гл.2, § 12-15; ОЛ-5 Д.8.1.
Упражнения
Занятия 1 – 2. Теория кривых.
ОЛ-3 §7; ДЛ-17 § 1 – 2, 7 – 9; ДЛ-18 § 4; ДЛ-5 § 2 –
4.
Занятия 3–4. Поверхности в пространстве. Первая
квадратичная форма поверхности.
ДЛ-17 § 10,11,13; ДЛ-18 § 5; ДЛ-5 § 7 – 8.
Занятие 5–6. Вторая квадратичная форма
поверхности. Главные направления и главные
кривизны поверхности. Гауссова и средняя кривизны
поверхности.
ДЛ-17 § 14,17; ДЛ-18 § 5; ДЛ-5 § 9.
Занятие 7. Линии кривизны. Асимптотические
линии. Минимальные поверхности. Геодезические
линии на поверхности.
ДЛ-18 § 5; ДЛ-18 § 5; ДЛ-5 § 10 – 11.
Занятие 8. Контроль по модулю 1 (РК №1).
42
Модуль 2: Риманова геометрия и тензорный анализ
Лекции
Лекция 8. Криволинейные системы координат в
области n-мерного пространства. Локальный базис
криволинейной системы координат. Длина кривой в
криволинейной системе координат. Функции gij , их
тензорными полями, их свойства. Симметричные и
кососимметричные
тензоры,
их
свойства.
Поливекторы и внешние формы. Внешнее
геометрический смысл и свойства. Вычисление углов
и объемов в криволинейной системе координат.
ОЛ-1 гл.3, § 6, пп.1 – 2, § 10, пп.1 – 2; ОЛ-2 гл.1, §
1,2, гл.3; ОЛ-5 1.1, 1.2;
ДЛ-4 гл.1, § 1 – 2.
Лекция 9. Риманова метрика (метрический тензор) в
области n-мерного пространства. Римановы и
псевдоримановы пространства. Длина кривой, угол
между кривыми, объем области в римановом
пространстве.
Примеры
римановых
и
псевдоримановых
пространств.
Пространство
Минковского.
ОЛ-1 гл.3, § 7, § 10, пп.1,2,5, гл.4, § 1,2 пп.1,2, § 3,
п.2; ОЛ-2 гл.1, § 2 – 4; ОЛ-5 1.3; ДЛ-4 гл.1, § 3.
Лекция 10. Гладкая k-мерная поверхность. Задача о
вычислении длины кривой на поверхности.
Индуцированная метрика на поверхности. Модели
геометрии Лобачевского.
ОЛ-2 гл.1, § 4; ОЛ-5 1.3.6; ДЛ-4 гл.1, § 3, гл.2, § 9 –
10.
Лекция 11. Тензоры как полилинейные функции.
ОЛ-1 гл.3, §5,6, пп.2 – 3, § 10, пп.3 – 4; ОЛ-2 гл.5, §
1 – 2; ОЛ-5 2.5 – 2.7; ДЛ-4 гл.3, § 16,17,19.
Лекция 14. Векторные поля. Производная по
направлению векторного поля, ее свойства.
Инвариантная форма записи векторного поля.
Коммутатор векторных полей, его свойства. Алгебра
Ли векторных полей. Базис модуля тензорных полей
в области евклидова пространства. Инвариантная
форма записи тензорного поля.
ОЛ-3 11.6 – 11.8; ДЛ-4 гл.3, § 23,24; ДЛ-10 гл.8, §
39; МП-2 § 5.
Лекция 15. Внешние дифференциальные формы.
Внешнее произведение дифференциальных форм.
Внешний дифференциал, его свойства. Градиент,
ротор и дивергенция как внешние дифференциалы в
Модуль
умножение, его свойства. Базис модуля
3
комплексе де Рама пространства R .
ДЛ-12 гл.7, Дополнение; ДЛ-13 гл.12, § 5, гл.15, §1.
Лекции 16 – 17. Ковариантное (инвариантное)
дифференцирование тензорных полей. Символы
Кристоффеля, их кинематический смысл. Закон
преобразования символов Кристоффеля. Теорема о
существовании
тензорной
операции
дифференцирования тензорных полей (без док-ва).
Дифференциальные операции векторного анализа в
криволинейных
координатах.
Ковариантное
дифференцирование вдоль кривой. Параллельный
перенос векторов. Геодезические. Уравнение
геодезических. Параллельный перенос векторов
вдоль геодезических.
ОЛ-1 гл.3, § 8,9 пп.1,2, гл.4, § 3 – 4; ОЛ-2 гл.5, § 3,4;
ОЛ-5 3.1 – 3.4; ДЛ-4 гл.4, § 28, 29.
qp  L  . Тензорное умножение. Тензорная
алгебра модуля. Базис модуля
 p  L .
qp  L  , координаты
(компоненты) тензора.
ОЛ-1 гл.3, § 5,6, пп.2 – 3, § 10, пп.3 – 4; ОЛ-2 гл.5, §
1 – 2; ОЛ-5 2.1 – 2.4;
ДЛ-4 гл.3, 16,17,19.
Лекции 12 – 13. Координатное определение тензора
и тензорного поля. Задание тензора (тензорного
поля) его компонентами в некоторой системе
координат.
Обратный
тензорный
признак.
Алгебраические операции над тензорами и
Упражнения
Занятие 9. Криволинейные системы координат.
ОЛ-5 1.1 – 1.2; ДЛ-18 § 2,3.
Занятие 10. Римановы метрики.
ОЛ-5 1.3; ДЛ-18 § 2,3.
Занятия 11 – 12. Тензоры и тензорные поля.
ОЛ-5 2.1 – 2.6; ДЛ-18.
Занятие 13. Контрольная работа.
Занятие 14. Векторные поля.
ДЛ-18 § 8; МП-2.
Занятие 15. Внешние дифференциальные формы.
ДЛ-18 §10; ДЛ-13; ОЛ-5 2.7.
Занятие 16. Ковариантное дифференцирование
тензорных полей.
ОЛ-5 3.1 - 3.4; ДЛ-18 § 9.
Занятие 17. Контроль по модулю (РК №2).
43
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнению текущих и
индивидуальных ДЗ, подготовке к контрольным мероприятиям.
Контрольные мероприятия и сроки их проведения
Модуль 1. Кривые и поверхности в пространстве
1. Домашнее задание №1 «Кривые и поверхности в пространстве»
Срок выдачи 1 неделя, срок
.
сдачи – 8 неделя
2. Контроль по модулю (РК № 1) «Кривые и поверхности в пространстве»
Срок проведения – 9 неделя
Модуль 2. Риманова геометрия и тензорный анализ
1. Домашнее задание №2 «Криволинейные системы координат»
Срок выдачи 8 неделя, срок сдачи – 15 неделя
2. Контрольная работа «Криволинейные системы координат»
Срок проведения – 13 неделя
3. Контроль по модулю (РК №2) «Риманова геометрия и тензорный анализ» Срок проведения – 17 неделя
Модуль 3. Экзамен
Литература
Основная литература (ОЛ)
1.
2.
3.
4.
5.
Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия: Первое знакомство. Изд.2-е. – М.: Едиториал УРСС,
2003. – 408 с.
Мищенко А.Ф., Фоменко А.Т. Курс дифференциальной геометрии и топологии. – М.: Изд-во «Факториалпресс», 2000. – 448 с.с
Хорькова Н.Г., Чередниченко А.В. Элементы дифференциальной геометрии и топологии. Кривые в
пространстве. – Изд-во МГТУ, 2007. – 48 с.
Канатников А.Н., Крищенко А.П., Четвериков В.Н. Дифференциальное исчисление функций многих
переменных. (Сер. Математика в техническом университете, вып. V) – М.: Изд-во МГТУ, 2000. – 456 с.
Хорькова Н.Г. Элементы дифференциальной геометрии и топологии. Риманова геометрия и тензорный анализ.
– Изд-во МГТУ, 2005. – 84 с.
Дополнительная литература (ДЛ)
1.
2.
3.
4.
5.
Рашевский П.К. Курс дифференциальной геометрии. Изд. 4–е.– М.:Едиториал УРСС, 2003.- 432 с.
Розендорн Э.Р. Задачи по дифференциальной геометрии. 3-е изд., испр. и доп. – М.: ФИЗМАТЛИТ, 2008 144
с.
Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения. Т.1. Изд-е 4-е,
исправленное и дополненное. – М.: Эдиториал УРСС, 1998. – 366 с.
Димитриенко Ю.И. Тензорное исчисление. – М.:Высшая школа, 2001. – 575 с.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1977. – 832 с.
Методические и учебные пособия (МП)
44
1.
2.
Дифференциальное исчисление функций многих переменных: Учебное пособие / Попов В.С., Пустовалова
Г.П., Хорькова Н.Г. и др.: под ред. Яковенко М.Г. – М.: Изд-во МГТУ, 1990. – 104 с.
Хорькова Н.Г., Четвериков В.Н. Элементы дифференциальной геометрии и топологии. Векторные поля на
многообразиях. Учебное пособие. – М.: Изд-во МГТУ, 1996. – 48 с.
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
для СМ3, 4, 6, 12
Дисциплина состоит из 3-х учебных модулей.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-5
10
Упражнения
1-7
14
Домашние задания текущие
1-7
6
Контроль по модулю №1
7
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
6-9
8
Упражнения
8-10
6
Домашние задания текущие
8-10
4
Контроль по модулю №2
11
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
10-17
16
Упражнения
11-17
14
Домашние задания текущие
11-17
10
Контроль по модулю №3
16
4
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
45
Примечание
Модуль 1:Ряды Фурье и функции комплексного переменного
Лекции
Лекция 1.Ортогональность тригонометрической
системы
функций
на
отрезке
.
Тригонометрические ряды Фурье и коэффициенты
Фурье. Теорема Дирихле (без док-ва). Разложение
функций в тригонометрические ряды Фурье на
отрезке
. Разложение в ряд Фурье четных и
нечетных функций.
точка. Задание кривых и областей на комплексной
плоскости. Функция комплексного переменного.
Понятие об элементарных функциях комплексного
переменного. Формулы Эйлера.
ОЛ-1 гл.1, гл.3 §3.1, ОЛ-8 гл.1 ч.1 §2,3, гл.2 §1, ОЛ-7
гл.1 §2-4, МП-2.
Лекция 4. Предел функции. Непрерывность
функции. Производная от функции комплексного
переменного. Условия Коши-Римана. Необходимые
и достаточные условия дифференцирования функции
комплексного переменного. Аналитичность функции
в точке и в области. Примеры.
ОЛ-2 3.1, 3.3, 3.6-3.9, ОЛ-3 гл.17, ОЛ-5 гл.12, ДЛ-6
гл.6, ДЛ-2 гл.14.
Лекция 2.Разложение функций в ряд Фурье на
произвольном отрезке длины 2l. Связь порядка
малости коэффициентов Фурье со свойствами
функций, разлагаемых в ряд Фурье. Разложение
функций по произвольной полной ортогональной
системе. Неравенство Бесселя и равенство
Парсеваля.
ОЛ-1 гл.2 §2.1, гл.3 §3.2, гл.4 §4.1-4.6, МП-1, МП-2.
ОЛ-2 3.1, 3.4, 3.5, 3.7, 3.8, ОЛ-3 гл.16,17, ОЛ-5 гл.12,
ДЛ-6 гл.5, гл.6, ДЛ-2 гл.14.
Лекция5. Геометрический смысл аргумента и модуля
производной. Понятие о конформном отображении.
Гармонические
функции
и
их
связь
с
аналитическими. Восстановление аналитической
функции по ее действительной или мнимой части.
Лекция 3.Комплексное переменное, комплексная
плоскость. Сфера Римана, бесконечно удаленная
ОЛ-1 гл.4 §4.7-4.9,ОЛ-8 гл.2 §2, гл.3 §1, ОЛ-7 гл.1 §4,
гл.6 §6, МП-2.
Упражнения
Занятие 1. Ряды Фурье.
ОЛ-10 гл.12: Ауд.: 480, 482, 484, 486, 488.
Дома: 481, 483, 485, 487.
или
ОЛ-11: Ауд.: 2672, 2673, 2677, 2697, 2698.
Дома: 2671, 2674, 2695, 2696.
Занятие 2.Неполные ряды Фурье.
ОЛ-10 гл.12: Ауд.: 493, 495, 497, 498.
Дома: 494, 499, 500.
или
ОЛ-11: Ауд.: 2683, 2684, 2687, 2689, 2702.
Дома: 2685, 2686, 2690, 2700.
Занятие 3. Действия над комплексными числами.
Кривые и области на комплексной плоскости.
Функции комплексного переменного.
МП-1, МП-2, ОЛ-6. Ауд.: 52, 53, 55, 57(а, б, г), 60(а,
в).
Дома: 54, 56, 58(в, д, е), 60(б, г).
или
МП-1, МП-2, ОЛ-10 гл.11 §1. Ауд.: 11.1, 3, 4, 7, 9, 10,
13, 20, 22.
Дома: 11.2, 5, 6, 8, 11, 12, 14, 21, 23.
Занятия 4-5.Функции комплексного переменного.
МП-1, МП-2, ОЛ-6. Ауд.: 62, 64, 67(а, в), 104(а, в),
114(а, в).
Дома: 63, 65, 67(б, д), 104(б, д), 114(б).
или
ОЛ-10 гл.11 § 1, 2. Ауд.: 11.27, 31, 32, 35, 37, 42, 43,
48, 51, 55, 56, 58, 59, 60, 63, 65, 67, 75, 77, 79, 83, 86,
87.
Дома: 11.28, 33, 34, 36, 38, 44,45, 49, 50, 53, 57, 61,
62, 64, 66, 76, 78, 81, 84, 90.
Занятие
6.Дифференцирование
функции
комплексного
переменного.
Определение
аналитической
функции
по
известной
действительной или мнимой части.
ОЛ-6. Ауд.: 104(а, в), 114(а, в).
Дома: 104(б, д), 114(б).
или
ОЛ-10 гл.11 § 1, 2. Ауд.: 11.113, 115, 116, 131, 132,
134, 136.
Дома: 11.112, 114, 117, 133, 135, 137.
Занятие 7.Контроль по модулю№1 (РК№1) «Ряды
Фурье и функции комплексного переменного».
Модуль 2:Комплексные степенные ряды
Лекции
Лекция 1.Интеграл от непрерывной функции
комплексного переменного, его свойства и
вычисление. Теорема Коши для односвязной и
многосвязной области. Независимость интеграла от
пути интегрирования. Формула Ньютона-Лейбница.
ОЛ-1 гл.5 §5.1-5.4, ОЛ-8 гл.2 §3,4, ОЛ-7 гл.1 §5, МП1, МП-2.
46
Лекция 2.Интегральная формула Коши. Формула
производной n-го порядка. Применение формул для
вычисления контурных интегралов.
Определение основных элементарных функций с
помощью степенных рядов.
ОЛ-1 гл.2, гл.3 §3.3-3.6, гл.6 §6.1-6.2, ОЛ-8 гл.4
§1,2,3, ОЛ-7 гл.2 §2, гл.4 §1, МП-1, МП-2.
ОЛ-1 гл.5 §5.5-5.7, ОЛ-8 гл.2 §5, ОЛ-7 гл.1 §6, МП-1,
МП-2.
Лекция 4. Теоремы о разложении аналитической
функции в ряды Тейлора иЛорана.
Лекция 3.Числовые и функциональные ряды с
комплексными членами. Абсолютная и условная
сходимости. Равномерная сходимость. Степенные
ряды. Теорема Абеля. Круг и радиус сходимости.
ОЛ-1 гл.6 §6.3-6.7, ОЛ-8 гл.4 §1,2,3, ОЛ-7 гл.2 §2,
гл.4 §1, МП-1, МП-2.
Упражнения
Занятие 1.Интегрирование функции комплексного
переменного. Вычисление контурных интегралов.
Интегральная формула Коши. Формула производной
n-го порядка.
ОЛ-6. Ауд.: 143, 147, 158, 174, 179, 212, 218, 264, 272.
Дома: 144, 149, 159,169, 180, 215, 265, 272, 275.
или
ОЛ-10 гл.11 §4. Ауд.: 11.231, 233, 235, 257, 259, 263,
265.
Дома: 11.232, 238, 258, 264, 268, 271.
Занятия 2-3.Степенные ряды. Разложение функций
в ряды Тейлора и Лорана.
ОЛ-10 гл.12 §3, 5. Ауд.: 12.165, 167, 171, 172, 176,
185, 190, 194, 201, 214, 216, 221, 227, 231, 237, 352,
358, 361, 368, 370.
Дома: 12.166, 168, 173, 177, 180, 191, 202, 215, 217,
225, 232, 238, 258, 264, 268, 271, 353, 354, 359, 360,
371, 373.
Модуль 3:Теория вычетов и операционное исчисление
Лекции
Лекция 1.Правильные и особые точки функции
комплексного переменного (включая бесконечно
удаленную). Классификация изолированных особых
точек. Связь типа особой точки с видом
лорановского разложения функции в окрестности
этой точки. Теорема Сохоцкого (без док-ва).
Лекция 5. Основные теоремы операционного
исчисления: линейности, подобия, смещения,
запаздывания,
о
дифференцировании
и
интегрировании оригиналов и изображений.
ОЛ-8 гл.7 §2, ОЛ-7 гл.8 §1, ДЛ-5 гл.2 §1-6, ОЛ-9 §6.2.
Лекция 6. Таблица оригиналов и изображений.
Нахождение
изображения
периодического
оригинала. Импульсные функции и их изображения.
ОЛ-1 гл.7, ОЛ-8 гл.4 §5,6, ОЛ-7 гл.4 §2, МП-1, МП-2.
Лекции 2-3.Вычет аналитической функции
в
изолированной особой точке. Вычет в бесконечно
удаленной точке. Основная теорема Коши о вычетах.
Применение вычетов к вычислению интегралов от
функций комплексного переменного по замкнутому
контуру.
ОЛ-8 гл.7 §2, ОЛ-7 гл.8 §1, ДЛ-5 гл.3 §1,4, гл.2 §3,
ОЛ-9 §6.2,6.3.
Лекция 7. Свертка оригиналов и ее изображение.
Формула обращения. Теоремы разложения. Интеграл
Дюамеля.
ОЛ-1 гл.8 §8.1-8.4, ОЛ-8 гл.5 §1,2, ОЛ-7 гл.5 §1,
МП-1, МП-2.
ОЛ-8 гл.7 §2, ОЛ-7 гл.8 §1, ДЛ-5 гл.2 §4, гл.4 §3, ОЛ9 §6.4.
Лекция 4.Оригинал и изображение. Теорема о
существовании
изображения.
Поведение
изображения в бесконечно удаленной точке.
Единичная функция Хевисайда и ее изображение.
Лекция 8. Операционный метод решения линейных
дифференциальных уравнений с постоянными
коэффициентами и систем таких уравнений.
ОЛ-8 гл.7 §1,2,4, ОЛ-7 гл.8 §11, ДЛ-5 гл.1 §1,2, ОЛ-9
§6.1.
ОЛ-8 гл.8 §1, ОЛ-7 гл.8 §1,3, ДЛ-5 гл.5 §1-4, ОЛ-9
§6.5.
Упражнения
Занятия 1-2.Изолированные особые точки, включая
бесконечно удаленную, их характер. Вычеты.
ОЛ-6. Ауд.: 277, 283, 295, 318, 325, 334.
Дома: 276, 280, 292, 315, 324, 332, 336.
или
ОЛ-10 гл.12 §5, 6. Ауд.: 12.382, 384, 387, 395, 398,
401, 408, 404, 414, 416, 424, 429.
Дома: 12.383, 391, 397, 402, 411, 413, 415, 419, 431,
432.
Занятие 3.Вычисление контурных интегралов с
помощью вычетов.
ОЛ-6. Ауд.: 338, 341, 348, 353, 356, 361.
Дома: 339, 347, 351, 357, 360.
или
47
ОЛ-10 гл.12 §6. Ауд.: 12.433, 435, 439, 441, 443, 445,
456, 463.
Дома: 12.434, 436, 440, 442, 444, 447, 459, 464.
Занятия
4-5.
Нахождение
изображений
и
оригиналов.
ОЛ-6. Ауд.: 524, 526, 529, 538, 540, 546, 555, 560, 564,
566, 569, 573, 576, 580, 583, 613, 625, 634, 635, 627.
Дома: 528, 536, 542, 547, 563, 565, 570, 574, 579, 620,
633.
или
ОЛ-10 гл.13 §1,2. Ауд.: 13.1, 2, 6, 9, 17, 20, 29, 37, 47,
53, 58, 74, 76, 78, 79, 82, 84, 86.
Дома: 13.3, 7, 8, 10, 19, 22, 26, 30, 40, 48, 52, 61, 75,
77, 80, 83, 85, 87.
Занятие 6. Теоремы разложения.
ОЛ-10 гл.13 §2. Ауд.: 13.88, 90, 93, 96, 98, 102, 104.
Дома: 13.89, 91, 94, 97, 99, 101,103.
Занятие 7. Применение операционного исчисления
к решению линейных дифференциальных уравнений
с постоянными коэффициентами и систем таких
уравнений.
ОЛ-6. Ауд.: 654, 657, 665, 683, 718, 720, 758.
Дома: 655, 666, 721, 760, 762.
или
ОЛ-10 гл.13 §3. Ауд.: 13.105, 111, 114, 117, 119, 129,
132, 137.
Дома: 13.107, 112, 115, 118, 121, 130, 134, 136, 138.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий,
подготовке к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Ряды Фурье и функции комплексного переменного»
Срок выдачи 1 неделя, срок сдачи – 7 неделя
2. Конт роль по модулю №1 (РК №1) «Ряды Фурье и функции комплексного переменного»
Срок проведения - 7 неделя
Модуль 2.
1. ДЗ №2 «Комплексные степенные ряды»
Срок выдачи 2 неделя, срок сдачи – 10 неделя
2. Контроль по модулю №2 (РК №2) «Комплексные степенные ряды».
Срок проведения – 11 неделя
Модуль 3.
1. ДЗ №3 «Теория вычетов и операционное исчисление»
Срок выдачи 9 неделя, срок сдачи части 1 – 13 неделя, части 2 – 15 неделя.
2. Контроль по модулю №3 (РК №3) «Теория вычетов и операционное исчисление».
Срок проведения – 16 неделя
Литература
1.
2.
3.
4.
5.
Основная литература (ОЛ)
Морозова В.Д. Теория функций комплексного переменного: Учеб. для вузов / Под ред. В.С. Зарубина, А.П.
Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. -520 с. (Сер. Математика в техническом
университете, Вып. X)
Власова Е.А. Ряды: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э.
Баумана, 2006. - 616 с. (Сер. Математика в техническом университете, Вып. IX)
Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов,т.2. -13 изд. - М.: Наука, 1985. 560 с.
Фролов С.В., Шостак Р.Я. Курс высшей математики, т.1.-М., Высшая школа, 1973.-480 с., т.2.-М., Высшая
школа, 1973. -400 с.
Бугров Я.С., Никольский С.М. Высшая математика: Дифференциальные уравнения, Кратные интегралы.
Ряды. Функции комплексного переменного. М.: Наука, 1984.-448 с.
48
6.
7.
8.
9.
10.
11.
1.
2.
3.
4.
5.
6.
1.
2.
3.
4.
5.
6.
Краснов М.Л., Киселев Л.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. Задачи и упражнения.-М., Наука, 1981.-215 с.
Свешников А.Г., Тихонов А.М. Теория функций комплексной переменной.-М., Наука, 1967.-304 с.
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости.-М., Наука, 1966.-331 с.
Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление: Учеб. для вузов/
Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1996. - 228 с. (Сер.
Математика в техническом университете, Вып. XI)
Сборник задач по математике для втузов. Специальные разделы математического анализа. Под ред. А.В.
Ефимова и Б.П.Демидовича. т. 2.-2-е изд. -М., Наука, 1986.-368 с.
Задачи и упражнения по математическому анализу для втузов. Под.ред. Б.П. Демидовича. М.: Интегралпресс, 1997.- 416 с.
Дополнительная литература (ДЛ)
Привалов И.И. Введение в теорию функций комплексного переменного. М.: Высш. шк., 1999. -432 с.
Шилов Г.Е. Математический анализ. Функции одного переменного. -М., Наука, 1976. -632 с.
Мышкис А.Д. Математика для втузов. Специальные курсы.-М., Наука, 1971. -632 с.
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1987. -688 с.
Шостак Р.Я. Операционное исчисление.- М.: Высшая школа. 1972 -252 с.
Смирнов В.И. Курс высшей математики. Т.2.- М.: ГИФМЛ, 1961.- 628 с.
Методические пособия
Ванько В.И., Галкин С.В., Морозова В.Д. Методические указания для самостоятельной работы студентов по
разделам "Теория функций комплексного переменного" и "Операционное исчисление", МВТУ, 1988. -28с.
Шостак Р.Я., Коган С.М., Хереско Т.А. Методическое пособие к выполнению домашнего задания по ТФКП,
МВТУ, 1976. -41 с.
Шостак Р.Я. Учебное пособие по операционному исчислению.- М.: МВТУ,1967. -100 с.
Голенко К.А., Хереско Т.А., Щетинина Н.Н. Методические указания для подготовки к контрольным работам
по курсу высшей математики, МВТУ, 1986. -36 с.
Нараленков К.М., Шарохина И.В. Тригонометрические ряды Фурье. – М.: Изд-во МГТУ, 2005. – 41 с.
Галкин С.В. Теория функций комплексного переменного и операционное исчисление. Учебное пособие - М.
Изд-во МГТУ им. Н.Э. Баумана, 2011 - 239с.
Рекомендуемые Интернет-сайты:
1. http://www.mathelp.spb.ru - лекции по высшей математике
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
для СМ1, 2, 5, 7, 8, 11, РК4
Дисциплина состоит из 3-х учебных модулей.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-3
6
Упражнения
1-7
14
Домашние задания текущие
1-7
6
Контроль по модулю №1
7
4
49
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
4-5
4
Упражнения
8-10
6
Домашние задания текущие
8-10
4
Контроль по модулю №2
11
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
6-8
7
Упражнения
11-17
14
Домашние задания текущие
11-17
10
Контроль по модулю №3
16
4
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Лекции
Примечание
Модуль 1:Ряды Фурье и функции комплексного переменного
Лекции
Лекция 1.Тригонометрическая система функций на
отрезке. Ряды Фурье по тригонометрической
системе. Коэффициенты Эйлера-Фурье. Теорема
Дирихле
о
разложении
функции
в
тригонометрический
ряд
Фурье.
Разложение
функций в тригонометрические ряды Фурье.
элементарных функций с помощью степенных рядов.
Формулы
Эйлера.
Вычисление
значений
элементарных функций.
ОЛ-1 гл.1, гл.3 §3.1, гл.2, гл.3 §3.3-3.6, гл.6 §6.1-6.2,
ОЛ-8 гл.1 ч.1 §2,3, гл.2 §1, гл.4 §1,2,3, ОЛ-7 гл.1 §2-4,
гл.4 §1,2,3, МП-1, МП-2.
ОЛ-2 3.1, 3.3-3.9, ОЛ-3 гл. 16, 17, ОЛ-5 гл.12, ДЛ-6
гл. 5, 6, ДЛ-2 гл.14.
Лекция 3.Предел функции. Непрерывность функции.
Производная от функции комплексного переменного.
Условия Коши-Римана. Необходимые и достаточные
условия дифференцирования функции комплексного
переменного. Аналитичность функции в точке и в
области. Гармонические функции и их связь с
аналитическими. Восстановление аналитической
функции по ее действительной или мнимой части.
Лекция 2.Комплексное переменное и комплексная
плоскость. Сфера Римана, бесконечно удаленная
точка. Числовые ряды с комплексными членами.
Необходимые и достаточные условия их сходимости.
Абсолютная и условная сходимость. Степенные ряды
с комплексными членами. Теорема Абеля. Круг и
радиус сходимости степенного ряда. Функции
комплексного переменного. Определение основных
ОЛ-1 гл.2 §2.1, гл.3 §3.2, гл.4 §4.1-4.9, ОЛ-7 гл.1 §4,
гл.6 §6, МП-1, МП-2.
Упражнения
Занятие 1. Ряды Фурье.
ОЛ-10 гл.12: Ауд.: 480, 482, 484, 486, 488.
Дома: 481, 483, 485, 487.
или
ОЛ-11: Ауд.: 2672, 2673, 2677, 2697, 2698.
Дома: 2671, 2674, 2695, 2696.
Занятие 2.Неполные ряды Фурье.
ОЛ-10 гл.12: Ауд.: 493, 495, 497, 498.
50
Дома: 494, 499, 500.
или
ОЛ-11: Ауд.: 2683, 2684, 2687, 2689, 2702.
Дома: 2685, 2686, 2690, 2700.
Занятие 3. Действия над комплексными числами.
Кривые и области на комплексной плоскости.
Функции комплексного переменного.
МП-1, МП-2, ОЛ-6. Ауд.: 52, 53, 55, 57(а, б, г), 60(а,
в).
Дома: 54, 56, 58(в, д, е), 60(б, г).
или
МП-1, МП-2, ОЛ-10 гл.11 §1. Ауд.: 11.1, 3, 4, 7, 9, 10,
13, 20, 22.
Дома: 11.2, 5, 6, 8, 11, 12, 14, 21, 23.
Занятия 4-5.Функции комплексного переменного.
МП-1, МП-2, ОЛ-6. Ауд.: 62, 64, 67(а, в), 104(а, в),
114(а, в).
Дома: 63, 65, 67(б, д), 104(б, д), 114(б).
или
ОЛ-10 гл.11 § 1, 2. Ауд.: 11.27, 31, 32, 35, 37, 42, 43,
48, 51, 55, 56, 58, 59, 60, 63, 65, 67, 75, 77, 79, 83, 86,
87.
Дома: 11.28, 33, 34, 36, 38, 44,45, 49, 50, 53, 57, 61,
62, 64, 66, 76, 78, 81, 84, 90.
Занятие
6.Дифференцирование
функции
комплексного
переменного.
Определение
аналитической
функции
по
известной
действительной или мнимой части.
ОЛ-6. Ауд.: 104(а, в), 114(а, в).
Дома: 104(б, д), 114(б).
или
ОЛ-10 гл.11 § 1, 2. Ауд.: 11.113, 115, 116, 131, 132,
134, 136.
Дома: 11.112, 114, 117, 133, 135, 137.
Занятие 7.Контроль по модулю№1 (РК№1) «Ряды
Фурье и функции комплексного переменного».
Модуль 2:Ряды Тейлора и Лорана
Лекции
Лекция 1.Интеграл от непрерывной функции
комплексного переменного, его свойства и
вычисление. Теорема Коши для односвязной и
многосвязной области. Независимость интеграла от
пути интегрирования. Формула Ньютона-Лейбница.
Интегральная формула Коши. Формула производной
n-го порядка. Применение формул для вычисления
контурных интегралов.
ОЛ-1 гл.5 §5.1-5.7, ОЛ-8 гл.2 §3-5, ОЛ-7 гл.1 §5, 6,
МП-1, МП-2.
Лекция 2.Теоремы о разложении аналитической
функции в ряды Тейлора иЛорана.
ОЛ-1 гл.6 §6.3-6.7, ОЛ-8 гл.4 §1,2,3, ОЛ-7 гл.2 §2,
гл.4 §1, МП-1, МП-2.
Упражнения
Занятие 1.Интегрирование функции комплексного
переменного. Вычисление контурных интегралов.
Интегральная формула Коши. Формула производной
n-го порядка.
ОЛ-6. Ауд.: 143, 147, 158, 174, 179, 212, 218, 264, 272.
Дома: 144, 149, 159,169, 180, 215, 265, 272, 275.
или
ОЛ-10 гл.11 §4. Ауд.: 11.231, 233, 235, 257, 259, 263,
265.
Дома: 11.232, 238, 258, 264, 268, 271.
Занятия 2-3.Степенные ряды. Разложение функций
в ряды Тейлора и Лорана.
ОЛ-10 гл.12 §3, 5. Ауд.: 12.165, 167, 171, 172, 176,
185, 190, 194, 201, 214, 216, 221, 227, 231, 237, 352,
358, 361, 368, 370.
Дома: 12.166, 168, 173, 177, 180, 191, 202, 215, 217,
225, 232, 238, 258, 264, 268, 271, 353, 354, 359, 360,
371, 373.
Модуль 3:Теория вычетов и операционное исчисление
Лекции
Лекция 1.Правильные и особые точки функции
комплексного переменного (включая бесконечно
удаленную). Классификация изолированных особых
точек. Связь типа особой точки с видом
лорановского разложения функции в окрестности
этой точки. Теорема Сохоцкого (без док-ва). Вычет
аналитической функции в изолированной особой
точке. Вычет в бесконечно удаленной точке.
Основная теорема Коши о вычетах. Применение
вычетов к вычислению интегралов от функций
комплексного переменного по замкнутому контуру.
ОЛ-1 гл.7, гл.8 §8.1-8.4, ОЛ-8 гл.4 §5,6, гл.5 §1,2,
ОЛ-7 гл.4 §2, гл.5 §1, МП-1, МП-2.
Лекции 2-3.Преобразование Лапласа. Оригинал и
изображение.
Теорема
о
существовании
изображения. Поведение изображения в бесконечно
удаленной точке. Единичная функция Хевисайда и ее
изображение. Основные теоремы операционного
исчисления: линейности, подобия, смещения,
запаздывания,
о
дифференцировании
и
интегрировании оригиналов и изображений. Свертка
оригиналов и ее изображение. Интеграл Дюамеля.
Передаточная
функция.
Формула
обращения
51
преобразования Лапласа. Теоремы разложения.
Операционный
метод
решения
линейных
дифференциальных уравнений с постоянными
коэффициентами и систем таких уравнений.
ОЛ-8 гл.7 §1,2,4, ОЛ-7 гл.8 §1, 3, ДЛ-5 гл.1 §1-6, гл.2
§1-6, гл.4 §3, гл.5 §1-4, ОЛ-9 §6.1-6.5.
Упражнения
Занятия 1-2.Изолированные особые точки, включая
бесконечно удаленную, их характер. Вычеты.
ОЛ-6. Ауд.: 277, 283, 295, 318, 325, 334.
Дома: 276, 280, 292, 315, 324, 332, 336.
или
ОЛ-10 гл.12 §5, 6. Ауд.: 12.382, 384, 387, 395, 398,
401, 408, 404, 414, 416, 424, 429.
Дома: 12.383, 391, 397, 402, 411, 413, 415, 419, 431,
432.
Занятие 3.Вычисление контурных интегралов с
помощью вычетов.
ОЛ-6. Ауд.: 338, 341, 348, 353, 356, 361.
Дома: 339, 347, 351, 357, 360.
или
ОЛ-10 гл.12 §6. Ауд.: 12.433, 435, 439, 441, 443, 445,
456, 463.
Дома: 12.434, 436, 440, 442, 444, 447, 459, 464.
Занятия
4-5.
Нахождение
изображений
и
оригиналов.
ОЛ-6. Ауд.: 524, 526, 529, 538, 540, 546, 555, 560, 564,
566, 569, 573, 576, 580, 583, 613, 625, 634, 635, 627.
Дома: 528, 536, 542, 547, 563, 565, 570, 574, 579, 620,
633.
или
ОЛ-10 гл.13 §1,2. Ауд.: 13.1, 2, 6, 9, 17, 20, 29, 37, 47,
53, 58, 74, 76, 78, 79, 82, 84, 86.
Дома: 13.3, 7, 8, 10, 19, 22, 26, 30, 40, 48, 52, 61, 75,
77, 80, 83, 85, 87.
Занятие 6. Теоремы разложения.
ОЛ-10 гл.13 §2. Ауд.: 13.88, 90, 93, 96, 98, 102, 104.
Дома: 13.89, 91, 94, 97, 99, 101,103.
Занятие 7. Применение операционного исчисления
к решению линейных дифференциальных уравнений
с постоянными коэффициентами и систем таких
уравнений.
ОЛ-6. Ауд.: 654, 657, 665, 683, 718, 720, 758.
Дома: 655, 666, 721, 760, 762.
или
ОЛ-10 гл.13 §3. Ауд.: 13.105, 111, 114, 117, 119, 129,
132, 137.
Дома: 13.107, 112, 115, 118, 121, 130, 134, 136, 138.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних
заданий, подготовке к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Ряды Фурье и функции комплексного переменного»
Срок выдачи 1 неделя, срок сдачи – 7 неделя
2. Конт роль по модулю №1 (РК №1) «Ряды Фурье и функции комплексного переменного»
Срок проведения - 7 неделя
Модуль 2.
1. ДЗ №2 «Ряды Тейлора и Лорана»
Срок выдачи 2 неделя, срок сдачи – 10 неделя
2. Контроль по модулю №2 (РК №2) «Комплексные степенные ряды».
Срок проведения – 11 неделя
Модуль 3.
1. ДЗ №3 «Теория вычетов и операционное исчисление»
Срок выдачи 9 неделя, срок сдачи части 1 – 13 неделя, части 2 – 15 неделя.
2. Контроль по модулю №3 (РК №3) «Теория вычетов и операционное исчисление».
Срок проведения – 16 неделя
52
Литература
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
7.
8.
9.
10.
11.
12.
7.
8.
9.
10.
11.
12.
Основная литература (ОЛ)
Морозова В.Д. Теория функций комплексного переменного: Учеб. для вузов / Под ред. В.С. Зарубина,
А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. -520 с. (Сер. Математика в техническом
университете, Вып. X)
Власова Е.А. Ряды: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им.
Н.Э. Баумана, 2006. - 616 с. (Сер. Математика в техническом университете, Вып. IX)
Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов,т.2. -13 изд. - М.: Наука,
1985. -560 с.
Фролов С.В., Шостак Р.Я. Курс высшей математики, т.1.-М., Высшая школа, 1973.-480 с., т.2.-М.,
Высшая школа, 1973. -400 с.
Бугров Я.С., Никольский С.М. Высшая математика: Дифференциальные уравнения, Кратные
интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1984.-448 с.
Краснов М.Л., Киселев Л.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. Задачи и упражнения.-М., Наука, 1981.-215 с.
Свешников А.Г., Тихонов А.М. Теория функций комплексной переменной.-М., Наука, 1967.-304 с.
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости.-М., Наука, 1966.-331 с.
Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление: Учеб. для
вузов/ Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1996. - 228 с.
(Сер. Математика в техническом университете, Вып. XI)
Сборник задач по математике для втузов. Специальные разделы математического анализа. Под ред.
А.В. Ефимова и Б.П.Демидовича. т. 2.-2-е изд. -М., Наука, 1986.-368 с.
Задачи и упражнения по математическому анализу для втузов. Под.ред. Б.П. Демидовича. М.:
Интеграл-пресс, 1997.- 416 с.
Дополнительная литература (ДЛ)
Привалов И.И. Введение в теорию функций комплексного переменного. М.: Высш. шк., 1999. -432 с.
Шилов Г.Е. Математический анализ. Функции одного переменного. -М., Наука, 1976. -632 с.
Мышкис А.Д. Математика для втузов. Специальные курсы.-М., Наука, 1971. -632 с.
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1987. 688 с.
Шостак Р.Я. Операционное исчисление.- М.: Высшая школа. 1972 -252 с.
Смирнов В.И. Курс высшей математики. Т.2.- М.: ГИФМЛ, 1961.- 628 с.
Методические пособия
Ванько В.И., Галкин С.В., Морозова В.Д. Методические указания для самостоятельной работы
студентов по разделам "Теория функций комплексного переменного" и "Операционное исчисление",
МВТУ, 1988. -28с.
Шостак Р.Я., Коган С.М., Хереско Т.А. Методическое пособие к выполнению домашнего задания по
ТФКП, МВТУ, 1976. -41 с.
Шостак Р.Я. Учебное пособие по операционному исчислению.- М.: МВТУ,1967. -100 с.
Голенко К.А., Хереско Т.А., Щетинина Н.Н. Методические указания для подготовки к контрольным
работам по курсу высшей математики, МВТУ, 1986. -36 с.
Нараленков К.М., Шарохина И.В. Тригонометрические ряды Фурье. – М.: Изд-во МГТУ, 2005. – 41 с.
Галкин С.В. Теория функций комплексного переменного и операционное исчисление. Учебное
пособие - М. Изд-во МГТУ им. Н.Э. Баумана, 2011 - 239с.
Рекомендуемые Интернет-сайты:
2. http://www.mathelp.spb.ru - лекции по высшей математике
53
ТФКП И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
(ВЫСШАЯ МАТЕМАТИКА)
для МТ и РК (кроме РК-5 и РК-6)
Дисциплина состоит из трех учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-2
2
Упражнения
1-2
6
Домашние задания текущие
1-2
4
3
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
3-12
10
Упражнения
3-12
20
Домашние задания текущие
3-12
10
14
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
13-17
6
Упражнения
13-17
6
Домашние задания текущие
13-17
6
17
2
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №3
54
Примечание
ЛЕ КЦ И И
Модуль 1: РЯДЫ ФУРЬЕ
в круге – в ряд Тейлора; аналитической в
кольце – в ряд Лорана. Дифференциальные
выражения для коэффициентов ряда Тейлора,
интегральные выражения для коэффициентов
ряда Тейлора и ряда Лорана.
ЛЕКЦИЯ 1. Ряд Фурье по ортогональной
системе функций. Коэффициенты Фурье.
Ортогональность
системы
тригонометрических функций на отрезках
[ ;  ] и L; L . Тригонометрические ряды
ЛЕКЦИЯ 6. Изолированные особые точки
функции, их классификация. Поведение
функции в окрестности различных типов
особых
точек.
Вычет
функции
в
изолированной особой точке. Равенство
вычета в точке z0 коэффициенту c1 ряда
Фурье и коэффициенты Эйлера-Фурье.
Теорема Дирихле (без док-ва). Разложение в
ряд Фурье периодических, четных и нечетных
функций. Неполные ряды Фурье.
Лорана функции f ( z ) по степеням ( z  z0 ) .
Вычисление вычета в полюсе (вывод
формулы). Теорема Каши о вычетах.
Приложение к вычислению интегралов.
Модуль 2: ТФКП
ЛЕКЦИЯ 2. Комплексные числа, комплексная
плоскость.
Функция
комплексного
переменного, ее геометрический смысл.
Однозначные и многозначные функции.
Примеры линейной и степенной функции.
Формула Эйлера как определение для ei .
Определение функций e z , sin z, cos z, sh z, ch z с
помощью
формулы
Эйлера.
Формулы,
связывающие эти функции. Логарифмическая
функция ln z , ее свойства. Вычисление z1z2 .
Модуль 3. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
ЛЕКЦИЯ 7. Оригинал и его изображение по
Лапласу. Свойства преобразования Лапласа:
аналитичность,
линейность,
дифференцирование
и
интегрирование
оригинала,
теорема
подобия,
теорема
смещения,
дифференцирование
и
интегрирование
изображения,
теорема
запаздывания.
Таблица
оригиналов
и
изображений.
ЛЕКЦИЯ 3. Предел функции комплексного
переменного, непрерывность. Производная
функции комплексного переменного, условия
Коши-Римана. Аналитичность (регулярность)
функции в области, в точке. Гармонические
функции, их связь с аналитическими
функциями. Восстановление аналитической
функции по ее действительной или мнимой
части. Геометрический смысл модуля и
аргумента производной.
ЛЕКЦИЯ 8. Методы восстановления оригинала
по
его
изображению.
Приложение
операционного
исчисления
к
решению
линейных дифференциальных уравнений с
постоянными коэффициентами и их систем.
П РА К ТИ Ч Е СК И Е З А Н Я ТИ Я
Модуль 1: РЯДЫ ФУРЬЕ
ЗАНЯТИЯ 1-2. Разложение функции в
тригонометрические ряды Фурье.
ЛЕКЦИЯ 4. Интеграл от непрерывной функции
комплексного переменного, методы его
вычисления: (1) параметризация пути; (2)
выражение
через
действительные
криволинейные
интегралы.
Основные
свойства и оценка интеграла (без док-ва).
Интеграл
от
аналитической
функции
комплексного переменного, его независимость
от пути интегрирования. Теорема Коши для
односвязной
и
многосвязной
областей.
Вычисление интегралов вида
C ( z  a )
n
Ауд: ОЛ-4, гл.12: № 480, 482, 484, 486, 488, 493,
495, 497, 498;
Дома: ОЛ-4, гл.12: № 484, 485, 487, 495, 496, 501
ЗАНЯТИЕ 3. Рубежный контроль по теме
"Ряды Фурье".
Модуль 2: ТФКП
ЗАНЯТИЕ 4. Действия над комплексными
числами.
Геометрия
на
комплексной
плоскости.
dz при
целом п. Интегральная формула Коши для
функции, аналитической в односвязной
области. Бесконечная дифференцируемость
аналитической функции и интегральная
формула для её п-й производной.
Ауд.: ОЛ-4, Гл.11, № 1, 3, 5, 7, 10, 13; 15, 17, 19;
или МП-2, Занятия 1 и 2.
ЛЕКЦИИ 5. Числовые ряды с комплексными
членами; необходимое условие, критерий
сходимости.
Абсолютная
и
условная
сходимость. Степенные ряды с комплексными
членами. Теорема о круге сходимости
степенного ряда. Двусторонние степенные
ряды (ряды Лорана), их область сходимости.
Разложение функции: аналитической функции
ЗАНЯТИЕ
5-6.
Элементарные
функции
комплексного переменного (КП), вычисление
их
значений
в
точке,
выделение
действительной
и
мнимой
частей.
Производная
функции
комплексного
переменного, восстановление аналитической
функции по ее действительной или мнимой
части.
Дома: ОЛ-4, Гл 11, № 2, 4, 6, 8, 12, 14, 16, 18;
или МП-2, Занятия 1 и 2.
55
Занятие 11 Вычисление интегралов по
замкнутому контуру от ФПК и несобственных
действительных интегралов с помощью
вычетов.
Ауд.: ОЛ-4, Гл.11, № 20, 22, 27, 53, 55, 57, 62, 64,
66, 67, 69, 80, 112, 117, 124, 131, 132.
Или МП-2, Занятие 4;
Дома: ОЛ-4, Гл. 11, № 21, 23, 26, 54, 56, 58, 63,
65, 68, 81, 113, 115, 123, 133, 137, или МП-2,
Занятие 4.
Ауд.: ОЛ-4, гл.12 № 435, 439, 440, 450, 456, 463;
или МП-2, Занятие 8;
ЗАНЯТИЯ 7 – 8. Числовые ряды, степенные
ряды в комплексной области, определение
круга сходимости. Двусторонние степенные
ряды (ряды Лорана), нахождение их области
сходимости.
Разложение
функции
комплексного переменного в ряд Тейлора и в
ряд Лорана.
Ауд.: ОЛ-4, гл.12 № 434, 436, 444, 460, 451, 458,
464; или МП-2, Занятие 8.
ЗАНЯТИЕ 12. Рубежный контроль по ТФКП
Модуль 3. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
ЗЗАНЯТИЯ 13-14. Нахождение изображений и
восстановление оригиналов.
Ауд.: или ОЛ-4, гл 12, №6, 12, 47, 165, 168, 181,
183, 189, 227, 231, 237, 352, 361, 368, 370, или
МП -2, Занятие 3.
Ауд.: ОЛ-4 гл. 13 № 1, 2, 6, 9, 17, 20, 29, 37, 47,
53, 58, 74, 76, 78, 79, 82, 84, 86.
Дома: ОЛ-4 гл. 13 № 3, 7, 8, 10, 19, 22, 26, 30, 40,
48, 52, 61, 75, 77, 80, 83, 85, 87.
Дома: ОЛ-4, гл.12, № 5, 11, 30, 84, 107, 166, 167,
172, 177, 191, 202, 232, 238, 258, 268, 353, 354,
359, 36, 371, или МП -2, Занятие 3.
функций
ЗАНЯТИЕ 15. Применение операционного
исчисления к решению дифференциальных
уравнений.
Ауд.: ОЛ-4, гл.11 № 230, 240, 257, 257, 259, 265,
265, 269; или МП-2, Занятие 6;.
Ауд.: ОЛ-4 гл. 13 № 105, 111, 117, 119, 129, 132,
137.
Дома: ОЛ-4, гл.11 № 231, 239, 258, 263, 266, 268,
или МП-2, Занятие 6.
Дома: ОЛ-4 гл. 13 № 107, 112, 115, 118, 121, 130,
134, 136, 138.
ЗАНЯТИЕ 10.. Особые точки аналитической
функции, их классификация. Вычеты.
ЗАНЯТИЕ
16
Контрольная
операционному исчислению.
ЗАНЯТИЕ
9.
Интегрирование
комплексного переменного
работа
Ауд.: ОЛ-4, гл.12 № 382, 386, 387, 392, 396, 408,
411, 417, 425, или МП-2, Занятие 8;
Дома: ОЛ-4, гл.12 № 383, 385, 388, 392, 395, 409,
412, 416, 426, или МП-2, Занятие 8.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к
выполнению контрольных работ и Рубежных контролей, выполнении индивидуальных ДЗ.
Контрольные мероприятия
Модуль 1: Ряды Фурье
1. Домашнее задание № 1 "Ряды Фурье. Выдача – 1 неделя, прием – 3 неделя.
2. Контрольная работа по теме "Ряды Фурье". Срок – 4 неделя.
Модуль 2: ТФКП
3. Домашнее задание № 2 "ТФКП". Выдача – 4 неделя, прием – 11 неделя.
4. Рубежный контроль по теме "ТФКП". Срок – 12 неделя.
Модуль 3:Операционное исчисление
5. Домашнее задание № 1 "Операционное исчисление», Выдача – 12 неделя, прием – 15 неделя.
6. Контрольная работа по теме " Операционное исчисление". Срок – 16 неделя.
ЛИТЕРАТУРА
56
по
Основная литература (ОЛ)
1.
Пискунов Н.С. Дифференциальное и интегральное исчисления, Т. 2, М.: Наука, 1985.
2.
Морозова В.Д. Теория функций комплексного переменного. Учебник для вузов (под ред.
В.С.Зарубина и А.П. Крищенко). – М.: МГТУ.– 2001 г. (серия «Математика в техническом
университете», вып X).
3.
Бугров Я.С., Никольский С.М. Высшая математика. Кратные интегралы. Ряды. Функции
комплексного переменного. – М.: Наука, 1985.
4.
Сборник задач по математике для втузов. Т.2 (под ред. Ефимова А.В., Демидовича Б.П.), М.:
Наука, 1986.
5.
Задачи и упражнения по математическому анализу для втузов. Под ред. Б.П. Демидовича, М.:
Интеграл-пресс, 1997.
Дополнительная литература
1.
2.
1968.
3.
4.
5.
1999.
6.
Кудрявцев Л.Д. Курс математического анализа. Т. 2, М.: Высшая школа, 1981.
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. М.: Наука,
Краснов М.Л., Киселев А.И. и др. Вся высшая математика, тт. 3 и 4, – М.: УРСС, 2001.
Зорич В.А. Математический анализ, т.2. – М.: МЦНМО, 1998.
Привалов И.И. Введение в теорию функций комплексного переменного. М,: Высшая школа. –
Шостак Р.Я. Операционное исчисление. М.: Высшая школа. – 1972.
Кафедральные издания и методические материалы
1.
Нараленков К. М., Шарохина И. В. Тригонометрические ряды Фурье: метод. указания к
выполнению домашнего задания / МГТУ им. Н. Э. Баумана. – М., 2005. – 38 с.
2.
Агаева Э.И., Ершова М.И., Зотина Р.С. Пособие по теории функций комплексного переменного. –
М.: МГТУ, 1992.
3.
Копаев А. В., Леванков В. И., Мастихин А. В. Теория функций комплексного переменного: метод.
указания к выполнению домашнего задания. – М.: МГТУ, 2012. – 38 с.
4.
Копаев А.В., Садыхов Г.С. Теория функций комплексного переменного. – М.: МГТУ, 1992.
5.
Алгазин О.Д., Богомолов В.Д., Копаев А В. Методы теории функций комплексного переменного в
прикладных задачах. – М.: МГТУ, 1993.
6.
Ванько В.И., Галкин С.В., Морозова В.Д. Методические указания для самостоятельной работы
студентов по разделам «Теория функций комплексного переменного» и «Операционное исчисление». – М.:
МВТУ,1988.
РЯДЫ, ТФКП И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
для РК-5 и Э5
Дисциплина состоит из двух учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-6
12
Упражнения
1-6
12
Домашние задания текущие
1-6
8
7
2
Контроль по модулю №1
57
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
7-17
22
Упражнения
7-17
22
Домашние задания текущие
7-17
12
17
2
Контроль по модулю №2
ЛЕ КЦ ИИ
Примечание
ЛЕКЦИЯ 6. Ряд Фурье по ортогональной
системе функций. Коэффициенты Фурье.
Ортогональность
системы
тригонометрических функций на отрезках [–π:
π] и L; L . Тригонометрические ряды Фурье
Модуль 1: РЯДЫ
ЛЕКЦИЯ 1. Числовые ряды. Признаки
сходимости (повторение).
ОЛ-1, гл. 16, §1-8; ОЛ-2, гл. 1 § 1.1 – 1.9; ОЛ-5
ч.1, гл.13, § 1–5.
и коэффициенты Эйлера-Фурье. Теорема
Дирихле (без док-ва). Разложение в ряд Фурье
периодических, четных и нечетных функций.
Неполные ряды Фурье.
ОЛ-1, гл. 17, § 1-7; ОЛ-2, гл 3; ОЛ-9, гл.10, § 14.
ЛЕКЦИЯ 2. Функциональные ряды. Область
сходимости
функционального
ряда.
Равномерная
сходимость.
Признак
Вейерштрасса
равномерной
сходимости.
Свойства равномерно сходящихся рядов:
непрерывность
суммы,
почленное
интегрирование и дифференцирование (без
доказательства). Степенные ряды. Теорема
Абеля.
ОЛ-1, гл. 16 § 9-15; ОЛ-2, гл.2, § 2.1, 2.2; ОЛ-5,
гл.1 § 1, 2, 4.
Модуль 2: ТФКП и Операционное исчисление
ЛЕКЦИЯ
7.
Комплексное
переменное,
комплексная плоскость. Задание кривых и
областей
в
комплексной
плоскости
уравнениями:
a Re( z )  bIm( z )  c; z  z0  R, arg( z  z0 )   ;
z  z1  z  z2  2a; z  z1  z  z2  2a.
ЛЕКЦИЯ 3.Радиус и интервал сходимости
степенного ряда. Свойства степенных рядов:
равномерная
сходимость,
непрерывность
суммы,
почленное
интегрирование
и
дифференцирование степенных рядов.
ОЛ-1, гл. 16 § 13-15; ОЛ-2, гл.2, § 2.5; ОЛ-5,
гл.1, § 4,5.
и соответствующими неравенствами. Функция
комплексного переменного, ее геометрический
смысл.
Однозначные
и
многозначные
функции. Примеры линейной и степенной
функции.
ОЛ-3, гл1, гл.3, § 3.1; ОЛ-10, гл. 1, § 2, гл.2, §
1,2.
ЛЕКЦИИ 4-5. Разложение вещественной
функции в степенной ряд, необходимое
условие. Ряд Тейлора и Маклорена. Критерий
разложимости функции в степенной ряд.
Достаточное условие разложимости функции в
ряд Тейлора. Разложение в ряд Маклорена
функций: e x , sin x, cos x, ln(1  x), arctg x, (1  x) ,
области пригодности этих
разложений.
Применение степенных рядов к вычислению
значений
функций
и
определённых
интегралов, решению дифференциальных
уравнений.
ОЛ-1, гл. 16, § 15-23; ОЛ-2, гл 2, § 2.5-2.9.
ЛЕКЦИЯ 8. Формула Эйлера как определение
для ei . Определение функций e z , sin z,
cos z, sh z, ch z с помощью формулы Эйлера.
Формулы,
связывающие
эти
функции.
Логарифмическая функция ln z , ее свойства.
Вычисление z1z2
ЛЕКЦИЯ 9 Предел функции комплексного
переменного, непрерывность. Производная
функции комплексного переменного, условия
Коши-Римана. Аналитичность (регулярность)
функции в области, в точке. Гармонические
функции, их связь с аналитическими
58
функциями. Восстановление аналитической
функции по ее действительной или мнимой
части. Геометрический смысл модуля и
аргумента производной. Однолистные и
многолистные функции.
ОЛ-3, гл. 3, § 3.2, гл.4; ОЛ-5, гл. 1 § 3, 4.
Оператор
обращения
интегрального
преобразования
Лапласа.
Свойства
преобразования
Лапласа:
аналитичность,
линейность,
дифференцирование
и
интегрирование оригинала, теорема подобия,
теорема смещения, дифференцирование и
интегрирование
изображения,
теорема
запаздывания.
Таблица
оригиналов
и
изображений.
ОЛ-5, гл.8, § 1, 2.
ЛЕКЦИЯ 10. Интеграл от непрерывной
функции комплексного переменного, методы
его вычисления: (1) параметризация пути; (2)
выражение
через
действительные
криволинейные
интегралы.
Основные
свойства и оценка интеграла. Интеграл от
аналитической
функции
комплексного
переменного, его независимость от пути
интегрирования.
Теорема
Коши
для
односвязной
и
многосвязной
областей.
Вычисление интегралов вида
C ( z  a )
n
ЛЕКЦИЯ
16.
Методы
восстановления
оригинала по его изображению. Приложение
операционного
исчисления
к
решению
линейных дифференциальных уравнений с
постоянными коэффициентами и их систем.
ОЛ-5, гл. 8, §3.
dz при
ПРА КТ И ЧЕ СК ИЕ ЗА Н Я ТИЯ
целом п. Интегральная формула Коши для
функции, аналитической в односвязной
области. Бесконечная дифференцируемость
аналитической функции и интегральная
формула для её п-й производной.
ОЛ-3, гл. 5, ОЛ-5, гл.1, § 5, 6.
Модуль 1: РЯДЫ
ЗАНЯТИЕ 1. Числовые ряды (повторение)
Ауд: ОЛ-6, гл.12: № 90, 92, 94, 95, 97, 99, 102,
103, 110, 112.
Дома: ОЛ-6, гл.12: № 91, 93, 96, 98, 100, 102,
104, 111.
10. Числовые ряды с комплексными членами;
необходимое условие, критерий сходимости.
Абсолютная
и
условная
сходимость.
Степенные ряды с комплексными членами,
теорема Абеля. Теорема о круге сходимости
степенного ряда. Теорема об умножении
степенных
рядов
(без
доказательства).
Разложение элементарных функций КП в ряд
Тейлора
ЗАНЯТИЯ 2-3. Степенные ряды. Разложение
функций в степенные ряды.
Ауд: ОЛ-6, гл.12: № 126, 129, 130, 165, 169, 171,
173, 175, 177, 183, 185, 216, 218, 226, 228, 231,
243, 245, 246.
Дома: ОЛ-6, гл.12: № 176, 178, 184, 193, 196,
200, 209, 207, 216, 219, 221, 222, 224, 227, 230,
232, 245.
ЗАНЯТИЕ 4. Применение степенных рядов.
Ауд: ОЛ-6, гл.12:№ 264, 268, 270, 295, 297, 299,
327, 329, 325.
Дома: ОЛ-6, гл.12: № 266, 273, 290, 296, 300,
311, 314, 327.
ОЛ-3, гл. 2; ОЛ-5, гл. 3, § 1
ЛЕКЦИЯ 12. Двусторонние степенные ряды
(ряды Лорана), их область сходимости.
Формулировка теорем о разложении функции:
аналитической функции в круге – в ряд
Тейлора; аналитической в кольце – в ряд
Лорана. Дифференциальные выражения для
коэффициентов ряда Тейлора, интегральные
выражения для коэффициентов ряда Тейлора
и ряда Лорана. Изолированные особые точки
функции, их классификация. Поведение
функции в окрестности различных типов
особых точек.
ОЛ-3, гл.2, § 2.5, гл.6, §6.3-6.6, гл.7; ОЛ-5, гл.2,
§ 1,2, гл.4, § 1.
ЛЕКЦИЯ 13. Связь нулей функции
полюсов функции
1
f ( z)
ЗАНЯТИЕ
5.
Разложение
функции
в
тригонометрические ряды Фурье.
Ауд: ОЛ-6, гл.12: № 480, 482, 484, 486, 488, 493,
495, 497, 498.
Дома: ОЛ-6, гл.12: № 484, 485, 487, 495, 496,
501.
ЗАНЯТИЕ 6. Рубежный контроль по теме
"Ряды".
Модуль 2: ТФКП и Операционное исчисление
ЗАНЯТИЕ 7. Действия над комплексными
числами.
Геометрия
на
комплексной
плоскости.
Ауд.: МП-2, Занятия 1 и 2.
Дома: МП-2, Занятие 1 и 2 или ОЛ-6, гл.11 № 1,
5, 6, 7, 12, 19, 21, 22, 25, 26.
f ( z) и
. Вычет функции в
изолированной особой точке. Равенство
вычета в точке z0 коэффициенту c1 ряда
Лорана функции f ( z ) по степеням ( z  z0 ) .
Вычисление вычета в полюсе (вывод
формулы).
ОЛ-3, гл.7, 8; ОЛ-10, гл.4, § 2, гл.5, § 1.
ЗАНЯТИЕ
8.
Элементарные
функции
комплексного переменного (КП), вычисление
их
значений
в
точке,
выделение
действительной
и
мнимой
частей.
Производная
функции
комплексного
переменного, восстановление аналитической
ЛЕКЦИИ 14-15. Оригинал и изображение.
Теорема о существовании изображения.
59
ЗАНЯТИЕ 12. Особые точки аналитической
функции,
их
классификация.
Вычеты.
Вычисление интегралов с помощью вычетов.
Ауд.: МП-2, Занятие 8.
Дома: МП-2, Занятие 8, или ОЛ-6, гл.12 № 383,
385, 388, 392, 395, 409, 412, 416, 426, 434, 436,
444, 460.
функции по ее действительной или мнимой
части.
Ауд.: МП-2, Занятие 4.
Дома: МП-2, Занятии 4 или ОЛ-6, гл.11 № 54,
56, 63, 66, 67, 81, 113, 115, 133, 135, 140.
ЗАНЯТИЯ 9 – 10. Числовые ряды, степенные
ряды в комплексной области, определение
круга сходимости. Двусторонние степенные
ряды (ряды Лорана), нахождение их области
сходимости.
Разложение
функции
комплексного переменного в ряд Тейлора и в
ряд Лорана.
Ауд.: МП -2, Занятие 3 или ОЛ-6, гл 12, №6, 12,
47, 165, 168, 181, 183, 189, 227, 231, 237, 352, 361,
368, 370.
Дома: МП -2, Занятие 3, или ОЛ-6, гл.12, № 5,
11, 30, 84, 107, 166, 167, 172, 177, 191, 202, 232,
238, 258, 268, 353, 354, 359, 36, 371.
ЗАНЯТИЯ 13-14. Нахождение изображений и
оригиналов.
Ауд.: ОЛ-6 гл. 13 № 1 2 6 9 17 20 29 37 47 53 58
74 76 78 79 82 84 86.
Дома: ОЛ-6 гл. 13 № 3 7 8 10 19 22 26 30 40 48 52
61 75 77 80 83 85 87.
ЗАНЯТИЕ 15. Применение операционного
исчисления к решению дифференциальных
уравнений.
Ауд.: ОЛ-6 гл. 13 № 105 111 117 119 129 132 137.
Дома: ОЛ-6 гл. 13 № 107 112 115 118 121 130 134
136 138.
ЗАНЯТИЕ 11. Интегрирование функций
комплексного переменного
Ауд.: МП-2, Занятие 6, или ОЛ-6, гл.11 № 230,
240, 257, 257, 259, 265, 265, 269.
Дома: МП-2, Занятие 6, или ОЛ-6, гл.11 № 231,
239, 258, 263, 266, 268.
ЗАНЯТИЕ 16. Рубежный контроль теме "ТФКП
и операционное исчисление".
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
контрольных работ и Рубежных контролей, выполнении индивидуальных ДЗ.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ
Модуль 1: РЯДЫ
1.
Домашнее задание № 1 "Ряды и их приложения ". Выдача – 1 неделя, прием – 8 неделя.
2.
Рубежный контроль по теме "Ряды". Срок – 9 неделя.
Модуль 2: ТФКП и Операционное исчисление
3.
Домашнее задание № 2 "ТФКП". Выдача – 10 неделя, прием – 14 неделя.
4.
Рубежный контроль по теме "ТФКП и операционное исчисление". Срок – 16 неделя.
ЛИТЕРАТУРА
Основная литература (ОЛ)
1.
2.
3.
4.
Пискунов Н.С. Дифференциальное и интегральное исчисления, Т. 2, М.: Интеграл-Пресс, 1996.
Власова Е.А. Ряды. Учебник для вузов (под ред. В.С.Зарубина и А.П. Крищенко). – М.: МГТУ.– 2001 г.
(серия «Математика в техническом университете», вып. IX)
Морозова В.Д. Теория функций комплексного переменного. Учебник для вузов (под ред. В.С.Зарубина
и А.П. Крищенко). – М.: МГТУ.– 2001 г. (серия «Математика в техническом университете», вып. X).
Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. Учебник
для вузов (под ред. В.С.Зарубина и А.П. Крищенко). – М.: МГТУ, –1996. (Серия «Математика в
техническом университете», вып. XI).
60
5.
6.
7.
1.
2.
3.
1.
2.
3.
4.
5.
6.
Бугров Я.С., Никольский С.М. Высшая математика. Кратные интегралы. Ряды. Функции
комплексного переменного. – М.: Наука, 2003.
Сборник задач по математике для втузов. Т.2 (под ред.Ефимова А.В., Демидовича Б.П.), М.: Наука,
1986.
Задачи и упражнения по математическому анализу для втузов. Под ред. Б.П. Демидовича, М.:
Интеграл-пресс, 1997.
Дополнительная литература (ДЛ)
Краснов М.Л., Киселев А.И. и др. Вся высшая математика, тт. 3 и 4, – М.: УРСС, 2001.
Зорич В.А. Математический анализ, т.2. – М.: МЦНМО, 1998.
Привалов И.И. Введение в теорию функций комплексного переменного. М,: Высшая школа. – 1999.
Методические пособия (МП)
Томашпольский В.Я., Шевченко М.Н., Янов И.О. Числовые ряды. Методические указания к типового расчета. –
М.: МГТУ, 2006.
Агаева Э.И., Ершова М.И., Зотина Р.С. Пособие по теории функций комплексного переменного. – М.: МГТУ,
1992.
Копаев А.В., Садыхов Г.С. Теория функций комплексного переменного. – М.: МГТУ, 1992.
Алгазин О.Д., Богомолов В.Д., Копаев А В. Методы теории функций комплексного переменного в прикладных
задачах. – М.: МГТУ 1993.
Зайцева Г.С., Лошкарев А.И. Интегральные преобразования и операционное исчисление. Методические
указания к типовому расчету. – М.: МГТУ, 1990.
Ванько В.И., Галкин С.В., Морозова В.Д. Методические указания для самостоятельной работы студентов по
разделам «Теория функций комплексного переменного» и «Операционное исчисление». – М.: МВТУ,1988.
Теория функций комплексного переменного и
гармонический анализ
для студентов факультета «Э», обучающихся по программе
«бакалавр»
Дисциплина состоит из 2-х учебных модулей и зачета.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-8
16
Упражнения
1-7
14
Домашние задания текущие
1-7
14
Контроль по модулю №1
8
2
Модуль 2
61
Примечание
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
9-17
18
Упражнения
9-16
16
Домашние задания текущие
9-16
16
Контроль по модулю №2
17
2
Примечание
Модуль 1: Гармонический анализ
Лекции.
ОЛ-1, гл. 1; ОЛ-2, гл.16, § 5-8; ОЛ-4, ч.1,
гл.13, § 3-5.
Лекции 1-2. Числовые ряды. Сходящиеся и
расходящиеся
ряды.
Необходимый
признак сходимости. Простейшие свойства
сходящихся рядов (почленное сложение
рядов, умножение ряда на число,
отбрасывание конечного числа членов
ряда).
Знакоположительные
ряды.
Признаки сравнения. Признаки Даламбера
и Коши. Интегральный признак Коши. Ряды
Дирихле.
Лекция 4. Функциональные ряды. Область
сходимости
функционального
ряда.
Равномерная
сходимость.
Признак
Вейерштрасса равномерной сходимости.
Свойства равномерно сходящихся рядов;
непрерывность
суммы,
почленное
интегрирование и дифференцирование
(без док-ва). Степенные ряды. Теорема
Абеля
ОЛ-1, гл. 2; ОЛ-2, гл.16, §9-13; ОЛ-4, ч.2,
гл.1, §1,2,4.
ОЛ-1, гл. 1; ОЛ-2, гл.16, §1-5; ОЛ-4
гл.13, § 1,2,4.
Лекция 5. Интервал, радиус и область
сходимости степенного ряда. Свойства
ч.1,
степенных
рядов:
равномерная
сходимость,
непрерывность
суммы,
почленное
интегрирование
и
дифференцирование.
Лекция 3. Знакопеременные ряды.
Абсолютная и условная сходимость.
Структура рядов, сходящихся абсолютно и
условно, их свойства. Знакочередующиеся
ряды. Признак Лейбница. Оценка суммы и
остатка ряда.
ОЛ-1, гл. 2; ОЛ-2, гл.16, §13-15; ОЛ-4, ч.2,
гл.1, § 4,5.
62
Лекции 6. Разложение функции в
степенной ряд. Ряд Тейлора и Маклорена.
Теорема о разложении функции в ряд
Тейлора. Разложение в ряд Маклорена
функций: e x ,sin x,cos x,ln 1  x  , 1  x  .
Теорема Дирихле (без док-ва). Разложение
в ряд Фурье периодических, четных и
нечетных функций. Неполные ряды Фурье.
Разложение функций в ряд Фурье на
произвольном отрезке длины 2l .
Разложение функций по произвольной
полной
ортогональной
системе.
Неравенство
Бесселя
и
равенство
Парсеваля. Полнота тригонометрической
системы.
ОЛ-1, гл. 2; ОЛ - 2, гл.16, §15-23.
Лекции 7-8. Ортогональность системы
тригонометрических функций на отрезках
  , и  l , l  . Тригонометрические ряды
ОЛ-1, гл. 3.4, 3.6; ОЛ-2, гл.17 ,§ 1-7, ОЛ-4,
ч.2, гл.10 , §1 - 4.
Фурье и коэффициенты Эйлера-Фурье.
Упражнения
Занятия 1-2. Знакоположительные
ряды.
или ОЛ-10: №2517 2522 2515 2532
2534-2544(четные) 2546 2548 2552
2556 2560 2594 2600 2602 2616
2618 2631 2633 2635.
Ауд.ОЛ-9, гл.12 №1 9 19 21 23 24
26 28 31 32 33 36 40 42 44 49
53-81 (нечетные),
Дома: ОЛ-9,гл.12: №125 127 128
166-180 (четные) 184 186 191 214
219 222 227232 240 244,
или ОЛ-10: № 2401 2405 2416
2417
2422
2425
24272467(нечетные).
или ОЛ-10: №2511 2520 2514 2527
2529 2531 2533 2545 2547 2549
2551 2557 2561 2595 2597 2603
2617 2619 2630 2634 2636.
Дома:ОЛ-9, гл.12: №3 10 20 22 25
27 34 35 37 41 43 50 54 5682(четные)
Занятие 6. Ряды Фурье.
или ОЛ-10 №2402 2406 2418 2420
2421 2426 2428-2468(четные).
Ауд. ОЛ-9, гл.12: №480 482 484
486 488,или ОЛ-10: № 2672 2673
2677 2697 2698.
Занятие 3. Знакопеременные ряды.
Ауд. ОЛ-9, гл.12: №90 92 94 95 97
99 101 103 110 112 ,
или ОЛ-10: №2470
2476 2478 2484(а,в ).
2472
Дома: ОЛ-9, гл.12: №481 483 485
487, или ОЛ-10: №2671 2674 2695
2696.
2474
Занятие 7. Неполные ряды Фурье.
Дома: ОЛ-9,гл.12: №91 93 96 98
100 102 104 111,
Ауд. ОЛ-9, гл.12: №493 495 497
498, или ОЛ-10: №2683 2684 2687
2689 2702.
или ОЛ-10: №2471-2479 (нечетные)
2482 2484 (б,г).
Дома: ОЛ-9, гл.12: №494 499 500,
или ОЛ-10: №2685 2686 2690
2700.
Занятия 4-5. Функциональные
ряды. Степенные ряды. Разложение
функций в степенные ряды.
Занятие 8. Аттестация № 1
Ауд. ОЛ-9, гл.12: №126 129 130
165 169 171 173 175 177 183 185
216 218 226 228 231 243 245 246
«Гармонический анализ»
63
Модуль 2: Теория функций комплексного переменного
Лекции.
Лекция 9. Комплексное переменное,
комплексная плоскость. Задание кривых и областей в
комплексной плоскости:
z  z 0  R, arg z  z 0    ,
функциями: линейной, дробно-линейной, функцией
Жуковского. Показательная функция и логарифм.
ОЛ-6 гл. 9-10.
z  z1  z  z 2  2a,
Лекция
13. Интеграл от непрерывной
функции комплексного переменного, его выражение
через действительные криволинейные интегралы,
основные свойства. Интеграл от аналитической
функции
комплексного
переменного,
его
независимость от пути интегрирования, формула
Ньютона - Лейбница. Теорема Коши для
односвязной и многосвязной областей.
z  z1  z  z 2  2a .
Функция
комплексного
переменного,
ее
геометрический
смысл.
Однозначные
и
многозначные функции. Примеры линейной и
степенной функции.
ОЛ-7 гл.2 §2; ОЛ-8 гл.1 §2, гл.2 §1,2., ОЛ-6, гл.1,3.
Лекция
10.
Ряды
с
Определение функций
комплексными
ОЛ-7 гл.2 § 4; ОЛ-8 гл.1 § 5, ОЛ-6, гл.5.
членами.
e z ,sin z,cos z,sh z,ch z с
Лекция
14.
Вычисление
интегралов
вида
l z  a  dz . Интегральная формула Коши для
помощью степенных рядов. Вывод формул,
связывающих эти функции. Логарифмическая
функция комплексного переменного, ее свойства:
выделение действительной и мнимой части,
многозначность,
главное
значение,
область
определения. Вычисление значений функций
n
функции,
аналитической
в
односвязной
и
многосвязной
области.
Вывод
интегральной
формулы производной n-го порядка. Бесконечная
дифференцируемость
функции
в
точке
аналитичности
e z ,sin z,cos z,sh z,ch z,ln z, z n .
z0 .
Вычисление интегралов
по
замкнутому контуру с помощью интегральной
формулы Коши и интегральной формулы n-ой
производной.
ОЛ-7 гл.4 §2,3; ОЛ-8 гл.2 §1,2, гл.3 §1, гл.4 §1. ОЛ-6,
гл.3, §3.3,3.5.
ОЛ-7 гл.2 § 4, 5, 6, ОЛ-8, гл.5.
Лекция 11. Предел функции комплексного
переменного, непрерывность. Производная функции
комплексного переменного, условия Коши-Римана.
Аналитичность функции в области, в точке.
Гармонические функции, их связь с аналитическими
функциями. Восстановление аналитической функции
по ее действительной или мнимой части.
Геометрический смысл модуля и аргумента
производной.
Однолистные
и
многолистные
функции.
Лекция 15. Ряды Лорана, их область сходимости.
Теоремы о разложении аналитической функции в
кольце в ряд Лорана, аналитической функции в круге
в ряд Тейлора. Интегральные коэффициенты ряда
Тейлора и ряда Лорана.
ОЛ-7 гл.2 § 4, 6; ОЛ-8 гл.2 § 1-2, ОЛ-6, гл.6.
Лекция 16. Изолированные особые точки функции,
их классификация. Поведение функции в окрестности
различных типов особых точек. Связь нулей функции
ОЛ-7 гл.2 §2; ОЛ-8 гл.1 §3,4., ОЛ-6, гл.3,4.
f  z  и полюсов функции
Лекция 12. Конформные отображения.
Основные свойства. Теорема Римана. Конформные
отображения, осуществляемые элементарными
1 . Вычет функции в
f z 
изолированной особой точке. Равенство вычета в
64
точке z0 коэффициенту C1 ряда Лорана функции
f  z по степеням
z  z .
0
комплексного переменного по замкнутому контуру
по замкнутому контуру.
Вычисление вычета в
полюсе (вывод формулы) и в существенно особой
точке. Основная теорема о вычетах. Применение
вычетов к вычислению интегралов от функции
ОЛ-7 гл.4 §1, 2, 3; ОЛ-8 гл.4 § 1, 2 , гл.5 § 1, ОЛ-6,
гл.7,8., §1, 2.
Лекция 17. Резерв.
Упражнения
Занятие 9. Действия с комплексными
числами (повторение). Геометрия на комплексной
плоскости. Функции комплексного переменного и
осуществляемые ими отображения.
ДЛ-6, Занятие 5 или ОЛ-9 гл.11:
Ауд.: № 11.138
11.144 11.146 11.171 11.184
111.189 11.191 11.193 11.195 11.199.
Дома: № 11.140 11.145 11.147 11.172 11.187 11.188
11.194 11.198 11.
Ауд.: ДЛ-6, Занятия 1, 2 или ОЛ-9 гл.11 №11.3 11.4
11.8 11.10 11.11 11.13 11.18 11.20 11.23 11.35
11.40 11.41.
Занятие 13. Интегрирование
комплексного переменного.
Дома: ДЛ-6, Занятия 1, 2 или ОЛ-9 гл.11 №11.1
11.5 11.6 11.7 11.12 11.19 11.21 11.22 11.36.
функций
ДЛ-6, Занятие 6 или ОЛ-9 гл.12:
Занятие 10. Числовые и функциональные
ряды с комплексными членами, определение их
области сходимости, степенные ряды.
Ауд.: №11.230 11.233 11.235 11.237 11.240 11.249
11.251 11.
ДЛ-6, Занятие 3 или ОЛ-9 гл.12:
Дома: №11.231 1.232 11.236 11.238 11.239 11.250
1.252.
Ауд.: №12.165 12.168 12.181 12.183 12.189 12.344
12.347 12.348.
Занятия 14. Разложение функций в ряды
Тейлора и Лорана.
Дома: №12.166 12.167 12.174 12.187 12.192 12.343
12.351 12.246.
ДЛ-6, Занятие 7 или ОЛ-9 гл.12:
Ауд.: №12.214 12.247 12.226 12.232 12.234 12.239
12.352 12.366 12.354.
Занятие
11. Элементарные функции
комплексного переменного, вычисление их значений
в точке, выделение действительной и мнимой
частей. Производная, отыскание аналитической
функции по ее действительной или мнимой части.
Дома: №12.215 12.216 12.227 12.231 12.233 12.238
12.245 12.355 12.360 12.369 12.368.
Занятие
15-16.
Особые
точки,
классификация. Вычисление вычетов в особых
точках. Применение вычетов к вычислению
интегралов от функции комплексного переменного
по замкнутому контуру
ДЛ-6, Занятие 4 или ОЛ-9 гл.11:
Ауд.: №11.53 11.55 11.62 11.64 11.65 11.80 11.112
11.116 11.131 11.132 .
Дома: №11.54 11.56 11.63 11.66 11.67 11.81 11.113
11.115 11.133 11.135 .
Занятие
отображения.
12.
Основные
ДЛ-6, Занятие 8 или ОЛ-9 гл.12:
Ауд.: №12.408 12.411 12.415 12.419 12.420 12.424
12.431 12.433 12.435 .
конформные
65
Дома: №12.409 12.414 12.416 12.421 12.423 12.426
12.432 12.434 12.436.
Занятие 17. Аттестация № 2 «Теория
функций комплексного переменного».
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
лабораторных работ, входному контролю готовности к выполнению лабораторной работы, оформлении отчетов по
лабораторным работам;
Контрольные мероприятия и сроки их проведения
1. ДЗ № 1. Часть 1. «Числовые ряды»
выполнения: выдача — 1-я неделя; прием — 4-я неделя.
2. ДЗ № 1. Часть 2. «Функциональные ряды»
выполнения: выдача — 4-я неделя; прием — 7-я неделя.
Сроки
Сроки
3. Контроль по модулю №1 (РК №1) «Ряды».
проведения – 8 неделя.
Срок
4. ДЗ №2. «Теория функции комплексного переменного»
выполнения: выдача — 9-я неделя; прием — 15-я неделя.
Сроки
5. Контроль по модулю №2 (РК №2) «Теория функции комплексного переменного»,
Срок проведения – 17 неделя.
Литература
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Основная литература (ОЛ)
Власова Е.А. Ряды. Под редакцией В.С.Зарубина, А.П. Крищенко.- М.: МГТУ.- 2006. 612с. (Серия
Математика в техническом университете, вып. IX).
Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2, 3изд. - М.: Наука,
1985.- 560с.
Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции
комплексного переменного. - М.: Наука. - 1989.- 464с.
Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1,2.- М.: Наука. - 1982, 616с.
Кудрявцев Л.Д. Курс математического анализа. - Т.1, 2.- М.: Высшая школа. 1981.- 614 с., 470с.
Морозова В.Д. Теория функций комплексного переменного. Под редакцией Зарубина В.С.,
Крищенко А.П. М.: МГТУ, 2000.
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное
исчисление. М.: Наука, 1986.
Свешников А.Г., Тихонов А.Н. Теория функций комплексного переменного. М.: Наука, 1986.
Сборник задач по математике для втузов, т.2. Под редакцией Ефимова А.В., Демидовича Б.П. М.: Наука,
1986.
Задачи и упражнения по математическому анализу для втузов. Под ред. Демидовича Б.П.- М.: Интегралпресс, 1997.- 416с
66
Дополнительная литература (ДЛ)
1. Краснов М.Л., Киселев Л.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. Задачи и упражнения. М.: Наука. – 1981.
2. Томашпольский В.Я., Шевченко М.Н., Янов И.О. Числовые ряды. Методические указания к
выполнению типового расчета. – М.: МГТУ. – 2006.
3. Дубограй И.В., Дьякова Л.Н., Скуднева О.В. Степенные ряды. Методические указания. -М.: Изд. МГТУ.
– 2005. – 57 с.
4. Нараленков К.М., Шарохина И..В., Тригонометрические ряды Фурье. Методические указания. -М.:
Изд. МГТУ. – 2005. – 40 с
5. Абрагин А.В., Дубровин В.М. Теория функций комплексного переменного. Методические указания к
выполнению домашнего задания. М.: МГТУ. – 2006.
6. Агаева Э.И., Ершова М.И., Зотина Р.С. Пособие по теории функций комплексного переменного. М.: МГТУ. –
1992.
7. Алгазин О.Д., Бутина Т.А., Дубровин В.М. Операционное исчисление. М: МГТУ. – 2012.
1.
Рекомендуемые Интернет-сайты:
Гордин М.П. Лекции по математическому анализу // http://energy.power.bmstu.ru/gormath/entermath.htm
Теория функций комплексного переменного, ряды
Фурье и операционное исчисление
для студентов факультета «Э», обучающихся по программе
«специалист»
Дисциплина состоит из 2-х учебных модулей и зачета.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-9
18
Упражнения
1-9
18
Домашние задания текущие
1-9
18
67
Примечание
Контроль по модулю №1
10
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
10-17
16
Упражнения
11-16
12
Домашние задания текущие
11-16
12
Контроль по модулю №2
17
2
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Примечание
Модуль 1: Теория функций комплексного переменного
Лекции.
Лекция 1. Комплексное переменное, комплексная
плоскость. Задание кривых и областей в
комплексной плоскости:
z  z 0  R, arg z  z 0    ,
Лекция 3.
Ряды
с
Определение функций
комплексными
членами.
z
e ,sin z,cos z,sh z,ch z с
помощью степенных рядов. Вывод формул,
связывающих эти функции. Логарифмическая
функция комплексного переменного, ее свойства:
выделение действительной и мнимой части,
многозначность,
главное
значение,
область
определения. Вычисление значений функций
z  z1  z  z 2  2a,
z  z1  z  z 2  2a .
Функция
комплексного
переменного,
ее
геометрический
смысл.
Однозначные
и
многозначные функции. Примеры линейной и
степенной функции.
e z ,sin z,cos z,sh z,ch z,ln z, z n .
ОЛ-1: гл. 4 §2, 3; ОЛ-2: гл. 2 §1, 2, гл. 3 §1, гл. 4 §1; ОЛ5: гл. 3 §3.3, 3.5.
ОЛ-1: гл. 2 §2; ОЛ-2: гл. 1 §2, гл. 2 §1, 2; ОЛ-5: гл. 1, 3.
Лекция 4. Конформные отображения. Основные
свойства.
Теорема
Римана.
Конформные
отображения элементарными функциями: линейной,
дробно-линейной,
функцией
Жуковского.
Показательная функция и логарифм.
Лекция 2.
Предел
функции
комплексного
переменного, непрерывность. Производная функции
комплексного переменного, условия Коши-Римана.
Аналитичность функции в области, в точке.
Гармонические функции, их связь с аналитическими
функциями. Восстановление аналитической функции
по ее действительной или мнимой части.
Геометрический смысл модуля и аргумента
производной.
Однолистные
и
многолистные
функции.
ОЛ-5: гл. 9, 10; ОЛ-2: гл 6.
Лекция 5. Интеграл от непрерывной функции
комплексного переменного, его выражение через
действительные
криволинейные
интегралы,
основные свойства. Интеграл от аналитической
функции
комплексного
переменного,
его
независимость от пути интегрирования, формула
ОЛ-1: гл. 2 §2; ОЛ-2: гл. 1 §3, 4; ОЛ-5: гл. 3, 4.
68
Ньютона-Лейбница. Теорема Коши для односвязной
и многосвязной областей.
Лекции 8-9. Изолированные особые точки функции,
их классификация. Поведение функции в окрестности
различных типов особых точек. Связь нулей функции
ОЛ-1: гл. 2 §4; ОЛ-2: гл. 1 §5; ОЛ-5: гл. 5.
Лекция 6. Вычисление интегралов вида
f  z  и полюсов функции
 z  a 
n
l
dz .
изолированной особой точке. Равенство вычета в
точке z0 коэффициенту C1 ряда Лорана функции
Интегральная формула Коши для функции,
аналитической в односвязной и многосвязной
области. Вывод интегральной формулы производной
n-го порядка. Бесконечная дифференцируемость
функции в точке аналитичности
z0 .
1 . Вычет функции в
f z 
f  z по степеням
z  z .
0
Вычисление вычета в
полюсе (вывод формулы) и в существенно особой
точке. Основная теорема о вычетах. Применение
вычетов к вычислению интегралов от функции
комплексного переменного по замкнутому контуру и
несобственных интегралов в действительной
области.
Вычисление
интегралов по замкнутому контуру с помощью
интегральной формулы Коши и интегральной
формулы n-ой производной.
ОЛ-1: гл. 2 §4, 5, 6; ОЛ-5: гл. 5.
ОЛ-1: гл. 4 §1, 2, 3; ОЛ-2: гл. 4 §1, 2, гл. 5 §1; ОЛ-5: гл.
7, 8.
Лекция 7. Ряды Лорана, их область сходимости.
Теоремы о разложении аналитической функции в
кольце в ряд Лорана, аналитической функции в круге
в ряд Тейлора. Интегральные коэффициенты ряда
Тейлора и ряда Лорана.
ОЛ-1: гл. 2 §4, 6; ОЛ-2: гл. 2 §1, 2; ОЛ-5: гл. 6.
Упражнения
Занятие 1. Действия с комплексными числами
(повторение). Геометрия на комплексной плоскости.
Функции
комплексного
переменного
и
осуществляемые ими отображения.
Дома: №12.166 12.167 12.174 12.187 12.192 12.343
12.351 12.246.
Занятие 3. Элементарные функции комплексного
переменного, вычисление их значений в точке,
выделение действительной и мнимой частей.
Производная, отыскание аналитической функции по
ее действительной или мнимой части.
ОЛ-3: Занятия 1, 2 или ОЛ-4 гл.11:
Ауд.: №11.3 11.4 11.8 11.10 11.11 11.13 11.18
11.20 11.23 11.35 11.40 11.41.
ОЛ-3: Занятие 4 или ОЛ-4 гл.11:
Дома: №11.1 11.5 11.6 11.7 11.12 11.19 11.21
11.22 11.36.
Ауд.: №11.53 11.55 11.62 11.64 11.65 11.80 11.112
11.116 11.131 11.132.
Занятие 2. Числовые и функциональные ряды с
комплексными членами, определение их области
сходимости, степенные ряды.
Дома: №11.54 11.56 11.63 11.66 11.67 11.81 11.113
11.115 11.133 11.135.
ОЛ-3: Занятие 3 или ОЛ-4 гл.12:
Занятие 4. Основные конформные отображения.
Ауд.: №12.165 12.168 12.181 12.183 12.189 12.344
12.347 12.348.
ОЛ-3: Занятие 5 или ОЛ-4 гл.11:
69
Ауд.: № 11.138 11.144 11.146 11.171
111.189 11.191 11.193 11.195 11.199.
11.184
Занятие 8.
Особые
точки,
классификация.
Вычисление вычетов в особых точках.
Дома: № 11.140 11.145
11.188 11.194 11.198.
11.187
ОЛ-3: Занятие 8 или ОЛ-4 гл.12:
11.147
11.172
Ауд.: №12.408 12.411 12.415 12.419 12.420 12.424
12.431.
Занятие 5. Интегрирование функций комплексного
переменного.
Дома: №12.409 12.414 12.416 12.421 12.423 12.426
12.432.
ОЛ-3: Занятие 6 или ОЛ-4 гл.12:
Ауд.: №11.230 11.233 11.235 11.237 11.240 11.249
11.251.
Занятие 9. Применение вычетов к вычислению
интегралов от функции комплексного переменного
по замкнутому контуру и несобственных интегралов
в действительной области.
Дома: №11.231 11.232 11.236 11.238 11.239 11.250
11.252.
ОЛ-3: Занятие 8 или ОЛ-4 гл.12:
Занятия 6-7. Разложение функций в ряды Тейлора и
Лорана.
Ауд.: №12.433 12.435 12.439 12.441 12.443 12.445
12.456 12.459 12.463.
ОЛ-3: Занятие 7 или ОЛ-4 гл.12:
Дома: №12.434 12.436 12.440 12.442 12.444 12.447
12.459 12.464.
Ауд.: №12.214 12.247 12.226 12.232 12.234 12.239
12.352 12.366 12.354.
Занятие 10. Рубежный контроль по
модулю
1
ТФКП.
Дома: №12.215 12.216 12.227 12.231 12.233 12.238
12.245 12.355 12.360 12.369 12.368.
Модуль 2: Ряды Фурье и операционное исчисление
Лекции.
Лекция 12. Разложение функций по произвольной
полной ортогональной системе. Неравенство Бесселя
и
равенство
Парсеваля.
Полнота
тригонометрической системы.
Лекции 10-11.
Ортогональность
системы
тригонометрических функций на отрезках   ,  и
 l, l  .
Тригонометрические
ряды
Фурье
и
ОЛ-8: гл. 3, 6.
коэффициенты Эйлера-Фурье. Комплексная форма
ряда Фурье. Теорема Дирихле (без док-ва).
Разложение в ряд Фурье периодических, четных и
нечетных функций. Неполные ряды Фурье.
Разложение функций в ряд Фурье на произвольном
отрезке длины 2l .
Лекция 13.
Понятие
об
интегральном
преобразовании. Преобразования Фурье и Лапласа,
связь между преобразованиями Фурье и Лапласа.
Оригинал и изображение. Теорема о существовании
изображения. Поведение изображения в бесконечно
удаленной точке. Единичная функция Хэвисайда и ее
изображение.
ОЛ-8: гл. 3, 4; ДЛ-8: гл. 17 §1-7; ДЛ-2: гл. 10 §1-4.
70
ОЛ-1: гл. 7 §1, 2, 4; ОЛ-2: гл. 8 §11; ОЛ-6: гл. 1 §1, 2;
ОЛ-7: гл. 5 §6.1; МП-2: гл. 1, 2 §1, 2.
ОЛ-1: гл. 7 §2; ОЛ-2: гл. 8 §1; ОЛ-6: гл. 3 §1, 4, гл. 2 §3;
ОЛ-7: §6.2, 6.3; МП-2: гл. 2 §3.
Лекция 14. Основные теоремы операционного
исчисления: линейности, подобия, смещения,
запаздывания,
о
дифференцировании
и
интегрировании оригиналов и изображений.
Теоремы о связи начальных и конечных значений
изображения и оригинала. Таблица оригиналов и
изображений.
Лекция 16. Свертка оригиналов и ее изображение.
Формулы
обращения.
Теоремы
разложения.
Интеграл Дюамеля.
ОЛ-1: гл. 7 §2; ОЛ-2: гл. 8 §1; ОЛ-6: гл. 2 §4, гл. 4 §3;
ОЛ-7: §6.4; МП-2: гл. 2, §4.
Лекция 17. Операционный метод решения линейных
дифференциальных уравнений с постоянными
коэффициентами и систем таких уравнений.
ОЛ-1: гл. 7 §2; ОЛ-2: гл. 8 §1; ОЛ-6: гл. 2 §1-6; ОЛ-7:
§6.2, 6.3; МП-2: гл. 2 §3.
ОЛ-1: гл. 8 §1; ОЛ-2: гл. 8 §1, 3; ОЛ-6: гл. 5 §1-4; ОЛ-7:
§6.5, МП-2: гл. 3, §1, 2.
Лекция 15.
Нахождение
изображения
периодического оригинала. Дельта-функция Дирака
и ее изображение. Импульсные функции и их
изображения.
Упражнения
или ОЛ-4 гл.13 §1, 2:
Занятие 11. Ряды Фурье.
Ауд.: ОЛ-4 гл.12 №12.480
12.486 12.488
12.482
Ауд.: №13.1 13.2 13.6 13.9 13.17 13.20 13.29 13.37
13.47 13.53 13.58 13.74 13.76 13.78 13.79 13.82
13.84 13.86.
12.484
или ДЛ-4 № 2672 2673 2677 2697 2698.
Дома: ОЛ-4 гл.12 №12.481 12.483 12.485
12.487
Дома: №13.3 13.7 13.8 13.10 13.19 13.22 13.26
13.30 13.40 13.48 13.52 13.61 13.75 13.77 13.80
13.83 13.85 13.87.
или МП-3 №2671 2674 2695 2696.
Занятие 15. Теоремы разложения.
Занятие 12. Неполные ряды Фурье.
ОЛ-4 гл.13 §2:
Ауд.: ОЛ-4 гл.12 №12.493 12.495 12.497
12.498 или ДЛ-4 №2683 2684 2687 2689
2702.
Ауд.: №13.88
13.104.
Дома: ОЛ-4 гл.12 №12.494 12.499 12.500
или ДЛ-10 №2685 2686 2690 2700.
Дома: №13.89 13.91 13.94 13.97 13.99 13.101
13.103.
Занятия 13-14.
оригиналов.
Нахождение
изображений
и
13.90
13.93
13.96
13.98
13.102
Занятие 16. Применение операционного исчисления
к решению линейных дифференциальных уравнений
с постоянными коэффициентами и систем таких
уравнений.
ДЛ-1:
ДЛ-1:
Ауд.: №524 526 529 538 540 546 555 560 564 566
569 573 576 580 613 625 634 635.
Ауд.: №654 657 665 683 718 720 758.
Дома: №655 666 721 760 762.
Дома: №528 536 542 547 563 565 570 574 579
620 627 633.
или ОЛ-4 гл.13 §3:
71
Ауд.: 13.105 13.111 13.114 13.117 13.119 13.129
13.132 13.137.
Занятие 17. Контроль по модулю 2 «Ряды Фурье и
операционное исчисление».
Дома: 13.107 13.112 13.115 13.118 13.121 13.130
13.134 13.136 13.138.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
лабораторных работ, входному контролю готовности к выполнению лабораторной работы, оформлении
отчетов по лабораторным работам;
Контрольные мероприятия и сроки их проведения
1. ДЗ № 1. Часть 1. «Комплексные числа. Функции комплексного переменного. Дифференцирование
функций комплексного переменного. Конформные отображения»
Сроки выполнения: выдача — 1-я неделя; прием — 4-я неделя.
2. ДЗ № 1. Часть 2. «Интегрирование функций комплексного переменного. Ряды Тейлора и Лорана. Теория
вычетов и её приложения»
Сроки выполнения: выдача — 5-я неделя; прием — 8-я неделя.
3. Контроль по модулю №1 (РК №1) «Теория функции комплексного переменного».
Срок проведения – 10 неделя.
4. ДЗ №2. Часть 1. «Ряды Фурье»
Сроки выполнения: выдача — 10-я неделя; прием — 12-я неделя.
5. ДЗ №2. Часть 2. «Операционное исчисление»
Сроки выполнения: выдача — 12-я неделя; прием — 15-я неделя.
6. Контроль по модулю №2 (РК №2) «Ряды Фурье и операционное исчисление»,
Срок проведения – 17 неделя.
Литература
1.
2.
3.
4.
5.
6.
7.
Основная литература (ОЛ)
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное
исчисление. М.: Наука, 1986.
Свешников А.Г., Тихонов А.Н. Теория функций комплексного переменного. М.: Наука, 1986.
Агаева Э.И., Ершова М.И., Зотина Р.С. Пособие по теории функций комплексного переменного. М.:
МГТУ, 1992.
Сборник задач по математике для втузов, т.2. Под редакцией Ефимова А.В., Демидовича Б.П. М.:
Наука, 1986.
Морозова В.Д. Теория функций комплексного переменного. Под редакцией Зарубина В.С.,
Крищенко А.П. М.: МГТУ, 2000.
Шостак Р.Я. Операционное исчисление. М.: Высшая школа, 1972.
Волков И.К. Канатников А.Н. Интегральные преобразования и операционное исчисление. Под
редакцией Зарубина В.С., Крищенко А.П. М.: МГТУ, 1996.
72
8. Власова Е.А. Ряды. Под редакцией В.С.Зарубина, А.П. Крищенко.- М.: МГТУ.- 2006. 612с. (Серия
Математика в техническом университете, вып. IX).
Дополнительная литература (ДЛ)
1. Краснов М.Л., Киселев Л.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. Задачи и упражнения. М.: Наука, 1981.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2, 13изд. - М.: Наука,
1985.- 560с.
3. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1,2.- М.: Наука. - 1982, 616с.
4. Задачи и упражнения по математическому анализу для втузов.
Под ред. Демидовича Б.П.- М.:
Интеграл-пресс, 1997.- 416с.
Методические пособия
1. Абрагин А.В., Дубровин В.М. Теория функций комплексного переменного. Методические указания
к выполнению домашнего задания. М.: МГТУ, 2006.
2. Лошкарев А.И., Облакова Т.В. Интегральные преобразования и операционное исчисление. М.:
МГТУ, 2007
3. Нараленков К.М., Шарохина И..В., Тригонометрические ряды Фурье. Методические указания. -М.:
Изд. МГТУ, 2005. 40 с
4. Алгазин О.Д., Бутина Т.А., Дубровин В.М. Операционное исчисление. М: МГТУ, 2012.
Рекомендуемые Интернет-сайты:
1. Гордин
М.П.
Лекции
по
математическому
анализу
//
http://energy.power.bmstu.ru/gormath/entermath.htm
Дополнительные главы математического анализа
4 семестр, спец. ИУ9
ЛИТЕРАТУРА
Основная литература (ОЛ)
Колмогоров А.Н., Фомин С.В., Элементы теории функций и функционального анализа, Наука, 1972. –
496 с.
Богачев В.И., Смолянов О.Г., Действительный и функциональный анализ: университетский курс. – М.Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2009. – 724 с.
Городецкий В.В., Нагнибида Н.И., Настасиев П.П., Методы решения задач по функциональному
анализу: Учебное пособие. – Киев: Высшая школа, 1990. – 479 с.
Дополнительная литература (ДЛ)
Богачев В.И., Основы теории меры. Том 1,2. – Москва-Ижевск: РХД, 2003.
Натансон И.П. Теория функций вещественной переменной – М.: Наука, 1974. – 480 с.
Халмош П. Теория меры. – М.: Изд-во «Факториал Пресс», 2003. – 256 с.
Шилов Г.Е., Гуревич Б.Л. Интеграл, мера и производная. – М.: Наука, 1967. – 220 с.
73
Дьяченко М.И., Ульянов П.Л., Мера и интеграл. – М.: Факториал, 1998. – 160 с.
Босс В. Лекции по математике. Функциональный анализ. – М.: Изд-во ЛКИ, 2007. – 216 с.
Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. – М.: Мир, 1967. – 252с.
Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления: В 3 т. Т. III – 8-е изд. – М.:
ФИЗМАТЛИТ, 2002. – 728 с.
Антоневич А.Б., Князев П.Н., Радыно Я.В., Задачи и упражнения по функциональному анализу. –
Минск: Высшая школа, 1978. – 205 с.
ЛЕКЦИИ
Модуль 1. Теория меры, конструкция интеграла Лебега
Лекции 1–2. Кольцо множеств, различные определения, их эквивалентность.
Теорема о пересечении колец. Теорема о существовании и единственности минимального
кольца, содержащего данную систему множеств. Полукольцо множеств. Сигма-алгебра
множеств, ее свойства. Борелевская сигма-алгебра. Мера на полукольце множеств.
Продолжение меры с полукольца, на наименьшее содержащее его кольцо. Счетная
аддитивность меры. Непрерывность меры. Связь непрерывности и счетной аддитивности..
Пример меры, не являющейся счетно-аддитивной. Теорема Каратеодори.
Лекции 3–4. Схема построения лебегова продолжения меры (без док-ва), случай
полукольца с единицей и без нее. Свойства меры Лебега. Теорема о существовании
неизмеримых по Лебегу множеств на Rn.
Лекция 5. Измеримые функции, измеримость по Лебегу, борелевость. Операции
над измеримыми функциями. Измеримость предела поточечно и почти всюду сходящейся
последовательности измеримых функций.
Лекциии 6–7. Теорема Егорова. Теорема Лузина. Фундаментальность и сходимость
по мере. Связь сходимости по мере и почти всюду в случае конечной и сигма-конечной
меры. Пример последовательности, сходящейся по мере и не сходящейся почти всюду.
Интеграл Лебега, его построение. Простые функции, интеграл Лебега для простых
функций, его свойства.
Лекции 8–9. Распространение определения интеграла Лебега с помощью
предельного перехода. Свойства интеграла Лебега. Неравенство Чебышева. Абсолютная
непрерывность интеграла Лебега. Критерий интегрируемости функции.
Модуль 2. Теория интеграла Лебега, действительный анализ
Лекции 10–12. Предельный переход под знаком интеграла Лебега: теоремы Лебега,
Б. Леви, Фату. Взаимосвязь интегралов Римана и Лебега. Полнота пространства L1(D).
Сходимость в среднем, ее связь со сходимостью почти всюду и сходимостью по мере.
Произведение мер.
Лекции 13–14. Теорема Фубини. Теорема Тонелли. Теорема Радона — Никодима.
Теорема Хана — Жордана.
Лекция 15. Связь интеграла с производной. Теорема Лебега о первообразной.
Лекции 16–17. Функции ограниченной вариации и абсолютно непрерывные
функции. Их свойства. Формула Ньютона — Лейбница. Формула интегрирования по
частям. Меры Лебега — Стилтьеса. Интеграл Лебега — Стилтьеса. Интеграл Римана —
Стилтьеса, его свойства, его связь с интегралом Лебега — Стилтьеса. Формула замены
переменных в интеграле Лебега. Приложения меры и интеграла Лебега в теории
вероятности.
74
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Теория меры, конструкция интеграла Лебега
Занятие 1. Канторово множество, его мощность. Системы множеств: кольцо,
полукольцо, сигма-алгебра; их свойства. Структура открытых множеств в Rn. Классы
множеств, порождающие борелевскую сигма-алгебру на прямой. Мощность борелевской
сигма-алгебры. Мера на кольце множеств, ее свойства. Счетная аддитивность меры.
Методическая разработка кафедры.
Занятие 2. Вычисление меры Лебега различных множеств. Меры Лебега —
Стилтьеса на прямой, примеры. Абсолютная непрерывность и сингулярность мер.
Дискретные меры. Канторова лестница, ее длина.
Методическая разработка кафедры.
Занятие 3. Измеримые и неизмеримые по Лебегу множества. Мощность сигмаалгебры всех измеримых по Лебегу множеств. Структура измеримых по Лебегу множеств.
Измеримые функции и их свойства.
Методическая разработка кафедры.
Занятия 4-5. Измеримые функции и их свойства. Сходимость по мере. Связь
сходимости по мере и почти всюду в случае конечной и сигма-конечной меры. Пример
последовательности, сходящейся по мере и не сходящейся почти всюду.
Методическая разработка кафедры.
Занятие 6. Вычисление интегралов Лебега. Связь интегралов Лебега и Римана.
Применение теорем о предельном переходе для вычисления интегралов Лебега.
Методическая разработка кафедры/
Занятие 7. Пространство L1(D), его свойства. Сходимость в среднем. Пространства
Lp(D). Неравенство Чебышева. Сходимости: равномерная, поточечная, почти всюду, по
мере, в среднем, в среднем квадратичном; их взаимосвязь.
Методическая разработка кафедры.
Занятия 8-9. Рубежный контроль.
Модуль 2. Теория интеграла Лебега, действительный анализ
Занятия 10-12. Абсолютно непрерывные функции. Функции ограниченной
вариации. Интеграл Лебега с переменным верхним пределом. Разложение функции
ограниченной вариации на сумму абсолютно непрерывной, сингулярной и функции
скачков. Связь с разложением мер. Абсолютная непрерывность заряда.
Методическая разработка кафедры
Занятия 13-14. Теорема Радона — Никодима. Случай заряда, построенного по
абсолютно непрерывной функции (сведение интеграла Лебега — Стилтьеса к интегралу
Лебега). Интеграл Римана — Стилтьеса, его свойства. Интегрирование по частям.
Вычисление интегралов Стилтьеса.
Методическая разработка кафедры
Занятие 15. Подготовка к рубежному контролю.
Занятия 16-17. Рубежный контроль по модулю 2.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ
Модуль 1. Теория меры, конструкция интеграла Лебега (1–10 неделя).
75
Рубежный контроль по модулю 1 (10 неделя).
Модуль 2. Теория интеграла Лебега, действительный анализ (11–17 неделя).
Рубежный контроль по модулю 2 (17 неделя).
Комплексный анализ
4 семестр, спец. ИУ9
ЛИТЕРАТУРА
Основная литература (ОЛ)
Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. – М.: Наука, 1967, – 304 с.
Маркушевич А.И. Теория аналитических функций: Т.1, 2. – М.: Наука, 1968.
Лаврентьев М.А., Шабат Б.В., Методы теории функций комплексного переменного. - М.: Наука, 1973, –
736 с.
Привалов И.И. Введение в теорию функций комплексного переменного. – М.: Физматгиз, 1960. – 444 с.
Шабат Б.В. Введение в комплексный анализ. Функции одного переменного: Учебник: В 2-х ч. Ч. 1. – 4е изд. – СПб.: Лань, 2004. – 336 с.
Сборник задач по теории аналитических функций / под ред. М.А. Евграфова. – М.: Наука, 1972, – 416 с.
Дополнительная литература (ДЛ)
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. - М.: Наука, 1966. – 331 с.
Волковыский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций комплексного
переменного. - М.: Наука, 1970. – 320 с.
Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. – М.: Наука, 1981.
Шабунин М., Половинкин Е., Карлов М. Сборник задач по теории функций комплексного переменного.
– М.: БИНОМ, Лаборатория знаний, 2006. – 362 с.
Леонтьева Т.А., Панферов В.С., Серов В.С. Задачи по теории функций комплексного переменного с
решениями. – М.: Мир, 2005. – 360 с.
ЛЕКЦИИ
Модуль 1. Элементарная теория
Лекции 1–2. Комплексные числа. Алгебраическая и тригонометрическая форма.
Возведение в степень и извлечение корней. Топология комплексной плоскости:
окрестности, предельные точки, граница множества, открытость, замкнутость, связность,
компакт, область. Расширенная комплексная плоскость и её топология.
Стереографическая
проекция,
сфера
Римана.
Предел
последовательности.
Функциональные последовательности, область сходимости, равномерная сходимость.
Функциональные ряды. Признак Вейерштрасса. Степенные ряды. Равномерная
сходимость. Круг и радиус сходимости. Теоремы Абеля. Предел функции.
Непрерывность. Определение и свойства функции ez. Показательная форма комплексного
числа. Основные элементарные функции комплексного переменного.
Лекции 3–4. Дифференцируемость функции комплексного переменного. Условия
Коши-Римана. Определение голоморфной функции в точке и в области. Свойства
комплексной производной. Производная сложной и обратной функции. Производная по
76
направлению. Обобщённые условия Коши-Римана. Геометрический смысл комплексной
производной. Понятие конформного отображения. Дифференцируемость в бесконечности.
Лекции 5–6. Дробно-линейные отображения (ДЛО) и их свойства. Геометрия
Лобачевского, модель Пуанкаре. Степенная функция и экспонента. Их основные
(максимальные) области конформности. Функция Жуковского.
Лекции 7–8. Многозначные функции, их непрерывные и голоморфные ветви.
Корень степени n и логарифм. Их основные ветви и области конформности. Общая
степенная и показательная функция. Тригонометрические и гиперболические функции.
Обратные тригонометрические функции. Функции arcsin(z), arctg(z). Обратный принцип
соответствия границ и принцип симметрии Римана — Шварца (б/д). Гармонические
функции, их связь с голоморфными. Метод конформных отображений для решения
краевых задач для уравнения Лапласа.
Модуль 2. Ряды и контурные интегралы
Лекция 9. Пути и кривые в C. Теорема Жордана (б/д). Приращение (полярного)
аргумента вдоль пути. Интеграл по комплексному переменному вдоль пути. Теорема о
существовании интеграла от непрерывной функции вдоль спрямляемого пути. Основные
свойства интеграла. Вычисление интеграла вдоль непрерывно-дифференцируемого пути.
Интеграл вдоль кривой. Оценка интеграла. Теорема Коши для односвязных областей.
Лекция 10. Интегральная теорема Коши для допустимых областей. Теорема Коши
для функций, голоморфных внутри области и непрерывных на границе. Комплексная
первообразная. Теорема о существовании первообразной в односвязной области. Формула
Ньютона-Лейбница. Интегральная формула Коши.
Лекция 11. Теорема о среднем. Принцип максимума модуля. Основная теорема
алгебры. Формула Коши для производных. Бесконечная дифференцируемость
голоморфных функций. Теорема Морера.
Лекция 12. Равномерная сходимость внутри области. Теоремы Вейерштрасса.
Степенные ряды, их свойства. Почленная дифференцируемость и интегрируемость
степенных рядов. Единственность разложения в степенной ряд. Теорема о разложении
голоморфной функции в ряд Тейлора. Эквивалентность голоморфности и аналитичности.
Табличные разложения в ряд Маклорена.
Лекции 13–14. Неравенства Коши для коэффициентов ряда Тейлора. Теорема
Лиувилля. Формула Тейлора. Теорема о нулях голоморфных функций. Локальная теорема
единственности, её следствия. Особые точки на границе круга сходимости. Обобщенные
степенные ряды. Кольцо сходимости. Теорема Лорана. Теорема об устранимой особой
точке. Изолированные особые точки и их классификация в терминах рядов Лорана.
Вычеты и их вычисление. Теорема Коши о вычетах и о полной сумме вычетов.
Модуль 3. Приложения ТФКП
Лекция 15. Правило Лопиталя для аналитических функций. Теорема Сохоцкого.
Большая теорема Пикара (б/д) и вывод из неё малой. Лемма Жордана. Логарифмический
вычет и его вычисление.
Лекция 16-17. Принцип аргумента. Теорема Руше. Элементы и их аналитическое
продолжение (непосредственное и по цепи). Многозначные аналитические функции и их
римановы поверхности, примеры n z и Ln z, понятие о точках ветвления. Продолжение
вдоль пути и его единственность. Аналитическое продолжение по близким и по
гомотопным путям. Теорема о монодромии. Аналитическое продолжение первообразной.
Полная аналитическая функция (ПАФ) в смысле Вейерштрасса: теорема Пуанкаре —
77
Вольтерра, голоморфные ветви, аналитичность ПАФ над точкой и над областью.
Критерий аналитичности ПАФ над областью. Количество значений аналитичной над
областью ПАФ. Изолированные особые точки неоднозначного характера; точки
ветвления.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Элементарная теория
Занятия 1–3. Операции над комплексными числами: сложение и вычитание,
умножение и деление. Сопряженные числа. Модуль и аргумент, тригонометрическая
форма записи. Возведение в степень и извлечение корня, формула Муавра. Решение
уравнений и неравенств с комплексными коэффициентами. Последовательности и ряды
комплексных чисел. Множества в комплексной плоскости. Стереографическая проекция.
Выделение действительной и мнимой части, модуля и аргумента функции комплексного
переменного. Изображение кривых. Элементарные функции и числовые выражения.
Функциональные ряды в комплексной плоскости.
Методическая разработка кафедры.
Занятие 4. Дифференцируемость функций комплексного переменного
восстановление голоморфной функции по ее действительной или мнимой части.
Методическая разработка кафедры.
и
Занятие 5. Дробно-линейные отображения и их свойства; применение ДЛО к
конформным отображениям областей.
Методическая разработка кафедры.
Занятие 6. Степенная функция, экспонента и тригонометрические функции.
Применение элементарных функций к конформным отображениям областей.
Методическая разработка кафедры.
Занятие 7. Принцип симметрии. Применение элементарных функций к
конформным отображениям областей. Перевод различных областей в верхнюю
полуплоскость посредством конформных однолистных отображений.
Методическая разработка кафедры.
Занятие 8. Рубежный контроль модулю.
Модуль 2. Ряды и контурные интегралы
Занятие 9. Интегрирование функций комплексного переменного. Теорема и
формула Коши. Вычисление интегралов с их помощью.
Методическая разработка кафедры.
Занятие 10. Разложение в степенной ряд. Нули голоморфных функций. Разложение
функции в ряд Лорана. Особые точки и их классификация.
Методическая разработка кафедры.
Занятия 11–12. Вычеты, их вычисление. Вычет в бесконечной точке. Вычисление
интегралов при помощи вычетов (с помощью вычетов внутри и снаружи области).
Методическая разработка кафедры.
Занятие 13. Интегралы по вещественной прямой. Вычисление вещественных
интегралов, содержащих тригонометрические функции.
Методическая разработка кафедры.
Занятие 14. Рубежный контроль по модулю.
78
Модуль 3. Приложения ТФКП
Занятие 15. Вычисление интегралов с помощью
Логарифмический вычет. Принцип аргумента. Теорема Руше.
Методическая разработка кафедры
леммы
Жордана.
Занятие 16. Гармонические функции, их связь с аналитическими функциями.
Свойства гармонических функций. Интеграл Пуассона. Решение задачи Дирихле для
уравнения Лапласа с помощью конформных отображений.
Методическая разработка кафедры
Занятие 17. Рубежный контроль по модулю.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ
Модуль 1. Элементарная теория (1–8 недели).
Рубежный контроль по модулю 1 (8 неделя).
Модуль 2. Ряды и контурные интегралы (9–14 недели).
Рубежный контроль по модулю 2 (14 неделя).
Модуль 3. Приложения ТФК (15–17 недели).
Рубежный контроль по модулю 3 (17 неделя).
Теория вероятностей и математическая статистика
4-й семестр 2012–2013, спец. БМТ-1,2
ЛИТЕРАТУРА
Основная литература (ОЛ)
Теория вероятностей. / В.А. Печинкин, О.И. Тескин, Г.М. Цветкова и др.; Под ред. В.С. Зарубина,
А.П. Крищенко. М.: Изд-во МГТУ им. Н.Э. Баумана, 1998. 456 с.
Математическая статистика. / В.Б. Горяинов, И.В. Павлов, Г.М. Цветкова и др.; Под ред. В.С. Зарубина,
А.П. Крищенко. М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. 424 с.
Сборник задач по математике для втузов. В четырех частях. Ч.4. / Под ред. А.В.Ефимова и А.С.
Поспелова. М.: Наука, 2003. 432 с.
Дополнительная литература (ДЛ)
Ширяев А.Н. Вероятность. М.: Наука, 1980. 576 с.
Ивченко Г.И., Медведев Ю.И. Математическая статистика. Учебное пособие для втузов. М.: Высш.
шк., 1984. 246 с.
Прохоров А.В., Ушаков В.Г., Ушаков Н.Г. Задачи по теории вероятностей. Основные понятия,
предельные теоремы, случайные процессы. Наука, 1986, 328 с.
Ивченко Г.И., Медведев Ю.И., Чистяков А.В. Сборник задач по математической статистике. М.:
Высш. шк., 1989, 256 с.
Сборник задач по теории вероятностей, математической статистике, теории случайных функций. Под
ред. А.А.Свешникова. М.: Наука, 1965. 656 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.
Учеб. пособие для студентов вузов М.: Высш. шк., 1998. 400 с.
Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. Учеб. пособие для втузов.
М.: Высш. шк., 2000. 366 с.
Методические пособия (МП)
Тескин О.И., Тверетинов Д.И., Северцев Н.А. Методические указания к решению задач по теории
вероятностей и математической статистике. М.: МВТУ, 1981. 58 с.
79
Панов В.Ф., Петрухина О.С., Сержантова М.М. Учебное пособие к проведению семинарских занятий
по теории вероятностей и математической статистике. М.: МВТУ, 1988. 29 с.
Тескин О.И., Пустовалова Г.П., Сержантова М.М. Учебное пособие по применению вероятностных
методов и статистических моделей в инженерных задачах. Ч. 1. М.: МВТУ, 1982. 52 с.
ескин О.И., Пустовалова Г.П., Сержантова М.М. Учебное пособие по применению вероятностных
методов и статистических моделей в инженерных задачах. Ч. 2. М.: МВТУ, 1983. 31 с.
ЛЕКЦИИ
МОДУЛЬ 1: Случайные события
Лекция 1. Случайное испытание. Элементарное событие и пространство
элементарных событий. Случайные события и их свойства. Комбинаторное и
геометрическое определение вероятности. Аксиоматическое определение вероятности.
Свойства вероятности. Теорема сложения вероятностей.
ОЛ-1: 1.1, 1.2, 2.1, 2.3, 1.3, 2.5.
Лекции 2-3. Условная вероятность. Теорема умножения. Независимые случайные
события. Формула полной вероятности. Формула Байеса. Биномиальная схема
независимых испытаний. Формула Бернулли и следствия из нее.
ОЛ-1: 3.1–3.3, 3.4–3.6.
МОДУЛЬ 2: Случайные величины
Лекция 4. Случайные величины. Функция распределения и ее свойства.
Дискретные случайные величины. Определение математического ожидания и дисперсии
дискретных случайных величин.
ОЛ-1: 4.1–4.3, 7.1–7.3.
Лекция 5. Непрерывные случайные величины. Плотность
вероятности и ее основные свойства. Функции от случайных величин.
ОЛ-1: 4.5, 6.1–6. 5.
распределения
Лекция 6. Основные вероятностные распределения: биномиальное, пуассоновское,
геометрическое, равномерное, экспоненциальное, нормальное. Математическое ожидание
и его свойства. Дисперсия и ее свойства.
ОЛ-1: 4.4, 4.6, 7.1, 7.3.
Лекция 7. Случайные векторы. Свойства функции распределения случайного
вектора. Дискретные случайные векторы.
ОЛ-1: 5.1, 5.2.
Лекция 8. Непрерывные случайные векторы. Свойства плотности распределения
вероятности непрерывного случайного вектора. Вероятность попадания случайного
вектора в прямоугольную и произвольную области.
ОЛ-1: 5.3.
Лекция 9. Ковариация и ее основные свойства. Коэффициент корреляции и его
основные свойства.
ОЛ-1: 7.4, 5.5.
Лекция 10. Условные законы распределения. Условные математическое ожидание и
дисперсия.
ОЛ-1: 8.1–8.2.
Лекция 11. Многомерное нормальное распределение. Линейные преобразования
нормально распределенных случайных величин. Метод линеаризации.
ОЛ-1: 5.5, 6.6.
80
Лекция 12. Неравенства Чебышева. Закон больших чисел в форме Чебышева.
Центральная предельная теорема. Теорема Муавра — Лапласа.
ОЛ-1: 9.1–9.4.
МОДУЛЬ 3: Математическая статистика
Лекция 13. Основные задачи математической статистики. Определение случайной
выборки, вариационного ряда, эмпирической функции распределения, гистограммы.
Теорема о сходимости эмпирической функции распределения к теоретической.
Выборочные числовые характеристики.
ОЛ-2: 1.1–1.2.
Лекция 14. Точечные оценки неизвестных параметров. Определение
несмещенности и состоятельности оценок. Эффективные оценки. Метод моментов. Метод
максимального правдоподобия.
ОЛ-2: 2.1, 2.2, 2.3.
Лекция 15. Интервальное оценивание. Общие методы построения доверительных
интервалов. Построение доверительных интервалов для математического ожидания
нормальной случайной величины при известной и неизвестной дисперсиях. Построение
доверительного интервала для дисперсии нормальной случайной величины при
неизвестном математическом ожидании. Доверительный интервал для параметра
биномиального распределения. Приближенные доверительные интервалы.
ОЛ-2: 3.1–3.3.
Лекция 16. Проверка статистических гипотез. Ошибки первого и второго рода при
проверке гипотез, мощность критерия. Общая схема проверки гипотез. Критерий
Неймана-Пирсона.
ОЛ-2: 4.1–4.3.
Лекция 17. Проверка гипотез о значении математическом ожидании нормальной
случайной величины при известной и неизвестной дисперсиях. Проверка гипотезы о
значении дисперсии нормальной случайной величины при неизвестном математическом
ожидании. Проверка гипотез о равенстве математических ожиданий двух нормальных
случайных величин, когда дисперсии неизвестны и равны. Проверка гипотез о равенстве
дисперсий двух нормальных случайных величин.
ОЛ-2: 4.5.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
МОДУЛЬ 1: Случайные события
Занятие 1. Пространство элементарных событий. Алгебра событий. Классическое
определение вероятностей. Элементы комбинаторики. Непосредственный подсчет
вероятностей. Геометрическое определение вероятностей.
Ауд.: ОЛ-1 (вопросы и задачи): 1.13, 1.15, 1.21, 2.17, 2.21, 2.25, 2.27, 2.29, 2.33, 2.35, 2.39
или
ОЛ-3: 18.1, 18.12, 18.14, 18.16, 18.66, 18.79, 18.90, 18.98, 18.100, 18.142, 18.153.
Дома: ОЛ-1 (вопросы и задачи): 1.12, 1.14, 1.20, 2.18, 2.22, 2.26, 2.28, 2.30, 2.32, 2.34, 2.38
или
ОЛ-3: 18.2, 18.13, 18.15, 1817, 18.67, 18.80, 18.91, 18.99, 18.101, 18.143, 18.154.
81
Занятие 2. Условная вероятность. Теоремы умножения и сложения. Формула
полной вероятности. Формула Байеса. Биномиальная схема независимых испытаний.
Формула Бернулли.
Ауд.: ОЛ-1 (вопросы и задачи): 3.21, 3.23, 3.25, 3.26, 3.28, 3.31, 3.33, 3.35, 3.37, 3.39, 3.40
или
ОЛ-3: 18.164, 18.176, 18.196, 18.229, 18.251, 18.325, 18.328, 18.336, 18.343, 18.348.
Дома: ОЛ-1 (вопросы и задачи): 3.22, 3.24, 3.27, 3.29, 3.30, 3.23 3.34, 3.36, 3.38 или
ОЛ-3: 18.165, 18.177, 18.197, 18.236, 18.252, 18.326, 18.332, 18.337, 18.345, 18.349.
МОДУЛЬ 2: Случайные величины
Занятие 3. Законы распределения одномерных случайных величин. Числовые
характеристики одномерных случайных величин. Законы распределения случайных
векторов. Числовые характеристики случайных векторов. (математическое ожидание,
дисперсия, ковариация, коэффициент корреляции).
Ауд.: ОЛ-1 (вопросы и задачи): 4.23, 4.20, 4.27, 4.31, 4.35, 5.29, 5.27, 5.32, 5.33, 5.38, 7.38,
7.39, 7.41 или
ОЛ-3: 18.258, 18.259, 18.261, 18.267, 18.269, 18.297, 18.352, 18.366, 18.260, 18.262, 18.268,
18.236, 18.271, 18.299, 18.356, 18.368.
Дома: ОЛ-1 (вопросы и задачи): 4.24, 4.26, 4.32, 3.34, 4.38, 5.35, 5.30, 5.34, 7.40, 7.42, 7.49.
Занятие 4. Функции от случайных величин. Функции от случайных векторов.
Условные законы распределения. Условные математическое ожидание и дисперсия.
Многомерное нормальное распределение.
Ауд.: ОЛ-1 (вопросы и задачи): 6.20, 6.21, 6.22(а), 6.23(а, б), 6.24, 8.12, 8.14, 8.16, 8.18, 8.20,
5.36, 5.38 или
ОЛ-3; 18.437, 18.444, 18.450, 18.455, 18.498, 18.378, 18.380, 18.404, 18.405, 18.406, 18.507,
19.514, 18.521, 18.529, 18.534, 18.423, 18.431.
Дома: ОЛ-1 (вопросы и задачи): 6.22(в), 6.23(в), 6.25, 8.13, 8.15, 8.17, 8.19, 5.37или
ОЛ-3: 18.438, 18.445, 18.451, 18.456, 18.499, 18.381, 18.407, 18.408, 18.409, 18.508, 19.516,
18.522, 18.530, 18.535, 18.424, 18.434.
Занятие 5. Неравенства Чебышёва. Закон больших чисел. Центральная предельная
теорема. Теорема Муавра — Лапласа. Метод статистических испытаний.
Ауд.: ОЛ-1 (вопросы и задачи): 9.18, 9.20, 9.21, 9.37 или
ОЛ-3: 18.542, 18.544, 18.550, 19.552, 18.556, 19.557, 18.564, 18.568, 18.581.
Дома: ОЛ-1 (вопросы и задачи): 9.36, 9.38 или
ОЛ-3: 18.543, 18.545, 18.551, 18.553, 18.558, 18.560, 18.565, 18.569, 18.570, 18.583.
МОДУЛЬ 3: Математическая статистика
Занятие 6. Метод моментов. Метод максимального правдоподобия.
Ауд.: ОЛ-2 (вопросы и задачи): 2.17, 2.19 или
ОЛ-3: 19.119, 19.121, 19.122, 19.124, 19.126, 19.132, 19.134.
Дома: ОЛ-2 (вопросы и задачи): 2.18 или
ОЛ-3: 19.120, 19.123, 19.125., 19.127, 19.133, 19.135.
82
Занятие 7. Интервальное оценивание.
Ауд:. ОЛ-2 (вопросы и задачи): 3.13, 3.15, 3.17, 3.19, 3.21, 3.23, 3.25, 3.27 или
ОЛ-3: 19.157, 19.159, 19.178, 19.183, 19.185, 19.191, 19.193.
Дома: ОЛ-2 (вопросы и задачи): 3.14, 3.16, 3.18, 3.20, 3.22, 3.24, 3.26, 3.28 или
ОЛ-3: 19.158, 19.160, 19.179., 19.184, 19.186, 19.192, 19.194.
Занятие 8. Проверка статистических гипотез в нормальной модели.
Ауд.: ОЛ-2 (вопросы и задачи): 4.18, 4.20, 4.22, 4.24, 4.26, 4.28, 4.30, 4.32, 4.34 или
ОЛ-3: 19.206, 19.208, 19.214, 19.219, 19.223, 19.225, 19.245, 19.248, 19.254.
Дома: ОЛ-2 (вопросы и задачи) 4.19, 4.21, 4.23, 4.25, 4.27, 4.29, 4.31, 4.33, 4.35 или
ОЛ-3: 19.207, 19.209, 19.215., 19.221, 19.224, 19.226, 19.246, 19.249, 19.255.
МАТЕРИАЛЫ ДЛЯ ПОДГОТОВКИ
Модуль 1: Случайные события
Вопросы для подготовки к рубежному контролю
Дать определение -алгебры событий.
Перечислить операции, определённые для случайных событий.
Дать классическое определение вероятности.
Дать геометрическое определение вероятности.
Дать аксиоматическое определение вероятности.
Дать определение достоверного события.
Дать определение невозможного события.
Дать определение несовместных событий.
Дать определение условной вероятности.
Дать определение независимых событий.
Дать определение полной группы событий.
Сформулировать основные свойства вероятности.
Сформулировать теорему умножения.
Сформулировать теорему сложения.
Сформулировать теорему о полной вероятности.
Сформулировать теорему Байеса.
Сформулировать теорему Бернулли.
Сформулировать следствия из теоремы Бернулли.
МОДУЛЬ 2: Случайные величины
Вопросы для подготовки к рубежному контролю
Вопросы для подготовки к рубежному контролю
Дать определение случайной величины.
Описать наиболее употребительные виды случайных величин (биномиальная, равномерно
распределенная, экспоненциальная, пуассоновская, нормальная).
Дать определения функции распределения и плотности распределения случайной
величины.
Дать определение дискретной и непрерывной случайных величин.
Сформулировать теоремы о свойствах плотности случайной величины.
Записать первое и второе неравенства Чебышева.
Сформулировать теорему Муавра — Лапласа.
83
Сформулировать центральную предельную теорему.
Сформулировать закон больших чисел в форме Бернулли и в форме Чебышева.
Дать определения математического ожидания случайной величины и сформулировать
теорему о его свойствах.
Дать определение дисперсии случайной величины и сформулировать теорему о ее
свойствах.
Дать определение начальных и центральных моментов.
Дать определение ковариации и коэффициента корреляции. Сформулировать теоремы о
свойствах ковариации и коэффициента колрреляции.
Дать определения функции распределения и плотности распределения случайного
вектора.
Описать наиболее употребительные виды случайных векторов (равномерно
распределенный, нормальный).
Дать определение ковариационной матрицы случайного вектора.
Сформулировать теорему о свойствах функции распределения случайного вектора
(двумерный случай).
Сформулировать теоремы о свойствах плотности распределения случайного вектора
(двумерный случай).
Сформулировать свойства двумерного нормального вектора.
Дать определения условной функции распределения и условной плотности распределения
случайного вектора.
Дать определение независимости случайных величин.
Дать определения условного математического ожидания и условной дисперсии случайной
величины.
Сформулировать теорему о свертке.
МОДУЛЬ 3: Математическая статистика
Вопросы для подготовки к рубежному контролю
Вопросы для подготовки к рубежному контролю
Определение законов распределения «хи-квадрат», Стьюдента, Фишера.
Определение и свойства выборочных функций распределения и плотности.
Определение несмещенности, состоятельности и эффективности точечных оценок.
Нахождение параметров равномерного распределения методом моментов. Нахождение
параметров биномиального, пуассоновского, равномерного, нормального и
экспоненциального распределений методом максимального правдоподобия.
Определение интервальной оценки, доверительного интервала (ДИ), уровня доверия.
Построение ДИ для математического ожидания нормально распределенной случайной
величины при известной и неизвестной дисперсии. Построение ДИ для дисперсии
нормально распределенной случайной величины.
Понятие критерия проверки гипотез. Определение критической области и уровня
значимости, ошибок первого и второго рода.
Построение оптимального критерия для математического ожидания нормально
распределенной генеральной совокупности при известной дисперсии для случая двух
простых гипотез.
Проверка гипотезы о математическом ожидании нормальной случайной величины и
гипотезы о равенстве математических ожиданий двух нормальных случайных
величин.
Проверка гипотезы о величине дисперсии нормальной случайной величины и гипотезы о
равенстве дисперсий двух нормальных случайных величин.
Критерий согласия Пирсона и его применение.
Метод наименьших квадратов оценивания параметров линейной модели.
84
Теория вероятностей и математическая статистика
4 семестр, спец. ИУ1, ИУ2
ЛИТЕРАТУРА
Основная литература (ОЛ)
Теория вероятностей: Учеб. для вузов/ В.А.Печинкин, О.И. Тескин, Г.М.Цветкова и др. / Под ред.
В.С.Зарубина, А.П.Крищенко. – М.: Изд-во МГТУ им. Н.Э.Баумана, 1998. – 456с.
Математическая статистика: Учеб. для вузов / В.Б. Горяинов, И.В. Павлов, Г.М. Цветкова и др. / Под
ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2001. – 424 с.
Пугачев В.С. Теория вероятностей и математическая статистика. – М.: Наука, 1979. – 496 с.
Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. Учеб. для
вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э.Баумана, 1996. – 228 с.
Краснов М.Л., Киселев Л.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление. Задачи и упражнения. М., Наука, 1981, -215 с.
Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа / Под
ред. А.В. Ефимова и Б.П. Демидовича. – 2-е изд. – М.: Наука, 1986. – 368 с.
Сборник задач по математике для втузов. Специальные курсы / Под ред. А.В.Ефимова. – М.: Наука,
1984. – 608 с.
Дополнительная литература (ДЛ)
Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648 с.
Бочаров П.П., Печинкин А.В. Теория вероятностей и математическая статистика. – М.: Гардарика,
1998, – 328 с.
Сборник задач по теории вероятностей, математической статистике, теории случайных функций / Под
ред. А.А. Свешникова. – М.: Наука, 1965. – 656 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей. – М.: Высшая школа, 1979. –
477 с.
Вентцель Е.С., Овчаров Л.А. Теория вероятностей. Задачи и упражнения. – М.: Наука, 1969. – 368 с.
ЛЕКЦИИ
Модуль 1. Операционное исчисление
Лекций по модулю 1 планом не предусмотрено.
Модуль 2. Теория вероятностей
Лекция 1. Случайное испытание. Элементарное событие и пространство
элементарных событий. Случайные события и их характеристические множества.
Комбинаторное, геометрическое и аксиоматическое определение вероятности.
ОЛ-1: 1.1, 1.2, 2.1, 2.3, 2.5.
Лекция 2. Вероятность реализации невозможного события. Теорема сложения,
монотонность: ( A  B)  ( P( A)  P( B)). Условная вероятность. Теорема умножения.
Независимые случайные события. Формула полной вероятности. Формула Байеса.
ОЛ-1: 2.5, 3.1–3.5.
Лекция 3. Независимые испытания. Биномиальная схема независимых испытаний.
Теорема Бернулли и следствия из нее.
ОЛ-1: 3.6, 4.1–4.2.
Лекция 4. Скалярные случайные величины. Функция распределения и ее свойства.
ОЛ-1: 4.1–4.2.
85
Лекция 5. Дискретные случайные величины. Биномиальное распределение и
распределение Пуассона. Непрерывные случайные величины. Плотность распределения
вероятностей и ее основные свойства. Равномерное и нормальное распределения.
Функция Лапласа.
ОЛ-1 4.3-4.6
Лекция 6. Понятие обобщенной плотности распределения вероятностей. Случайные
векторы.
Функция распределения случайного вектора и ее основные свойства.
Дискретные случайные векторы.
ОЛ-3: гл.2, §3; ОЛ-1: 5.1, 5.2.
Лекция 7. Непрерывные случайные векторы. Свойства плотности распределения
вероятностей непрерывного случайного вектора. Независимые случайные величины.
Функции случайных величин.
ОЛ-1: 5.3, 5.4; ОЛ-3: гл.5, §§2–3.
Лекция 8. Математическое ожидание и его свойства. Дисперсия и ее свойства.
ОЛ-1: 7.1–7.3.
Лекция 9. Ковариация и ее основные свойства. Коэффициент корреляции и его
основные свойства. Ковариационная матрица и ее основные свойства.
ОЛ-1: 7.4.
Лекции 10–11. Закон больших чисел и его основное содержание. Неравенства
Чебышева. Теорема Чебышева. Теорема Бернулли. Центральная предельная теорема.
Теорема Муавра — Лапласа.
ОЛ-1: 9.1, 9.2, 9.4.
Модуль 3. Математическая статистика
Лекция 12. Основная задача математической статистики. Случайная выборка и ее
закон распределения. Выборка и выборочное пространство. Выборочная характеристика и
выборочный закон распределения. Задача оценивания параметров законов распределения
наблюдаемых случайных величин. Понятие точечной оценки. Несмещенность точечной
оценки. Выборочное среднее – несмещенная оценка для математического ожидания.
Выборочная дисперсия – смещенная оценка для дисперсии.
ОЛ-2: 1.1, 1.2, 2.1.
Лекция 13. Эффективность точечной оценки. Выборочное среднее – эффективная
оценка в подклассе линейных несмещенных оценок. Состоятельность точечной оценки.
Теорема Рао и следствия из нее. Метод максимального правдоподобия построения
точечных оценок.
ОЛ-2: 2.1.
Лекция 14. Интервальные оценки — основные понятия. Построение интервальных
оценок. Интервальная оценка для математического ожидания случайной величины
 ( ) N (m,  2 ) при известной дисперсии и ее анализ.
ОЛ-2: 3.1–3.3.
Лекции 15–16. Проверка статистических гипотез — основные понятия и
определения. Проверка простых параметрических гипотез. Критерий Неймана — Пирсона
и примеры его применения. Проверка сложных параметрических гипотез. Равномерно
наиболее мощный критерий и примеры его построения.
ОЛ-2: 4.1-4.5.
Лекция 17. Резерв.
86
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Операционное исчисление
Занятие 1. Нахождение изображений и оригиналов.
ОЛ-4: 6.1–6.3
Ауд.: ОЛ-5: 524, 526, 529, 538, 540, 546, 555, 560, 564, 566, 569, 573, 576, 580, 583, 613, 625,
634, 635, 627.
или ОЛ-6: 13.1, 13.2, 13.6, 13.9, 13.17, 13.20, 13.29, 13.37, 13.47, 13.53, 13.58, 13.74, 13.76,
13.78, 13.79, 13.82, 13.84, 13.86.
Дома: ОЛ-5: 528, 536, 542, 547, 563, 565, 570, 574, 579, 620, 633.
или ОЛ-6: 13.3, 13.7, 13.8, 13.10, 13.19, 13.22, 13.26, 13.30, 13.40, 13.48, 13.52, 13.61, 13.75,
13.77, 13.80, 13.83, 13.85, 13.87.
Занятие 2. Теоремы разложения. Изображения периодических функций.
ОЛ-4: 6.4, ОЛ-4: 6.3
Ауд.: ОЛ-6: 13.88, 13.90, 13.93, 13.96, 13.98, 13.102, 13.104.
Дома: ОЛ-6: 13.89, 13.91, 13.94, 13.97, 13.99, 13.101, 13.103.
Занятие 3. Применение операционного исчисления к решению линейных
дифференциальных уравнений с постоянными коэффициентами и систем таких
уравнений.
ОЛ-4: 6.5
Ауд.: ОЛ-5: 654, 657, 665, 683, 718, 720, 758.
или ОЛ-6: 13.105, 13.111, 13.114, 13.117, 13.119, 13.129, 13.132, 13.137.
Дома: ОЛ-5: 655, 666, 721, 760, 762.
или ОЛ-6: 13.107, 13.112, 13.115, 13.118, 13.121, 13.130, 13.134, 13.136, 13.138.
Занятие 4. Рубежный контроль по модулю 1.
Модуль 2. Теория вероятностей (случайные события) для спец. ИУ1,3
Занятие 5. Элементы комбинаторики. Пространство элементарных событий.
Алгебра событий.
ОЛ-1, гл.1 (вопросы и задачи): 1.12, 1.13, 1.14, 1.15, 1.17, 1.20, 1.21.
Занятия 6–7. Классическое определение вероятностей. Непосредственный подсчет
вероятностей.
ОЛ-1, гл.2 (вопросы и задачи): 2.17, 2.18, 2.19, 2.20, 2.21, 2.23, 2.26, 2.28, 2.29, 2.32, 2.33,
2.34, 2.35, 2.36, 2.37, 2.39.
Занятие 8. Условная вероятность. Теоремы сложения и умножения.
ОЛ-1, гл.3 (вопросы и задачи): 3.21, 3.22, 3.23, 3.24, 3.25, 3.26.
Занятие 9. Формула полной вероятности. Формула Байеса.
ОЛ-1, гл.3 (вопросы и задачи): 3.30, 3.31, 3.28, 3.32, 3.33.
Занятие 10. Биномиальная схема независимых испытаний. Формула Бернулли и
следствия из нее.
ОЛ-1, гл.3 (вопросы и задачи): 3.34, 3.35, 3.36, 3.37, 3.38, 3.39, 3.40.
Занятие 11. Рубежный контроль по модулю 2.
87
Модуль 2. Теория вероятностей (случайные события) для спец. ИУ2,4
Занятие 5. Анализ постановок и методов решений задач ДЗ «Случайные события».
Подготовка к рубежному контролю по модулю 2.
Занятие 6. Рубежный контроль по модулю 2.
Модуль 3. Теория вероятностей (случайные величины) для спец.
ИУ1,3
Занятие 12. Случайные величины и их законы распределения.
ОЛ-1, гл.4 (вопросы и задачи): 4.23, 4.27, 4.31, 4.33, 4.34, 4.38.
ОЛ-1, гл.5 (вопросы и задачи): 5.29, 5.32, 5.34, 5.38.
Занятие 13. Функции от случайных величин.
ОЛ-1, гл.6 (вопросы и задачи): 6.20– 6.24, 6.28.
Занятие 14. Числовые характеристики случайных величин.
ОЛ-1, гл.7 (вопросы и задачи): 7.38–7.40, 7.44, 7.48, 7.52–7.54.
Занятие 15. Закон больших чисел.
ОЛ-1, гл.9 (вопросы и задачи): 9.14–9.18, 9.36, 9.38.
Занятие 16. Рубежный контроль по модулю 3.
Занятие 17. Резерв.
Модуль 3. Теория вероятностей (случайные величины) для спец.
ИУ2,4
Занятие 7. Анализ постановок и методов решений задач ДЗ «Случайные
величины». Подготовка к рубежному контролю по модулю 3.
Занятие 8. Рубежный контроль по модулю 3.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ
Модуль 1. Операционное исчисление (5 неделя для ИУ1,3 и 9 неделя для ИУ2,4;
максимум 18 баллов, минимум 9 баллов).
Домашнее задание №1 «Операционное исчисление» (выдача 1 неделя, прием 4 неделя
для спец. ИУ1,3 и 8 неделя для спец. ИУ2,4).
Рубежный контроль по модулю 1 (5 неделя для спец. ИУ1,3 и 9 неделя для спец. ИУ2,4).
Модуль 2. Теория вероятностей (случайные события) (13 неделя, максимум 30 баллов,
минимум 15 баллов).
Домашнее задание №2. «Теория вероятностей (случайные события)», (выдача 5 неделя,
прием 13 неделя).
Рубежный контроль по модулю 2 (13 неделя).
Модуль 3. Теория вероятностей (случайные величины) (16 неделя, максимум 42 балла,
минимум 22 балла).
Домашнее задание №3. «Теория вероятностей (случайные события)», (выдача 12 неделя,
прием 16 неделя).
Рубежный контроль по модулю 3 (16 неделя).
88
СИСТЕМНЫЙ АНАЛИЗ
для ИБМ
Дисциплина состоит из трех учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-6
12
Упражнения
1-6
18
Домашние задания текущие
1-6
8
7
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
7-11
10
Упражнения
1-11
15
Домашние задания текущие
1-11
10
12
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
12-17
6
Упражнения
12-17
9
Домашние задания текущие
12-17
8
17
2
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №3
89
Примечание
Лекция 10. Понятие графа и орграфа. Задача о
кратчайшем пути, алгоритм Дейкстры. Задача о
максимальном
потоке,
алгоритм
ФордаФалкерсона. Минимальный разрез.
ЛЕКЦИИ
Модуль 1. Линейное программирование
Лекция 1. Экономические задачи, сводимые к
задачам линейного программирования (ЛП).
Виды задач ЛП и способы перехода от одного
вида к другому. Угловая точка канонической
задачи ЛП. Базисная допустимая форма.
Лекция 11. Динамическое программирование.
Функции Беллмана. Уравнения Беллмана.
Примеры
задач
динамического
программирования: о распределении средств, о
рюкзаке, о замене оборудования.
Лекция 2. Основная теорема линейного
программирования. Симплекс-метод. Полные и
укороченные симплекс-таблицы. Метод
искусственного базиса.
Модуль 3. Принятие решений в условиях
неопределенности
Лекция 3. Двойственность задач линейного
программирования. Таблица соответствий.
Основная теорема двойственности. Условия
дополняющей нежёсткости. Теорема о
приращениях. Экономический смысл
двойственных переменных и условий
дополняющей нежёсткости в задаче о наилучшем
использовании ресурсов.
Лекция 12. Матричные игры с природой.
Оптимизация по критериям Байеса, Вальда,
Сэвиджа и Гурвица. Конечные игры двух лиц с
нулевой суммой. Чистые стратегии. Матрица
игры. Седловая точка. Смешанные стратегии.
Лекция 4. Транспортная задача. Закрытая и
открытая модели. Теорема о существовании
оптимального решения. Выбор опорного плана.
Лекции 14. Биматричные игры. Кооперативные
игры. Оптимальность по Парето. Задачи
многокритериальной оптимизации.
Лекция 5. Проверка оптимальности опорного
плана транспортной задачи.
Перекачки по
циклам. Случаи вырождения. Модификации
транспортной задачи.
Лекция 15. Определение нечеткого множества.
Операции над нечеткими множествами объединение,
сумма,
пересечение,
произведение, отрицание; законы де Моргана.
Алгебра нечетких множеств и ее отличие от
алгебры множеств. Теоремы о сведении нечетких
множеств к теории случайных множеств.
Лекция 13. Критерий оптимальности смешанных
стратегий. Сведение к задаче ЛП и решение игры.
Основная теорема теории игр.
Лекция 6. Целочисленные задачи ЛП. Метод
ветвей и границ. Задачи о назначениях и о
коммивояжере
как
частный
случай
целочисленных ЗЛП. Другие методы решения
целочисленных задач ЛП.
Лекция 16. Применение нечетких множеств к
принятию решений. Задачи с лингвистическими
переменными.
Модуль 2. Прикладные задачи
математического программирования
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Лекции 7-8. Необходимые условия условного
экстремума, их геометрический смысл для
функции
двух
переменных.
Теорема
о
приращениях (доказательство для случая двух
переменных
с
одним
ограничением).
Стандартная
задача
нелинейного
программирования. Множители Лагранжа, их
экономический смысл. Задача о потребительском
выборе.
Модуль 1. Линейное программирование
Лекция 9. Выпуклые множества, выпуклые и
вогнутые функции. Теорема Куна –Таккера.
Доказательство основных теорем линейного
программирования как следствий теоремы Куна –
Таккера.
Занятия 5 – 6. Двойственность в задачах ЛП.
Экономический
смысл
двойственных
переменных.
Занятие 1. Постановка задачи линейного
программирования
(ЗЛП).
Формализация
экономических задач.
Занятие 2. Графическое решение задачи ЛП.
Угловые точки.
Занятие 3. Симплекс-метод.
Занятие 4. Метод искусственного базиса.
Занятие 7. Транспортная задача.
90
Занятие
8.
назначениях
Модификации
ТЗ.
Задача
о
Модуль 3. Принятие решений в условиях
неопределенности
Занятие 18. Игры с природой. Составление
матрицы игры и ее анализ по критериям Байеса,
Вальда, Сэвиджа и Гурвица.
Занятие 9. Рубежный контроль по модулю 1.
Модуль 2. Прикладные задачи
математического программирования
Занятие
10.
Задача
Целочисленные задачи ЛП.
Занятие 19. Седловая точка в игре двух лиц.
Смешанные стратегии. Графическое решение игр
коммивояжера.
2  2 и 2n.
Занятия 11-12. Условия Куна – Таккера. Задача о
потребительском выборе. Выпуклые функции.
Занятие 20. Исключение заведомо невыгодных
стратегий. Сведение матричной игры к ЗЛП и ее
решение.
Занятие 13. Способы задания графов и орграфов.
Алгоритм Дейкстры в задаче о кратчайшем пути.
Занятие 21. Биматричные игры.
многокритериальной оптимизации.
Занятие 14. Задачи о максимальном потоке и о
минимальном разрезе.
Задачи
Занятие 22-23. Нечеткие множества.
применение к принятию решений.
Занятие 15. Алгоритм Беллмана в задаче о пути в
слоистом
графе.
Формализация
задач
динамического программирования.
Занятие 24. Рубежный контроль по модулю 3.
Занятие 16. Задача о распределении средств.
Задача о рюкзаке.
Занятие 17. Рубежный контроль по модулю 2.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к
выполнению контрольных работ и Рубежных контролей, выполнении индивидуальных ДЗ.
Контрольные мероприятия
Модуль 1. Линейное программирование
1. ДЗ №1 срок 8 неделя
2. Рубежный контроль № 1 срок 9 неделя
Модуль 2. Прикладные задачи математического программирования
3. ДЗ №2 срок 12 неделя
4. Рубежный контроль № 2 срок 13 неделя
Модуль 3. Принятие решений в условиях неопределенности
5. ДЗ №3 срок 15 неделя
6. Рубежный контроль № 3 срок 16 неделя.
91
Их
Литература
Основная литература
1. Волков И.К., Загоруйко Е.А. Исследование операций: Учебник для вузов. Под ред. Зарубина В.С, Крищенко
А.П.- М.: Изд. МГТУ им. Н.Э. Баумана, 2000. – 436 с. (Серия математика в техническом университете, Вып.
XX).
2. Грешилов А.А. Математические методы принятия решений. Учебное пособие для вузов. – М.: Изд. МГТУ
им. Н.Э. Баумана, 2006. – 584 с.
3. Орлов А.И. Принятие решений. Теория и методы разработки управленческих решений. – М. ИКЦ «МарТ»;
Ростов н/Д: Издательский центр «Март», 2005. -496 с.
4. Исследование операций в экономике. Под ред. Н. Ш. Кремера. М.: Юрайт, 2011, – 430 с.
5. Аттетков А.В., Галкин СВ., Зарубин В.С. Методы оптимизации. Учебник для вузов / под ред. В.С.Зарубина,
А.П.Крищенко. – М.: МГТУ им. Н.Э. Баумана, 2001.- 436с. (Серия математика в техническом университете,
Вып. XIV)
6. Косоруков О.А., Мищенко А.В. Исследование операций. Учебник / Под общ. ред. Н.П. Тихомирова – М.:
Изд-во «Экзамен», 2003.
7. Сборник задач по математике для втузов. Ч. 4. Методы оптимизации. Уравнения в частных производных.
Интегральные уравнения. (Под ред. А.В. Ефимова) – М.: Наука, 1990.
8. Грешилов А.А., Лебедев А.Л. Компьютерные обучающие пособия для решения задач математической
статистики и математического программирования: учеб. пособие (с расчетными программами на
оптическом диске) – М.: Изд-во МГТУ им. Н.Э.Баумана, 2011.
Дополнительная литература
1. Костевич Л.С., Лапко А. А.. Исследование операций. Теория игр. М, 2008 г., 368 с.
2. Вагнер Г. Основы исследования операций: Пер. с англ.- М.: Мир, 1972 -(в 3-х томах).
3. Грешилов А.А. Прикладные задачи математического программирования. Учебное пособие для вузов.
– М.: ЛОГОС, 2006. – 286 с.
4. Калихман И.Л. Сборник задач по математическому программированию. – М.: Высшая школа, 1975. –
270 с.
5. Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах: Учебное
пособие для вузов – М.: Высшая школа, 1979. – 126 с.
6. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: учебное пособие для университетов.М.:Высшая школа, 1998.- 304 с.
7. Штойер Р. Многокритериальная оптимизация. Теория, расчет и приложения. - М.: Радио и связь,
1992. – 504 с.
8. Антонов А.В. Системный анализ – М.: Высшая школа, 2008, – 456 с.
Кафедральные издания и методические материалы
1. Исмагилов Р.С., Калинкин А.В., Станцо В.В. Нелинейное и динамическое программирование. – М.:
Изд. МГТУ им. Н.Э. Баумана, 2007. – 40 с.
2. Исмагилов Р.С., Калинкин А.В., Станцо В.В. Графы. – М.: Изд. МГТУ им. Н.Э. Баумана, 1999. – 40
с.
3. Исмагилов Р. С., Калинкин А. В. Элементы математического программирования.– М.: МГТУ им.
Н.Э. Баумана, 1999, 24 с.
4. Васильев Н. С., Станцо В. В. Двойственность в линейном программировании и теория матричных
игр. – М.: МГТУ им. Н. Э. Баумана, 2010. – 45 с.
5. Титов А.В., Калинкин А.В. Математическая логика. Нечеткие множества и формальные системы. –
М.: МГТУ им. Н. Э. Баумана, 2008. – 31 с
Электронные ресурсы
1.
Козлов В.Н. Системный анализ и принятие решений. Учебное пособие. Спб., 2008, – 220 с.–
PDF: http://hoster.bmstu.ru/~fn1/?page_id=30
92
ПРИКЛАДНАЯ СТАТИСТИКА
для ИБМ-4, ИБМ-5 и ИБМ-6
Дисциплина состоит из двух учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-7
14
Упражнения
1-7
7
Лабораторные работы
1-7
7
Домашние задания текущие
1-7
7
8
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
8-17
22
Упражнения
8-17
10
Лабораторные работы
8-17
10
Домашние задания текущие
8-17
8
17
2
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Лекция 2. Модели законов распределения
вероятностей, наиболее распространенные в
практике статистических исследований. Модели,
используемые
для
описания
механизмов
генерации реальных социально-экономических
данных, и модели, используемые при реализации
техники статистических исследований.
Лекции
Модуль 1. Элементы математической
статистики
Лекция
1.
Введение.
Основные задачи
прикладной статистики. Качество, структура и
объем данных. Разновидности анализа данных.
Контролируемые переменные и переменные
отклика. Цели исследования. Особенности задач
прикладной статистики.
Лекция
3.
эмпирическая
93
Выборочные
функция
характеристики:
распределения,
гистограмма, полигон частот, выборочные
моменты, выборочные квантили, коэффициенты
асимметрии
и
эксцесса,
выборочный
коэффициент
корреляции.
Асимптотические
свойства выборочных характеристик. Выборочное
среднее и выборочная медиана – как решение
экстремальных задач математической статистики.
Лекция
15.
Понижение
размерности
исследуемого многомерного признака. Отбор
наиболее информационных показателей.
Лекция 16. Обзорная лекция.
Практические занятия
Модуль 1. Элементы математической
статистики
Лекции 4-5. Оценки параметров распределений.
Свойства
оценок,
методы
оценивания.
Информация по Фишеру и эффективные оценки.
Интервальное оценивание.
Занятие
1.
Описательная
статистика.
Выборочные характеристики и их свойства.
Смещенность выборочной дисперсии.
Занятие
2.
Оценивание
параметров
распределений. Метод моментов и метод
максимального
правдоподобия.
Оценки
параметров
для
основных
моделей
распределений вероятностей.
Лекция 6. Оценивание параметров основных
моделей распределения вероятностей.
Лекция 7. Проверка статистических гипотез.
Проверка гипотез о параметрах распределений.
Модуль 2. Элементы прикладной статистики
Занятие 3. Проверка гипотез о параметрах для
основных моделей распределений.
Лекции 8-9. Критерии согласия: критерий «хиквадрат» Пирсона, критерий КолмогороваСмирнова, критерий Андерсона – Дарлинга.
Критерии однородности для двух выборок.
Непараметрические критерии однородности:
критерии сдвига и масштаба. Проверка гипотезы
симметрии
распределения.
Гипотезы
о
независимости.
Занятие 4. Непараметрические критерии
согласия.
Критерии
Колмогорова-Смирнова,
критерий Андерсона-Дарлинга, критерий «хиквадрат» Пирсона.
Модуль 2. Элементы прикладной статистики
Занятие 5. Дисперсионный анализ. Проверка
гипотезы об однородности дя двуз выборок и для
парных наблюдений.
Лекция
10.
Дисперсионный
анализ.
Однофакторный
анализ.
Многофакторный
анализ. Таблицы сопряженности.
Занятие
6.
Корреляционный
анализ.
Коэффициент корреляции и его свойства.
Ранговая
корреляция
и
коэффициенты
корреляции Спирмена и Кендалла.
Лекции 11-12. Корреляционный анализ. Анализ
связей между количественными переменными.
Коэффициент
корреляции.
Корреляционное
отношение и функциональная зависимость
между переменными. Анализ связей между
порядковыми (ординальными) переменными.
Ранговые коэффициенты корреляции Спирмена и
Кендалла.
Анализ
связей
между
классификационными
(номинальными)
переменными.
Занятие 7. Линейная регрессия. Оценки
параметров постой линейной регрессии с
использованием метода наименьших квадратов и
метода Тейла. Сведение нелинейных моделей к
модели множественной линейной регрессии.
Занятие 8. Резерв.
Лабораторные работы.
Модуль 1. Элементы математической
статистики
1. Моделирование случайных чисел с заданным
законом распределения. Стандартные процедуры
моделирования (в среде Exel), метод обратной
функции,
другие
методы.
Проверка
выполнимости закона больших чисел методами
статистического моделирования. Выборочное
среднее и выборочная медиана как оценки центра
распределения для распределений Гаусса и Коши.
Лекции 13-14. Исследование вида зависимости
между количественными переменными. Простая
линейная регрессия. Оценка параметров по
методу наименьших квадратов и по методу
Тейла. Множественная линейная регрессия.
Отбор значимых факторов. Нелинейные модели,
сводящиеся к модели множественной линейной
регрессии. Мультиколлинеарность и отбор
существенных
факторов
(предикторов).
Непараметрическое оценивание регрессии.
2.
Описательная
статистика.
Нахождение
основных эмпирических характеристик выборки.
94
Построение
графиков
гистограммы
эмпирической функции распределения.
и
5. Дисперсионный анализ. Проверка гипотез об
однородности двух выборок и построение
доверительного интервала для параметра сдвига с
использованием распределения Стьюдента и
распределения Манна-Уитни. Проверка гипотезы
об однородности парных наблюдений с
использованием рангового критерия Вилкоксона.
3. Статистическое моделирование и исследование
свойств оценок параметров. Сравнение трех
оценок параметра  в модели xi  R(0,  ) :
оценка метода моментов- удвоенное выборочное
среднее,
оценка
метода
максимального
правдоподобия- старший член вариационного
ряда(с поправкой на смещенность), удвоенная
выборочная медиана.
6. Линейный регрессионный анализ. Простая
линейная регрессия. Оценки параметров по
методу наименьших квадратов и по методу Тейла.
Параметрические
и
непараметрические
доверительные интервалы для коэффициентов
регрессионной модели.
4. Построение доверительных интервалов для
параметров
нормального
распределения.
Построение доверительного интервала для
теоретического среднего с использованием
центральной предельной теоремы. Построение
непараметрического доверительного интервала
для теоретического среднего с использованием
знаково-рангового распределения Вилкоксона.
7. Множественная линейная регрессии, отбор
существенных факторов. Нелинейные модели,
сводимые к модели множественной линейной
регрессии. Выбор модели, наиболее адекватно
описывающей представленный данные.
Модуль 2. Элементы прикладной статистики
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
лабораторных работ, входному контролю готовности к выполнению лабораторной работы, оформлении отчетов по
лабораторным работам.
Контрольные мероприятия
Модуль 1. Элементы математической статистики
1. Домашнее задание №1
2. Рубежный контроль №1
Модуль 1. Элементы прикладной статистики
3. Домашнее задание №2
4. Рубежный контроль №2
Литература
Основная литература
1. Горяинов В.Б., Павлов И.В. и др. Математическая статистика М.: Изд-во МГТУ им.Н.Э. Баумана, 2001. – 423с.
2. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Финансы и статистика, Москва, 1983, – 472с.
3. Орлов А. И. Прикладная статистика. Учебник для вузов. — М.: Экзамен, 2006. — 672 с.
4. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. / Под ред. В.Э. Фигурнова. М.: ИнфраМ, 2002.
95
Дополнительная литература
5. Орлов А. И. Эконометрика. Учебник для вузов. Изд. 3-е, исправленное и дополненное. — М.: Изд-во
«Экзамен», 2004. — 576 с.
6. Лагутин М.Б. Наглядная математическая статистика. М.: Бином, Лаборатория знаний, 2007. 472 с.
7. Гмурман Г.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2003, 479м.
8. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ-ДАНА, 2004. – 573 с.
9. Кокс Д., Снелл Э. Прикладная статистика. Принципы и примеры. Москва 1984, «Мир», 202 стр.
Кафедральные издания и методические материалы
10. Карташов Г.Д., Павлов И.В., Тимонин В.И. Методические указания к выполнению типового расчета по
математической статистике. – М.: МГТУ, 1995.
11. Карташов Г.Д., Павлов И.В., Тимонин В.И. Проверка статистических гипотез. М.: Изд-во МГТУ им.Н.Э. Баумана,
1995.
Электронные ресурсы
12. Айвазян С.А., Мхитарян В.С. Прикладная статистика в примерах и задачах. ЮНИТИ, Москва, 2001, – 272 стр.,
DjVu: http://hoster.bmstu.ru/~fn1/?page_id=30.
13. Сорокин О.Д. Прикладная статистика на компьютере. Новосибирск, 2009,– 223 стр. PDF:
http://hoster.bmstu.ru/~fn1/?page_id=30.
14. Валеев С.Г., Клячкин В.Н. Практикум по прикладной статистике. Ульяновск, 2008, – 124 стр. DjVu:
http://hoster.bmstu.ru/~fn1/?page_id=30
КРАТНЫЕ ИНТЕГРАЛЫ И ТФКП
4 семестр, спец. ИУ-3
ЛИТЕРАТУРА
Основная литература (ОЛ)
Гаврилов В.Р., Иванова Е.Е. Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. –
М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 492 с.
Морозова В.Д. Теория функций комплексного переменного. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. –
520 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 2. – М.: Наука, 1985. – 560 с.
Задачи и упражнения по математическому анализу для втузов. Под ред. Б.П. Демидовича. – М.:Наука, 1970. –
472 с.
Краснов М.Л., Киселев Л.И., Макаренко Г.И. Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. Задачи и упражнения. – М.: Наука, 1981. – 215 с.
Дополнительная литература (ДЛ)
Ильин В.А., Позняк Э.Г. Основы математического анализа: Ч. 2. – М.: Наука, 1980. – 448 с.
Кудрявцев Л.Д. Курс математического анализа. – М.: Высшая школа,1981. – 584 с.
Свешников А.Г., Тихонов А.М. Теория функций комплексной переменной. – М.: Наука, 1967. – 304 с.
Методические пособия (МП)
Ванько В.И., Галкин С.В., Морозова В.Д. Методические указания для самостоятельной работы студентов по
разделам «Теория функций комплексного переменного» и «Операционное исчисление», МВТУ, 1988. – 28 с.
Шостак Р.Я., Коган С.М., Хереско Т.А. Методическое пособие к выполнению домашнего задания по ТФКП,
МВТУ, 1976. – 41 с.
96
Голенко К.А., Хереско Т.А., Щетинина Н.Н. Методические указания для подготовки к контрольным работам
по курсу высшей математики, МВТУ, 1986. – 36 с.
ЛЕКЦИИ
Модуль 1. Кратные интегралы
Лекция 1. Двойной интеграл. Свойства двойного интеграла. Замена переменных в
двойном интеграле.
ОЛ-1 1.1-1.7, 1.9; ОЛ-4 гл.14 § 1–3, 6.
Лекция 2. Тройной интеграл. Свойства тройного интеграла.
ОЛ-1 2.1-2.4; ОЛ-4 гл.14 § 11, 12.
Лекция 3. Криволинейный интеграл второго рода. Свойства криволинейного интеграла.
ОЛ-1 5.4-5.6; ОЛ-4 гл.3 § 1–2.
Лекция 4. Формула Грина. Условие независимости криволинейного интеграла от пути
интегрирования в односвязной области.
ОЛ-1 5.7–5.8; ОЛ-4 гл.15 § 3–4.
Лекция 5. Вычисление криволинейного интеграла от полного дифференциала. Интеграл
по поверхности. Свойства интеграла по поверхности.
ОЛ-1 5.9, 6.1–6.4; ОЛ-4 гл.15 § 4.
Лекция 6. Поверхностный интеграл второго рода. Скалярное поле, векторное поле.
Формула Остроградского-Гаусса. Дивергенция.
ОЛ-1 6.6–6.10, 7.1–7.5; ОЛ-4 гл.15 § 5,6,8.
Лекция 7. Формула Стокса. Вихрь (ротор) векторного поля и его свойства.
Потенциальное векторное поле, Лапласово поле.
ОЛ-1 6.8, 7.3–7.7; ОЛ-4 гл.15 § 7.
Лекция 8. Оператор Гамильтона. Векторные дифференциальные операции второго
порядка.
ОЛ-1 |8.1-8.4; ОЛ-4 гл.15 § 9.
Лекции 9. Криволинейные ортогональные координаты (КООК). Коэффициенты Ламе.
Дифференциальные операции в КООК.
ОЛ-1 Д.8.1; ДЛ-1 гл.6 §3.
Модуль 2. Функциональные ряды
Лекция 10. Функциональные ряды. Равномерная сходимость. Степенные ряды. Теорема
Абеля.
ОЛ-2 2.1-2.5; ОЛ-4 гл.16 §9-13.
Лекция 11. Основные свойства степенных рядов. Ряд Тейлора. Приложения степенных
рядов.
ОЛ-2 2.5–2.8; ОЛ-4 гл.16 §14–17.
Модуль 3. ТФКП
Лекция 12. Комплексная функция комплексного переменного. Функциональные ряды в
С. Основные трансцендентные функции комплексного переменного и их свойства. Формулы
Эйлера. Основные трансцендентные функции комплексного переменного и их свойства.
Формулы Эйлера.
ОЛ-3 3.1 3.3–3.5; ОЛ-5 гл.1 §1–2.
97
Лекция 13. Предел функции комплексного переменного. Непрерывность и производная
функции комплексного переменного. Условия Коши — Римана. Аналитичность функции в
области и в точке. Аналитичность основных элементарных функций комплексного
переменного.
ОЛ-3 3.2, 4.1-4.3, 4.6; ОЛ-5 гл.1 §2–3.
Лекция 14. Интеграл от непрерывной функции комплексного переменного, Интегральная
формула Коши.
ОЛ-3 5.1–5.5; ОЛ-5 гл.1 §4–5.
Лекция 15. Разложение аналитической функции в ряд Тейлора и ряд Лорана.
ОЛ-3 6.1–6.6; ОЛ-5 гл.1 §6.
Лекция 16. Классификация изолированных особых точек аналитической функции по
виду ее разложения в ряд Лорана в окрестности этих точек.
ОЛ-3 7.2–7.4; ОЛ-5 гл.1 §7.
Лекции 17. Вычет аналитической функции в ее изолированной особой точке. Вычет в
бесконечно удаленной точке. Применение вычетов.
ОЛ-3 8.1–8.4; ОЛ-5 гл.1 §8.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Теория поля
Занятия 1. Расстановка пределов и вычисление двойных интегралов в декартовых
координатах.
ОЛ-5: Ауд.: 2113, 2118, 2121, 2124, 2125, 2131, 2132, 2134, 2137, 2139, 2151.
Дома: 2115, 2117, 2120, 2123, 2142, 2126, 2130, 2133, 2135, 2136, 2138, 2140, 2142, 2150, 2153,
2138, 2153.
Занятие 2. Вычисление двойных интегралов в полярных координатах. Вычисление
площадей плоских фигур.
ОЛ-5 Ауд.: 2160, 2162, 2166, 2168, 2178, 2181, 2183.
Дома: 2163, 2161, 2165, 2167, 2171, 2177, 2180.
Занятие 3. Вычисление объемов. Вычисление площади поверхности.
ОЛ-5 Ауд.: 2194, 2196, 2198, 2202; 2213, 2215, 2219, 2220, 2231.
Дома: 2195, 2197, 2199, 2200, 2201; 2214, 2216, 2218, 2222.
Занятие 4. Вычисление тройных интегралов.
ОЛ-5 Ауд.: 2240, 2241, 2255, 2257, 2260, 2268
Дома: 2250, 2253, 2256, 2242, 2262, 2263, 2247, 2264.
Занятие 5. Вычисление криволинейных интегралов. Приложения криволинейных
интегралов.
ОЛ-5 Ауд.: 2312, 2323, 2327, 2328, 2332, 2337, 2344.
Дома: 2313, 2315, 2316, 2324, 2329, 2335, 2338, 2345.
Вычисление криволинейного интеграла от полного дифференциала. Отыскание функции по ее
полному дифференциалу.
ОЛ-5 Ауд.: 2318(а,в,д), 2319(а,в), 2322(а,в), 2326(а,в).
98
Дома: 2318(а,г), 2319(б,г), 2322(б,г), 2326(б,г).
Занятие 6. Поверхностные интегралы. Теория поля.
ОЛ-5 Ауд.: 2349, 2350, 2357, 2366; 2373, 2375, 2377.
Дома: 2365, 2351, 2356, 2357; 2372, 2374, 2376, 2380, 2385(в).
Ауд.: 2383, 2384, 2385.
Дома: ОЛ-5 гл.7:2389, 2391, 2386, 2388, 2394, 2398(1)
Занятие 7. Рубежный контроль по модулю 1 (лекции №1-9, семинары № 1-6).
Модуль 2. Функциональные ряды
Занятие 7. Степенные ряды. Интервал сходимости.
ОЛ-5 Ауд. 2526, 2528, 2530, 2533, 2534, 2540, 2545, 2547, 2549, 2551, 2553, 2554, 2557, 2559,
2560, 2563.
Дома. 2527, 2529, 2531, 2538, 2546, 2548, 2550, 2552, 2556, 2558, 2561, 2563.
Занятие 8. Разложение функции в ряды.
ОЛ-5 Ауд.: 2592, 2594, 2596-2598, 2600, 2631, 2633, 2635, 2637, 2601, 2602, 2611, 2615, 2606,
2619, 2617.
Дома: 2595, 2599, 2632, 2636, 2638, 2607, 2608, 2616, 2618, 2630.
Приложение степенных рядов.
ОЛ-5 Ауд.: 2644, 2646, 2648, 2654, 2657.
Дома: 2642, 2645, 2653.
Занятие 9. Рубежный контроль по модулю 2 (лекции № 7-8, семинары № 7-8
Модуль 3. ТФКП
Занятие 10. Числовые и степенные ряды с комплексными членами. Вычисление
значений элементарных функций комплексного переменного.
ОЛ-5 Ауд. 2485, 2487, 2488, 2490, 2492, 2566, 2567, 2570. ОЛ-7: 59, 62, 64.
Дома. 2486, 2489, 2491, 2564, 2555. ОЛ-5: 60, 63, 65.
Занятие 11. Вычисление значений элементарных функций комплексного переменного.
Проверка аналитичности функций и нахождение производных. Нахождение аналитической
функции по ее действительной или мнимой части.
ОЛ-6 Ауд. 66(а,б,г) 70, 104, 106, 114, 117(а,б,е), 140, 142, 148.
Дома. 66(в,д,е) 69, 105, 115, 117(в,г,д), 141, 145, 147.
Занятие 12. Интегральная формула Коши. Разложение аналитической функции в ряды
Тейлора и Лорана.
ОЛ-6 Ауд. 168, 170, 172, 174, 250, 252, 258.
Дома. 167, 169, 171, 173, 251, 253, 257.
Занятие 13. Разложение аналитических функций в ряды Тейлора и Лорана.
ОЛ-6 Ауд. 265, 267, 269, 271, 273, 275.
Дома. 266, 268, 270, 272, 274.
99
Занятие 14. Нули аналитической функции. Изолированные особые точки и их
классификация.
ОЛ-6 Ауд. 276, 278, 290, 292, 294, 302, 304 306.
Дома. 277, 291, 293, 295, 297, 301, 305, 307.
Занятие 15. Изолированные особые точки и вычеты в них. Применение вычетов к
вычислению контурных интегралов.
ОЛ -6 Ауд. 316, 318, 322, 324, 328, 338, 348, 350, 352.
Дома. 319, 321, 323, 325, 327, 339, 347, 351, 353.
Занятие 16. Аттестационная работа №3 «ТФКП» (лекции 12–17, семинары 12-17).
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ
Модуль 1 (максимум 27 баллов, минимум 14 баллов).
Домашнее задание №1: “Кратные и криволинейные интегралы. Теория поля” (2–6 нед.).
Рубежный контроль по модулю (7 нед.).
Модуль 2 (максимум 20 баллов, минимум 12 баллов).
Домашнее задание №2 “Функциональные ряды” (7–8 нед.).
Рубежный контроль по модулю (9 нед.).
Модуль 3 (максимум 43 балла, минимум 34 баллов).
Рубежный контроль по модулю (17 нед.).
Математическая логика и теория алгоритмов
4 семестр, спец. ИУ3
ЛИТЕРАТУРА
Основная литература
Мендельсон Э. Введение в математическую логику. – М.: Наука, 1971. – 320 с.
Кушнер Б.А. Лекции по конструктивному математическому анализу. – М.: Наука, 1973. – 448 с.
Белоусов А.И., Ткачев С.Б. Дискретная математика. – 3-е изд. – М.: Изд. МГТУ им. Н.Э. Баумана, 2004. – 744 с.
Дополнительная литература
Математическая логика в программировании: Сб. статей: Пер. с англ. – М.: Мир, 1991. – 408 с.
Верещагин Н.К., Шень А. Языки и исчисления. – М.: МЦНМО, 2000. – 291 с.
ЛЕКЦИИ
Модуль 1. Теория алгоритмов
Лекция 1. Предпосылки возникновения математической логики и теории алгоритмов.
Проблемы математического определения алгоритма и доказательства. Интуитивная концепция
алгоритма. Понятие конструктивного объекта. Алфавит, слово, язык, словарная функция.
100
ОЛ-1, предисловие; ОЛ-2, введение; ОЛ-3, Д1.1, 7.1.
Лекция 2. Машины Тьюринга. Вычислимость по Тьюрингу. Тезис Тьюринга. Понятие
нормального алгорифма Маркова. Основные примеры. Вычислимость по Маркову. Принцип
нормализации.
ОЛ-3, Д7.4; ОЛ-1, гл. 5, §2.
ОЛ-1, гл. 5, §1; ОЛ-2, §1, пп. 1.1 – 1.4, 1.9.
Лекция 3. Эквивалентность алгорифмов. Теорема о переводе. Способы сочетания
нормальных алгорифмов.
ОЛ-1, гл. 5, §1; ОЛ-2, §1, пп. 1.5– 1.7.
Лекция 4. Универсальный алгорифм. Разрешимые и перечислимые множества. Перечислимые
множества и области применимости нормальных алгорифмов. Проблема применимости для
нормальных алгорифмов и доказательство ее неразрешимости.
ОЛ-1, гл. 5, §1; ОЛ-2, §1, пп. 1.7– 1.8; ОЛ-2, §§2, 3; ОЛ-2, §§2, 3.
Модуль 2. Математическая логика
Лекция 5. Понятие формальной теории. Аксиомы и правила вывода. Выводимость и
доказуемость. Примеры теорий. Исчисление высказываний (ИВ).
ОЛ-1, гл. 1, §4; конспект лекций.
Лекция 6. Теорема дедукции для ИВ. Правила естественного вывода. Примеры
построения доказательств в ИВ.
ОЛ-1, гл. 1, §4; конспект лекций.
Лекция 7. Полнота и непротиворечивость ИВ.
ОЛ-1, гл. 1, §4; конспект лекций; ДЛ-2, гл.1, гл. 2: 2.1, 2.2.
Лекции 8. Понятие алгебраической системы. Операции и предикаты. Термы и формулы.
Понятие интерпретации. Выполнимость, истинность и логическая общезначимость. Аксиомы и
правила вывода исчисления предикатов 1-го порядка (ИП1).
ОЛ-3, 4.1; ОЛ-1, гл. 2, §§ 1 – 4.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Теория алгоритмов
Занятия 1-2. Программирование вычислимых функций на машинах Тьюринга и
нормальных алгорифмах Маркова.
ОЛ-3, задачи 7.37, 7.38; МРК.
Занятие 3-4. Построение разрешающих алгоритмов для разрешимых множеств. Анализ
некоторых неразрешимых проблем.
МРК.
Модуль 2. Математическая логика
Занятия 5-6. Построение доказательств в исчислении высказываний.
ОЛ-1, упр. к. гл. 1; ДЛ-4, упр. к гл. 2, 5.
Занятия 7-8. Построение доказательств в исчислении предикатов.
ОЛ-1, упр. к гл. 1; ДЛ-4, упр. к гл. 3, 5.
101
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ
Модуль 1 Теория алгоритмов (8 неделя, максимум 45 баллов, минимум 25 баллов).
Домашнее задание №1 «Теория алгоритмов» (выдача 3 неделя, прием 9 неделя).
Рубежный контроль по модулю 1 (12 неделя).
Модуль 2. Математическая логика (16 неделя, максимум 45 баллов, минимум 25 баллов).
Домашнее задание №2 «Исчисление высказываний» (выдача 9 неделя, прием 13 неделя).
Рубежный контроль по модулю (16 неделя).
Математическая логика и теория алгоритмов
4 семестр, спец. ИУ7
ЛИТЕРАТУРА
Основная литература
Э. Мендельсон. Введение в математическую логику. – М.: Наука, 1971. – 320 с.
Б.А. Кушнер. Лекции по конструктивному математическому анализу. – М.: Наука, 1973. – 448 с.
А.А. Марков, Н.М. Нагорный. Теория алгорифмов. – М.: Наука, 1984. – 432 с.
А.И. Белоусов, С.Б. Ткачев. Дискретная математика.- 4-е изд. - М.: Изд. МГТУ им. Н.Э. Баумана, 2006. – 744 с.
А.Н. Колмогоров, А.Г. Драгалин. Математическая логика.- 3-е изд. – М.: КомКнига, 2006. – 240 с.
С.В. Яблонский. Введение в дискретную математику.- 3-е изд. – М.: Высшая школа, 2002. – 384 с.
Г.П. Гаврилов, А.А. Сапоженко. Задачи и упражнения по курсу дискретной математики. – М.: Наука, 1992. –
408 с.
И.А. Лавров, Л.Л. Максимова. Задачи по теории множеств, математической логике и теории алгоритмов. – М.:
Наука, 1975. – 240 с.
Дополнительная литература
Математическая логика в программировании: Сб. статей: Пер. с англ. – М.: Мир, 1991. – 408 с.
Н.К. Верещагин, А. Шень. Языки и исчисления. – М.: МЦНМО, 2000. – 291 с.
Н. Катленд. Вычислимость: введение в теорию рекурсивных функций. – М.: Мир, 1983. – 256 с.
Ч. Чень, Р. Ли. Математическая логика и автоматическое доказательство теорем. – М.: Наука, 1983. – 360 с.
ЛЕКЦИИ
Модуль 1. Теория алгоритмов
Лекция 1. Предпосылки возникновения математической логики и теории алгоритмов.
Проблемы математического определения алгоритма и доказательства. Интуитивная концепция
алгоритма. Понятие конструктивного объекта. Алфавит, слово, язык, словарная функция.
ОЛ-1, предисловие; ОЛ-2, введение; ОЛ-4, Д1.1, 7.1.
Лекция 2. Машины Тьюринга. Вычислимость по Тьюрингу. Тезис Тьюринга.
ОЛ-4, Д7.4; ОЛ-1, гл. 5, §2.
Лекция 3. Понятие нормального алгорифма Маркова. Основные примеры. Вычислимость
по Маркову. Принцип нормализации.
ОЛ-1, гл. 5, §1; ОЛ-2, §1, пп. 1.1 – 1.4, 1.9.
Лекция 4. Эквивалентность алгорифмов. Теорема о переводе. Способы сочетания
нормальных алгорифмов: теорема композиции.
ОЛ-1, гл. 5, §1; ОЛ-2, §1, пп. 1.5– 1.7.
102
Лекция 5. Способы сочетания нормальных алгорифмов: теоремы объединения, разветвления и
повторения. Универсальный алгорифм.
ОЛ-1, гл. 5, §1; ОЛ-2, §1, пп. 1.7– 1.8.
Лекция 6. Разрешимые и перечислимые множества. Перечислимые множества и области
применимости нормальных алгорифмов.
ОЛ-2, §§2, 3.
Лекция 7. Проблема применимости для нормальных алгорифмов и доказательство ее
неразрешимости.
ОЛ-2, §§2, 3.
Лекция 8. Понятие частично рекурсивной функции. Подстановка, рекурсия, минимизация. Тезис
Черча.
ОЛ-5, Дополнительные главы, гл. 2, §§3, 4; ОЛ-6, ч. I, гл.4, §§4-7; ДЛ-3, гл. 2, 3.
Лекция 9. Нумерация рекурсивных функций. S-m-n-теорема.
ДЛ-3, гл. 4.
Модуль 2. Булевы функции
Лекции 10-11. Булевы функции, равенство функций, суперпозиция, формулы. Реализация
булевых функций стандартными формулами. ДНФ, СДНФ, минимизация в классе ДНФ.
ОЛ-4, 6.1 – 6.6.
Лекции 12-13. Полные и замкнутые множества булевых функций. Классы Поста.
Критерий Поста функциональной полноты.
ОЛ-4 6.7.
Модуль 3. Математическая логика
Лекция 14. Понятие формальной теории. Аксиомы и правила вывода. Выводимость и
доказуемость. Примеры теорий. Исчисление высказываний (ИВ).
ОЛ-1, гл. 1, §4..
Лекция 15. Теорема дедукции для ИВ. Правила естественного вывода. Примеры
построения доказательств в ИВ.
ОЛ-1, гл. 1, §4.
Лекция 16. Полнота и непротиворечивость ИВ.
ОЛ-1, гл. 1, §4; ДЛ-2, гл.1, гл. 2: 2.1, 2.2.
Лекции 17–18. Понятие алгебраической системы. Операции и предикаты. Термы и
формулы. Понятие интерпретации. Выполнимость, истинность и логическая общезначимость.
Аксиомы и правила вывода исчисления предикатов 1-го порядка (ИП1).
ОЛ-4, 4.1; ОЛ-1, гл. 2, §§ 1 – 4.
Лекции 19-20. Теорема дедукции для ИП1. Примеры доказательств. Полнота и
непротиворечивость ИП1. Теории первого порядка. Проблемы полноты и разрешимости.
ОЛ-1, гл. 2, §§ 3, 4, 8; ДЛ-2, 4.1 – 4.5.
Лекции 21–22. Метод резолюций для ИВ и ИП1.
ДЛ-4, гл. 5.
103
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятия 1-2. Машины Тьюринга и нормальные алгорифмы.
ОЛ-4, задачи 7.37, 7.38; ОЛ-8, ч. III, §2; МРК.
Занятие 3. Рекурсивные функции.
ОЛ-7, гл. V, §2; ОЛ-8, ч. III, §1; ДЛ-3, упр. к главам 2 и 3; МРК.
Занятие 4. Построение минимальной ДНФ для булевой функции.
ОЛ-4, задачи 6.11 – 6.18.
Занятие 5. Полные множества булевых функций.
ОЛ-4, задачи 6.21-6.25.
Занятие 7. Исчисление высказываний.
ОЛ-1, упр. к. гл. 1; ДЛ-4, упр. к гл. 2, 5.
Занятие 8. Исчисление предикатов.
ОЛ-1, упр. к гл. 1; ДЛ-4, упр. к гл. 3, 5.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ
Модуль 1 Теория алгоритмов (7 неделя, максимум 30 баллов, минимум 16 баллов).
Домашнее задание №1 «Теория алгоритмов» (выдача 2 неделя, прием 5 неделя).
Рубежный контроль по модулю 1 (7 неделя).
Модуль 2. Булевы функции ( 11 неделя, максимум 30 баллов, минимум 16 баллов).
Домашнее задание №2 «Булевы функции» (выдача 7 неделя, прием 10 неделя).
Модуль 3. Математическая логика (16 неделя, максимум 30 баллов, минимум 18 баллов).
Домашнее задание №3 «Исчисление высказываний» (выдача 9 неделя, прием 15 неделя).
Рубежный контроль по модулю (16 неделя).
Дискретная математика
4 семестр 2012–13, спец. ИУ6
ЛИТЕРАТУРА
Основная литература (ОЛ)
1. Белоусов А.И., Ткачев С.Б. Дискретная математика. – Изд. 2-е. – М: Изд-во МГТУ им. Н.Э. Баумана, 2002. –
744 с.
2. Яблонский С.В. Введение в дискретную математику. – Изд. 2-е. – М.: Наука, 1986. – 384 с.
3. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. – Изд. 2-е. – М.: Наука, 1992. –
408 с.
4. Лекции по теории графов. / В.А. Емеличев, О.И. Мельников, В.И. Сарванов, Р.И. Тышкевич. – М.: Наука,
1990. – 383 с.
5. Винберг Э.Б.. Курс Алгебры. – М.: Факториал, 2002. – 544 с.
6. Кострикин А.И. Введение в алгебру. Основы алгебры. – М.: Физматлит, 1994. – 320 с.
Дополнительная литература (ДЛ)
1. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976. – 400 с.
104
2. Кофман А. Введение в прикладную комбинаторику. – М.: Наука, 1975. – 480 с.
3. Шиханович Ю.А. Введение в современную математику. – М.: Наука, 1965. – 376 с.
4. Сборник задач по алгебре / Под ред. А.И. Кострикина. – М.: Наука, 1987. –352 с.
5. Лавров И.М., Максимова Л.М. Задачи по теории множеств, математической логике и теории алгоритмов. –
М.: Наука, 1975. – 240 с.
6. П.С.Александров, А.Н.Колмогоров, Введение в теорию функций действительного переменного, М.: 1933,
270 с.
Методические пособия (МП)
1. Белоусов А.И., Мартынов Б.В., Щетинин А.Н. Лекции по дискретной математике. – М: изд-во МГТУ им.
Н.Э. Баумана, 1994.
2. Виноградова М.С., Ткачев С.Б. Булевы функции. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 32 с.
ЛЕКЦИИ
МОДУЛЬ 1. Элементы теории множеств и высшей алгебры
Лекция 1. Предмет и метод дискретной математики. Множества. Операции над
множествами. Декартово произведение. Отображения. Метод характеристических функции.
Композиция отображений. Обратное отображение. Теорема об обратном отображении.
ОЛ-1 1, конспект лекций, ОЛ-2, МРК; ОЛ-6
ДЛ-1, ДЛ5, ДЛ-6; МРК.
Лекция 2. Бинарное отношение. Способы задания бинарных отношений. Отношения
эквивалентности и фактор-множества. Частично упорядоченные множества. Супремум и
инфимум. Мощность множества. Счетные и несчетные множества.
ОЛ-1 1; ОЛ-2, ОЛ-3, ОЛ7 МРК; конспект лекций;
ДЛ-3, ДЛ-5, ДЛ6
Лекция 3. Полугруппы, группы. Гомоморфизм и изоморфизм. Подгруппа. Циклическая
подгруппа. Порядок элемента. Теоремы Кэли и Лагранжа.
ОЛ-5, ОЛ-6, ОЛ-1 2, ОЛ-1, МРК; конспект лекций; ДЛ-1, ДЛ-4.
Лекции 4-5. Полукольца, кольца и поля. Решение уравнения ax=b в группе и системы
линейных уравнений над полем. Идемпотентные полукольца. Замкнутые идемпотентные
полукольца. Решение линейных уравнений в замкнутых полукольцах.
ОЛ-1, 3, МП-1, конспект лекций, МРК, ДЛ1.
МОДУЛЬ 2. Булевы функции
Лекция 6-7. Булевы функции, равенство функций, суперпозиция, формулы. Реализация
булевых функций стандартными формулам: ДНФ, СДНФ, полиномы Жегалкина. Минимизация
в классе ДНФ. Карты Карно, алгоритм Блейка
ОЛ-1 6, ОЛ-2, ОЛ-3, МП-1, МП-2, конспект лекций, МРК.
Лекции 8–9. Полные системы булевых функций. Классы Поста. Критерий Поста.
ОЛ-1 6, МРК; конспект лекций; ОЛ-2, ОЛ-3, МП-1, МП-2.
МОДУЛЬ 3. Введение в теорию графов
Лекция 10. Простые и ориентированные графы. Подграфы. Изоморфизм. Маршруты,
пути, циклы, связность. Матричные представления графа. Деревья.
ОЛ-4 гл.1; ОЛ-1 5, конспект лекций, ОЛ-3, ДЛ-3.
Лекции 11. Взвешенные графы. Остовное дерево минимального веса. теорема Кирхгофа
(формулировка) и алгоритм Краскала.
105
ОЛ-4 гл.2; ОЛ-1 5, конспект лекций.
Лекция 12. Задача о достижимости и задача о кратчайшем пути в ориентированном
графе. Алгоритмическое и алгебраическое решения. Методы систематического обхода вершин
графа: поиск в глубину и поиск в ширину.
ОЛ-4, гл.2, ОЛ-1 5, конспект лекций.
МОДУЛЬ 4. Языки, автоматы и грамматики
Лекция 13-14. Алфавит, слово, язык. Операции над языками, регулярные языки и
регулярные выражения. Мощность множества регулярных языков. Существование
нерегулярных языков. Понятие конечного автомата-распознавателя как взвешенного орграфа.
Язык. допускаемый КА. Теорема Клини. Детерминизация КА. Регулярность дополнения
регулярного языка. Лемма о разрастании для регулярных языков. Примеры нерегулярных
языков.
ОЛ-1 7, ОЛ-7, конспект лекций.
Лекции 15. Конечные детерминированные автоматы с выходом. Задача о минимальном
покрывающем автомате. Эквивалентные состояния. Процедура минимизации.
ДЛ-1; МРК; конспект лекций; ОЛ-1 7.
Лекции 16-17. Языки порожденные грамматиками. Иерархия Хомского. Праволинейные
грамматики и регулярные языки. НК грамматики и задача распознавания. Счетность множества
языков, порожденных грамматиками, и существование языков не порождаемых грамматиками.
ОЛ-1 7, конспект лекций, ОЛ-7.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
МОДУЛЬ 1. Элементы теории множеств и высшей алгебры
Занятия 1-2. Множества. Доказательство теоретико-множественных равенств методом
характеристических функций и методом двух включений. Отображения. Проверки
биективности, инъективности, сюрьективности. Бинарные отношения, проверка их свойств,
порядки, эквивалентности. Классы эквивалентности. Наибольшие и наименьшие элементы,
максимальные и минимальные элементы.
МРК; ОЛ-3, ДЛ-5, ОЛ-1.
Занятие 3-4. Группы, примеры, подгруппы, циклические подгруппы, порядки элементов.
Группа перестановок. Решение уравнений в группах. Полукольца, кольца и поля. Решение
уравнений и систем уравнений в полях. Решение уравнений в группах и систем уравнений в
полях. Решение уравнения x=ax+b в полукольцах.
МРК, ОЛ-1, ДЛ-4, ОЛ5, ОЛ6, ОЛ-1 2.
Занятие 5 (первая половина). Рубежный контроль по модулю 1. (18-30 баллов)
МОДУЛЬ 2. Булевы функции
Занятие 5-6 (вторая половина). Булевы функции. СДНФ, СКНФ, полином Жегалкина,
фиктивные переменные. Сокращенная ДНФ (карты Карно и алгоритм Блейка). Тупиковые
формы (функция Патрика). Разбор типового Домашнего задания
ОЛ-3, гл.1 § 3-4; ОЛ-1 задача 6.4, 6.7, 6.8,6.11 МП-2.
Занятие 7-8. Полные системы булевых функций. Реализация стандартных булевых
функций с помощью функций полной системы. Разбор типового Домашнего задания.
ОЛ-3 гл.2; ОЛ-1 задачи 6.13–6.25, МП-2.
106
Занятие 9. Рубежный контроль по модулю 2. (9-15 баллов)
МОДУЛЬ 3. Введение в теорию графов
Занятия 10-11. Графы и матрицы. Вычисления в идемпотентных полукольцах. Поиск
матриц достижимости и стоимости кратчайших путей.
ОЛ4, упражнения, ОЛ3, гл.4.
Занятия 12. Алгоритмы на графах. Поиск в ширину. Поиск в глубину. Алгоритм
Краскала.
ОЛ4, упражнения, ОЛ3, гл.4.
Занятие 13. Рубежный контроль по модулю 3. (13-22 балла).
МОДУЛЬ 4. Языки, автоматы и грамматики
Занятия 14-15. Регулярные языки и регулярные выражения. Построение автомата по
регулярному выражению. Вычисление языка автомата. Построение автомата по регулярному
выражению. Детерминизация автоматов. Автомат для дополнения языка. Примеры грамматик.
Грамматика регулярного языка.
ОЛ-1 задачи 7.10, 7.14, 7.15, 7.16, МРК.
Занятие 16. Минимизация детерминированных атвоматов с выходом
ОЛ-1 задачи 7.17, 7.20, 7.21, ДЛ-1, МРК.
Занятия 17. Рубежный контроль по модулю 4 (20–33 балла).
МАТЕРИАЛЫ ДЛЯ ПОДГОТОВКИ
МОДУЛЬ 1: Введение в анализ
Вопросы для подготовки
Множества, равенство множеств, стандартные операции над множествами.
Характеристическая функция множества. Свойства характеристических функций.
Отображения множеств. Cюръективные, инъективные и биективные отображения. Операция
суперпозиции отображений.
Обратное отображение. Единственность обратного отображения. Теорема существования
обратного отображения (формулировка).
Бинарные отношения, отношения эквивалентности, классы эквивалентности, теорема о
разбиении на классы эквивалентности (формулировка).
Отношения порядка, максимальный (минимальный) элемент, инфинум и супремум.
Мощность множества, счетные множества, их свойства, мощность отрезка.
Полугруппы, группы, подгруппы, гомоморфизмы, изоморфизмы.
Группа перестановок.
Циклическая группа. Циклическая подгруппа. Порядок элемента. Теорема Лагранжа.
Решения уравнений в группах.
Полукольца, кольца, делители нуля, поля, примеры конечных полей.
Решение систем уравнений в полях.
Идемпотентные полукольца, замкнутые полукольца, решение уравнения x=ax+b.
Типовые задачи рубежного контроля
Записать характеристическую функцию симметрической разности множеств A и B через
характеристические функции самих множеств A и B.
Как устроены классы эквивалентности, заданной на множестве целых чисел так: два целых
числа эквивалентны, если они дают одинаковый остаток при делении на 6.
Найти минимальные (максимальные) элемент в заданном отношении порядка.
107
В группе перестановок
указать все подгруппы, изоморфные группе вычетов
(относительно сложения).
Найти порядок элемента 3 в мультипликативной группе вычетов по модулю 13.
Решить уравнение в группе перестановок, движений плоскости, множеств.
Решить систему уравнений в поле вычетов по модулю 7.
Решить уравнение в полукольце подмножеств.
МОДУЛЬ 2: Булевы функции
Вопросы для подготовки
Булевы функции, способы задания, существенные и фиктивные переменные, отношение
равенства.
Суперпозиция булевых функций. Формулы над множеством элементарных функций.
Стандартные формулы: СДНФ. СКНФ, полином Жегалкина.
Задача о минимизации ДНФ, меры сложности ДНФ, сокращенные ДНФ, алгоритм Блейка.
Тупиковые ДНФ, карта Карно для трех и четырех переменных. Теорема о тупиковости
минимальной ДНФ. Функция Патрика.
Контактные схемы, метод каскадов.
Замкнутые классы: классы функций сохраняющих константу, класс самодвойственных
функций, класс монотонных функций класс линейных функций.
Теорема Поста о полноте, построение заданной функции из функций полной системы.
Типовые задачи рубежного контроля
Для булевой функции трех переменных с изображающим числом #01101110 найти СДНФ,
СКНФ, полином Жегалкина.
Разложить данную булеву функцию трех переменных по первым двум переменным с пмощью
теоремы о разложении..
Показать, что данная булева функция трех переменных не является монотонной. Указать все
пары соседних наборов значений переменных, на которых
нарушается условие
монотонности. С помощью функций системы
реализовать отрицание.
Найти сокращенную ДНФ для функции #0111 1001 0110 0101.
Домашнее задание
Для заданной булевой функции 4х переменных построить карту Карно, выписать сокращенную
ДНФ. Найти ядро булевой функции, выписать функцию Патрика, найти все тупиковые
ДНФ, нарисовать соответствующие покрытия на карте Карно, выписать все минимальные
ДНФ.
Для двух заданных булевых функций
трех переменных построить сокращенные ДНФ.
Исследовать систему
на полноту. Если система не полна, дополнить ее до полной
системы функцией
так, чтобы система
не имела полных подсистем. В
полученной в результате полной системе реализовать следующие элементарные булевы
функции: константы, отрицание, конъюнкцию и дизъюнкцию.
МОДУЛЬ 3: Введение в теорию графов
Вопросы для подготовки
Графы, вершины, ребра, степень вершины, изоморфизмы графов.
Подграфы, пути, циклы, остовы, связный граф.
Графы и матрицы: матрица смежности, матрица Кирхгофа, матрица инцидентности, матрица
ориентированной инцидентности.
Деревья.
Взвешенные графы. Задача о поиске остова наименьшего веса. Алгоритмы Краскала и Прима
108
поиска остова наименьшего веса.
Ориентированные графы, матрица смежности, матрица достижимости, их связь. Вычисление
матрицы достижимости.
Взвешенные ориентированные графы, задача о кратчайшем пути, матрица стоимости
кратчайших путей, ее связь с матрицей смежности. Вычисление матрицы стоимости.
Алгоритмы перечисления: поиск в глубину и поиск в ширину.
Алгоритм Дейкстры поиска кратчайшего пути.
Типовые задачи рубежного контроля.
Сколько компонент связности может иметь граф с 5 вершинами и двумя ребрами?
Сколько ребер может иметь неориентированное дерево с 2012 вершинами?
Сколько циклов может быть у связного графа с 2012 вершинами и 2012 ребрами?
Выполнить поиск в глубину (в ширину) для данного ориентированного графа.
Выполнить алгоритм Краскала для данного взвешенного графа.
Решив линейную систему уравнений в полукольце (R  , max, ) , вычислить первый столбец
матрицы стоимостей кратчайших путей графа, матрица смежности которого имеет вид
.
МОДУЛЬ 4: Языки, автоматы и грамматики
Вопросы для подготовки
Алфавит, слово, язык, множество языков над данным алфавитом, его мощность, операции над
языками. Идемпотентное замкнутое полукольцо языков.
Регулярные операции и регулярные языки. Мощность множества регулярных языков.
Регулярные языки и автоматы. Построение языка по автомату и автомата по языку. Поиск
языка автомата с помощью итерации матрицы смежности.
Детерминизация. Автомат для дополнения.
Лемма о разрастании для регулярных языков, примеры нерегулярных языков.
Языки, порожденные грамматиками. Иерархия Хомского.
Грамматики и автоматы-распознаватели. Место регулярных языков в иерархии Хомского.
Существование не регулярных контекстно-свободных языков.
Типовые задачи рубежного контроля
Показать, что язык
над алфавитом
является регулярным.
Построить для него автомат и грамматику. Является ли полученная грамматика контекстносвободной?
Для автомата с выходом, заданного таблицей выписать все пары 2-неэкввалентных состояний.
Детерминизировать данный автомат.
Построить автомат, без пустых переходов, реализующий объединение данных языков.
Построить грамматику, порождающую данный язык.
Найти язык, порожденный данной праволинейной грамматикой.
Домашнее задание
Для конечного автомата M={{a,b},{q1,q2,q3},{q1, q2},{q3}, δ(q1,a) = {q1,q3}, δ(q1,b) = { q1 , q2},
δ(q2,a) = {q1}, δ(q2,b) = { q1 ,q3}, δ(q3,b) = {q1} }, где M = {{Алфавит}, {множество
состояний}, {начальные состояния}, {заключительные состояния}, функция переходов}},
нарисовать граф автомата, найти язык
порожденный автоматом. Детерминизировать
автомат. Построить автомат, допускающий язык
над алфавитом
. Построить автоматы для языков
,
,
. Исключить из них
109
переходы, помеченные пустым словом.
Для автомата с выходом, заданного таблицей, построить граф автомата, найти минимальный
автомат, построить граф минимального автомата. Если состояния q4 и q5 исходного
автомата не эквивалентны, то выписать различающую их входную последовательность.
Теоретические вопросы к экзамену,
не вошедшие в вопросы для подготовки к модулям
Теорема существования обратного отображения.
Теорема о разбиении на классы эквивалентности.
Теорема о мощности отрезка.
Теорема о мощности множества отображений из данного множества в двухэлементное
Теорема Кэли.
Теорема Лагранжа.
Теорема о конечной области целостности без делителей нуля.
Естественный порядок в идемпотентном полукольце.
Индуктивно упорядоченные множества, их непрерывные отображения, теорема о неподвижной
точке. Примеры.
Теорема о разложении.
Теорема о представлении булевой функции в виде полинома Жегалкина, метод неопределенных
коэффициентов.
Полином Жегалкина и существенные переменные булевой функции.
Теорема существования тупиковой минимальной ДНФ.
Теорема об сокращенной ДНФ монотонной функции.
Теорема Поста о полноте.
Покрытия и морфизмы автоматов, их связь.
Теорема о минимальности фактор автомата.
Теорема о связи k-эквивалентностей и эквивалентности.
Теорема о корректности алгоритма Краскала.
Теорема о связи матрицы смежности и матрицы достижимости.
Теорема о связи матрицы смежности и матрицы стоимостей кратчайших путей.
Мощность множества регулярных языков.
Поиск языка автомата с помощью итерации матрицы смежности.
Теорема Клини.
НК-грамматики. Языки, порожденные НК-грамматиками в иерархии Хомского.
Задача распознавания в НК-грамматиках.
Мощность множества языков, порожденных грамматиками, существование нерегулярных
контекстно-свободных языков.
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
для ФН-2
Дисциплина состоит из 2-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-7
28
Упражнения
1-9
18
110
Примечание
Домашние задания текущие
1-9
14
Контроль по модулю №1
10
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
8-17
40
Упражнения
10-17
16
Домашние задания текущие
10-17
12
Контроль по модулю №2
17
4
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Примечание
Модуль 1:Метрические, нормированные и гильбертовы пространства
Лекции
Лекции 1-2.Понятие метрического пространства
(МП), аксиомы метрики, предел последовательности
элементов МП. Открытые и замкнутые множества,
предельная точка. Плотные, всюду плотные, нигде не
плотные множества. Непрерывные функции в
метрических пространствах. Основные метрические
пространства. Неравенства Гельдера и Минковского.
ОЛ-1, гл. 2,
Лекции 7-8. Линейные пространства. Линейные
многообразия.
Бесконечномерные
линейные
многообразия.
Прямая
сумма
линейных
многообразий. Нормированные пространства (НП).
Банаховы пространства (БП). Примеры. Лемма
Рисса. Подпространства НП. Эквивалентность норм
в
конечномерных
линейных
пространствах.
Замкнутость
конечномерных
линейных
многообразий. Критерий локальной компактности
НП.
§1,2, ОЛ-3, гл.1, §2.
Лекция 3.Полные МП. Пополнение МП. Теорема о
вложенных множествах в МП.
ОЛ-1, гл.3, §1,3, ОЛ-3, гл.2, §1, ОЛ-5 §5.1-5.3, ОЛ-6
§4.1.
ОЛ-1, гл.2, §3, ОЛ-3, гл. 2, §3.
Лекция 9. Ряды в НП. Критерий Коши сходимости
ряда. Теоремы об абсолютно сходящихся рядах в БП.
БП со счетным базисом и сепарабельные
пространства.
Лекция 4.Принцип сжимающих отображений.
Примеры применения принципа сжимающих
отображений. Свойства интегрального оператора
Вольтерра и его степени.
ОЛ-4, гл.1, §5,ОЛ-5 §5.4-5.7.
ОЛ-1, гл.2, §4, ОЛ-3, гл.1, §3, ОЛ-6 §4.2.
Лекции 10-11. Гильбертово пространство (ГП).
Примеры. Непрерывность скалярного произведения.
Равенство параллелограмма. Расстояние от точки до
замкнутого выпуклого множества. Расстояние от
точки
до подпространства.
Ортогональность
элементов ГП. Ортогональное дополнение к
подпространству. Разложение ГП в прямую сумму
подпространства и его ортогонального дополнения.
Критерий всюду плотности линейного многообразия
в ГП.
Лекция 5. Сепарабельные пространства. Примеры
сепарабельных и несепарабельных пространств.
ОЛ-1, гл. 2, §7, ОЛ-3, гл. 2, §2.6, ОЛ-5, §5.4.
Лекция 6. Компактные множества в МП. Свойства
отображений,
непрерывных на компактных
множествах. Критерий компактности множеств в МП
(теорема Хаусдорфа). Критерии относительной
компактности множеств в пространствах
и .
ОЛ-1, гл.2, §7, ОЛ-3, гл.2, §2.6, ОЛ-6 §4.2.
ОЛ-1, гл.3, §4, ОЛ-3 гл.4, §1, ОЛ-4, гл.1, §6, ОЛ-5
§6.1-6.3, ОЛ-6 §5.1.
111
Лекции 12-13. Ортонормированные системы (ОНС) и
ряды Фурье
в
ГП.
Неравенство Бесселя.
Ортонормированные базисы в ГП. Критерии
базисности ортонормированной системы в ГП.
Равенство Парсеваля. Замкнутые ОНС как
ортонормированные
базисы.
Полные
ортонормированные системы (ПОНС). ПОНС как
ортонормированные базисы.
Лекция 14. Процесс ортогонализации Грама Шмидта. Теорема о существовании в каждом
сепарабельном ГП счетного ортонормированного
базиса. Изоморфизм гильбертовых сепарабельных
пространств. Теорема Рисса - Фишера.
ОЛ-1, гл.4, §6, ОЛ-3, гл.4, §1, ОЛ-4, гл.1, §6, ОЛ-5
§6.6-6.7.
ОЛ-1, гл.4, §6, ОЛ-3, гл.4, §1, ОЛ-4, гл.1, §6, ОЛ-5
§6.4-6.5.
Упражнения
Занятие 1.Элементы теории множеств. Мощность
множества. Эквивалентные множества. Счетные
множества и множества мощности континуума.
ОЛ-1, гл.1, §3.
Занятие 2.Основные понятия в метрических
пространствах.
ОЛ-6, гл.1, §6, ОЛ-12, Задачи: 1.1-1.12
Занятие 3. Полнота метрических пространств.
ОЛ-6, гл.1, §6, ОЛ-12, Задачи: 2.1-2.4.
Занятие 4.Принцип сжимающих отображений.
ОЛ-6, гл.1, §6, гл. 6 §24, ОЛ-12, Задачи: 2.5-2.10.
Занятие 5.Компактные множества в метрических
пространствах.
ОЛ-6, гл.1, §6, ОЛ-12, Задачи: 3.1-3.8.
Занятие 6.Нормированные пространства.
ОЛ-6, гл.1, §1, ОЛ-12, Задачи: 4.1-4.4.
Занятие 7.Банаховы пространства.
ОЛ-6, гл.1, §2, ОЛ-12, Задачи: 4.5-4.9.
Занятие 8. Гильбертовы пространства. Расстояние
от элемента до подпространства.
ОЛ-6, гл.1, §3, ОЛ-12, Задачи: 5.1-5.6
Занятие
9. Ортонормированные
базисы
в
гильбертовых пространствах.
ОЛ-6, гл.1, §3, 5, ОЛ-12, Задачи: 5.7-5.8.
Модуль 2:Линейные операторы и интегральные уравнения
Лекции
Лекции 1-2.Элементы теории множеств. Системы
множеств: полукольцо, кольцо, алгебра,
сигмаалгебра. Мера на полукольце. Продолжение меры с
полукольца на порожденное им минимальное кольцо.
Свойства меры. Счетно-аддитивная мера, ее
продолжение с полукольца на минимальное кольцо.
Внешняя мера и ее свойства. Лебегово продолжение
меры. Измеримые по Лебегу множества. Свойства
меры Лебега.
вид непрерывных ЛФ в некоторых БП. Общий вид
непрерывных ЛФ в ГП.
ОЛ-1, гл.4, §1, ОЛ-3, гл.2, §2, ОЛ-4, гл.4, §16,17, ОЛ6 §4.4, 5.2.
Лекция8. Сопряженные пространства. Сильная и
слабая
сходимости.
Второе
сопряженное
пространство.
ОЛ-1, гл.4, §2,3, ОЛ-3, гл.2, §2.5, ОЛ-4, гл,4, §17, ОЛ6 § Д.5.1.
ОЛ-1, гл.1, гл.5, §1-3. ОЛ-3, гл.3, §1, ОЛ-5 §7.1.
Лекции 3-4.Измеримые функции и их свойства.
Сходимость почти всюду. Интеграл Лебега на
множестве конечной меры. Свойства интеграла
Лебега.
Сигма-аддитивность
и
абсолютная
непрерывность
интеграла
Лебега. Предельный
переход под знаком интеграла Лебега. Сравнение
интеграла Лебега с интегралом Римана.
Лекция
9.
Расширение
понятия
функции.
Пространство основных функций. Обобщенные
функции. Действия над обобщенными функциями.
ОЛ-1, гл.4, §5.
Лекции 10-11. Линейные операторы в НП.
Линейные ограниченные (непрерывные) операторы
в
БП. Норма опреатора. Нормированное
пространство линейных ограниченных операторов.
Принцип равномерной ограниченности (теорема
Банаха - Штейнгауза). Обратные операторы.
Теорема Банаха об обратном операторе.
ОЛ-1, гл.5, §5, ОЛ-3, гл.3 §2,3, ОЛ-5 §7.2-7.3.
Лекция 5.Банаховы пространства
и их свойства.
,
,
ОЛ-1, гл.7, §1,2,ОЛ-5 §7.4-7.5.
ОЛ-1, гл.4, §5, ОЛ-3, гл.2, §3.3, ОЛ-4, гл.2, §10, 11,
12, ОЛ-6 §4.3- 4.5.
Лекции6-7.
Линейные
функционалы
(ЛФ).
Ограниченные ЛФ, непрерывные ЛФ, их связь.
Норма ЛФ. Примеры. Теорема Хана - Банаха о
продолжении ограниченного ЛФ, следствия. Общий
Лекция 12. Спектр линейного оператора. Регулярные
значения оператора. Резольвента.
Собственные
112
значения
оператора.
и собственные элементы линейного
ОЛ-1, гл.4, §6, ОЛ-2, гл.6, §1,2,3, ОЛ-3, гл.4, §2, ОЛ4, гл.5, §20,21,22, ОЛ-6, §4.6, 5.4, 5.5.
ОЛ-1, гл.4, §5, ОЛ-4, гл.4, §18, гл.6, §24, ОЛ-6, §4.6.
Лекции 16-17. Интегральные уравнения Фредгольма.
Классификация
интегральных
уравнений.
Однородное уравнение Фредгольма второго рода.
Собственные функции и собственные значения
однородного уравнения Фредгольма второго рода.
Разложение по собственным функциям. Краевая
задача на собственные значения (задача Штурма Лиувилля).
Лекция 13. Сопряженные операторы в НП.
Сопряженные операторы в ГП. Самосопряженные
операторы. Положительно определенные операторы.
ОЛ-1, гл.4, §5, ОЛ-4, гл.4, §18, гл.6, §24, ОЛ-6, §5.2,
Д.5.1.
Лекции 14-15. Вполне непрерывные (компактные)
операторы и их свойства. Спектр вполне
непрерывного оператора в НП. Спектр вполне
непрерывного самосопряженного (симметрического)
оператора в ГП. Теорема Гильберта - Шмидта.
Однородные
и
неоднородные
операторные
уравнения.
Уравнения с вполне непрерывными
симметрическими
операторами.
Примеры
интегральных уравнений.
ОЛ-1, гл.9, §1,2, ОЛ-7, гл.1, 3-5.
Лекции 18-19. Неоднородное уравнение Фредгольма
второго рода. Теоремы Фредгольма. Уравнения
Вольтерра второго рода. Резольвента для уравнения
Вольтерра. Интегральное уравнение Фредгольма
первого рода.
ОЛ-1, гл.9, §1,2, ОЛ-7, гл.6-8.
Лекция 20. Резерв.
Упражнения
Занятие 1. Мера Лебега. Измеримые функции.
Интеграл Лебега.
ОЛ-6, гл.1, §4.
Занятие 2.Линейные ограниченные функционалы и
их нормы. Сопряженные пространства.
ОЛ-6, гл.3, §11-13, ОЛ-12, Задачи: 6.1-6.2.
Занятие 3. Линейные ограниченные операторы.
Норма линейного оператора.
ОЛ-6, гл.2, §7-8, ОЛ-12, Задачи: 6.3.
Занятие 4.Обратные линейные операторы.
Л-6, гл.2, §9.
Занятие 5.Сопряженные операторы.
Л-6, гл.3, §14.
Занятие 6.Спектр оператора. Резольвента.
Л-6, гл.5, §19.
Занятие
7.
Самосопряженные
операторы.
Компактные операторы. Спектр самосопряженного
компактного оператора.
Л-6, гл.5, §20, ОЛ-12, Задачи: 6.4-6.5.
Занятие 8. Интегральные уравнения Фредгольма.
Л-6, гл.5, §21.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий,
подготовке к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Основные понятия функционального анализа»
Срок выдачи 1 неделя, срок сдачи – 8 неделя
2. Контроль по модулю №1 (РК №1) «Основные понятия функционального анализа».
Срок проведения – 10 неделя
Модуль 2.
1. ДЗ №2 «Функционалы, операторы, интегральные уравнения»
Срок выдачи 8 неделя, срок сдачи – 15 неделя
2. КР «Функционалы и операторы»
Срок проведения - 13 неделя
3. Контроль по модулю №2 (РК №2) «Функциональный анализ».
Срок проведения – 16 неделя
113
Литература
Основная литература (ОЛ)
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. - М.: Наука, 1981. - 542
с.
2. Люстерник Л.А., Соболев В.Н. Элементы функционального анализа. - М.: Наука, 1965. - 520 с.
3. Садовничий В.А. Теория операторов. - М.: Изд-во МГУ, 1986. - 368~с.
4. Треногин В.А. Функциональный анализ. - М.: Наука, 1980. - 495 с.
5. Власова Е.А. Ряды. - М.: Изд-во МГТУ, 2000. -612 с.
6. Власова Е.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики. - М.: Изд-во
МГТУ, 2001. -700 с.
7. Васильева А.Б., Тихонов Н.А. Интегральные уравнения. - М.: Изд-во МГУ, 1989. - 158 с.
8. Треногин В.А., Писаревский В.М., Соболева Т.С. Задачи и упражнения по функциональному анализу. - М.:
Наука, 1984. - 256 с.
9. Власова Е.А., Феоктистов В.В., Чадов В.Б. Введение в прикладной функциональный анализ. - М.: Изд-во
МГТУ, 1994. - 54 с.
10. Феоктистов В.В. Бесконечномерные пространства и применение функционального анализа в математической
физике. - М: Изд-во МГТУ, 1995. - 54 с.
11. Власова Е.А., Нараленков К.М., Пугачев О.В. Функциональный анализ. – М.: Изд-во МГТУ, 2005. – 64 с.
12. Власова Е.А., Красновский Е.Е., Марчевский И.К. Функциональный анализ. –М: Изд-во МГТУ, 2009, - 77 с.
1.
1.
2.
3.
4.
Дополнительная литература (ДЛ)
Вулих Б.З. Краткий курс теории функций вещественной переменной. - М.: Наука, 1973. - 304 с.
Пугачев В.С. Лекции по функциональному анализу. - М.: Изд-во МАИ, 1996. - 744 с.
Канторович Л.В., Акилов Г.П. Функциональный анализ. - М.: Наука, 1977. - 744 с.
Кириллов А.А., Гвишиани А.Д. Теоремы и задачи функционального анализа. - М.: Наука, 1988. 398 с.
Рекомендуемые Интернет-сайты:
1. http://www.mathelp.spb.ru - лекции по высшей математике
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
для ФН-4
Дисциплина состоит из 3-х учебных модулей.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-4
4
Упражнения
1-6
12
Домашние задания текущие
1-6
10
Контроль по модулю №1
5
2
114
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
5-10
6
Упражнения
7-10
8
Домашние задания текущие
7-10
5
Контроль по модулю №2
10
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
11-17
7
Упражнения
11-17
14
Домашние задания текущие
10-17
5
Контроль по модулю №3
15
4
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Примечание
Модуль 1:Метрические и нормированные и пространства
Лекции
Лекция 1.. Понятие метрического пространства
(МП), аксиомы метрики, предел последовательности
элементов
МП.
Непрерывные
функции
в
метрических пространствах. Основные метрические
пространства. Неравенства Гельдера и Минковского.
Полные МП. Пополнение МП. Теорема о вложенных
шарах в МП. Принцип сжимающих отображений.
Свойства интегрального оператора Вольтерра и его
степени. Сепарабельные пространства. Компактные
множества в МП.
Свойства отображений,
непрерывных на компактных множествах. Критерии
относительной
компактности
множеств
в
метрических пространствах.
ОЛ-1, гл. 2, §1-4, 7, ОЛ-3, гл.1, §2, 3, гл. 2, §2.6, 3, ,
ОЛ-5, §5.4, ОЛ-6 §4.2 .
Лекция 2.Нормированные
пространства
(НП).
Банаховы
пространства
(БП).
Примеры.
Подпространства НП. Эквивалентность норм
в
конечномерных линейных пространствах. Критерий
локальной компактности НП. Ряды в НП. Критерий
Коши сходимости ряда. Теоремы об абсолютно
сходящихся рядах в БП. БП со счетным базисом и
сепарабельные пространства.
ОЛ-1, гл.3, §1,3, ОЛ-3, гл.2, §1, ОЛ-4, гл.1, §5, ОЛ-5
§5.1-5.7, ОЛ-6 §4.1.
Упражнения
Занятие 1.Основные понятия в метрических
пространствах.
ОЛ-6, гл.1, §6, ОЛ-12, Задачи: 1.1-1.12
Занятие 2. Полнота метрических пространств.
ОЛ-6, гл.1, §6, ОЛ-12, Задачи: 2.1-2.4.
Занятие 3.Принцип сжимающих отображений.
ОЛ-6, гл.1, §6, гл. 6 §24, ОЛ-12, Задачи: 2.5-2.10.
Занятие 4.Компактные множества в метрических
пространствах.
ОЛ-6, гл.1, §6, ОЛ-12, Задачи: 3.1-3.8.
Занятие 5.Нормированные пространства.
ОЛ-6, гл.1, §1, ОЛ-12, Задачи: 4.1-4.4.
Занятие 6.Банаховы пространства.
ОЛ-6, гл.1, §2, ОЛ-12, Задачи: 4.5-4.9.
115
Модуль 2:Гильбертовы пространства и линейные функционалы
Лекции
Лекция 1.Гильбертово пространство (ГП). Примеры.
Непрерывность скалярного произведения. Равенство
параллелограмма.
Расстояние
от
точки
до
подпространства. Ортогональность элементов ГП.
Ортогональное дополнение к подпространству.
Разложение ГП в прямую сумму подпространства и
его ортогонального дополнения.
ортогонализации Грама - Шмидта. Теорема о
существовании в каждом сепарабельном
ГП
счетного ортонормированного базиса. Изоморфизм
гильбертовых сепарабельных пространств.
ОЛ-1, гл.4, §6, ОЛ-3, гл.4, §1, ОЛ-4, гл.1, §6, ОЛ-5
§6.4-6.7.
Лекция
3.Линейные
функционалы
(ЛФ).
Ограниченные ЛФ, непрерывные ЛФ, их связь.
Норма ЛФ. Примеры. Теорема Хана - Банаха о
продолжении ограниченного ЛФ, следствия. Общий
вид непрерывных ЛФ в некоторых БП. Общий вид
непрерывных ЛФ в ГП. Сопряженные пространства.
Сильная и слабая сходимости. Обобщенные функции
и их свойства.
ОЛ-1, гл.3, §4, ОЛ-3 гл.4, §1, ОЛ-4, гл.1, §6, ОЛ-5
§6.1-6.3, ОЛ-6 §5.1.
Лекции 2.Ортонормированные системы (ОНС) и
ряды Фурье
в
ГП.
Неравенство Бесселя.
Ортонормированные базисы в ГП. Критерии
базисности ортонормированной системы в ГП.
Равенство Парсеваля. Замкнутые ОНС как
ортонормированные
базисы.
Полные
ортонормированные системы (ПОНС). ПОНС как
ортонормированные
базисы.
Процесс
ОЛ-1, гл.4, §1-3, §5, ОЛ-3, гл.2, §2, ОЛ-4, гл.4, §16,17,
ОЛ-6 §4.4, 5.2.
Упражнения
Занятие 1.. Гильбертовы пространства. Расстояние
от элемента до подпространства.
ОЛ-6, гл.1, §3, ОЛ-12, Задачи: 5.1-5.6.
Занятие
2.Ортонормированные
базисы
в
гильбертовых пространствах.
ОЛ-6, гл.1, §3, 5, ОЛ-12, Задачи: 5.7-5.8.
Занятие 3.Линейные ограниченные функционалы и
их нормы. Сопряженные пространства.
ОЛ-6, гл.3, §11-13, ОЛ-12, Задачи: 6.1-6.2.
Занятие 4. Рубежный контроль №1.
Модуль 3:Линейные операторы и интегральные уравнения
Лекции
Лекция 1.Линейные операторы в НП. Линейные
ограниченные (непрерывные) операторы в БП.
Норма оператора. Нормированное пространство
линейных ограниченных операторов. Обратные
операторы. Теорема Банаха об обратном операторе.
Спектр линейного оператора. Регулярные значения
оператора. Резольвента. Собственные значения и
собственные элементы линейного оператора.
непрерывного самосопряженного (симметрического)
оператора в ГП. Теорема Гильберта - Шмидта.
ОЛ-1, гл.4, §5, 6, ОЛ-2, гл.6, §1,2,3, ОЛ-3, гл.4, §2,
ОЛ-4, гл.4, гл.5, §20,21,22, §18, гл.6, §24, ОЛ-6, §4.6,
5.2, 5.4, 5.5, Д.5.1.
Лекции 3-4.Интегральные уравнения Фредгольма.
Классификация
интегральных
уравнений.
Однородное уравнение Фредгольма второго рода.
Собственные функции и собственные значения
однородного уравнения Фредгольма второго рода.
Разложение
по
собственным
функциям.
Неоднородное уравнение Фредгольма второго рода.
Теоремы Фредгольма.
ОЛ-1, гл.4, §5, ОЛ-3, гл.2, §3.3, ОЛ-4, гл.2, §10, 11,
12, гл.4, §18, гл.6, §24, ОЛ-6 §4.3- 4.5, §4.6.
Лекции
2.Сопряженные
операторы
в
НП.
Сопряженные операторы в ГП. Самосопряженные
операторы. Понятие о вполне непрерывном
операторе. Вполне непрерывные операторы в
гильбертовом пространстве.
Спектр вполне
ОЛ-1, гл.9, §1,2, ОЛ-7, гл.1, 3-5, гл. 6-8.
Упражнения
Занятия1-2. Линейные ограниченные операторы.
Норма линейного оператора.
ОЛ-6, гл.2, §7-8, ОЛ-12, Задачи: 6.3.
Занятие 3.Обратные линейные операторы.
Л-6, гл.2, §9.
Занятие 4.Сопряженные операторы.
Л-6, гл.3, §14.
Занятие 5.Спектр оператора. Резольвента.
Л-6, гл.5, §19.
Занятие 6. Рубежный контроль №2.
Занятие 7 .Резерв.
116
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних
заданий, подготовке к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Основные понятия функционального анализа»
Срок выдачи 1 неделя, срок сдачи – 5 неделя
Модуль 2.
1. Контроль по модулю №1 (РК №1) «Основные понятия функционального анализа».
Срок проведения – 10 неделя
Модуль 3.
1. ДЗ №2 «Функционалы, операторы, интегральные уравнения»
Срок выдачи 8 неделя, срок сдачи – 15 неделя
2. Контроль по модулю №2 (РК №2) «Функциональный анализ».
Срок проведения – 15 неделя
Литература
Основная литература (ОЛ)
13. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. - М.: Наука,
1981. - 542 с.
14. Люстерник Л.А., Соболев В.Н. Элементы функционального анализа. - М.: Наука, 1965. - 520 с.
15. Садовничий В.А. Теория операторов. - М.: Изд-во МГУ, 1986. - 368~с.
16. Треногин В.А. Функциональный анализ. - М.: Наука, 1980. - 495 с.
17. Власова Е.А. Ряды. - М.: Изд-во МГТУ, 2000. -612 с.
18. Власова Е.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики. - М.: Издво МГТУ, 2001. -700 с.
19. Васильева А.Б., Тихонов Н.А. Интегральные уравнения. - М.: Изд-во МГУ, 1989. - 158 с.
20. Треногин В.А., Писаревский В.М., Соболева Т.С. Задачи и упражнения по функциональному анализу. М.: Наука, 1984. - 256 с.
21. Власова Е.А., Феоктистов В.В., Чадов В.Б. Введение в прикладной функциональный анализ. - М.: Издво МГТУ, 1994. - 54 с.
22. Феоктистов В.В. Бесконечномерные пространства и применение функционального анализа в
математической физике. - М: Изд-во МГТУ, 1995. - 54 с.
23. Власова Е.А., Нараленков К.М., Пугачев О.В. Функциональный анализ. – М.: Изд-во МГТУ, 2005. – 64
с.
24. Власова Е.А., Красновский Е.Е., Марчевский И.К. Функциональный анализ. –М: Изд-во МГТУ, 2009, 77 с.
5.
6.
7.
8.
Дополнительная литература (ДЛ)
Вулих Б.З. Краткий курс теории функций вещественной переменной. - М.: Наука, 1973. - 304 с.
Пугачев В.С. Лекции по функциональному анализу. - М.: Изд-во МАИ, 1996. - 744 с.
Канторович Л.В., Акилов Г.П. Функциональный анализ. - М.: Наука, 1977. - 744 с.
Кириллов А.А., Гвишиани А.Д. Теоремы и задачи функционального анализа. - М.: Наука, 1988. 398 с.
Рекомендуемые Интернет-сайты:
1. http://www.mathelp.spb.ru - лекции по высшей математике
АНАЛИТИЧЕСКАЯ ХИМИЯ
(для бакалавров Э–9, 4 семестр)
Дисциплина состоит из 3-х учебных модулей
117
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 1
Модуль 1
Сроки проведения или
выполнения, недели
1-6
1-6
1-6
6
Трудоемкость, Примечания
часы
6
8
8
2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 2
Модуль 2
Сроки проведения или
выполнения, недели
7 - 10
7 - 10
8 - 11
11
Трудоемкость, Примечания
часы
4
10
9
2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Контроль по модулю 2
Модуль 3
Сроки проведения или
выполнения, недели
11 - 17
11 - 17
16
Трудоемкость, Примечания
часы
7
10
2
МОДУЛЬ1:Теоретические основы аналитической химии
Лекции
Лекция 1. Химический анализ. Аналитическая
химия как теоретическая основа химического
анализа. Понятие об аналитическом сигнале.
Качественный анализ. Количественный анализ.
Стадии химического анализа. Отбор и подготовка
пробы к анализу. Разложение пробы. Основные
закономерности протекания химических реакций,
использование законов химической кинетики и
термодинамики для получения аналитического
сигнала.
переносом протона. Автопротолиз растворителя.
Равновесия в водных растворах. Количественные
характеристики
процессов
диссоциации,
гидролиза.
Влияние
на
растворимость
электролитов
температуры,
введения
одноименного иона. Солевой эффект. Реакции с
переносом электрона, их применение в
качественном и количественном анализе.
Определение показателей качества природных и
сточных вод. Реакции с переносом электронных
пар с образованием донорно-акцепторных
связей. Применение комплексных соединений в
химическом анализе.
ОЛ-1, ОЛ-3.
Лекция 2. Типы химических реакций,
применяемых в аналитической химии. Реакции с
ОЛ-2.
Лабораторные работы
Занятие1.Знакомство с химической посудой и оборудованием аналитической лаборатории. Расчеты в
аналитической химии с использованием понятий «концентрация», «эквивалент».
Занятие2. Приготовление растворов точной концентрации.
Занятие3, 4.Измерение рН в растворах кислот и оснований. Буферные растворы.
Занятие5.Аналитические реакции катионов.
118
Занятие6.Контроль модуля1
МОДУЛЬ2:Классические методы количественного химического анализа
Лекции
Лекция 3. Классический количественный
анализ. Гравиметрия. Стадии гравиметрического
анализа.
Требования,
предъявляемые
к
осаждаемой и гравиметрической формам.
Образование и старение осадков. Соосаждение
как одна из форм загрязнения осадка. Примеры
гравиметрических определений.
Расчет кривых титрования. Индикаторы метода.
Выбор индикатора. Расчет ошибок титрования.
Примеры определений. Использование метода
нейтрализации для определения показателей
качества
природных
и
сточных
вод.
Комплексонометрическое титрование. Понятие о
комплексонах. Металлохромные индикаторы.
Примеры
определений.
Осадительное
и
окислительно-восстановительное
титрование.
Фиксирование точки эквивалентности в данных
методах Примеры определений.
ОЛ-2, ОЛ-3.
Лекция
4.
Титриметрический
анализ
(титриметрия).
Требования
к
реакциям,
используемым в титриметрии. Классификация
методов титриметрии. Метод нейтрализзации.
ОЛ-1.
Лабораторные работы
Занятие 7, 8Определение качества природной воды и пищевых продуктов: определение содержания
растворенного СО2, кислотности воды или молока, щелочности, карбонатной жесткости воды.
Занятие 9, 10. Комплексонометрическое титрование: определение содержания ионов Ca2+, Mg2+, Fe3+ в
водопроводной и природной водах, ионов Cu2+ в растворах.
Занятие 11 .Контроль модуля 2.
МОДУЛЬ3:Физико-химические методы анализа
Лекции
Лекция 5.Физико-химические методы анализа.
Классификация методов. Оптические методы.
Абсорбционная спектроскопия (фотометрия).
Закон Бугера-Ламберта-Бера-основной закон
фотометрии.
Спектрофотометрия,
фотоколориметрия.
Метод
калибровочного
графика. Фотоколориметрическое титрование.
Колориметрия.
качественного и количественного определения
состава смеси.
Обработка хроматограмм.
Принципиальная схема хроматографа, виды
детекторов.
ОЛ-1, ОЛ-4.
Лекция 8. Ионообменная хроматография.
Ионообменники. Константа ионного обмена,
обменная емкость ионита. Примеры разделения
компонентов смеси методом ионообменной
хроматографии.
Экстракция
как
метод
разделения и концентрирования веществ. Виды
экстракционных
процессов.
Константа
распределения.
Расчеты
при
проведении
экстракционных
процессов.
Экстракция
в
химическом анализе.
ОЛ-3, ОЛ-4.
Лекция 6.
Электрохимические
методы
анализа.
Классификация
методов.
Потенциометрия. Электроды индикаторные и
сравнения.
Хлорсеребряный
электрод,
стеклянный электрод. Потенциометрическое
титрование.
Ионометрия.
Ионоселективные
электроды.
Кондуктометрия
и
кондуктометрическое титрование. Полярография.
ОЛ-3, ОЛ-4.
Литература: ОЛ-3, ОЛ-4.
Лекция
7.
Хроматография.
Виды
хроматографии. Неподвижная фаза и носитель.
Газовая хроматография (ГХ). Газожидкостная
хроматография (ГЖХ). Виды хроматограмм.
Применение ГХ и ГЖХ для разделения веществ,
119
Лабораторные работы.
Занятие 12, 13. Фотометрия. Определение содержания Fe3+ в водопроводной или природной воде.
Занятие 14. Количественное и качественное обнаружение катионов методом осадочной хроматографии в
колонке и на бумаге.
Занятие 15. Разделение ионов Cu2+, Zn2+, Mg2+ методом экстракции.
Занятие 16 .Контроль модуля 3.
Домашние задания
ДЗ 1.Равновесия в водных растворах сильных электролитов. Выдача -01 неделя, сдача–05 неделя
ДЗ 2.Равновесия в водных растворах слабых электролитов. Выдача – 06 неделя, сдача - 11неделя
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций; подготовке к выполнению и
защите лабораторных работ; выполнении индивидуального домашнего задания. Каждое домашнее
задание включает в себя 5 практических и расчетных задач. Самостоятельная работа является как
домашней, так и аудиторной (в том числе под контролем преподавателя на консультациях, где разбираются
трудные вопросы из материала лекций, типовые варианты домашних и контрольных заданий, а также
демонстрируются возможности использования математических программ при обработке результатов
лабораторных работ).
Самостоятельная работа является как домашней, так и аудиторной под контролем преподавателя (КСР)
Зачетная работа
Итоговый контроль по дисциплине проводится на 17 неделе для студентов, которые неудовлетворительно
освоили содержание модулей (т.е. для студентов, набравших менее 60 баллов).
ЛИТЕРАТУРА
Основная литература(ОЛ)
1.
2.
3.
4.
Харитонов Ю.А. Аналитическая химия. Аналитика. В 2-х кн. М.: Высшая школа, 2001.
Васильев В.П. Аналитическая химия. В 2-х кн. М.: Дрофа, 2002.
Кунце У., Шведт Г. Основы качественного и количественного анализа. М.: Мир, 1997.
Отто М. Современные методы аналитической химии. М.: Техносфера, 2003.
Методические пособия, изданные в МГТУ (МП)
5.
В.Н. Горячева, И.В. Татьянина, В.Н., Ж.Н. Каблучая, А.М. Голубев, Е.А. Якушева. Методические
указания к выполнению домашнего задания по курсу аналитической химии с примерами решения
задач. Методические указания. М.: Изд. МГТУ им. Н.Э. Баумана. 2009. 36 с.
6.
В.Н. Горячева, И.В. Татьянина, В.Н., Ж.Н. Каблучая, А.М. Голубев, Е.А. Якушева. Сборник задач по
курсу аналитической химии. Учеб.пособие. М.: Изд. МГТУ им. Н.Э. Баумана. 2010. 23 с.
7.
Горячева В.Н., Татьянина И.В., Харитонова Л.К. и др. Методические указания к лабораторным
работам по аналитической химии. М.: изд-во МГТУ им. Н.Э. Баумана, 2002.
8.
Горячева В.Н., Татьянина И.В., Хмарцева Л.А. и др. Аналитические реакции некоторых
органических анионов. Методические указания к выполнению лабораторной работы. М.: изд-во
МГТУ, 2004.
120
9.
Горячева В.Н., Татьянина И.В., Овчаренко Л.П. и др. Аналитическая химия. Ч.1.Классические
методы количественного анализа. М.: изд-во МГТУ, 2005.
10.
Смирнов А.Д., Голубев А.М., Горячева В.Н. и др. Аналитическая химия. Ч.2. Количественный
анализ. М.: изд-во МГТУ, 2007.
11.
Слитиков П.В., Каблучая Ж.Н., Горячева В.Н. и др. Применение методов хроматографии в
аналитической химии. Методические указания к лабораторной работе. М.: изд-во МГТУ. 2007.
12.
Татьянина И.В., Горячева В.Н., Сабельникова Т.М. и др. Экстракция как метод разделения и
концентрирования веществ на примере разделения ионов Cu(II), Zn(II),Mg(II). М.: изд-во МГТУ, 2008.
Электронныеучебныепособия(ЭП)
13. Координационные соединения: электронное учебное пособие / Татьянина И.В., Горячева В.Н.,
Каблучая Ж.Н. − ФГУП НТЦ «Информрегистр», № 0321002693, от 29.12.2010.
14. Горячева В.Н., Татьянина И.В., Смирнов А.Д., Каблучая Ж.Н., Голубев А.М. Аналитическая химия:
электронное учебное издание: курс лекций по дисциплине «Аналитическая химия». Часть 1.
Классические методы количественного анализа. − ФГУП «Информрегистр», № 0321201047, от
26.04.2012.
15. Горячева В.Н., Татьянина И.В., Смирнов А.Д., Каблучая Ж.Н., Голубев А.М. Аналитическая химия:
электронное учебное издание: курс лекций по дисциплине «Аналитическая химия». Часть 2.
Количественный анализ (оптические, рентгенофазовый и рентгеноструктурный методы. − ФГУП
«Информрегистр», № 0321201048, от 26.04.2012.
Интернет – источники
1. http://window.edu.ru/catalog?p_rubr=2.2.74.7
2. http://www.ximicat.com/index.php?razdel=obs
3. http://rushim.ru/books/books.htm
ФИЗИЧЕСКАЯ ХИМИЯ
(для бакалавров ФН-4)
Дисциплина состоит из 3-х учебных модулей
Модуль 1
Виды аудиторных занятий и Сроки проведения или
самостоятельной работы
выполнения, недели
Лекции
8
Лабораторные работы
8
Домашнее задание текущее
Не предусмотрено
Контроль по модулю 1
8
Трудоемкость, Примечания
часы
18
10
2
Модуль 2
Виды аудиторных занятий и Сроки проведения или
самостоятельной работы
выполнения, недели
Лекции
13
Лабораторные работы
13
Домашнее задание текущее
Не предусмотрено
Контроль по модулю 2
13
Модуль 3
121
Трудоемкость, Примечания
часы
9
4
2
Виды аудиторных занятий и Сроки проведения или
самостоятельной работы
выполнения, недели
Лекции
17
Лабораторные работы
17
Контроль по модулю 2
17
Трудоемкость, Примечания
часы
7
3
2
МОДУЛЬ 1: Физико-химическое состояние вещества
Лекции
Фазовые равновесия в однокомпонентных
гетерогенных
системах.
Температурная
зависимость давления насыщенного пара.
Уравнение
Клапейрона
–
Клаузиуса.
Эмпирическое правило Трутона. Примеры
фазовых диаграмм. Применение правила фаз
Гиббса. Фазовые переходы: первого и
второго
рода,
монотропные
и
энантиотропные.
МОДУЛЬ 1: Физико-химическое состояние
вещества
Лекции
Лекции 1- 4. Химическая термодинамика.
Функции состояния – внутренняя
энергия, энтальпия. Функции процесса –
теплота, работа. Расчет функций состояния в
изопроцессах. Закон Гесса и следствия из
него.
Первый
закон
термодинамики.
Температурная зависимость стандартного
теплового эффекта реакции. Закон Кирхгофа.
Второй и третий законы термодинамики.
Энтропия.
Уравнение
Клаузиуса.
Зависимость энтропии от температуры,
давления и объема. Изменение энтропии в
процессах.
Уравнение
Больцмана.
Температурная зависимость стандартной
энтропии химической реакции. Критерии
направленности процесса. Уравнение Гиббса
– Гельмгольца. Методы расчета стандартной
энергии Гиббса химических реакций.
Системы переменного состава. Химический
потенциал. Условия равновесия.
Двухкомпонентные системы. Метод
физико-химического анализа. Применение
правила фаз Гиббса. Виды равновесий.
Физико-химические
основы
перегонки
растворов. Равновесие «жидкий раствор –
кристалл».
Расчеты
по
диаграммам
состояния.
Трехкомпонентные
системы.
Применение
правила
фаз
Гиббса.
Графическое изображение состава. Типы
диаграмм состояния.
Лекции 7 – 10. Растворы
Классификация
растворов.
Межмолекулярное
и
химическое
взаимодействие. Парциальные молярные
величины. Уравнение Гиббса – Дюгема.
Теплоты
растворения
и
разбавления.
Давление насыщенного пара компонента над
раствором. Законы Рауля и Генри.
Растворимость
газов.
Коллигативные
свойства.
Идеальные,
неидеальные,
предельно
разбавленные
растворы.
Экстракция.
Активность.
Коэффициент
активности. Первое и второе стандартные
состояния. Методы определения активности
и коэффициента активности компонентов
раствора.
Лекции 5 – 6. Фазовые равновесия.
Фаза,
компонент,
число
термодинамических
степеней
свободы.
Правило фаз Гиббса. Однокомпонентные
гомогенные
системы.
Расчет
термодинамических функций идеальных
газов по их спектрам. Определение
параметров молекул по спектральным
данным. Химический потенциал компонента
в идеальных газовых растворах. Реальные
газы. Уравнение состояния с вириальными
коэффициентами. Другие формы уравнения
состояния.
Принцип
соответственных
состояний. Фугитивность и активность.
Химический потенциал реального газа.
Лекции 11 — 13. Химическое равновесие
122
Термодинамическая
теория
химического
сродства.
Химическая
переменная. Закон действующих масс.
Стандартная термодинамическая константа
равновесия
и
способы
ее
расчета.
Статистический метод расчета констант
равновесия
газофазных
реакций.
Эмпирические константы равновесия, их
связь со стандартной термодинамической
константой равновесия. Расчет состава
равновесной смеси. Уравнения изотермы,
изобары и изохоры химической реакции.
Влияние внешних факторов на смещение
химического
равновесия.
Химическое
равновесие в гетерогенных системах.
Лабораторные работы
Занятие 1. Исследование веществ методом электронного парамагнитного резонанса
Занятие 2. Спектрофотометрическое определение концентрации веществ в растворах
Занятие 3. Физико-химическое равновесие в системе фенол – вода.
Контроль выполнения модуля 1. Срок – 8 неделя.
МОДУЛЬ 2: Физико-химическое описание химических процессов
Лекции
Потенциометрия и ее применение.
Типы электрохимических источников тока и
топливных элементов.
МОДУЛЬ 2: Физико-химическое описание
химических процессов
Лекции
Лекции 17 — 19. Химическая кинетика.
Кинетика
гомогенных
реакций.
Кинетические
кривые.
Скорость,
молекулярность, порядок и константа
скорости реакции. Факторы, влияющие на
скорость реакции. Формальная кинетика.
Элементарные
необратимые
реакции
различных
порядков.
Время
полупревращения. Методы определения
частного порядка реакции по компоненту.
Сложные
реакции:
обратимые,
параллельные, последовательные. Метод
лимитирующей стадии. Метод стационарных
концентраций.
Теории
химической
кинетики:
активных
столкновений
и
активированного
комплекса.
Мономолекулярные реакции в газовой
фазе. Схема Линдемана.
Цепные
реакции и их механизм. Неразветвленные и
разветвленные
процессы.
Предельные
явления
в
разветвленных
процессах.
Фотохимические реакции.
Гомогенные
реакции в жидкой фазе. Быстрые и
медленные
реакции.
Уравнение
Лекции 14 — 16. Электрохимия.
Растворы
электролитов.
Электролитическая диссоциация. Средняя
ионная
активность
электролита.
Коэффициент
активности.
Электростатическая
теория
сильных
электролитов
Дебая
–
Хюккеля.
Термодинамические
свойства
ионов.
Движение ионов в электрическом поле.
Электрическая проводимость растворов
электролитов. Электрическая подвижность
ионов.
Числа
переноса.
Уравнение
Кольрауша.
Кондуктометрия
и
ее
применение.
Константа
и
степень
диссоциации слабого электролита. Закон
разведения Оствальда.
Электрохимические
реакции.
Термодинамическая
теория
ЭДС.
Электродные
потенциалы.
Уравнения
Нернста и Петерса. Типы электродов и
электрохимических цепей. Диаграмма Пурбе.
123
Смолуховского.
Бьеррума.
Уравнение
Бренстеда
–
Аврами.
Гетерогенные
процессы
диффузионным лимитированием.
с
Гетерогенные реакции. Кинетика
зародышеобразования
новой
фазы.
Уравнения степенного типа, Ерофеева –
Лабораторные работы
Занятие 4. Экспериментальное определение термодинамических характеристик гальванического
элемента.
Занятие 5. Потенциометрическое титрование
Занятие 6. Кинетика разложения пероксида водорода при гомогенном катализе
Контроль выполнения модуля 2. Срок – 13 неделя.
МОДУЛЬ 3: Управление физико-химическими процессами
Лекции
переходных металлов. Ферментативный
катализ. Уравнение Михаэлиса – Ментен.
МОДУЛЬ 3: Управление физикохимическими процессами
Гетерогенный катализ. Основные
стадии процесса. Роль адсорбции. Закон
действующих
поверхностей.
Изотерма
адсорбции Лэнгмюра. Уравнение Лэнгмюра
– Хиншельвуда. Лимитирующие стадии
гетерогенно-каталитической
реакции.
Механизм Ридиэла – Или.
Лекции 20 — 25. Катализ
Активность
и
селективность
катализатора. Механизмы каталитического
действия.
Автокатализ,
ингибирование.
Гомогенный катализ. Кинетическое
описание
кислотно-основного
катализа.
Уравнение Бренстеда. Катализ комплексами
Лабораторные работы
Занятие 7. Изучение адсорбции уксусной кислоты на активированном угле.
Контроль выполнения модуля 3. Срок – 17 неделя.
124
Домашние задания
не предусмотрено
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций; подготовке к выполнению и
защите лабораторных работ; выполнении индивидуального домашнего задания. Каждое домашнее
задание включает в себя 5 практических и расчетных задач. Самостоятельная работа является как
домашней, так и аудиторной (в том числе под контролем преподавателя на консультациях, где разбираются
трудные вопросы из материала лекций, типовые варианты домашних и контрольных заданий, а также
демонстрируются возможности использования математических программ при обработке результатов
лабораторных работ).
Самостоятельная работа является как домашней, так и аудиторной под контролем преподавателя (КСР)
Зачетная работа
Итоговый контроль по дисциплине проводится на 17 неделе для студентов, которые неудовлетворительно
освоили содержание модулей (т.е. для студентов, набравших менее 60 баллов).
ЛИТЕРАТУРА
Основная литература (ОЛ)
1.
Стромберг А.Г., Семченко Д.П. Физическая химия. М.: Высшая школа.1999. 528 с.
2.
Физическая химия. Под ред. К.С.Краснова. М.: Высшая школа. 1995. Т. 1. 512 с. Т. 2. 320 с.
Дополнительная литература (ДЛ)
1.
Краткий
справочник
физико-химических
А.М.Пономаревой. Л.: Химия. 1983.
величин.
Под
ред.
А.А.Равделя,
2.
Задачи по физической химии / В. В. Еремин, С. И. Каргов, И. А. Успенская и др. – М.: Изд-во
“Экзамен”, 2003. – 320 с.
3.
Методические разработки кафедры к лабораторным работам
Методические пособия, изданные в МГТУ (МП)
1.
Химическая термодинамика. Методические указания. / Е. Е. Гончаренко, В. А. Батюк, Н. М.
Елисеева и др. М.: Изд-во МГТУ, 1994.
2.
Сборник контрольных вопросов и задач для защиты лабораторных работ по курсу химии:
Метод. указания /С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др.; Под ред. А.М. Голубева М.: Изд-во МГТУ им.Н.Э. Баумана, 2009. – 84 с.
Электронные учебные пособия (ЭП)
125
1.
Современная химия в техническом университете. Химия элементов и их соединений:
электронное учебное пособие / Ермолаева В.И., Волков А.А., Горшкова В.М., Слынько Л.Е.ФГУП НТЦ «Информрегистр», № 0320801585, от 4.08.08
Интернет – источники
1.
2.
3.
http://window.edu.ru/catalog?p_rubr=2.2.74.7
http://www.ximicat.com/index.php?razdel=obs
http://rushim.ru/books/books.htm
ОРГАНИЧЕСКАЯ ХИМИЯ
(для бакалавров Э-9)
Дисциплина состоит из 3-х учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоемкость,
часы
Лекции
1-6
12
Лабораторные работы
1-6
6
Домашнее задание текущее
1-6
14
Контроль по модулю 1
6
2
Примечания
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоемкость,
часы
Лекции
7 - 12
12
Лабораторные работы
7 - 12
6
Домашнее задание текущее
8 - 12
14
Контроль по модулю 2
12
2
126
Примечания
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоемкость,
часы
Лекции
13 - 17
10
Лабораторные работы
13 - 17
5
Контроль по модулю 3
17
2
Примечания
МОДУЛЬ1: Строение и классификация органических соединений. Механизмы органических
реакций. Предельные, непредельные углеводороды.
Лекции
Лекция 1. Предмет органической химии. Содержание курса. Пути формирования органической химии как
науки, ее место среди естественных наук. Основные природные источники органических соединений нефть, природный газ, угли, торф, сланцы и методы их переработки Общие понятия об органических
загрязняющих веществах. Особенности строения атома углерода.
Основные положения теории
химического строения органических веществ А. М. Бутлерова.
ОЛ - 1, Гл. 1; ОЛ -1, Гл. 1, ОЛ-3, Гл. 1, 2.
Лекция 2. Классификация органических соединений. Ациклические и циклические органические
соединения. Гомологические ряды. Функциональные группы. Общие понятия о химической номенклатуре.
Понятие о пространственном строении органических молекул. Изомерия. Общие сведения о механизмах
органических реакций. Основы качественного и количественного анализа органических соединений.
Лекция 3. Предельные углеводороды - алканы. Особенности строения, номенклатура, изомерия.
Физические и химические свойства алканов гомологического ряда метана. Метан, пропан, бутан - газы
бытового назначения. Высшие алканы как составные части бензина, моторных топлив, смазочных масел. Их
свойства, применение, влияние на окружающую среду.
ОЛ - 1, Гл. 1; ОЛ - 2, Гл.1; ОЛ - 3, Гл. 4
Лекция 4. Непредельные углеводороды – алкены и алкадиены. Особенности строения, получение,
номенклатура, изомерия. Физические и химические свойства. Отдельные представители, их свойства.
Использование этилена и пропилена в качестве сырья для получения органических соединений,
пластических масс и композиционных материалов. Характеристики важнейших типов синтетических
каучуков.
Меры безопасности при работе с непредельными углеводородами.
ОЛ - 1, Гл. 2, 3; ОЛ - 2, Гл. 1;ОЛ - 3, Гл. 5, 7.
Лекция 5. Непредельные углеводороды – алкины. Особенности строения, получение, номенклатура,
изомерия. Физические и химические свойства алкинов. Ацетилен, его свойства и применение в
127
химической промышленности. Отдельные представители, их свойства и применение в
промышленности.
химической
ОЛ - 1, Гл. 4; ОЛ - 2, Гл. 1; ОЛ - 3, Гл. 6.
Лекция 6. Ароматические углеводороды (арены). Особенности строения бензольного кольца. Теоретические
представления о гибридизации атома углерода в бензольном кольце. Изомерия и номенклатура аренов.
Физические и химические свойства бензола и его производных. Особенности химических реакций.
Ориентирующее влияние заместителей в бензольном кольце. Применение бензола и его производных.
Загрязняющее действие на окружающую среду.
ОЛ - 1, Гл. 8; ОЛ - 3, Гл. 9.
Лабораторные работы
Занятие 1. Синтез сложного эфира.
Занятие 2. Очистка продукта реакции этерификации методом перегонки.
Занятие 3. Контроль модуля 1.
МОДУЛЬ 2: Ароматические углеводороды. Производные углеводородов.
Кислородсодержащие углеводороды. Циклические углеводороды.
Лекции
Лекция 7. Производные углеводородов. Моно - и полигалогенпроизводные предельных углеводородов.
Строение, номенклатура и изомерия. Физические и химические свойства.
Галогенпроизводные
непредельных углеводородов. Строение, номенклатура, изомерия, Физические и химические свойства.
Отдельные представители, их свойства и применение. Загрязняющее действие на окружающую среду.
Ароматические галагенпроизводные. Строение, номенклатура, физические и химические свойства.
Применение и получение.
ОЛ - 1, Гл. 2; ОЛ - 2, Гл. 2; ОЛ - 3, Гл. 12, 19.
Лекция 8. Кислородсодержащие углеводороды. Одноатомные и высшие спирты. Строение, номенклатура,
изомерия. Физические и химические свойства. Отдельные представители одноатомных и многоатомных
спиртов (метиловый и этиловый спирты, виниловый спирт, этиленгликоль, глицерин и др.). Получение и
применение. Загрязняющее действие на окружающую среду.
ОЛ - 1, Гл. 3; ОЛ - 2, Гл. 3; ОЛ - 3, Гл. 13.
Лекция 9. Альдегиды и кетоны алифатических соединений. Строение, номенклатура, изомерия. Физические
и химические свойства. Отдельные представители альдегидов и кетонов (формальдегид, этаналь, пропанон
и др.). Получение и применение. Загрязняющее действие на окружающую среду.
ОЛ - 1, Гл. 3; ОЛ - 2, Гл. 4; ОЛ - 3, Гл. 13.
Лекция 10. Фенолы и ароматические спирты, ароматические альдегиды, кетоны и карбоновые кислоты.
Строение, номенклатура, изомерия. Физические и химические свойства. Отдельные представители
ароматических кислородсодержащих угдеводородов (бензиловый спирт, бензойная кислота и др.). Высшие
жирные кислоты, мыла. Получение и применение. Загрязняющее действие на окружающую среду.
128
ОЛ - 1, Гл. 8; ОЛ - 3, Гл. 13.
Лекция 11. Циклические углеводороды. Карбоциклические углеводороды (алициклические и
ароматические). Особенности строения. Номенклатура, изомерия, способы получения, физические и
химические свойства, применение. Терпены - особая группа природных алициклических соединений
(лимонел, камфора, скипидар и др.) Их свойства и применение.
ОЛ - 1, Гл. 7; ОЛ - 2, т. 2; ОЛ - 3, Гл. 10, 11.
Лекция 12. Гетероциклические соединения. Общая характеристика. Влияние природы гетероатома на
свойства гетероциклических соединений. Номенклатура. Свойства пяти - и шестичленных гетероциклов.
Отдельные представители (фуран, тиофен, пиррол, пиридин и др.), их свойства и применение. Понятие об
алкалоидах (никотин, хинин, папаверин и др.).
ОЛ - 1, Гл. 9; ОЛ - 2, т. 2; ОЛ - 3, Гл. 23.
Лабораторные работы
Занятие 4. Идентификация продукта реакции этерификации и определение его строения.
Занятие 5. Качественные реакции в органической химии.
Занятие 6. Контроль модуля 2.
МОДУЛЬ 3: Азот- и серосодержащие углеводороды. Биологически активные
органические соединения. Полимеры.
Лекции
Лекция 13. Азот- и серосодержащие углеводороды. Органические соединения азота: нитросоединения,
амины, аминоспирты, амиды кислот, ароматические амины, ароматические азосоединения (азокрасители)
и др. Строение, номенклатура, физические и химические свойства. Отдельные представители, их получение
и применение.
ОЛ - 1, Гл. 8, 9; ОЛ - 2, Т. 2; ОЛ - 3, Гл. 23.
Лекция 14. Органические соединения серы: тиоспирты, тиоэфиры, сульфокислоты, сульфосоединения
ароматического ряда. Строение, номенклатура, физические и химические свойства. Отдельные
представители, их получение и применение.
ОЛ - 1, Гл. 9; ОЛ - 2, Т. 2; ОЛ - 3, Гл. 23.
Лекции 15. Биологически активные органические соединения. Пестициды и гербициды. Строение, свойства
и свойства. Социальные и экономические аспекты применения пестицидов и гербицидов. Липиды: жиры,
масла и воски. Строение, свойства и применение. Стероиды, гормоны и витамины. Строение, способы
применения, биологическая активность.
ОЛ - 1, Гл. 9; ОЛ - 2, т. 2; ОЛ - 3, Гл. 26.
129
Лекция 16. Аминокислоты, пептиды и белки. Структура, физические и химические свойства. Биосинтез
белка. Углеводы и нуклеиновые кислоты. Структура. Реакции углеводов.
ОЛ - 1, Гл. 6; ОЛ - 2, Гл. 8; ОЛ - 3, Гл. 22.
Лекция 17. Полимерные материалы. Классификация, способы получения синтетических полимеров:
реакции полимеризации и поликонденсации. Релаксационные явления в полимерах. Деструкция в
полимерах. Отдельные представители, их применение. Пластмассы. Загрязняющее действие на
окружающую среду.
ОЛ - 1, Гл. 11, 12; ОЛ - 2, т. 2.
Лабораторные работы
Занятие 7. Разделение жидких смесей органических веществ методом перегонки. Обработка результатов
эксперимента с помощью компьютерной программы «L-микро».
Занятие 8. Контроль модуля 3.
Домашние задания
ДЗ 1. Строение и классификация органических соединений. Механизмы органических реакций.
Предельные, непредельные углеводороды. Выдача - 1 неделя, сдача - 7 неделя.
ДЗ 2. Ароматические углеводороды. Производные углеводородов. Кислородсодержащие углеводороды.
Циклические углеводороды. Выдача - 8 неделя, сдача – 12 неделя.
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к
выполнению лабораторных работ, входному контролю готовности к выполнению лабораторной работы,
выполнении индивидуального задания по тематике лабораторной работы, которое расценивается как
защита лабораторной работы. Индивидуальное задание включает в себя 3-5 практических и расчетных
задач. Самостоятельная работа является как домашней, так и аудиторной под контролем преподавателя
(КСР)
ЛИТЕРАТУРА
Основнаялитература (ОЛ)
1.
2.
3.
4.
5.
6.
7.
Артеменко А.И. Органическая химия: Учебник для вузов. -4-е изд., перераб. и доп. – М.: Высш.шк., 2000.
– 558 с.
Шабаров Ю.С. Органическая химия: Учебник для вузов в 2-х томах, - 3-е изд., стер. – М.: Химия, 2000. –
846 с.
Грандберг И.И. Органическая химия: Учебник для вузов.-5-е изд., стер.- М: Дрофа, 2002.- 671 с.
Березин Б.Д., Березин Д.Б. Курс современной органической химии: Учеб. пособие для вузов. – М:
Высш.шк.,1999.-767 с.
Нейланд О.Я. Органическая химия: Учебник для вузов. – М.:Высш.шк., 1990. – 750с.
Швехгеймер М.-Г.А., Кобранов К.И. Органическая химия: Учебник для вузов. –М.: Высш.шк.,1994.-542 с.
Органическая химия: Методические указания по выполнению домашнего задания. Составители:
130
8.
Хмарцева Л.А., Кадушечкина Р.С., Степанов М.Б. и др., - Муром: Изд. – полиграфический центр МИ
ВлГУ, 2007. – 28 с.
Методические указания к лаб. раб. «Синтез и физико-химическое исследование продуктов реакции
этерификации» / Сост.: Хмарцева Л.А., Степанов М.Б., Голубев А.М. и др. – Муром. ИПЦ МИ ВлГУ, 2000. 14 с.
Методические пособия, изданные в МГТУ (МП)
Решение типовых задач по органической химии для различных классов соединений/Л.А. Хмарцева, М.Б.
Степанов, Якушева Е.А., А.М. Голубев,– М.: Изд-во МГТУ им. Н.Э. Баумана, 2012. – 60 с.
Изучение кинетики полимеризации метилметакрилата/ Л.А. Хмарцева, М.Б. Степанов, А.М. Голубев,–
М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. – 11 с.
Методические указания к лабораторной работе по курсу органической химии. Разделение жидких
органических веществ методом перегонки. Обработка результатов эксперимента с помощью
компьютерной программы «L-микро» /Л.А. Хмарцева, М.Б. Степанов, Якушева Е.А., А.М. Голубев,–
М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. – 10 с.
Методические указания к лабораторной работе «Синтез и физико-химическое исследование продуктов
реакции этерификации»/Л.А.Хмарцева, М.Б.Степанов, Р.С.Кадушечкина, Н.М.Елисеева, Е.А. Якушева,–
М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. – 14 с.
Интернет – источники
http://window.edu.ru/catalog?prubr=2.2.74.7.4
http://www.ximicat.com/index.php?razdel=neo
3.
http://rushim.ru/books/books.htm
НЕОРГАНИЧЕСКАЯ ХИМИЯ
(для бакалавровЭ-9)
Дисциплина состоит из 2-х учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 1
Сроки проведения или
выполнения, недели
1-6
1-6
1-6
6
Трудоемкость, Примечания
часы
6
6
11
2
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 2
Сроки проведения или
выполнения, недели
7 - 17
7 - 17
8 - 15
16
131
Трудоемкость, Примечания
часы
6
6
12
2
МОДУЛЬ1: Закономерности протекания реакций в растворах
Лекции
Лекция1. Растворы. Классификация растворов.
Способы выражения состава раствора.
Растворимость.
Энергетика
образования
растворов.
Коллигативные
свойства
разбавленных растворов Закон Раулядляне
электролитов. Понятие об осмосе. Осмотическое
давление. Уравнение Вант-Гоффа .Изотонические
растворы. Отклонение свойств растворов кислот,
оснований и солей от закона Рауля и уравнения
Вант-Гоффа.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.11-12; ОЛ-3, Гл.6
Лекция2. Растворы электролитов. Электрическая
проводимость
электролитов.
Слабые
электролиты.
Теория
электролитической
диссоциации Аррениуса. Степень и коэффициент
диссоциации. Закон Рауля для электролитов.
Уравнение Вант-Гоффа для электролитов.
Равновесие
диссоциации
в
растворах
электролитов. Константа диссоциации. Закон
разбавления
Оствальда.
Электролитическая
диссоциация воды. Ионное произведение воды.
Водородный игидроксидный показатели-pH, pOH.
Буферные растворы.
Лекция3. Понятие о сильных электролитах.
Активность и коэффициент активности. Ионное
равновесие в системе раствор – осадок.
Произведение растворимости. Реакции обмена в
электролитах. Гидролиз солей.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.13-14; ОЛ-3, Гл.7
Лабораторные работы
Занятие1. Определение концентрации раствора методом кислотно-основного титрования.
Занятие2. Растворы электролитов.
Занятие3. Закономерности протекания реакций в растворах неэлектролитов и электролитов.
Занятие4. Контроль модуля 1.
МОДУЛЬ2: Электрохимические процессы в электролитах
Лекции
Лекция4.
Окислительно-восстановительные
реакции в электролитах.
Окислители и
восстановители.
Возникновение
скачка
потенциала на границе металл — электролит.
Электродные процессы.
Электрохимические
цепи
обратимые
и
необратимые
Понятие
об
электроде
и
электродном потенциале. Уравнение Нернста для
электродного потенциала и электродвижущей
силы (ЭДС) электрохимической цепи. Типы
электродов. Стандартный водородный электрод.
Ряд стандартных электродных потенциалов.
Определение
направления
окислительновосстановительных реакций.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.16-17; ОЛ-3, Гл.16, 17
Лекция5.
Гальванический
элемент.
Классификация
гальванических
элементов.
Химические и концентрационные гальванические
элементы. Элемент Даниэля – Якоби. Расчет
электродного потенциала и электродвижущей
силы гальванического элемента. Химические
источники тока (ХИТ). Первичные и вторичные
ХИТ. Аккумуляторы.
Лекция6. Электролиз. Потенциал разложения
электролита. Последовательность разряда ионов
на электродах. Законы Фарадея. Применение
электрохимических процессов в технике.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.16-17; ОЛ-3, Гл 16, 17
Лекция7. Коррозия и защита металлов.
Классификация коррозионных процессов по виду
разрушений и активности коррозионных сред.
Типы коррозионных процессов. Показатели
коррозии: глубинный, массовый, объемный,
токовый. Химическая коррозия. Кинетика
окисления металлов. Защитные свойства пленок.
Лекция8.
Электрохимическая
коррозия.
Механизм
электрохимической
коррозии.
Водородная и кислородная деполяризация.
Влияние различных факторов на скорость
коррозии. Примеры коррозионных процессов.
Методы защиты металлов от коррозии.
ОЛ —1, Гл.6; ОЛ — 2, Гл.18; ОЛ-3, Гл.18, 19
Лабораторные работы
132
Занятие5. Окислительно-восстановительные реакции.
Занятие6. Коррозия и защита металлов.
Занятие7. Электрохимические процессы.
Занятие8. Контроль модуля 2.
Домашние задания
ДЗ 1. Закономерности протекания реакций в растворах. Выдача - 1 неделя, сдача-7неделя.
ДЗ 2. Электрохимические процессы вэлектролитах. Выдача - 8 неделя, сдача - 15неделя.
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
лабораторных работ, входному контролю готовности к выполнению лабораторной работы, выполнении
индивидуального задания по тематике лабораторной работы, которое расценивается как защита
лабораторной работы. Индивидуальное задание включает в себя 3-5 практических и расчетных задач.
Самостоятельная работа является как домашней, так и аудиторной под контролем преподавателя (КСР).
ЛИТЕРАТУРА
Основнаялитература(ОЛ)
1. Карапетьянц М.Х., Дракин С.И. Общая и неорганическаяхимия. М.:Химия,2000 –593с.
2. Горбунов А.И., Филиппов Г.Г.,Федин В.И. Химия. М.:Изд-воМГТУим.Н.Э.Баумана,2007.– 586 с.
3. Гуров А.А. ,Бадаев Ф.З., Овчаренко Л.П., Шаповал В.Н.Химия. М.: Изд-во МГТУ им. Н.Э. Баумана,
2004 .- 748с.
Методические пособия, изданные в МГТУ(МП)
4. Методические указания к выполнению лабораторных работ по неорганической химии/
В.И.Ермолаева, Н.Н.Двуличаская, В.М.Горшкова, Л.Е.Слынько. – М.: Изд-во МГТУ им. Н.Э.Баумана,
2009. –103с.
5. Теоретические основы неорганической химии: метод. указания/ В.И.Ермолаева, Н.Н.Двуличанская.М.: Изд-во МГТУ им. Н.Э.Баумана, 2011.-61с.
6. Методические указания к выполнению домашнего задания по курсу неорганической химии/
ЕрмолаеваВ.И., ДвуличанскаяН.Н., ХмарцеваЛ.А. и др.-М.:Изд-во МГТУ им. Н.Э. Баумана, 2003. –
48с.
7. Сборник контрольных вопросов и задач для защиты лабораторных работ по курсу химии: Метод.
указания/ С.Л.Березина, А.М.Голубев, Е.Е.Гончаренко и др.; Под ред. А.М.Голубева- М.:Изд-во МГТУ
им. Н.Э. Баумана, 2009. – 84с.
Электронные учебные пособия (ЭП)
8. Методические указания к выполнению домашнего задания по курсу неорганической химии:
электронное
учебное
пособие/
ЕрмолаеваВ.И.,
ДвуличанскаяН.Н.,
ХмарцеваЛ.А.ФГУПНТЦ«Информрегистр», № 0321000438,от14.12.2010.
9. Теоретические основы химии: электронное учебное издание: Методические указания к решению
задач
по
курсу
«Неорганическаяхимия»/
ЕрмолаеваВ.И.,
ДвуличанскаяН.Н.ФГУПНТЦ«Информрегистр», № 0321002540,от14.12.2010.
Интернет – источники
1. http://window.edu.ru/catalog?prubr=2.2.74.7.4
2. http://www.ximicat.com/index.php?razdel=neo
3. http://rushim.ru/books/books.htm
133
Химия
(для специальности судебная компьютерно-техническая экспертиза)
Дисциплина состоит из 3-х учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоемкость,
часы
Лекции
1 –7
8
Лабораторные работы
1 –7
14
Домашнее задание текущее
2–7
12
Контроль по модулю 1
7
4
Примечания
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоемкость,
часы
Лекции
8– 12
10
Лабораторные работы
8– 12
10
Домашнее задание текущее
8 – 12
12
Контроль по модулю 2
12
4
Примечания
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
134
Трудоемкость,
часы
Примечания
Лекции
13 – 17
16
Лабораторные работы
13 – 17
10
Домашнее задание текущее
13 – 16
12
Контроль по модулю 1
17
4#
МОДУЛЬ1:Строение вещества. Основные законы химии
Лекции
Лекция1.Химия как раздел естествознания, значение химии для науки и технологии. Вещество и его
строение. Понятие о квантово-механической модели атома водорода. Вероятностный характер процессов в
микромире: принцип неопределенности Гейзенберга, волна де-Бройля, волновое уравнение Шредингера.
Квантовые числа. Атомная орбиталь. Формы орбиталей.
ОЛ – 1, Гл.3; ОЛ – 2, Гл. 1; ОЛ − 3, Р-л I: Гл. 2; ОЛ – 4, Гл. 1; ДЛ − 6, 10.
Лекция2.Строение многоэлектронных атомов. Принцип Паули. Правила Хунда и Клечковского. Принцип
минимальной энергии. Электронные конфигурации атомов. Энергетические характеристики атомов:
энергия ионизации, сродство к электрону, электроотрицательность. Периодические свойства элементов.
Периодический закон Д.И. Менделеева.
ОЛ – 1, Гл.3; ОЛ – 2, Гл. 1; ОЛ − 3, Р-л I: Гл. 2; ОЛ – 4, Гл. 2.
Лекция3.Химическая связь. Характеристики связи: энергия, длина, валентный угол, полярность. Типы связи.
Понятие о методе валентных связей. Гибридизация атомныхорбиталей. σ - и π - связи. Геометрическая
конфигурация молекул. Электрический момент диполя молекулы. Метод Гиллеспи.
ОЛ – 1, Гл. 4; ОЛ – 3, Р-л II: Гл. 3, Р-л II: Гл. 1, 3; ОЛ - 4, Гл. 2.
Лекция 4. Ионная связь и ее особенности. Межмолекулярные взаимодействия. Водородная связь.
Металлическая связь и особенности строения металлов. Основные физические и химические свойства
металлов.
ОЛ – 1, Гл. 4; ОЛ – 3, Р-л II: Гл. 4, Р-л II: Гл. 4, 5; ОЛ - 4, Р-л IV: Гл. 11; ДЛ − 5, 10.
Лабораторныеработы
Занятие1.Основные понятия и законы химии
Занятие2.Основные классы неорганических соединений
Занятие3.Определение концентрации раствора методом титрования
Занятие4. Жесткость воды
Занятие 5. Строение атомов и химическая связь
135
Занятие 6. Химические свойства металлов и их соединений
Занятие 7.Контроль модуля1
МОДУЛЬ2:Основные закономерности протекания химических процессов
(термодинамика, кинетика)
Лекции
Лекция5.Элементы химической термодинамики. Первый закон термодинамики. Термодинамические
функции: энтальпия и внутренняя энергия. Тепловой эффект реакции. Закон Гесса. Термохимические
расчеты.
ОЛ – 1, Гл. 5; ОЛ – 2, Гл. 6; ОЛ – 3, Р-л V: Гл. 1; ОЛ – 4, Гл. 5; ДЛ − 6, 8.
Лекция 6. Второй закон термодинамики. Понятие об энтропии. Изменение энтропии в процессах. Третий
закон термодинамики. Расчет абсолютных значений стандартных энтропий веществ. Объединенное
уравнение первого и второго законов. Термодинамические критерии направленности химических процессов.
Энергия Гиббса.
ОЛ – 1, Гл. 6; ОЛ – 2, Гл. 7; ОЛ – 3, Р-л V: Гл. 2; ОЛ – 4, Гл. 5; ДЛ − 6, 8.
Лекция 7.Химическое равновесие в гомогенной системе. Константа равновесия. Уравнения изотермы,
изобары, изохоры химической реакции. Особенности равновесия в гетерогенных системах.
ОЛ – 1, Гл. 10 − 12; ОЛ – 2, Гл. 10 − 12; ОЛ – 3, Р-л V: Гл. 3; ОЛ – 4, Гл. 6; ДЛ − 6, 8.
Лекция 8. Элементы химической кинетики. Понятие о скорости реакции. Зависимость скорости реакции от
концентрации (закон действующих масс). Кинетические уравнения реакций нулевого, 1-го и 2-го порядков.
Лекция 9. Зависимость скорости реакции от температуры. Правило Вант-Гоффа. Уравнение Аррениуса.
Понятие об энергии активации. Энергетическая диаграмма реакции. Особенности кинетики гетерогенных
процессов. Гомогенный и гетерогенный катализ.
ОЛ – 1, Гл. 7 – 9; ОЛ – 2, Гл. 10; ОЛ – 3, Р-л V: Гл. 4; ОЛ – 4, Гл. 7; ДЛ − 6, 10.
Лабораторныеработы
Занятие8.Химическая термодинамика
Занятие9.Химическое равновесие в гомогенных системах
Занятие10.Закономерности протекания химических процессов
Занятие 11. Химическая кинетика
Занятие12.Контрольмодуля2
МОДУЛЬ3:Основыэлектрохимических процессов
Лекции
136
Лекции 10. Растворы. Классификация растворов. Энергетика образования растворов. Понятие о
термодинамике идеальных растворах. Закон Рауля и следствия из него. Осмос. Растворы электролитов.
ОЛ – 1, Гл. 13; ОЛ – 2, Гл. 11; ОЛ – 3, Р-л III: Гл. 2; ОЛ – 4, Гл. 8; ДЛ − 8.
Лекция 11. Теория электролитической диссоциации Аррениуса. Сильные и слабые электролиты. Степень
диссоциации. Константа диссоциации. Закон разбавления Оствальда. Электролитическая диссоциация
воды. Ионное произведение воды. Водородный (рН) и гидроксидный (рОН) показатели. Активность и
коэффициент активности.
ОЛ – 1, Гл. 14; ОЛ – 2, Гл.12, 13; ОЛ – 3, Р-л III: Гл. 2; ОЛ – 4, Гл. 8; ДЛ − 6, 10.
Лекция 12. Ионное равновесие в системе раствор – осадок. Произведение растворимости. Диссоциация
комплексных ионов. Константа нестойкости. Реакции обмена в электролитах. Гидролиз солей.
ОЛ – 1, Гл. 14; ОЛ – 2, Гл. 13; ОЛ – 3, Р-л III: Гл. 2; ОЛ – 4, Гл. 8; ДЛ − 6.
Лекция 13. Возникновение двойного электрического слоя на границе металл - электролит. Электродный
потенциал. Уравнение Нернста для электродного потенциала и электродвижущей силы (ЭДС)
электрохимической цепи. Стандартный водородный электрод. Ряд стандартных электродных потенциалов.
Гальванический элемент Даниэля-Якоби.
ОЛ – 1, Гл. 16 – 17; ОЛ – 2, Гл. 17 – 18; ОЛ – 4, Гл. 9; ДЛ − 5, 10.
Лекция 14. Электролиз. Ряды разряжаемости ионов. Законы Фарадея. Химические источники тока,
первичные элементы и аккумуляторы. Коррозия металлов. Классификация коррозионных процессов по
виду разрушений и активности коррозионных сред.
ОЛ – 1, Гл. 17; ОЛ – 2, Гл. 13; ОЛ – 4, Гл. 9; ДЛ − 6, 8.
Лекция 15-16. Электрохимическая коррозия. Механизм электрохимической коррозии. Водородная и
кислородная деполяризация. Контактная коррозия и коррозия сплавов. Влияние различных факторов на
скорость коррозии. Примеры коррозионных процессов. Защита металлов и сплавов от коррозии.
Механические и электрохимические методы защиты.
ОЛ – 1, Гл. 18 – 19; ОЛ – 2, Гл. 22 – 23; ОЛ – 4, Гл. 9; ДЛ − 6, 8.
Лекция 17. Обзорная лекция. Практическое применение химических процессов. Химия и экология.
Безотходные химические производства.
ОЛ – 4; ДЛ – 9
Лабораторныеработы
Занятие13.Окислительно-восстановительные реакции
Занятие14. Растворы электролитов
Занятие15.Закономерности протекания электрохимических процессов
Занятие 16. Коррозия металлов и защита металлов от коррозии
Занятие17.Контрольмодуля3
137
Домашние задания
ДЗ 1.Строение атомов и химическая связь. Химические свойства металлов. Выдача -2неделя, сдача-7неделя.
ДЗ 2.Закономерности протекания химических процессов (термодинамика, равновесие, кинетика). Выдача 8 неделя, сдача - 12неделя.
ДЗ 3. Электрохимические явления и процессы (электролиты, гальванические элементы, электролиз,
коррозия металлов). Выдача − 13 неделя, сдача – 16 неделя.
Самостоятельнаяработа
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к
выполнению лабораторных работ, входному контролю готовности к выполнению лабораторной работы,
выполнении индивидуального задания по тематике лабораторной работы, которое расценивается как
защита лабораторной работы. Индивидуальное задание включает в себя 2−4 практических и расчетных
задач. Самостоятельная работа является как домашней, так и аудиторной под контролем преподавателя
(КСР).
Литература
Основная литература (ОЛ)
Гуров А.А., Бадаев Ф.З., Овчаренко Л.П., Шаповал В.Н. Химия. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. −
748 с.
Горбунов А.И., Гуров А.А.. Филиппов Г.Г., Шаповал В.Н. Теоретические основы общей химии. – М.:
МГТУ, 2001. − 719 с.
Ахметов Н.С. Общая и неорганическая химия. М.: Высшая школа, 1998. – 743 с.
Коровин Н.В. Общая химия. М.: Высшая школа, 1998. – 557 с.
Дополнительная литература (ДЛ)
Лидин Р.А., Молочко В.А., Андреева Л.Л. Химические свойства неорганических соединений. – М.: Химия,
1996.
Лидин Р.А., Молочко В.А., Андреева Л.Л. Задачи по общей и неорганической химии. – М.: Гуманитар. Изд.
Центр ВЛАДОС, 2004.
Фримантл М. Химия в действии. М.: Мир. – 1998. Т.1 – 528 с., Т.2. – 620 с.
Задачи по общей и неорганической химии: учеб.пособие для студентов высш. учеб. заведений / Р.А. Лидин,
В.А. Молочко, Л.Л. Андреева; под ред. Р.А. Лидина. – М.: Гуманитар. изд. центр Владос, 2004. – 383 с.
Сборник задач и упражнений по общей и неорганической химии: учеб. Пособие для студентов высш.
учеб.заведений / под ред. Павлова Н.Н. – М.: Дрофа, 2005. – 240 с.
Пузаков С.А., Попков В.А., Филиппова А.А. Сборник задач и упражнений по общей химии: учеб.пособие
для студентов высш. учеб. Заведений. − М.: Высшая школа, 2004. – 254 с.
Методические пособия, изданные в МГТУ (МП)
138
Березина С.Л., Голубев A.M., Горшкова В.М. и др. Лабораторный практикум по курсу химии для
технических университетов, ч. 1, ч. 2: Методические указания. /Под ред. Фадеева Г.Н. – М.: МГТУ, 2005,
2009.
Сборник контрольных вопросов и задач для защиты лабораторных работ по курсу химии: Метод.указания
/С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др.; Под ред. А.М. Голубева - М.: Изд-во МГТУ им.Н.Э.
Баумана, 2009. – 84 с.
Методические указания к выполнению домашнего задания по курсу общей химии: Методические указания /
Бадаев Ф.З., Голубев А.М., Горшкова В.М. и др.; под ред. Ермолаевой В.И. − М.: МГТУ, 2003. − 48 с.
Методические разработки кафедры к лабораторным работам.
Интернет – источники
http://window.edu.ru/catalog?prubr=2.2.74.7.4
http://www.ximicat.com/index.php?razdel=neo
http://rushim.ru/books/books.htm
Теоретическая механика
2 курс 4 семестр 2012/2013 уч.г. для студентов ф-та ИУ (гр. ИУ1-41,42)
Дисциплина состоит из 3-х учебных модулей и экзамена
Модуль 1
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
1-2
4
Упражнения и КСР
1-2
4
Домашние задания текущие
1-3
3
5
2
Контроль по модулю № 1
139
Модуль 2
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
3-9
14
Упражнения и КСР
3-9
14
Домашние задания текущие
4-10
7
10
2
Контроль по модулю № 2
Модуль 3
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
10-17
18
Упражнения и КСР
10-17
18
Домашние задания текущие
11-17
7
17
4
Контроль по модулю № 3
Модуль 4.
Экзамен
МОДУЛЬ 1: ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Лекции
Лекция
1,2.
Предмет
динамики.
Основные понятия и определения.
Постоянные и переменные силы:
зависимость
силы
от
времени,
положения точки и ее скорости. Аксиомы
динамики
Ньютона.
Инерциальная
система отсчета.
Дифференциальные
уравнения
движения
материальной
точки в векторной форме и в проекциях
на декартовы и естественные оси
координат. Две основные задачи
динамики для материальной точки.
Интегрирование
дифференциальных
уравнений движения материальной
точки. Интегралы уравнений движения.
Постоянные
интегрирования,
их
определение по начальным условиям.
Случай несвободного движения точки,
понятие о динамических реакциях.
Неинерциальная
система
отсчета.
Дифференциальное уравнение движения
точки относительно неинерциальной
системы
отсчета.
Переносная
и
кориолисова силы инерции. Частные
случаи.
Принцип
относительности
классической
механики.
Случай
относительного покоя. Примеры.
ОЛ-1, ГЛ. 13, § 13.1-13.5.
140
Практические занятия (семинары и КСР)
Занятие 1. Динамика материальной
точки в инерциальной системе отсчета.
ОЛ4-27.7, 27.22, 27.65, ОЛ3-8.11(8.10)
(ауд.); ОЛ3-8.1, 8.9, МП-2 (дома).
Занятие 2. Динамика материальной
точки в неинерциальной системе отсчета
ОЛ4-27.53, 33.9, ОЛ3-8.39(8.38) (ауд.);
ОЛ3-8.40(8.39), 8.44(8.43), МП 1,2,3, ДЗ 1
(дома).
МОДУЛЬ 2: ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
Лекции
Лекции 3. Механическая система. Центр
масс системы и его координаты.
Классификация сил, действующих на
механическую систему: силы внешние и
внутренние. Свойства внутренних сил
системы.
Лекции 4. Геометрия масс. Моменты
инерции системы и твердого тела
относительно точки и оси. Радиус
инерции.
Центробежные
моменты
инерции. Вычисления момента инерции
тела относительно оси, проходящей
через данную точку в заданном
направлении.
Эллипсоид
инерции.
Главные оси инерции. Свойства главных
и главных центральных осей инерции.
Тензор инерции.
Дифференциальные уравнения движения
механической системы. Теорема о
движении центра масс системы. Закон
сохранения движения центра масс.
Количество движения материальной
точки
и
механической
системы.
Элементарный импульс силы и импульс
силы за конечный промежуток времени,
его проекции на координатные оси.
Теорема об изменении количества
движения
материальной
точки
в
дифференциальной
и
интегральной
формах. Законы сохранения количества
движения системы. Дифференциальные
уравнения поступательного движения
твердого тела. Примеры.
ОЛ-1, ГЛ. 14, § 14.2,14.6-14.8
Студенты
прорабатывают
самостоятельно тему:
Теорема
Штейнера.
Вычисление
моментов инерции тел простейшей
формы.
ОЛ-1,ГЛ.14,§ 14.3-14.5.
Лекции 5. Момент количества движения
точки относительно центра и оси.
Главный момент количеств движения
(кинетический момент) механической
ОЛ-1, ГЛ. 14, § 14.1, ГЛ.15 § 15.1-15.4, §
16.1
141
системы относительно центра и оси.
Кинетический момент твердого тела
относительно
оси
вращения.
Кинетический момент твердого тела при
сферическом движении.
Лекция 7. Элементарная и полная работа
силы.
Мощность.
Работа
равнодействующей
силы.
Работа
внутренних сил системы, работа сил,
приложенных к твердому телу, при его
различных движениях. Кинетическая
энергия точки и системы точек.
Вычисление кинетической энергии при
сложном движении (теорема Кенига).
Кинетическая энергия твердого тела в
различных случаях его движений.
Теорема об изменении кинетической
энергии
для
точки
и
системы
материальных точек. Примеры: ОЛ438.31, ОЛ3-9.78.
Теорема об изменении кинетического
момента системы. Законы сохранения
кинетического
момента.
Дифференциальное уравнение вращения
твердого тела вокруг неподвижной оси.
Примеры
ГЛ. 15, § 15.5, ОЛ-1, ГЛ. 14 § 14.2, 14.3.
Студенты
прорабатывают
самостоятельно следующие тему:
ОЛ-1, ГЛ. 15, § 15.6, 15.8.
Движение точки под действием
центральной
силы.
Понятие
о
секторной
скорости.
Теорема
площадей.
Лекции 8. Потенциальное силовое поле.
Элементарная и полная работа силы в
потенциальном силовом поле. Силовая
функция и потенциальная энергия поля.
Условия
существования
силовой
функции. Поверхности уровня и их
свойства. Примеры вычисления силовых
функций: однородного поля силы
тяжести, линейной силы упругости. Закон
сохранения
полной
механической
энергии системы.
ОЛ-1, ГЛ. 15, § 15.5
Лекции 6. Кёнигова система отсчета.
Кинетический
момент
системы
в
сложном
движении.
Теорема
об
изменении
кинетического
момента
системы
материальных
точек
в
относительном движении по отношению
к центру масс. Дифференциальные
уравнения плоского движения твердого
тела. Пример ОЛ3-10.2. Динамические
уравнения
Эйлера.
Интегрирование
задачи о движении тяжелого твердого
тела с одной неподвижной точкой:
случаи Эйлера, Лагранжа, Ковалевской.
ОЛ-1, ГЛ. 15, § 15.7.
Лекция 9. Принцип Даламбера для точки
и системы материальных точек. Сила
инерции материальной точки. Главный
вектор и главный момент сил инерции в
общем и частных случаях движения
твердого тела. Определение с помощью
принципа Даламбера динамических
реакций при несвободном движении
точки и механической системы - метод
кинетостатики. Примеры.
ОЛ-1, ГЛ. 15, § § 15.1-15.3, § 15.5, ГЛ. 14, §
14.2.
ОЛ-1, ГЛ. 15, § 15.5, ГЛ. 16, § 16.1. Л1,ГЛ.16,§ 16.1, 6.2.
ОЛ-1, ГЛ. 17, § § 17.1-17.3.
142
Практические занятия (семинары и КСР)
Занятие 3. Теоремы о движении центра
масс и изменении количества движения.
ОЛ4-35.20, 35.10,35.11, ОЛ3-19.4 (ауд.);
ОЛ3-9.9,9.10 (9.11),9.12(9.11), МП-4,5,6,13
(дома).
Занятие 7. Теорема об изменении
кинетической энергии. ОЛ4-38.20, 38.28,
38.31, ОЛ3-9.59 (9.57) (ауд.); ОЛ3-9.46
(9.44), 9.47 (9.45), МП-4,5,6,13(дома).
Занятие
8.
ОЛ3-9.92.
Примеры
выполнения ДЗ 2 (ауд.), ДЗ 2, МП-4,5,6,13
(дома).
Занятие 4. Теорема об изменении
кинетического момента. ОЛ4-37.50,
37.52, ОЛ3-9.17(9.18) (ауд.); ОЛ39.19(9.20),9.20(9.21), МП-4,5,6,13 (дома).
Занятие 9. Принцип Даламбера. ОЛ441.17, 41.21 (ауд.); ОЛ4-41.19, 41.22
(дома).
Занятие
5.
ОЛ4-37.43,
ОЛ39.34(9.35),9.37 (ауд.); ОЛ3-9.29 (9.30),
9.26 (9.27) (дома).
Занятие 6. Плоское движение твердого
тела ОЛ4-39.7, ОЛ3-10.7, 10.8 (ауд.); ОЛ310.4, 10.6, МП-13 (дома).
МОДУЛЬ 3: АНАЛИТИЧЕСКАЯ МЕХАНИКА. МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКОЙ
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Лекции 10-11. Связи и их классификация.
Возможные перемещения точки и
механической системы. Обобщенные
координаты. Вариации обобщенных
координат. Число степеней свободы
голономной системы. Элементарная
работа
силы
на
возможном
перемещении.
Идеальные
связи.
Принцип
возможных
перемещений
(принцип
Лагранжа).
Пример.
Обобщенные силы. Различные способы
вычисления
обобщенных
сил.
Обобщенные
силы
в
случае
потенциального силового поля. Условия
равновесия механической системы в
обобщенных силах. Равновесие системы
в потенциальном поле.
ОЛ-1, ГЛ. 18, § § 18.1-18.4.
Лекции 12. Общее уравнение динамики
(объединенный принцип ДаламбераЛагранжа). Уравнения Лагранжа 2-го
рода: вывод и методика применения.
Примеры.
ОЛ-1, ГЛ. 18, § 18.5.
Лекции 13. Малые колебания системы с
одной степенью свободы. Понятие об
устойчивом
положении
равновесия
механической
системы.
Теорема
Лагранжа-Дирихле (без доказательства).
143
Понятие о силах линейно-вязкого
сопротивления и их влиянии на
устойчивость положения равновесия.
Дифференциальные уравнения малых
свободных колебаний системы с одной
степенью свободы в общем случае (при
учете
сил
линейно-вязкого
сопротивления). Свободные колебания
консервативной системы с одной
степенью свободы. Период, частота, фаза
и амплитуда колебаний.
Собственные и вынужденные колебания.
Основные
свойства
установившихся
вынужденных колебаний. Амплитудночастотная
и
фазочастотная
характеристики. Резонанс при наличии и
отсутствии сил вязкого сопротивления.
ОЛ-1,ГЛ.19,§ 19.3
ОЛ-1,ГЛ.16,§ 16.2.
Лекция 16-17. Элементы приближенной
теории гироскопа. Основные понятия и
допущения.
Кинетический
момент
быстровращающегося
гироскопа.
Теорема Резаля. Особенности движения
оси
гироскопа.
Закон
прецессии.
Гироскопический момент. Определение
гироскопических
реакций,
правило
Жуковского.
Примеры
применения
гироскопов в технике.
ОЛ-1, ГЛ.19, § 19.1-19.2
Лекции 14-15. Свободные колебания
системы при наличии сил линейновязкого сопротивления. Характеристики
затухания: декремент, логарифмический
декремент. Апериодические затухающие
движения. Вынужденные колебания.
Обобщенная возмущающая сила. Вывод
и интегрирование дифференциального
уравнения вынужденных колебаний.
ОЛ-1,ГЛ.16,§ 16.2.
Практические занятия (семинары и КСР)
Занятие 13. ОЛ3-12.28, 12.40 (ауд.); ДЗ 3,
МП-7,9,11 (дома).
Занятие 10. Принцип возможных
перемещений.
ОЛ3-11.10(11.12),
11.5(11.6), 11.3(11.4), 11.9(11.11) (ауд.);
ОЛ3-11.7 (11.8), ОЛ4-46.22, МП-11 (дома).
Занятие 14. ОЛ3-14.4, ОЛ4-54.4, 54.18
(ауд.); ОЛ4-54.3, 54.20, ОЛ3-14,20 (дома).
Занятие 15. ОЛ3-14.43, 14,44 (ауд.); ОЛ454.20, ОЛ3-14.42, 14.46 (дома).
Занятие 11. Общее уравнение механики.
ОЛ4-47.6, 47.9, 47.12, 47.17 (ауд.); ОЛ447.13,47.16, МП-11 (дома).
Занятие 16. ОЛ3-14.45, 14.53 (ауд.); ОЛ314.50, 14.54, ДЗ 4 (дома).
Занятие 12. Уравнения Лагранжа 2 рода.
ОЛ3-12.9, 12.26,12.23 (ауд.); ОЛ3-12.10,
12.21, МП-7,9 (дома).
Занятие 17. ОЛ3-15.1, ОЛ4-40.3, 40.7
(ауд.); ОЛ3-15.4, 15.2 (дома).
144
Самостоятельная подготовка
В самостоятельную работу студентов входят изучение теории по каждой теме,
выполнение текущего задания, выполнение, сдача и защита ДЗ, контроль по модулю.
Студент допускается к экзамену (итоговый 4 модуль) при условии выполненных и
защищенных ДЗ.
Контрольные мероприятия и сроки их проведения
МОДУЛЬ 1:
Сроки выполнения модуля: 1-я неделя - 5-я неделя.
Защита домашнего задания № 1 на 4 неделе.
Письменная работа проводится по материалам семинаров 1 – 2 и лекций 1 – 2 на 5-й
неделе.
МОДУЛЬ 2:
Сроки выполнения модуля: 6-я неделя - 11-я неделя.
Защита домашнего задания № 2 на 10 неделе.
Письменная работа проводится по материалам семинаров 3 – 9 и лекций 3 – 9 на 10-й
неделе.
МОДУЛЬ 3:
Сроки выполнения модуля: 11-я неделя - 17-я неделя.
Защита домашнего задания № 3 на 13 неделе.
Письменная работа проводится по материалам семинаров 10 – 12 и лекций 10 – 12 на 13й неделе.
Защита домашнего задания № 4 на 15 неделе.
Письменная работа проводится по материалам семинаров 14 – 16 и лекций 13 – 15 на 16й неделе.
МОДУЛЬ 4 ИТОГОВЫЙ (экзамен)
Срок выставления общей оценки за 4 модуль – экзаменационная сессия.
145
Основная и дополнительная литература
1.
2.
3.
4.
Основная литература (ОЛ)
Курс теоретической механики. Под ред. К.С. Колесникова. – М.: Изд. МГТУ, 2000,
2002, 2005, 2011.
Никитин Н.Н. Курс теоретической механики. Изд.4е и посл. – М.: Высшая школа,
1983, 1990, 2003.
Сборник задач по теоретической механике. Под ред. К.С. Колесникова. – М.:
Наука, 1989, 2007, 2008.
Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука, 1981,
1986.
Дополнительная литература (ДЛ)
1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 2. – М.:
Наука, 1998.
2. Маркеев А.П. Теоретическая механика. – М.: Наука, 1990.
3. Лойцянский Л.Г. Лурье А.И. Курс теоретической механики. - М.: Наука, ч.1, 1982,
ч.2, 1983 и след.
Методические пособия, изданные в МГТУ (МП)
1. Саратов Ю.С., Баранов В.Н., Нарская Н.Л. Динамика материальной точки.
Методические указания к курсовой работе по теоретической механике. – Изд. МГТУ, 1999.
2. Баранов В.Н., Феоктистова О.П., Саратов Ю.С., Щеглова Н.Н. Динамика
материальной точки. Методические указания к решению задач и выполнению курсовой
работы. – М.: Изд. МГТУ, 2002.
3. Дубинин В.В., Никитин Н.Н., Феоктистова О.П. Общие теоремы динамики. Метод.
указания по выполнению курсовой работы по разделу курса теоретической механики
«Динамика». – Изд. МВТУ, 1984.
4. В.В. Дубинин, А.Ю. Карпачев, А.В. Ремизов. Общие теоремы динамики.
Методические указания к выполнению курсового задания. – М.: МГТУ, 2006.
5. Дронг В.И., Максимов Г.М., Огурцов А.И. Уравнения Лагранжа 2 рода. Метод.
указания к курсовой работе по динамике. – Изд. МВТУ, 1985.
6. Уравнения Лагранжа 2 рода. Метод. указания к выполнению курсовой работы и
решению задач. Под ред.Дронга В.И. – Изд. МГТУ, 1988.
7. Саратов Ю.С., Русанов П.Г., Тушева Г.М. Метод. указания к курсовой работе по
динамике. Раздел «Колебания линейной системы с одной степенью свободы». – Изд.
МВТУ, 1985.
8. Ильин М.М., Пожалостин А.А., Тушева Г.М. Колебания линейной системы с одной
степенью свободы. Метод.указания к выполнению курсовой работы по разделу курса
теоретической механики «Динамика». – Изд. МГТУ, 2002.
9. Н.В. Борохова, М.М. Ильин, Г.М. Тушева. Колебания линейной системы с одной
степенью свободы. Методические указания к выполнению домашних заданий по разделу
курса «Теоретическая механика». – Изд. МГТУ, 2005.
Рекомендуемые Интернет-сайты
1. http://hoster.bmstu.ru/~fn3/
146
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Календарный план 2 курс 4 семестр 2012/2013 уч. г.
для студентов факультетов СМ (СМ1-41, СМ1-42, СМ2-41, СМ3-41, СМ3-42, СМ4-41, СМ4-42,
СМ6-41, СМ6-42, СМ8-41, СМ8-42, СМ9-41, СМ9-42, СМ10-41, СМ10-42, СМ12-41), РК (РК4-41,
РК4-42), МТ.
Дисциплина состоит из 3-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-3
6
Практические занятия
1-4
6
Домашние задания
1-4
6
5
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
5-9
10
Практические занятия
5-11
6
Домашние задания
5-12
6
13
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
147
Примечание
Лекции
10-17
16
Практические занятия
13-17
6
Домашние задания
13-16
6
16
2
Контроль по модулю №3
Модуль 4. Экзамен
МОДУЛЬ 1. ДИНАМИЧЕСКИЕ РЕАКЦИИ
Лекции
Лекции 1-2. Приведение сил инерции тела,
вращающегося вокруг неподвижной оси, к
началу координат на оси вращения.
Получение выражений для проекций
главного вектора и главного момента сил
инерции на оси декартовой системы
координат.
Определение
реакций
подшипников твердого тела, вращающегося
вокруг неподвижной оси. Статические и
динамические
составляющие
реакций.
Частные случаи. Понятие статической и
динамической
уравновешенности
тела.
Пояснения к выполнению 1-го домашнего
задания.
ОЛ-1, гл. 17, §§ 17.1-17.6.
Лекции 3-4. Основные положения теории
удара. Общие теоремы динамики для удара.
Изменение угловой скорости при ударе по
вращающемуся телу. Фазы удара. Ударные
импульсы для двух фаз удара. Удар точки о
неподвижную поверхность. Коэффициент
восстановления. Примеры. Центр удара.
Условия отсутствия ударных реакций в
опорах вращающегося тела. Теорема Карно.
ОЛ-1, гл. 20, §§ 20.1-20.6
Практические занятия
Занятие 1. Динамические реакции
В аудитории: ОЛ-5: 13.21 (13.19),
(13.26), 13.32 (13.31)
В аудитории: ОЛ-5: 13.10(13.8), 13.9(13.7),
13.14(13.12)
Дома: ОЛ-5: 13.30 (13.39) ДЗ1, МП 1, 5, 6
Дома: ОЛ-5: 13.11(13.9), 13.6(13.13)
Занятие 3. Основы теории удара
Занятие 2. Динамические реакции
В аудитории: ОЛ-6: 44.2, 44.25
Дома: ОЛ-5: 16.20
148
13.27
.
МОДУЛЬ 2. МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ
СВОБОДЫ. СВОБОДНЫЕ КОЛЕБАНИЯ
Лекции
Лекции
5-6.
Положение
равновесия
механической
системы.
Нахождение
положений
равновесия
из
условий
равновесия, выраженных в обобщенных
силах. Примеры. Устойчивость положения
равновесия. Теорема Лагранжа – Дирихле.
Силы сопротивления, пропорциональные
первой степени скоростей точек, линейновязкое
сопротивление.
Диссипативная
функция Релея. Связь между полной
механической энергией и диссипативной
функцией.
Влияние
сил
вязкого
сопротивления на устойчивость положения
равновесия системы.
Дифференциальное уравнение движения
системы с одной степенью свободы в случае
малых
отклонений
от
положения
равновесия.
Свободные
колебания
консервативной системы с одной степенью
свободы.
Элементы
гармонических
колебаний. Примеры.
ОЛ-1, гл. 19, § 19.3.
Лекция 9. Свободные движения системы с
линейно-вязким
сопротивлением.
Затухающее
колебательное
движение.
Постоянная времени затухающих колебаний,
декремент колебания, логарифмический
декремент,
добротность
системы.
Затухающие неколебательные движения.
Основные свойства свободных колебаний.
Пример: Л6-32.67.
ОЛ-1, гл. 19, §§ 19.1, 19.2.
Лекции 7-8. Понятие о малых движениях
системы около устойчивого положения
равновесия. Приближенные выражения для
кинетической и потенциальной энергий и
диссипативной функции Релея в системе с
одной
степенью
свободы.
ОЛ-1, гл. 19, § 19.3, ОЛ-7, гл. 2.
Практические занятия
Занятие 4.
Дома: ОЛ-5: 14.21, 14.26, МП 2,3
В аудитории: ОЛ-6: 32.1, 32.2, 32.3, ОЛ5-14.1
Занятие 6.
Дома: ОЛ-5: 14.4, 14.14, ОЛ-7, гл.2
В аудитории: ОЛ-5: 14.29, ОЛ-6: 32.64, 32.62
Занятие 5.
Дома: ОЛ-5: 14.31, 14.33, ДЗ 2
В аудитории: ОЛ-5: 14.6, 14.22
МОДУЛЬ 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
149
Лекции
Лекции 10-11. Вынужденные колебания.
Определение обобщенной возмущающей
силы при различных способах возбуждения.
Интегрирование
дифференциального
уравнения вынужденных колебаний при
наличии линейно-вязкого сопротивления.
Установившиеся вынужденные колебания.
Частный случай – консервативная система,
резонанс
в
консервативной
системе.
Амплитудно-частотная и фазо-частотная
характеристики системы. Исследование
коэффициента динамичности и фазового
сдвига
при
силовом
возбуждении.
Исследование коэффициента динамичности
в случае инерционного возбуждения.
системы.
Устойчивость
положения
равновесия консервативной системы с двумя
степенями свободы. Критерий Сильвестра.
Пример.
Вывод
дифференциальных
уравнений малых колебаний консервативной
системы с двумя степенями свободы.
Парциальные
системы
и
парциальные
частоты.
Интегрирование
дифференциальных уравнений свободных
колебаний. Уравнение частот, исследование
его корней. Коэффициенты распределения
амплитуд. Главные колебания, формы
главных
колебаний.
Нормальные
координаты. Пример: Л6-55.4. Особенности
описания малых колебаний систем с n
степенями свободы.
Лекция
12.
Основные
свойства
установившихся вынужденных колебаний.
Пояснения и пример выполнения ДЗ.
ОЛ-1, гл. 19, §§ 19.7, 19.8.
Лекция 16. Вынужденные колебания в
консервативной системе с двумя степенями
свободы
в
случае
гармонического
возбуждающего
воздействия.
Частные
случаи. Эффект динамического гашения
колебаний. Примеры.
ОЛ-1, гл. 19, § 19.4.
Лекция 13. Вынужденные колебания в
системе с одной степенью свободы в случае
периодического,
но
негармонического
вынуждающего воздействия и в случае
произвольного вынуждающего воздействия.
Основы виброзащиты. Примеры.
ОЛ-1, гл. 19, § 19.9.
Лекция 17. Движение точки переменной
массы.
Дифференциальные
уравнения
движения. 1-я и 2-я задачи Циолковского.
Пример.
ОЛ-1, гл. 19, §§ 19.4-19.6.
Лекции
14-15.
Кинетическая
и
потенциальная энергии системы с двумя
степенями
свободы.
Выражения
для
кинетической и потенциальной энергии для
случая малых колебаний механической
ОЛ-1, гл. 21, МП 8.
Практические занятия
Занятие 7.
Занятие 8.
В аудитории: ОЛ-5: 14.42, 14.44, 14.46
В аудитории: ОЛ-5: 14.52, Задачи типа ДЗ
Дома: ОЛ-5: 14.43, 14.47
Дома: ОЛ-5: 14.51, ДЗ 2, 3, МП 2,3
150
Дома: ОЛ-5: 14.80
Занятие 9.
В аудитории: ОЛ-6: 55.9, 55.7, ОЛ5-14.73
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
В самостоятельную работу студента входят: изучение теории по каждой теме; выполнение текущих
заданий и письменных работ (контроль по модулю); выполнение и защита ДЗ.
Студент допускается к экзамену (итоговый 4 модуль) при условии, что он выполнил и защитил все ДЗ.
Контрольные мероприятия и сроки их проведения
МОДУЛЬ 1.
Домашнее задание № 1 «Динамические реакции подшипников»
Объем в часах – 6. Сроки выполнения: выдача – 1-я неделя, прием – 4-я неделя.
Методические пособия МП – 1, 5, 6.
Письменная работа № 1. Материал модуля «Динамические реакции». Проводится по лекциям 1,
2, практическим занятиям 1, 2 и методическим пособиям МП 1, 5, 6 на 5-ой неделе.
МОДУЛЬ 2.
Домашнее задание № 2. «Малые колебания – определение параметров процесса».
Объем в часах – 6. Сроки выполнения: выдача – 5-я неделя, прием – 12-я неделя.
Письменная работа № 2. Материал Модуля 2. Проводится по лекциям 6-10, семинарам 4, 5 и
методическим пособиям МП 2-3 на 12 неделе.
МОДУЛЬ 3.
Домашнее задание № 3. «Малые колебания – исследование колебательного процесса».
Объем в часах – 6. Сроки выполнения: выдача – 12-я неделя, прием – 16-я неделя.
Письменная работа № 3. Материал модуля 3. Проводится по лекциям 11, 12, семинарам 6, 7 и
методическим пособиям МП 2, 3 на 16-ой неделе.
МОДУЛЬ 4. ИТОГОВЫЙ (экзамен)
Срок выставления оценки за 4 модуль – экзаменационная сессия.
Литература (ОЛ)
151
1.
Дронг В.И., Дубинин В.В., Ильин М.М., Колесников К.С., Космодемьянский В.А.,
Назаренко Б.П., Панкратов А.А., Русанов П.Г., Саратов Ю.С., Степанчук Ю.М., Тушева Г.М.,
Шкапов П.М. Курс теоретической механики. / Под общ.ред. Колесникова К.С. Изд. 1 и
последующие – М.: Изд. МГТУ, 2000, 2002, 2005, 2011.
2.Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. Изд. 4 и
последующие – М.: Высшая школа, 1983, 1990, 2003
3.Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 1, 2. – М.: Наука, 1971,
1985.
4.Ильин М.М., Колесников К.С., Саратов Ю.С. Теория колебаний: Учебник для вузов / Под общ.ред.
К.С. Колесникова. – М.: Изд. МГТУ, 2001, 2003. (Серия Механика в техническом университете, т. 4).
5.Сборник задач по теоретической механике. Под ред. К.С. Колесникова. – М.: Наука, 1983, 1989,
2007, 2008.
6.Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука, 1981, 1986.
Методические пособия, изданные в МГТУ (МП)
1. Занозин П.В., Ефремова Л.Е., Плешаков Ю.Д. Динамические реакции подшипников.
Метод.указания по выполнению курсовой работы. – Изд. МВТУ, 1986.
2. Ильин М.М., Пожалостин А.А., Тушева Г.М. Колебания линейной системы с одной степенью
свободы. Метод.указания к выполнению курсовой работы по разделу курса теоретической
механики «Динамика». – Изд. МГТУ, 2002.
3. Н.В. Борохова, М.М. Ильин, Г.М. Тушева. Колебания линейной системы с одной степенью
свободы. Методические указания к выполнению домашних заданий по разделу курса
«Теоретическая механика». – Изд. МГТУ, 2005.
4. Динамика. Метод.указания по проведению практических занятий с использованием моделей и
приборов по курсу «Теоретическая механика». – Изд. МГТУ, 1988.
5. Борохова Н.В., Ефремова Л.Е., Панкратов А.А., Шкапов П.М. Динамические реакции
подшипников. Метод. указания к выполнению курсовой работы. / Под ред. Саратова Ю.С. – Изд.
МГТУ, 1990.
6. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный комплекс
«Динамические реакции подшипников» ТМл-06М. Изд. МГТУ, 2009.
7. Баркин Ю.В., Дронг В.И., Панкратов А.А. Движение точки переменной массы. – Изд. МГТУ, 1992.
Рекомендуемые Интернет-сайты
1. http://hoster.bmstu.ru/~fn3/
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
для студ. каф. ИУ2 (4 семестр)
Дисциплина состоит из 3-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
152
Трудоёмкость,
часы
Примечание
Лекции
1-4
8
Практические занятия
1-6
6
Лабораторные работы
1-6
6
Домашние задания
1
6
Контроль по модулю №1
8
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
5-8
8
Практические занятия
7-12
6
Лабораторные работы
4-5
4
Домашние задания
2
6
Контроль по модулю №2
13
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
9-17
18
Практические занятия
13-17
6
Лабораторные работы
6-8
6
Домашние задания
3
6
Контроль по модулю №3
16
2
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Примечание
Модуль 1: Аналитическая механика
Лекции
Лекция 1. Связи и их классификация. Возможные
перемещения точки и механической системы.
Обобщенные координаты. Вариации обобщенных
координат. Число степеней свободы голономной
системы. Элементарная работа силы на возможном
перемещении. Идеальные связи.
ОЛ-1, гл. 17, §§ 17.1-17.3.
153
Лекция 2. Принцип возможных перемещений.
Пример. Общее уравнение динамики. Пример.
Обобщенные силы. Различные способы вычисления
обобщенных сил. Обобщенные силы в случае
потенциального силового поля. Условия равновесия
в обобщенных силах. Равновесие системы в
потенциальном поле.
Лекции 3-4. Общее уравнение динамики в
обобщенных силах. Уравнения Лагранжа 2 рода.
Вывод и методика применения. Примеры: ОЛ5-12.30,
12.14.
ОЛ-1, гл. 18, § 18.5
ОЛ-1, гл. 18, § § 18.1-18.4.
Практические занятия
Занятие 1. Принцип возможных перемещений
Занятие 3. Уравнения Лагранжа 2 рода
В аудитории: ОЛ-5: 11.10(11.12), 11.5(11.6),
11.3(11.4), 11.9(11.11)
Дома: ОЛ-5: 11.7(11.8); ОЛ6-46.22
В аудитории: ОЛ-5: 12.9, 12.26, 12.23
Дома: ОЛ-5: 12.10, 12.21
.
Занятие 2. Общее уравнение механики
В аудитории: ОЛ-6: 47.6, 47.9, 47.12, 47.17
Дома: ОЛ-6: 47.13,47.16
Лабораторные работы
Лабораторная работа 1. «Свободные колебания
физического маятника».
МП-8.
Лабораторная работа 3. «Качение тел одинаковой
массы с разными моментами инерции».
МП-10
Лабораторная работа 2. «Колебания двойного
маятника».
МП-9.
.
Модуль 2: Малые колебания механической системы с одной степенью
свободы. Свободные колебания
Лекции
Лекция 5. Основные положения и допущения
линейной теории колебаний. Нахождение положений
равновесия из условий равновесия, выраженных в
обобщенных силах. Примеры.
Устойчивость
положения равновесия. Теорема Лагранжа –
Дирихле. Влияние сил вязкого сопротивления на
устойчивость положения равновесия системы.
Нахождение положений устойчивого положения
равновесия для систем с одной степенью свободы.
Лекции 6-7. Понятие о малых движениях системы
около
устойчивого
положения
равновесия.
Приближенные выражения для кинетической и
потенциальной энергий и диссипативной функции
Релея в системе с одной степенью свободы.
Физический
смысл
диссипативной
функции.
Дифференциальное уравнение движения системы с
одной степенью свободы в случае малых отклонений
от положения равновесия. Свободные колебания
ОЛ-1, гл. 19, §§ 19.1, 19.2.
154
консервативной системы с одной степенью свободы.
Элементы гармонических колебаний. Примеры.
декремент, добротность системы. Затухающие
неколебательные движения. Пример: ОЛ6-32.67.
ОЛ-1, гл. 19, § 19.3.
ОЛ-1, гл. 19, § 19.3, Л-7, гл. 2
Лекция 8. Свободные движения системы с линейновязким сопротивлением. Затухающее колебательное
движение.
Постоянная
времени
затухающих
колебаний, декремент колебания, логарифмический
Практические занятия
Занятие 4. Свободные колебания консервативной
системы с одной степенью свободы.
Занятие 6. Движение системы с одной степенью
свободы
при
наличии
линейно-вязкого
сопротивления.
В аудитории: ОЛ-6: 32.1,32.2,32.3; ОЛ-5: 14.1
Дома: ОЛ-5: 14.4
В аудитории: ОЛ-5: 14.29, ОЛ-6: 32.64, 32.62
Дома: ОЛ-5: 14.31, 14.33
Занятие 5. Свободные колебания консервативной
системы с одной степенью свободы (продолжение)
.
В аудитории: ОЛ5: 14.6, 14.22
Дома: ОЛ-5: 14.21, 14.26
Лабораторные работы
Лабораторная работа 4. «Исследование гироскопических давлений».
МП-11.
Модуль 3: Вынужденные колебания механической системы с одной степенью
свободы. Основы теории устойчивости движения
Лекции
Лекции 9-10. Вынужденные колебания. Определение
обобщенной силы при различных способах
возбуждения. Интегрирование дифференциального
уравнения вынужденных колебаний при наличии
линейно-вязкого сопротивления. Частный случай –
консервативная система, резонанс в консервативной
системе. Собственные и вынужденные колебания.
Амплитудно-частотная
и
фазо-частотная
характеристики
системы.
Исследование
коэффициента динамичности и фазового сдвига.
Исследование коэффициента динамичности в случае
вынужденного относительного движения. Основные
свойства установившихся вынужденных колебаний.
Примеры.
Лекция 11. Вынужденные колебания в системе с
одной степенью свободы в случае периодического,
но негармонического вынуждающего воздействия и в
случае произвольного вынуждающего воздействия.
Основы виброзащиты.
ОЛ-1, гл. 19, §§ 19.4-19.6.
Лекции 12-13. Кинетическая и потенциальная
энергии системы с двумя степенями свободы.
Устойчивость
положения
равновесия
консервативной системы с двумя степенями
свободы. Критерий Сильвестра. Пример. Вывод
дифференциальных уравнений малых колебаний в
консервативной системе с двумя степенями свободы.
Парциальные системы и парциальные частоты.
ОЛ-1, гл. 19, § 19.4.
155
Интегрирование
дифференциальных
уравнений
свободных
колебаний.
Уравнение
частот,
исследование
его
корней.
Коэффициенты
распределения амплитуд. Главные колебания, формы
главных колебаний. Нормальные координаты.
Пример: ОЛ6-55.4.
координаты. Определение устойчивости движения
применительно к фазовым координатам.
ОЛ-4: гл.1, §§ 1.1-1.2
Лекция 16.
Линеаризация
дифференциальных
уравнений возмущенного движения. Уравнения
первого приближения. Устойчивость движения
линейных систем. Характеристическое уравнение
дифференциальных уравнений первого приближения
(линейных) и анализ его возможных корней.
Критерии
устойчивости
линейных
систем.
Алгебраический критерий Гурвица. Границы
применимости линейной теории устойчивости.
Теоремы А.М.Ляпунова об устойчивости по первому
приближению.
ОЛ-1, гл. 19, §§ 19.7, 19.8.
Лекция
14.
Вынужденные
колебания
в
консервативной системе с двумя степенями свободы
в
случае
гармонического
возбуждающего
воздействия.
Частные
случаи.
Эффект
динамического гашения колебаний.
ОЛ-1, гл. 19, § 19.9.
Лекции 15. Основные понятия теории устойчивости
движения: невозмущенное и возмущенное движения;
возмущения (отклонения) обобщенных координат и
скоростей. Определение устойчивости движения по
А.М.Ляпунову (применительно к обобщенным
координатам и скоростям). Дифференциальные
уравнения возмущенного движения. Фазовые
ОЛ-4: гл.1, §§ 1.3-1.5, 1.8.
Лекция 17. Движение точки переменной массы.
Уравнение И.В.Мещерского. Первая и вторая задачи
К.Э.Циолковского.
ОЛ-1: гл. 21; МП 16.
Практические занятия
Занятие
7.
Вынужденные
колебания
консервативной системы с одной степенью свободы.
В аудитории: ОЛ-5: Л5-14.52
Дома: ОЛ-5: 14.51
В аудитории: ОЛ-5: 14.42,14.44,14.46
Дома: ОЛ-5: 14.43, 14.47
Занятие 9. Свободные колебания консервативной
системы с двумя степенями свободы.
Занятие 8. Вынужденные колебания системы с
одной степенью свободы при наличии линейновязкого сопротивления.
В аудитории: ОЛ-6: 55.9, 55.7; ОЛ-5: 14.73
Дома: ОЛ-5: 14.80
.
Лабораторные работы
Лабораторная работа 6. «Вынужденные колебания
системы с инерционным возмущением».
МП-13.
Лабораторная работа 8. «Двухстепенной
гироскоп».
МП-15..
Лабораторная работа 7. «Вынужденные колебания
системы с одной степенью свободы».
МП-14.
.
Самостоятельная подготовка
Модуль 1:


Проработка курса лекций, учебников, методических пособий по темам лекций 1 – 4, семинаров 1 - 3 и
лабораторных работ 1 – 3.
Выполнение домашнего задания № 1
156

Подготовка к письменным работам 1.1 и 1.2
Домашнее задание № 1 «Уравнения Лагранжа II рода».
Сроки выполнения: выдача – 2-я неделя, прием – 8-я неделя.
Объем в часах: 6.
Методические пособия: МП-2,3.
Письменная работа 1.1 по теме «Аналитическая механика» (лекции 1-3, практические занятия 1-2)
Срок проведения: 5-я неделя.
Письменная работа 1.2 по теме «Уравнения Лагранжа 2-го рода» (лекции 1-4, практическое занятие 3).
Срок проведения: 8-я неделя.
Модуль 2:



Проработка курса лекций, учебников, методических пособий по темам лекций 5 – 8, семинаров 4 – 6 и
лабораторных работ 4 – 5
Выполнение домашнего задания № 2
Подготовка к письменной работе 2
Домашнее задание № 2 «Малые колебания – определение параметров процесса».
Сроки выполнения: выдача – 8-я неделя, прием – 13-я неделя.
Объем в часах: 6.
Методические пособия: МП-4,5.
Письменная работа2 по теме «Свободные колебания механической системы с одной степенью свободы»
Срок проведения: 13 неделя.
Модуль 3:



Проработка курса лекций, учебников, методических пособий по темам лекций 9 – 14, семинаров 7, 8 и
лабораторных работ 6, 7
Выполнение домашнего задания № 3
Подготовка к письменной работе 3
Домашнее задание № 3 «Малые колебания – исследование колебательного процесса».
Объем в часах: 6.
Методические пособия: МП-4,5.
Письменная работа 3 по теме «Вынужденные колебания механической системы с одной степенью свободы»
Срок проведения: 15 неделя.
Контрольные мероприятия и сроки их проведения
МОДУЛЬ 1
Домашнее задание №1 «Уравнения Лагранжа 2 рода»
срок выполнения: 2 – 8 недели
Письменная работа 1.1. «Аналитическая механика»
срок проведения – 5 неделя
157
Письменная работа 1.2. «Уравнения Лагранжа 2 рода»
срок проведения – 8 неделя
Лабораторная работа 1. «Свободные колебания физического маятника»
срок проведения – 2 неделя
Лабораторная работа 2. «Колебания двойного маятника»
срок проведения – 4 неделя
Лабораторная работа 3. «Качение тел одинаковой массы с разными моментами инерции»
срок проведения – 6 неделя
Срок выставления общей оценки за модуль – 8 неделя
МОДУЛЬ 2
Домашнее задание №2 «Малые колебания – определение параметров процесса»
срок выполнения: 8 – 13 неделя
Письменная работа 2. «Свободные колебания механической системы с одной степенью свободы»
срок проведения – 13 неделя
Лабораторная работа 4. «Исследование гироскопических давлений»
срок проведения – 8 неделя
Лабораторная работа 5. «Исследование динамических реакций»
срок проведения – 10 неделя
Срок выставления общей оценки за модуль – 13 неделя
МОДУЛЬ 3
Домашнее задание №3 «Малые колебания – исследование колебательного процесса»
срок выполнения:13 – 15 недели
Письменная работа 3. «Вынужденные колебания механической системы с одной степенью свободы»
срок проведения – 15 неделя
Лабораторная работа 6. «Вынужденные колебания системы с инерционным возмущением»
срок проведения – 12 неделя
Лабораторная работа 7. «Вынужденные колебания системы с одной степенью свободы»
срок проведения – 14 неделя
Письменная работа 4. «Основы теории устойчивости движения»
срок проведения – 16 неделя
Лабораторная работа 8. «Двухстепенной гироскоп»
срок проведения – 16 неделя
Срок выставления общей оценки за модуль – 16 неделя
158
МОДУЛЬ 4: ИТОГОВЫЙ (экзамен)
Срок выставления оценки за 4 модуль – экзаменационная сессия.
Литература
Основная литература (ОЛ)
5. Курс теоретической механики / Под ред. К.С.Колесникова. – М.: Изд. МГТУ, 2000, 2002 2005, 2011.
6. Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. – М.: Высшая школа, 1974,
1983, 1990 и более поздние издания.
7. Ильин М.М., Колесников К.С., Саратов Ю.С. Теория колебаний: Учебник для вузов / Под общ. ред. К.С.
Колесникова. – М.: Изд. МГТУ, 2001, 2003. (Серия Механика в техническом университете, т. 4).
8. Алфутов Н.А., Колесников К.С. Устойчивость движения и равновесия / Под общ. ред. К.С. Колесникова. – М.:
Изд. МГТУ, 2001, 2003.
5. Сборник задач по теоретической механике / Под ред. К.С.Колесникова – М.: Наука, 1989, 2007, 2008 и более
поздние издания.
6. Мещерский И.В. Сборник задач по теоретической механике М.: Наука, 1981, 1986 и более поздние издания.
11.
12.
13.
14.
Дополнительная литература (ДЛ)
Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 1, 2. – М.: Наука, 1971, 1985
Бабаков Н.Н. Теория колебаний. – М.: Наука, 1971
Яблонский А.А., Норейко С.С. Курс теории колебаний – СПб.: Изд. «Лань», 2003
Меркин Д.Р. Введение в теорию устойчивости движения – СПб.: Изд. «Лань», 2003
Методические пособия, изданные в МГТУ (МП)
5. Темнов А.Н., Лямин В.И. Аналитическая механика. – Изд. МГТУ, 1990.
6. Дронг В.И., Максимов Г.М., Огурцов А.И. Уравнения Лагранжа 2 рода. Метод. указания к курсовой работе по
динамике. – Изд. МВТУ, 1985.
7. Уравнения Лагранжа 2 рода. Метод. указания к выполнению курсовой работы и решению задач. Под
ред.Дронга В.И. – Изд. МГТУ, 1988.
8. Ильин М.М., Пожалостин А.А., Тушева Г.М. Колебания линейной системы с одной степенью свободы.
Метод.указания к выполнению курсовой работы по разделу курса теоретической механики «Динамика». – Изд.
МГТУ, 2002.
9. Н.В. Борохова, М.М. Ильин, Г.М. Тушева. Колебания линейной системы с одной степенью свободы.
Методические указания к выполнению домашних заданий по разделу курса «Теоретическая механика». – Изд.
МГТУ, 2005.
10. Решение задач по курсу «Теоретическая механика» с использованием ЭВМ. Под ред. Г.М. Максимова и
Е.Н. Солохина. – Изд. МГТУ, 1988.
11. Динамика. Метод.указания по проведению практических занятий с использованием моделей и приборов
по курсу «Теоретическая механика». – Изд. МГТУ, 1988.
12. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В., Косачев С.Л. Автоматизированный лабораторный
комплекс «Свободные колебания физического маятника» ТМл-01М.: Метод. Указания - М.: Изд-во МГТУ им.
Н.Э. Баумана, 2006. - 16 с.: ил.
13. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный комплекс «Двойной
маятник» ТМл-02М.: Учебное пособие - М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. - 20 с.
14. Дубинин В.В., Солохин Е.Н., Иванникоа В.А., Назаренко Б.П. Лабораторный аппаратно-программный
комплекс ТМЛ-20МР. Метод. указания - М.: Изд-во МГТУ им. Н.Э. Баумана, 1998. - 20 с.: ил.
15. Дубинин В.В., Жигулёвцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный комплекс
«Двухстепенной гироскоп» ТМл-09М : Метод. Указания - М.: Изд-во МГТУ им. Н.Э. Баумана, 2011. - 21 с.: ил.
16. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный комплекс
«Динамические реакции подшипников» ТМЛ-06М: Метод. указания - М.: Изд-во МГТУ им. Н.Э. Баумана,
2009. - 40 с.: ил.
159
17. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный комплекс
«Вынужденные колебания механической системы с инерционным возмущением» ТМЛ-07М: Метод. указания
- М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – 17 с.: ил.
18. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный комплекс
«Вынужденные колебания системы с одной степенью свободы» ТМл-08М: Метод. указания - М.: Изд-во
МГТУ им. Н.Э. Баумана, 2005. - 18 с.: ил.
19. Дубинин В.В., Жигулёвцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный комплекс
«Двухстепенной гироскоп» ТМл-09М : Метод. Указания - М.: Изд-во МГТУ им. Н.Э. Баумана, 2011. - 16 с.: ил.
20. Баркин Ю.В., Дронг В.И., Панкратов А.А. Движение точки переменной массы. – Изд. МГТУ, 1992.
Рекомендуемые Интернет-сайты
1. http://hoster.bmstu.ru/~fn3/
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для УЦ1,2-41
Дисциплина состоит из 3-х учебных модулей и экзамена
Модуль 1
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
1-5
9
Упражнения
1-4
8
Домашние задания текущие
1-4
5
Контроль по модулю № 1
5-6
2
Модуль 2
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
5-9
9
Упражнения
5-11
14
Домашние задания текущие
5-11
12
13
4
Контроль по модулю № 2
160
Модуль 3
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
10-17
16
Упражнения
12-17
12
Домашние задания текущие
12-17
7
17
4
Контроль по модулю № 3
Модуль 1: Кинематика точки и кинематика
простейших движений твёрдоготела
Лекции
Лекция 1.
Введение.
Кинематика.
Введение в курс «Теоретическая механика».
Предмет механики. Теоретическая механика
как одна из фундаментальных физикоматематических наук; ее значение и место
среди других естественных и технических
наук.
Траектория точки. Скорость точки. Ускорение
точки. Способ задания движения точки в
декартовых
координатах.
Определение
траектории точки по уравнениям ее
движения. Проекции скорости на оси
декартовых координат.
Определение
модуля и направления вектора скорости по
его проекциям на оси декартовых
координат. Проекции ускорения точки на оси
декартовых координат. Определение модуля
и направления вектора ускорения. Примеры.
ОЛ-1, гл.1, пп. 1.1-1.4.
Кинематика.
Предмет
кинематики.
Пространство и время. Системы отсчета.
Кинематика
точки.
Способы
задания
движения точки. ОЛ-1, гл.1, п.1.1
Лекция 2. Кинематика точки. Векторный
способ
задания
движения
точки.
ускорения
по
осям
естественного
трехгранника. Касательное и нормальное
ускорения. Примеры. ОЛ-1, гл.1, п.1.5.
Лекция 4. Кинематика твёрдого тела.
Понятие абсолютно твердого тела. Задание
движения твердого тела, число степеней
свободы. Теорема о проекциях скоростей
двух точек твердого тела. Простейшие
движения тела. Поступательное движение
твердого тела. Теорема о траекториях,
скоростях и ускорениях точек твердого тела
при поступательном движении. Число
степеней свободы, уравнения движения.
Вращение
твердого
тела
вокруг
неподвижной оси. Угол поворота, уравнение
движения.
Угловая скорость и угловое
Лекция 3. Кинематика точки.
Естественный способ задания движения
точки. Модуль и направление скорости.
Естественные оси и их орты. Разложение
161
час) Векторные и скалярные формулы для
скоростей и ускорений точек тела,
вращающегося вокруг неподвижной оси.
Примеры. ОЛ-1, гл.2, пп.2.1-2.3.
ускорение твердого тела, вращающегося
вокруг неподвижной оси. ОЛ-1, гл.2, пп.2.12.3.
Лекция 5. Кинематика твёрдого тела. (1
Упражнения
Семинары 1-3.
час.)
Кинематика точки (5
Семинары 3-4. Кинематика простейших
движений твердого тела (3 час.)
Кинематика точки. Траектория. Скорость
и ускорение точки при координатном и
естественном
способе
задания
ее
движения. ОЛ-2,3.
Поступательное движение твёрдого тела и
вращение тела вокруг неподвижной оси.
ОЛ-2,3.
Модуль 2: Кинематика плоского движения твёрдого тела
и кинематика сложного движения точки
Лекции
Векторы угловой скорости и углового
ускорения. Скорости и ускорения точек
тела. ОЛ-1, гл. 4, пп. 4.1-4.6.
Лекция 5. Кинематика твёрдого тела.
Плоское движение твердого тела.
Движение плоской фигуры в ее
плоскости. Разложение
движения на
поступательное вместе с полюсом и
вращение вокруг полюса.
Примеры.
ОЛ-1, гл. 3, пп. 3.1-3.4.
Лекция 8.
Кинематика
движения точки.
сложного
Сложное движение точки. Абсолютное,
относительное и переносное движения
точки. Полная и локальная производные
вектора. Формула Бура. Скорость и
ускорение точки при сложном движении.
Теорема о сложении скоростей. Теорема о
сложении ускорений (теорема Кориолиса).
Правило Жуковского. ОЛ-1, гл. 6, пп. 6.1-6.4.
Лекция 6. Кинематика твёрдого тела.
Теорема о скоростях точек твердого тела
при плоском движении. Мгновенный
центр скоростей. Определение скоростей
точек тела с помощью мгновенного
центра скоростей. Теорема об ускорениях
точек твердого тела при плоском
движении. Мгновенный центр ускорений.
Примеры. ОЛ-1, гл. 3, пп. 3.3-3.8.
Лекция 9.
Кинематика
движения твердого тела.
сложного
Сложение поступательных движений твердого тела.
Лекция 7. Кинематика твёрдого тела.
Сложение вращательных движений твердого тела вокруг
пересекающихся и параллельных осей. Пара вращений. ОЛ-1,
гл. 7, пп. 7.1-7.4.
Движение
твёрдого
тела
вокруг
неподвижной
точки
(сферическое
движение). Число степеней свободы. Углы
Эйлера. Мгновенная ось вращения.
Упражнения
Семинары 5-8. Кинематика плоского
движения твердого тела.
Скорости и ускорения точек твердого
тела, движущегося плоскопараллельно.
162
МЦС, МЦУ тела.
ОЛ-2,3.
движение точки. Разложение абсолютного
движения на относительное и переносное.
Абсолютные скорость и ускорение точки.
ОЛ-2,3.
Семинары 9-11. Кинематика сложного
движения точки.
Прямая и обратная задачи на сложное
Модуль 3: Статика
Лекции
Теорема о приведении произвольной
системы сил к данному центру - основная
теорема статики. Главный вектор и
главный момент системы сил, формулы
для их вычисления. Условия равновесия
произвольной системы сил. Частные
случаи системы сил: система сходящихся
сил, система параллельных сил, плоская
система сил - условия равновесия. ОЛ-1,
гл. 8, п. 8.6, гл. 9, п.9.1.
Лекция 10. Статика твёрдого тела.
Введение в статику. Предмет статики,
общая характеристика инженерных задач,
решаемых методами статики. Основные
понятия и определения статики: сила,
система
сил,
эквивалентные
и
уравновешенные
системы
сил,
равнодействующая. Аксиомы статики.
Связи и реакции связей. Основные виды
связей и их реакции (гладкая опора, нить,
цилиндрический и сферический шарнир,
подпятник,
невесомый
стержень
с
шарнирами на концах и др.). Примеры.
ОЛ-1, гл. 8, пп.8.1-8.2.
Лекция 14. Статика твёрдого тела.
Система тел. Силы внешние и внутренние.
Условия равновесия
системы тел.
Статически определимые и статически
неопределимые системы. Распределенные
силы. Примеры. ОЛ-1, гл. 9, п.9.2-9.4.
Лекция 11. Статика твёрдого тела.
Условия равновесия сходящейся системы
сил. Теорема о трех непараллельных силах.
Алгебраический и векторный моменты
силы относительно точки. Моменты силы
относительно оси.
Связь векторного
момента силы относительно точки с
моментом
силы
относительно
оси,
проходящей через эту точку. Аналитические
выражения момента силы относительно осей
координат. Примеры. ОЛ-1, гл. 8, пп.8.3-8.4.
Лекция 15. Статика твёрдого тела.
Трение скольжения. Законы Кулона. Угол и
конус
трения.
Равновесие
тела
на
шероховатой поверхности. Примеры. ОЛ-1,
гл. 10.
Лекция 16. Статика твёрдого тела.
Трение качения. Коэффициент трения
качения. Примеры решения
задач по
статике. ОЛ-1, гл. 10.
Лекция 12. Статика твёрдого тела.
Лекция 17. Центр параллельных сил и
центр тяжести.
Пара сил. Теорема о сумме моментов сил,
составляющих пару.
Векторный и
алгебраический
момент
пары.
Эквивалентность пар. Сложение пар.
Условие равновесия системы пар сил.
Лемма о параллельном переносе силы.
ОЛ-1, гл. 8, пп.8.5-8.6.
Приведение системы параллельных сил к
равнодействующей. Центр параллельных
сил. Формулы для радиус-вектора центра
параллельных сил. Центр тяжести тела.
ОЛ-1, гл.11, пп. 11.1-11.3.
Лекция 13. Статика твёрдого тела.
Упражнения
163
абсолютно твердому телу и к системе
твердых тел. Равновесие твердых тел на
шероховатой поверхности. ОЛ-2,3.
Семинары 12-17. Статика
Равновесие плоской (сходящейся и
произвольной)
и
пространственной
произвольной систем сил, приложенных к
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, в выполнении
текущих еженедельных заданий, получаемых студентом на семинарских занятиях на дом для
закрепления пройденного материала, в выполнении ДЗ, в подготовке к контрольным
мероприятиям по модулям.
Контрольные мероприятия и сроки их проведения
1. ДЗ № 1 - «Кинематика точки и простейшие движения твёрдого тела».
Срок выдачи - 1 неделя, срок сдачи– 5 неделя.
2. Контроль по модулю 1: срок проведения – 5-6 неделя.
3. ДЗ №2 – «Кинематика плоского движения твёрдого тела»
Срок выдачи - 5 неделя, срок сдачи– 9 неделя.
4. ДЗ № 3 - «Кинематика сложного движения точки»
Срок выдачи - 9 неделя, срок сдачи– 13 неделя.
5. Контроль по модулю 2: срок проведения – 13 неделя.
6. ДЗ № 4 – «Статика»
Срок выдачи - 12 неделя, срок сдачи– 14 неделя.
7. Контроль по модулю 3: срок проведения – 17 неделя.
Литература
Основная учебная литература (ОЛ)
1. Курс теоретической механики: учебник для вузов/В.И.Дронг, В.В.Дубинин, М.М.Ильин и др.
Под общ. ред. К.С.Колесникова. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2007. -736 с.
2. Мещерский И.В. Задачи по теоретической механике: Учебное пособие. - С-Пб.: Лань,
2010. – 448 с.
3. Колесников К.С., Блюмин Г.Д., Дронг В.И., Дубинин В.В.,Ильин М.М., Огурцов А.И., Пожалостин
А.А., Саратов Ю.С. Сборник задач по теоретической механике. - М.: Наука, 2007. – 448 с.
Дополнительная учебная литература (ДЛ)
1. Никитин Н.Н. Курс теоретической механики: Учебник для машиностроительных и
приборостроительных специальностей вузов. – 6-е изд., перераб. и доп. – М.:
Высшая школа, 2005. – 719 с.
2. Тарг С.М. Краткий курс теоретической механики. Учебник. – М.: Высшая школа,
2008. -415 с.
164
3. Чуркин В.М. Теоретическая механика в решениях задач из сборника
И.В.Мещерского: Кинематика. Учебное пособие. - М.: Книжный дом “Либроком”,
2010. – 384 с.
Методические пособия
1. Горина Т.И., Кинелёв В.Г. Кинематика точки. Кинематика простейших движений твердого
тела. Методические указания по выполнению курсовой работы // Под ред. Дубинина В.В.М.: МВТУ им. Н.Э.Баумана, 1979.
2. Горина Т.И., Назаренко Б.П., Русанов П.Г. Методические указания по выполнению курсовой
работы по разделу «Кинематика плоского движения твердо тела». - М.: МВТУ им.
Н.Э.Баумана, 1982.
3. Дубинин В.В., Карпачев А.Ю., Назаренко Б.П., Северова Л.В. Кинематика плоского
движения твердо тела. Методические указания по решению задач и выполнению
курсового задания. - М.: МГТУ им. Н.Э.Баумана, 2004.
4. Занозин П.В., Пилюгина Н.Н., Тушева Г.М. Кинематика сложного движения точки. - М.:
МВТУ им. Н.Э.Баумана, 1980.
5. Борохова Н.В., Бурмистров Б.А., Гридина Г.А., Кинелёв В.Г., Курдин В.С., Орфаницкая Л.П.
Плоская статика. Пространственная статика. Методические указания к курсовой работе по
теоретической механике. - М.: МВТУ им. Н.Э.Баумана, 1986.
Рекомендуемые Интернет-сайты
10. http://hoster.bmstu.ru/~fn3/
Теоретическая механика для студентов ф-та ФН
(2 курс 4 семестр 2012/2013 уч.г.)
Дисциплина содержит 3 учебных модуля и экзамен
Модуль 1
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
1-3
6
Упражнения
1-2
4
Домашние задания текущие
1-3
3
5
2
Контроль по модулю № 1
Модуль 2
165
Виды аудиторных занятий и Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
4-10
14
Упражнения
3-9
14
Домашние задания текущие
4-10
7
10
2
Контроль по модулю № 2
Модуль 3
Виды аудиторных занятий и
Сроки проведения или Трудоёмкость, Примечание
Самостоятельной работы
выполнения, недели
часы
Лекции
11-17
14
Упражнения
10-17
16
Домашние задания текущие
11-17
7
Контроль по модулю № 3, №4
13, 16
4
Модуль 4.
Экзамен
166
МОДУЛЬ 1: ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Лекции
Лекция 1. Предмет динамики. Основные
понятия
и
определения:
масса,
материальная точка, сила. Постоянные и
переменные силы. Зависимость силы от
времени, положения точки и ее скорости.
Аксиомы
динамики
Ньютона.
Инерциальная
система
отсчета.
Дифференциальные уравнения движения
материальной точки в векторной форме
и в проекциях на декартовы и
естественные оси координат. Две
основные
задачи
динамики
для
материальной точки. Решение первой
задачи динамики.
Вторая задача
динамики.
Интегрирование
дифференциальных уравнений движения
материальной
точки.
Постоянные
интегрирования, их определение по
начальным
условиям.
Случай
несвободного движения точки. Понятие о
динамических реакциях.
Лекция 2. Относительное движение
материальной
точки.
Динамика
относительного движения. Переносная и
кориолисова силы инерции. Принцип
относительности классической механики.
Случай относительного покоя. Движение
материальной точки вблизи поверхности
Земли.
ОЛ-1, ГЛ. 13, § 13.5, 13.6.
Лекция 3. Движение точки под
действием центральной силы. Секторная
скорость, теорема площадей. Первая и
вторая формулы Бине. Вывод закона
всемирного тяготения из законов
Кеплера. Вывод законов Кеплера из
закона всемирного тяготения. Задача
двух тел.
ОЛ-1, ГЛ. 22, § 22.1-22.5.
ОЛ-1, ГЛ. 13, § 13.1-13.4.
Практические занятия
Занятие 1. Динамика материальной
точки в инерциальной системе отсчета.
ОЛ4-27.7, 27.22, 27.65, ОЛ3-8.11(8.10)
(ауд.); ОЛ3-8.1, 8.9, МП-2 (дома).
Занятие 2. Динамика материальной
точки в неинерциальной системе отсчета
ОЛ4-27.53, 33.9, ОЛ3-8.39(8.38) (ауд.);
ОЛ3-8.40(8.39), 8.44(8.43), МП 1,2, ДЗ 1
(дома).
МОДУЛЬ 2: ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
Лекции
167
Лекция 4. Механическая система. Масса
системы. Центр масс системы и его
координаты.
Классификация
сил,
действующих на механическую систему:
силы внешние и внутренние. Равенство
нулю главного вектора и главного
момента внутренних сил.
Кинетический момент твердого тела при
сферическом движении. Теорема об
изменении
кинетического
момента
системы.
Закон
сохранения
кинетического
момента.
Дифференциальное уравнение вращения
твердого тела вокруг неподвижной оси.
Пример.
Моменты инерции системы и твердого
тела относительно оси и полюса. Радиус
инерции. Формула для вычисления
момента инерции относительно оси
любого направления. Центробежные
моменты инерции. Эллипсоид инерции.
Главные оси инерции. Свойства главных
и главных центральных осей инерции.
Тензор инерции.
ОЛ-1, ГЛ. 15, § 15.5, ОЛ-1, ГЛ. 14 § 14.2,
14.3.
Лекция 7. Кёнигова система отсчета.
Кинетический
момент
системы
в
сложном
движении.
Теорема
об
изменении
кинетического
момента
системы
материальных
точек
в
относительном движении по отношению
к центру масс. Дифференциальные
уравнения плоского движения твердого
тела. Пример ОЛ3-10.2. Динамические
уравнений
Эйлера.
Интегрирование
задачи о движении тяжелого твердого
тела с одной неподвижной точкой,
случаи Эйлера, Лагранжа, Ковалевской.
Студенты
прорабатывают
самостоятельно тему: вычисление
моментов инерции однородных тел
простейшей формы.
ОЛ-1,ГЛ.14,§ 14.1-14.7.
Лекции 5, 6. Дифференциальные
уравнения
движения
механической
системы. Теорема о движении центра
масс
системы.
Закон
сохранения
движения центра масс. Количество
движения
материальной
точки
и
механической системы. Элементарный
импульс силы и импульс силы за
конечный
промежуток
времени,
проекции на координатные оси. Теорема
об изменении количества движения
материальной
точки
в
дифференциальной и конечной формах.
Законы сохранения количества движения
системы. Момент количества движения
точки относительно центра и оси.
Главный момент количеств движения
(кинетический момент) механической
системы относительно центра и оси.
Кинетический момент твердого тела
относительно
оси
вращения.
ОЛ-1, ГЛ. 15, § § 15.1-15.3, § 15.5, ГЛ. 14, §
14.2.
ОЛ-1, ГЛ. 15, § 15.5, ГЛ. 16, § 16.1. Л1,ГЛ.16,§ 16.2.
Лекция 8. Элементарная и полная работа
силы.
Мощность.
Работа
равнодействующей
силы.
Работа
внутренних сил системы, работа сил,
приложенных к твердому телу, при его
различных движениях. Кинетическая
энергия точки и системы точек.
Вычисление кинетической энергии при
сложном движении (теорема Кенига).
Кинетическая энергия твердого тела в
различных случаях его движений.
Теорема об изменении кинетической
энергии
для
точки
и
системы
168
материальных точек. Примеры: ОЛ438.31, ОЛ3-9.78.
ОЛ-1, ГЛ. 15, § 15.7.
Лекция 10. Принцип Даламбера для
точки и системы материальных точек.
Сила инерции материальной точки.
Главный вектор и главный момент сил
инерции в общем и частных случаях
движения твердого тела. Определение с
помощью
принципа
Даламбера
динамических реакций при несвободном
движении точки и механической системы
- метод кинетостатики. Примеры.
ОЛ-1, ГЛ. 15, § 15.6, 15.8.
Лекция 9. Потенциальное силовое поле.
Элементарная и полная работа силы в
потенциальном силовом поле. Силовая
функция и потенциальная энергия поля.
Условия
существования
силовой
функции. Поверхности уровня и их
свойства. Примеры вычисления силовых
функций: однородного поля силы
тяжести, линейной силы упругости, поля
притяжения по закону Ньютона. Закон
сохранения
полной
механической
энергии системы.
ОЛ-1, ГЛ. 17, § § 17.1-17.3.
Практические занятия
Занятие 3. Теоремы о движении центра
масс и изменении количества движения.
ОЛ4-35.20, 35.10,35.11, ОЛ3-19.4 (ауд.);
ОЛ3-9.9, 9.10(9.11), 9.12(9.11), МП-3-5
(дома).
Занятие 7. Теорема об изменении
кинетической энергии. ОЛ4-38.20, 38.28,
38.31, ОЛ3-9.59 (9.57) (ауд.); ОЛ3-9.46
(9.44), 9.47 (9.45), МП-3-5(дома).
Занятие
8.
ОЛ3-9.92.
Примеры
выполнения ДЗ 2 (ауд.); ДЗ 2, МП-3-5
(дома).
Занятие 4. Теорема об изменении
кинетического
момента.
ОЛ4-37.50,
37.52,
ОЛ3-9.17(9.18)
(ауд.);
ОЛ39.19(9.20), 9.20(9.21), МП-3-5 (дома).
Занятие 9. Принцип Даламбера. ОЛ441.17, 41.21 (ауд.); ОЛ4-41.19, 41.22
(дома).
Занятие 5. ОЛ4-37.43, ОЛ3-9.34(9.35),
9.37 (ауд.); ОЛ3-9.29 (9.30), 9.26 (9.27)
(дома).
Занятие 6. Плоское движение твердого
тела ОЛ4-39.7, ОЛ3-10.7, 10.8 (ауд.); ОЛ310.4, 10.6 (дома).
169
МОДУЛЬ 3: АНАЛИТИЧЕСКАЯ МЕХАНИКА. МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКОЙ
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Лекции
Лекция 11. Связи и их классификация.
Возможные перемещения точки и
механической системы. Обобщенные
координаты. Вариации обобщенных
координат. Число степеней свободы
голономной системы. Элементарная
работа
силы
на
возможном
перемещении.
Идеальные
связи.
Принцип возможных перемещений.
Пример. Обобщенные силы. Различные
способы вычисления обобщенных сил.
Обобщенные
силы
в
случае
потенциального силового поля. Условия
равновесия в обобщенных силах.
Равновесие системы в потенциальном
поле.
Лекции 14-15. Затухающие колебания
системы
при
наличии
вязкого
сопротивления.
Характеристики
затухания: декремент, логарифмический
декремент. Апериодические затухающие
движения. Вынужденные колебания.
Интегрирование
дифференциального
уравнения.
Установившиеся
вынужденные колебания. Основные
свойства установившихся вынужденных
колебаний. Амплитудно-частотная и
фазочастотная характеристики. Резонанс
при наличии и отсутствии вязкого
сопротивления.
ОЛ-1,ГЛ.19,§ 19.3
ОЛ-1,ГЛ.16,§ 16.2.
ОЛ-1, ГЛ. 18, § § 18.1-18.4.
Лекция 16-17. Элементы приближенной
теории гироскопа. Основные понятия и
допущения.
Кинетический
момент
быстровращающегося
гироскопа.
Теорема Резаля. Особенности движения
оси
гироскопа.
Закон
прецессии.
Гироскопический момент. Определение
гироскопических
реакций,
правило
Жуковского.
Примеры
применения
гироскопов в технике.
Лекция 12. Общее уравнение динамики в
обобщенных силах. Уравнения Лагранжа
2 рода. Вывод и методика применения.
Примеры.
ОЛ-1, ГЛ. 18, § 18.5.
Лекция
13.
Дифференциальные
уравнения малых колебаний системы с
одной степенью свободы в общем случае
(при
наличии
линейной
восстанавливающей силы, вязкого трения
и возмущающей силы). Понятие о
диссипативных
силах.
Свободные
колебания консервативной системы с
одной степенью свободы. Фаза, период,
частота и амплитуда колебаний.
ОЛ-1,ГЛ.16,§ 16.2.
ОЛ-1, ГЛ.19, § 19.1-19.2
170
Практические занятия
Занятие 10. Принцип возможных
перемещений.
ОЛ3-11.10(11.12),
11.5(11.6), 11.3(11.4), 11.9(11.11) (ауд.);
ОЛ3-11.7 (11.8), ОЛ4-46.22 (дома).
Занятие 15. ОЛ3-14.43, 14,44 (ауд.); ОЛ454.20, ОЛ3-14.42, 14.46, МП 8-10 (дома).
Занятие 16. ОЛ3-14.45, 14.53 (ауд.); ОЛ314.50, 14.54, МП -8-10, ДЗ 4 (дома).
Занятие 11. Общее уравнение механики.
ОЛ4-47.6, 47.9, 47.12, 47.17 (ауд.); ОЛ447.13,47.16 (дома).
Занятие 17. ОЛ3-15.1, ОЛ4-40.3, 40.7
(ауд.); ОЛ3-15.4, 15.2 (дома).
Занятие 12. Уравнения Лагранжа 2 рода.
ОЛ3-12.9, 12.26,12.23 (ауд.); ОЛ3-12.10,
12.21, МП-6,7 (дома).
Занятие 13. ОЛ3-12.28, 12.40 (ауд.); ДЗ 3,
МП-6,7 (дома).
Занятие 14. ОЛ3-14.4, ОЛ4-54.4, 54.18
(ауд.); ОЛ4-54.3, 54.20, ОЛ3-14,20 (дома).
Самостоятельная подготовка
В самостоятельную работу студентов входят изучение теории по каждой теме, выполнение
текущего задания, выполнение и защита ДЗ, контроль по модулю.
Студент допускается к экзамену (итоговый 4 модуль) при условии выполнения и защиты всех
ДЗ.
Контрольные мероприятия и сроки их проведения
МОДУЛЬ 1
Сроки выполнения модуля: 1-я неделя - 5-я неделя.
Защита домашнего задания № 1 на 4 неделе.
Письменная работа №-1 (контроль по модулю) проводится по материалам семинаров 1 – 2 и
лекций 1 – 3 на 5-й неделе.
МОДУЛЬ 2
Сроки выполнения модуля: 5-я неделя - 11-я неделя.
Защита домашнего задания № 2 на 10 неделе.
171
Письменная работа №2 (контроль по модулю) проводится по материалам семинаров 3 – 9 и
лекций 4 – 10 на 10-й неделе.
МОДУЛЬ 3
Сроки выполнения модуля: 11-я неделя - 17-я неделя.
Защита домашнего задания № 3 на 13 неделе.
Письменная работа №2 проводится по материалам семинаров 10 – 13 и лекций 11 – 12 на 13-й
неделе.
Защита домашнего задания № 4 на 16 неделе.
Письменная работа проводится по материалам семинаров 14 – 16 и лекций 13 – 16 на 16-й
неделе.
МОДУЛЬ 4 ИТОГОВЫЙ (экзамен)
Срок выставления общей оценки за 4 модуль – экзаменационная сессия.
Основная и дополнительная литература
Основная литература (ОЛ)
5. Курс теоретической механики. Под ред. К.С. Колесникова. – М.: Изд. МГТУ, 2000, 2002,
2005, 2011.
6. Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. – М.:
Высшая школа, 1974, 1983, 1990.
7. Сборник задач по теоретической механике. Под ред К.С. Колесникова. – М.: Наука, 1989,
2007, 2008.
8. Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука, 1981, 1986.
Дополнительная литература (ДЛ)
4. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 2. – М.: Наука, 1998.
5. Маркеев А.П. Теоретическая механика. – М.: Наука, 1990.
6. Голубев Ю.Ф. Основы теоретической механики. – М.: Изд-во МГУ, 1992г. и след.
7. Журавлев В.Ф. Основы теоретической механики. – М.: Наука. Физматлит, 1997 и след.
Методические пособия, изданные в МГТУ (МП)
11. Саратов Ю.С., Баранов В.Н., Нарская Н.Л. Динамика материальной точки. Методические
указания к курсовой работе по теоретической механике. – Изд. МГТУ, 1999.
12. Баранов В.Н., Феоктистова О.П., Саратов Ю.С., Щеглова Н.Н. Динамика материальной точки.
Методические указания к решению задач и выполнению курсовой работы. – М.: Изд. МГТУ, 2002.
172
13. Дубинин В.В., Никитин Н.Н., Феоктистова О.П. Общие теоремы динамики. Метод. указания
по выполнению курсовой работы по разделу курса теоретической механики «Динамика». – Изд.
МВТУ, 1984.
14. В.В. Дубинин, А.Ю. Карпачев, А.В. Ремизов. Общие теоремы динамики. Методические
указания к выполнению курсового задания. – М.: МГТУ, 2006.
15. Дубинин В.В., Дубровина Г.И., Карпачев А.Ю. Общие теоремы динамики. Учебное пособие.
М. МГТУ, 2010.
16. Дронг В.И., Максимов Г.М., Огурцов А.И. Уравнения Лагранжа 2 рода. Метод. указания к
курсовой работе по динамике. – Изд. МВТУ, 1985.
17. Уравнения Лагранжа 2 рода. Метод. указания к выполнению курсовой работы и решению
задач. Под ред.Дронга В.И. – Изд. МГТУ, 1988.
18. Саратов Ю.С., Русанов П.Г., Тушева Г.М. Метод. указания к курсовой работе по динамике.
Раздел «Колебания линейной системы с одной степенью свободы». – Изд. МВТУ, 1985.
19. Ильин М.М., Пожалостин А.А., Тушева Г.М. Колебания линейной системы с одной
степенью свободы. Метод.указания к выполнению курсовой работы по разделу курса
теоретической механики «Динамика». – Изд. МГТУ, 2002.
20. Н.В. Борохова, М.М. Ильин, Г.М. Тушева. Колебания линейной системы с одной степенью
свободы. Методические указания к выполнению домашних заданий по разделу курса
«Теоретическая механика». – Изд. МГТУ, 2005.
Рекомендуемые Интернет-сайты
21. http://hoster.bmstu.ru/~fn3/
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
для ПС (4 семестр)
План дисциплины во втором семестре состоит из 3-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-4
8
Семинары
1-4
8
Домашнее задание № 1
Письменная работа № 1
Письменная работа № 2
1-6
3
5
8
2
2
Контроль по модулю №1
7
173
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
5-6
4
5
2
7-10
8
7
2
9
Семинары
Лабораторные работы № 1-4
Письменная работа № 3
Защита лаб. работ № 1-4
7-10
Контроль по модулю №2
10
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
7-17
22
Семинары
6-9
7
Лабораторные работы № 5-8
11-14
9
Домашнее задание № 2
Письменная работа № 4
Домашнее задание № 3
Письменная работа № 5
Защита лаб. работ № 5-6
9-12
12
12-15
15
12-15
8
2
8
2
8
Контроль по модулю №2
16
Примечание
Модуль 1: Аналитическая механика. Уравнения Лагранжа 2-го рода
Лекции
Лекция 1. Связи и их классификация.
Возможные
перемещения
точки
и
механической
системы.
Обобщенные
координаты.
Вариации
обобщенных
координат.
Число
степеней
свободы
голономной системы. Элементарная работы
силы на возможном перемещении. Идеальные
связи. Обобщенные силы.
ОЛ-1, Гл. 18, § 18.1−18.3.
Лекции
2.
Различные
способы
вычисления обобщенных сил. Обобщенные
силы в случае потенциального силового поля.
Примеры.
Принцип
возможных
перемещений. Пример. Условия равновесия в
обобщенных силах. Равновесие системы в
потенциальном силовом поле.
ОЛ-1, Гл. 18, § 18.3−18.4.
Лекции
3-4.
Общее
уравнение
динамики в обобщенных силах. Уравнение
Лагранжа 2 рода. Вывод и методика
применения. Примеры: Л3-12.30, 12.14.
ОЛ-1, Гл. 18, § 18.4−18.5.
174
Семинары
Занятие
1.
Принцип
возможных
перемещений. Определение неизвестных сил
при равновесии механических систем.
Ауд.:
ОЛ4–11.10(11.12),
11.3(11.4),
11.9(11.11), 11.5(11.6)
Дома: ОЛ4-11.7(11.8), Л5–46.22, МП 3.
Занятие 2. Общее уравнение динамики.
Определение сил и ускорений при движении
механических систем.
Ауд.: ОЛ5–47.6, 47.9, 47. 12, 47.17
Дома: ОЛ5–47.13,47.16, МП 3
Занятие 3. Уравнение Лагранжа 2 рода.
Составление дифференциальных уравнений
движения механических систем.
Ауд.: ОЛ4–12.9, 12.26,12.23
Дома: ОЛ4–12.10,12.21, МП 4–7
Занятие 4. Уравнение Лагранжа 2 рода.
Составление дифференциальных уравнений
движения механических систем.
Ауд.: ОЛ4–12.28,12.40.
Дома: ДЗ-1, МП 1–3,5.
Модуль 2: Теория удара
Лекции
Лекция 5. Основные положения теории
удара. Общие теоремы динамики для удара.
Изменение угловой скорости при ударе по
вращающемуся телу. Удар точки о
неподвижную поверхность. Коэффициент
восстановления. Фазы удара. Ударные
импульсы для двух фаз удара.
ОЛ-1, Гл. 20, § 20.1-20.5, Л-2, Гл. 9(13),
§ 1-4.
Лекция 6. Теорема Карно. Удар двух
тел при поступательном движении. Центр
удара. Условия отсутствия ударных реакций
в опорах вращающегося тела.
ОЛ-1, Гл. 20, § 20.5-20.7,20.10, Л-2, Гл.
9(13), § 5-7.
Семинары
Занятие 5. Основные положения теории
удара. Общие теоремы динамики для удара.
Определение кинематических характеристик
движения систем при ударе.
Ауд.: ОЛ5–44.2, 44.26, 44.28.
Дома: ОЛ5–44.27.
Лабораторные работы
Лабораторная работа № 1 «Качение
тел одинаковой массы с разными моментами
инерции» - проводится на 7-ой неделе. Объем
в часах − 2.
Методическое пособие МП-7.
Лабораторная работа № 2
«Исследование гироскопических давлений» проводится на 8-ой неделе. Объем в часах −
2.
Методическое пособие МП-8.
Лабораторная работа № 3
«Двухстепенной гироскоп»- проводится на 9ой неделе. Объем в часах − 2.
Методическое пособие МП-9.
Лабораторная работа № 4
«Динамические реакции подшипников»проводится на 10-ой неделе. Объем в часах −
3.
Методическое пособие МП-10.
Модуль 3: Теория колебаний. Колебания линейной системы
175
Теоретическая механика
176
Лекции
Лекции 7-8. Положение равновесия
механической
системы.
Нахождение
положений
равновесия
из
условий
равновесия, выраженных в обобщенных
силах. Примеры. Устойчивость положения
равновесия. Теорема Теорема Лагранжа –
Дирихле.
Силы
сопротивления,
пропорциональные первой степени скоростей
точек,
линейно-вязкое
сопротивление.
Диссипативная функция Релея. Связь между
полной
механической
энергией
и
диссипативной функцией. Влияние сил
вязкого сопротивления на устойчивость
положения равновесия системы.
ОЛ-1, Гл. 19.1, § 16.2, ОЛ-2, , Гл. 7, § 1.
Лекция
9.
Дифференциальное
уравнение малых колебаний системы с одной
степенью свободы. Свободные колебания
консервативной системы с одной степенью
свободы.
Элементы
гармонических
колебаний. Математический и физический
маятники. Примеры Л5-14.1,14.4.
ОЛ-1, Гл. 19, § 19.2, ОЛ-2, Гл. 7(11), § 23.
Лекция 10. Свободные движения
системы с линейно-вязким сопротивлением.
Затухающее
колебательное
движение.
Декремент колебаний, логарифмический
декремент,
добротность
системы.
Затухающие неколебательные движения.
Пример Л6-32.67.
ОЛ-1, Гл. 19, § 19.3, ОЛ-2, Гл. 7(11), § 23.
Лекция 11. Вынужденные колебания.
Способы
возбуждения.
Определение
обобщенной силы при различных способах
возбуждения.
Интегрирование
дифференциального уравнения вынужденных
колебаний
системы.
Собственные
и
вынужденные колебания. Пояснения к
домашнему заданию.
ОЛ-1, ГЛ. 19, § 19.4, ОЛ-2, Гл. 7(11), §
2-3.
Лекция 12. Резонанс при линейновязком сопротивлении и при отсутствии
сопротивления. Амплитудно-частотная и
фазо-частотная характеристики системы.
Основные
свойства
установившихся
вынужденных колебаний. Пояснения к
домашнему заданию.
ОЛ-1, ГЛ. 19, § 19.4, ОЛ-2, Гл. 7(11), §
2-3.
Лекция 13. Вынужденные колебания в
системе с одной степенью свободы в случае
периодического,
но
негармонического
вынуждающего воздействия и в случае
произвольного вынуждающего воздействия.
Основы теории регистрирующих приборов.
Основы виброзащиты.
ОЛ-1, Гл. 19, § 19.4, 19.5, 19.6, ОЛ-2, Гл.
7(11), § 2-3.
Лекция
14.
Кинетическая
и
потенциальная энергия системы с двумя
степенями свободы. Устойчивость положения
равновесия системы с двумя степенями
свободы. Критерий Сильверста. Вывод
дифференциальных
уравнений
малых
колебаний консервативной системы с двумя
степенями
свободы.
Интегрирование
дифференциальных уравнений свободных
колебаний.
Парциальные
частоты
и
парциальные системы. Уравнение частот,
исследование его корней.
ОЛ-1, Гл. 19, § 19.8, ОЛ-2, Гл. 7(11), § 4.
Лекция
15-16.
Коэффициенты
распределения амплитуд. Формы главных
колебаний.
Нормальные
координаты.
Вынужденные колебания в консервативной
системе с двумя степенями свободы в случае
гармонического возбуждающего воздействия.
Эффект динамического гашения колебаний.
ОЛ-1, ГЛ. 19, § 19.9, ОЛ-2, Гл. 7(11), §
4.
Лекция 17. Элементы космонавтики.
Первые интегралы уравнений движения
точки под действием центральной силы.
Исследование
траекторий
движения.
Формулы для космических скоростей.
ОЛ-1, Гл. 22, § 22.1−22.4, ОЛ-2, , Гл. 10,
§ 1−4.
Семинары
176
Занятие
6.
Свободные
колебания
консервативной системы с одной степенью
свободы. Составление дифференциальных
уравнений
колебаний
консервативной
системы и их решение.
Ауд.: ОЛ5–32.1, 32.2, 32.3.
Дома: ОЛ4–14.3, Л5–32.16.
Занятие
7.
Свободные
движения
механической системы с одной степенью
свободы с учетом вязкого трения. Получение
уравнений движения
Ауд.: ОЛ4–14.1, 14.6, 14.22, 14.29.
Дома: ОЛ5–32.74.
Занятие 8. Вынужденные колебания.
Определение
обобщенной
силы
при
различных
способах
возбуждения.
Интегрирование
дифференциального
уравнения вынужденных колебаний системы.
Собственные и вынужденные колебания.
Пояснения к домашнему заданию.
Ауд.: ОЛ4–14.42, 14.44, 14.45.
Дома: ОЛ5–32.81.
Занятие 9. Вынужденные колебания.
Интегрирование
дифференциального
уравнения вынужденных колебаний системы.
Амплитудно-частотная и фазо-частотная
характеристики системы. Пояснения к
домашнему заданию.
Ауд.: ОЛ4–14.41, 14.52. Задачи типа ДЗ №
2,3.
Дома: –14.43, Л4–14.45, МП 8–9.
Лабораторные работы
Лабораторная работа № 5 «Свободные
колебания
физического
маятника»
−
проводится на 11-ой неделе. Объем в часах −
2. Методическое пособие МП-11.
Лабораторная работа № 6
«Вынужденные колебания системы с одной
степенью свободы» − проводится на 12-ой
неделе. Объем в часах − 2.
Методическое пособие МП 12.
Лабораторная
работа
№
7
«Вынужденные колебания механической
системы с инерционным возмущением» −
проводится на 13-ой неделе. Объем в часах −
2.
Методическое пособие МП 13.
Лабораторная работа № 8 «Двойной
маятник» − проводится на 14-ой неделе.
Объем в часах − 2.
Методическое пособие МП 14.
Модуль 4: Экзамен
Экзамен проводится по материалам модулей 1-4.
Самостоятельная подготовка



Проработка курса лекций, учебников, методических пособий по темам лекций 1 – 17,
семинаров 1 – 9
Выполнение домашних заданий №№ 1–3.
Подготовка к письменным работам №№ 1–5 и их написание.
Контрольные мероприятия и сроки их проведения
МОДУЛЬ 1:
Домашнее задание № 1 «Уравнения Лагранжа 2-го рода».
Методические пособия МП – 1-4.
Сроки выполнения: выдача – 1-я неделя, прием – 6 неделя.
Письменная работа 1. Тема работы: применение принципа возможных перемещений и общего
уравнения динамики для определения неизвестных сил и ускорений в механической системе.
Проводится по материалам лекций 1–3 и семинаров 1–2.
Методические пособия МП 1–4.
Срок проведения – 3 неделя.
177
Письменная работа 2. Тема работы: составление дифференциальных уравнений движения
системы с помощью уравнений Лагранжа 2-го рода. Проводится по материалам лекций 3–4 и
семинаров 3–4.
Методические пособия МП 1–4.
Срок проведения – 5 неделя.
Срок выставления общей оценки за модуль 1 – 7 неделя.
МОДУЛЬ 2:
Письменная работа № 3. Тема работы: определение кинематических характеристик движения
систем при ударе с помощью общих теорем динамики. Проводится по материалам лекций 5–6 и
семинара 5.
Срок проведения – 7 неделя.
Лабораторные работы. Оформление отчетов по установленному образцу и защита лабораторных работ:
Лабораторная работа № 1 «Качение тел одинаковой массы с разными моментами инерции» проводится на 7-ой неделе.
Методическое пособие МП-7.
Лабораторная работа № 2 «Исследование гироскопических давлений» - проводится на 8-ой неделе.
Методическое пособие МП-8.
Лабораторная работа № 3 «Двухстепенной гироскоп»- проводится на 9-ой неделе.
Методическое пособие МП-9.
Лабораторная работа № 4 «Динамические реакции подшипников»- проводится на 10-ой неделе.
Методическое пособие МП-10.
Срок выставления общей оценки за модуль 2 – 10 неделя.
МОДУЛЬ 3.
Домашнее задание № 2. «Малые колебания – определение параметров процесса».
Сроки выполнения: выдача – 9-я неделя, прием – 12-я неделя.
Методические пособия МП 5,6.
Письменная работа 4 по теме «Колебания линейной системы с одной степенью свободы».
Проводится по материалам лекций 7–10 и практических занятий 6,7 на 12-ой неделе.
Методические пособия МП 5,6.
Домашнее задание № 3. «Малые колебания – исследование характеристик системы»
Сроки выполнения: выдача – 12-я неделя, прием – 15-я неделя.
Методические пособия МП 5,6.
Письменная работа № 5 по теме «Вынужденные колебания линейной системы с одной степенью
свободы». Проводится по материалам лекций 11–13 и практических занятий 7–8 на 16-ой неделе.
Лабораторные работы. Оформление отчетов по установленному образцу и защита лабораторных работ:
Лабораторная работа № 5 «Свободные колебания физического маятника». Проводится на
11-ой неделе.
Методическое пособие МП-11.
Лабораторная работа № 6 «Вынужденные колебания системы с одной степенью свободы».
Проводится на 12-ой неделе.
Методическое пособие МП 12,13.
Лабораторная работа № 7 «Вынужденные колебания механической системы с
инерционным возмущением». Проводится на 13-ой неделе.
Методическое пособие МП 13.
Лабораторная работа № 8 «Двойной маятник» − проводится на 14-ой неделе.
Методическое пособие МП 14
Срок выставления общей оценки за модуль 3 – 16 неделя.
МОДУЛЬ 4. ЭКЗАМЕН
178
▼ Основная и дополнительная литература
Основная литература (ОЛ)
1.
Курс теоретической механики. Под ред. К.С. Колесникова. – М.: Изд. МГТУ, 2000, 2002,
2005, 2011.
2.
Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. – М.:
Высшая школа, 1974, 1983, 1990, (2003).
3.
Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 2. – М.: Наука,
1971, 1985.
4.
Сборник задач по теоретической механике. Под ред К.С. Колесникова. – М.: Наука, 1989,
2007.
5. Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука, 1981, 1986.
6.
Ильин М.М., Колесников К.С., Саратов Ю.С. Теория колебаний. Под ред. К.С.
Колесникова. – М.: Изд. МГТУ, 2001.
7. Журавлев В.Ф. Основы теоретической механики. – М.: Наука, Физматлит. 1997.
Методические пособия, изданные в МГТУ (МП)
1. Витушкин В.В., Максимов Г.М., Избранные принципы аналитической механики. Уравнения
Лагранжа 2-го рода: Метод. указания к выполнению курсовой работы по теоретической
механике. Под ред. Дубинина В.В.М. – Изд-во МГТУ им. Н.Э. Баумана, 2012.
2. Максимов Г.М., Русанов П.Г. Избранные принципы аналитической механики. Уравнения
Лагранжа 2-го рода: Учеб.пособие. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002.
3. Витушкин В.В., Максимов Г.М., Русанов П.Г. Избранные принципы аналитической механики.
Уравнения Лагранжа 2-го рода: Метод. указания к выполнению курсовой работы по
теоретической механике. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
4. Лямин В.И., Темнов А.Н. Аналитическая механика. М.: Изд-во МГТУ им. Н.Э. Баумана, 1990.
5. Ильин М.М., Пожалостин А.А., Тушева Г.М. Колебания линейной системы с одной степенью
свободы. Методические указания к выполнению курсовой работы по разделу курса
теоретической механики «Динамика».-Изд. МГТУ, 2002.
6. Борохова Н.В., Ильин М.М., Тушева Г.М. Колебания линейной системы с одной степенью
свободы. Методические указания к выполнению домашних заданий по разделу курса
«Теоретическая механика». Под ред. Ильина М.М. – Изд. МГТУ, 2005.
7. Дубинин В.В., Солохин Е.Н., Иванникоа В.А., Назаренко Б.П. Лабораторный аппаратнопрограммный комплекс ТМЛ-20МР. Метод. указания - М.: Изд-во МГТУ им. Н.Э. Баумана,
1998. - 20 с. : ил.
8. Дубинин В.В., Жигулёвцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный
комплекс для изучения гироскопических давлений ТМл-04М : Метод. Указания - М.: Изд-во
МГТУ им. Н.Э. Баумана, 2007. - 16 с.: ил.
9. Дубинин В.В., Жигулёвцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный
комплекс «Двухстепенной гироскоп» ТМл-09М : Метод. Указания - М.: Изд-во МГТУ им. Н.Э.
Баумана, 2011. - 21 с.: ил.
10. Дубинин В.В., Жигулёвцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный
комплекс «Динамические реакции подшипников» ТМл-09М: Метод. Указания - М.: Изд-во
МГТУ им. Н.Э. Баумана, 2011. - 21 с.: ил.
11. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В., Косачев С.Л. Автоматизированный
лабораторный комплекс «Свободные колебания физического маятника» ТМл-01М.: Метод.
Указания - М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. - 16 с.: ил.
12. Дубинин В.В., Жигулёвцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный
комплекс «Вынужденные колебания системы с одной степенью свободы» ТМл-08М: Метод.
указания - М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. - 18 с.: ил.
179
13. Дубинин В.В., Жигулёвцев Ю.Н., Витушкин В.В. Автоматизированный лабораторный
комплекс «Вынужденные колебания механической системы с инерционным возмущением»
ТМЛ-07М: Метод. указания - М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – 17 с.: ил.
14. Дубинин В.В., Жигулевцев Ю.Н., Витушкин В.В., Косачев С.Л. Автоматизированный
лабораторный комплекс «Двойной маятник» ТМл-02М.: Учеб. пособие - М.: Изд-во МГТУ им.
Н.Э. Баумана, 2010. - 34 с.: ил.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Для студентов ГУИМЦ ( УЦ1,2-41)
2 курс, 4 семестр
▼ Аудиторные занятия
4.
Лекции
скоростей двух точек твердого тела. Простейшие
движения тела. Поступательное движение твердого тела.
МОДУЛЬ 1:
Теорема о траекториях, скоростях и ускорениях точек
Лекция 1. Введение. Кинематика. Введение в курс
«Теоретическая механика». Предмет механики изучение механического движения и механического
взаимодействия материальных объектов; содержание
разделов механики. Теоретическая механика как одна из
фундаментальных физико-математических наук; ее
значение и место среди других естественных
и
технических наук. Основные исторические этапы
развития механики.
твердого тела при поступательном движении. Число
степеней свободы, уравнения движения. Вращение
твердого тела вокруг неподвижной оси. Угол поворота,
уравнение движения.
ускорение
Лекция 5. Кинематика твёрдого тела. (1 час). Плоское
движение твердого тела. Движение плоской фигуры в ее
плоскости. Разложение движения на поступательное
вместе с полюсом и вращение вокруг полюса. Примеры.
ОЛ-1, гл. 3, пп. 3.1-3.4.
Лекция 6. Кинематика твёрдого тела. Теорема о
скоростях точек твердого тела при плоском движении.
Мгновенный центр скоростей. Определение скоростей
точек тела с помощью мгновенного центра скоростей.
Теорема об ускорениях точек твердого тела при плоском
движении. Мгновенный центр ускорений. Примеры. ОЛ1, гл. 3, пп. 3.3-3.8.
Естественный способ задания движения точки. Модуль
и направление скорости. Естественные оси и их орты.
Разложение ускорения по осям естественного
трехгранника. Касательное и нормальное ускорения.
Примеры. ОЛ-1, гл.1, п.1.5.
твёрдого
тела.
вокруг
МОДУЛЬ 2:
Лекция 3. Кинематика точки.
Кинематика
вращающегося
Лекция 5. Кинематика твёрдого тела. (1 час)
Векторные и скалярные формулы для скоростей и
ускорений
точек
тела,
вращающегося
вокруг
неподвижной оси. Примеры. ОЛ-1, гл.2, пп.2.1-2.3.
Лекция 2. Кинематика точки. Векторный способ
задания движения точки. Траектория точки. Скорость
точки. Ускорение точки. Способ задания движения
точки в декартовых координатах. Определение
траектории точки по уравнениям ее движения.
Проекции скорости на оси декартовых координат.
Определение модуля и направления вектора скорости по
его проекциям на оси декартовых координат. Проекции
ускорения точки на оси декартовых координат.
Определение модуля и направления вектора ускорения.
Примеры. ОЛ-1, гл.1, пп. 1.1-1.4.
4.
тела,
неподвижной оси. ОЛ-1, гл.2, пп.2.1-2.3.
Кинематика. Предмет кинематики. Пространство и
время. Системы отсчета. Кинематика точки. Способы
задания движения точки. ОЛ-1, гл.1, п.1.1
Лекция
твердого
Угловая скорость и угловое
Лекция 7. Кинематика твёрдого тела. Движение
твёрдого тела вокруг неподвижной точки (сферическое
движение). Число степеней свободы. Углы Эйлера.
Мгновенная ось вращения. Векторы угловой скорости и
углового ускорения. Скорости и ускорения точек тела.
ОЛ-1, гл. 4, пп. 4.1-4.6.
Понятие
абсолютно твердого тела. Задание движения твердого
тела, число степеней свободы. Теорема о проекциях
180
Примеры. ОЛ-1, гл. 9, п.9.2-9.4.
Лекция 8. Кинематика сложного движения точки.
Сложное движение точки. Абсолютное, относительное и
переносное движения точки. Полная и локальная
производные вектора. Формула Бура. Скорость и ускорение
точки при сложном движении. Теорема о сложении
скоростей. Теорема о сложении ускорений (теорема
Кориолиса). Правило Жуковского. ОЛ-1, гл. 6, пп. 6.1-6.4.
Лекция 15. Статика твёрдого тела. Трение скольжения.
Законы Кулона. Угол и конус трения. Равновесие тела
на шероховатой поверхности. Примеры. ОЛ-1, гл. 10.
Лекция 16. Статика твёрдого тела. Трение качения.
Коэффициент трения качения. Примеры решения задач
по статике. ОЛ-1, гл. 10.
Лекция 9. Кинематика сложного движения твердого
Лекция 17. Центр параллельных сил и центр тяжести.
Приведение
системы
параллельных
сил
к
равнодействующей. Центр параллельных сил. Формулы
для радиус-вектора центра параллельных сил. Центр
тяжести тела. ОЛ-1, гл.11, пп. 11.1-11.3.
тела. Сложение поступательных движений твердого
тела. Сложение вращательных движений твердого тела
вокруг пересекающихся и параллельных осей. Пара
вращений. ОЛ-1, гл. 7, пп. 7.1-7.4.
5.
МОДУЛЬ 3:
Семинары
МОДУЛЬ 1:
Лекция 10. Статика твёрдого тела.
Введение в статику. Предмет статики, общая
характеристика инженерных задач, решаемых методами
статики. Основные понятия и определения статики: сила,
система сил, эквивалентные и уравновешенные системы
сил, равнодействующая. Аксиомы статики. Связи и
реакции связей. Основные виды связей и их реакции
(гладкая опора, нить, цилиндрический и сферический
шарнир, подпятник, невесомый стержень с шарнирами
на концах и др.). Примеры. ОЛ-1, гл. 8, пп.8.1-8.2.
Семинары 1-3. Кинематика точки (5 час.)
Кинематика точки. Траектория. Скорость и ускорение
точки при координатном
и естественном способе
задания ее движения. ОЛ-2,3.
Семинары 3-4. Кинематика простейших движений
твердого тела (3 час.)
Поступательное движение твёрдого тела и вращение
тела вокруг неподвижной оси. ОЛ-2,3.
Лекция 11.
Статика твёрдого тела. Условия
равновесия сходящейся системы сил. Теорема о трех
непараллельных силах. Алгебраический и векторный
моменты силы относительно точки. Моменты силы
относительно оси. Связь векторного момента силы
относительно точки с моментом силы относительно оси,
проходящей через эту точку. Аналитические выражения
момента силы относительно осей координат. Примеры.
ОЛ-1, гл. 8, пп.8.3-8.4.
МОДУЛЬ 2:
Семинары 5-8.
твердого тела.
Кинематика плоского движения
Скорости и ускорения точек твердого тела, движущегося
плоскопараллельно. МЦС, МЦУ тела. ОЛ-2,3.
Семинары 9-11.
точки.
Лекция 12. Статика твёрдого тела. Пара сил. Теорема
о сумме моментов сил, составляющих пару. Векторный
и алгебраический момент пары. Эквивалентность пар.
Сложение пар. Условие равновесия системы пар сил.
Лемма о параллельном переносе силы. ОЛ-1, гл. 8,
пп.8.5-8.6.
Кинематика сложного движения
Прямая и обратная задачи на сложное движение точки.
Разложение абсолютного движения на относительное и
переносное. Абсолютные скорость и ускорение точки.
ОЛ-2,3.
Лекция 13.
Статика твёрдого тела. Теорема о
приведении произвольной системы сил к данному
центру - основная теорема статики. Главный вектор и
главный момент системы сил, формулы для их
вычисления. Условия равновесия произвольной системы
сил. Частные случаи системы сил: система сходящихся
сил, система параллельных сил, плоская система сил условия равновесия. ОЛ-1, гл. 8, п. 8.6, гл. 9, п.9.1.
МОДУЛЬ 3:
Семинары 12-17. Статика.
Равновесие плоской и пространственной системы сил,
приложенной к твердому телу и к системе твердых тел.
Равновесие на шероховатой поверхности. ОЛ-2,3.
Лекция 14. Статика твёрдого тела. Система тел. Силы
внешние и внутренние. Условия равновесия системы
тел.
Статически определимые и статически
неопределимые
системы.
Распределенные
силы.
181
▼ Самостоятельная подготовка
МОДУЛЬ 1:
Проработка курса лекций, учебников проводится по темам лекций 1 – 5 и семинаров 1 – 4.
Выполнение домашнего задания №1 – Кинематика точки и простейших движений твердо тела.
Сроки выполнения: выдача — 1-я неделя; прием — 4-я неделя.
Методическое пособие МП-1.
Подготовка к защите ДЗ № 1 в форме контрольной работы по теме семинаров 1 – 4.
МОДУЛЬ 2:
Проработка курса лекций, учебников проводится по темам лекций 5 – 9 и семинаров 5 – 11.
Выполнение домашнего задания № 2 - Кинематика плоского движения твердого тела.
Сроки выполнения: выдача — 5-я неделя; прием — 9-я неделя.
Методические пособия МП-2,3,4.
Подготовка к защите ДЗ № 2 в форме контрольной работы по теме семинаров 5 – 8.
Выполнение домашнего задания № 3 - Кинематика сложного движения точки.
Сроки выполнения: выдача — 9-я неделя; прием — 13-я неделя.
Методические пособия МП-5,6.
Подготовка к защите ДЗ № 3 в форме контрольной работы по теме семинаров 9 – 11.
МОДУЛЬ 3:
Проработка курса лекций, учебников проводится по темам лекций 10 – 17 и семинаров 12 – 17.
Выполнение домашнего задания № 4 - Статика.
Сроки выполнения: выдача — 13-я неделя; прием — 16-я неделя.
Методические пособия МП-7.
Подготовка к защите ДЗ № 4 в форме контрольной работы по теме семинаров 12 – 17.
МОДУЛЬ 4:
Экзамен.
▼ Основная и дополнительная литература
1.
2.
3.
4.
5.
6.
1.
2.
3.
4.
Основная литература (ОЛ)
Курс теоретической механики: учебник для вузов/В.И.Дронг, В.В.Дубинин, М.М.Ильин и др. Под
общ. ред. К.С.Колесникова.- М.: Изд-во МГТУ им. Н.Э.Баумана, 2007. - 736 с.
Мещерский И.В. Задачи по теоретической механике: Учебное пособие. –C.Пб.: Лань, 2010.. – 448 с.
Колесников К.С.,
Блюмин Г.Д., Дронг В.И., Дубинин В.В.,Ильин М.М., Огурцов А.И.,
Пожалостин А.А., Саратов Ю.С. Сборник задач по теоретической механике.-М.:Наука, 2007.. – 448
с.
Дополнительная литература (ДЛ)
Никитин Н.Н. Курс теоретической механики: Учебник для машиностроительных и
приборостроительных специальностей вузов. – 6-е изд., перераб. и доп. – М.: Высшая школа, 2005.–
719 с.
Тарг С.М. Краткий курс теоретической механики. Учебник. – М.: Высшая школа, 2009. - 415 с.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. – М.:
Наука, тт. 1-3, 1996 г.
Методические пособия, изданные в МГТУ (МП)
Горина Т.И., Кинелёв В.Г. Кинематика точки. Кинематика простейших движений твердого тела.
Методические указания по выполнению курсовой работы//Под ред. Дубинина В.В.- М.: МВТУ им.
Н.Э.Баумана, 1979.
Горина Т.И., Назаренко Б.П., Русанов П.Г. Методические указания по выполнению курсовой работы
по разделу «Кинематика плоского движения твердо тела». - М.: МВТУ им. Н.Э.Баумана, 1982.
Кинематика плоского движения твердо тела//Под ред. Назаренко Б.П. - М.: МВТУ им. Н.Э.Баумана,
1989.
Дубинин В.В., Карпачев А.Ю., Назаренко Б.П., Северова Л.В. Кинематика плоского движения
твердо тела. Методические указания по решению задач и выполнению курсового задания. - М.:
МГТУ им. Н.Э.Баумана, 2004.
182
5.
6.
7.
Занозин П.В., Пилюгина Н.Н., Тушева Г.М. Кинематика сложного движения точки. - М.: МВТУ им.
Н.Э.Баумана, 1980.
Дубинин В.В., Гатауллина Г.И., Тушева Г.М. Методические указания к выполнению курсовой
работы и решению задач по теме «Кинематика сложного движения точки». - М.: МГТУ им.
Н.Э.Баумана, 2005.
Борохова Н.В., Бурмистров Б.А., Гридина Г.А., Кинелёв В.Г., Курдин В.С., Орфаницкая Л.П.
Плоская статика. Пространственная статика. Методические указания к курсовой работе по
теоретической механике. - М.: МВТУ им. Н.Э.Баумана, 1986.
ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
для специальности РК-5 (бакалавр), 2 курс, 4 семестр
Дисциплина состоит из 2-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Лекции
10.
Упражнения
11.
Лабораторные работы
12.
Домашние задания текущие
13.
Контроль модуля
Сроки проведения или
выполнения, недели
1-8
1-8
1-8
Трудоёмкость,
часы
Примечание
16
8
8
1-8
10
8
1
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
9-17
18
9-17
9
14.
Упражнения
15.
Лабораторные работы
16.
Домашние задания текущие
9-14
10
17.
Контроль модуля
17
1
9-16
183
9
Примечание
Лекции
Модуль 1: Линейные электрические цепи. Основы анализа и расчета
электрических цепей. Переходные процессы в линейных электрических
цепях
Лекция 1. Общие сведения об электрических
цепях и их классификация. Задачи анализа и
расчета линейных электрических цепей.
Источники электропитания Топология и
эквивалентные преобразования
электрических цепей.
нагрузки. Символический метод расчета.
Понятие о круговых диаграммах.(
Электрические измерения и приборы).
Мощность в цепях синусоидального тока.
ОЛ -1 2.8 – 2.11, 2.15 – 2.20; ОЛ – 2 2.8 – 2
-9; ОЛ – 4 1.1 – 1.5; ОЛ -14.
Основные законы (закон Ома и законы
Кирхгофа) расчета электрических цепей.
Режимы работы электрических цепей. Расчет
электрических цепей с одним источником
энергии. ОЛ-1 1.1-1.5 ; ОЛ-2 1.1- 1.4; ОЛ -13
Лекция5. Резонансные явления в
электрических цепях синусоидального тока
(резонанс напряжений и резонанс токов).
Условия возникновения резонансных
режимов. Соотношение параметров и
векторные диаграммы при резонансе. Расчет
электрических цепей при несинусоидальных
периодических входных воздействиях.
Показание приборов при несинусоидальных
воздействиях. Мощность в цепях при
несинусоидальном входном напряжении
Лекция 2. Расчет электрических цепей с
несколькими источниками. Метод
контурных токов, метод узлового
напряжения, принцип суперпозиции, метод
эквивалентного генератора. Энергетические
соотношения, режимы работы, баланс
мощностей. ОЛ-1 1.6 – 1.10; ОЛ-2 1.5 –
1.9; ОЛ -13
ОЛ -1 2.12 -2.14; ОЛ -2 2.10 -1.13; ОЛ -14.
ОЛ -1 5.1- 5.6; ОЛ -2 5.1 -5.6.
Лекция 3. Особенности анализа
электрических цепей с нелинейными
элементами. Графоаналитический метод
расчета нелинейных цепей.
Лекция 6. Понятие о трехфазных
электрических цепях. Преимущества
трехфазных цепей. Схемы соединений фаз
источника и приемника. Соотношения
между фазными и линейными
напряжениями источника. Соединение
приемников звездой и треугольником.
Симметричная нагрузка. Несимметричная
нагрузка. Роль нейтрального провода.
Мощность трехфазных цепей. Измерение
мощности в трехфазных цепях. Метод двух
ваттметров. ОЛ -1 3.1 -3.4; ОЛ -2 3.1 – 3.5.
ОЛ -1 3.5; ОЛ -2 3.6 – 3.7.
Свойство односторонней проводимости р–n
перехода. Полупроводниковые диоды и
схемы выпрямления. Общие представления
и способы построения источников
вторичного электропитания. ОЛ -1 1.16- 1.17;
ОЛ -2 1 -13. ОЛ – 4 2.2; 5.1 – 5.2
Лекция 4. Основные законы и методы
расчета электрических цепей
синусоидального тока. Векторные
диаграммы при различных характерах
184
Лекция 7. Причины и необходимые условия
возникновения переходных процессов.
Энергетические соотношения при
переходных процессах. Законы коммутации.
Классический метод расчета переходных
процессов. Независимые и зависимые
начальные условия. Определения начальных
условий, корней характеристического
уравнения и постоянных интегрирования.
Постоянная времени цепи и время
переходного процесса. Переходные
процессы в цепи с последовательным
соединением конденсатора и резистора.
Подключение и отключение источника
постоянной э.д.с. Подключение индуктивной
катушки к источнику постоянной э.д.с.
Отключение индуктивной катушки от
источника постоянного напряжения и
замыкание ее на резистор.
ОЛ -1 4.1; ОЛ – 2 4.1 – 4.2.
4.2, 4.7, 4.8; ОЛ -2 4.2 -4.4.
ОЛ -1 ОЛ -1
Модуль 2: Электромагнитные устройства и электрические машины
Лекция 8. Понятие о магнитных цепях.
Свойства ферромагнитных материалов.
Основные величины, используемые при
анализе и расчете магнитных цепей.
Основные законы магнитных цепей. Задачи
расчета и анализа магнитных цепей с
постоянными магнитодвижущими силами.
Допущения, используемые при расчете.
Аналогия методов расчета магнитных и
электрических цепей.
ОЛ -1 6.1 – 6.5;
ОЛ -2 6.1 – 6.3.
Потери и к.п.д. трансформатора. Внешняя
характеристика трансформатора.
Определение параметров и
эксплуатационных характеристик
трансформатора по паспортным данным и
опытам холостого хода и короткого
замыкания. Трехфазные трансформаторы.
Особенности трансформаторов малой
мощности. ОЛ -1 8.1 – 8.4; ОЛ -3 1.1 1.4.
ОЛ -1 8.7;
Лекция 9. Магнитные цепи при переменной
магнитодвижущей силе. Катушка со сталью.
Потери в стали. Допущения, используемые
при расчете подобных магнитных цепей.
Уравнения, схема замещения и векторная
диаграмма идеализированной обмотки.
Уравнения, схема замещения и векторная
диаграмма реальной катушки.
ОЛ -1 6.10 – 6.15; ОЛ – 2
ОЛ -3 1.5 – 1.8.
Лекция 11. Устройство трехфазного
асинхронного двигателя. Вращающееся
магнитное поле. Принцип действия
асинхронного двигателя. ЭДС обмотки
статора. ЭДС, частота тока ротора,
скольжение. Ток и эквивалентная схема фазы
обмотки ротора.
ОЛ -1 10.1 – 10.7;
6.5.
ОЛ – 3 3.1 – 3.7.
Лекция 12. Электромагнитная мощность и
потери асинхронного двигателя. Момент,
развиваемый двигателем. Схема замещения
асинхронного двигателя. Механическая
характеристика асинхронного двигателя.
Расчет и построение механической
характеристики по паспортным данным.
Лекция 10. Назначение, устройство и
принцип действия трансформатора. Режим
холостого хода трансформатора.
Коэффициент трансформации. Работа
трансформатора с нагрузкой. Уравнения,
схема замещения, векторная диаграмма
трансформатора.
185
ОЛ -1 10.9 – 10.13;
смешанного возбуждения. Механические
характеристики и способы регулирования
частоты вращения двигателей постоянного
тока. Тормозные режимы работы двигателей
(режим противовключения, генераторный
режим, режим динамического торможения).
Особенности применения двигателей
постоянного тока с различными способами
возбуждения.
ОЛ -1 9.11 – 9.19; ОЛ -3
2.9 – 2.13.
ОЛ -3 3.8 – 3.10.
Лекция 13. Пуск асинхронного двигателя.
Двигатели с улучшенными пусковыми
свойствами. Регулирование частоты
вращения асинхронного двигателя.
Тормозные режимы работы. Однофазные
асинхронные двигатели.
ОЛ -1
3.14.
10.14 – 10.19;
ОЛ -3
3.11 –
Лекция 16. Классификация генераторов
постоянного тока по способу возбуждения.
Схемы включения генераторов. Основные
характеристики генераторов постоянного
тока: характеристика холостого хода,
внешняя характеристика, регулировочная
характеристика. Потери энергии и КПД
машин постоянного тока. Машины
постоянного тока малой мощности.
Лекция 14. Назначение и устройство
машин постоянного тока. Принцип действия
машин постоянного тока в генераторном и
двигательном режимах. ЭДС якоря и
электромагнитный момент. Явление реакции
якоря. Способы возбуждения машин
постоянного тока.
ОЛ -1 9.1 – 9.6;
ОЛ – 3
2.1 – 2.6.
Лекция 15. Пуск двигателя постоянного
тока. Двигатели параллельного,
независимого, последовательного и
ОЛ -1 9.6 – 9.10, 9.23;
2.8, 2.14
ОЛ -3
2.7 –
Лекция 17.. Резервная.
2. Упражнения
источниками ЭДС. Метод контурных токов.
Баланс мощности в разветвленных цепях с
несколькими источниками.
Модуль 1
Ауд.: ОЛ -1 гл.1: 1.55 – 1.57, 1.59, 1.64, 1.68,
1.69.
Занятие 1. Эквивалентные структурные
преобразования линейных электрических
цепей. Расчет токов и напряжений в цепях
постоянного тока с применением законов
Кирхгофа.
Дома: ОЛ -1 гл.1: по варианту домашнего
задания.
Дома: ОЛ -1 гл. 1: по варианту домашнего
задания.
Занятие 3. Расчет токов и напряжений в
электрических цепях однофазного
синусоидального тока. Построение
векторных диаграмм.
Занятие 2. Расчет разветвленных
электрических цепей с несколькими
. Резонанс напряжений и токов в
электрических цепях. Резонансные режимы в
Ауд.: ОЛ -1 гл.1: 1.2, 1.3 – 1.8.
186
разветвленных цепях. Ауд.: ОЛ -6 гл.2: 2.2,
2.3, 2 .6, 2.20, 2.24, 2.26, 2.27.
треугольником для случаев симметричной и
несимметричной нагрузок. Ауд.: ОЛ -1 гл.3
3.6 – 3.9, 3.22 – 3.25, 3.28 – 3.38.Дома: ОЛ -1
гл.3 по варианту домашнего задания .
Занятие5. Расчет переходных процессов в
электрических цепях 1) при
последовательном и параллельном
соединении элементов R,L; 2) при
последовательном и параллельном
соединении элементов R,C.
Ауд.: ОЛ -1 гл.2 2.122 – 2.124, 2.144 – 2.147,
2.154, 2.155.
Ауд.: ОЛ -1 гл.4 4.4, 4.5, 4.14, 4.15, 4.17, 4.22
– 4.26.
Дома: ОЛ -1 гл.2 по варианту домашнего
задания.
Дома: ОЛ -1 гл.4 по варианту домашнего
задания.
Занятие 4. Расчет токов, напряжений и
мощности в трехфазных электрических цепях
при соединении фаз потребителя звездой и
Расчет и построение искусственных
механических характеристик асинхронных
двигателей при различных способах
регулирования частоты вращения. Расчет
энергетических показателей.
Модуль 2
Занятие 6. Рубежный контроль по модулю 1
(45 мин). Расчет магнитных цепей с
постоянной магнитодвижущей силой.
Прямая и обратная задачи расчета
неразветвленных и симметричных
разветвленных магнитных цепей. Расчет
магнитных цепей с переменной
магнитодвижущей силой. Расчет параметров
схемы замещения реальной индуктивной
катушки.
Ауд.: ОЛ -6 гл.10 10.17 – 10.20, 10.23, 10.32,
10.42.
10.45 – 10.48, 10.50, 10.55, 10.62, 10.66,
10.69.
Дома: ОЛ -6 гл.10 10.28, 10.31, 10.37, 10.40,
10.41. 10.51, 10.54, 10.56, 10.57.
Занятие 8. Расчет и построение
естественной механической характеристики
по паспортным данным для двигателей
постоянного тока параллельного и
независимого возбуждения. Способы
регулирования частоты вращения.
Ауд.: ОЛ -1 гл.6.1 6.31, 6.34 – 6.36, 6.38,6.39.
гл. 6.2 6.90 – 6.98, 6.100, 6.102.
Дома: ОЛ -1 гл.6.1 6.43, 6.45, 6.52. 6.2 6.104,
6.110, 6.115.
Ауд.: ОЛ -6 гл.9 9.32, 9.35 – 9.38, 9.44, 9.50,
9.53.
Дома: ОЛ -6 гл.9 9.26, 9.27,9.28, 9.40, 9.42,
9.43.
Занятие 7. Расчет и построение
естественных скоростной и механической
характеристик трехфазных асинхронных
двигателей по паспортным и каталожным
данным.
Занятие 9. Рубежный контроль по модулю 2.
187
3. Лабораторные работы
Модуль 1
1. Исследование линейных
электрических цепей постоянного
тока
Экспериментальное исследование
источника постоянного напряжения:
режимов его работы, внешней
характеристики. Также исследуется
разветвленная электрическая цепь с двумя
источниками. Расчет параметров цепи
производится методом непосредственного
использования законов Кирхгофа, что
является
закреплением теоретического курса.
Изучаются используемые в работе приборы
магнитоэлектрической системы и
рассчитываются погрешности измерений.
2 Исследование линейных электрических
цепей синусоидального тока.
Экспериментальное исследование
электрической цепи синусоидального тока
при последовательном и параллельном
соединении катушки индуктивности и
конденсатора. Определение режима
резонанса.
Модуль 2
4 Исследование двигателя постоянного
тока параллельного возбуждения.
Изучение технических данных и основных
свойств двигателя, электрической схемы
установки, последовательности пуска и
способов регулирования частоты вращения,
экспериментальное снятие механических
характеристик двигателя постоянного тока.
3 .Исследование асинхронного
электродвигателя с короткозамкнутым
ротором.
Исследование пусковых и
регулировочных свойств трехфазного
асинхронного электродвигателя с
короткозамкнутым ротором,
экспериментальное определение
основных технических данных двигателя
и снятие механической характеристики
Самостоятельная подготовка
Самостоятельная работа студента заключается в выполнении домашних заданий, проработке
материала лекций, подготовке к выполнению лабораторных работ, подготовке к мероприятиям
контроля модулей, оформлении отчетов по лабораторным работам
188
Контрольные мероприятия и сроки их проведения
1. Домашнее задание №1 (часть 1) «Расчет электрических цепей постоянного тока»
Срок выдачи 1 неделя, срок сдачи - 4 неделя
2. Домашнее задание №1(часть 2) «Расчет электрических цепей переменного тока »
Срок выдачи 1 неделя, срок сдачи - 9 неделя
3.Домашнее задание №2 « Анализ и расчет характеристик двигателей электроприводов постоянного и
переменного тока.»
Срок выдачи 8 неделя, срок сдачи - 16 неделя
Контроль по модулю №1 (РК №1) «Линейные электрические цепи».
Срок проведения – 8 неделя
Контроль по модулю №2 (РК №2) «Асинхронные двигатели. Машины постоянного тока»
Срок проведения –16неделя
Экзамен
Условием получения отметки о сдаче 1 и 2 модулей семестра является выполнение домашних заданий,
выполнение и защита лабораторных работ, положительное написание контрольных работ по защите модулей с
получением баллов по бально-рейтинговой системе.
Литература
Основная литература (ОЛ)
1. А.С. Касаткин, М.В. Немцов Электротехника : учеб. для вузов М: Издательский центр « Академия» , 2008.- 544с.
2. Л.А. Бессонов Электрические цепи: учебник. М : Гардарики, 2007.-701 с.
3.В.Г. Герасимов ,Х.Э. Зайдель и др.Сборник задач по электротехнике и основам электроники. М: Высш. шк. 1987.- 288с.
4. Д.Н. Липатов Вопросы и задачи по электротехнике для программированного обучения. М: Энергоатомиздат.1984г.-360с.
5. Б.Ф. Токарев. Электрические машины. М: Энергоатомиздат ,1990.-248 с.
Дополнительная литература(ДЛ)
1. Борисов Ю.М., Липатов Д.H., Зорин Ю.Н. «Электротехника».- М.: Энергоатомиздат,1985 – 552 с.
2. «Электротехника и электроника». Кн.1. «Электрические и магнитные цепи». / Под ред. В.Г.
Герасимова.- М.: Энергоатомиздат,1996 – 288 с.
3. «Электротехника и электроника. Кн.2. Электромагнитные устройства и электрические машины» /
Под ред. В. Г. Герасимова.- М.: Энергоатомиздат,1997-272 с.
4. «Электротехника и электроника» Кн.3. «Электрические измерения и основы электроники» / Под
ред. В. Г. Герасимова.- М.: Энергоатомиэдат,1998 – 432 с.
189
Методические пособия
1. Электрические цепи постоянного тока: электронное учебное издание: методические
рекомендации к изучению курса лекций по дисциплине «Электротехника и электроника» / Мисеюк
О.И. – ФГУП НТЦ «Информрегистр», №0321100935 от 27.04.2011.
2. Электрические цепи однофазного синусоидального тока: электронное учебное издание:
методические рекомендации к изучению курса лекций по дисциплине «Электротехника и
электроника» /Волченсков В.Н.– ФГУП НТЦ «Информрегистр», №0321100936 от 27.04.2011.
3. Волченсков В.И., Дробышев Г.Ф. Методические указания к выполнению домашнего задания
по курсу «Электротехника и электроника» по теме «Расчет линейных цепей постоянного тока».
Изд-во МГТУ, 2011, 30 с.
4. Волченсков В.И. Методические указания к выполнению домашнего задания по курсу
«Электротехника и электроника» по теме «Расчет линейных цепей синусоидального тока». Издво МГТУ, 2011, 27 с.
5. Волченсков В.И. Методические указания к выполнению домашнего задания по курсу
«Электротехника и электроника» по теме «Исследование трехфазных асинхронных двигателей с
фазным ротором». Изд-во МГТУ, 2009, 42 с.
2. Домашнее задание №1(часть 2) «Расчет электрических цепей переменного тока »
ЭЛЕКТРОТЕХНИКА
для специальности СМ -7, СМ -11 (бакалавр) 4 семестр
Дисциплина состоит из 3-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Лекции
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
1-4
6
18.
Упражнения
1-4
4
19.
Лабораторные работы
1-4
4
20.
Домашние задания текущие
1-4
10
21.
Тест по модулю
4
1
190
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
5-9
14
Лекции
22.
Упражнения
5-9
7
23.
Лабораторные работы
5-9
4
24.
Домашние задания текущие
5-9
10
25.
Тест по модулю
10
1
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
10-16
14
Лекции
26.
Упражнения
10-16
6
27.
Лабораторные работы
10-16
8
28.
Домашние задания текущие
10-16
20
29.
Тест по модулю
16
1
Примечание
Модуль 1: Электрические цепи постоянного тока. Основы анализа и расчета
электрических цепей
Лекции
Лекция 1. Общие сведения об электрических
цепях и их классификация. Задачи анализа и
расчета линейных электрических цепей.
Источники электропитания. Элементы
электрических цепей: линейные:
(резистивный, индуктивный, емкостной) и
нелинейные (диод, транзистор).
Математические модели, схемы замещения
и вольтамперные характеристики этих
элементов. ОЛ-1 1.1-1.6; ОЛ-2 1.1- 1.4.
Основные законы (закон Ома и законы
Кирхгофа) расчета электрических цепей.
Режимы работы электрических цепей.
Расчет электрических цепей с одним
источником энергии. Расчет электрических
цепей с несколькими источниками. ОЛ-1
1.7,1.9 – 1.10; ОЛ-2 1.5 – 1.9; ДЛ -5.
Лекция 3.. Метод контурных токов;
принцип суперпозиции, метод
эквивалентного генератора. Энергетические
соотношения, баланс мощностей.
Особенности анализа электрических цепей с
Лекция 2. Топология и эквивалентные
преобразования электрических цепей.
191
Мостовые электрические цепи. ОЛ-1 1.111.15; 6.1-6.3; ОЛ-2 1.10-1.13; ДЛ -5..
нелинейными элементами.
Графоаналитический метод расчета
нелинейных цепей.
Упражнения
Занятие 1. Эквивалентные структурные преобразования линейных электрических цепей. Расчет
токов и напряжений в цепях постоянного тока с применением законов Кирхгофа. Ауд.: ОЛ -4
гл.1: 1.2, 1.3 – 1.8. Дома: ОЛ -4 гл. 1: по варианту домашнего задания.
Занятие 2. Расчет разветвленных электрических цепей с несколькими источниками ЭДС.
Баланс мощности в разветвленных цепях с несколькими источниками. Расчет электрических
цепей с нелинейными элементами графическим методом пересечения характеристик Ауд.: ОЛ 4 гл.1: 1.55 – 1.57, 1.59, 1.64, 1.68, 1.69, 1.106-1.109. Дома: ОЛ -4 гл.1: по варианту домашнего
задания.
Лабораторные работы
1. Исследование линейных электрических цепей постоянного тока
Экспериментальное исследование источника постоянного напряжения: режимов его
работы, внешней характеристики. Также исследуется разветвленная электрическая цепь с
двумя источниками. Расчет параметров цепи производится методом непосредственного
использования законов Кирхгофа, что является закреплением теоретического курса.
Изучаются используемые в работе приборы магнитоэлектрической системы и
рассчитываются погрешности измерений.
Модуль 2: Электрические цепи синусоидального тока. Переходные процессы.
Лекции
Лекция 4. Способы представления
гармонически изменяющихся функций
(временные диаграммы, векторные
величины и комплексные числа).
Действующее значение синусоидальной
величины. Резистивный, индуктивный и
емкостной элементы в цепи
синусоидального тока. ОЛ -1 2.1 - 2.8; ОЛ 2 2.1 – 2.7; ДЛ -6.
(Электрические измерения и приборы).
Мощность в цепях синусоидального тока.
ОЛ -1 2.9 - 2.20; ОЛ – 2 2.8 – 2 -9; ДЛ -6.
Лекция 6. Резонансные явления в
электрических цепях синусоидального тока
(резонанс напряжений и резонанс токов).
Условия возникновения резонансных
режимов. Соотношение параметров и
векторные диаграммы при резонансе. ОЛ -1
2.21; ОЛ -2 2.10 -1.13; ДЛ -6.
Лекция 5. Основные законы и методы
расчета электрических цепей
синусоидального тока. Векторные
диаграммы при различных характерах
нагрузки. Символический (комплексный)
метод расчета цепей синусоидального тока.
Понятие о круговых диаграммах.
Лекция 7. Расчет электрических цепей при
несинусоидальных периодических входных
воздействиях. Показание приборов при
несинусоидальных воздействиях. Мощность
192
в цепях при несинусоидальном входном
напряжении. ОЛ -1 4.1- 43; ОЛ -2 5.1 -5.6.
процессов. Энергетические соотношения
при переходных процессах. Законы
коммутации. Классический метод расчета
переходных процессов. Независимые и
зависимые начальные условия. Определения
начальных условий, корней
характеристического уравнения и
постоянных интегрирования. Постоянная
времени и время переходного процесса. ОЛ
-1 5.1- 5.3; ОЛ – 2 4.1 – 4.2.
Лекция 8. Понятие о трехфазных
электрических цепях. Преимущества
трехфазных цепей. Схемы соединений фаз
источника и приемника. Соотношения
между фазными и линейными
напряжениями источника. Соединение
приемников звездой. Симметричная
нагрузка. Несимметричная нагрузка. Роль
нейтрального провода. Соединение
приемников треугольником. Симметричная
нагрузка. Несимметричная нагрузка.
Мощность трехфазных цепей. Измерение
мощности в трехфазных цепях. Метод двух
ваттметров ОЛ -1 3.1 -3.8; ОЛ -2 3.1 – 3.7.
Лекция 10. Переходные процессы в цепи
с последовательным соединением
конденсатора и резистора. Подключение и
отключение источника постоянной э.д.с.
Подключение индуктивной катушки к
источнику постоянной э.д.с. Отключение
индуктивной катушки от источника
постоянного напряжения и замыкание ее на
резистор. ОЛ -1 5.4- 5.6; ДЛ -2 4.2 -4.4.
Лекция 9. Причины и необходимые
условия возникновения переходных
Упражнения
Занятие 3. Рубежный контроль по модулю
1 (45мин). Расчет токов и напряжений в
электрических цепях однофазного
синусоидального тока. Построение
векторных диаграмм. Ауд.: ОЛ -4 гл.2: 2.2,
2.3, 2 .6, 2.20, 2.24, 2.26, 2.27. Дома: ОЛ -4
гл.2: по варианту домашнего задания.
цепях при соединении фаз потребителя
звездой и треугольником для случаев
симметричной и несимметричной
нагрузок.Ауд.: ОЛ -4 гл.3 3.6 – 3.9, 3.22 –
3.25, 3.28 – 3.38. Дома: ОЛ -4 гл.3 по
варианту домашнего задания
Занятие 6. Расчет переходных процессов в
электрических цепях: 1) при
последовательном и параллельном
соединении элементов R,L; 2) при
последовательном и параллельном
соединении элементов R,C. Рубежный
контроль по модулю 2 (45мин.) Ауд.: ОЛ -4
гл.4 4.4, 4.5, 4.14, 4.15, 4.17, 4.22 –
4.26.Дома: ОЛ -4 гл.4 по варианту
домашнего задания.
Занятие 4. Резонанс напряжений и токов в
электрических цепях. Резонансные режимы
в разветвленных цепях. Ауд.: ОЛ -4 гл.2
2.122 – 2.124, 2.144 – 2.147, 2.154,
2.155.Дома: ОЛ -4 гл.2 по варианту
домашнего задания.
Занятие 5. Расчет токов, напряжений и
мощности в трехфазных электрических
Лабораторные работы
2. Исследование линейных электрических цепей синусоидального тока.
193
Экспериментальное исследование электрической цепи синусоидального тока при
последовательном и параллельном соединении катушки индуктивности и конденсатора.
Определение режима резонанса.
Модуль 3: Электромагнитные устройства и электрические машины
Лекции
Лекция 11. Понятие о магнитных цепях.
Свойства ферромагнитных материалов.
Основные величины, используемые при
анализе и расчете магнитных цепей.
Основные законы магнитных цепей. Задачи
расчета и анализа магнитных цепей с
постоянными магнитодвижущими силами.
Допущения, используемые при расчете.
Аналогия методов расчета магнитных и
электрических цепей. Последовательность
расчета симметричных и несимметричных
разветвленных магнитных цепей с
постоянными магнитами. ОЛ -1 7.1 – 7.6;
ОЛ -2 6.1 – 6.4.
опытам холостого хода и короткого
замыкания. ОЛ -1 9.1 – 9.9; ОЛ -5 1.1 1.8.
Лекция 14. Устройство трехфазного
асинхронного двигателя. Вращающееся
магнитное поле. Принцип действия
асинхронного двигателя. ЭДС обмотки
статора. ЭДС, частота тока ротора,
скольжение. Ток и эквивалентная схема
фазы обмотки ротора. Электромагнитная
мощность и потери асинхронного двигателя.
Момент, развиваемый двигателем.
Механическая характеристика
асинхронного двигателя. Расчет и
построение механической характеристики
по паспортным данным. ОЛ -1 14.1 – 14.5;
14.12-14.15. ОЛ – 5 3.1 – 3.10.
Лекция 12. Магнитные цепи при
переменной магнитодвижущей силе.
Катушка со сталью. Потери в стали.
Допущения, используемые при расчете
подобных магнитных цепей. Уравнения,
схема замещения и векторная диаграмма
идеализированной обмотки. Уравнения,
схема замещения и векторная диаграмма
реальной катушки. ОЛ -1 8.1 – 8.5;
2 6.5.
Лекция15. Пуск асинхронного двигателя.
Двигатели с улучшенными пусковыми
свойствами. Регулирование частоты
вращения асинхронного двигателя.
Тормозные режимы работы. Однофазные
асинхронные двигатели. ОЛ -1 14.16 –
14.18;
ОЛ -5 3.11 – 3.14.
ОЛ –
Лекция 13. Назначение, устройство и
принцип действия трансформатора. Режим
холостого хода трансформатора.
Коэффициент трансформации. Работа
трансформатора с нагрузкой. Уравнения,
схема замещения, векторная диаграмма
трансформатора. Потери и к.п.д.
трансформатора. Внешняя характеристика
трансформатора. Определение параметров и
эксплуатационных характеристик
трансформатора по паспортным данным и
Лекция 16. Назначение и устройство
машин постоянного тока. Принцип действия
машин постоянного тока в генераторном и
двигательном режимах. ЭДС якоря и
электромагнитный момент. Явление
реакции якоря. Способы возбуждения
машин постоянного тока. Пуск двигателей
постоянного тока. ОЛ -1 13.1 – 13.11;
ОЛ – 5 2.1 – 2.6.
194
Лекция 17. Двигатели параллельного,
независимого, последовательного и
смешанного возбуждения. Механические
характеристики, способы регулирования
частоты вращения двигателей постоянного
тока. Тормозные режимы работы двигателей
:режим противовключения, генераторный
режим, режим динамического торможения.
Особенности применения двигателей
постоянного тока с различными способами
возбуждения. ОЛ -1 13.13 – 13.15; ОЛ -5
2.9 – 2.13.
Примечание: материал, заключенный в
скобки, выносится на самостоятельную
проработку.
Упражнения
Занятие 7. Расчет магнитных цепей с
переменной магнитодвижущей силой.
Расчет параметров схемы замещения
реальной индуктивной катушки. Расчет
конструктивных параметров
трансформатора (размеров сердечника,
параметров обмоток). Потери
трансформатора. Ауд.:ОЛ -4 гл. 6.2 6.90 –
6.98, 6.100, гл.8 8.12, 8.44, 8.52.Дома: ОЛ -4
6.2 6.104, 6.110, 6.115, 8.62, 8.63, 8.67.
способах регулирования частоты вращения.
Расчет энергетических показателей. Ауд.:
ОЛ -4 гл.10 10.17 – 10.20, 10.23, 10.32,
10.42, 10.66, 10.69.Дома: ОЛ -4 гл.10 10.
28, 10. 37, 10.40,10.51, 10.54, 10.56, 10.57.
Занятие 9 Расчет и построение
естественной механической характеристики
по паспортным данным для двигателей
постоянного тока параллельного и
независимого возбуждения. Способы
регулирования частоты вращения.
Рубежный контроль по модулю 3. Ауд.:ОЛ 4 гл. .9 9.32, 9.35 – 9.38, 9.44, 9.50, 9.53.
Дома: ОЛ -4 гл. 9 9.26, 9.27,9.28, 9.40, 9.42,
9.43
Занятие 8. Расчет и построение
естественных скоростной и механической
характеристик трехфазных асинхронных
двигателей по паспортным и каталожным
данным. Расчет и построение
искусственных механических характеристик
асинхронных двигателей при различных
Лабораторные работы
3. .Исследование асинхронного
электродвигателя с
короткозамкнутым ротором.
4. Исследование двигателя постоянного
тока параллельного возбуждения.
Изучение
технических
данных
и
основных свойств двигателя, электрической
схемы установки, последовательности пуска
и
способов
регулирования
частоты
вращения,
экспериментальное
снятие
механических характеристик двигателя.
Исследование пусковых и регулировочных
свойств трехфазного асинхронного
электродвигателя с короткозамкнутым
ротором, экспериментальное определение
основных технических данных двигателя и
снятие механической характеристики.
Самостоятельная подготовка
Самостоятельная работа студента заключается в выполнении домашних заданий, проработке
материала лекций, подготовке к выполнению лабораторных работ, подготовке к мероприятиям
контроля модулей, оформлении отчетов по лабораторным работам
Контрольные мероприятия и сроки их проведения
195
1. ДЗ №1 (часть 1) «Расчет электрических цепей постоянного тока»
Срок выдачи 1 неделя, срок сдачи - 4 неделя
2. ДЗ №1(часть 2) «Расчет электрических цепей переменного тока »
Срок выдачи 1 неделя, срок сдачи - 9 неделя
3.ДЗ№2 « Анализ и расчет характеристик двигателей электроприводов постоянного и переменного тока.»
Срок выдачи 8 неделя, срок сдачи - 16 неделя
Контроль по модулю №1 (РК №1) «Цепи постоянного тока».
Срок проведения – 4 неделя
Контроль по модулю №2 (РК №2) «Цепи переменного тока. Переходные процессы»
Срок проведения –9неделя
Контроль по модулю №3 (РК №3) «Асинхронные двигатели. Машины постоянного тока»
Срок проведения –16неделя
Экзамен
Условием получения отметки о сдаче 1, 2 и 3 модуля семестра является выполнение домашних заданий,
выполнение и защита лабораторных работ, положительным написанием контрольной работы по защите модуля с
получением баллов по балльно-рейтинговой системе.
Литература
Основная литература (ОЛ)
1. А.С. Касаткин, М.В. Немцов Электротехника : учеб. для вузов М: Издательский центр « Академия» , 2008.544с.
2. Л.А. Бессонов Электрические цепи: учебник. М : Гардарики, 2007.-701 с.
3.В.Г. Герасимов ,Х.Э. Зайдель и др.Сборник задач по электротехнике и основам электроники. М: Высш. шк.
1987.- 288с.
4. Д.Н. Липатов Вопросы и задачи по электротехнике для программированного обучения. М:
Энергоатомиздат.1984г.-360с.
5. Б.Ф. Токарев Электрические машины. М: Энергоатомиздат ,1990.-345с.
Дополнительная литература (ДЛ))
1. Борисов Ю.М., Липатов Д.H., Зорин Ю.Н. «Электротехника».- М.: Энергоатомиздат,1985 – 552 с.
2. «Электротехника и электроника». Кн.1. «Электрические и магнитные цепи». / Под ред. В.Г. Герасимова.- М.:
Энергоатомиздат,1996 – 288 с.
3. «Электротехника и электроника. Кн.2. Электромагнитные устройства и электрические машины» / Под ред. В. Г.
Герасимова.- М.: Энергоатомиздат,1997-272 с.
4. «Электротехника и электроника» Кн.3. «Электрические измерения и основы электроники» / Под ред. В. Г.
Герасимова.- М.: Энергоатомиэдат,1998 – 432 с.
5.Электрические цепи постоянного тока: электронное учебное издание: методические рекомендации к изучению
курса лекций по дисциплине «Электротехника и электроника» / Мисеюк О.И. – ФГУП НТЦ «Информрегистр»,
№0321100935 от 27.04.2011.
6. Электрические цепи однофазного синусоидального тока: электронное учебное издание: методические
рекомендации к изучению курса лекций по дисциплине «Электротехника и электроника» /Волченсков В.Н.– ФГУП
НТЦ «Информрегистр», №0321100936 от 27.04.2011..
196
Рекомендуемые Интернет-сайты:
1. .Методические материалы для изучения курса «Электротехника и электроника» http://hoster.bmstu.ru/moodle,2012г.
2. Методические материалы для изучения курса «Электротехника» http//hoster. bmstu.ru//~fn7
ЭЛЕКТРОТЕХНИКА
для специальности СМ -7, СМ -11 (специалист) 4 семестр
Дисциплина состоит из 3-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Лекции
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
1-4
11
30.
Упражнения
1-4
6
31.
Лабораторные работы
1-4
9
32.
Домашние задания текущие
1-4
10
33.
Контроль модуля
5
1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
5-9
18
34.
Упражнения
5-9
10
35.
Лабораторные работы
5-9
9
36.
Домашние задания текущие
5-9
10
37.
Контроль модуля
10
1
197
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
10-16
22
Лекции
38.
Упражнения
10-16
18
39.
Лабораторные работы
10-16
16
40.
Домашние задания текущие
10-16
20
41.
Контроль модуля
17
1
Примечание
Модуль 1: Электрические цепи постоянного тока. Основы анализа и расчета
электрических цепей
Лекции
Лекция 1. Общие сведения об электрических
цепях и их классификация. Задачи анализа и
расчета линейных электрических цепей.
Источники электропитания. Элементы
электрических цепей: линейные:
(резистивный, индуктивный, емкостной) и
нелинейные (диод, транзистор).
Математические модели, схемы замещения
и вольтамперные характеристики этих
элементов. ОЛ-1 1.1-1.5 ; ОЛ-2 1.1- 1.4;
ДЛ -2
Лекция 2. Топология и эквивалентные
преобразования электрических цепей.
Лекция 3. Расчет электрических цепей с
несколькими источниками. Метод
контурных токов, метод узлового
напряжения, принцип суперпозиции, метод
эквивалентного генератора. Энергетические
соотношения, режимы работы, баланс
мощностей. ОЛ-1 1.12-1.15; ОЛ-2 1.101.12; ДЛ -2
Лекция 4. Особенности анализа
электрических цепей с нелинейными
элементами. Графоаналитический метод
расчета нелинейных цепей. Мостовые
электрические цепи. ОЛ -1 1.16- 1.17; ОЛ -2
1.13.
Основные законы (закон Ома и законы
Кирхгофа) расчета электрических цепей.
Режимы работы электрических цепей.
Расчет электрических цепей с одним
источником энергии. ОЛ-1 1.6 – 1.10;
ОЛ-2 1.5 – 1.9; ДЛ -2
Лекция 5. Свойство односторонней
проводимости р–n перехода.
Полупроводниковые диоды и схемы
выпрямления. Общие представления и
способы построения источников вторичного
электропитания. ОЛ – 4 2.2; 5.1 – 5.2.
Упражнения
Занятие 1. Эквивалентные структурные
постоянного тока с применением законов
преобразования линейных электрических
Кирхгофа. Ауд.: ОЛ -6 гл.1: 1.2, 1.3 – 1.8.
цепей. Расчет токов и напряжений в цепях
198
Дома: ОЛ -6 гл. 1: по варианту домашнего
задания.
Применение метода эквивалентного
генератора при расчете нелинейных
электрических цепей.
Занятие 2. Расчет разветвленных
электрических цепей с несколькими
источниками ЭДС. Метод контурных токов.
Баланс мощности в разветвленных цепях с
несколькими источниками. Ауд.: ОЛ -6
гл.1: 1.55 – 1.57, 1.59, 1.64, 1.68, 1.69.
Ауд.: ОЛ -6 гл.1: 1.101 – 1.104, 1.106 –
1.109. Дома: ОЛ -6 гл.1: по варианту
домашнего задания.
Дома: ОЛ -6 гл.1: по варианту домашнего
задания.
Занятие 3. Расчет электрических цепей с
нелинейными элементами графическим
методом пересечения характеристик.
Лабораторные работы
приборы магнитоэлектрической системы
и рассчитываются погрешности
измерений.
1. Исследование линейных электрических
цепей постоянного тока
Экспериментальное исследование
источника постоянного напряжения:
режимов его работы, внешней
характеристики. Также исследуется
разветвленная электрическая цепь с
двумя источниками. Расчет параметров
цепи производится методом
непосредственного использования
законов Кирхгофа, что является
закреплением теоретического курса.
Изучаются используемые в работе
2
Исследование выпрямителей.
Исследование однополупериодных и
двухполупериодных схемы нерегулируемых
выпрямителей с емкостными фильтрами и
без сглаживающих фильтров. Изучение
осциллограмм и внешних характеристик
выпрямителей. Знакомство на практике с
работой осциллографа и мультиметра.
Модуль 2: Электрические цепи синусоидального тока. Переходные процессы в
линейных электрических цепях
Лекции
Лекция 6. Способы представления
гармонически изменяющихся функций
(временные диаграммы, векторные
величины и комплексные числа).
Действующее значение синусоидальной
величины. Резистивный, индуктивный и
емкостной элементы в цепи
синусоидального тока. ОЛ -1 2.1 - 2.7; ОЛ
-2 2.1 – 2.7; ДЛ -3.
Лекция 7. Основные законы и методы
расчета электрических цепей
синусоидального тока. Векторные
диаграммы при различных характерах
199
нагрузки. Символический метод расчета.
Понятие о круговых диаграммах.(
Электрические измерения и приборы).
Мощность в цепях синусоидального тока.
ОЛ -1 2.8 – 2.11, 2.15 – 2.20; ОЛ – 2 2.8 – 2
-9; ОЛ – 4 1.1 – 1.5; ДЛ -3.
Несимметричная нагрузка. Мощность
трехфазных цепей. Измерение мощности в
трехфазных цепях. Метод двух ваттметров.
ОЛ -1 3.5; ОЛ -2 3.6 – 3.7.
Лекция 12. Причины и необходимые
условия возникновения переходных
процессов. Энергетические соотношения
при переходных процессах. Законы
коммутации. Классический метод расчета
переходных процессов. Независимые и
зависимые начальные условия. Определения
начальных условий, корней
характеристического уравнения и
постоянных интегрирования. Постоянная
времени и время переходного процесса. ОЛ
-1 4.1; ОЛ – 2 4.1 – 4.2.
Лекция 8. Резонансные явления в
электрических цепях синусоидального тока
(резонанс напряжений и резонанс токов).
Условия возникновения резонансных
режимов. Соотношение параметров и
векторные диаграммы при резонансе. ОЛ -1
2.12 -2.14; ОЛ -2 2.10 -1.13; ДЛ -3.
Лекция 9. Расчет электрических цепей при
несинусоидальных периодических входных
воздействиях. Показание приборов при
несинусоидальных воздействиях. Мощность
в цепях при несинусоидальном входном
напряжении. ОЛ -1 5.1- 5.6; ОЛ -2 5.1 5.6.
Лекция 13. Переходные процессы в цепи
с последовательным соединением
конденсатора и резистора. Подключение и
отключение источника постоянной э.д.с.
Подключение индуктивной катушки к
источнику постоянной э.д.с. Отключение
индуктивной катушки от источника
постоянного напряжения и замыкание ее на
резистор. ОЛ -1 4.2, 4.7, 4.8; ОЛ -2 4.2 4.4.
Лекция 10. Понятие о трехфазных
электрических цепях. Преимущества
трехфазных цепей. Схемы соединений фаз
источника и приемника. Соотношения
между фазными и линейными
напряжениями источника. Соединение
приемников звездой. Симметричная
нагрузка. Несимметричная нагрузка. Роль
нейтрального провода. ОЛ -1 3.1 -3.4; ОЛ
-2 3.1 – 3.5.
Лекция 14. Подключение катушки
индуктивности к источнику
синусоидального напряжения. Переходные
процессы в цепи с последовательным
соединением резистора, индуктивной
катушки и конденсатора. ОЛ -1 4.9; ОЛ -2
4.5, 4.6.
Лекция11. Соединение приемников
треугольником. Симметричная нагрузка.
Упражнения
Занятие 4. Рубежный контроль по модулю 1
в разветвленных цепях. Ауд.: ОЛ -6 гл.2
(30 мин). Расчет токов и напряжений в
2.122 – 2.124, 2.144 – 2.147, 2.154, 2.155.
электрических цепях однофазного
Дома: ОЛ -6 гл.2 по варианту домашнего
синусоидального тока. Построение
задания.
векторных диаграмм. Ауд.: ОЛ -6 гл.2: 2.2,
Занятие 6. Расчет токов, напряжений и
2.3, 2 .6, 2.20, 2.24, 2.26, 2.27. Дома: ОЛ -6
мощности в трехфазных электрических
гл.2: по варианту домашнего задания.
цепях при соединении фаз потребителя
звездой и треугольником для случаев
Занятие 5. Резонанс напряжений и токов в
симметричной и несимметричной нагрузок.
электрических цепях. Резонансные режимы
200
соединении элементов R,C. Ауд.: ОЛ -6 гл.4
4.4, 4.5, 4.14, 4.15, 4.17, 4.22 – 4.26. Дома:
ОЛ -6 гл.4 по варианту домашнего задания.
Ауд.: ОЛ -6 гл.3 3.6 – 3.9, 3.22 – 3.25, 3.28 –
3.38.
Дома: ОЛ -6 гл.3 по варианту домашнего
задания
Занятие 8. Расчет переходных процессов в
электрических цепях с последовательным
соединением элементов R, L, C. Ауд.: ОЛ -6
гл.4 4.76, 4.77.
Занятие 7. Расчет переходных процессов в
электрических цепях 1) при
последовательном и параллельном
соединении элементов R,L; 2) при
последовательном и параллельном
Лабораторные работы
3. Исследование линейных электрических
цепей синусоидального тока.
Экспериментальное исследование
электрической цепи синусоидального
тока при последовательном и
параллельном соединении катушки
индуктивности и конденсатора.
Определение режима резонанса.
Экспериментальное исследование
трехфазной электрической цепи при
соединении потребителей звездой и
треугольником при различных режимах для
измерения активной мощности цепи
используется метод двух ваттметров.
Построение векторных диаграмм для
исследуемых режимов.
4. Исследование трехфазных электрических
цепей.
Модуль 3: Электромагнитные устройства и электрические машины
Лекции
Лекция 15. Понятие о магнитных цепях.
Свойства ферромагнитных материалов.
Основные величины, используемые при
анализе и расчете магнитных цепей.
Основные законы магнитных цепей. Задачи
расчета и анализа магнитных цепей с
постоянными магнитодвижущими силами.
Допущения, используемые при расчете.
Аналогия методов расчета магнитных и
электрических цепей. ОЛ -1 6.1 – 6.5;
ОЛ -2 6.1 – 6.3.
Лекция 17. Магнитные цепи при
переменной магнитодвижущей силе.
Катушка со сталью. Потери в стали.
Допущения, используемые при расчете
подобных магнитных цепей. Уравнения,
схема замещения и векторная диаграмма
идеализированной обмотки. Уравнения,
схема замещения и векторная диаграмма
реальной катушки. ОЛ -1 6.10 – 6.15; ОЛ
– 2 6.5.
Лекция 18. Назначение, устройство и
принцип действия трансформатора. Режим
холостого хода трансформатора.
Коэффициент трансформации. Работа
трансформатора с нагрузкой. Уравнения,
схема замещения, векторная диаграмма
трансформатора. ОЛ -1 8.1 – 8.4; ОЛ -3
1.1 -1.4.
Лекция 16. Расчет неразветвленных
магнитных цепей при постоянных
магнитодвижущих силах. Прямая и
обратная задачи. Последовательность
расчета симметричных и несимметричных
разветвленных магнитных цепей с
постоянными магнитами. ОЛ -1 6.6 – 6.7;
ОЛ -2
6.4.
201
Лекция 19. Потери и к.п.д.
трансформатора. Внешняя характеристика
трансформатора. Определение параметров и
эксплуатационных характеристик
трансформатора по паспортным данным и
опытам холостого хода и короткого
замыкания. Трехфазные трансформаторы.
Особенности трансформаторов малой
мощности. ОЛ -1 8.7; ОЛ -3 1.5 – 1.8.
двигательном режимах. ЭДС якоря и
электромагнитный момент. Явление
реакции якоря. Способы возбуждения
машин постоянного тока. ОЛ -1 9.1 – 9.6;
ОЛ – 3 2.1 – 2.6.
Лекция 24. Пуск двигателя постоянного
тока. Двигатели параллельного,
независимого, последовательного и
смешанного возбуждения. Механические
характеристики, способы регулирования
частоты вращения двигателей постоянного
тока. Тормозные режимы работы двигателей
:режим противовключения, генераторный
режим, режим динамического торможения.
Особенности применения двигателей
постоянного тока с различными способами
возбуждения. ОЛ -1 9.11 – 9.19; ОЛ -3
2.9 – 2.13.
Лекция 20. Устройство трехфазного
асинхронного двигателя. Вращающееся
магнитное поле. Принцип действия
асинхронного двигателя. ЭДС обмотки
статора. ЭДС, частота тока ротора,
скольжение. Ток и эквивалентная схема
фазы обмотки ротора. ОЛ -1 10.1 – 10.7;
ОЛ – 3 3.1 – 3.7.
Лекция 21. Электромагнитная мощность
и потери асинхронного двигателя. Момент,
развиваемый двигателем. Схема замещения
асинхронного двигателя. Механическая
характеристика асинхронного двигателя.
Расчет и построение механической
характеристики по паспортным данным. ОЛ
-1 10.9 – 10.13; ОЛ -3 3.8 – 3.10.
Лекция 25. Классификация генераторов
постоянного тока по способу возбуждения.
Схемы включения генераторов. Основные
характеристики генераторов постоянного
тока: характеристика холостого хода,
внешняя характеристика, регулировочная
характеристика. Потери энергии и КПД
машин постоянного тока. Машины
постоянного тока малой мощности. ОЛ -1
9.6 – 9.10, 9.23;
ОЛ -3
2.7 – 2.8, 2.14
Лекция 22. Пуск асинхронного
двигателя. Двигатели с улучшенными
пусковыми свойствами. Регулирование
частоты вращения асинхронного двигателя.
Тормозные режимы работы. Однофазные
асинхронные двигатели. ОЛ -1 10.14 –
10.19;
ОЛ -3 3.11 – 3.14.
Лекция 26. Резервная.
Примечание: материал, заключенный в
скобки, выносится на самостоятельную
проработку.
Лекция 23. Назначение и устройство
машин постоянного тока. Принцип действия
машин постоянного тока в генераторном и
неразветвленных и симметричных
разветвленных магнитных цепей. Ауд.:ОЛ 6 гл.6.1 6.31, 6.34 – 6.36, 6.38,6.39. Дома:
ОЛ -6 гл.6.1 6.43, 6.45, 6.52.
Упражнения
Занятие 9. Рубежный контроль по модулю 2
(45 мин). Расчет магнитных цепей с
постоянной магнитодвижущей силой.
Прямая и обратная задачи расчета
202
Занятие 10. Расчет магнитных цепей с
переменной магнитодвижущей силой.
Расчет параметров схемы замещения
реальной индуктивной катушки. Ауд.: ОЛ -6
гл. 6.2 6.90 – 6.98, 6.100, 6.102. Дома: ОЛ -6
6.2 6.104, 6.110, 6.115.
Занятие 14. Расчет и построение
искусственных механических характеристик
асинхронных двигателей при различных
способах регулирования частоты вращения.
Расчет энергетических показателей. Ауд.:
ОЛ -6 гл.10 10.45 – 10.48, 10.50, 10.55,
10.62, 10.66, 10.69. Дома: ОЛ -6 гл.10
10.28, 10.31, 10.37, 10.40, 10.41.
Занятие 11. Расчет конструктивных
параметров трансформатора (размеров
сердечника, параметров обмоток). Потери
трансформатора. Ауд.: ОЛ -6 гл.8 8.12,
8.44, 8.52, 8.66.Дома: ОЛ -6 гл.8 8.62, 8.63,
8.67.
Занятие15-16. Расчет и построение
естественной механической характеристики
по паспортным данным для двигателей
постоянного тока параллельного и
независимого возбуждения. Способы
регулирования частоты вращения.
Занятие 12. Расчет параметров схемы
замещения трансформатора, его
электрических и эксплуатационных
параметров. Ауд.: ОЛ -6 гл.8 8.21 – 8.27,
8.32, 8.35, 8.56. Дома: ОЛ -6 гл.8 8.31, 8.33,
8.34, 8.39.
Ауд.: ОЛ -6 гл.9 9.32, 9.35 – 9.38, 9.44,
9.50, 9.53. Дома: ОЛ -6 гл.9 9.26, 9.27,9.28,
9.40, 9.42, 9.43.
Занятие 17. Рубежный контроль по модулю
Занятие 13. Расчет и построение
естественных скоростной и механической
характеристик трехфазных асинхронных
двигателей по паспортным и каталожным
данным. Ауд.: ОЛ -6 гл.10 10.17 – 10.20,
10.23, 10.32, 10.42. Дома: ОЛ -6 гл.10
10.51, 10.54, 10.56, 10.57.
3.
Лабораторные работы
5. .Исследование асинхронного
электродвигателя с
короткозамкнутым ротором.
6. Исследование свойств асинхронного
двигателя при частотном регулировании.
Исследование основных характеристик и
параметров асинхронного двигателя при
частотном
регулировании,
а
также
устройство и принцип работы частотного
преобразователя
7.
7.Исследование двигателя постоянного
тока параллельного возбуждения.
Исследование пусковых и регулировочных
свойств трехфазного асинхронного
электродвигателя с короткозамкнутым
ротором, экспериментальное определение
основных технических данных двигателя и
снятие механической характеристики.
Изучение
технических
данных
и
основных свойств двигателя, электрической
схемы установки, последовательности пуска
203
и
способов
регулирования
частоты
вращения,
экспериментальное
снятие
механических характеристик двигателя.
8.
Исследование
постоянного тока.
Исследование
основных
свойств
и
характеристик генератора постоянного тока
при различных способах его возбуждения.
генераторов
.
Самостоятельная подготовка
Самостоятельная работа студента заключается в выполнении домашних заданий, проработке
материала лекций, подготовке к выполнению лабораторных работ, подготовке к мероприятиям
контроля модулей, оформлении отчетов по лабораторным работам
Контрольные мероприятия и сроки их проведения
1. ДЗ №1 (часть 1) «Расчет электрических цепей постоянного тока»
Срок выдачи 1 неделя, срок сдачи - 4 неделя
2. ДЗ №1(часть 2) «Расчет электрических цепей переменного тока »
Срок выдачи 1 неделя, срок сдачи - 9 неделя
3.ДЗ№2 « Анализ и расчет характеристик двигателей электроприводов постоянного и переменного тока.»
Срок выдачи 8 неделя, срок сдачи - 16 неделя
Контроль по модулю №1 (РК №1) «Цепи постоянного тока».
Срок проведения – 4 неделя
Контроль по модулю №2 (РК №2) «Цепи переменного тока. Переходные процессы»
Срок проведения –9 неделя
Контроль по модулю №3 (РК №3) «Асинхронные двигатели. Машины постоянного тока»
Срок проведения –17 неделя
Экзамен
Условием получения отметки о сдаче 1, 2 и 3 модуля семестра является выполнение домашних заданий,
выполнение и защита лабораторных работ, положительным написанием контрольной работы по защите модуля с
получением баллов по балльно-рейтинговой системе.
Литература
Основная литература (ОЛ)
1. А.С. Касаткин, М.В. Немцов Электротехника : учеб. для вузов М: Издательский центр « Академия» , 2008.544с.
2. Л.А. Бессонов Электрические цепи: учебник. М : Гардарики, 2007.-701 с.
3.В.Г. Герасимов ,Х.Э. Зайдель и др.Сборник задач по электротехнике и основам электроники. М: Высш. шк.
1987.- 288с.
4. Д.Н. Липатов Вопросы и задачи по электротехнике для программированного обучения. М:
Энергоатомиздат.1984г.-360с.
5. Б.Ф. Токарев Электрические машины. М: Энергоатомиздат ,1990.-345с.
Дополнительная литература (ДЛ))
1. Борисов Ю.М., Липатов Д.H., Зорин Ю.Н. «Электротехника».- М.: Энергоатомиздат,1985 – 552 с.
2. «Электрические цепи постоянного тока: электронное учебное издание: методические рекомендации к изучению
курса лекций по дисциплине «Электротехника и электроника» / Мисеюк О.И. – ФГУП НТЦ «Информрегистр»,
№0321100935 от 27.04.2011.
204
3. Электрические цепи однофазного синусоидального тока: электронное учебное издание: методические
рекомендации к изучению курса лекций по дисциплине «Электротехника и электроника» /Волченсков В.Н.– ФГУП
НТЦ «Информрегистр», №0321100936 от 27.04.2011..
4. «Электротехника и электроника» Кн.3. «Электрические измерения и основы электроники» / Под ред. В. Г.
Герасимова.- М.: Энергоатомиэдат,1998 – 432 с.
5 Электротехника и электроника». Кн.1. «Электрические и магнитные цепи». / Под ред. В.Г. Герасимова.- М.:
Энергоатомиздат,1996 – 288 с.
6. «Электротехника и электроника. Кн.2. Электромагнитные устройства и электрические машины» / Под ред. В. Г.
Герасимова.- М.: Энергоатомиздат,1997-272 с.
Рекомендуемые Интернет-сайты:
3. .Методические материалы для изучения курса «Электротехника и электроника» http://hoster.bmstu.ru/moodle,2012г.
4. Методические материалы для изучения курса «Электротехника» http//hoster. bmstu.ru//~fn7
Теория механизмов и машин
Квалификация (степень) - специалист
Виды учебной работы
Объем в часах по семестрам
04 семестр
05 семестр
Всего
17 недель
17 недель
Лекции
34
34
-
Семинары
Лабораторные работы
17
17
17
17
-
Самостоятельная работа
51
51
-
Курсовое проектирование
51
-
51
Трудоемкость, час
Трудоемкость, зачетные
единицы
Проверка знаний:
170
119
51
5,5
4
1,5
экз. (диф.зачет)
дифф. зачет
Модуль 1
Домашнее задание №1
Контрольная работа №1
Модуль 2
Домашнее задание №2
Контрольная работа №2
Самостоятельная проработка
материала
Объем, час
Контрольные мероприятия
Кол.
Баллы (max)
8
1
1
1
20
15
6
1
51
1
1
20
15
205
Итоги бально-рейтинговой аттестации:
Отлично
85
Хорошо
70
Удовлетворительно
60
Неделя
План КМ
Объем (час)
Баллы
Отлично
Хорошо
Удовлетворительно
1
2
3
4
Виды контрольных мероприятий
5 6 7 8 9 10 11 12 13 14
ДЗ 1 КР 1 М1
ДЗ 2
15
КР2
35
16
М2
17
35
Контроль знаний (4 семестр)
экзамен
30
Литература
Основная литература
1.
Теория механизмов и механика машин. Под ред. Фролова К.В, Тимофеева Г.А.-М.: Изд. МГТУ,
2002, 2004, 2009, 2012
2.
Попов С.А.,
Тимофеев Г.А.
Курсовое проектирование по
теории механизмов и
механике машин.-М.: Высшая школа, 2002, 2005, 2008.
Дополнительная литература
3.
Артоболевский И.И. Теория механизмов и машин.-М.: Наука,1988.
4.
Попов С.А., Черная Л.А. Математическое и программное обеспечение расчетов
кинематических характеристик: Учебное пособие. -М.: Изд. МГТУ, 1991.
5.
Леонов И.В. Динамика машинного агрегата при неустановившихся режимах движения:
Учебное пособие.-М.: Изд. МГТУ, 1990.
6.
Конспект лекций по новым разделам курса ТММ: Учебное пособие. Под ред. К.В.
Фролова, Д.М. Лукичева.-М.: Изд.М ВТУ, 1986.
7.
Динамика машинного агрегата: Учебное пособие. Под ред. Б.И.Крюкова.-М.: Изд.
МВТУ, 1988.
206
8.
Мусатов А.К. Кинематические и динамические характеристики механизмов и машин:
Учебное пособие.М.:Изд. МВТУ, 1987.
9.
Проектирование механизмов с высшими кинематическими парами: Учебное пособие.
Под ред.А.К.Мусатова.-М.: Изд.МВТУ,1989.
10.
Силовой расчет, уравновешивание, проектирование механизмов: Учебное пособие. Под
ред. А.К. Мусатова.-М.: Изд.МГТУ,1990.
11.
Головин А.А. Проектирование сложных рычажных механизмов: Учебное пособие. М.:
Изд. МГТУ, 1995.
12.
Тимофеев Г.А. Теория механизмов и машин: курс лекций. М.: Высшее образование,
2010.- 356 с.
13.
Теория механизмов и механика машин: Учебное пособие. Под ред. Г.А.Тимофеева.- М.:
Изд. МГТУ, 2002.
14.
Тарабарин В.Б, Кузенков В.В., Фурсяк Ф.И. Методические указания к выполнению
лабораторных работ по курсу ТММ.- М.: Изд. МГТУ, 2009.
15.
Теория механизмов и машин. Курсовое проектирование: Учебное пособие. Под ред. Г.А.
Тимофеева, Н.В. Умнова.-М.: Изд. МГТУ, 2010, 2012
ЛЕКЦИИ
Модуль 1. Механика машин
Лекция 1. Введение. Проблемы теории механизмов и механики машин. Понятие о
машинном агрегате Основные виды машин и механизмов и их элементы.
Л-1: Введение, гл.1 : П1.1, 1.2; Л-2: П1.1; Л-7: Введение; Л-8: П1,2; Л-12: Л-1.
Лекция 2. Строение и кинематика механизмов. Классификация кинематических пар.
Число степеней свободы механизма. Структурный анализ и синтез механизмов. Избыточные
связи и способы их устранения при проектировании.
Л-1: гл.2; Л-2: П2.1, 2.2; Л-8: П2, 3; Л-12: Л-2, Л-3.
Лекция 3. Кинематическое исследование плоских рычажных механизмов графическим
методом;
цикловые
кинематические
графики.
Кинематическое
исследование
плоских
рычажных механизмов аналитическим методом с применением ЭВМ.
Л-1: П3.1, 3.2, 3.3, 3.5; Л-4; Л-8;П4.5; Л-12: Л-5; Л-15: гл.2.
Лекция 4. Динамика машин. Силы, действующие в машинах. Общая методика силового
расчета механизмов. Силовой расчет многозвенных рычажных механизмов ( без учета трения);
применение ЭВМ.
207
Л-1: П1.3, 6.1, 6.2; Л-5: гл.4; Л-7: П5.1-5.4; Л-8: П8; Л-10: гл.1; Л-12: Л-6.
Лекция*(материал для самостоятельной проработки). Трение и его виды. Трение в
кинематических парах .
Силовой расчет механизмов с учетом трения. Самоторможение.
Механический к.п.д. системы механизмов.
Л-1: П8.1, П6.3-6.5; Л-3: П43-45, 49-51, 56, 64; Л-10: гл.2 ; Л-12: Л-26.
Лекция 5. Расчетные схемы машинных агрегатов. Механические характеристики
двигателей и рабочих машин. Динамическая модель машинного агрегата и ее параметры.
Приведение сил. Приведение масс.
Л-1: П1,3, 4.1, 4.2; Л-5: П2,1-2.3; Л-6: П2.1, 2.2; Л-7: П1.2, 1.4; Л-8: П8-10.
Лекция
6.
Уравнение
дифференциальной форме.
движения
машинного
Режимы движения
агрегата
в
энергетической
машинного агрегата. Определение
и
закона
движения при переходном процессе. Безударный останов механизма.
Л-5: П2.2, 2.3; Л-8: П11, 12; Л-1: П1.4, П4.3, 4.4; Л-12; Л-7; Л-15: гл.3.
Л-1: П4.5-4.7; Л-5: П4.2- 4.4; Л-8: П13, 14 ; Л-12: Л-7; Л-15: гл.3.
Лекция 7. Динамический анализ и синтез при установившемся режиме.
Л-1: П4.8, 4.9; Л-6: П2.3-2.5; Л-7: П2.3; Л-8: П15, 16 ; Л-12: Л-8.
Лекция 8. Уравновешивание механизмов.
Виды
неуравновешенности рычажных
механизмов и их статическое уравновешивание. Виды неуравновешенности роторов
(статическая, моментная, динамическая). Балансировка роторов.
Л-1: П7.5, 7.6; Л-3: П59-62; Л-10: гл.3, 4 ; Л-12: Л-10, 11.
Лекция* (материал для самостоятельной проработки). Основы виброзащиты человекаоператора и машины. Виброизоляция. Динамическое виброгашение.
Л-1: гл.7; Л-6: гл.4; Л-7: гл.3; Л-12: Л-12.
Модуль 2. Механизмы с высшими кинематическими парами
Лекция 9. Механизмы с высшими парами. Основная теорема зацепления, скольжение
профилей, угол давления. Эвольвента окружности, ее уравнения и свойства. Элементы
прямозубого эвольвентного колеса и основные расчетные зависимости. Элементы и свойства
эвольвентного зацепления.
Л-1: П3.7, гл.9: П9.2-9.4, П9.7; Л-9: П1.1; Л-12: Л-13.
Л-1: П11.1-11,5; Л-9: П1.2-1.5; Л-12: Л-14; Л-15: гл.5.
Лекция 10. Методы нарезания зубчатых колес. Станочное зацепление. Определение
основных размеров зубчатого эвольвентного колеса. Подрезание и заострение зубьев.
208
Л-1: П11.6-11.8; Л-2: П6.2-6.5; Л-9: П1.6-1.8; Л-12: Л-14.
Лекция 11. Эвольвентная зубчатая передача, ее основные параметры и качественные
показатели. Цилиндрическая передача, составленная из косозубых колес, особенности ее
расчета.
Л-1: П11.9-11.11; Л-2: П6.6; Л-9: П1.9-1.11; Л-12: Л-16.
Лекция * (материал для самостоятельного изучения).
Выбор расчетных значений
коэффициентов смещения. Применение ЭВМ для оптимизации параметров зубчатой передачи.
Л-1: П11.11, гл. 12: 12.2; Л-2: П6.2- 6.4; Л-3: П108; Л-12: Л-15, Л-21.
Лекция 12. Червячная передача, ее кинематика и геометрический расчет.
Коническая
зубчатая передача, ее кинематика и геометрический расчет.
Л-1: П12.1; Л-3: П107; Л-9: гл.3; Л-12: Л-20.
Лекция 13.
Многозвенные зубчатые передачи с
неподвижными
осями колес.
Планетарные зубчатые механизмы, методы их кинематического исследования. Проектирование
планетарных редукторов по заданному передаточному отношению.
Л-1: П3-7, гл.10: П10.1-10.4; Л-2: П7.1, 7.2, 7.4; Л-9: П1.12, 2.1, 2.2; Л-12: Л-18.
Л-1: П10.4; Л-2: П7.3; Л-9: П2.3; Л-12: Л-18; Л-15: гл.5.
Лекция 14. Кулачковые механизмы и их основные параметры. Построение графика
перемещения толкателя по заданной форме профиля кулачка. Угол давления. Влияние угла
давления на работоспособность и размеры механизма.
Л-1: П14.1, 14.2; Л-9: П4.1, 4.2; Л-12: Л-22; Л-15: гл.7.
Лекция 15.
. Проектирование
кулачковых
механизмов оптимальных размеров по
допустимому углу давления. Определение координат профиля кулачка. Проектирование
кулачковых механизмов с использованием ЭВМ.
Л-1: П14.3-14.4; Л-2; П8.3-8.6; Л-9: П4.3-4.5; Л-12: Л-23; Л-15: гл.7.
Л-1: П14.6; Л-2: П8.7; Л-9: П4.6, 4.7; Л-12: Л-23; Л-15: гл.3.
Лекция 16. Проектирование кинематических схем плоских рычажных механизмов по
заданным условиям с применением ЭВМ.
Л-1: гл.13; Л-2: П2.3; Л-3: П110; Л-10: гл.5; Л-11: гл.3; Л-12: Л-4; Л-15: гл.1.
Лекция 17. Манипуляторы, область применения, технические характеристики и
кинематика.
Л-1: П17.1-17.3; Л-6: П3.1-3.3; Л-10: гл.6; Л-12: Л-24, 25.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
209
Модуль 1. Механика машин.
1 занятие. Структурный анализ и синтез механизмов.
Л-1: П3.4, 3.6; Л-8: П4,5; Л-13; Л-12: Л-5.
2 занятие. Кинематические характеристики механизмов.
Л-1: П2.1-2.5; Л-8: П2,3; Л-13; Л-12: Л-3.
3 занятие. Параметры динамической модели.
Л-1: П3.1, 3.3, 3.5; Л-12; Л-13; Л-12: Л-5, Л-1: П4.2, 4.3; Л-8: П9, 10, 11; Л-15: гл.2.
4 занятие. Силовой расчет механизмов.
Л-1: П6.1, 6.2; Л-10; гл.1; Л-13; Л-12: Л-9; Л-15: гл.4.
5 занятие. Контрольная работа №1.
Л-1: П4.4, 4.5, 4.8, 4.9; Л-8: П12-16; Л-12: Л-7,8 ; Л-15: гл.3.
Модуль 2. Механизмы с высшими кинематическими парами
6 занятие. Синтез цилиндрической зубчатой передачи.
Л-1: П11.1-11.3, 11.5, 11.7, 11.9; Л-9: П1.2, 1.3, 1.5, 1.7, 1.9; Л-12: Л-14.
7 занятие. Проектирование многозвенных планетарных зубчатых механизмов.
Л-1: П10.4; Л-9: П2.1, 2.2; Л-12: Л-17; Л-15: гл.6.
8 занятие. Контрольная работа № 2.
Домашние задания
Модуль 1. Механика машин.
Домашнее задание 1 «Структурный и кинематический анализ рычажного механизма».
1.
Структурный анализ: изобразить структурную схему заданного рычажного
механизма, обозначить на ней звенья и кинематические пары (КП), определить
число звеньев, вид и класс КП, подсчитать число подвижностей и число
избыточных связей для плоского и пространственного механизма, провести
структурный анализ плоского механизма по Ассуру - вычертить первичный
механизм и структурные группы, определить в них число звеньев и КП,
подвижность на плоскости и в пространстве, для пространственных групп
удалить избыточные связи (снижением классов КП без введения местных
подвижностей).
2.
Графоаналитическое исследование кинематики: для заданного положения
механизма вычертить в масштабе кинематическую схему механизма и по ней
решить графически задачу о положениях; записать векторные уравнения для
210
скоростей и алгебраические для угловых скоростей, построить в масштабе план
скоростей и определить по нему скорости всех точек, обозначенных на
механизме, и угловые скорости всех звеньев; аналогичным путем решить
задачу о ускорениях.
3.
Аналитическое исследование кинематики: для заданного механизма изобразить
эквивалентную систему векторных контуров и записать векторные уравнения
их замкнутости; спроецировать эти уравнения на оси координат и, оперируя с
уравнениями проекций, последовательно решить задачи о положениях,
скоростях и ускорениях ( как минимум аналитическое решение провести
только для выходного звена механизма). Полученные аналитическим и графоаналитическим методами результаты кинематического анализа свести в
таблицу. Если использовались компьютерные программы, то в таблице
приводятся и результаты расчета на ЭВМ.
4.
Для выходного звена механизма построить цикловые диаграммы функции
положения, скорости и ускорения (или первой и второй передаточных
функций) от обобщенной координаты  1.
Срок выдачи 1/2 неделя, срок сдачи 7/8 неделя
Трудоемкость 8 часов
Модуль 2. Механизмы с высшими кинематическими парами
Домашнее задание 2 «Силовой анализ рычажного механизма».
1. Вычертить в масштабе кинематическую схему механизма в заданном положении,
показать на ней приложенные внешние силы и моменты, записать рядом со схемой
постановку задачи: что дано и что требуется определить.
2. На базе структурного анализа механизма определить число неизвестных в силовом
расчете. Определить главные векторы и главные моменты сил инерции. Провести
кинетостатический расчет механизма по звеньям и группам Ассура. Для каждого
рассматриваемого элемента системы: изобразить в масштабе его расчетную схему с
приложенными внешними силами и моментами, включая инерционные нагрузки и
реакции, записать векторные уравнения сил и алгебраические уравнения моментов,
вычертить в масштабе планы сил. Составить таблицу результатов силового расчета
(число уравнений должно равняться числу неизвестных в силовом расчете).
211
Срок выдачи 7 неделя, срок сдачи 13 неделя
Трудоемкость 5 часов
Проведение контрольных мероприятий
Модуль 1. Механика машин.
Контрольная работа № 1 «Движение механизма под действием приложенных сил»
Срок проведения 9-10 недели
Модуль 2. Механизмы с высшими кинематическими парами.
Контрольная работа № 2 «Механизмы с высшими кинематическими парами»
Срок проведения 15-16 недели
Типовые примеры контрольных работ
Контрольная работа № 1 «Движение механизма под действием приложенных сил» (см.
приложение 1)
Контрольная работа № 2 «Механизмы с высшими кинематическими парами» (см.
приложение 2)
Вопросы для подготовкам к защитам ДЗ и экзамену
Модуль 1. Механика машин
1. Что называется машиной? Какие машины Вы знаете? Что такое машинный агрегат?
2. Что называется механизмом, кинематической цепью? Какие виды кинематических цепей
существуют? Что называют кинематической парой, как их классифицируют?
3. Как происходит замыкание кинематических пар в кинематической цепи?
4. Что называют звеном, какие виды звеньев существуют? Чем отличается деталь от звена?
5. Сформулируйте определения прямой и обратной задач динамики.
6. Что понимается под динамической моделью механизма?
7. С какой целью производится приведение сил и моментов в механизме? Какое условие
положено в основу приведения сил и моментов?
8. Какое условие положено в основу замены масс и моментов инерции при приведении?
9. Напишите формулу кинетической энергии для кривошипно-ползунного механизма.
10. Какие факторы вызывают периодические и непериодические колебания угловой скорости
динамической модели?
11. Какие основные режимы движения машин Вы знаете?
212
12. Чем характеризуются переходные режимы движения машины?
13. Запишите уравнение движения в дифференциальной форме и покажите как им можно
пользоваться?
14. Как определяется продолжительность переходного процесса?
15. Как оценивается неравномерность хода машины? Как её можно уменьшить?
16. Сформулируйте основное назначение маховой массы (маховика)? В каких случаях маховик
необходим и когда он не требуется?
17. Какова цель установки маховика в машине? Чем следует руководствоваться при выборе места
установки маховика в машине?
18. В каких случаях маховик необходим и когда он не требуется?
19. Выведите формулу для расчёта дополнительных маховых масс при постоянном приведённом
моменте инерции машины?
20. В чём состоит задача уравновешивания?
21. Какие виды неуравновешенности механизмов Вы знаете? Объясните каждый из видов
неуравновешенности.
22. Сформулируйте условия полного уравновешивания механизмов машины.
23. Что является мерой статической и динамической неуравновешенностей?
24. Расскажите о методе замещающих масс при уравновешивании.
25. С какой целью и как устанавливаются корректирующие массы (противовесы)?
26. Как произвести полное статическое уравновешивание (шарнирного четырёхзвенника),
кривошипно-ползунного механизма?
27. Сформулируйте, что такое статическая, моментная и динамическая неуравновешенность
ротора?
28. В чём состоят причины дисбаланса вращающихся деталей?
29. Какие методы виброзащиты Вы знаете?
30. Какой метод виброзащиты называется виброизоляцией? В чём суть этого метода? В каких
случаях он эффективен?
31. Что такое динамическое гашение колебаний? В каких случаях оно применяется?
Модуль 2. Механизмы с высшими кинематическими парами
1. Что называется высшей кинематической парой?
2. Назовите известные Вам механизмы с высшими кинематическими парами?
3. Как записывается условие существования высшей кинематической пары?
4. Дайте определение основной теоремы зацепления.
213
5. Дайте определение линии зацепления в эвольвентной передаче.
6. Запишите уравнения описывающее эвольвенту
7. Сформулируйте основные свойства эвольвенты.
8. Что называется эвольвентной зубчатой передачей?
9. Изменяется ли передаточное отношение эвольвентной передачи при изменении
межосевого расстояния?
10. Что называют зубчатым колесом?
11. Расскажите об основных элементах зубчатого колеса.
12. Запишите формулы окружного и углового шагов эвольвентного зубчатого колеса.
13. Какие методы изготовления зубчатых колёс Вы знаете?
14. В чём заключается сущность изготовления эвольвентных колёс методом огибания?
15. Дайте определение станочного зацепления.
16. Выведите формулы для определения основных размеров зубчатого колеса ( ra ,
s, h ) используя
схему станочного зацепления.
17. Запишите условия отсутствия подрезания в станочном зацеплении.
18. Что такое
z min ? Выведите формулу для определения z min .
19. Что такое
xmin ? Выведите формулу для xmin .
20. Выведите формулу для определения угла зацепления эвольвентной передачи внешнего
зацепления.
21. Какая эвольвентная передача называется передачей без смещения?
22. По каким признакам классифицируют зубчатые передачи?
23. Перечислите основные качественные показатели цилиндрической эвольвентной передачи?
24. Что такое коэффициент торцевого перекрытия? Выведите формулу для
 .
25. Как записывается формула для коэффициента осевого перекрытия   ?
26. Какой зубчатый механизм называется сложным?
27. Какой механизм называется планетарным?
28. Как определить передаточное отношение одной из схем планетарного механизма
аналитическим способом?
29. Какова цель применения метода обращения движения при кинематическом анализе
планетарного механизма?
30. Как используются графический (аналитический) метод для определения угловых скоростей
зубчатых колёс планетарных механизмов?
31. Как формулируется задача кинематического синтеза планетарного механизма?
214
32. Какие основные условия необходимо выполнить при синтезе многосателлитного планетарного
механизма? Перечислите их.
33. Запишите условие соседства для однорядного планетарного механизма с K=3 ?
34. Как обеспечивается условие сборки многосателлитного планетарного механизма?
35. Как определяются числа зубьев (любой из схем) планетарного механизма методом
сомножителей?
36. Определите числа зубьев однорядного планетарного механизма с
u14  5
и К=3.
37. Для каких целей используются конические зубчатые передачи?
38. Укажите достоинства и недостатки конических зубчатых передач
39. Каковы особенности расчёта геометрии конических колёс и передач?
40. Как определяются углы вершин начальных конусов в конической прямозубой передаче при
известном передаточном отношении и межосевом угле?
41. Какие пространственные передачи относятся к гиперболоидным?
42. Какие виды винтовых передач используются в машинах? Укажите их достоинства и недостатки.
43. Какие виды червячных передач используются в машинах?
44. Расскажите о способах изготовления червяков и червячных колёс?
45. Назовите достоинства и особенности кулачковых механизмов, обусловившие их широкое
применение в различных машинах и приборах?
46. Каковы недостатки кулачковых механизмов?
47. Изобразите схемы наиболее распространенных плоских и пространственных кулачковых
механизмов.
48. Как подразделяются кулачковые механизмы по способу замыкания высшей пары?
49. Перечислите основные фазы движения толкателя кулачкового механизма и соответствующие им
углы поворота кулачка?
50. Расскажите об основных этапах синтеза кулачковых механизмов
51. Как определить положение центра вращения кулачка в механизме с поступательно движущемся
толкателем при заданном допустимом угле давления?
52. Как определить положения центра вращения кулачка при заданном допустимом угле давления
и межосевом расстоянии в механизме с качающимся коромысловым толкателем?
53. Из каких соображений выбирается величина радиуса ролика кулачкового механизма?
54. Как
по
теоретическому
(центровому)
профилю
кулачка
(конструктивный) профиль?
55. Что такое манипулятор, автооператор, промышленный робот?
56. Для чего предназначены промышленные роботы?
215
построить
действительный
57. В
чём
заключаются
особенности
структуры
кинематических
цепей
манипуляторов
промышленных роботов?
58. От чего зависят двигательные возможности манипулятора промышленного робота?
59. Что такое подвижность манипулятора ? Как она определяется?
60. Дайте определение рабочего пространства, зоны обслуживания манипулятора и его
маневренности (на любом примере)
ЛАБОРАТОРНЫЕ РАБОТЫ
1.
Структурный анализ плоских рычажных механизмов.
2.
Индикаторная диаграмма и механические характеристики компрессора.
3.
Определение КПД редуктора.
4.
Построение эвольвентных зубьев методом огибания.
5.
Динамическая балансировка роторов.
6.
Синтез кинематических схем рычажных механизмов.
7.
Структура и качественные показатели манипуляторов.
8.
Исследование процесса трения в поступательной кинематической паре.
Последовательность выполнения лабораторных работ по подгруппам
Недели
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Лаб.
1
1
12
12
10
10
4
4
5
5
17
17
8
8
9
9
работы
12
12
1
1
4
4
10
10
17
17
5
5
9
9
8
8
216
Приложение 1
Контрольная работа № 1 «Движение механизма под действием приложенных
сил»
217
Приложение 2
Контрольная работа № 2 «Механизмы с высшими парами»
218
Теория механизмов и машин
Квалификация (степень) – бакалавр
Объем в часах по семестрам
04 семестр
05 семестр
Всего
17 недель
17 недель
Виды учебной работы
Лекции
34
34
-
Семинары
Лабораторные работы
17
17
17
17
-
Самостоятельная работа
51
51
-
Курсовое проектирование
51
-
51
Трудоемкость, час
Трудоемкость, зачетные
единицы
Проверка знаний:
170
119
51
5,5
4
1,5
дифф. зачет
дифф. зачет
Объем, час
Контрольные мероприятия
Кол.
Баллы (max)
8
1
1
1
20
15
6
1
51
1
1
20
15
Модуль 1
Домашнее задание №1
Контрольная работа №1
Модуль 2
Домашнее задание №2
Контрольная работа №2
Самостоятельная проработка
материала
Итоги бально-рейтинговой аттестации:
Отлично
85
Хорошо
70
Удовлетворительно
60
Неделя
План КМ
Объем (час)
Баллы
1
2
3
4
Виды контрольных мероприятий
5 6 7 8 9 10 11 12 13 14
ДЗ 1 КР 1 М1
ДЗ 2
35
219
15
КР2
16
М2
35
17
Отлично
Хорошо
Удовлетворительно
Контроль знаний (4 семестр)
Диф. зачет
30
Литература
Основная литература
1.
Теория механизмов и механика машин. Под ред. Фролова К.В, Тимофеева Г.А.-М.: Изд.
МГТУ, 2002, 2004, 2009, 2012
2.
Попов С.А.,
Тимофеев Г.А.
Курсовое проектирование по
теории механизмов и
механике машин.-М.: Высшая школа, 2002, 2005, 2008.
Дополнительная литература
3.
Артоболевский И.И. Теория механизмов и машин.-М.: Наука,1988.
4.
Попов С.А., Черная Л.А. Математическое и программное обеспечение расчетов
кинематических характеристик: Учебное пособие. -М.: Изд. МГТУ, 1991.
5.
Леонов И.В. Динамика машинного агрегата при неустановившихся режимах движения:
Учебное пособие.-М.: Изд. МГТУ, 1990.
6.
Конспект лекций по новым разделам курса ТММ: Учебное пособие. Под ред. К.В.
Фролова, Д.М. Лукичева.-М.: Изд.М ВТУ, 1986.
7.
Динамика машинного агрегата: Учебное пособие. Под ред. Б.И. Крюкова.-М.: Изд.
МВТУ, 1988.
8.
Мусатов А.К. Кинематические и динамические характеристики механизмов и машин:
Учебное пособие. М.:Изд. МВТУ, 1987.
9.
Проектирование механизмов с высшими кинематическими парами: Учебное пособие.
Под ред. А.К.Мусатова.-М.: Изд.МВТУ,1989.
10.
Силовой расчет, уравновешивание, проектирование механизмов: Учебное пособие. Под
ред. А.К. Мусатова.-М.: Изд.МГТУ,1990.
11.
Головин А.А. Проектирование сложных рычажных механизмов: Учебное пособие. М.:
Изд. МГТУ, 1995.
12.
Тимофеев Г.А. Теория механизмов и машин: курс лекций. М.: Высшее образование,
2010.- 356 с.
220
13.
Теория механизмов и механика машин: Учебное пособие. Под ред. Г.А.Тимофеева.- М.:
Изд. МГТУ, 2002.
14.
Тарабарин В.Б, Кузенков В.В., Фурсяк Ф.И. Методические указания к выполнению
лабораторных работ по курсу ТММ.- М.: Изд. МГТУ, 2009.
15.
Теория механизмов и машин. Курсовое проектирование: Учебное пособие. Под ред. Г.А.
Тимофеева, Н.В. Умнова.-М.: Изд. МГТУ, 2010, 2012
ЛЕКЦИИ
Модуль 1. Механика машин
Лекция 1. Введение. Проблемы теории механизмов и механики машин. Понятие о
машинном агрегате. Основные виды машин и механизмов и их элементы.
Л-1: Введение, гл.1: П1.1, 1.2; Л-2: П1.1; Л-7: Введение; Л-8: П1,2; Л-12: Л-1.
Лекция 2. Строение и кинематика механизмов. Классификация кинематических пар.
Число степеней свободы механизма. Структурный анализ и синтез механизмов. Избыточные
связи и способы их устранения при проектировании. Кинематические характеристики
механизмов.
Л-1: гл. 2; Л-2: П2.1, 2.2; Л-8: П2, 3; Л-12: Л-2, 3.
Лекция 3. Кинематическое исследование плоских рычажных механизмов аналитическим
методом с использованием ЭВМ.
Л-1: П3.1, 3.3, 3.5; Л-4; Л-12: Л-5; Л-15: гл.2.
Лекция 4. Динамика машин. Расчетные схемы машинных агрегатов. Механические
характеристики двигателей и рабочих машин. Приведение масс. Приведение сил. Динамическая
модель машинного агрегата.
Л-1: П1.3, 4.1-4.3; Л-5: П2.1-2.3; Л-6: П2.1, 2.2; Л-8: П8-11; Л-12: Л-7.
Лекция
5.
Уравнение
движения
машинного
агрегата
в
энергетической
и
дифференциальной форме.
Режимы движения машинного агрегата. Установившийся режим. Понятие о маховых
массах и их роль в машинном агрегате.
Л-1: П1.4, 4.4, 4.8; Л-5: П2.2, 2.3; Л-8: П12, 15; Л-12: Л-7.
Лекция 6. Определение закона движения машинного агрегата при установившемся
режиме работы и способы его обеспечения. Неустановившееся движение. Определение закона
неустановившегося движения машинного агрегата.
221
Л-1: П4.5, 4.9, 6.3, 6.5; Л-5: П4.2-4.4; Л-6: П2.3-2.5;
Лекция 7. Силовой расчет механизма без учета трения аналитическим способом с
использованием ЭВМ.. Статическое уравновешивание рычажных механизмов.
Л-1: П6.1, 6.2; Л-3: П59-61; Л-5: гл.4; Л-10: П1.1, 1.2, гл.3; Л-12: Л-6.
Краткие сведения о КПД механизма. Учет трения в кинематических парах механизма
(материал для самостоятельного изучения)
Л-7: П2.3, 4.2, 5.5; Л-8: П13, 14, 16; Л-10: П2-1. ; Л-12: Л-8, Л-26.
Лекция 8. Виды неуравновешенности роторов. Уравновешевание роторов.
Основы
виброзащиты человека-оператора и машины. Виброизоляция и динамическое виброгашение.
Л-1: гл. 7; Л-3: П62; Л-6: гл.4; Л-7: гл.3; Л-10: гл.4; Л-12: Л-10, 11.
Модуль 2. Механизмы с высшими кинематическими парами
Лекция 9.
передача.
Кинематика высшей кинематической пары.
Цилиндрическая зубчатая
Элементы эвольвентного зубчатого колеса и основные расчетные зависимости.
Эвольвентное зацепление, его свойства. Эвольвентная зубчатая передача.
Л-1: П3.7, 9.2-9.4, 9.7, 11.1-11.5, 11.9; Л-2: П6.6; Л-9: П1.1-1.5, 1-9; Л-12: Л-13.
Лекция 10. Станочное зацепление.
Подрезание и заострение зубьев. Определение
основных размеров зубчатого колеса и передачи. Применение ЭВМ. Качественные показатели
эвольвентной зубчатой передачи.
Л-1: П11.6-11.8, 11.10, 11.11; Л-2: П6.2-6.5; Л-9: П1.6-1.8, 1-10, 1.11; Л-12: Л-15.
Лекция 11. Планетарные механизмы. Кинематическое исследование планетарных
механизмов.
Л-1: П3.7, П10.4; Л-2: П7.1, 7.2, 7.4; Л-9: П2.1, 2.2; Л-12: Л-18.
Лекция 12. Проектирование планетарных редукторов по заданному передаточному
отношению.
Л-1: П10.4; Л-2: П7.3; Л-9: П2.3; Л-12: Л-18; Л-15: гл.5.
Лекция 13. Кулачковые механизмы и их основные параметры. Построение графика
перемещения толкателя по заданной форме профиля кулачка. Понятие об угле давления в
кулачковом механизме.
Л-1: П14.1-14.3; Л-2: П8.5; Л-9: П4.1-4.3; Л-12: Л-22.
Лекция 14. Формула для определения угла давления. Определение оптимальных
размеров кулачкового механизма по допустимому углу давления.
Л-1: П14.4; Л-2: П8.3-8.6; Л-9: П4.4, 4.5; Л-12: Л-22, 23.
Лекция 15. Синтез кулачковых механизмов по заданному закону движения толкателя и
допустимому углу давления.
222
Л-1: П14.6; Л-2: П8.7; Л-9: П4.6, 4.7; Л-12: Л-23.
Лекция 16. Проектирование кинематических схем плоских рычажных механизмов по
заданным условиям с применением ЭВМ.
Л-1: гл.13; Л-2: П2.3; Л-3: П110; Л-10: гл.5; Л-11: гл3; Л-12: Л-4.
Лекция 17. Манипуляторы, область применения, технические характеристики и
кинематика.
Л-1: П17.1-17.3; Л-6: П3.1-3.3; Л-10: гл.6; Л-12: Л-24, 25.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Механика машин
1 занятие. Построение планов скоростей и ускорений рычажных механизмов.
Л-1: П3.4, 3.6; Л-8: П4,5; Л-13; Л-12: Л-5.
2 занятие. Структурный анализ и синтез механизмов; устранение избыточных связей.
Л-1: П2.1-2.5; Л-8: П2,3; Л-13; Л-12: Л-3.
3 занятие. Силовой расчет механизмов.
Л-1: П6.1, 6.2; Л-10; гл.1; Л-13; Л-12: Л-9; Л-15: гл.4.
4 занятие. Динамическая модель и ее параметры
Л-1: П4.4, 4.5, 4.8, 4.9; Л-8: П12-16; Л-12: Л-7,8 ; Л-15: гл.3.
5 занятие. Контрольная работа №1.
Модуль 2. Механизмы с высшими кинематическими парами
6 занятие. Элементы эвольвентного зубчатого колеса, станочного и рабочего
зацеплений.
Л-1: П11.1-11.3, 11.5, 11.7, 11.9; Л-9: П1.2, 1.3, 1.5, 1.7, 1.9; Л-12: Л-14.
7 занятие. Планетарные механизмы (кинематический анализ и синтез)
Л-1: П10.4; Л-9: П2.1, 2.2; Л-12: Л-17; Л-15: гл.6.
8 занятие. Контрольная работа № 2.
ДОМАШНИЕ ЗАДАНИЯ
Модуль 1. Механика машин
Домашнее задание 1 Структурный и кинематический анализ рычажного механизма.
223
1. Структурный анализ: изобразить структурную схему заданного рычажного механизма,
обозначить на ней звенья и кинематические пары (КП), определить число звеньев, вид и
класс КП, подсчитать число подвижностей и число избыточных связей для плоского и
пространственного механизма, провести структурный анализ плоского механизма по
Ассуру - вычертить первичный механизм и структурные группы, определить в них число
звеньев и КП, подвижность на плоскости и в пространстве, для пространственных групп
удалить избыточные связи (снижением классов КП без введения местных
подвижностей).
2. Графоаналитическое исследование кинематики: для заданного положения механизма
вычертить в масштабе кинематическую схему механизма и по ней решить графически
задачу о положениях; записать векторные уравнения для скоростей и алгебраические для
угловых скоростей, построить в масштабе план скоростей и определить по нему
скорости всех точек, обозначенных на механизме, и угловые скорости всех звеньев;
аналогичным путем решить задачу о ускорениях.
3. Аналитическое исследование кинематики: для заданного механизма изобразить
эквивалентную систему векторных контуров и записать векторные уравнения их
замкнутости; спроецировать эти уравнения на оси координат и, оперируя с уравнениями
проекций, последовательно решить задачи о положениях, скоростях и ускорениях ( как
минимум аналитическое решение провести только для выходного звена механизма ).
Полученные аналитическим и графо-аналитическим методами результаты
кинематического анализа свести в таблицу. Если использовались компьютерные
программы, то в таблице приводятся и результаты расчета на ЭВМ.
Срок выдачи 1/2 неделя, срок сдачи 7/8 неделя
Трудоемкость 8 часов
Модуль 2. Механизмы с высшими кинематическими парами
Домашнее задание 2 “Кинетостатический силовой расчет рычажного механизма”.
1.
Вычертить в масштабе кинематическую схему механизма в заданном положении, показать на ней
приложенные внешние силы и моменты, записать рядом со схемой постановку задачи: что дано и
что требуется определить.
2.
На базе структурного анализа механизма определить число неизвестных в силовом расчете.
Определить главные векторы и главные моменты сил инерции. Провести кинетостатический
расчет механизма по звеньям и группам Ассура. Для каждого рассматриваемого элемента
224
системы: изобразить в масштабе его расчетную схему с приложенными внешними силами и
моментами, включая инерционные нагрузки и реакции, записать векторные уравнения сил и
алгебраические уравнения моментов, вычертить в масштабе планы сил. Составить таблицу
результатов силового расчета (число уравнений должно равняться числу неизвестных в силовом
расчете).
Срок выдачи 7 неделя, срок сдачи 13 неделя
Трудоемкость
5 часов
Проведение контрольных мероприятий
Модуль 1. Механика машин.
Контрольная работа № 1 «Движение механизма под действием приложенных сил»
Срок проведения 9-10 недели
Модуль 2. Механизмы с высшими кинематическими парами.
Контрольная работа № 2 «Механизмы с высшими кинематическими парами»
Срок проведения 15-16 недели
Типовые примеры контрольных работ
Контрольная работа № 1 «Движение механизма под действием приложенных сил» (см.
приложение 1)
Контрольная работа № 2 «Механизмы с высшими кинематическими парами» (см.
приложение 2)
Вопросы для подготовкам к защитам ДЗ и экзамену
Модуль 1. Механика машин
1. Что называется машиной? Какие машины Вы знаете? Что такое машинный агрегат?
2. Что называется механизмом, кинематической цепью? Какие виды кинематических цепей
существуют? Что называют кинематической парой, как их классифицируют?
3. Как происходит замыкание кинематических пар в кинематической цепи?
4. Что называют звеном, какие виды звеньев существуют? Чем отличается деталь от звена?
5. Сформулируйте определения прямой и обратной задач динамики.
6. Что понимается под динамической моделью механизма?
7. С какой целью производится приведение сил и моментов в механизме? Какое условие
положено в основу приведения сил и моментов?
225
8. Какое условие положено в основу замены масс и моментов инерции при приведении?
9. Напишите формулу кинетической энергии для кривошипно-ползунного механизма.
10. Какие факторы вызывают периодические и непериодические колебания угловой скорости
динамической модели?
11. Какие основные режимы движения машин Вы знаете?
12. Чем характеризуются переходные режимы движения машины?
13. Запишите уравнение движения в дифференциальной форме и покажите как им можно
пользоваться?
14. Как определяется продолжительность переходного процесса?
15. Как оценивается неравномерность хода машины? Как её можно уменьшить?
16. Сформулируйте основное назначение маховой массы (маховика)? В каких случаях маховик
необходим и когда он не требуется?
17. Какова цель установки маховика в машине? Чем следует руководствоваться при выборе места
установки маховика в машине?
18. В каких случаях маховик необходим и когда он не требуется?
19. Выведите формулу для расчёта дополнительных маховых масс при постоянном приведённом
моменте инерции машины?
20. В чём состоит задача уравновешивания?
21. Какие виды неуравновешенности механизмов Вы знаете? Объясните каждый из видов
неуравновешенности.
22. Сформулируйте условия полного уравновешивания механизмов машины.
23. Что является мерой статической и динамической неуравновешенностей?
24. Расскажите о методе замещающих масс при уравновешивании.
25. С какой целью и как устанавливаются корректирующие массы (противовесы)?
26. Как произвести полное статическое уравновешивание (шарнирного четырёхзвенника),
кривошипно-ползунного механизма?
27. Сформулируйте, что такое статическая, моментная и динамическая неуравновешенность
ротора?
28. В чём состоят причины дисбаланса вращающихся деталей?
29. Какие методы виброзащиты Вы знаете?
30. Какой метод виброзащиты называется виброизоляцией? В чём суть этого метода? В каких
случаях он эффективен?
31. Что такое динамическое гашение колебаний? В каких случаях оно применяется?
226
Модуль 2. Механизмы с высшими кинематическими парами
4. Что называется высшей кинематической парой?
5. Назовите известные Вам механизмы с высшими кинематическими парами?
6. Как записывается условие существования высшей кинематической пары?
7. Дайте определение основной теоремы зацепления.
8. Дайте определение линии зацепления в эвольвентной передаче.
9. Запишите уравнения описывающее эвольвенту
10. Сформулируйте основные свойства эвольвенты.
11. Что называется эвольвентной зубчатой передачей?
12. Изменяется ли передаточное отношение эвольвентной передачи при изменении
межосевого расстояния?
13. Что называют зубчатым колесом?
14. Расскажите об основных элементах зубчатого колеса.
15. Запишите формулы окружного и углового шагов эвольвентного зубчатого колеса.
16. Какие методы изготовления зубчатых колёс Вы знаете?
17. В чём заключается сущность изготовления эвольвентных колёс методом огибания?
18. Дайте определение станочного зацепления.
19. Выведите формулы для определения основных размеров зубчатого колеса ( ra ,
s, h ) используя
схему станочного зацепления.
20. Запишите условия отсутствия подрезания в станочном зацеплении.
21. Что такое
z min ? Выведите формулу для определения z min .
22. Что такое
xmin ? Выведите формулу для xmin .
23. Выведите формулу для определения угла зацепления эвольвентной передачи внешнего
зацепления.
24. Какая эвольвентная передача называется передачей без смещения?
25. По каким признакам классифицируют зубчатые передачи?
26. Перечислите основные качественные показатели цилиндрической эвольвентной передачи?
27. Что такое коэффициент торцевого перекрытия? Выведите формулу для
28. Как записывается формула для коэффициента осевого перекрытия   ?
29. Какой зубчатый механизм называется сложным?
30. Какой механизм называется планетарным?
227
 .
31. Как определить передаточное отношение одной из схем планетарного механизма
аналитическим способом?
32. Какова цель применения метода обращения движения при кинематическом анализе
планетарного механизма?
33. Как используются графический (аналитический) метод для определения угловых скоростей
зубчатых колёс планетарных механизмов?
34. Как формулируется задача кинематического синтеза планетарного механизма?
35. Какие основные условия необходимо выполнить при синтезе многосателлитного планетарного
механизма? Перечислите их.
36. Запишите условие соседства для однорядного планетарного механизма с K=3 ?
37. Как обеспечивается условие сборки многосателлитного планетарного механизма?
38. Как определяются числа зубьев (любой из схем) планетарного механизма методом
сомножителей?
39. Определите числа зубьев однорядного планетарного механизма с
u14  5
и К=3.
40. Для каких целей используются конические зубчатые передачи?
41. Укажите достоинства и недостатки конических зубчатых передач
42. Каковы особенности расчёта геометрии конических колёс и передач?
43. Как определяются углы вершин начальных конусов в конической прямозубой передаче при
известном передаточном отношении и межосевом угле?
44. Какие пространственные передачи относятся к гиперболоидным?
45. Какие виды винтовых передач используются в машинах? Укажите их достоинства и недостатки.
46. Какие виды червячных передач используются в машинах?
47. Расскажите о способах изготовления червяков и червячных колёс?
48. Назовите достоинства и особенности кулачковых механизмов, обусловившие их широкое
применение в различных машинах и приборах?
49. Каковы недостатки кулачковых механизмов?
50. Изобразите схемы наиболее распространенных плоских и пространственных кулачковых
механизмов.
51. Как подразделяются кулачковые механизмы по способу замыкания высшей пары?
52. Перечислите основные фазы движения толкателя кулачкового механизма и соответствующие им
углы поворота кулачка?
53. Расскажите об основных этапах синтеза кулачковых механизмов
54. Как определить положение центра вращения кулачка в механизме с поступательно движущемся
толкателем при заданном допустимом угле давления?
228
55. Как определить положения центра вращения кулачка при заданном допустимом угле давления
и межосевом расстоянии в механизме с качающимся коромысловым толкателем?
56. Из каких соображений выбирается величина радиуса ролика кулачкового механизма?
57. Как
по
теоретическому
(центровому)
профилю
кулачка
построить
действительный
(конструктивный) профиль?
58. Что такое манипулятор, автооператор, промышленный робот?
59. Для чего предназначены промышленные роботы?
60. В
чём
заключаются
особенности
структуры
кинематических
цепей
манипуляторов
промышленных роботов?
61. От чего зависят двигательные возможности манипулятора промышленного робота?
62. Что такое подвижность манипулятора ? Как она определяется?
63. Дайте определение рабочего пространства, зоны обслуживания манипулятора и его
маневренности (на любом примере)
ЛАБОРАТОРНЫЕ РАБОТЫ
9.
Структурный анализ плоских рычажных механизмов.
10.
Индикаторная диаграмма и механические характеристики компрессора.
11.
Определение КПД редуктора.
12.
Построение эвольвентных зубьев методом огибания.
13.
Динамическая балансировка роторов.
14.
Синтез кинематических схем рычажных механизмов.
15.
Структура и качественные показатели манипуляторов.
16.
Исследование процесса трения в поступательной кинематической паре.
Последовательность выполнения лабораторных работ по подгруппам
Недели
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Лаб.
1
1
12
12
10
10
4
4
5
5
17
17
8
8
9
9
работы
12
12
1
1
4
4
10
10
17
17
5
5
9
9
8
8
229
Приложение 1
Контрольная работа № 1 «Движение механизма под действием приложенных
сил»
230
Приложение 2
Контрольная работа № 2 «Механизмы с высшими парами»
231
Физическая Культура
4 семестр
Теория
Лекция
Психологические основы умственного труда и интеллектуальной деятельности. Средства
физической культуры в регулировании работоспособности.
Психофизическая характеристика интеллектуальной деятельности и учебного труда
студента. Динамика работоспособности студентов в учебном году и факторы ее определяющие.
Основные принципы изменения психофизиологического состояния студентов в период
экзаменационной сессии, критерии нервно-эмоционального и психофизического утомления.
Оздоровительно-реабилитационная и адаптивная физическая культура. Особенности
использования средств физической культуры для оптимизации работоспособности,
профилактики нервно-эмоционального и психофизического утомления студентов, повышение
эффективности учебного труда (2 часа).
В течение семестра
По графику учебного отделения
- Методика и особенности занятий избранным видом спорта или системой физических
упражнений, 1 час (по тематике учебных отделений).
Практика
17 недель
- Занятия по планам учебных отделений (видов спорта) (4 часа в неделю).
Контрольные упражнения
В течение семестра
- контрольные упражнения вида спорта по графику учебного отделения.
ЗАЧЕТНЫЕ ТРЕБОВАНИЯ
По системе балльно-рейтинговой оценки
университета проставляются с учетом модулей.
результатов
успеваемости
студентов
Внимание!
Медицинская справка не является основанием для освобождения от занятий и получения зачета
по физическому воспитанию.
Студенты, освобожденные по состоянию здоровья от практических занятий на длительный
срок, зачисляются в специальное учебное отделение для освоения доступных им разделов
учебной программы с начала учебного семестра или сразу после получения медицинской
справки.
Студенты, находящиеся на дообследовании должны зарегистрироваться в специальном
отделении до получения ими мед.заключения (справки).
232