(2 балла) ТОЛЬКО ОТВЕТ
реклама

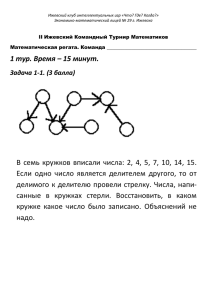
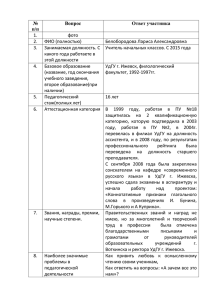
Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 1 тур. Время – 10 минут. Задача 1-1. (1 балл) ТОЛЬКО ОТВЕТ В корзине лежат красные и синие шарики, причем синие составляют 3/5 общего количества. После этого число красных шариков удвоили. Какую долю теперь составляют синие шарики? Красные составляют 2/5. Синие – 3 части Красные -2 части, а стали 4 части, итого синих осталось 3/7 Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 1 тур. Время – 10 минут. Задача 1-2. (2 балла) ТОЛЬКО ОТВЕТ В зоомагазине продают больших и маленьких птиц. Большая птица стоит вдвое дороже маленькой. Одна дама купила 5 больших птиц и 3 маленьких, а другая - 5 маленьких и 3 больших. При этом первая дама заплатила на 200 рублей больше. Сколько стоит каждая птица? Первая дама купила 13 маленьких Вторая – 11 маленьких Маленькая стоит 100 Большая – 200 Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 1 тур. Время – 10 минут. Задача 1-3. (3 балла) ОТВЕТ С ОБОСНОВАНИЕМ ̅̅̅ . Сравните числа ̅̅̅̅̅ Пусть ̅̅̅̅ 𝑎𝑑 < ̅̅̅ 𝑏𝑐 и 𝑎𝑐 ̅̅̅ > ̅𝑏𝑑 𝑎𝑏𝑐 и ̅̅̅̅̅ 𝑏𝑎𝑑 . Значит, a=b, значит d<c. ̅̅̅̅̅ 𝑎𝑏𝑐 > ̅̅̅̅̅ 𝑏𝑎𝑑 Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 2 тур. Время – 15 минут. Задача 2-1. (2 балла) ТОЛЬКО ОТВЕТ Найдите ребро куба, если площадь его поверхности численно равна ¾ от его объема. Пусть ребро куба равно x. 6xx = ¾ xxx 64/3 = x X=8 x Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 2 тур. Время – 15 минут. Задача 2-2. (3 балла) Сколько существует пар натуральных чисел (M,N), что выполняется равенство M/2 = 6/N? MN = 12 M = 1, 2, 3, 4, 6, 12. Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 2 тур. Время – 15 минут. Задача 2-3. ( 5 баллов) Ответ обоснуйте На доске написаны в строку 2013 целых чисел. Докажите, что можно стереть одно число так, что сумма оставшихся чисел будет чётной. Если все написанные числа – НЕЧЕТНЫЕ, то их сумма – НЕЧЕТНАЯ. Тогда можно вычеркнуть любое число. Если там все числа четные, то сумма четная, и опять вычеркиваем любое. Если есть и четные, и нечетные, то ПОДБЕРЕМ, какое вычеркнуть. Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 3 тур. Время – 20 минут. Задача 3-1. (4 балла) Если из количества учеников 6A вычесть 23 и полученную разность умножить на 23, то получится столько же, как если бы из этого числа вычли 13 и разность умножили бы на 13. Сколько же там учеников? Пусть учеников в классе x. Из первого равенства получим 23(x–23) = 23x – 529 Из второго 13(x–13) = 13x–169. 23х–529 = 13x–169 23x–360 = 13x 10х = 360 X=36 Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 3 тур. Время – 20 минут. Задача 3-2. ( 5 баллов) ТОЛЬКО ОТВЕТ Каждый рабочий, копая канаву поодиночке, справился бы с этой работой за 36 часов. Какое наименьшее число рабочих надо нанять, чтобы канава была вырыта раньше, чем за 2 часа 50 минут? 2 часа 50 минут = это 2 5/6 часа, то есть 17/6 часа. Значит, надо за один час сделать > 6/17 работы. Один рабочий за час делает 1/36 часть работы. Осталось 6/17 : 1/36 = 12 12/17 < 13 Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 3 тур. Время – 20 минут. Задача 3-3. ( 7 баллов) Назовем фигуру, расположенную в клетчатом прямоугольнике 68, змейкой, если она состоит из клеток, имеющих общие границы по стороне, и каждая клетка змейки, за исключением крайних, имеет ровно двух соседних ( по стороне). Соприкосновение двух клеток змейки по углу возможно (см.рис.). Нарисуйте змейку длиной 31. Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 4 тур. Время – 25 минут. Задача 4-1. ( 4 балла) ОТВЕТ Анна сходила в ресторан «Вечерний». Там ей очень понравилось, и она решила дать 10% чаевых от того счета, который сама подсчитала. Но пока она находилась в ресторане, уже стукнуло 6 часов вечера, и на любой счет появилась вечерняя наценка в 15%. В итоге она вместе с чаевыми и наценкой заплатила 2750 руб. Сколько бы она заплатила, если бы не давала чаевых и ушла бы до 18.00? Сначала счет составлял 100% Анна хотела дать еще 10% Ресторан сам добавил 15% Итого получилось оплата 125% от первоначальной суммы, и это 2750 руб. Значит, 25% = 2750:5 = 550, 100% = 5504 = 2200 руб. Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 4 тур. Время – 25 минут. Задача 4-2. ( 6 баллов) ОБОСНОВАНИЕ Дети загадали натуральное число и произнесли следующие девять фраз: «Число делится на 2», «Число делится на 3, но не делится на 2», «Число делится на 4, но не делится на 3», . . . , «Число делится на 10, но не делится на 9». Могут ли быть верными одновременно 5 фраз? Если да - приведите пример, если нет, обоснуйте. Если верная какая-то фраза, то следующая точно неверна. Фраз 9. Чтобы было верно пять из них, должны быть верны все фразы про четные числа. Но тогда все про нечетные – неверны. Значит, число не делится на 5 и делится на 10, такого не бывает. Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 4 тур. Время – 25 минут. Задача 4-3. (10 баллов) ОБОСНОВАНИЕ В автомобильных гонках участвовало три машины – A, B, C. На дистанцию сначала ушла машина А, потом В, потом С. На трассе машину А обогнали 3 раза, машину В – пять раз, а машину С – 8 раз. В каком порядке они могли прийти к финишу? Машина С была последняя. Её никто не мог обогнать, пока она сама не обогнала этого «гонщика». И снова так же. Но машину С обгоняли 8 раз, а машины А и B – в сумме тоже 8 раз, значит, это всегда только С. Но в итоге С все равно осталась последней, а А и B вообще друг друга не обгоняли. Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 5 тур. Время – 20 минут. Задача 5-1. ( 3 балла) Ответ+ пример Какое наибольшее число сторон может иметь фигура, являющаяся общей частью треугольника и выпуклого четырехугольника? Нарисуйте пример Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 5 тур. Время – 20 минут. Задача 5-2. (4 балла) ПРИМЕР Расставьте цифры от 1 до 8 по кругу так, чтобы каждое число делилось на разность своих соседей. 61725384 Ижевский клуб интеллектуальных игр «Что? Где? Когда?» МБОУ Экономико-математический лицей № 29 г. Ижевска Республиканский ресурсный центр по математике Центр математического образования школьников, УдГУ V Ижевский Командный Турнир Математиков Математическая регата, 16 марта 2013г. Команда ____________________________________ 5 тур. Время – 20 минут. Задача 5-3. ( 8 баллов) ОБОСНОВАНИЕ Несколько (больше пяти) шариков выложены в ряд. Каждый покрашен в какой-то цвет. Оказалось, что среди любых трёх шариков, идущих подряд, хотя бы два — красные, а среди любых шести шариков, идущих подряд, хотя бы два — синие. Сколько среди них желтых? Ответ обоснуйте Среди первых шести шариков – хотя бы 4 красных Среди первых шести шариков – хотя бы 2 синих. На желтых места, увы, просто нет.