ГЛАВА 4. ТЕОРЕМА ОБ ИЗМЕНЕНИИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ
реклама

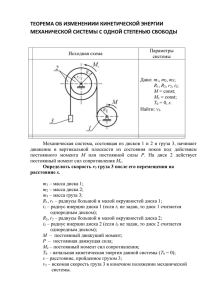
ГЛАВА 4. ТЕОРЕМА ОБ ИЗМЕНЕНИИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Теорема в форме дифференциального уравнения: T P dT P, dt или где в левой части уравнения представлена полная производная по времени от кинетической энергии (КЭ) системы (или механизма) T , т.е. скорость ее нарастания (убывания). Кинетическая энергия равна мощности приложенных внешних и внутренних сил. Здесь Здесь Tсистемы Tзвеньев , P Pсил Fi vi M j j (1) Fi – приложенная сила, vi – скорость точки приложения силы, M j – момент пары сил, приложенной к звену, j – угловая скорость звена механизма. Теорема (1) для механизма с одной степенью свободы, с голономными связями, с выбранной обобщенной координатой q , приводится к виду: aq Q a при 2T P , Q 2 q q (2) или q bQ 0 при q2 P ba , Q 2T q 1 (3) Из (3) следует, что обобщенное ускорение механизма q прямо пропорционально обобщенной силе механизма пропорциональности b. Коэффициент Q с коэффициентом пропорциональности b равен обратному коэффициенту инерции a , т.е. – отношению квадрата обобщенной скорости q 2 к двойной кинетической энергии 2T механизма и с обобщенной силой Q , равной мощности P системы приложенных внешних и внутренних сил, деленной на обобщенную скорость механизма q . Замечание. Если в качестве обобщенной координаты q принять декартову координату x или y , то коэффициент a называется приведенной массой механизма и обозначается a mпр. , если q принять угол поворота, то коэффициент a называется приведенной массой механизма и обозначается a J пр . Теорема об изменении кинетической энергии на произвольном конечном интервале времени в форме «первого интеграла энергии»: T T0 A (5) Уравнение (5) может быть прочитано как: приращение кинетической энергии любой механической системы за конечный интервал времени [t0 , t ] равно работе всех сил (внешних и внутренних), приложенных к системе за этот промежуток времени. Работа силы или пары сил в общем случае равна определенному интегралу по времени от мощности силы или пары сил: t A P(t )dt (Нм≡Дж) t0 Рассмотрим несколько случаев: 1) мощность и работа постоянной силы на направленном прямолинейном перемещении s равна P F v Fv cos Fvv, A Fs cos Fs s , где Fv , Fs - проекции силы на скорость v и направление перемещения s 2) мощность и работа силы сухого трения при неизменном направлении движения s Pf Fvv fNv , Af Fs s fN s , где f – коэффициент трения, N – нормальное давление на негладкую поверхность. 3) работа силы тяжести при перемещении «вверх» или «вниз»: A hG где h - разность высот между начальным и конечным положениями 4) мощность и работа пары сил трения качения с моментом M к : P M к N 0 , A M к N 0 , где M к N -момент трения качения, - коэффициент трения качения 5) мощность и работа постоянного момента M пары сил: P M M , A M , где M – проекция M на направление , – угол поворота пары сил. Теорема об изменении кинетической энергии для одностепенного механизма с постоянным коэффициентом инерции 1 a q 2 q02 A , при 2 В случае постоянной мощности t A Pdt сил (6) t0 P const , (постоянной обобщенной силы Q ) имеем динамическое уравнение энергии q 2 q02 2bQq , при b a 1 const Q Пример выполнения задания P const q (7) Рис.1 Пример решения задачи Одностепенной механизм (рис. 1) состоит из трех подвижных твердых тел – звеньев, соединенных нерастяжимым тросом: ползуна 1 массой m1 , колеса 2 массой m2 , радиуса r2 , центрального радиуса инерции i2 и колеса 3 массой m3 , радиуса r3 , радиуса инерции i3 . В начальное мгновение t0 0 механизм не имел скорости. Принимая за обобщенную координату q направленное смещение s груза 1, т.е. полагая q s , найти скорость груза v s , как функцию перемещения s . При этом считать, что имеется сухое трение груза об опору с известным коэффициентом трения f и момент трения качения с коэффициентом трения δ; заданы углы α и β наклонной поверхности. Все величины заданы в СИ. Решение: Пусть s – обобщенное перемещение механизма, s v – обобщенная скорость, s - обобщенное ускорение. Покажем механизм в движении, в его произвольном «положительном состоянии», когда фазовые координаты s 0 , s 0 . Покажем веса G1 , G2 , G3 , а также - идеальные (не имеющие мощности) реакции голономных связей: N1 , N 2 , N3 , где, очевидно, N1 G1 cos , N3 G3 cos . Имеем силы трения и моменты пар сил трения F1 fN1 fG1 cos , M 3 N3 G3 cos . Звено 1 - выполняет прямолинейное поступательное движение, Звено 2 – вращательное движение с угловой скоростью 2 v , r2 Звено 3 – плоское движение со скоростью центра масс v3 v , угловой скоростью Найдем v . r3 мощность системы сил, приложенных к механизму посредством скалярного умножения сил на скорости их точек приложения: P G1 v F1 v N1 v G2 O N 3 v3 G3 v3 M 3 , или P G1v sin F1v G3v sin M 3 v r3 Обобщенная сила механизма по обобщенной координате s (обобщенная скорость v ) находится из мощности приложенных сил P по формуле Q P P s v Окончательное выражение для обобщенной силы Q G1 sin F1 G3 sin M3 r3 или Q m1 g sin fm1 g cos m3 g sin m3 g cos r3 (9) Из выражения (9) видно, что обобщенная сила не зависит от времени Q const , поэтому работа системы сил на перемещении из начального положения ( s 0 ) в произвольное конечное положение ( s 0 ) равна s A Qds Qs (Нм≡Дж), (10) 0 где Q – получено ранее (9). Теперь найдем к кинетической энергии механизма в произвольном его состоянии, задаваемом векторной строкой [ s v 0, s 0 ] Она состоит из кинетической энергии трех подвижных звеньев. mv2 1) кинетическая энергия поступательного движения звена равна 2 2) вращательного движения mv2 J z w2 miz2 w2 , 2 2 3) плоского движения: l 2 milz2 w2 , где lz – ось, проведенная через 2 центр масс перпендикулярной плоскости движения. Находим двойную кинетическую энергию механической системы 2T m1v 2 m2i22 w22 m3v 2 m3i32 w32 или m2i22 m3i32 2 2T m1 2 m3 2 v r2 r3 Общий множитель при квадрате обобщенной скорости в двойной кинетической энергии называется приведенным коэффициентом инерции механизма, или, более точно для данного случая - приведенной массой механизма (т.к. в качестве обобщенной была выбрана линейная координата): m2i22 m3i32 a m1 2 m3 2 r2 r3 (11) Подставляя результаты (11) и (9) в (7) и учитывая условие задачи v0 0 . получаем ответ q 2 2bQq при q s, q v , или m3 g cos 2 m1 g sin fm1 g cos m3 g sin r3 2 s, v 2 2 mi mi m1 22 2 m3 323 r2 r3 (7) Выражение (7) дает взаимосвязь между перемещением s груза (1) и его скоростью v . Варианты заданий: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22