Рассеяние Ми

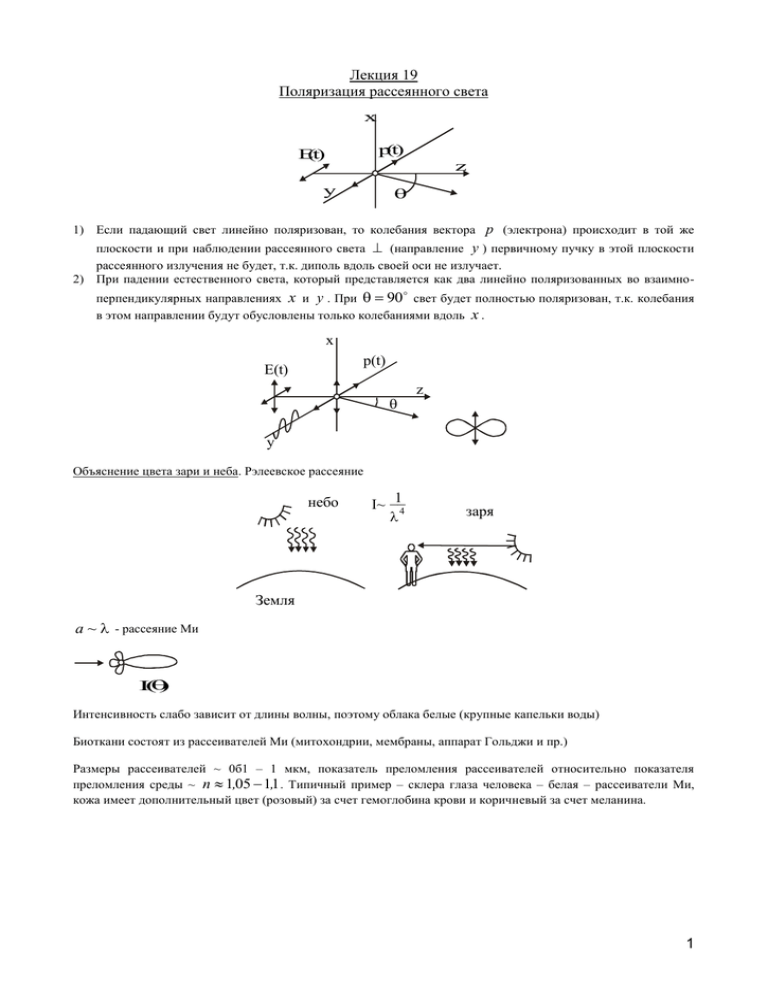
Лекция 19
Поляризация рассеянного света
x
p(t)
E(t)
z

y
1) Если падающий свет линейно поляризован, то колебания вектора p (электрона) происходит в той же
плоскости и при наблюдении рассеянного света  (направление y ) первичному пучку в этой плоскости
рассеянного излучения не будет, т.к. диполь вдоль своей оси не излучает.
2) При падении естественного света, который представляется как два линейно поляризованных во взаимноперпендикулярных направлениях x и y . При   90 свет будет полностью поляризован, т.к. колебания
в этом направлении будут обусловлены только колебаниями вдоль x .

x
p(t)
E(t)

z
y
Объяснение цвета зари и неба. Рэлеевское рассеяние
небо
1
I~ __
4

заря
Земля
a ~  - рассеяние Ми

I
Интенсивность слабо зависит от длины волны, поэтому облака белые (крупные капельки воды)
Биоткани состоят из рассеивателей Ми (митохондрии, мембраны, аппарат Гольджи и пр.)
Размеры рассеивателей ~ 0б1 – 1 мкм, показатель преломления рассеивателей относительно показателя
преломления среды ~ n  1,05  1,1 . Типичный пример – склера глаза человека – белая – рассеиватели Ми,
кожа имеет дополнительный цвет (розовый) за счет гемоглобина крови и коричневый за счет меланина.
1
I p,отн.ед.
область
геометрической
оптики
20
10
16
10
резонансная обл.
рассеяние Ми
12
10
k
108
2
1/2
4
10
0
10
Рэлеевс.
обл.
-4
4
10
k
-4
10
4
1/ 
-2
10
0
10
2
10
4
10
6
10
Зависимость интенсивности рассеяния от радиуса рассеивателя
8
10
10
10
___
2a
ka= 
a и длины волны  .
Рассеяние Ми
2a
- характерный размер, a ~ 

В больших частицах много молекул, т.е. много элементарных диполей (рассеивателей). Отличие от Рэлеевского
рассеяния
1) При рассеянии Рэлея все элементарные рассеиватели находятся в поле одной и той же волны и излучают
когерентно. При рассеянии Ми элементарные рассеиватели находятся не в одинаковых электромагнитных
полях.
2) При рассеянии Рэлея излучение от элементарных рассеивателей (одной и той же частицы) интерферируют
при одинаковой разности фаз независимо от направления. В рассеянии Ми необходимо учитывать различия
в фазах излучения элементарных рассеивателей и разность фаз, вносимую в наблюдаемое излучение
конечным расстоянием между элементарными рассеивателями.

a~ __
4
a> 
рассеяние вперед
Рассеяние Рэлея и Ми – упругое рассеяние
Квазиупругое рассеяние
Движущаяся частица
k
p

kз
k

k з - волновой вектор зондирующего излучения

2n
kз  kз 




2n

k  k р  kз 
 2 sin

2


k р ~ kз
2



i  t k r t 
E pj  E p 0 e 0 j

r j t  означает, что рассеиватель j движущийся.






r j t   r0 j  v j t   j  k rj t   k r0 j  k v j t 

 
d j
 Dj  k v j  k  v j  cos 
dt


 - угол между вектором k и направлением движения частицы v j
4n

 sin  v j  cos 

2
По сдвигу частоты света при квазиупругом рассеянии света определяют скорость движения
частиц – эритроцитов, лимфоцитов и др. – доплеровские измерители скорости кровотока.
Dj 
Неупругое рассеяние
1. Рассеяние Мандельштама-Бриллюэна
Дифракция света на звуковой волне. Амплитуда дифрагированной волны изменяется гармонически с частотой
 звуковой волны, поскольку звуковая волна в твердом теле или жидкости создает волну плотности вещества,
т.е. волну показателя преломления и коэффициента пропускания в направлении дифракционных максимумов,
nd sin     . Поэтому наблюдаемая в направлении дифракционных максимумов напряженность ЭМВ света
описывается формулой
E t   A0 cos t  cos t 
A0
cos  t  cos  t 
2
В среде (кристалле) оптическая длина пути nd sin    . Частота звуковой волны
2v з 2v з n sin  4v з n sin  2
n


v 


 4v з   sin  2n  з   sin , т.к.
d


c
2
2
 c 

2 sin  sin 
2

v 
  2n  з   sin - формула М-Б
2
 c 

спектр
рассеяния
недиф. комп.
  
стоксовый антистоксовый
компонент компонент
d
vз
x
d - период решетки (длина волны звук. волн)
2

d  v з  Tз
Tз
2. Комбинационное рассеяние
Собственные колебания молекул, как механических систем, приводит к модуляции оптических свойств среды
на частоте  , следовательно, рассеянный свет может быть представлен в виде:
E t   A0 1   cos t  cos t ,
 - и  - определяются строением вещества (молекул вещества)
3
A
_
_
1
A
2
_
_
1
A
2




  
Спектр рассеяния (комбинационное или рамановское (Раман))
Применение упругого, квазиупругого и неупругого рассеяния
1. Цитометры – счетчики клеток разных типов.
2.
3.
4.
Доплеровские измерители скорости потоков клеток.
Нефелометры – измерители размеров частиц.
КР-микроскопы – строение биотканей и клеток на уровне молекул.
нефелометр
ФП
+ _
БУ
А
цитометр
Д
ФП
спектр-анализатор
ФП
Д
I
vk
коррелометр
~ vk

анемометр
Вращение плоскости поляризации
Соотношение Френеля:  

n g  nd  l
0


Френель показал, что оптическая активность, какова бы не была ее физическая природа, означает наличие в
среде кругового двойного лучепреломления – неодинаковой скорости распространения лучей, поляризованных
по правому и левому кругу. Наличие этих волн дает линейно поляризованную волну, но т.к. скорости
распространения этих волн различны, то плоскость колебаний линейно поляризованных волн, входящих и
выходящих из оптически активной среды повернуты друг относительно друга на определенный угол  .
Пусть v d  v g ,
d  droit - правый, g  gauch - левый, т.е. право-поляризованная волна опережает лево-
поляризованную.
4
 d     g   или  

1
d   g
2

С другой стороны:


z 
z 
c
c
 ,  g   t 
, vd 
 d   t 
, vg 
 vg 
nd
ng
 vd 


 d   g l
l


n g  nd 
n g  nd , z  l - толщина образца.
2
2c
0




A
A

g
 

g
d
d
z=0
z=l
A
A
n g  n d - правовращ.
n g  n d - левовращ.
Очень чувствительный метод исследования веществ, включая биологические n g  n d ~10-10
  ~ 0,01
Определение сахара в моче, в других биожидкостях, например, водянистой влаге глаза человека.
Эффект Доплера в оптике
a
S
1
v

B
v - скорость движения источника S1 относительно приемника В
c
- скорость распространения света в среде. S1 B  a
n
t1 - момент времени начала движения.
Волна, испущенная в момент времени t1 достигнет точки В в момент времени
an
1  t1 
c
Волна, испущенная в момент времени t 2  t1   достигнет точки В в момент времени
a  vn
2  t2 
c
т.к. к моменту времени t 2 расстояние между источником и приемником сделается равным a  v в
зависимости от направления движения. Итак, волны, испущенные источником за время   t 2  t1 , действуют
на приемник в течение времени
vn
 vn 
 1 

c
c 

Если  0 - частота источника, то за время  им будет испущено N   0  волн, следовательно, частота,
N
воспринимаемая приемником,  

   2  1   
5
0
0
 vn 

  0 1 

c 
 vn  1  vn

1  
c
c 

vn  удаление

   0 1 

c  приближение


S
2
S
1
v


B
BS 2  BS1  S1S 2 cos 
v  S1 B  a
BS2  a  vcos  

v
Доплеровские анемометры, доплеровские микроскопы для мониторинга скорости кровотока в сосудах и
микроциркуляции крови в тканях.
Элементы нелинейной оптики
1. Самофокусировка.
n  n0  n2 E 2
лазерный
пучок
Е0
а -радиус
пучка
Е=0
а
гауссово распределение
Разность фаз между центральным и крайними лучами
2
n2 E 2 l сф

ср
ед
а
lсф
l сф  a 
n0
2n 2 E 2
«линза», наведенная внешним оптическим полем с гауссовым распределением
2.
Просветление (индуцированная прозрачность)
6
мощный
пучок
среда
l
слабыйпучок
Для слабого пучка
I  I 0 e l
  f I м ощного пучка 
  0 ,   0 - усиление
3.
Самодифракция.
x
I1

I2
нелинейная среда
Для интерференционной схемы с двумя пучками, распространяющимися под углом
 друг к другу

 2
I  I1  I 2  2 I1 I 2  cos  n0 2 x sin 
2

 4
 
n  n0  n2 I1  I 2   2n2 I1 I 2  cos  n0 sin  x 

2
 


n x 
Период наведенной решетки в среде d
d
d


2
4

  2 
n0 sin

2
2n0 sin
Основы нелинейной теории дисперсии
n  n0  n2 E 2
Мы связали коэффициент поглощения с показателем преломления через аномальную дисперсию, т.е. через
заселенность уровней в атомах, составляющих вещество. Очевидно, что заселенность уровней должна зависеть
от интенсивности поля (эффективность переходов). С другой стороны, нелинейная (квадратичная) зависимость
от поля может быть реализована через изменение плотности среды за счет эффекта электрострикции (сжатия
среды под действием электрического поля)
u
p
p
1  2
p
 E
8 
 - диэлектрическая проницаемость,  - плотность среды
n
7
Возможен и тепловой механизм нелинейности
n
u
T , T ~ E2
T
Электронная теория
mr  eEt   F , E  E0 e it , F  kr ,
u r  
kr 2
,
2
квазиупругая сила
kr 2 1
1
 m r 3  mr 4  ...
2 3
4

ангармонич еская
составляющая
Смещение r будет уже на частотах  , 2 , 3 и т.д.
u r  
Генерация гармоник
нелинейный
кристалл
анизотропный
кристалл
КДП
P(2 )
 

гидрофосфат
калия
фильтр
на 
-0,1
1  1,06 мкм
 2  0,53 мкм
o
0
0,1
0 ,
0=41,5o
B
C
n2 E 2  n0 , однако большая длина ВС и малый диаметр дают сильные нелинейные эффекты
 
Для двух плоских волн с частотами 1 , 2 и волновыми векторами k1 , k 2 , амплитудами A1 , A2 ,
дипольный момент, индуцированный в среде, имеет составляющую, пропорциональную выражению
(учитывается только квадратичная ангармоничность)






 
 
~ A1 A2 cos 1   2 t  k1  k 2 r и ~ A1 A2 cos 1  2 t  k1  k 2 r
1  2 и имеющих постоянную фазу в
 
 
 
плоскостях, перпендикулярным векторам k1  k 2 . В направлениях k1  k 2 и k1  k 2 среда должна
генерировать, следовательно, излучение с частотами 1  2 и 1  2 , соответ. скорости
пространственного изменения фазы диполей, например, для 1  2
 
12
v  1  2  k1  k 2  1  2  k12  k 22  2k1k 2 cos  ,
 
 
т.е. зависимость от угла  между векторами k1 , k 2 , т.е. синфазность по k1  k 2 не соответствует
 
синфазности по k1  k 2 , что позволяет подбором угла  усиливать один процесс и подавлять другой.
В среде создается ансамбль диполей, колеблющихся с частотами


8