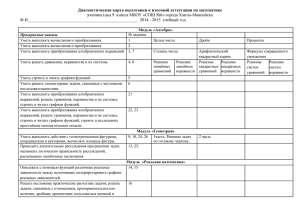
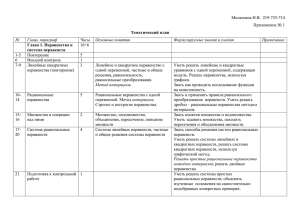
9 класс - Лицей №6

Муниципальное автономное общеобразовательное учреждение лицей № 6
Октябрьского района городского округа город Уфа
Республики Башкортостан
02.77
Рассмотрена и принята
на заседании МО
учителей математики,
информатики и физики
протокол № 1 от «26»
августа 2015 г.
Согласована с
заместителем директора
по УВР
«26» августа 2015 г.
Утверждена
приказом директора
МАОУ лицей № 6
№ 285 от «27» августа
2015 г.
Рабочая программа
Наименование учебного предмета: Алгебра
Класс 9а
Срок реализации рабочей программы: 2015-2016 учебный год
Рабочая программа составлена на основе: Программы основного общего
образования по математике, 2009, одобрены Министерством образования и науки
РФ; Программы. Алгебра 7-9 классы, А.Г. Мордкович, 2009
Рабочую программу составила Селезнева Наталья Алексеевна
Уфа 2015 г.
1. Пояснительная записка
Статус документа
Данная рабочая программа ориентирована на обучающихся 9-х классов и реализуется на основе
следующих нормативно - правовых документов:
 Закона Российской Федерации «Об образовании в Российской Федерации» от 29.12.2012г.
№273 ФЗ;
 Федерального компонента государственного образовательного стандарта, утвержденного
Приказом Минобразования РФ от 05.03.2004г. № 1089;
 Программы основного общего образования по математике, 2009, одобрены Министерством
образования и науки РФ;
 Программы. Алгебра 7-9 классы, А.Г. Мордкович, 2009;
 Федерального перечня учебников;
 Требований к оснащению образовательного процесса в соответствии с содержательным
наполнением учебных предметов федерального компонента государственного
образовательного стандарта.
 Учебным планом МАОУ лицей №6 на 2015-2016 учебный год (приказ «Об утверждении
учебного плана МАОУ лицей №6 на 2015-2016 учебный год» от 27.08.2015 г. №279).
Данная рабочая программа
 конкретизирует содержание предметных тем образовательного стандарта на базовом
уровне;
 дает примерное распределение учебных часов по разделам курса и рекомендуемую
последовательность изучения разделов алгебры с учетом межпредметных и
внутрипредметных связей, логики учебного процесса, возрастных особенностей
обучающихся.
Структура документа
Примерная программа по алгебре включает:
 пояснительную записку;
 цели и задачи изучения алгебры;
 основное содержание с примерным распределением учебных часов по разделам курса,
 требования к уровню подготовки обучающихся;
 календарно-тематическое планирование;
 литературу и средства обучения.
На реализацию данной программы отводится 136 часов в год, 4 часа в неделю.
Цели и задачи изучения алгебры
Общеучебные цели изучения курса:
-овладение математическими знаниями необходимыми для применения в практической
деятельности, для изучения физики и химии, для продолжения образования;
-развитие интереса к предмету, формирование понимания значимости алгебры;
-развитие способностей, творческой активности;
-формирование опыта решения разнообразных задач, планирования деятельности;
-ясного, точного и грамотного изложения своих мыслей.
Задачи:
- развить представление о числе и роли вычислений в человеческой практике;
-сформировать практические навыки выполнения устных, письменных, инструментальных
вычислений, развить вычислительную культуру;
-овладеть символическим языком алгебры, выработать формально-оперативные алгебраические
умения и научиться применять их к решению математических и нематематических задач;
-изучить свойства и графики элементарных функций, научиться использовать функциональнографические представления для описания и анализа реальных зависимостей;
-получить представления о статистических закономерностях в реальном мире и о различных
способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
-развить логическое мышление и речь – умения логически обосновывать суждения, проводить
несложные систематизации, приводить примеры и контрпримеры,
-использовать различные языки математики (словесный, символический, графический) для
иллюстрации, интерпретации, аргументации и доказательства;
-сформировать представления об изучаемых понятиях и методах как важнейших средствах
математического моделирования реальных процессов и явлений.
Изучение алгебры на ступени основного общего образования направлено на достижение
следующих целей:





овладение системой математических знаний и умений, необходимых для применения в
практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для
полноценной жизни в современном обществе: ясность и точность мысли, критичность
мышления, интуиция, логическое мышление, элементы алгоритмической культуры,
пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и
техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой
культуры, понимание значимости математики для научно-технического прогресса;
развитие вычислительных и формально-оперативных алгебраических умений до уровня,
позволяющего уверенно использовать их при решении задач математики и смежных предметов
(физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений
и неравенств как основного средства математического моделирования прикладных задач,
осуществление функциональной подготовки школьников. В ходе изучения курса обучающиеся
овладевают приёмами вычислений на калькуляторе;
Основные развивающие и воспитательные цели
Развитие:

Ясности и точности мысли, критичности мышления, интуиции, логического
мышления, элементов алгоритмической культуры, пространственных представлений,
способности к преодолению трудностей;
 Математической речи;
 Сенсорной сферы, двигательной моторики;
 Внимания, памяти;
 Навыков само и взаимопроверки.
 Формирование представлений об идеях и методах математики как универсального
языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
 Культуры личности, отношения к математике как к части общечеловеческой
культуры, понимание значимости математики для научно-технического прогресса;
 Волевых качеств;
 Коммуникабельности;
 Ответственности.
Целью изучения курса алгебры в 9 классе является:
систематизация и обобщение сведения о преобразованиях алгебраических выражений и
решении уравнений с одной переменной, систем уравнений второй степени, вырабатывается
умение решать системы уравнений и применять их при решении текстовых задач; знакомство
обучающихся с важнейшими функциональными понятиями и с графиками квадратичной функции
общего вида, действиями над степенями с целыми показателями, решение квадратных неравенств
графическим методом, знакомство с методом интервалов при решении неравенств, решение
систем неравенств; планирования и осуществления алгоритмической деятельности, выполнения
заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач,
требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения,
постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи,
использования различных языков математики (словесного, символического, графического),
свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и
доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их
обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных
информационных источников, включая учебную и справочную литературу, современные
информационные технологии.
2. Содержание рабочей программы и общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих
содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия;
элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности
они отражают богатый опыт обучения математике в нашей стране, учитывают современные
тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед
школьным образованием цели на информационно емком и практически значимом материале.
Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным
образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых
для повседневной жизни. Она служит базой для всего дальнейшего изучения математики,
способствует логическому развитию и формированию умения пользоваться алгоритмами.
Изучение алгебры нацелено на формирование математического аппарата для решения задач
из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает
значение математики, как языка для построения математических моделей, процессов и
явлений реального мира (одной из основных задач изучения алгебры является развитие
алгоритмического мышления, необходимого, в частности, для освоения курса информатики;
овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит
свой специфический вклад в развитие воображения, способностей к математическому
творчеству. Другой важной задачей изучения алгебры является получение школьниками
конкретных знаний о функциях как важнейшей математической модели для описания и
исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных,
периодических и др.), для формирования у обучающихся представлений о роли математики в
развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся
обязательным компонентом школьного образования, усиливающим его прикладное и
практическое значение. Этот материал необходим, прежде всего, для формирования
функциональной грамотности – умений воспринимать и анализировать информацию,
представленную в различных формах, понимать вероятностный характер многих реальных
зависимостей, производить простейшие вероятностные расчёты. Изучение основ
комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт
числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о
современной картине мира и методах его исследования, формируется понимание роли
статистики как источника социально значимой информации, и закладываются основы
вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать
практические навыки выполнения устных, письменных, инструментальных вычислений,
развить вычислительную культуру;
овладеть
символическим
языком
алгебры,
выработать
формально-оперативные
алгебраические умения и научиться применять их к решению математических и
нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функциональнографические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты
и методы планиметрии, познакомиться с простейшими пространственными телами и их
свойствами;
получить представления о статистических закономерностях в реальном мире и о различных
способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный
характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить
несложные систематизации, приводить примеры и контрпримеры, использовать различные
языки математики (словесный, символический, графический) для иллюстрации,
интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах
математического моделирования реальных процессов и явлений.
1. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ, НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ
(36 ч)
Целое уравнение и его корни. Решение уравнений третьей и четвертой степени с одним
неизвестным с помощью разложения на множители и введения вспомогательной переменной.
Уравнение с двумя переменными и его график. Уравнение окружности. Решение систем,
содержащих одно уравнение первой, а другое второй степени. Решение задач методом
составления систем. Решение систем двух уравнений второй степени с двумя переменными.
Рациональные неравенства. Решение систем неравенств.
Цель – выработать умение решать простейшие системы, содержащие уравнения второй
степени с двумя переменными, и решать текстовые задачи с помощью составления таких
систем, решать рациональные неравенств и их системы.
Знать методы решения уравнений и неравенств:
а) разложение на множители;
б) введение новой переменной;
в) графический способ;
г) метод интервалов.
Уметь решать целые уравнения методом введения новой переменной
Уметь решать системы 2 уравнений с 2 переменными графическим способом
Уметь решать уравнения с 2 переменными способом подстановки и сложения
Уметь решать задачи «на работу», «на движение» и другие составлением систем уравнений.
Уметь решать неравенства методом интервалов.
2.ФУНКЦИИ (29 ч)
Квадратичная функция
Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного
трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного
трехчлена. Функция y=ax2+bx+с, её свойства, график. Простейшие преобразования графиков
функций. Решение неравенств второй степени с одной переменной. Решение рациональных
неравенств методом интервалов.
Цель – выработать умение строить график квадратичной функции и применять графические
представления для решения неравенств второй степени с одной переменной.
Знать основные свойства функций, уметь находить промежутки знакопостоянства,
возрастания, убывания функций
Уметь находить область определения и область значений функции, читать график функции
Уметь решать квадратные уравнения, определять знаки корней
Уметь выполнять разложение квадратного трехчлена на множители
Уметь строить график функции у=ах2 , выполнять простейшие преобразования графиков
функций
Уметь строить график квадратичной функции, выполнять простейшие преобразования
графиков функций
Уметь строить график квадратичной функции» находить по графику нули функции,
промежутки, где функция принимает положительные и отрицательные значения.
Уметь построить график функции y=ax2 и применять её свойства. Уметь построить график
функции y=ax2 + bx + с и применять её свойства
Уметь находить токи пересечения графика Квадратичной функции с осями координат. Уметь
разложить квадратный трёхчлен на множители.
Уметь решать квадратное уравнение.
Уметь решать квадратное неравенство алгебраическим способом. Уметь решать квадратное
неравенство с помощью графика квадратичной функции
Уметь решать квадратное неравенство методом интервалов. Уметь находить множество
значений квадратичной функции.
Уметь решать неравенство ах2 +вх+с≥0 на основе свойств квадратичной функции
Степенная функция. Корень n-й степени
Четная и нечетная функции. Функция y=xn, Определение корня n-й степени.
Цель – ввести понятие корня n-й степени.
Знать определение и свойства четной и нечетной функций
Уметь строить график функции у=хn, знать свойства степенной функции с натуральным
показателем, уметь решать уравнения хn=а при: а) четных и б)нечетных значениях n.
Знать определение корня n- й степени, при каких значениях а имеет смысл выражение .
Уметь выполнять простейшие преобразования и вычисления выражений, содержащих корни,
применяя изученные свойства арифметического корня n-й степени.
Знать, что степень с основанием, равным 0 определяется только для положительного дробного
показателя и знать, что степени с дробным показателем не зависят от способа записи r в виде
дроби.
Знать свойства степеней с рациональным показателем, уметь выполнять простейшие
преобразования выражений, содержащих степени с дробным показателем.
Уметь выполнять преобразования выражений, содержащих степени с дробным показателем.
3. ПРОГРЕССИИ (22 ч)
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов
прогрессии.
Цель – дать понятие об арифметической и геометрической прогрессиях как числовых
последовательностях особого вида.
Добиться
понимания
терминов
«член
последовательности»,
«номер
члена
последовательности», «формула n –го члена арифметической прогрессии»
Знать формулу n –го члена арифметической прогрессии, свойства членов арифметической
прогрессии, способы задания арифметической прогрессии
Уметь применять формулу суммы n –первых членов арифметической прогрессии при решении
задач
Знать, какая последовательность является геометрической, уметь выявлять, является ли
последовательность геометрической, если да, то находить q
Уметь вычислять любой член геометрической прогрессии по формуле, знать свойства членов
геометрической прогрессии
Уметь применять формулу при решении стандартных задач
Уметь применять формулу S =
в
при решении практических задач
1 q
Уметь находить разность арифметической прогрессии
Уметь находить сумму n первых членов арифметической прогрессии. Уметь находить
любой член геометрической прогрессии. Уметь находить сумму n первых членов
геометрической прогрессии. Уметь решать задачи.
5. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ (18 ч)
Комбинаторные задачи. Перестановки, размещения, сочетания. Вероятность случайного
события
Знать формулы числа перестановок, размещений, сочетаний и уметь пользоваться ими.
Уметь пользоваться формулой комбинаторики при вычислении вероятностей.
6. ПОВТОРЕНИЕ (28 ч)
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс
алгебры 9 класса).
Региональный компонент реализуется приблизительно в 20% тем курса в виде задач
практического содержания, содержащих реальные факты.
3. Требования к уровню подготовки обучающихся
В ходе преподавания алгебры в 9 классе, работы над формированием у обучающихся
перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они
овладевали умениями общеучебного характера, разнообразными способами деятельности,
приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и
конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач,
требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения,
постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи,
использования различных языков математики (словесного, символического, графического),
свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и
доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их
обоснования;
поиска, систематизации, анализа и классификации информации, использования
разнообразных информационных источников, включая учебную и справочную литературу,
современные информационные технологии.
В результате изучения алгебры обучающийся должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их
применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить
примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения
понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры
статистических закономерностей и выводов;
смысл
идеализации,
позволяющей
решать
задачи
реальной
действительности
математическими методами, примеры ошибок, возникающих при идеализации.
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях
и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять
подстановку одного выражения в другое; выражать из формул одну переменную через
остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с
алгебраическими дробями; выполнять разложение многочленов на множители; выполнять
тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и
преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним,
системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат,
проводить отбор решений, исходя из формулировки задачи;
распознавать арифметические и геометрические прогрессии; решать задачи с применением
формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу;
находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при
решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики.
использовать приобретенные знания и умения в практической деятельности и повседневной
жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между
реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с
использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при
исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
4. Критерии оценивания обучающихся
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
 работа выполнена полностью;
 в логических рассуждениях и обосновании решения нет пробелов и ошибок;
 в решении нет математических ошибок (возможна одна неточность, описка, которая не
является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
 работа выполнена полностью, но обоснования шагов решения недостаточны (если умение
обосновывать рассуждения не являлось специальным объектом проверки);
 допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или
графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
 допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или
графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
 допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными
умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой
теме или значительная часть работы выполнена не самостоятельно.
 Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение
задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за
решение более сложной задачи или ответ на более сложный вопрос, предложенные
обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если обучающийся:
 полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
 изложил материал грамотным языком, точно используя математическую терминологию и
символику, в определенной логической последовательности;
 правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
 показал умение иллюстрировать теорию конкретными примерами, применять ее в новой
ситуации при выполнении практического задания;
 продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и
устойчивость используемых при ответе умений и навыков;
 отвечал самостоятельно, без наводящих вопросов учителя;
 возможны одна – две неточности при освещение второстепенных вопросов или в выкладках,
которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5»,
но при этом имеет один из недостатков:
 в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
 допущены один–два недочета при освещении основного содержания ответа, исправленные
после замечания учителя;
 допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в
выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
 неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда
последовательно), но показано общее понимание вопроса и продемонстрированы умения,
достаточные для усвоения программного материала (определены «Требованиями к
математической подготовке учащихся» в настоящей программе по математике);
 имелись затруднения или допущены ошибки в определении математической терминологии,
чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
 ученик не справился с применением теории в новой ситуации при выполнении практического
задания, но выполнил задания обязательного уровня сложности по данной теме;
 при достаточном знании теоретического материала выявлена недостаточная сформированность
основных умений и навыков.
Отметка «2» ставится в следующих случаях:
 не раскрыто основное содержание учебного материала;
 обнаружено незнание учеником большей или наиболее важной части учебного материала;
 допущены ошибки в определении понятий, при использовании математической терминологии, в
рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких
наводящих вопросов учителя.
Отметка «1» ставится, если:
 обучающийся обнаружил полное незнание и непонимание изучаемого учебного материала или
не смог ответить ни на один из поставленных вопросов по изученному материалу.
1. Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и
негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
- незнание определения основных понятий, законов, правил, основных положений теории,
незнание формул, общепринятых символов обозначений величин, единиц их измерения;
- незнание наименований единиц измерения;
- неумение выделить в ответе главное;
- неумение применять знания, алгоритмы для решения задач;
- неумение делать выводы и обобщения;
- неумение читать и строить графики;
- неумение пользоваться первоисточниками, учебником и справочниками;
- потеря корня или сохранение постороннего корня;
- отбрасывание без объяснений одного из них;
- равнозначные им ошибки;
- вычислительные ошибки, если они не являются опиской;
- логические ошибки.
3.2. К негрубым ошибкам следует отнести:
- неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата
основных признаков определяемого понятия или заменой одного - двух из этих признаков
второстепенными;
- неточность графика;
- нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение
логики, подмена отдельных основных вопросов второстепенными);
- нерациональные методы работы со справочной и другой литературой;
- неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
- нерациональные приемы вычислений и преобразований;
- небрежное выполнение записей, чертежей, схем, графиков.
I. Работа учителя по осуществлению единых требований к устной и письменной речи
обучающихся
Воспитание речевой культуры обучающихся может успешно осуществляться только в результате
целенаправленных и квалифицированных действий всего педагогического коллектива.
1. Учителю необходимо: тщательно продумывать ход изложения материала на уроке,
правильность и точность всех формулировок, вопросов; грамотно оформлять все виды записей (на
доске, в журнале, в дневниках учащихся и т. п.); писать разборчивым почерком.
2. Не допускать в своей речи неправильно построенных предложений и оборотов, нарушения норм
произношения, небрежности в выборе слов и неточности в формулировках определений, заданий.
3. Систематически проводить работу по обогащению и конкретизации словаря учащихся, по
ознакомлению с терминологией изучаемого предмета. При объяснении новых терминов - слова
четко произносить, записывать на доске и в тетрадях, постоянно проверять усвоение их значения и
правильное употребление. Использовать таблицы, плакаты с трудными по написанию и
произношению словами, относящимися к данной учебной дисциплине, к данному разделу
программы.
4. Большое внимание уделять формированию на всех уроках умений анализировать, сравнивать,
сопоставлять изученный материал, при ответе приводить необходимые доказательства, делать
выводы и обобщения.
5. Учить обучающихся работать с книгой, пользоваться разнообразной справочной литературой,
каталогами и картотекой, таблицами.
6. Следить за аккуратным ведением тетрадей, грамотным оформлением всех записей в них.
7. Исправлять допущенные ошибки.
8. Контролировать наличие у обучающихся тетрадей по учебным предметам, соблюдение
установленного в школе порядка их оформления, ведения, соблюдение единого орфографического
режима.
9. Использовать все формы внеклассной работы (олимпиады, конкурсы, факультативные,
кружковые занятия, диспуты, семинары, КВН и т.п.) для совершенствования речевой
математической культуры учащихся.
II. Требования к речи обучающихся
Обучающиеся должны уметь:
— излагать материал логично и последовательно;
— отвечать громко, четко, с соблюдением логических ударений, пауз и правильной интонации.
Для речевой культуры обучающихся важны и такие умения, как умение слушать и понимать речь
учителя и товарищей, внимательно относиться к высказываниям других, умение поставить вопрос,
принять участие в обсуждении проблемы.
III. О письменных работах и тетрадях обучающихся
1. О видах письменных работ
1.1. Основными видами классных и домашних письменных работ обучающихся являются
обучающие работы.
1.2. По математике проводятся текущие и итоговые письменные контрольные работы,
самостоятельные работы, контроль знаний в форме теста.
Текущие контрольные работы имеют целью проверку усвоения изучаемого и проверяемого
программного материала; их содержание и частотность определяются учителем с учетом степени
сложности изучаемого материала, а также особенностей обучающихся каждого класса. Для
проведения текущих контрольных работ учитель может отводить весь урок или только часть его.
Итоговые контрольные работы проводятся:
- после изучения наиболее значимых тем программы,
- в конце учебной четверти,
- в конце полугодия.
В целях предупреждения перегрузки обучающихся время проведения текущих и итоговых
контрольных работ определяется общешкольным графиком, составляемым руководителями школ
по согласованию с учителями. В один рабочий день следует давать в классе только одну
письменную текущую или итоговую контрольную работу. При планировании контрольных работ
в каждом классе необходимо предусмотреть равномерное их распределение в течение всей
четверти, не допуская скопления письменных контрольных работ к концу четверти, полугодия.
Не рекомендуется проводить контрольные работы в первый день четверти, в первый день после
праздника, в понедельник.
Самостоятельные работы или тестирование могут быть рассчитаны как на целый урок, так и на
часть урока, в зависимости от цели проведения контроля.
2. Количество и назначение тетрадей обучающихся
2.1. Для выполнения всех видов обучающих работ обучающиеся должны иметь в VII—IX классах
3 рабочие тетради (2 по алгебре и 1 по геометрии);
2.2. Для контрольных работ по математике выделяются специальные тетради, которые в течение
всего учебного года хранятся в школе и выдаются ученикам для выполнения контрольных работ и
работ над ошибками в VII—IX классах 2 тетради для контрольных работ (1 по алгебре и 1 по
геометрии);
3. Порядок ведения тетрадей обучающимися.
Все записи в тетрадях учащиеся должны проводить с соблюдением следующих требований:
3.1. Писать аккуратным, разборчивым почерком.
3.2. Единообразно выполнять надписи на обложке тетради: указывать, для чего предназначена
тетрадь (для работ по алгебре, для контрольных работ).
3.3. Указывать дату выполнения работы. В тетрадях по математике число и месяц записываются
цифрами на полях тетради.
3.4. Писать на отдельной строке название темы урока.
3.5. Обозначать номер упражнения, указывать вид выполняемой работы (самостоятельная работа,
тест), указывать, где выполняется работа (классная или домашняя).
Например:
Классная работа.
№ 124.
3.6. Соблюдать красную строку.
3.7. Между классной и домашней работой отступать 4 клеточки, между заданиями – 2 клеточки.
3.8. Чертежи и построения выполнять карандашом — с применением линейки и циркуля.
4. Порядок проверки письменных работ учителями.
4.1. Тетради обучающихся, в которых выполняются обучающие классные и домашние работы по
математике, проверяются в 7 – 9 классах ежедневно проверяются работы у слабых и 2 раза в
неделю - наиболее значимые – у всех остальных;
4.2. Все виды контрольных работ проверяют у всех обучающихся.
4.3. Учитель соблюдает следующие сроки проверки контрольных работ в 9 – 11 классах – работы
проверяются либо к уроку следующего дня, либо через один – два урока.
4.4. Учитель проводит работу над ошибками после проверки контрольных работ и хранит тетради
контрольных работ обучающихся в течение учебного года.
4.5. В проверяемых работах учитель отмечает и исправляет допущенные ошибки, руководствуясь
следующим:
- при проверке тетрадей и контрольных работ обучающихся V —XI классов по математике
учитель только подчеркивает и отмечает на полях допущенную ошибку, которую исправляет сам
обучающийся;
- подчеркивание ошибок производится учителем только красной пастой (красными чернилами,
красным карандашом).
4.6. Все контрольные работы оцениваются учителем с занесением оценок в классный журнал.
Оценки за самостоятельные работы (тесты), если они не запланированы на весь урок, могут
выставляться выборочно, на усмотрение учителя.
Классные и домашние письменные работы по математике оцениваются; оценки в журнал могут
быть выставлены за наиболее значимые работы по усмотрению учителя.
При оценке письменных работ обучающихся учителя руководствуются соответствующими
нормами оценки знаний, умений и навыков школьников.
4.7. После проверки письменных работ обучающимся дается задание по исправлению ошибок
или выполнению заданий, предупреждающих повторение аналогичных ошибок.
Работа над ошибками осуществляется в тех же тетрадях, в которых выполнялись соответствующие
письменные работы.
5. Календарно-тематическое планирование
№
урока
Название раздела,
темы
1
Повторение.
Решение уравнений
Повторение.
Неравенства,
системы
Повторение.
Решение задач
Повторение
Стартовый
Тест 1
Повторение
Стартовый
Тест 2
Повторение
Стартовый
Тест 3
4
Линейные
и квадратные
неравенства
Изучение
нового
материала
5
Линейные
и квадратные
неравенства
Закрепление
2
3
Тип урока
Элементы
обязательного
минимума
образования
Требования к
уровню подготовки
обучающихся
Формы контроля
Рациональные неравенства и их системы (16 ч.)
Определения
Иметь представление
Текущий
линейного и
о решении линейных
квадратного
и квадратных
неравенств,
неравенств с одной
неравенства с
переменной.
модулем,
Знать, как проводить
графический способ исследование
решения
функции на
неравенств.
монотонность.
Уметь:
– решать линейные и
квадратные
неравенства с одной
переменной,
содержащие модуль;
– решать неравенства,
используя графики.
Определения
Иметь представление
Самоконтроль,
линейного и
о решении линейных
взаимоконтроль
квадратного
и квадратных
неравенств,
неравенств с одной
неравенства с
переменной.
модулем,
Знать, как проводить
графический способ исследование
решения
функции на
неравенств.
монотонность.
Домашнее
задание
С. 5-12 §1, №1.1,
1.3, 1.5
С. 5-12 §1, №1.7,
1.9, 1.11
Дата урока
Коррекция
(с указанием
причин)
6
Линейные
и квадратные
неравенства
Закрепление
Понятия линейного
и квадратного
неравенств,
неравенства с
модулем,
графический способ
решения
неравенств.
7
Рациональные
неравенства
Изучение
нового
материала
Понятия
рационального и
дробнорационального
неравенств, метод
интервалов,
равносильное
преобразование
неравенства.
8
Рациональные
Закрепление
Понятия
Уметь:
– решать линейные и
квадратные
неравенства с одной
переменной,
содержащие модуль;
– решать неравенства,
используя графики.
Иметь представление
о решении линейных
и квадратных
неравенств с одной
переменной.
Знать, как проводить
исследование
функции на
монотонность.
Уметь:
– решать линейные и
квадратные
неравенства с одной
переменной,
содержащие модуль;
– решать неравенства,
используя графики.
Иметь представление
о решении
рациональных
неравенств методом
интервалов.
Знать и применять
правила
равносильного
преобразования
неравенств
Уметь решать
дробно-рациональные
неравенства методом
интервалов.
Иметь представление
Индивидуальный
С. 5-12 §1, №1.13,
1.15, 1.17
Текущий
С. 12-23 §2, №2.1,
2.3, 2.5
Математический
С. 12-23 §2, №2.7,
неравенства
рационального и
дробнорационального
неравенств, метод
интервалов,
равносильное
преобразование
неравенства.
9
Рациональные
неравенства
Закрепление
Понятия
рационального и
дробнорационального
неравенств, метод
интервалов,
равносильное
преобразование
неравенства.
10
Рациональные
неравенства
Закрепление
Понятия
рационального и
дробнорационального
неравенств, метод
интервалов,
равносильное
преобразование
неравенства.
о решении
рациональных
неравенств методом
интервалов.
Знать и применять
правила
равносильного
преобразования
неравенств
Уметь решать
дробно-рациональные
неравенства методом
интервалов.
Иметь представление
о решении
рациональных
неравенств методом
интервалов.
Знать и применять
правила
равносильного
преобразования
неравенств
Уметь решать
дробно-рациональные
неравенства методом
интервалов.
Иметь представление
о решении линейных
и квадратных
неравенств с одной
переменной.
Знать, как проводить
исследование
функции на
монотонность.
Уметь:
– решать линейные и
квадратные
неравенства с одной
диктант
2.9, 2.11
Индивидуальный
С. 12-23 §2,
№2.13, 2.15, 2.17
Самостоятельная
работа
С. 12-23 §2,
№2.19, 2.21, 2.23
11
Рациональные
неравенства
Закрепление
Понятия
рационального и
дробнорационального
неравенств, метод
интервалов,
равносильное
преобразование
неравенства.
12
Множества и
операции над ними
Изучение
нового
материала
Понятия множества,
объединения,
пересечения
множеств, пустое
множество
13
Множества и
операции над ними
Закрепление
Понятия множества,
объединения,
пересечения
множеств, пустое
множество
14
Системы
рациональных
неравенств
Изучение
нового
материала
Понятия
системы
неравенств,
двойного
переменной,
содержащие модуль;
– решать неравенства,
используя графики.
Иметь представление
о решении линейных
и квадратных
неравенств с одной
переменной.
Знать, как проводить
исследование
функции на
монотонность.
Уметь:
– решать линейные и
квадратные
неравенства с одной
переменной,
содержащие модуль;
– решать неравенства,
используя графики.
Знать определение
простейших понятий
теории множеств.
Уметь задавать
множества,
производить
операции над
множествами
Знать определение
простейших понятий
теории множеств.
Уметь задавать
множества,
производить
операции над
множествами
Знать способы
решения систем
рациональных
Текущий
С. 12-23 §2,
№2.25, 2.27, 2.29
Текущий
С. 23-40 §3, №3.1,
3.3, 3.5
Текущий
С. 23-40 §3, №3.7,
3.9, 3.11
Индивидуальный
С. 40-48 §4, №4.1,
4.3, 4.5
неравенства,
графический метод
решения
систем
неравенств.
15
Системы
рациональных
неравенств
Закрепление
Понятия системы
неравенств,
двойного
неравенства,
графический метод
решения систем
неравенств.
16
Системы
Закрепление
Понятия системы
неравенств.
Уметь:
- решать системы
линейных и
квадратных
неравенств,
-решать двойные
неравенства,
-решать системы
простых
рациональных
неравенств методом
интервалов,
– решать системы
квадратных
неравенств,
используя
графический метод.
Знать способы
решения систем
рациональных
неравенств.
Уметь:
- решать системы
линейных и
квадратных
неравенств,
-решать двойные
неравенства,
-решать системы
простых
рациональных
неравенств методом
интервалов,
– решать системы
квадратных
неравенств,
используя
графический метод.
Знать способы
Текущий
Самостоятельная
С. 40-48 §4, №4.7,
4.9, 4.11
С. 40-48 §4,
рациональных
неравенств
17
Системы
рациональных
неравенств
неравенств,
двойного
неравенства,
графический метод
решения систем
неравенств.
Закрепление
Понятия системы
неравенств,
двойного
неравенства,
графический метод
решения систем
неравенств.
решения систем
рациональных
неравенств.
Уметь:
- решать системы
линейных и
квадратных
неравенств,
-решать двойные
неравенства,
-решать системы
простых
рациональных
неравенств методом
интервалов,
– решать системы
квадратных
неравенств,
используя
графический метод.
Знать способы
решения систем
рациональных
неравенств.
Уметь:
- решать системы
линейных и
квадратных
неравенств,
-решать двойные
неравенства,
-решать системы
простых
рациональных
неравенств методом
интервалов,
– решать системы
квадратных
неравенств,
используя
работа
№4.13, 4.15, 4.17
Текущий
С. 40-48 §4,
№4.19, 4.21, 4.23
18
Обобщающий урок
по теме:
«Рациональные
неравенства и их
системы»
Закрепление
19
Контрольная работа
№1 «Рациональные
неравенства и их
системы»
Контроль и
оценка знаний
Понятия линейного
и квадратного
неравенств,
неравенства с
модулем,
рационального и
дробнорационального
неравенств, системы
неравенств,
двойного
неравенства, метод
интервалов,
равносильное
преобразование
неравенства,
графический способ
решения неравенств
и их систем.
Понятия линейного
и квадратного
неравенств,
неравенства с
модулем,
рационального и
дробнорационального
неравенств, системы
неравенств,
двойного
неравенства, метод
интервалов,
равносильное
преобразование
неравенства,
графический способ
решения неравенств
и их систем.
графический метод.
Уметь решать
рациональные
неравенства и
системы
рациональных
неравенств.
Уметь решать
рациональные
неравенства и
системы
рациональных
неравенств.
Индивидуальный
С. 40-48 §4,
№4.25, 4.27, 4.29
Письменный
фронтальный
контроль
С. 40-48 §4,
№4.31, 4.33, 4.35
Системы уравнений (20 ч.)
20
Основные понятия.
Системы уравнений
Изучение
нового
материала
Понятие о решении
системы уравнений
и неравенств,
равносильные
преобразования.
21
Основные понятия.
Системы уравнений
Закрепление
Понятие о решении
системы уравнений
и неравенств,
равносильные
преобразования.
22
Основные понятия.
Системы уравнений
Закрепление
Понятие о решении
системы уравнений
и неравенств,
равносильные
преобразования.
23
Методы решения
систем уравнений
Изучение
нового
материала
Методы
подстановки,
алгебраического
сложения, введения
Иметь понятие о
решении системы
уравнений и
неравенств.
Знать равносильные
преобразования
уравнений и
неравенств с двумя
переменными.
Уметь определять
понятия, приводить
доказательства.
Иметь понятие о
решении системы
уравнений и
неравенств.
Знать равносильные
преобразования
уравнений и
неравенств с двумя
переменными.
Уметь определять
понятия, приводить
доказательства.
Иметь понятие о
решении системы
уравнений и
неравенств.
Знать равносильные
преобразования
уравнений и
неравенств с двумя
переменными.
Уметь определять
понятия, приводить
доказательства.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
Индивидуальный
С. 49-67 §5, №5.1,
5.3, 5.5
Текущий
С. 49-67 §5, №5.7,
5.9, 5.11
Самостоятельная
работа
С. 49-67 §5,
№5.13, 5.15, 5.17
Индивидуальный
С. 68-74 §6, №6.1,
6.3, 6.5
новых переменных.
24
Методы решения
систем уравнений
Закрепление
Методы
подстановки,
алгебраического
сложения, введения
новых переменных.
25
Методы решения
систем уравнений
Закрепление
Методы
подстановки,
алгебраического
сложения, введения
новых переменных.
26
Методы решения
систем уравнений
Закрепление
Методы
подстановки,
алгебраического
сложения, введения
новых переменных.
методом
подстановки,
методом
алгебраического
сложения, методом
введения новых
переменных.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
методом
подстановки,
методом
алгебраического
сложения, методом
введения новых
переменных.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
методом
подстановки,
методом
алгебраического
сложения, методом
введения новых
переменных.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
методом
подстановки,
методом
алгебраического
сложения, методом
введения новых
переменных.
Текущий
С. 68-74 §6, №6.7,
6.9, 6.11
Самостоятельная
работа
С. 68-74 §6,
№6.13, 6.15, 6.17
Текущий
С. 68-74 §6,
№6.19, 6.21, 6.23
27
Методы решения
систем уравнений
Закрепление
Методы
подстановки,
алгебраического
сложения, введения
новых переменных.
28
Методы решения
систем уравнений
Закрепление
Методы
подстановки,
алгебраического
сложения, введения
новых переменных.
29
Методы решения
систем уравнений
Закрепление
Методы
подстановки,
алгебраического
сложения, введения
новых переменных.
30
Методы решения
систем уравнений
Практикум
Методы
подстановки,
алгебраического
сложения, введения
новых переменных.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
методом
подстановки,
методом
алгебраического
сложения, методом
введения новых
переменных.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
методом
подстановки,
методом
алгебраического
сложения, методом
введения новых
переменных.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
методом
подстановки,
методом
алгебраического
сложения, методом
введения новых
переменных.
Знать алгоритм
метода подстановки.
Уметь решать
системы уравнений
методом
подстановки,
методом
Текущий
С. 68-74 §6,
индивидуальные
задания
Математический
диктант
С. 68-74 §6,
индивидуальные
задания
Индивидуальный
С. 68-74 §6,
индивидуальные
задания
Самостоятельная
работа
С. 68-74 §6,
индивидуальные
задания
31
Системы уравнений
как математические
модели реальных
ситуаций
Изучение
нового
материала
Математическая
модель
реальной
ситуации.
32
Системы уравнений
как математические
модели реальных
ситуаций
Закрепление
Математическая
модель реальной
ситуации.
33
Системы уравнений
как математические
модели реальных
ситуаций
Изучение
нового
материала
Математическая
модель реальной
ситуации.
алгебраического
сложения, методом
введения новых
переменных.
Знать, как составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Знать, как составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Знать, как составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Текущий
С. 75-82 §7, №7.1,
7.3, 7.5
Текущий
С. 75-82 §7, №7.7,
7.9, 7.11
Текущий
С. 75-82 §7,
№7.13, 7.15, 7.17
34
Системы уравнений
как математические
модели реальных
ситуаций
Закрепление
Математическая
модель реальной
ситуации.
35
Системы уравнений
как математические
модели реальных
ситуаций
Закрепление
Математическая
модель реальной
ситуации.
36
Системы уравнений
как математические
модели реальных
ситуаций
Закрепление
Математическая
модель реальной
ситуации.
37
Системы уравнений
как математические
модели реальных
ситуаций
Практикум
Математическая
модель реальной
ситуации.
Знать, как составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Знать, как составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Знать, как составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Знать, как составлять
математические
модели реальных
ситуаций и работать с
Индивидуальный
С. 75-82 §7,
№7.19, 7.21, 7.23
Групповой
С. 75-82 §7,
№7.25, 7.27, 7.29
Текущий
С. 75-82 §7,
№7.31, 7.33, 7.35
Тренировочный
тест (подготовка к
ОГЭ)
С. 75-82 §7,
№7.37, 7.39, 7.41
38
Обобщающий урок
по теме: «Системы
уравнений»
Закрепление
Нелинейные
системы уравнений
с двумя
переменными,
математическая
модель реальной
ситуации.
39
Контрольная работа
№2
«Системы
уравнений»
Контроль и
оценка знаний
Нелинейные
системы уравнений
с двумя
переменными,
математическая
модель реальной
ситуации.
40
Определение
числовой функции.
Область
определения,
область значений
функции
Изучение
нового
материала
Определения
числовой функции,
области
определения,
области значения
функции, графика
функции.
составленной
моделью.
Уметь составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь решать
Текущий
простые нелинейные
системы уравнений
двух переменных
различными
методами, составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Уметь решать
Письменный
простые нелинейные
фронтальный
системы уравнений
контроль
двух переменных
различными
методами, составлять
математические
модели реальных
ситуаций и работать с
составленной
моделью.
Числовые функции (29 ч.)
Знать определения
Индивидуальный
числовой функции,
области определения,
области значения
функции, графика
функции.
Уметь находить
область определения
функции.
С. 75-82 §7, тест 4
С. 75-82 §7, тест 5
С. 83-91 §8, №8.1,
8.3, 8.5
41
Определение
числовой функции.
Область
определения,
область значений
функции
Закрепление
Определения
числовой функции,
области
определения,
области значения
функции, графика
функции.
42
Определение
числовой функции.
Область
определения,
область значений
функции
Закрепление
Определения
числовой функции,
области
определения,
области значения
функции, графика
функции.
43
Определение
числовой функции.
Область
определения,
область значений
функции
Закрепление
Определения
числовой функции,
области
определения,
области значения
функции, графика
функции.
44
Определение
числовой функции.
Область
определения,
область значений
функции
Практикум
Определения
числовой функции,
области
определения,
области значения
функции, графика
функции.
45
Способы задания
функций
Изучение
нового
материала
Аналитический,
графический,
табличный,
словесный способы
Знать определения
числовой функции,
области определения,
области значения
функции, графика
функции.
Уметь находить
область определения
функции.
Знать определения
числовой функции,
области определения,
области значения
функции, графика
функции.
Уметь находить
область определения
функции.
Знать определения
числовой функции,
области определения,
области значения
функции, графика
функции.
Уметь находить
область определения
функции.
Знать определения
числовой функции,
области определения,
области значения
функции, графика
функции.
Уметь находить
область определения
функции.
Знать способы
задания функции:
аналитический,
графический,
Групповой
С. 83-91 §8, №8.7,
8.9, 8.11
Текущий
С. 83-91 §8,
№8.13, 8.15, 8.17
Текущий
С. 83-91 §8,
№8.19, 8.21, 8.23
Тренировочный
тест (подготовка к
ОГЭ)
С. 83-91 §8, тест 6
Текущий
С. 91-96 §9, №9.1,
9.3,9.5
задания функции.
46
Способы задания
функций
Закрепление
Аналитический,
графический,
табличный,
словесный способы
задания функции.
47
Способы задания
функций
Закрепление
Аналитический,
графический,
табличный,
словесный способы
задания функции.
табличный,
словесный.
Уметь:
-при задании
функции применять
различные способы:
аналитический,
графический,
табличный,
словесный,
- решать графически
уравнения.
Знать способы
задания функции:
аналитический,
графический,
табличный,
словесный.
Уметь:
-при задании
функции применять
различные способы:
аналитический,
графический,
табличный,
словесный,
- решать графически
уравнения.
Знать способы
задания функции:
аналитический,
графический,
табличный,
словесный.
Уметь:
-при задании
функции применять
различные способы:
аналитический,
графический,
Индивидуальный
С. 91-96 §9, №9.7,
9.9. 9.11
Самостоятельная
работа
С. 91-96 §9,
№9.13, 9.15. 9.17
48
Свойства функций
Изучение
нового
материала
Монотонность,
наибольшее и
наименьшее
значения функции,
ограниченность,
выпуклость и
непрерывность.
49
Свойства функций
Закрепление
Монотонность,
наибольшее и
наименьшее
значения функции,
ограниченность,
выпуклость и
непрерывность.
табличный,
словесный,
- решать графически
уравнения.
Знать свойства
функции:
монотонность,
наибольшее и
наименьшее значения
функции,
ограниченность,
выпуклость и
непрерывность.
Уметь исследовать
функции на
монотонность,
наибольшее и
наименьшее
значение,
ограниченность,
выпуклость и
непрерывность.
Знать свойства
функции:
монотонность,
наибольшее и
наименьшее значения
функции,
ограниченность,
выпуклость и
непрерывность.
Уметь исследовать
функции на
монотонность,
наибольшее и
наименьшее
значение,
ограниченность,
выпуклость и
непрерывность.
Текущий
С. 97-109 §10,
№10.1, 10.3. 10.5
Индивидуальный
С. 97-109 §10,
№10.7, 10.9, 10.11
50
Свойства функций
Закрепление
Монотонность,
наибольшее и
наименьшее
значения функции,
ограниченность,
выпуклость и
непрерывность.
51
Свойства функций
Практикум
Монотонность,
наибольшее и
наименьшее
значения функции,
ограниченность,
выпуклость и
непрерывность.
52
Свойства функций
Закрепление
Монотонность,
наибольшее и
наименьшее
значения функции,
Знать свойства
функции:
монотонность,
наибольшее и
наименьшее значения
функции,
ограниченность,
выпуклость и
непрерывность.
Уметь исследовать
функции на
монотонность,
наибольшее и
наименьшее
значение,
ограниченность,
выпуклость и
непрерывность.
Знать свойства
функции:
монотонность,
наибольшее и
наименьшее значения
функции,
ограниченность,
выпуклость и
непрерывность.
Уметь исследовать
функции на
монотонность,
наибольшее и
наименьшее
значение,
ограниченность,
выпуклость и
непрерывность.
Знать свойства
функции:
монотонность,
наибольшее и
Групповой
С. 97-109 §10,
№10.13, 10.15,
10.17
Индивидуальный
С. 97-109 §10,
№10.19. 10.21,
10.23
Самостоятельная
работа
С. 97-109 §10,
№10.25. 10.27,
10.29
ограниченность,
выпуклость и
непрерывность.
53
Четные и нечетные
функции
Изучение
нового
материала
Понятия четной и
нечетной функции,
алгоритм
исследования
функции на
чётность и
нечётность.
54
Четные и нечетные
функции
Закрепление
Понятия четной и
нечетной функции,
алгоритм
исследования
функции на
чётность и
нечётность.
наименьшее значения
функции,
ограниченность,
выпуклость и
непрерывность.
Уметь исследовать
функции на
монотонность,
наибольшее и
наименьшее
значение,
ограниченность,
выпуклость и
непрерывность.
Знать понятия четной
и нечетной функции,
алгоритм
исследования
функции на чётность
и нечётность.
Уметь применять
алгоритм
исследования
функции на четность
и строить графики
четных и нечетных
функций.
Знать понятия четной
и нечетной функции,
алгоритм
исследования
функции на чётность
и нечётность.
Уметь применять
алгоритм
исследования
функции на четность
и строить графики
четных и нечетных
функций.
Текущий
С. 110-115 §11,
№11.1, 11.3, 11.5
Индивидуальный
С. 110-115 §11,
№11.7, 11.9, 11.11
55
Четные и нечетные
функции
Закрепление
Понятия четной и
нечетной функции,
алгоритм
исследования
функции на
чётность и
нечётность.
56
Обобщающий урок
«Числовая функция.
Свойства функции»
Закрепление
57
Контрольная работа
Закрепление
Определения
числовой функции,
области
определения,
области значения
функции, графика
функции,
аналитический,
графический,
табличный,
словесный способы
задания функции,
монотонность,
наибольшее и
наименьшее
значения функции,
ограниченность,
выпуклость и
непрерывность,
Понятия четной и
нечетной функции,
алгоритм
исследования
функции на
чётность и
нечётность.
Определения
Знать понятия четной
и нечетной функции,
алгоритм
исследования
функции на чётность
и нечётность.
Уметь применять
алгоритм
исследования
функции на четность
и строить графики
четных и нечетных
функций.
Уметь применять
полученные знания
на практике.
Уметь применять
Самоконтроль
С. 110-115 §11,
№11.13, 11.15,
11.17
Индивидуальный
С. 110-115 §11,
№11.19, 11.21,
11.23
Письменный
С. 110-115 §11,
№3
«Числовая функция.
Свойства функции»
58
Функции
yx
n
n  N  ,
их свойства и
графики
59
Функции
Изучение
нового
материала
числовой функции,
области
определения,
области значения
функции, графика
функции,
аналитический,
графический,
табличный,
словесный способы
задания функции,
монотонность,
наибольшее и
наименьшее
значения функции,
ограниченность,
выпуклость и
непрерывность,
Понятия четной и
нечетной функции,
алгоритм
исследования
функции на
чётность и
нечётность.
Степенная функция
с натуральным
показателем.
Закрепление
Степенная функция
полученные знания
на практике.
Знать о понятии
степенной функции с
натуральным
показателем, о
свойствах и графике
функции.
Уметь:
- определять графики
функций с четным и
нечетным
показателем,
-строить и читать
графики степенных
функций.
Знать о понятии
фронтальный
контроль
№11.25, 11.27,
11.29
Текущий
С. 115-122 §12,
№12.1, 12.3, 12.5
Индивидуальный
С. 115-122 §12,
y  xn
n  N  ,
с натуральным
показателем.
их свойства и
графики
60
Функции
yx
n
n  N  ,
Закрепление
Степенная функция
с натуральным
показателем.
Изучение
нового
материала
Степенная функция
с целым
отрицательным
показателем.
их свойства и
графики
61
Функции
yx
n
n  N 
, их свойства и
графики
степенной функции с
натуральным
показателем, о
свойствах и графике
функции.
Уметь:
- определять графики
функций с четным и
нечетным
показателем,
-строить и читать
графики степенных
функций.
Знать о понятии
степенной функции с
натуральным
показателем, о
свойствах и графике
функции.
Уметь:
- определять графики
функций с четным и
нечетным
показателем,
-строить и читать
графики степенных
функций.
Знать о понятии
степенной функции с
отрицательным
целым показателем, о
свойствах и графике
функции.
Уметь:
- определять графики
функций с четным и
нечетным
отрицательным
целым показателем,
-решать графически
№12.7, 12.9, 12.11
Групповой
С. 115-122 §12,
№12.13, 12.15,
12.17
Текущий
С. 122 -128 §13,
№13.1, 13.3, 13.5
62
Функции
yx
n
n  N 
, их свойства
графики
63
Функции
yx
n
Степенная функция
с целым
отрицательным
показателем.
Закрепление
Степенная функция
с целым
отрицательным
показателем.
и
n  N 
, их свойства и
графики
Закрепление
уравнения,
-строить графики
степенных функций с
любым показателем
степени,
-читать свойства по
графику функции,
-строить графики
функций по
описанным
свойствам.
Знать о понятии
степенной функции с
отрицательным
целым показателем, о
свойствах и графике
функции.
Уметь:
- определять графики
функций с четным и
нечетным
отрицательным
целым показателем,
-решать графически
уравнения,
-строить графики
степенных функций с
любым показателем
степени,
-читать свойства по
графику функции,
-строить графики
функций по
описанным
свойствам.
Знать о понятии
степенной функции с
отрицательным
целым показателем, о
свойствах и графике
Текущий
Самостоятельная
работа
С. 122 -128 §13,
№13.7, 13.9, 13.11
С. 122 -128 §13,
№13.13, 13.15,
13.17
64
Функция у=3√х, её
свойства и график
Изучение
нового
материала
Функция
кубического корня.
65
Функция у=3√х, её
свойства и график
Закрепление
Функция
кубического корня.
функции.
Уметь:
- определять графики
функций с четным и
нечетным
отрицательным
целым показателем,
-решать графически
уравнения,
-строить графики
степенных функций с
любым показателем
степени,
-читать свойства по
графику функции,
-строить графики
функций по
описанным
свойствам.
Знать определение
функции кубического
корня, её свойства.
Уметь:
– определять график
функции кубического
корня,
– строить график
функции кубического
корня,
– читать свойства по
графику функции.
Знать определение
функции кубического
корня, её свойства.
Уметь:
– определять график
функции кубического
корня,
– строить график
функции кубического
Текущий
С. 128-135 §14,
№14.1, 14.3, 14.5
Взаимоконтроль
С. 128-135 §14,
№14.7, 14.9, 14.11
66
Функция у=3√х, её
свойства и график
Практикум
Функция
кубического корня.
67
Обобщающий урок
«Степенная
функция»
Закрепление
68
Контрольная работа
№4
«Степенная
функция»
Контроль и
оценка знаний
Степенные функции
с натуральным
показателем и с
целым
отрицательным
показателем,
функция
кубического корня.
Степенные функции
с натуральным
показателем и с
целым
отрицательным
показателем,
функция
кубического корня.
69
Числовые
последовательности
Изучение
нового
материала
Понятие
последовательности
, n-го члена
последовательности
.
корня,
– читать свойства по
графику функции.
Знать определение
функции кубического
корня, её свойства.
Уметь:
– определять график
функции кубического
корня,
– строить график
функции кубического
корня,
– читать свойства по
графику функции.
Уметь строить
графики и описывать
свойства
элементарных
функций.
Уметь строить
графики и описывать
свойства
элементарных
функций.
Тренировочный
тест (подготовка к
ОГЭ)
С. 128-135 §14,
№14.13, 14.15,
14.17
Текущий
С. 128-135 §14,
№14.19, 14.21,
14.23
Письменный
фронтальный
контроль
С. 128-135 §14,
№14.25, 14.27,
14.29
Прогрессии (22 ч.)
Знать понятие
Текущий
последовательности,
n-го члена
последовательности.
Уметь вычислять n-й
член
последовательности,
задавать формулой n-
С. 136-145 §15,
№15.1, 15.3, 15.5
70
Числовые
последовательности
Закрепление
Понятие
последовательности
, n-го члена
последовательности
.
71
Числовые
последовательности
Закрепление
Понятие
последовательности
, n-го члена
последовательности
.
72
Арифметическая
прогрессия
Изучение
нового
материала
Арифметическая
прогрессия,
формула n-го члена
арифметической
прогрессии.
73
Арифметическая
прогрессия
Закрепление
Арифметическая
прогрессия,
формула n-го члена
арифметической
прогрессии.
й член.
Знать понятие
последовательности,
n-го члена
последовательности.
Уметь вычислять n-й
член
последовательности,
задавать формулой nй член.
Знать понятие
последовательности,
n-го члена
последовательности.
Уметь вычислять n-й
член
последовательности,
задавать формулой nй член.
Знать определение
арифметической
прогрессии, формулу
n-го члена
арифметической
прогрессии.
Уметь использовать
индексные
обозначения, решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать определение
арифметической
прогрессии, формулу
n-го члена
арифметической
Групповой
С. 136-145 §15,
№15.7, 15.9, 15.11
Индивидуальный
С. 136-145 §15,
№15.13, 15.15,
15.17
Текущий
С. 145-156 §16,
№16.1, 16.3, 16.5
Самоконтроль
С. 145-156 §16,
№16.7, 16.9, 16.11
74
Арифметическая
прогрессия
Закрепление
Арифметическая
прогрессия,
формула n-го члена
арифметической
прогрессии.
75
Арифметическая
прогрессия
Изучение
нового
материала
Арифметическая
прогрессия,
формула суммы п
первых членов
арифметической
прогрессии
прогрессии.
Уметь использовать
индексные
обозначения, решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать определение
арифметической
прогрессии, формулу
n-го члена
арифметической
прогрессии.
Уметь использовать
индексные
обозначения, решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать формулы
суммы n первых
членов для
арифметической
прогрессии.
Уметь использовать
индексные
обозначения, решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
Взаимоконтроль
С. 145-156 §16,
№16.13, 16.15,
16.17
Текущий
С. 145-156 §16,
№16.19, 16.21,
16.23
76
Арифметическая
прогрессия
Закрепление
Арифметическая
прогрессия,
формула суммы п
первых членов
арифметической
прогрессии
77
Арифметическая
прогрессия
Закрепление
Арифметическая
прогрессия,
формула суммы п
первых членов
арифметической
прогрессии
78
Арифметическая
прогрессия
Закрепление
Арифметическая
прогрессия,
формула суммы п
первых членов
арифметической
прогрессии
применением
изучаемых формул.
Знать формулы
суммы n первых
членов для
арифметической
прогрессии.
Уметь использовать
индексные
обозначения, решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать формулы
суммы n первых
членов для
арифметической
прогрессии.
Уметь использовать
индексные
обозначения, решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать формулы
суммы n первых
членов для
арифметической
прогрессии.
Уметь использовать
индексные
обозначения, решать
Индивидуальный
С. 145-156 §16,
№16.25, 16.27,
16.29
Текущий
С. 145-156 §16,
№16.31, 16.33,
16.35
Индивидуальный
С. 145-156 §16,
№16.37, 16.39,
16.41
79
Арифметическая
прогрессия
Практикум
Арифметическая
прогрессия,
формула суммы п
первых членов
арифметической
прогрессии
80
Геометрическая
прогрессия
Изучение
нового
материала
Геометрическая
прогрессия,
формулы n-го члена
геометрической
прогрессии.
81
Геометрическая
прогрессия
Закрепление
Геометрическая
прогрессия,
формулы n-го члена
геометрической
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать формулы
суммы n первых
членов для
арифметической
прогрессии.
Уметь использовать
индексные
обозначения, решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать определение
геометрической
прогрессии, формулы
n-го члена
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать определение
геометрической
прогрессии, формулы
n-го члена
Самостоятельная
работа
С. 145-156 §16,
№16.43, 16.45,
16.47
Текущий
С. 147-150, п. 26,
№ 610,612, 613
Взаимоконтроль
С. 156-172 §17,
№17.1, 17.3, 17.5
прогрессии.
82
Геометрическая
прогрессия
Закрепление
Геометрическая
прогрессия,
формулы n-го члена
геометрической
прогрессии.
83
Геометрическая
прогрессия
Закрепление
Геометрическая
прогрессия,
формулы n-го члена
геометрической
прогрессии.
84
Геометрическая
прогрессия
Изучение
нового
Геометрическая
прогрессия,
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать определение
геометрической
прогрессии, формулы
n-го члена
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать определение
геометрической
прогрессии, формулы
n-го члена
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать геометрическая
прогрессия –
Самоконтроль
С. 156-172 §17,
№17.7, 17.9, 17.11
Текущий
С. 156-172 §17,
№17.13, 17.15,
17.17
Текущий
С. 156-172 §17,
№17.19, 17.21,
85
Геометрическая
прогрессия
материала
формула суммы п
первых
членов
геометрической
прогрессии.
Закрепление
Геометрическая
прогрессия,
формула суммы п
первых
членов
геометрической
прогрессии.
последовательность
особого вида,
формулы n-го члена
геометрической
прогрессии, формулы
n членов для
геометрической
прогрессии, для
бесконечно
убывающей
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать геометрическая
прогрессия –
последовательность
особого вида,
формулы n-го члена
геометрической
прогрессии, формулы
n членов для
геометрической
прогрессии, для
бесконечно
убывающей
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
17.23
Взаимоконтроль
С. 156-172 §17,
№17.25, 17.27,
17.29
86
Геометрическая
прогрессия
Закрепление
Геометрическая
прогрессия,
формула суммы п
первых
членов
геометрической
прогрессии.
87
Геометрическая
прогрессия
Закрепление
Геометрическая
прогрессия,
формула суммы п
первых
членов
геометрической
прогрессии.
применением
изучаемых формул.
Знать геометрическая
прогрессия –
последовательность
особого вида,
формулы n-го члена
геометрической
прогрессии, формулы
n членов для
геометрической
прогрессии, для
бесконечно
убывающей
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать геометрическая
прогрессия –
последовательность
особого вида,
формулы n-го члена
геометрической
прогрессии, формулы
n членов для
геометрической
прогрессии, для
бесконечно
убывающей
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
Самостоятельная
работа
С. 156-172 §17,
№17.31, 17.33,
17.35
Текущий
С. 156-172 §17,
№17.37, 17.39,
17.41
88
Геометрическая
прогрессия
Закрепление
Геометрическая
прогрессия,
формула суммы п
первых
членов
геометрической
прогрессии.
89
Обобщающий урок
«Арифметическая и
геометрическая
прогрессии»
Практикум
90
Контрольная работа
№5
«Арифметическая и
Контроль и
оценка знаний
Арифметическая и
геометрическая
прогрессии,
формулы
n-го
члена, суммы п
первых
членов
арифметической и
геометрической
прогрессий.
Метод
математической
индукции.
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Знать геометрическая
прогрессия –
последовательность
особого вида,
формулы n-го члена
геометрической
прогрессии, формулы
n членов для
геометрической
прогрессии, для
бесконечно
убывающей
геометрической
прогрессии.
Уметь решать
упражнения и задачи,
в том числе
практического
содержания с
непосредственным
применением
изучаемых формул.
Уметь применять
полученные знания
при решении задач.
Уметь применять
полученные знания
при решении задач.
Математический
диктант,
взимоконтроль
С. 156-172 §17,
№17.43, 17.45,
17.47
Текущий
С. 156-172 §17,
№17.49, 17.51,
17.53
Письменный
фронтальный
контроль
С. 156-172, §17,
тест 7
геометрическая
прогрессии»
91
Комбинаторные
задачи
Изучение
нового
материала
92
Комбинаторные
задачи
Закрепление
93
Комбинаторные
задачи
Закрепление
Элементы комбинаторики, статистики и теории вероятности (18 ч.)
Простейшие
Знать, как решать
Текущий
С. 173-182 §18,
комбинаторные
простейшие
№18.1, 18.3, 18.5
задачи, дерево
комбинаторные
возможных
задачи, рассматривая
вариантов, правило
дерево возможных
умножения.
вариантов, правило
умножения.
Уметь решать
простейшие
комбинаторные
задачи, рассматривая
дерево возможных
вариантов, правило
умножения.
Простейшие
Знать, как решать
Индивидуальный С. 173-182 §18,
комбинаторные
простейшие
№18.7, 18.9, 18.11
задачи, дерево
комбинаторные
возможных
задачи, рассматривая
вариантов, правило
дерево возможных
умножения.
вариантов, правило
умножения.
Уметь решать
простейшие
комбинаторные
задачи, рассматривая
дерево возможных
вариантов, правило
умножения.
Простейшие
Знать, как решать
Групповой
С. 173-182 §18,
комбинаторные
простейшие
№18.13, 18.15,
задачи, дерево
комбинаторные
18.17
возможных
задачи, рассматривая
вариантов, правило
дерево возможных
умножения.
вариантов, правило
умножения.
Уметь решать
простейшие
94
Статистика - дизайн
информации
Изучение
нового
материала
Статистические
методы обработки
информации,
числовые
характеристики
информации.
95
Статистика - дизайн
информации
Закрепление
Статистические
методы обработки
информации,
числовые
характеристики
информации.
96
Статистика - дизайн
Закрепление
Статистические
комбинаторные
задачи, рассматривая
дерево возможных
вариантов, правило
умножения.
Знать статистические
методы обработки
информации,
числовые
характеристики
информации.
Уметь указывать
общий ряд данных
измерений,
наименьшую и
наибольшую
варианты, определять
кратность варианты,
процентную частоту,
строить
многоугольник
процентных частот.
Знать статистические
методы обработки
информации,
числовые
характеристики
информации.
Уметь указывать
общий ряд данных
измерений,
наименьшую и
наибольшую
варианты, определять
кратность варианты,
процентную частоту,
строить
многоугольник
процентных частот.
Знать статистические
Текущий
С. 182-196 §19,
№19.1, 19.3, 19.5
Взаимоконтроль
С. 182-196 §19,
№19.7, 19.9, 19.11
Текущий
С. 182-196 §19,
информации
методы обработки
информации,
числовые
характеристики
информации.
97
Простейшие
вероятностные
задачи
Изучение
нового
материала
Классическое
определение
вероятности,
понятия случайное
событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
98
Простейшие
вероятностные
задачи
Закрепление
Классическое
определение
вероятности,
понятия случайное
событие,
достоверное и
невозможное
события,
несовместные
методы обработки
информации,
числовые
характеристики
информации.
Уметь указывать
общий ряд данных
измерений,
наименьшую и
наибольшую
варианты, определять
кратность варианты,
процентную частоту,
строить
многоугольник
процентных частот.
Знать классическую
вероятностную схему,
классическое
определение
вероятности, понятия
случайное событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
Уметь находить
вероятность события.
Знать классическую
вероятностную схему,
классическое
определение
вероятности, понятия
случайное событие,
достоверное и
невозможное
события,
№19.13, 19.15,
19.17
Групповой
С. 196-209 §20,
№20.1, 20.3, 20.5
Текущий
С. 196-209 §20,
№20.7, 20.9, 20.11
события, события,
противоположные
данному событию.
99
Простейшие
вероятностные
задачи
Закрепление
Классическое
определение
вероятности,
понятия случайное
событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
100
Простейшие
вероятностные
задачи
Закрепление
Классическое
определение
вероятности,
понятия случайное
событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
101
Простейшие
вероятностные
задачи
Практикум
Классическое
определение
вероятности,
понятия случайное
несовместные
события, события,
противоположные
данному событию.
Уметь находить
вероятность события.
Знать классическую
вероятностную схему,
классическое
определение
вероятности, понятия
случайное событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
Уметь находить
вероятность события.
Знать классическую
вероятностную схему,
классическое
определение
вероятности, понятия
случайное событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
Уметь находить
вероятность события.
Знать классическую
вероятностную схему,
классическое
определение
Текущий
С. 196-209 §20,
№20.13, 20.15,
20.17
Индивидуальный
С. 196-209 §20,
№20.19, 20.21,
20.23
Самостоятельная
работа
С. 196-209 §20,
№20.25, 20.27,
20.29
событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
102
Экспериментальные
данные и
вероятности
событий
Изучение
нового
материала
Статистическая
устойчивость,
статистическая
вероятность.
103
Экспериментальные
данные и
вероятности
событий
Закрепление
Статистическая
устойчивость,
статистическая
вероятность.
104
Экспериментальные
данные и
вероятности
событий
Закрепление
Статистическая
устойчивость,
статистическая
вероятность.
105
Экспериментальные
данные и
Закрепление
Статистическая
устойчивость,
вероятности, понятия
случайное событие,
достоверное и
невозможное
события,
несовместные
события, события,
противоположные
данному событию.
Уметь находить
вероятность события.
Иметь представление
о статистической
устойчивости,
статистической
вероятности.
Уметь решать
простейшие
статистические
задачи.
Иметь представление
о статистической
устойчивости,
статистической
вероятности.
Уметь решать
простейшие
статистические
задачи.
Иметь представление
о статистической
устойчивости,
статистической
вероятности.
Уметь решать
простейшие
статистические
задачи.
Иметь представление
о статистической
Текущий
С. 209-215 §21,
№21.1, 21.3, 21.5
Текущий
С. 209-215 §21,
№21.7, 21.9, 21.11
Самостоятельная
работа
С. 209-215 §21,
№21.13, 21.15,
21.17
Текущий
С. 209-215 §21,
№21.19, 21.21,
вероятности
событий
статистическая
вероятность.
106
Экспериментальные
данные и
вероятности
событий
Практикум
Статистическая
устойчивость,
статистическая
вероятность.
107
Обобщающий урок.
«Элементы
комбинаторики,
статистики и теории
вероятностей»
Контрольная работа
№6
«Элементы
комбинаторики,
статистики и теории
вероятностей»
Закрепление
Простейшие
комбинаторные и
вероятностные
задачи.
Контроль и
оценка знаний
Простейшие
комбинаторные и
вероятностные
задачи.
108
устойчивости,
статистической
вероятности.
Уметь решать
простейшие
статистические
задачи.
Иметь представление
о статистической
устойчивости,
статистической
вероятности.
Уметь решать
простейшие
статистические
задачи.
Уметь решать
простейшие
комбинаторные и
вероятностные
задачи.
Знать понятия:
перестановки,
размещения,
сочетания;
относительной
частоты, случайного
события, различные
подходы к
определению
вероятности
случайного события,
формулы для
подсчета числа
перестановок,
размещений,
сочетаний.
Уметь применять
теоретические знания
для решения задач.
21.23
Тренировочный
тест (подготовка к
ОГЭ)
С. 209-215 §21,
тест 8
Текущий
С. 209-215 §21,
тест 9
Письменный
фронтальный
контроль
С. 209-215 §21,
тест 10
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
Повторение.
Вычисления.
Повторение.
Вычисления.
Повторение.
Тождественные
преобразования
Повторение.
Тождественные
преобразования
Повторение.
Уравнения и
системы уравнений
Повторение.
Уравнения и
системы уравнений
Повторение.
Неравенства
Повторение.
Неравенства
Повторение.
Функции
Повторение.
Функции
Повторение.
Построение
графиков
Повторение.
Построение
графиков
Повторение.
Решение текстовых
задач
Повторение.
Решение текстовых
задач
Повторение.
Решение текстовых
Итоговое повторение (28 ч.)
Знать математические
Все виды
термины и формулы,
контроля
различные методы
решения задач,
пропорций,
уравнений и
неравенств, систем
уравнений и
неравенств, графики
основных
элементарных
функций и их
свойства, способы
преобразования
выражений.
Уметь правильно
употреблять
математические
термины и формулы,
применять различные
методы при решении
задач, пропорций,
уравнений и
неравенств, систем
уравнений и
неравенств,
выполнять
преобразование
различных
выражений.
Тест 11
Индивидуальные
задания
Тест 12
Индивидуальные
задания
Тест 13
Индивидуальные
задания
Тест 15
Индивидуальные
задания
Тест 16
Индивидуальные
задания
Тест 17
Тест 2
Тест 18
Индивидуальные
задания
Индивидуальные
задания
124
125
126
127
128
129
130
131
132
133
134
135
136
задач
Повторение.
Решение
нестандартных
задач
Повторение.
Решение
нестандартных
задач
Повторение.
Решение
нестандартных
задач
Повторение. Чтение
графиков
Повторение. Чтение
графиков
Повторение. Чтение
графиков
Повторение. Работа
с таблицами
Повторение. Работа
с таблицами
Повторение. Работа
с таблицами
Повторение.
Решение
практических задач
Повторение.
Решение
практических задач
Итоговая
контрольная работа.
Итоговый урок
Тест 19
Индивидуальные
задания
Индивидуальные
задания
Тест 20
Индивидуальные
задания
Индивидуальные
задания
Тест 21
Индивидуальные
задания
Индивидуальные
задания
Тест 22
Индивидуальные
задания
Описание учебно-методического и материально-технического обеспечения
образовательного процесса
1. Литература:
1) А.Г. Мордкович, Л.А. Александрова и др. Алгебра: учебник для 9 класса
общеобразовательных учреждений. - М: Мнемозина, 2009 г.
2) Алгебра – 9. Рабочая тетрадь (М.С. Мильштейн), Алгебра – 9. Контрольные работы (Л.А.
Александрова), Алгебра, 7-9. Тесты (А.Г. Мордкович, Е.Е. Тульчинская);
3) Математика 5-11 классы: нетрадиционные формы организации контроля на уроках / авт.сост. М.Е. Козина, О.М. Фадеева. - Волгоград, Учитель, 2007;
4) Н.П.Кострикина. Задачи повышенной трудности в курсе алгебры 7-9 классов - М :
Просвещение», 1991;
5) Математика 5-11 классы: нетрадиционные формы организации контроля на уроках / авт.сост. М.Е. Козина, О.М. Фадеева. - Волгоград, Учитель, 2007;
6) Конструирование современного урока математики: кн. для учителя / С.Г. Манвелов. – М.:
Просвещение,2005.
2. Интернет-ресурсы
1) Я иду на урок математики (методические разработки). - Режим доступа: www.festival. 1
september.ru
2) Уроки, конспекты. - Режим доступа: www.pedsovet.ru
3) http://www.informika.ru; http://www.ed.gov.ru; http://www.edu.ru
4) http://www.kokch.kts.ru/cdo
5) Педагогическая мастерская, уроки в Интернет и многое другое. – Режим доступа: http://
teacher.fio.ru
6) Новые технологии в образовании. – Режим доступа: http://edu.secna.ru/main
7) Мегаэнциклопедия Кирилла и Мефодия. – Режим доступа: http://mega.km.ru
8) Сайты энциклопедий, например. – Режим доступа: http://www.rubricon.ru; http://www.encyclopedia.ru
9) http://pedsovet.su/
10) Общероссийский проект «Школа цифрового века».
3. Технические средства обучения:
1) DVD-плеер (видеомагнитофон).
2) Телевизор.
3) Компьютер.
4) Видеопроектор.
4. Учебно-практическое оборудование:
1) Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления
таблиц, схем.
2) Штатив для таблиц,
3) Ящики для хранения таблиц.
4) Укладка для аудиовизуальных средств (слайдов, таблиц и др.)
6.