1.10 С.Н. Карамбиров.
реклама
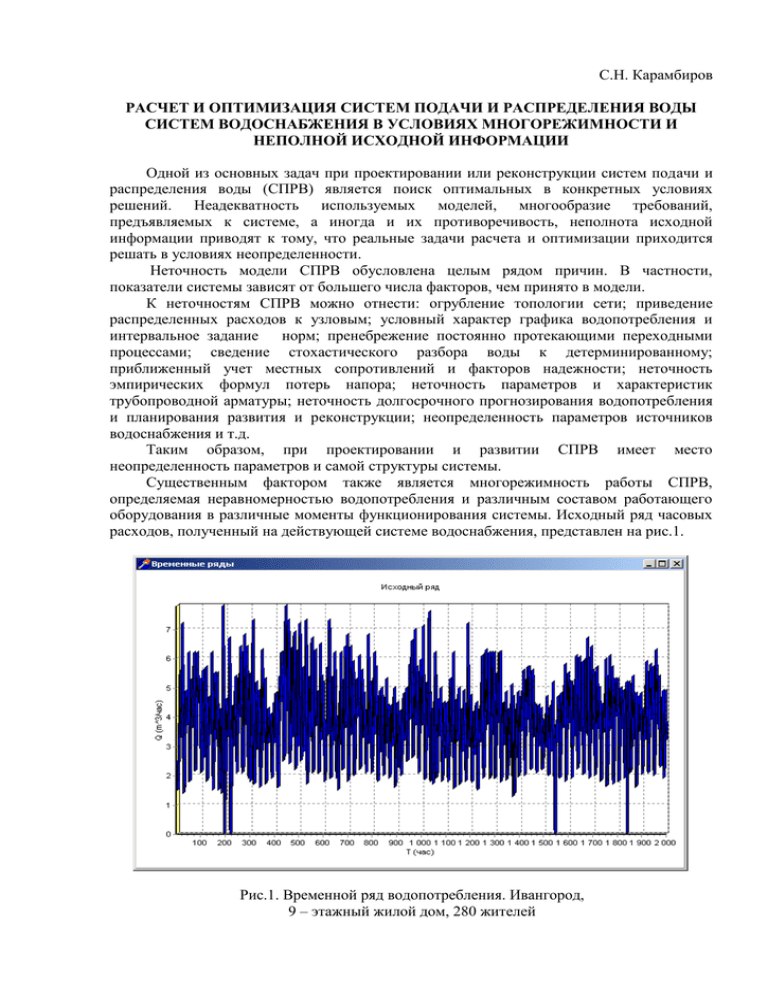
С.Н. Карамбиров РАСЧЕТ И ОПТИМИЗАЦИЯ СИСТЕМ ПОДАЧИ И РАСПРЕДЕЛЕНИЯ ВОДЫ СИСТЕМ ВОДОСНАБЖЕНИЯ В УСЛОВИЯХ МНОГОРЕЖИМНОСТИ И НЕПОЛНОЙ ИСХОДНОЙ ИНФОРМАЦИИ Одной из основных задач при проектировании или реконструкции систем подачи и распределения воды (СПРВ) является поиск оптимальных в конкретных условиях решений. Неадекватность используемых моделей, многообразие требований, предъявляемых к системе, а иногда и их противоречивость, неполнота исходной информации приводят к тому, что реальные задачи расчета и оптимизации приходится решать в условиях неопределенности. Неточность модели СПРВ обусловлена целым рядом причин. В частности, показатели системы зависят от большего числа факторов, чем принято в модели. К неточностям СПРВ можно отнести: огрубление топологии сети; приведение распределенных расходов к узловым; условный характер графика водопотребления и интервальное задание норм; пренебрежение постоянно протекающими переходными процессами; сведение стохастического разбора воды к детерминированному; приближенный учет местных сопротивлений и факторов надежности; неточность эмпирических формул потерь напора; неточность параметров и характеристик трубопроводной арматуры; неточность долгосрочного прогнозирования водопотребления и планирования развития и реконструкции; неопределенность параметров источников водоснабжения и т.д. Таким образом, при проектировании и развитии СПРВ имеет место неопределенность параметров и самой структуры системы. Существенным фактором также является многорежимность работы СПРВ, определяемая неравномерностью водопотребления и различным составом работающего оборудования в различные моменты функционирования системы. Исходный ряд часовых расходов, полученный на действующей системе водоснабжения, представлен на рис.1. Рис.1. Временной ряд водопотребления. Ивангород, 9 – этажный жилой дом, 280 жителей Детальный учет всех перечисленных обстоятельств практически невозможен. Выходом из положения может быть использование методов принятия решения в условиях неопределенности. В ряде случаев при построении модели, ввиду отсутствия полной информации, решающее значение имеют сведения, полученные от эксперта, отражающие смысловые особенности системы и сформулированные им на естественном языке [2]. Описание системы в этом случае носит приближенный характер. Для использования имеющейся информации при построении модели оптимизируемой системы вводится понятие нечеткого множества, которое позволяет формализовать словесное описание объекта. Нечеткое описание используется, когда задается не точное значение параметра, а некоторое множество возможных его значений с той или иной степенью «уверенности» эксперта. Элементы нечеткого множества А могут обладать некоторым свойством в разной степени и, следовательно, принадлежать данному множеству с разной степенью A 1. Чем ближе A(x) к единице, тем выше степень принадлежности х к А. Выбор функции принадлежности основан на качественной информации эксперта. Использование сходных условий, дополнительная информация и опыт проектирования позволяют построить функции принадлежности интересующих параметров. При этом можно косвенно учесть несколько факторов неопределенности. Применение нечетких («мягких») ограничений расширяет область допустимых решений и позволяет учесть противоречивые цели отдельных подсистем, которые не позволяют получить оптимальное решение в детерминированной постановке. Интервальные и нечеткие подходы хорошо зарекомендовали себя при решении широкого круга задач. Нечеткое моделирование технических и экономических систем реализовано в пакетах MATLAB, fuzzyTECH, FuzzyXL, CubiCalc, Rule Maker и др. Вместе с тем эти методы не нашли широкого применения при проектировании и эксплуатации систем подачи и распределения воды, состоящих из водозаборных сооружений, насосных станций, резервуаров, станций подкачки, арматуры, потребителей, водоводов и распределительных сетей [3]. Рассмотрим вариант нечеткой постановки задачи, связанный с неопределенностью водопотребления, задаваемого в СНиП интервально (таблице). Расчетные расходы воды Степень благоустройства районов жилой Удельное хозяйственно–питьевое Застройки водопотребление л/сутчел Застройка зданиями, оборудованными внутренним водопроводом и канализацией: Без ванн 125 – 160 С ванными и местными водонагревателями 160 – 230 С централизованным горячим водоснабжением 230 – 350 Лицо, принимающее решение, задает узловые расходы в виде функций принадлежности, например, вида, представленного на рис 2, показывающие «степень ожидаемости» водопотребления. Функции принадлежности водопотребления промышленными и другими предприятиями определяются в каждом случае индивидуально. 1 Mu 0,8 0,6 0,4 0,2 0 Q Рис. 2. Функция принадлежности водопотребления Зная функции принадлежности узловых расходов, можно провести расчеты и вычислить функции принадлежности результатов гидравлической увязки сети - расходов участков, напоров в узлах, подач водопитателей (нечеткое потокораспределение). Типичный вид функции принадлежности свободного напора в узле сети представлен на рис.3. Результаты можно использовать для оценки изменения величин потокораспределения, резервов саморегулирования системы и выявления «критических» параметров. Возможно и конструктивное применение теории нечетких множеств в расчетах СПРВ. Для этого рассмотрим требуемую функцию принадлежности требуемых узловых напоров в задаче оптимизации (рис.4), отражающую наше пожелание иметь свободные напоры не меньше требуемых, но не больше допустимых. Предполагается, что для водопотребления с заданным значением функции принадлежности решена задача синтеза СПРВ и получен ее «базовый» стоимостной показатель (интегральные дисконтированные затраты) –Z1. H(м) Рис.3 Функция принадлежности напора в узле 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 Нтреб. Hдоп. Рис.4. Функция принадлежности требуемых свободных напоров При изменении узловых расходов в пределах отличной от нуля функции принадлежности, изменяются и экономические показатели системы, При этом интерес представляют только решения, для которых Z<Z1, что может быть закреплено в соответствующей функции принадлежности (рис. 5). Z1 Z Рис. 5 Функция принадлежности интегральных дисконтированных затрат Для фиксированного набора неопределенных параметров с заданными функциями принадлежности i можно подобрать параметры системы и получить функцию принадлежности решения, как минимум i (наихудший случай): = min i. Заметим, что в i входят функции принадлежности узловых расходов, свободных напоров и экономического показателя Z. В соответствии с принципом Беллмана-Заде [2] оптимальным будет решение, которое максимизирует функцию (лучшее из худшего): опт = max . Рассмотрим один из вариантов приближенного решения задачи: 1. Задаемся вектором узловых расходов Q, с одинаковыми значениями функции принадлежности Q. 2. Определяем параметры системы и, для увеличения значения функции принадлежности Z, проводим ее оптимизацию, например, методом линейного программирования. 3. Для полученного решения находим функцию принадлежности . 4. Повторяя шаги 1-3 находим максимальное значение и соответствующие ему параметры системы. Пример изменения функции цели нечеткой оптимизации и Z/Z1 от Q показан на рис.6. Рис.6. График изменения функции цели и Z/Z1 нечеткой оптимизации Видно, что функция принадлежности пересечения состоит из двух типов ветвей: линейной, которую определяет функция принадлежности узловых расходов, и нелинейной, задаваемой экономическим функционалом. Максимум этой функции, то есть решение задачи, является «компромиссом» между рассматриваемыми неопределенностями. Нечеткое обеспечение подач водопитателей Как правило, график подач водопитателей определяют до гидравлического расчета, исходя из расчетного ступенчатого графика водопотребления. В большинстве случаев выбор диаметров производят на час наибольшего транзита или на час наибольшего водопотребления [1]. После подбора параметров и увязки сети расчетные подачи, обычно, не совпадают с требуемыми. Нечеткая постановка задачи позволяет приблизить расчетные и требуемые подачи. Для примера рассмотрим систему с контррезервуаром, имеющую два водопитателя – насосную станцию и башню. В качестве расчетных примем случаи максимального и минимального водопотребления, причем в час Qmin башня должна пополняться. Пусть удалось получить начальное приближение параметров системы, причем в час Qmax вода поступает из башни, а в час Qmin – в башню, однако подачи водопитателей могут не совпадать с требуемыми. Не имеет смысла требовать точного совпадения подач, так же, как ставить требования приближения подач, не считаясь с экономическими показателями. Вместе с тем, решение задачи можно получить, если «смягчить» требования, то есть допустить возможность их нарушения с той или иной степенью и искать подачи, «близкие» к заданным. В этом случае можно поставить задачу оптимизации, когда ищется максимум пересечения функций принадлежности требуемых подач. Рассмотрим формирование такой целевой функции: находим первое приближение параметров системы, обеспечивающее для башни: в час Qmax - подачу из башни, в час Qmin - подачу в башню; задавшись исходными диаметрами, выбираем в качестве допустимых для каждого участка диаметры на размер больше и на размер меньше выбранного; задаем функции принадлежности требуемых подач для часа Qmax и Qmin, удовлетворяющие условиям ij(Qдостij) > 0, где Qдостij – достигнутая подача i–го водопитателя в j–й час (например j = 1 – час Qmax, j = 2 – час Qmin), и не допускающие смены знака подачи водопитателя (рис.7). Так как для любого часа Qij = Qj =const, где Qj – водопотребление объекта в j–й час, достаточно ограничиться функциями принадлежности одного водопитателя, например, башни. Подачи башни в выбранный час, например, Qmax независимо варьируются в пределах значений функции принадлежности (рис.7); из возможных диаметров выбираем, для каждого участка, текущий. Таким образом, получаем реализацию переменных; при фиксированных диаметрах и текущих подачах определяем требуемые напоры у водопитателей в час Qmax , и, в случае их допустимости (рис.7), подбираем параметры и проводим гидравлические расчеты для максимального и минимального водопотребления с возможным регулированием подач водопитателей; находим значения функций принадлежности подач башни в выбранные часы и их min, то есть целевую функцию, показывающую степень близости подач к требуемым; продолжая варьировать переменными задачи, находим максимум функции цели опт max min i . i 2 В подобной ситуации для решения задачи наиболее эффективны методы случайного поиска. На основе этих методов автором был разработан алгоритм решения поставленной задачи направленным случайным поиском с самообучением. Сравнивая полученные на каждом шаге значения, находим оптимальное решение, соответствующее подачам, наиболее близким к требуемым. Расчеты показали хорошую сходимость метода. Типичный ход оптимизационного процесса представлен на рис.8. В более общем случае может быть поставлена задача приближения к требуемым подачам на заданном множестве часовых интервалов. Выше отмечалось, что задача обеспечения требуемых подач водопитателей тесно связана с экономическими факторами. Рассмотрим одно из возможных расширений поставленной задачи – нахождение «разумного» компромисса между требуемыми подачами водопитателей и стоимостными характеристиками системы. Б 1 Час Qmax ---- Час Qmin 0,5 Qдост2 Qтр2 Qтр1 QБ Рис.7. Функции принадлежности требуемых подач башни ( Б) В рассмотренную выше схему легко добавить экономический показатель с функцией принадлежности типа, показанного на рис 5, тогда опт max min i . i 3 Таким образом, получена задача многокритериальной оптимизации, которая может быть решена описанным выше способом. Без требований на подачи водопитателей этот метод может использоваться для традиционной оптимизации СПРВ. Аналогично учитываются другие факторы неопределенности. Рис.8 Ход процесса приближения к требуемым подачам водопитателей Стохастическая неопределенность На основе рассмотрения водопотребления как многомерного случайного вектора и системы нелинейных уравнений для стационарного гидравлического расчета СПРВ развит метод стохастического потокораспределения в сети. Установившееся потокораспределение в сети моделируется системой уравнений (1), которая описывает, соответственно, первый, второй законы Кирхгофа в узловой форме и напорно-расходные характеристики насосных станций, станций подкачки и регулирующих задвижек. При этом насосные станции (НС) моделируются узлами, а станции подкачки и задвижки – участками. Некоторые водопитатели - НС моделируют скважины, подающие воду непосредственно в сеть. При этом коммуникации водозаборов подземных вод входят в расчетную схему. q pn Qi i (H i ) 0 , i 1,.., m; p,ni (Z H ) - (Z H ) - sign(q ) S q 0 , i, j 1,.., m I - I - I ; i j j ij ij ij cп зд i S Hj H j hвj - H Hj 2 q вj q вj 0, j 1,.., k; kj S спi H i2 - H i1 - H спi 2 qiу qiу 0, iу I cп ; k cni 8 iy H i1 - H i2 qiу qiу 0 , iу I зд . g d 4 iy (1) где Qi-полезный расход воды в i-м узле(л/c); (H) -функция, учитывающая изменение расхода воды в узле от напора; Hi – свободный напор в i-м узле(м); qpn – расход участка, смежного с i–м узлом (л/c); qij – расход в участке (л/c), соединяющем узлы i и j; mколичество узлов; I – множество участков сети (1..n); Iсп – множество участков – станций подкачки; Iзд - множество участков – задвижек; k - число водопитателей; Sij– коэффициент гидравлического сопротивления участка между узлами i и j; kj - число параллельно работающих насосов j–го водопитателя; Zi - геодезическая высота i-го узла сети (м); qв j -подача j-го водопитателя (л/c); HHj, SHj - коэффициенты аналитического выражения характеристик насосов водопитателей (для башен SHj=0); Hспi, Scпi –то же для станций подкачки в iy–м участке; Hi1, Hi2-напор в начале и в конце участка -станции подкачки или задвижки (м); iy, diy –коэффициент сопротивления и диаметр задвижки в iy-м участке; hвj - высота всасывания j–го водопитателя; для скважин hвj= -zст +zнас+qвj/qуд; zст- отметка статического уровня; qуд - удельный дебит скважины (л/c/м); zнас - отметка насоса (м). Вектор узловых расходов: Q = (Q11 ... Qmm) - случайный вектор. Будем считать, что Q подчиняется совместному нормальному закону распределения с ковариационной ~ матрицей K Q и средним значением Q. В общем виде систему (1) можно записать так F(x) = 0, T где F(x)=(f1(x)...fr(x)) — вектор-функция, состоящая из уравнений системы (2), r = n+m+k – размерность системы. Вектор неизвестных x имеет следующую структуру X = (q1... qnH1 ... Hm qHc 1...qHc k)T (2) (3) Дополним вектор водопотребления Q до размерности системы, приписав к нему n+k нулей. Последние можно рассматривать как дисперсии и ковариации случайных величин, плотность распределения которых fi(x) = (x); i = m + 1, .., r, (4) где (x) - дельта-функция Дирака. Ковариационная матрица вектора Q будет иметь вид ~ K Q m m 0 KQ = 0 0 r r . (5) Поскольку водопотребление узлов является случайным вектором, случайным будет и вектор решения x. Перепишем (2) в виде F(x) = Q. (6) Тогда решение системы (6) можно записать в виде x = F-1(Q). (7) Так как F(x) нелинейная по x вектор-функция, то и F-1(Q) также будет нелинейной. Ввиду того, что определение распределения нелинейных функций случайных величин является достаточно сложной задачей, для определения характеристик вектора х применим метод линеаризации, который состоит в замене нелинейных функций в окрестности решения достаточно близкими к ним линейными. При этом вектор x будет иметь многомерное нормальное распределение с математическим ожиданием: x F-1(Q) (8) и ковариационной матрицей Kx [F ´]-1 KQ[F ´]-1 , (9) где звездочкой обозначена операция транспонирования, а матрица f 1 f 1 ... x1 xr F´= .................. . f r f r x ... x 1 r x x (10) Доверительный интервал пьезометрических линий при стохастическом расчете для схемы с контррезервуаром показан на рис.9. Этот метод отражает лишь основные свойства стохастических процессов, происходящих в системе, и позволяет оценить интервалы возможных изменений интересующих величин. На базе стохастического расчета СПРВ разработан метод стохастической оптимизации, в котором оптимизируется математическое ожидание экономического функционала при известных вероятностных характеристиках решения, определяемых по начальному (текущему) приближению стохастического расчета. В узлах сети должны поддерживаться напоры, обеспечивающие заданную вероятность отказа подачи воды Poi, то есть P (Hi < Hoi) Poi . (11) У водопитателей вероятность превышения напора Hвi над предельным значением Hдоп i, определяемым из прочностных условий, не должна превышать некоторого заданного значения Pвi P (Hвi > Hдоп i) Pвi (12) Выполнить эти требования можно с помощью специальных ограничений в методе линейного программирования. В функцию цели и в систему ограничений входят элементы ковариационной матрицы решения стохастического расчета. Рис.9 Интервалы изменения напоров для схемы с контррезервуаром Выводы Для решения многих задач потокораспределения и оптимизации, в том числе многокритериальной, автором предлагается использовать нечеткие переменные и методы направленного случайного поиска с самообучением, которые позволяют формально учесть требования, существующие, в настоящее время, в форме представлений и пожеланий. Примером такой задачи может служить, разработанная автором, многорежимная оптимизация системы по экономическому фактору с приближением подач водопитателей, в характерные периоды, к требуемым значениям. Показано, что получаемые решения не требуют округления и корректировки. Нечеткие и стохастические расчеты потокораспределения хорошо согласуются между собой по интервалам изменения решений. Дальнейшее развитие таких методов представляется очень перспективным. Библиографический список 1. Абрамов Н.Н., Поспелова М.М., Сомов М.А. и др. Расчет водопроводных сетей: Учебное пособие для вузов. М.: Стройиздат. 1983. 278 с.. 2. Заде Л. Понятие лингвистической переменной и его применение к понятию приближенных решений. М.: Мир. 1976. 3. Николадзе Г.И., Сомов М.А. Водоснабжение: Учеб. для вузов. М.: Стройиздат. 1995. 688 с.
