ПАЛОЧКА-ВЫРУЧАЛОЧКА
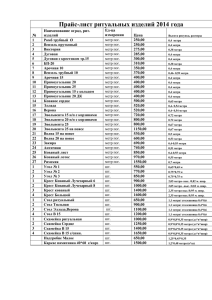
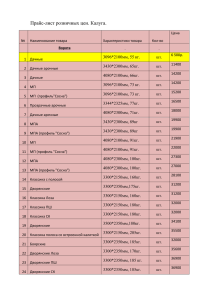
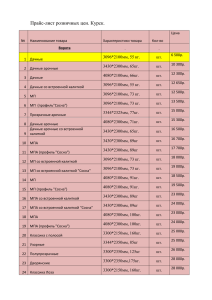
реклама

ПАЛОЧКА-ВЫРУЧАЛОЧКА Научно-методический материал (обобщение опыта) педагог Решетова Марина Георгиевна МКОУ «ООШ № 164» Кемеровская область, Таштагольский район, поселок Амзас 1 СОДЕРЖАНИЕ Перевод внесистемных единиц в СИ………….………………………………………………3 Говорящие приставки……………………………………………………………………….3 Длина, площадь, объем………………………………………………………………………4 Волшебная лесенка………..…………………………………………………………….4 Квадрат и куб……………..……………………………………………………………..5 Скорость и плотность………………………………………………………………………...6 Запоминание формул…………..………………………………………………………………..6 Работа с формулами………….………………………………………………………………….6 Вычисления по формулам………………………………………………………………………7 2 Физику и математику в школе должны изучать все дети. У каждого из них разные способности, склонности, предпочтения. Есть дети, которые все «схватывают на лету», а есть а есть и такие у которых все «очень сложно». Именно эти дети больше всего нуждаются в помощи, ведь к началу 7 класса они пришли с огромным багажом пробелов в знаниях, умениях и навыках, да еще с «пугалкой», которую им часто твердили родители: «Это еще что, вот начнется физика (алгебра, геометрия, химия и т.д)». В результате всего этого у них уже сформировалась начальная установка «Ничего не понимаю», «Это мне никогда не выучить» и т.п. Как можно помочь таким ученикам? Как разубедить их, изменить их настроение, отношение к изучаемому предмету? Это сложная задача и каждый учитель решает ее по-своему. За многие годы учительской деятельности мной был накоплен материал, который в одних случаях помогает детям увидеть уже хорошо знакомые действия, а в других – дает подсказку, как легче справиться с проблемами. Я привожу нетрадиционные формы запоминания, приемы работы с физическими величинами и формулами. Перевод внесистемных единиц в СИ При решении задач необходимо еще при анализе условий перевести все физические величины в СИ. Здесь моментами, которые могут вызвать трудность могут быть: 1. Применение дольных и кратных приставок. 2. Перевод в СИ линейных, квадратных и кубических величин. 3. Перевод в СИ единиц скорости и плотности. Говорящие приставки Здесь хорошо сделать небольшой экскурс в урок русского языка. Вспомним, что слова имеют корень и приставку. Пользуясь таблицей дольных и кратных приставок (она в кабинете всегда перед глазами) и уже хорошо знакомым единицам измерения грамм и метр, разберем следующие случаи: Возьмем корень грамм Кило = 1000, значит КИЛОграмм = 1000 грамм Мили=0,001, значит МИЛИграмм=0,001грамма И обратно: грамм = 0,001 КИЛОграмма грамм = 1000 МИЛИграммов При переводе граммов в килограммы следует вместо приставки произнести ее численное значение. ПРИМЕР: 285 милиграмм – 280 тысячных грамма = 0,280 г 15 грамм – 15 тысячных килограмма = 0.015 кг Возьмем корень МЕТР КИЛОМЕТР=1000 МЕТРОВ МЕТР=0,001 КИЛОМЕТРА 3 ДЕЦИМЕТР =0,1 МЕТРА МЕТР=10 ДЕЦИМЕТРОВ САНТИМЕТР=0,01 МЕТРА МЕТР=100 САНТИМЕТРОВ МИЛИМЕТР=0,001 МЕТРА МЕТР=1000 МИЛИМЕТРОВ ПРИМЕР: 25 КИЛОМЕТРОВ =25 тысяч МЕТРОВ=25000 м 54 САНТИМЕТРА= 54 сотых МЕТРА=0,54 м 28 МИЛИМЕТРОВ=28 тысячных МЕТРА=0,028 м Именно проговаривая дважды приставку, сначала в виде приставки, а затем в виде ее численного значения ученик произносит величину в виде десятичной дроби, которую потом записывает. Длина, площадь и объем Волшебная лесенка Нарисуем лесенку. С одной стороны возле ступенек расставим единицы длины, а с другой стороны укажем, во сколько раз эти величины отличаются друг от друга. Дальше, рассуждая, сто длина, выраженная в сантиметрах выглядит больше, чем в метрах, расставляем стрелки, указывая, что переводя метры в сантиметры, будем умножать, а переводя сантиметры в метры – делить на все числа, которые стоят с обратной стороны лесенки. Если нужно перевести в СИ квадратные или кубические единицы, то разницу между ними тоже нужно возвести в квадрат или куб. ПРИМЕР: 76 см2 =76:100:100=0,0076 м2 см 10 дм 10 м 4 см² 10² дм² м² 10² Квадрат и куб Если рядом нет таблицы дольных и кратных приставок 1 м · 1м = 1м2 100см · 100 см = 10000см2 1м 1м2 = 10000см2 1м 1м 1м 1 м · 1м · 1 м = 1м3 1 м 100см · 100 см · 100 см = 1000000см3 1м3 = 1000000см3 5 Скорость, и плотность При переводе скорости из внесистемных единиц в СИ нужно километры, сантиметры, миллиметры переводить в метры, а часы, минуты и т.д. в секунды. Дальше надо придерживаться определенной формы записи: км 72 ч = 72 км 1 час м 72000м =20 с 3600с При переводе единиц плотности в СИ действуют аналогично: г 56 см 3= 56г 1см3 0,056кг 0,000001м3 кг =56000 м3 Запоминание формул Формулы, конечно, надо знать наизусть. Однако есть такое свойство человеческой памяти – забывать то, чем не пользуешься постоянно. Но есть некоторые приемы, которые позволяют закрепить в памяти некоторые факты, если они имеют какую-нибудь зацепку. Этот прием я подсмотрела в журнале «Физика в школе». Один мой коллега предложил давать формулам имена, в которых звучит их содержание. Особенно ценно в этом приеме еще и то, что названия ученики могут придумывать сами. ПРИМЕР: Масса = ров m=ρ·v Ауитка A=UIt Рожа F=ρgh Жираф F=gρV Свита, свет S=vt Рельс R=ρ 𝑙 𝑠 Еще один способ для тех, кто знает или обращает внимание на единицы измерения величин. НАПРИМЕР: Скорость измеряется в метр υ= секунда = путь время = м с , значит, чтобы найти скорость, надо метры делить на секунды. 𝑆 𝑡 6 Работа с формулами Многие учащиеся испытывают затруднения при преобразовании формул. Здесь хорошей палочкой-выручалочкой станет магический треугольник. Любую формулу, записанную в виде произведения величин. Можно вписать в треугольник, разбитый на части. Букву, стоящую перед знаком равенства вписывают в верхнюю часть треугольника, а остальные – в нижние ячейки в произвольном порядке. F m U a I R (𝑡2 - 𝑡1 ) m Q C Теперь обращаем внимание, что каждый треугольник, по сути, является двухэтажной конструкцией, как и простая дробь, т.е. имеет числитель – верхнюю часть и знаменатель – нижнюю часть. Чтобы выразить из формулы искомую величину, нужно просто закрыть ее рукой. Тогда перед нами останется либо один этаж, т.е. все величины будут записаны в ряд через знаки умножения, либо в виде дроби с числителем и знаменателем, 7 Вычисления по формулам Есть еще один способ, как справиться с формулой при решении задач. И хотя методисты меня осудят, я частенько его применяю, ведь, если нельзя выйти через дверь, приходится лезть через окно. Нужно просто показать ученикам, что формула, после того, как в нее подставить значения всех известных величин превращается в обыкновенное простейшее линейное уравнение, которое они хорошо умеют решать. Если же и этого недостаточно, можно заменить искомую величину привычной буквой Х.Существенным недостатком является то, что нет возможности проверить правильность решения, определив размерность найденной величины, и при подставлении значений в формулу единицы измерения тоже не вписываются. Но здесь опять же, цель оправдывает средства этим приемом пользуются только самые слабые ученики при решении простейших задач, а для них и это уже результат. Основной моей целью было помочь ученикам запомнить «сухие» формулы, создать более комфортную атмосферу на уроке, облегчить процесс приобретения и сохранения знаний. Хочется надеяться, что мой опыт и идеи, собранные по крупицам помогут ученикам по- иному взглянуть на предмет физики и почувствовать себя хотя бы немного увереннее. 8