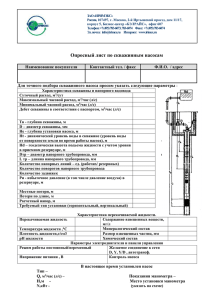
УП_Гидравлика, гидр привод и газ дин

Министерство образования Российской Федерации
Владивостокский государственный университет
экономики и сервиса
________________________________________________________
С.А. ОСТРЕНКО
В.В. ПЕРМЯКОВ
ГИДРАВЛИКА,
ГИДРАВЛИЧЕСКИЙ ПРИВОД
И ГАЗОВАЯ ДИНАМИКА
Учебное пособие
Владивосток
Издательство ВГУЭС
2003
1
ББК 22.253.3
О 76
Рецензенты: Е.Н. Минаев, д-р техн. наук, профессор;
В.П. Рогов, канд. техн. наук, доцент
О 76
Остренко С.А., Пермяков В.В.
ГИДРАВЛИКА, ГИДРАВЛИЧЕСКИЙ ПРИВОД
И ГАЗОВАЯ ДИНАМИКА: Учебное пособие. – Владивосток: Изд-во ВГУЭС, 2003. – 132 с.
В работе представлены задачи по гидравлике, гидравлическим машинам, гидроприводам и газовой динамике с кратким изложением теории по каждому из разделов, а также справочный
материал для их решения.
Для студентов специальности 23.01.00 – "Эксплуатация и
обслуживание транспортных и технологических машин и оборудования (автомобильный транспорт)".
ББК 22.253.3
©
2
Издательство Владивостокского
государственного университета
экономики и сервиса, 2003
ВВЕДЕНИЕ
Грамотная эксплуатация и обслуживание транспортных машин и
оборудования невозможны без знаний законов гидравлики и газовой
динамики, а также без умения приложения их для решения практических задач: определения давления в жидкостях, сопротивления каналов,
сил, действующих на тела, помещенные в поток. Кроме того, будущие
специалисты должны иметь представление о принципах работы и основных характеристиках гидравлических машин, гидродинамических
передач и объемных гидроприводов, широко распространенных на автомобильном транспорте.
Учебное пособие состоит из трех частей. В первой части представлены задачи по гидростатике, динамике несжимаемой жидкости, расчетам гидравлических систем, гидравлическим машинам. Вторая часть
посвящена гидравлическим передачам и гидроприводам. В третьей –
рассмотрены особенности процессов, происходящих в сжимаемых средах, и собраны задачи, связанные с одномерным изоэнтропическим течением газа, со скачками уплотнения и течениями с трением при наличии энергообмена.
Каждый раздел имеет в своем составе теоретическую часть, задачи
(некоторые из них многовариантны) и справочный материал. Главы,
предполагаемые для самостоятельного изучения студентами, снабжены
примерами расчетов. Все это позволяет использовать данную работу
для обучения по заочной форме.
При составлении (первая и вторая части подготовлены С.А. Остренко, третья – В.В. Пермяковым) использованы задачи из следующих
первоисточников.
Давидсон В.Е. Основы газовой динамики в задачах. – М.: Высшая
школа, 1965. 224 с.
Золотов С.С., Амфилохиев В.Б., Фаддеев Ю.И. Задачник по гидромеханике для судостроителей: Учеб. пособие. 2-е изд., перераб. и доп. –
Л.: Судостроение, 1984. 232 с.
Остренко С.А., Пермяков В.В. Гидрогазодинамика и гидравлические системы: Сб. задач. – Владивосток: Изд-во ВГУЭС, 1997. 120 с.
Примеры расчетов по гидравлике: Учеб. пособие для вузов /
А.Д. Альтшуль, В.И. Калицун, Ф.Г. Майрановский, П.П. Пальгунов;
Под ред. А.Д. Альтшуля. – М.: Стройиздат, 1977. 255 с.
Сборник задач по машиностроительной гидравлике: Учеб. пособие
для машиностроительных вузов / Д.А. Бутаев, З.А. Калмыкова, Л.Г. Подвидз и др.; Под ред. И.И. Куколевского и Л.Г. Подвидза. 4-е изд., перераб. – М.: Машиностроение, 1981. 464 с.
3
Часть 1
ГИДРАВЛИКА И ГИДРАВЛИЧЕСКИЕ СИСТЕМЫ
Свойства жидкостей
Основной механической характеристикой жидкости является плотность, определяемая для однородной жидкости отношением ее массы М
к объему W:
  M W , кг/м3.
Значения плотностей капельных жидкостей при температуре 20 оС
приведены в таблице П-1.
Сопротивление жидкостей изменению своего объема характеризуется коэффициентом объемного сжатия, который равен относительному
изменению объема жидкости при изменении давления на единицу:
W 
W
, Па -1 ,
W  p
где W – изменение объема W, соответствующее изменению давления
на величину p.
Связь между плотностями жидкости при различных давлениях
можно представить в виде
 p2   p1 
1
.
1  W   p1  p2 
Величина, обратная коэффициенту объемного сжатия, представляет
собой объемный модуль упругости:
E  1 W , Па .
Коэффициент температурного расширения характеризует относительное изменение объема жидкости при изменении температуры на
один градус:
t 
W
, K -1 ,
W  t
где W – изменение объема W, соответствующее изменению температуры на величину t.
Для воды при нормальных условиях можно принимать
W  1 2 109 , Па -1, t  1 10000, K-1 .
Расчет плотности жидкости при различных температурах выполняют по формуле
4
t2  t1 
1
.
1   t  t2  t1 
Значение коэффициентов объемного сжатия и температурного
расширения воды при различных температурах и давлениях приведены
в табл. П 1.2 и П 1.3 соответственно.
Сопротивление жидкости изменению своей формы характеризуется
их динамической вязкостью (внутренним трением) , Пас. Отношение
динамической вязкости жидкости к ее плотности называют кинематической вязкостью:
    , м2 с .
Поверхностное натяжение жидкости обусловлено силами взаимного притяжения молекул поверхностного слоя, стремящимися сократить
свободную поверхность жидкости. Оно характеризуется коэффициентом поверхностного натяжения , Н/м. Вследствие поверхностного
натяжения жидкость, имеющая криволинейную поверхность, испытывает дополнительное усилие, увеличивающее или уменьшающее давление
в жидкости на величину
1 1
pпов       ,
 r1 r2 
где r1 и r2 – главные радиусы кривизны рассматриваемого элемента поверхности.
В трубках малого диаметра d дополнительное давление от поверхностного натяжения приводит к изменению уровня жидкости в них на
высоту
hпов 
4 
,
 g d
где g – ускорение свободного падения.
Задачи
Задача 1. В отопительной системе здания содержится W  0,4 м 3
воды. Сколько воды дополнительно войдет в расширительный сосуд
при нагревании от 20 до 90оС?
Задача 2. При гидравлических испытаниях внутренних систем водоснабжения допускается падение испытательного давления в течение
10 минут на p  49 кПа . Определить допустимую величину утечки
W при испытании системы вместимостью W  80 м 3 .
5
Задача 3. Для аккумулирования дополнительного объема охлаждающей жидкости, вытесняемой из системы охлаждения двигателя в результате ее нагрева, к системе охлаждения в верхней точке присоединяют расширительный бачок, сообщающийся с атмосферой. Определить наименьший объем расширительного бачка, при котором полное
его опорожнение исключается. Допустимое колебание температуры
жидкости в системе в процессе работы двигателя 90–100˚С. Объем системы W  5  10 3 м3 . Охлаждающая жидкость – вода.
Задача 4. Канистра вместимостью W  20 л была доверху заполнена бензином, температура которого составляла 20˚С. Какое избыточное
давление создастся в канистре в случае хранения ее в боксе при температуре 35˚С. Деформацией канистры пренебречь.
Задача 5. Определить высоту подъема воды в стеклянном капилляре диаметром d  1 мм при температуре воды t1  20o C и t1  80o C .
Зависимость коэффициента поверхностного натяжения воды от температуры имеет вид  t  0,076  0,00015 t (м  С) .
Гидравлический удар
Гидравлическим ударом называют резкое повышение давления,
возникающее в напорном трубопроводе при внезапном торможении
потока жидкости. Он представляет собой колебательный процесс (в реальной жидкости – затухающий), возникающий в упругом трубопроводе
с капельной жидкостью при внезапном изменении ее скорости. Гидравлический удар чаще всего возникает при быстром закрытии или открытии крана или иного устройства управления потоком. Повышение давления в трубопроводе в результате гидравлического удара определяют
по формуле Н.Е. Жуковского:
pуд    V0 
1
 Eж  2    r   Eс 
   V0  c,
где  – плотность жидкости, кг/м 3; V0 – начальная скорость течения
жидкости, м/с; Еж – среднее для данного pуд значение адиабатного
модуля упругости жидкости, Па; r – радиус трубопровода, м;  – толщина стенки, м; Е с – модуль упругости материала стенки, Н/м 2 (для
стали Ст 3 модуль упругости равен (1,5–2)1011 Н/м2, а для чугуна –
(1,0–1,3)1011 Н/м2; с – скорость распространения ударной волны, м/с.
Когда уменьшение скорости в трубе происходит не до нуля, а до
значения V1, возникает неполный гидравлический удар и формула Жуковского приобретает вид
6
pуд    V0  V1   c.
Формулы Жуковского справедливы для прямого гидравлического
удара, который имеет место при очень быстром закрытии крана, когда
время закрытия соответствует следующему условию:
t зак  t 0  2  l c,
где t0 – фаза гидравлического удара, l – длина участка трубопровода до
крана.
При tзак  t0 возникает непрямой гидравлический удар, при котором
ударная волна, отразившись от резервуара, возвращается к крану раньше,
чем он будет полностью закрыт. Повышение давления в этом случае pуд
при условии, что скорость потока при закрытии крана уменьшается, а
давление возрастает линейно по времени определяют по формуле
pуд  pуд  t0 tзак    V0  2  l tзак .
Задачи
Задача 1. Определить величину повышения давления в стальной
водопроводной трубе, если скорость воды в ней до удара была V = 1 м/с,
диаметр трубы d = 0,5 м и толщина стенок  = 0,005 м.
Задача 2. В стальном трубопроводе длиной l = 20 м, диаметром
d = 0,1 м и толщиной стенок  = 0,003 м расход воды Q = 0,02 м3/с. Температура воды 20˚С. Определить наименьшее время закрытия задвижки
tмин, чтобы повышение давления в конце трубопровода pмакс, вызванное
гидравлическим ударом, было не более 400 кПа. Чему будет равно повышение давления в случае мгновенного закрытия задвижки?
Задача 3. В конце системы, состоящей
из двух последовательно соединенных стальных трубопроводов, установлена задвижка.
Определить повышение давления перед задвижкой при ее закрытии за 0,2 секунды. Расход воды Q = 0,02 м3/с; диаметры трубопроводов: d1 = 0,2 м, d2 = 0,1 м;
длина: l1 = 100 м, l2 = 200 м. Определить наименьшее время закрытия
задвижки, исключающее прямой гидравлический удар. Толщина стенок
трубопроводов  = 0,005 м. Температура воды 20оС.
Задача 4. Вода в количестве Q перекачивается по чугунной трубе
диаметром d, длиной L, толщиной стенки . Свободный конец трубы
снабжен затвором. Определить время закрытия затвора при условии,
что повышение давления в трубе p вследствие гидравлического удара
не превысит 10 кг/см2. Как изменится давление при мгновенном закрытии затвора?
7
Вариант
Величина
Q, м3/мин
d, мм
L, м
1
2
3
4
5
6
7
8
9
10
0,35
1,41
3,18
5,66
8,85
12,7
8,85
5,66
3,18
1,41
50
100
150
200
250
300
250
200
150
100
1200 1400 1600 2000 1500 1100 1300 1500 1700 1200
, мм
7
8,5
9,5
10,5
11,5
12,5
11,5
10,5
9,5
8,5
Задача 5. Горизонтальная труба служит
для отвода жидкости в количестве Q из
большого открытого бака. Свободный конец
трубы снабжен краном. Определить ударное
повышение давления в трубе перед краном,
если диаметр трубы d, длина L, толщина
стенки
, а материал стенки – сталь. Кран закрывается за время tзак по закону,
обеспечивающему линейное уменьшение скорости жидкости в трубе
перед краном в функции от времени.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
Б
В
М
Б
Г
К
Н
М
В
М
Q, л/с
0,2
10
0,5
0,3
0,2
0,2
0,2
0,1
0,5
15
d, мм
16
55
22
16
16
18
16
10
20
70
L, м
20
1000
50
25
20
25
25
10
50
1500
, мм
2
3
2
2
2
3
2
2
2
3
tзак, с
0,5
2,0
0,7
0,8
0,6
0,7
0,6
0,2
0,6
2,0
Ж
Обозначения: Б – бензин; В – вода; Г – глицерин; Ж – жидкость;
К – керосин; М – масло трансформаторное; Н – нефть.
Задача 6. Определить время закрытия задвижки, установленной на
свободном конце стального водопровода диаметром d, длиной L и толщиной стенки  при условии, чтобы максимальное повышение давления
в водопроводе было бы в три раза меньше, чем при мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия задвижки повышение давления распространится до сечения, находящегося на расстоянии 0,7 L от задвижки?
8
Вариант
Величина
1
2
3
4
5
6
7
8
9
10
d, мм
100
150
200
250
300
250
200
150
100
50
L, м
1900 1700 1850 1750 1450 1900 1600 1800 1500 2000
, мм
7
8
8
10
12
11
10
9
8
6
Гидростатика
Гидростатическое давление р представляет собой напряжение сжатия в точке, расположенной внутри покоящейся жидкости. Оно действует по нормали к поверхности тела, помещенного в жидкость. Гидростатическое давление зависит от положения рассматриваемой точки
внутри жидкости и от внешнего давления, приложенного к ее свободной
поверхности. В наиболее распространенном случае, когда из массовых
сил действует только сила тяжести, гидростатическое давление в точке,
находящейся на глубине h, определяют по основному уравнению гидростатики
p  p0    g  h ,
где р0 – внешнее давление на свободной поверхности жидкости, которое
передается всем точкам этой жидкости и по всем направлениям без изменения (закон Паскаля).
Сила суммарного давления жидкости Р на плоскую стенку равна
произведению смоченной площади стенки S и гидростатического давления в центре тяжести этой площади рс, т.е.
P  pc  S    g  hc  S ,
где hc – глубина погружения центра тяжести смоченной площади стенки.
Точка приложения равнодействующей сил давления (центр давления) для наклонных стенок лежит ниже центра тяжести стенки. Его положение определяют по формуле
ld  lc 
Jc
,
S  lc
где Jс – момент инерции смоченной площадки стенки относительно
горизонтальной оси, проходящей через центр тяжести этой площадки;
lс и ld – соответственно расстояния центра тяжести стенки и центра
давления от линии пересечения плоскости стенки со свободной поверхностью.
9
Формулы для определения центра тяжести и момента инерции плоских фигур
относительно оси, проходящей через центр
тяжести, приведены в приложении (см.
табл. П 1.6).
Сила суммарного давления жидкости Р
на цилиндрическую поверхность может
быть представлена геометрической суммой
ее составляющих: горизонтальной Рг и вертикальной Рв, т.е.
P  Pг2  Pв2 .
Горизонтальная составляющая силы суммарного давления жидкости на цилиндрическую стенку равна силе суммарного давления жидкости на вертикальную проекцию площади Sв этой стенки:
Pг    g  hc  Sв  pc  Sв .
Вертикальная составляющая равна весу жидкости в объеме тела
давления:
Pв    g  W .
Телом давления называют объем жидкости, ограниченный данной
криволинейной поверхностью, вертикальной поверхностью, проведенной через нижнюю образующую криволинейной поверхности, и свободной поверхностью жидкости.
На тело, погруженное в жидкость, действует Рвыт выталкивающая
сила, равная весу вытесненного объема жидкости Wпогр (закон Архимеда)
Pвыт    g  Wпогр .
Задачи
Задача 1. Определить силу суммарного давления на торцевую
плоскую стенку цилиндрической цистерны диаметром d  2,4 м и точку ее приложения. Высота горловины hг  0,6 м . Цистерна заполнена
бензином до верха горловины (рис. 1).
10
Задача 2. Определить силы, разрывающие горизонтальную, наполненную бензином цистерну длиной l  10 м по сечениям 1 – 1 и 2 – 2
при условиях задачи 1 (рис. 1).
Задача 3. Простейший ареометр (прибор для определения плотности жидкостей), выполненный из круглого стержня диаметром d  8 мм
и прикрепленного к его основанию металлического шарика диаметром
d ш  5 мм , имеет вес G  0,006 Н . Определить плотность жидкости ,
если ареометр цилиндрической частью погружается в нее на глубину
h  1,5 см .
Задача 4. Определить плотность бревна круглого (квадратного) сечения, если из пресной воды выступает 1/4 его диаметра (стороны).
Задача 5. Какой вес должны иметь
поршни, чтобы находиться в баке с водой в заданных на рисунке положениях при показании манометра рм гПа?
Что произойдет с давлением и с поршнями, если левый из них “перегрузить”
на Gx Н?
h1 = 0,5 м; h2 = 2,0 м; h3 = 1,0 м;
d1 = -0,5 м; d2 = 3-0,5 м; d3 = 2-0,5 м.
Варианты
Величины
1
2
3
4
5
6
7
8
9
10
рм, гПа
588
500
400
300
350
400
450
500
600
650
Gx, Н
3680 3000 2500 2000 2500 3000 3000 5000 4500 4000
Задача 6. Бензин под избыточным давлением р = 30 кПа подводится к поплавковой камере карбюратора по трубке диаметром d = 4 мм.
Шаровой поплавок массой 25 г и игла
массой 12 г, перекрывающая доступ бензина, укреплены на рычаге (а = 40 мм,
b = 15 мм), который может поворачиваться
вокруг неподвижной оси О.
Определить радиус поплавка из условия, что в момент открытия
отверстия поплавок погружен наполовину в жидкость. Трением в шарнирах и массой рычага пренебречь.
11
Задача 7. Определить силу, развиваемую гидравлическим прессом, работающим с помощью ручного плунжерного насоса. Усилие на рукоятке Q, вес
поршня пресса G2, вес плунжера
насоса G1, геометрические размеры установки: a, b, d, D.
Варианты
Величины
1
2
3
4
5
6
7
8
9
10
Q, H
245
260
240
230
200
210
220
230
240
250
G1, H
196
200
210
200
190
180
170
180
190
200
G2, H
1964 2000 2100 2000 2100 1900 1800 1700 1600 1800
a, м
0,2
0,1
0,2
0,3
0,2
0,1
0,2
0,3
0,2
0,2
b, м
1,8
1,0
2,0
2,5
2,5
1,5
2,0
2,5
2,0
2,4
d, м
0,02
0,03 0,035 0,04
0,02
0,03
0,04
0,05
0,04
0,03
D, м
0,2
0,3
0,4
0,35
0,5
0,6
0,6
0,5
0,35
0,4
Задача 8. Замкнутый резервуар разделен на
две части плоской перегородкой, имеющей квадратное отверстие со стороной а, закрытое крышкой. Давление над жидкостью Ж в левой части
резервуара определяется показаниями манометра
рм, давление воздуха в правой части – показаниями мановакуумметра рв. Определить величину и
точку приложения результирующей силы давления на крышку.
Вариант
Величина
1
2
3
4
5
6
7
8
9
10
Ж
В
Б
К
В
Мтр
Г
Н
К
Мтурб
Б
рм, кг/см2
0,8
0,9
0,7
0,8
0,5
0,9
1,0
0,3
1,0
0,5
кг/см2
0,1
0,1
0,2
0,2
0,3
0,3
0,1
0,1
0,2
0,2
a, мм
200
300
400
100
200
300
200
100
400
200
b, мм
500
3000 1300
600
500
400
500
300
600
300
рв,
12
Обозначения: Б – бензин, В – вода, Г – глицерин, Ж – жидкость,
К – керосин, Мтр – масло трансформаторное, Мтурб – масло турбинное,
Н – нефть.
Задача 9. Определить предварительное
поджатие x пружины, нагружающей дифференциальный предохранительный клапан, необходимое для того, чтобы клапан открывался
при давлении р = 3 МПа. Диаметры поршней:
D1 = 22 мм; D2 = 20 мм, а жесткость пружины
С =8 Н/мм.
Динамика идеальной жидкости
Интегрирование дифференциального уравнения движения идеальной (невязкой) жидкости вдоль линии тока для установившегося движения приводит к уравнению Бернулли:
V2 p
  g  z  c, либо
2

 V 2
2
 pgz c ,
где с – постоянная интегрирования.
Данное уравнение выражает закон сохранения удельной механической энергии, отнесенной к единице массы жидкости. Член V 2 2 характеризует кинетическую энергию, p  – потенциальную энергию давления, а g  z – потенциальную энергию положения.
Порядок использования уравнения Бернулли. На линии тока выбирают точки 1 и 2. В одной из них (например точке 1) должны быть известны скорость V1, давление p1 и координата z1, а для другой точки –
любые две из величин, входящих в это уравнение (обычно p2 и z2). Применив уравнение Бернулли к этим точкам, получим:
p1 
  V12
2
   g  z1  p2 
  V2 2
2
   g  z2
и найдем неизвестную величину (в данном случае – V2).
Если неизвестными являются две величины (V2 и р2), то дополнительно привлекают уравнение неразрывности. Для течения по трубам и
каналам с площадью проходного сечения S уравнение неразрывности
имеет вид
Vcp  S  Q,
где Vcp – средняя скорость течения; Q – объемный расход жидкости.
13
При расчетах обтекания тел жидкостью используют коэффициент
давления в данной точке p , который представляет отношение избыточного давления (по сравнению с давлением в невозмущенном потоке p )
к скоростному напору невозмущеного потока, т.е.
2
V 
p  p
 1    .
2
  V 2
 V 
p
В идеальной жидкости коэффициент давления не зависит от рода
жидкости (плотности ) и скорости набегающего потока V , являясь
функцией лишь безразмерных координат.
Задачи
Задача 1. Центробежный вентилятор засасывает воздух из атмосферы через сопло. К
цилиндрической части сопла с диаметром
200 мм присоединена трубка, опущенная в бак
с водой. Высота поднятия воды в трубке h мм.
Определить расход воздуха через сопло (температура воздуха 15оС, давление 101,6 кПа).
Варианты
Величина
h, мм
1
2
3
4
5
6
7
8
9
10
250
300
350
400
500
550
600
700
750
800
Задача 2. Найти скорость течения воды на оси
трубы, если показание ртутного дифференциального
манометра, подсоединенного к трубке динамического
напора и к статическому отверстию, равно h. Плотность ртути – 13600 кг/м3.
Варианты
Величина
h, мм рт.ст.
1
2
3
4
5
6
7
8
9
10
300
200
100
250
340
400
500
600
550
440
14
Задача 3. Вода вытекает из резервуара по расширяющейся трубе – диффузору. Пренебрегая потерями, определить, при каком уровне воды H1 в
резервуаре давление в узком сечении диффузора
станет теоретически равным нулю. d1 = 100 мм;
d2 = 150 мм; значения H2 приведены в таблице.
Варианты
Величина
H2, м
1
2
3
4
5
6
7
8
9
10
1,15
1,00
0,90
0,80
0,70
0,60
0,65
0,75
0,85
0,95
Задача 4. Бензин, температура которого 20˚С,
перетекает из топливного бака бензопилы в находящийся перед карбюратором бачок постоянного
уровня по трубопроводу с внутренним диаметром
d = 3 мм.
Определить расход бензина Q при напоре
H = 0,4 м при полностью открытом поплавковом
клапане.
Задача 5. Выход воды из горизонтальной песколовки выполнен в виде
сужения с плавно закругленными стенками. Ширина песколовки В = 3 м. Расход ливневой воды Q = 0,9 м3/с. Определить глубину воды в отводящем канале h2, если ширина его b = 0,8 м.
Дно канала – горизонтальное.
Задача 6. Для заполнения водой тендера на ходу поезда в специально устроенный между рельсами лоток с водой опускается труба приемного устройства диаметром D = 200 мм так, что входное сечение трубы располагается навстречу потоку.
Суммарный коэффициент потерь в приемном устройстве, отнесенный к средней скорости в трубе,  = 2, а высота подъема воды
h = 3 м.
Определить время t, необходимое для заполнения тендера объемом W = 10 м3 при
скорости поезда V = 36 км/ч.
15
При какой наименьшей скорости vmin поезда это приемное устройство перестанет работать?
Указание. Использовать уравнение Бернулли для относительного
V2
w2
движения
h
 1    , где w – скорость в трубе.
2 g
2 g
Динамика вязкой несжимаемой жидкости
Общая задача гидродинамики вязкой несжимаемой жидкости сводится к решению системы дифференциальных уравнений движения:
u
u
u
u
1  p
u
v
 w
X 
    2u,
t
 x
 y
 z
  x
v
v
v
v
1  p
u
v
 w
Y  
    2 v,
t
 x
 y
 z
  y
w
w
w
w
1  p
u
v
 w
Z 
  2w
t
 x
 y
 z
  z
и уравнения неразрывности:
u v w


 0,
 x  y  z
где u, v, w – проекции вектора скорости на оси координат; X, Y, Z – проекции вектора напряжений массовых сил на оси координат;  – плотность жидкости; р – давление;     – коэффициент кинематической
вязкости жидкости ( – коэффициент динамической вязкости жидкости); 2   2  x 2   2  y 2   2  z 2 – оператор Лапласа.
Для решения этой системы уравнений необходимо задать начальные (для неустановившегося течения) и граничные условия. Наиболее
распространенным граничным условием для течений вязкой жидкости
является условие “прилипания”, согласно которому относительная скорость движения жидкости на границе соприкосновения ее с поверхностью твердого тела равна нулю.
Точные решения уравнений движения (уравнений Навье – Стокса)
получены лишь для простейших течений, для которых можно предсказать заранее характер траекторий частиц жидкости.
Для большинства задач, представляющих практический интерес,
используют приближенные уравнения, полученные из полных путем
отбрасывания слагаемых, имеющих в рассматриваемом случае несущественное значение. К числу такого рода решений относят решения задач
о пограничном слое и о медленных движениях жидкости. Последние
16
справедливы для течений, в которых роль сил инерции по сравнению с
силами вязкости пренебрежимо мала. Например, сопротивление шара
радиусом r0 при равномерном прямолинейном движении со скоростью
V в неограниченном объеме несжимаемой вязкой жидкости при условии V  ro   1 2 определяют по формуле Стокса:
F  6      ro  V .
Невозможность получить теоретическое решение уравнений движения вязкой жидкости приводит к необходимости опытного определения интересующих характеристик движения как на натурном объекте,
так и на модели. Модельные эксперименты следует проводить с соблюдением условий гидродинамического подобия, которые включают условия геометрического и кинематического подобий. Подобные процессы
имеют одинаковые критерии подобия, т.е. одинаковые безразмерные
комплексы, составленные из величин, характеризующих рассматриваемое явление (течение). Гидродинамические критерии подобия определяют соотношения сил различной природы, действующих в потоке.
Критерии гидродинамического подобия получают непосредственно
из уравнений движения, приведенных к безразмерному виду путем
представления всех размерных величин в долях от характерных для потока величин: характерного линейного размера L0, характерного времени t0, характерной скорости V и разности давлений р.
Основными критериями гидродинамического подобия являются:
Sh 
Re 
Lo
– критерий Струхаля; Fr 
V  to
V  Lo

– критерий Рейнольдса; Eu 
V
g  Lo
– критерий Фруда;
2  p
  V 2
– критерий Эйлера.
В сложных случаях движения для полного гидродинамического
подобия двух геометрически и кинематически подобных потоков требуется одновременное равенство всех критериев подобия. В случае
отличия хотя бы одного из критериев в рассматриваемых потоках подобие считается частичным. В таком случае моделируются только те
силы, которые учитываются в равных для обоих потоков критериях.
Часто встречаются течения, при которых некоторые силы не играют
важной роли. Например, при установившемся движении в трубе, если в
ней нет ни поверхностных волн, ни кавитации, критерии Струхаля,
Фруда и Эйлера не играют никакой роли при моделировании. Равенство критериев Рейнольдса в этом случае обеспечивает динамическое
подобие потоков.
17
Задачи
Задача 1. Найти закон распределения скорости и касательного напряжения в слое вязкой
жидкости толщиной h, находящейся между
двумя параллельными неограниченными плоскостями, если верхняя плоскость движется по
отношению к нижней с постоянной скоростью
V0 (рис. а). Получить выражение средней скорости, погонного (на 1 м “размаха” по оси z)
расхода q и падения давления для двух случаев:
безнапорного течения  p  x  0 и напорного
течения  p  x  0 (рис. б).
Задача 2. Поршень прямоугольного сечения a  b  100  50 мм, длиной L = 100 мм движется с постоянной
скоростью V0 в сосуде с минеральным
маслом МС–20 при температуре 20˚С,
вытесняя его через постоянный по
периметру зазор h = 1 мм. Используя
решение предыдущей задачи, определить усилие F, необходимое для перемещения поршня с этой скоростью.
Варианты
Величина
V0, см/с
1
2
3
4
5
6
7
8
9
10
1
1,5
2
3
4
5
6
7
8
9
Задача 3. Найти закон распределения скорости, давления и касательного
напряжения в поперечном сечении установившегося прямолинейно-параллельного ламинарного течения вязкой жидкости вдоль наклонной неограниченной плоскости при наличии свободной
поверхности с постоянным давлением.
Определить погонный расход жидкости. Заданными величинами считать глубину жидкости h и угол наклона плоскости 
Примечание. В качестве граничного условия на свободной поверхности принять отсутствие на ней касательных напряжений.
18
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
h, мм
10
2
3
4
5
10
2
3
4
5
о
10
15
20
25
30
10
15
20
25
30
Задача 4. Алюминиевый шарик (относительная плотность А = 2,6), имеющий диаметр d = 4 мм, свободно падает в жидкости, относительная плотность которой  = 0,9.
Определить динамическую вязкость жидкости, если
шарик, двигаясь равномерно, прошел путь s = 15 см за время t = 30 с.
Указание. Воспользоваться формулой Стокса для силы
сопротивления жидкости, действующей на медленно движущийся шарик. Относительной плотностью называют величину, равную отношению плотности какого-либо вещества к плотности воды.
Задача 5. Определить среднюю скорость движения воды в опытном
трубопроводе, изготовленном в масштабе KL = 1:5, на котором производят испытания по определению коэффициента сопротивления клапанов
систем при движении моторного топлива со средней скоростью Vн.
Температуры в условиях модельных и натурных испытаниях равны
(tм = tн = 10˚С). Найти масштаб разности давлений между сходственными точками KP, если плотность натурной жидкости н = 870 кг/м3.
Варианты
Величина
Vн, м/с
1
2
3
4
5
6
7
8
9
10
0,5
0,75
1,0
1,5
0,5
0,75
1,0
1,5
0,5
1,5
Задача 6. Можно ли удовлетворить условиям подобия в силах трения для модели подводного судна при испытании в бассейне и аэродинамической трубе с открытой рабочей частью? Длина судна Lн, скорость
Vн, расчетная температура воды tн = 4˚С. Температура воды в бассейне и
воздуха в аэродинамической трубе tм = 15˚С. Скорость буксировки моделей Vм в бассейне ограничена значением 5 м/с, скорость продувки в
аэродинамической трубе – значением 30 м/с.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
Lн, м
30
40
50
60
70
80
90
100
110
120
Vн, м/с
5
6
7
8
9
10
11
12
13
14
19
Распыливание топлива в дизелях1
Истечение топлива из отверстия приводит к образованию струи с
шероховатой поверхностью, динамически взаимодействующей с воздушной средой. Скорость относительного движения воздуха и струи увеличивается над выпуклостями и снижается во впадинах, что приводит,
в соответствии с уравнением Бернулли, к изменению давления вдоль нее.
Благодаря этому увеличивается амплитуда и усиливается неустойчивость
движения струи, результатом чего является дробление ее на капли на некотором расстоянии Lc от
выходного отверстия форсунки. При высоком значении относительной скорости вместо распада на
одиночные капли происходит дробление струи на
множество мелких частиц,
размеры которых меняются в широких пределах. Этот процесс дробления называют распылом.
При расчетах характеристик процесса распыливания (длины
сплошного участка струи Lc, среднего диаметра капель dк, длины волны
lопт, соответствующей наибольшей неустойчивости струи, приводящей к
ее дроблению, границ различных режимов распада струи) пользуются
следующими безразмерными величинами:
M 
d
 V 2  dc
12

;   k  c ;   2 ; We  1 1
,
1    d c
2
1

где 1 – коэффициент динамической вязкости топлива; 1 – плотность
топлива;  – коэффициент поверхностного натяжения топлива; dc –
диаметр отверстия сопла; k – волновое число ( k  2   l ); We – критерий Вебера; V1 – осевая скорость движения жидкости в струе.
Граница области перехода от волнообразного распада струи к распыливанию (граничное значение критерия Вебера Wг3) для форсунок с
Лышевский А.С. Распыливание топлива в судовых дизелях. – Л.: Судостроение, 1971. 248 с.
1
20
цилиндрическими сопловыми отверстиями при отсутствии внутри них
специальных устройств, возмущающих проходящую жидкость, описывается уравнением
Wг3  266  M 0,133   0,8 .
При выполнении условия We  Wг3 обеспечивается получение режима распыливания топлива.
На процесс распада струи оказывает значительное влияние скорость истечения, вязкость топлива и среда, в которую происходит его
впрыск.
При малых скоростях истечения топлив значение <1. Для
M  1 8 пользуются следующими зависимостями:
 для определения длины сплошного участка струи
Lc
 C  We  1  3  M ;
dc
 для определения диаметра капель, образующихся при распаде
струй из:
топлив с пренебрежимо малой вязкостью


dк 3 3  2

 ;
dc
2
маловязких топлив
dк 3 3  2

  1  M ;
dc
2
топлив большой вязкости
dк 3 3  2

  1  3  M .
dc
2
При больших скоростях истечения значение >>1. Распад струи
маловязкого топлива происходит, главным образом, под воздействием
коротковолновых возмущений, максимальная частота которых соответствует значению
1
3
Для таких условий расчет ведут по формулам
 опт     We .
Lc 3  3
C


,
dc
2
  We  
21
где С – эмпирический коэффициент (С=12);
dк
9 
.
3
dc
2    We
При промежуточных значениях скорости истечения маловязкого
топлива развиваются осесимметричные возмущения, которые приводят
к распаду струи при значении параметра опт, равном
 опт  0,705  exp 0,155    We  .
В этом случае длину сплошной части струи рассчитывают по формуле
Lc
 1,09  C  We  exp  0,24    We  ,
dc
где С – эмпирический коэффициент (С=12),
а диаметр капель – по зависимости
dк 3
 6,66  exp  0,155    We  .
dc
Основное влияние на параметры распада струи вязкого топлива при
значительных скоростях движения оказывают силы инерции, характеризуемые критериями  и We. Силы вязкости играют второстепенную
роль. В предположении об отсутствии поперечного потока воздуха и
волнообразных несимметричных возмущений расчет ведут по следующим зависимостям:
Lc
M 0,308
 C  0,71 1, 21 ,
dc
We  
где С – эмпирический коэффициент (С=372);
dк
M 0, 073
 3,01 
.
dc
  We 0, 266
Пример 1. Проверить, обеспечивается ли распыливание топлива
ДТ-2 форсункой с диаметром сопла dc = 0,38 мм, если минимальное
давление подачи р1 = 7 МПа, средние давление и температура воздуха в
камере сгорания р2 = 3,5 МПа и T2 = 730 К, коэффициент расхода форсунки с = 0,6, а физические свойства топлива при 50˚С имеют следующие значения: коэффициент динамической вязкости 1 = 48810-4 Пас;
плотность 1 = 886 кг/м3; коэффициент поверхностного натяжения
 = 3510-3 Н/м. Плотность воздуха 2 = 1,23 кг/м3 при температуре
T0 = 293 К и атмосферном давлении р0 = 0,1 МПа.
22
Скорость истечения топлива:
V1   c 
2

  p1  p2   0,6


2
7  10 6  3,3  10 6  53,5 м/с.
886
Критерии We и M равны:
We 
M
V12  1  d c

12
1  d c  


53,52  886  0,38  10 3
 27360 ;
35  10 3
488 10 
4 2
886  0,38  10 3  35  10 3
 0,202 .
Плотность воздуха в камере сгорания:
2  0 
p2 T0
3,5  10 6 293
  1,23
 17 ,3 кг/м 3 .
p0 T2
0,1  10 6 730
Соотношение плотностей:

 2 17 ,3

 0,0195 .
1 886
Граничное значение критерия Вебера равно:
Wг3  266  M 0,133   0,8  266  0,2020,133  0,01950,8  5017 .
Так как значение критерия Вебера значительно превышает граничное, то распыл топлива обеспечивается.
Пример 2. Определить параметры дробления струи маловязкого топлива, которое подается форсункой с диаметром отверстия dc = 0,22 мм и коэффициентом расхода с = 0,6 в среду воздуха плотностью 2 = 17,5 кг/м3
при р1 – р2 = 3,5 МПа. Плотность топлива и его поверхностное натяжение равны 1 = 865 кг/м3 и  = 2710-3 Н/м.
Скорость истечения топлива:
V1   c 
2

  p1  p2   0,6


2
3,5  10 6  54 м/с.
865
Значения критериев:
We 
V12  1  d c



54 2  865  0,22  10 3
 20400 ;
27  10 3
 2 17 ,5

 0,0202 .
1 865
23
Так как   We велико, то распад струи происходит под воздействием коротковолновых возмущений с >> 1. Значение критерия , соответствующее распаду струи, равно
1
3
1
3
 опт     We   0,0202  20400  137 .
При этом значении  длина сплошного участка струи:
Lc  d c
 0,22  10 3
3 3
12

2   We  
3 3
12
 0,118  10 3 м,
2 0,0202  20400  0,0202
почти отсутствует, а средний размер капель составит:
dк  dc  3
9 
9 
 0,22  10 3  3
 0,715  10 3 м .
2    We
2  0,0202  20400
Пример 3. Определить длину сплошного участка струи для условий
работы форсунки, указанных в примере 1, при р1 = 10 МПа.
Скорость истечения топлива:
V1   c 
2

  p1  p2   0,6


2
10  10 6  3,3  10 6  73 м/с.
886
Значение критерия Вебера:
We 
V12  1  d c


73 2  886  0,38  10 3
 51000 .
35  10 3
Используя значения М и  из примера 1, определим длину сплошного участка по формуле для вязких топлив:
Lc  d c 372
M 0,308
0,202 0,308
 0,38  10 3  372
 8,4  10 3 м.
0 , 71 1, 21
We 
51000 0, 710,0195 1, 21
Пример 4. Оценить параметр Lс и наиболее вероятный размер капель первичного дробления в момент максимального давления впрыска
топлива (р1 = 40 МПа, р2 = 4,5 МПа и T2 = 1700 К) для параметров форсунки и характеристик топлива, указанных в примере 1.
Скорость истечения топлива:
V1   c 
2

  p1  p2   0,6


2
40  10 6  4,5  10 6  170 м/с.
886
24
Плотность воздуха в камере сгорания:
2  0 
p2 T0
4,5  10 6 293
  1,23
 9,5 кг/м 3 .
p0 T2
0,1  10 6 1700
Значения критериев:
We 
V12  1  d c



170 2  886  0,38  10 3
 277000 ;
35  10 3
 2 9,5

 0,0107 .
1 886
Величина критерия М остается такой же, как и в примере 1
(М = 0,202).
Длину сплошной части струи определим по формуле для вязких
топлив:
Lc  d c  372 
M 0,308
0,202 0,308
 0,38  372 
 2,87 мм.
0 , 71
1, 21
We  
277000 0,71  0,0107 1, 21
Так как значение критерия We велико, то силы вязкости не будут
оказывать решающего влияния на качество дробления, поэтому при
оценке наиболее вероятного диаметра капель первичного дробления
струи воспользуемся следующей формулой для вязких топлив:
d к  d c  3,01 
M 0,073
0,202 0,073
 0,38  3,01 
 0,122 мм.
0 , 266
  We 
0,0107  277000 0,266
Основы гидравлических расчетов систем
Потери напора на трение
При равномерном движении жидкости в трубах потери давления на
трение как при ламинарном, так и при турбулентном режимах движения
рассчитывают по формуле Дарси–Вейсбаха:
p тр   
l  V 2

,
d
2
где  – коэффициент гидравлического трения; l – длина трубопровода;
d – его диаметр;  – плотность жидкости; V – средняя скорость ее течения.
Коэффициент гидравлического трения зависит от режима движения
жидкости, значения критерия Рейнольдса:
Re 
V d
25

и состояния стенок трубы, которое характеризуется относительной шероховатостью:
  э d ,
где э – эквивалентная равномерно-зернистая шероховатость (см. табл. П 1.7)
(т.е. такая высота неровностей, образованных песчинками одинакового
размера, которая при расчете дает одинаковое с действительной шероховатостью значение коэффициента гидравлического трения).
При ламинарном режиме течения коэффициент гидравлического
трения рассчитывают по формуле
  64 Re .
При турбулентном режиме течения весь диапазон значений чисел
Рейнольдса, в зависимости от относительной шероховатости, разбивают
на области, каждой из которых соответствует своя формула для расчета
коэффициента гидравлического трения:
область гидравлически гладких труб 2300  Re  10  :
  0,3164 Re0,25 – формула Блазиуса;
переходная область 10   Re  500  :

  0,11    68 Re

0 , 25
– формула А.Д. Альтшуля;
квадратичная область Re  500  :
  0,11  
0, 25
– формула Б.Л. Шифринсона.
В случае течения жидкости по трубам, форма поперечного сечения
которых отличается от круга, в приведенных выше формулах используют вместо d эквивалентный диаметр:
dэ  4  S П ,
где S – площадь поперечного сечения трубы; П – полный смоченный
периметр трубы.
Коэффициент гидравлического трения при ламинарном течении в
трубах различной формы рассчитывают по формуле
  A Re ,
где А – коэффициент, численное значение которого зависит от формы
поперечного сечения трубы (см. табл. П 1.8).
Пропускная способность трубопроводов в период эксплуатации
снижается. Вследствие коррозии и образования отложений в трубах ше26
роховатость их увеличивается, что в первом приближении можно оценить по формуле
t  o    t ,
где о – абсолютная шероховатость новых труб, мм; t – абсолютная
шероховатость через t лет эксплуатации, мм;  – коэффициент, характеризующий быстроту возрастания шероховатости, мм/год (см. табл. П 1.9).
Сифоном называют соединяющий два резервуара трубопровод,
часть которого расположена выше уровня жидкости в напорном резервуаре. Допускаемое возвышение верхней точки сифона определяют по
формуле
p  p
hc  в
,
 g
где p – потеря давления на участке от напорного резервуара до верхней
точки сифона. Минимально допускаемое давление в верхней точке сифона должно быть выше давления насыщения при данной температуре.
Местные потери давления в трубах
Местные сопротивления, к которым относят арматуру, фасонные
части трубопроводов и прочее оборудование, вызывают изменения величины и (или) направления скорости движения жидкости на отдельных
участках трубопроводов, что приводит к потерям давления в них. Потери давления определяют по формуле Вейсбаха:
pм      V 2 2 .
Значения коэффициентов местных сопротивлений зависят от
конфигурации местного сопротивления и режима течения жидкости
перед ним.
При внезапном сужении трубопровода (резком изменении площади
проходного сечения от S1 до S2) коэффициент местного сопротивления
2
1 
 c    1 ,


где  – коэффициент сжатия струи, который можно определить по формуле А.Д. Альтшуля:
  0,57 
где
n
0,043
,
1,1  n
S2
.
S1
27
Коэффициент местного сопротивления диафрагмы, расположенной
внутри трубы постоянного сечения (отнесенный к сечению трубопровода):
2
 1

 д  
 1 ,
 nд  

где nд = So / S – отношение площади отверстия диафрагмы So к площади
сечения трубы S.
При движении жидкости с малыми числами Рейнольдса коэффициенты местных сопротивлений ориентировочно определяют по формуле
А.Д. Альтшуля:

A
  кв ,
Re
где  кв – значение коэффициента местного сопротивления в квадратичной области; Re – число Рейнольдса, отнесенное к нестесненному сечению трубопровода.
Значения параметра А и  кв для некоторых местных сопротивлений
приведены в приложении (см. табл. П 1.10).
Если расстояние между отдельными местными сопротивлениями
достаточно велико для того, чтобы искажение эпюры скоростей, вызванное одним из них, не сказывалось на следующем, потери давления
во всех местных сопротивлениях суммируют. Для этого необходимо,
чтобы местные сопротивления отстояли друг от друга на расстояние,
превышающее lвл, определяемое по формулам:
для турбулентного движения
lвл d  12
  50 ,
где  – коэффициент трения трубы, на которой расположено местное
сопротивление;
при малых числах Рейнольдса
lвл d  1,25  Re .
Задачи
Задача 1. Для ограничения расхода воды в водопроводной линии
установлена диафрагма. Избыточное давление в трубе до и после диафрагмы постоянно и равно соответственно р1 = 63,7 кПа и р2 = 20,5 кПа.
Диаметр трубы D = 0,076 м. Определить необходимый диаметр отверстия диафрагмы d с таким расчетом, чтобы расход в линии был равен
Q = 0,0059 м3/с.
28
Задача 2. Определить потери давления в радиаторе, если расход масла Q  2  104 м3/с.
Диаметр коллектора d 0  0,03 м, диаметр трубок
d тр  0,01 м, их длина l тр  1 м, количество – 4.
Плотность масла   900 кг/м3. Коэффициент
кинематической вязкости   6,5  10 5 м2/с.
Задача 3. Найти потери давления
pм на преодоление местных сопротивлений при движении воды в стальном
трубопроводе диаметром d = 0,025 м
при повороте на угол  = 90˚ без вставки и со вставкой. Найти наименьшую
длину вставки lвл, при которой отсутствует взаимное влияние двух местных
сопротивлений. Скорость воды V = 5 м/с, температура воды 20˚С.
Задача 4. По гидравлически гладкой горизонтальной трубе диаметром d перекачивают бензин с расходом Q при температуре 10˚С. Найти
перепад давления на длине L, равной 5 метрам.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
d, мм
50
60
15
10
15
20
22
25
28
32
Q, л/с
6
6
2
2
2
4
4
4
4
4
Задача 5. При какой разности уровней h расход моторного топлива М3 (t = 40˚С,   900 кг/м3)
через сифонный трубопровод будет равен Q?
Определить давление в сечении В–В, если
при общей длине L, равной 20 метрам, расстояние
от начала трубопровода до сечения В–В составляет 15 метров, а диаметр d – 50 миллиметров.
Варианты
Величина
Q, л/с
1
2
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
11
12
29
Задача 6. Вычислить изменение потери давления и потребной
мощности в гидравлически гладком трубопроводе диаметром d и длиной L, равной 100 метрам, по которому перекачивается моторное топливо М3 с расходом Q при подогреве его с 10 до 40˚С.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
d, мм
80
90
100
110
120
100
110
120
100
150
Q, л/с
15
15
25
25
25
50
50
50
75
75
Задача 7. В цистерны подается вода с расходом
Qо, равным 10 литров в секунду, и сливается по вертикальному трубопроводу диаметром d, длиной L,
равной 2 метрам. Определить уровень воды H, считая
трубопровод гидравлически гладким, а коэффициент
местной потери напора (местного сопротивления) в
кране А –  равным 2,0. Найти давление в сечении
К – К, расположенном на расстоянии 2 метра от места
слива.
Варианты
Величина
d, мм
1
2
3
4
5
6
7
8
9
10
40
50
60
70
80
40
50
60
70
80
Задача 8. Чему должно быть равно избыточное давление воздуха над поверхностью керосина (t = 20˚С) при расходе Q? Трубопровод гидравлически гладкий; d = 10 мм;
L = 1 м; коэффициент местных потерь давления в кране  = 2,5; H = 3 м.
Варианты
Величина
Q, л/с
1
2
3
4
5
6
7
8
9
10
0,2
0,4
0,6
0,8
1,0
0,2
0,4
0,6
0,8
1,0
Задача 9. Вода перепускается из одного резервуара в другой по
трубопроводу переменного сечения. Определить расход при показанных
30
на рисунке уровнях H1 и H2, полагая,
что режим течения соответствует
квадратичной области с относительной эквивалентной зернистой шероховатостью   1 400 . Определить
время выравнивания уровней.
Варианты
Величина
H1, м
H2, м
1
8
2
2
10
5
3
15
7
4
20
13
5
25
15
6
8
3
7
10
6
8
15
8
9
20
12
10
25
14
Задача 10. Найти расход в магистральном трубопроводе диаметром
200 мм, если в параллельной ветви диаметром 50 мм и длиной 7 м расходомер показывает Q2. Коэффициент потерь напора в расходомере 
считать
равным 1,5; коэффициенты трения в обоих
ветвях ( и  одинаковы и равны 0,025.
Варианты
Величина
Q2, л/с
1
2
2
4
3
5
4
7
5
10
6
9
7
8
8
6
9
3
10
11
8
В
7,5
8
70
9
Б
8
6
70
10
Г
6
15
60
Задача 11. Жидкость подается в открытый верхний бак по вертикальной трубе длиной L и диаметром d за счет давления воздуха в нижнем замкнутом
резервуаре. Определить давление воздуха р, при котором расход будет равен Q. Принять коэффициенты
сопротивления: вентиля в, равным 8,0; входа в трубу
вх – 5,0; выхода в бак вых – 1,0. Эквивалентная шероховатость стенок трубы э равна 0,2 мм.
Варианты
Величина
Ж
Q, л/с
L, м
d, мм
1
В
4
6
50
2
М
8
8
70
3
Б
0,7
10
20
4
К
1,5
6
30
5
Г
2,5
8
40
6
В
10
10
80
7
М
6
12
60
Обозначения: Б – бензин; В – вода; Г – глицерин; Ж – жидкость;
К – керосин; М – масло трансформаторное.
31
Задача 12. Определить диаметр трубопровода, по которому подается жидкость Ж с расходом Q из условия получения в нем максимально
возможной скорости при сохранении ламинарного режима. Температура
жидкости t равна 20˚С.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
Ж
К
Б
В
Г
М
В
М
Б
В
К
Q, л/с
12
3,5
0,05
4,5
650
1,0
120
3,5
0,5
10
Обозначения: Б – бензин; В – вода; Г – глицерин; Ж – жидкость;
К – керосин; М – масло индустриальное.
Задача 13. Масляный радиатор состоит из четырех параллельных
трубок эллиптического поперечного сечения.
Определить потерю hп напора в радиаторе при расходе масла Q = 0,2 л/с,
если а = 20 мм, b = 4 мм, длина каждой
трубки l = 300 мм и кинематическая вязкость масла  = 1,510-4 м2/с.
Потерями напора на входе в трубку
и выходе из нее, а также влиянием начального участка пренебречь. Размеры коллектора полагать большими по сравнению с поперечным сечением трубки.
Указание. Для трубы эллиптического поперечного сечения при
  a 3  b3
p
установившемся ламинарном течении Q  2
, где а и b –

2
4  l
a b
полуоси эллипса.
Задача 14. Определить давление нагнетания р насоса в начале масляной линии, подающей смазку к трем коренным
подшипникам коленчатого вала
автомобильного двигателя, если
подача насоса Q = 50 см3/с.
Размеры: d = 6 мм; d1 = 4 мм;
d0 = 40 мм; L = 1000 мм; l =
200 мм; s = 50 мм; а = 6 мм.
Зазоры в подшипниках считать
концентрическими и равными  = 0,06 мм.
32
Кинематическая вязкость масла  = 0,3610-4 м2/с, его плотность
 = 900 кг/м3. Течение в трубах и зазорах считать ламинарным. Потери
напора в фильтре hф = 5 м. Влияние вращения вала не учитывать. Сопротивлением распределительного канала пренебречь, считая, что к
каждому подшипнику подается расход Q/3.
Ответ:
128  l 3  s  a  
Q
128    L  Q
p 4 
 

   g  hф  2,7 МПа .
3 
3


d
d


 d4
0
 1

Задача 15. По сифонному трубопроводу, для которого задан напор
H = 6 м, необходимо подавать расход воды Q = 50 л/с при условии, чтобы вакуумметрическая высота в сечениях трубопровода не превышала
7 м. Опасное сечение С расположено выше
начального уровня воды на h = 4 м, длина
восходящей линии трубопровода для этого
сечения l1 = 100 м, а нисходящей линии
l2 = 60 м. Трубопровод снабжен приемным
клапаном с сеткой (к = 5) и задвижкой.
Определить диаметр трубопровода d и коэффициент сопротивления
задвижки , удовлетворяющие условиям задачи.
Указание. Пренебречь потерями в поворотах, а коэффициент потерь на трение рассчитывать по формуле для старых водопроводных
труб:   0,02 d 1 3 .
Задача 16. Смазочное масло (относительная плотность  = 0,8,
 = 610-6 м2/с) подводится к подшипникам коленчатого вала по системе трубок, состоящей из пяти одинаковых участков, каждый длиной
l = 500 мм и диаметром d = 4 мм.
1. Сколько смазки нужно подать
к узлу А системы, чтобы каждый подшипник получил ее не менее 8 см3/с?
2. Как изменится потребное количество смазки, если участки АВ
заменить трубой диаметром D = 8 мм?
Давление на выходе из трубок в
подшипники считать одинаковым, местными потерями и скоростными напорами пренебречь.
33
Истечение жидкости из отверстий и насадков
Истечение из малых отверстий в тонкой стенке сосуда
Отверстие можно считать малым, если его высота меньше одной
десятой части напора, под которым происходит истечение.
Скорость вытекания жидкости из открытого сосуда через отверстие
определяют по формуле
V    2  g  H    2  p  ,
где H и p – напор и избыточное давление в центре отверстия;  – коэффициент скорости, учитывающий потери напора, обусловленные протеканием жидкости через отверстие.
При истечении из закрытого сосуда с давлением р на поверхности
жидкости в среду с давлением ро скорость истечения находят по формуле
V  
2

 g  H   p  po  .
Расход жидкости, вытекающей из отверстия равен:
Q    So  V    So 
2

 g  H   p  po  ,
где  – коэффициент сжатия струи; Sо – площадь сечения отверстия;  –
коэффициент расхода отверстия.
Число Рейнольдса при истечении из отверстий определяют по скорости истечения, т.е. для истечения из открытого сосуда оно имеет вид
Re H 
d  2 g  H

.
При истечении с большими значениями числа Рейнольдса
(ReH>100000) можно принимать следующие значения коэффициентов
истечения:  = 0,62 – 0,63; 0,97 – 0,98;  = 0,61.
При истечении с малыми числами Рейнольдса все коэффициенты
истечения зависят от значений ReH. Для определения коэффициента
расхода используют приближенные формулы:
при ReH < 25

Re H
;
25,2  Re H

Re H
;
1,5  1,4  Re H
при 25 < ReH < 300
34
при 300 < ReH < 10000
  0,592  0,27 Re1H6 ;
при ReH > 10000
  0,592  5,5
Re H .
При истечении жидкостей с малой вязкостью через отверстия малого диаметра и при небольших напорах на коэффициент расхода оказывает влияние поверхностное натяжение.
Истечение из насадков и коротких труб
Короткую трубку l  3  4  d  , присоединенную к отверстию для
изменения характеристик истечения, называют насадком. Формула расхода для насадков та же, что и для отверстий в тонкой стенке. Отличие в
расходе учитывают с помощью коэффициента расхода насадка н. Для
насадков разных типов в автомодельной относительно числа Рейнольдса области истечения значения коэффициентов расхода приведены в
приложении П 1.11.
При истечении из коротких трубопроводов следует учитывать не
только местные сопротивления, но и потери на трение. При этом расчетная зависимость имеет вид
Q   c  S o  2  p  ,
где  c  1
1    l d    – коэффициент расхода системы (при исте-
чении под уровень –  c  1
  l d    ).
Истечение при переменном напоре
Истечение при переменном напоре обычно имеет место при опорожнении или наполнении резервуаров.
Дифференциальное уравнение процесса опорожнения открытого
резервуара произвольной формы при отсутствии притока в него жидкости имеет вид
S z  dz  Qz dt ,
где Sz – площадь свободной поверхности жидкости в резервуаре (в общем случае зависит от вертикальной координаты z); dz – понижение
уровня жидкости за время dt; Qz – расход жидкости через выпускное
отверстие.
Истечение жидкости под действием переменного напора является
неустановившимся, однако, если площадь поперечного сечения резер35
вуара достаточно велика по сравнению с площадью выходного отверстия, то переменная скорость опускания уровня жидкости будет весьма
малой. В этом случае локальными ускорениями частиц жидкости можно
пренебречь, рассматривать процесс истечения за бесконечно малый
промежуток времени как установившийся. Мгновенный расход при этих
условиях определяется по формуле
Qz    S o  2  g  z ,
где  – коэффициент расхода выпускного устройства, отнесенный к
площади Sо выходного отверстия.
При квадратичном режиме истечения коэффициент расхода можно
принимать постоянным в течение всего процесса. Тогда для резервуара
с постоянной по высоте площадью поперечного сечения время частичного опорожнения сосуда от начального уровня Ho до произвольного
уровня H находят по формуле
t
2S
  So  2  g



Ho  H .
Коэффициент расхода  выпускного устройства определяется его
конструкцией.
Время полного опорожнения резервуара при переменном напоре в
два раза больше времени истечения того же объема жидкости при постоянном напоре, равном начальному уровню Ho.
При истечении жидкостей с большой вязкостью (ReH < 10) время
опорожнения рассчитывают по формуле
t
H
29  S 
 lg o ,
g  d  So
H
где S – площадь горизонтального сечения резервуара,  – кинематическая вязкость жидкости.
Задачи
Задача 1. Какое избыточное давление воздуха
нужно поддерживать в баке, чтобы его опорожнение происходило в два раза быстрее, чем при атмосферном давлении над уровнем воды? Каким
будет время опорожнения бака?
Диаметр бака D = 800 мм, его начальное заполнение H = 900 мм. Истечение происходит через
цилиндрический насадок диаметром d = 25 мм и высотой h = 100 мм,
коэффициент расхода которого  = 0,82.
36
Задача 2. Открытая цистерна диаметром
D = 2,4 м и длиной L = 6 м, полностью заполненная
бензином, опоражнивается через сливную трубу,
диаметр и длина которой d = 50 мм и l = 7 м, а выходное сечение находится на уровне нижней точки
цистерны. Суммарный коэффициент местных сопротивлений в трубе  = 8, а коэффициент сопротивления трения  = 0,025.
Определить время опорожнения цистерны.
Задача 3. Пневматический амортизатор шасси с диаметром цилиндра D = 120 мм в начальном положении заряжен воздухом под избыточным давлением р0 = 3,2 МПа, который занимает часть высоты цилиндра
а0 = 150 мм.
Определить время и осадку цилиндра под действием постоянной нагрузки G = 50 кН, внезапно приложенной к амортизатору, если жидкость перетекает через
отверстие диаметром d = 3 мм (коэффициент расхода
 = 0,8).
Плотность жидкости (спиртоглицериновая смесь)
 = 1120 кг/м3.
Указание. Дифференциальное уравнение процесса
истечения:
S  dx  Q  dt ,
где S – площадь поршня; dx – осадка цилиндра за время dt.
Расход через отверстие:
Q    s 2
p1  p

,
где p1  G S – постоянное давление над поршнем; р – переменное давление воздуха при занимаемой им высоте x, p   p0  pат   a0 x  pат
(рат = 0,1 МПа – атмосферное давление).
Подставляя в уравнение процесса истечения выражения для Q и p,
после преобразования получаем
dt  
S
 s 2
p1  p €˜

x
 dx ,
x  a1

где а1 – высота объема воздуха в конце процесса:
p  pат
a1  0
 a0 .
p1  pат
37
Задача 4. К цилиндру гидравлического
амортизатора, где в качестве пружины используется сжимаемая под нагрузкой жидкость,
приложена сила Р = 400 кН.
Считая стенки цилиндра абсолютно
жесткими, определить величину опускания x0
цилиндра относительно поршня амортизатора
(прямой ход) и время t обратного хода при
внезапном прекращении действия силы Р.
Дроссельное отверстие в поршне имеет
диаметр d0 = 4 мм, его коэффициент расхода
 = 0,6. Модуль упругости жидкости принять постоянным Е = 12108 Н/м2.
Объем жидкости в ненагруженном цилиндре V = 5500 см3. Диаметр
штока D = 100 мм. Силами инерции жидкости и цилиндра, а также силами трения пренебречь.
Ответ:
x0 
2S
P V
P V

 10 c ,
 3 см ; t 
2
ES
ES
  s0  2  g
где s0    d02 4 и S    D 2 4 .
Задача 5. Для понижения давления на некотором участке гидросистемы применяют редукционный клапан, схема которого показана на
рисунке.
Пренебрегая трением и считая, что сила
давления на клапан определяется выражением
P  p2    d 2 4 , определить редуцированное
давление р2, которое будет иметь место при
расходе через клапан Q = 0,6 л/с, если давление на входе в клапан р1 = 10 МПа. Вычислить
для этого случая подъем y клапана, приняв коэффициент расхода  = 0,6.
Как изменится расход через клапан и его подъем, если редуцированное давление изменится до р2 = 7 МПа при том же давлении р1.
Жесткость пружины с = 235 Н/мм, ее сжатие l = 2 мм. Диаметр клапана d = 10 мм. Плотность жидкости  = 900 кг/м3.
Задача 6. Для защиты гидросистемы от недопустимого повышения
давления применяют предохранительный клапан. Открытие клапана и
перепуск жидкости в линию слива происходит в тот момент, когда сила
давления жидкости на клапан становится равной силе натяжения пружины, прижимающей клапан к седлу.
Особенность показанной на рисунке конструкции состоит в том,
что при открытом клапане поток жидкости в нем проходит последовательно через два сопротивления – клапанную щель (d0, y) и дроссельные
38
отверстия (d1), благодаря чему в промежуточной между этими сопротивлениями камере создается некоторое избыточное давление р1, которое дает дополнительное усилие сжатия клапанной
пружины.
Определить внешний диаметр клапана D, если требуется, чтобы при расходе
через клапан Q = 2 л/с давление р в подводящем патрубке перед клапаном было
равно давлению открытия клапана р = р0 = 2,5 МПа. Определить при
этом подъем клапана y. Диаметр подвода do = 15 мм.
Коэффициент расхода клапана 0 принять равным коэффициенту
расхода дроссельного отверстия 1 : 0 = 1 = 0,6. Число отверстий i = 4,
диаметр каждого d1 = 4,5 мм. Жесткость пружины с = 600 Н/мм. Плотность жидкости  = 900 кг/м3.
Насосы и их работа на сеть
Центробежные насосы
Насосом называют машину, преобразующую механическую энергию двигателя в энергию потока жидкости.
Рабочий процесс насоса характеризуется его основными параметрами: подачей, напором, мощностью, КПД и допустимым вакуумом.
Напором H называют энергию, сообщаемую единице веса жидкости, проходящей через насос. Его измеряют в метрах столба перекачиваемой жидкости и определяют по формуле
H
pвых  pвх V 2вых  V 2вх

 z,
g
2 g
где pвых и pвх – давления на выходе из насоса и на его входе, Па; Vвых и
Vвх – средние скорости на выходе из насоса и на его входе, м/с; z – расстояние по вертикали между точками присоединения манометра и вакуумметра, м;  – плотность жидкости, кг/м3.
Полезную мощность определяют как произведение объемного расхода жидкости на напор:
NП    g  H  Q .
Полный КПД насоса представляет собой отношение полезной
мощности к подведенной (к мощности на валу). Он учитывает все виды
потерь в насосе: гидравлические г, объемные о и механические м:
N
  П  г  o  м .
N
39
Всасывающую способность насоса характеризуют вакуумметрической высотой всасывания:
H вак 
pa  pвх
V 2вх
 hг 

g
2 g
h ,
w
где hг – геометрическая высота расположения всасывающего патрубка
насоса над уровнем жидкости, м; hw – потери напора во всасывающей
линии, м.
Допустимый вакуум – это разряжение во всасывающем патрубке
насоса, обеспечивающее бескавитационную его работу.
Условием бескавитационной работы насоса является кавитационный запас – разность между удельной энергией потока на входе насоса
и энергией, соответствующей давлению парообразования:
 p
V 2вх 
p
  П ,
h   вх 
   g 2 g    g
Кавитация возникает в случае, если максимальное падение динамического напора на входе hmax будет равно критическому значению.
С.С. Руднев, обобщая опытные данные, получил следующую формулу:
34
 n Q 
 ,
hmax  10  
 c 


где n – число оборотов вала, об/мин; Q – подача, м3/с; с – опытный коэффициент, характеризующий конструкцию насоса.
Величина с для всех геометрически подобных машин постоянна и
находится в пределах 800–1500. Чем больше величина с, тем лучше всасывающая способность насоса.
Характеристиками насоса называют графические зависимости
между основными рабочими параметрами машины: между напором и
подачей (H – Q), мощностью и подачей (N – Q), КПД и подачей ( – Q),
допустимым вакуумом и подачей (Hвак – Q).
С помощью теории подобия получены условия пропорциональности:
Q1 n1
 ;
Q2 n2
2
H1  n1 
  ;
H 2  n2 
3
N1  n1 
  ,
N 2  n2 
позволяющие производить пересчет характеристик имеющихся в наличии насосов на другую частоту вращения (индексы 1 и 2 соответствуют
подобным режимам работы одного и того же насоса).
Для сравнения центробежных насосов различной конструкции с
целью выбора в качестве базовой той модели, которая наилучшим образом отвечает поставленной задаче, используют критерий, получивший
40
название коэффициента быстроходности. Его значение определяют по
следующей зависимости:
Q
.
H3 4
Насос, работающий на сеть, должен обеспечить равенство создаваемого им напора потребному напору в сети, который определяется по
общей формуле
p  pн
H потр  zк  zн   к
  hw ,
g
c  3,65  n 
где (zк – zн) – геодезические отметки уровней жидкости в конечной и
начальной точках сети, м; рк и рн – избыточные давления в приемном и
напорном резервуарах, Па;  – плотность перекачиваемой жидкости,
кг/м3; g – ускорение свободного падения, м/с2; hw – суммарные потери
напора в трубопроводах сети, м.
Точку пересечения характеристики насоса с кривой потребного
напора называют рабочей точкой.
Параллельное соединение насосов используют для увеличения подачи. Суммарную характеристику нескольких насосов получают сложением подач отдельных насосов при постоянных напорах.
Последовательное соединение центробежных насосов используют
для повышения напора. Суммарную характеристику получают сложением напоров отдельных насосов при постоянных их подачах.
Задачи
Задача 1. Центробежный насос производительностью Q работает
при частоте вращения n. Определить допустимую высоту всасывания,
если диаметр всасывающей трубы d, а ее длина L.
Коэффициент кавитации в формуле Руднева принять равным с. Температура воды t = 20˚С. Коэффициент сопротивления колена к = 0,2. Коэффициент сопротивления входа в трубу вх = 1,8. Эквивалентная шероховатость стенок трубы э = 0,15 мм.
Варианты
Величина
1
Q, л/с
d, мм
L, м
n, об/мин
с
2
3
4
5
6
7
8
9
10
15
25
35
62
30
22
14
100
53
32
100 125 150 200 150 125 100 250 200 150
2,5
2,8
3,5
5
3,6
3
2,5
5,8
4,8
3,2
2860 2850 2740 1470 2500 2890 1475 1450 1500 2000
1000 1100 1200 800 1000 900 1200 800 900 1000
41
Задача 2. Центробежный насос подает воду с расходом Q из колодца в открытый напорный бак по трубе диаметром d на высоту H. Определить коэффициент быстроходности и коэффициент полезного действия насоса, если мощность на валу насоса Nе, частота вращения n, а
суммарный коэффициент сопротивления системы с равен 12.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
Q, л/с
15
25
36
63
36
25
15
25
36
15
H, м
10
8
9
20
15
12
10
5
8
16
d, мм
100
125
150
200
150
125
100
125
150
100
Nе, кВт
2,3
3,2
5,0
17,3
7,7
4,4
2,3
2,3
4,6
3,4
n, об/мин
3000 2500 2000 1500 3000 2000 2800 3000 2500 2700
Задача 3. Вода перекачивается насосом из открытого бака А в расположенный ниже резервуар В, в котором поддерживается постоянное
давление рв по трубопроводу общей длиной L и диаметром d. Разность уровней воды в баках h. Определить напор, создаваемый насосом при подаче в бак В
расхода воды Q. Принять суммарный коэффициент
местных сопротивлений c равным 6,5. Эквивалентная
шероховатость стенок трубопровода э = 0,15 мм.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
рв, кг/см2
1,7
(а)
0,75
(и)
1,8
(а)
1,8
(а)
0,8
(и)
0,2
(в)
0,2
(и)
0,25
(в)
0,3
(в)
0,9
(а)
L, м
90
112
225
180
135
113
90
225
180
135
d, мм
100
125
250
200
150
125
100
250
200
150
H, м
2,0
2,5
3,0
3,5
4,0
1,0
5,0
0,5
0
2,0
Q, л/с
15
25
98
63
36
24
14
100
62
35
Обозначения: (а) – абсолютное давление; (и) – избыточное давление; (в) – вакуумметрическое давление
Задача 4. Определить производительность и напор насоса (рабочую
точку) при подаче воды в открытый резервуар из колодца на высоту H
42
по трубопроводу диаметром d, длиной L с коэффициентом гидравлического трения  равным 0,03, и суммарным коэффициентом местных
сопротивлений с = 1,2. Как изменится подача и напор насоса, если частота вращения рабочего колеса уменьшится на 10%?
Данные, необходимые для построения характеристики центробежного насоса (H – Q), приведены в таблице.
Q
0
0,2Q0
0,4Q0
0,6Q0
0,8Q0
1,0Q0
H
1,0H0
1,05H0
1,0H0
0,88H0
0,65H0
0,35H0
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
H, м
30
45
6
30
30
60
60
6
15
15
d, мм
200
100
250
100
50
80
100
200
70
300
L, м
6
25
40
15
60
7
36
8
12
280
Qо, м3/с
0,7
0,1
0,3
0,1
0,01
0,1
0,1
0,3
0,03
0,3
Hо, м
100
150
20
100
100
200
200
20
50
50
Задача 5. Два одинаковых насоса работают параллельно и подают
воду в открытый резервуар из колодца на высоту H по трубопроводу
диаметром d, длиной L с коэффициентом гидравлического трения
 = 0,03 и суммарным коэффициентом местных сопротивлений с = 30.
Определить рабочую точку (подачу и напор) при совместной работе насосов на сеть. Как изменится суммарная подача и напор, если частота вращения рабочего колеса одного из насосов увеличится на 10%?
(Данные, необходимые для построения характеристики Q – H, те же, что
и в задаче 4.)
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
H, м
24
30
45
40
60
30
25
40
50
60
d, мм
310
185
180
180
200
170
1330
170
190
250
L, м
320
190
185
190
210
175
125
175
200
260
0,05
0,06
0,07
0,065
0,10
0,05
0,025
0,06
0,08
0,15
80
100
150
130
200
100
80
140
160
200
Qо,
м3/с
Hо, м
43
Задача 6. Два одинаковых насоса работают последовательно и подают воду в открытый резервуар из колодца на высоту H. Определить
рабочую точку (напор и подачу) при совместной работе насосов на сеть,
если коэффициент сопротивления сети (системы) c равен 1200, а диаметр
трубопровода d. Как изменяются суммарный напор и подача, если частота
вращения рабочего колеса одного из насосов увеличится на 12%? (Данные, необходимые для построения характеристики Q – H, те же, что и в
задаче 4).
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
H, м
60
24
30
45
40
60
30
25
40
50
d, мм
260
320
195
190
190
210
180
135
180
200
Qо, м3/с
0,15
0,05
0,06
0,07 0,065 0,10
0,05 0,025 0,06
0,08
Hо, м
200
80
100
150
100
160
130
200
80
140
Насосы объемного типа
В объемном насосе процесс нагнетания осуществляется за счет
непосредственного вытеснения жидкости рабочим органом. К этому
типу машин относят поршневые, шестеренные, винтовые, ротационные
лопастные насосы (пластинчатые).
Поршневые насосы. Основные геометрические параметры:
D – диаметр поршня; r – радиус кривошипа; l – длина шатуна;
S  2  r – ход поршня.
Рабочий объем:
q  
D2
 S.
4
Средняя теоретическая подача:
n
,
60
где n – число оборотов коленчатого вала (число двойных ходов поршня)
в минуту.
Действительная подача меньше теоретической на величину утечек,
учитываемых объемным КПД:
Qт  q 
Q  Qт  o .
44
Закон изменения подачи во времени:
Q   
D2
r


 r     sin  
sin 2 ,
4
2l


где – угловая скорость вращения вала; –угол поворота вала.
Из формулы видно, что подача насоса изменяется по синусоидальному закону, т.е. носит пульсирующий характер. Для уменьшения неравномерности подачи и сглаживания пульсаций применяют многоцилиндровые насосы.
Неравномерность подачи оценивают коэффициентом неравномерности:

Qmax  Qmin
.
Qcp
Поршневые машины аксиального типа. Рабочий объем машины
определяют из геометрических соотношений:
q  
d2
 D  tg  z ,
4
где d – диаметр поршня; D – диаметр окружности, на которой расположены оси цилиндров;  – угол наклона шайбы ( D  tg  S – ход поршня); z – число цилиндров.
Средняя теоретическая подача аксиально-поршневого насоса:
n
,
60
Аксиально-поршневые машины принципиально обратимы. Момент, развиваемый аксиально-поршневым гидромотором, равен
Wт  q 
pq
,
2 
где р – перепад давления жидкости в гидромоторе.
Шестеренные машины. Процесс нагнетания жидкости осуществляется за счет ее переноса во впадинах шестерен. При инженерных расчетах подача насоса может быть определена по приближенной формуле,
основанной на допущении, что количество жидкости, подаваемой за
один оборот вала, равно сумме объемов впадин между зубьями. При
этом принимают объем впадины равным объему зуба. Следовательно,
объем вытесняемой жидкости равен:
M
W  b z f ,
где b – толщина зуба; z – число зубьев; f – площадь впадины.
45
Поскольку, как правило, шестерни одинаковы, то рабочий объем
машины:
q  2b z  f .
Считая, что высота зуба равна двум модулям (2m), а его ширина –
половине шага (t/2), получим
f  m  t.
Выразив модуль и шаг через диаметр начальной окружности dн
( m  d н z, t    d н z ), найдем формулу для величины рабочего объема:
2    dн  b
 2    d н  m  b.
z
2
q
Теоретическая подача:
n 2    dн  b  n
n

 2    dн  m  b .
60
z  60
60
2
Qт  q 
Из формулы видно, что для увеличения подачи необходимо уменьшать количество зубьев (обычно z = 6–12).
Шестеренные машины обратимы. Момент, развиваемый шестеренным гидромотором, равен:
M 
pq
.
2 
Задачи
Задача 1. Определить полезную мощность насоса объемного гидропривода, если внешняя нагрузка на поршень силового гидроцилиндра
F, скорость рабочего хода V, диаметр поршня D1, диаметр штока D2. Механический
КПД гидроцилиндра м равен 0,96, объемный КПД о = 0,97. Общая длина трубопровода системы L, диаметр трубопровода d,
суммарный коэффициент местных сопротивлений с = 20. Рабочая жидкость в системе –
спиртоглицериновая смесь ( = 1210 кг/м3,
 = 1,2 см2/с).
Указание. Напор насоса затрачивается
на перемещение поршня, нагруженного силой F, и на преодоление гидравлических потерь в трубопроводах системы.
46
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
F, кН
50
60
70
80
90
100
90
80
70
60
V, см/с
4
9,5
12,5
8,6
3,5
5,6
3,4
11
8
5,3
D1, мм
110
120
130
138
145
155
145
138
130
120
D2, мм
36
40
44
46
48
52
48
46
43
40
L, м
10
15
12
10
8
14
12
10
8
12
d, мм
15
20
25
22
14
20
15
25
20
15
Задача 2. Определить средний объемный коэффициент полезного
действия, максимальную теоретическую подачу и степень неравномерности подачи поршневого насоса двойного действия с диаметром цилиндра D, ходом поршня S и диаметром штока d при n двойных ходах
(оборотах рабочего вала) в минуту, заполняющего мерный бак емкостью W в течение tс.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
D, мм
200
300
250
100
200
300
150
250
300
280
S, мм
150
250
200
60
250
300
100
250
350
250
d, мм
50
75
62,5
25
50
75
40
62,5
75
70
n, об/мин
50
60
70
60
80
60
50
75
60
90
0,52
1,45
3,5
0,2
1,16
3,7
3,0
80
50
100
80
70
90
80
W, м3
t, с
1,13 0,077 0,86
60
100
50
Задача 3. Поршневой насос простого действия с диаметром цилиндра D, ходом поршня S, числом двойных ходов в минуту n и объемным
КПД о = 0,9 подает рабочую жидкость в систему гидропривода. При
какой частоте вращения должен работать включенный параллельно шестеренчатый насос с начальным диаметром шестерни dн, шириной шестерен b, числом зубьев z = 30 и объемным КПД о = 0,86, чтобы количество подаваемой жидкости удвоилось?
47
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
D, мм
80
90
100
110
120
70
90
100
110
80
S, мм
200
260
160
220
180
240
280
300
320
340
n, об/мин
60
75
50
65
55
70
80
85
90
95
dн, мм
64
72
80
88
96
56
72
80
88
64
b, мм
50
65
40
55
45
60
70
75
80
85
Задача 4. Поршневой насос двойного действия подает воду в количестве Q из колодца в открытый резервуар на высоту H по трубопроводу
длиной L, диаметром d; коэффициент гидравлического трения  = 0,03 и
суммарный коэффициент местных сопротивлений с = 20. Определить
размеры цилиндра и мощность электродвигателя, если отношение хода
поршня к его диаметру (S:D) равно 1,0; число двойных ходов в минуту
n, отношение диаметра штока к диаметру поршня (d:D) составляет 0,15;
объемный коэффициент полезного действия о = 0,9; полный коэффициент полезного действия  = 0,7.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
Q л/с
30
50
65
150
200
150
100
60
120
200
H, м
10
15
20
15
10
25
20
30
35
25
L, м
20
25
30
35
40
35
30
25
20
40
d, мм
100
150
200
250
300
250
200
150
250
300
n, об/мин
100
90
80
70
60
90
80
70
60
100
Задача 5. Определить мощность шестеренного насоса, используемого в объемной гидропередаче для перемещения поршня гидроцилиндра, если внешняя нагрузка поршня при рабочем ходе (справа налево)
Р = 5000 Н, скорость рабочего хода V = 0,15 м/с, диаметр поршня
D1 = 50 мм, диаметр штока D2 = 20 мм.
Рабочая жидкость в системе – спирто-глицериновая смесь плотностью  = 1235 кг/м3 и кинематической вязкостью  = 1,210-4 м2/с. Общая
длина трубопровода системы l = 11 м, диаметр d = 10 мм.
48
Местные потери в обратном клапане,
кране управления и фильтре выражаются
через относительные эквивалентные длины
труб, равные соответственно lэ/d = 50, 40, 60.
Какова мощность насоса при обратном
ходе поршня, если преодолеваемое при
этом усилие равно 1000 Н?
Указание. Напор насоса в данной установке равен сумме перепада пьезометрических напоров по обе стороны поршня и потерь напора в трубопроводах:
4 P
Hн 
 hП .
  D12  D22    g


Задача 6. Пластинчатый насос, подача которого Q = 1 л/с, нагнетает масло в верхний бак из двух баков с одинаковыми уровнями. Всасывающие трубы имеют равные диаметры d1 = d2 = 20 мм и равные приведенные длины l1 = l2 = 4 м. Диаметр и приведенная длина напорной трубы d3 = 20 мм и l3 = 6 м.
Определить напор насоса Hн и мощность двигателя Nдв при высоте подъема Hст = 5 м, если кинематическая вязкость масла  = 0,510-4 м2/с, его плотность
 = 900 кг/м3 и КПД насоса  = 0,7.
Как изменится напор насоса, если уровень в левом баке будет ниже, чем в правом, на z = 2 м?
Указание. При разнице z уровней в баках потери
напора в левой и правой всасывающих трубах связаны
уравнением hп1  z  hп2 ; решая его совместно с Q1  Q2  Qн , находим
расходы Q1 и Q2 во всасывающих трубах. Для установления зависимости потерь напора от расхода предварительно следует определить режим движения в трубах.
Задача 7. Шестеренный бензонасос, подача которого Qн = 4 л/с, снабжен
обводной трубой, возвращающей часть его подачи на сторону всасывания. Статический напор установки Hст = 8 м.
Диаметр основного трубопровода d1 = 50 мм, его
приведенная длина l1 = 50 м ( = 0,025). Диаметр обводной трубы d0 = 32 мм, ее суммарный коэффициент сопротивления (включая частично прикрытый вентиль)  = 33.
1. Определить подачу в верхний бак и мощность,
потребляемую насосом (КПД насоса  = 70%, плотность
бензина  = 750 кг/м3).
2. При каком наименьшем значении  обводной
трубы подача в верхний бак прекратится?
49
3. Какую мощность будет потреблять насос при выключенной обводной трубе?
Указание. Характеристика шестеренного насоса в координатах
Hн – Qн может быть приближенно изображена вертикальной прямой
Qн = const.
Гидродвигатели
Силовым гидроцилиндром называют гидродвигатель с поступательным движением выходного звена. Отношение усилия на гидроцилиндре Fдв к усилию, приложенному к поршневому насосу Fн, называют
передаточным отношением i. Если пренебречь падением давления в
линиях связи, то ввиду равенства давлений в насосе и гидроцилиндре
(рн = рдв) получим:
Fдв S дв

 i,
Fн
Sн
где Sдв и Sн – площади поршней гидроцилиндра и насоса, м 2.
Если пренебречь сжимаемостью жидкости, то объемы, описываемые поршнями, равны:
S дв  lдв  S н  lн ,
где lдв и lн – перемещения поршней гидроцилиндра и насоса, м.
Объем жидкости, вытесняемой поршнем (гидроцилиндра либо
насоса) в единицу времени:
Q  S V ,
где V – скорость движения поршня, м/с.
Мощность рассматриваемых гидромашин определяют по формуле
N  F  V  p  Q.
Гидродвигатели вращательного движения называют гидромоторами.
Рабочим объемом гидромотора qм называют объем жидкости, проходящий через него за один оборот вала при перепаде давлений, равном
нулю. Расход жидкости через гидромотор, который в идеальном случае
при отсутствии утечек равен подаче насоса, вычисляют по уравнению:
Qм 
qм  nм
,
60
где nм – число оборотов вала гидромотора в минуту.
50
Теоретическая скорость вращения вала гидромотора
nм  nн 
qн
,
qм
где индексы “м” и “н” относятся к гидромотору и насосу соответственно.
Выходная мощность гидропередачи равна мощности гидромотора:
N м  pм  Qм .
Обычно в гидроприводе в качестве выходного параметра рассматривают не мощность, а момент, который определяют по формуле
Mм 
Nм
м

pм  Qм
p q
 м м,
2    nм 60
2 
где  – угловая скорость вала гидромотора, 1/с.
В реальных условиях объемные потери, связанные с утечками,
приводят к снижению скорости вращения вала гидромотора, что учитывают объемным КПД:
o 
nм
,
nмт
где nмт – теоретическая скорость вращения вала.
Влияние внутренних сопротивлений приводит к снижению момента на выходном валу, что учитывают с помощью гидравлического КПД:
т 
Mм
,
M мт
где Mмт – теоретический момент на выходном валу.
КПД гидропередачи определяют по формуле

N вых
 o  г  мех ,
N вх
где мех – механический КПД передачи.
Как и в любой гидравлической системе мощность, теряемая в гидропередаче, превращается в теплоту. Для нормальной работы системы
ее необходимо отводить за счет охлаждения элементов гидропривода.
Задачи
Задача 1. Для подъема груза массой G = 10,2 т со скоростью
V = 0,16 м/с используются два параллельно работающих гидроцилиндра диаметром D = 100 мм. Расстояние между осями гидроцилиндров
L = 5 м.
51
При укладке груза его центр тяжести может
смещаться от среднего положения на а = 250 мм.
1. Каким должен быть коэффициент сопротивления дросселя Д1 или Д2 в одной из ветвей
напорного трубопровода насоса, чтобы груз поднимался без перекашивания? Коэффициент сопротивления полностью открытого дросселя в
другой ветви трубопровода принимать равным
нулю.
2. Какими будут при этом подача насоса и
развиваемое им давление?
Диаметр трубопровода d = 12 мм. Плотность рабочей жидкости
 = 880 кг/м3.
Потерями напора в трубопроводах системы, а также трением и
утечками в гидроцилиндрах пренебречь.
Задача 2. Силовой гидравлический цилиндр нагружен силой F и делает n двойных
ходов в минуту. Длина хода поршня h, диаметр поршня D, диаметр штока d. Определить
давление масла, потребную подачу и среднюю скорость поршня. Механический коэффициент полезного действия гидроцилиндра
мех = 0,95, а объемный КПД о = 0,98.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
F, кН
90
80
70
60
50
60
70
80
90
100
h, см
100
115
120
100
110
105
120
130
105
112
n, об/мин
12
10
20
11
10
20
25
20
10
15
D, мм
145
150
130
120
110
120
130
140
145
155
d, мм
50
50
45
40
40
40
45
45
50
52
Задача 3. Перемещение поршней гидроцилиндров с диаметром D = 25 см осуществляется подачей
рабочей жидкости ( = 1,5 cм2/с,  = 1400 кг/м3) по
трубам 1 и 2 одинаковой эквивалентной длины
L = 20 м и диаметром d = 5 см. Определить силу F2,
при которой скорость перемещения второго поршня
была бы в два раза больше скорости первого поршня. Расход в магистрали Q, первый поршень нагружен силой F1.
Указание. На перемещение поршней затрачивается одинаковый
суммарный напор, считая от точки А.
52
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
F1, кН
5,50
8,25
11,0
13,7
16,5
4,13
6,90
9,60
12,4
15,1
Q, л/с
6
9
12
15
18
4,5
7,5
10,5
13,5
16,5
Задача 4. Шестеренный насос объемной гидропередачи подает масло (вязкость  = 0,310-4 м2/с, относительная плотность  = 0,92) в гидроцилиндр (диаметры поршня и штока D1 = 100 мм и D2 = 40 мм),
нагруженный усилием Р = 3300 Н.
Характеристика насоса при n = const задана в виде зависимости подачи насоса Qн и его КПД  от развиваемого насосом давления рн.
Напорная труба, идущая от насоса к гидроцилиндру, имеет приведенную длину l1 = 2 м и диаметр d = 15 мм; сливная труба гидроцилиндра имеет размеры l2 = 8 м (приведенная длина с учетом сопротивления
полностью открытого дросселя В), d = 15 мм.
Насос снабжен перепускной трубой с дросселем А и переливным
клапаном С, характеристика которого задана в виде зависимости между
расходом Qк через клапан и давлением насоса рн.
1. Определить скорость Vп рабочего хода поршня и мощность Nдв,
потребляемую насосом при закрытом дросселе А и полностью открытом
дросселе В.
2. Сравнить мощность, потребляемую насосом при уменьшении
скорости поршня до V’п = 0,25Vп двумя способами – прикрытием дросселя В при полностью закрытом дросселе А и открытием дросселя А при
полностью открытом дросселе В.
Задача 5. Для системы по условию задачи 4 при закрытом дросселе
А и полностью открытом дросселе В определить:
1. Нагрузку Р1, при которой откроется переливной клапан С. Какими будут при этой нагрузке скорость Vп1 рабочего хода поршня и мощность Nдв1, потребляемая насосом?
2. При какой нагрузке Р2 поршень остановится? Какова будет при
этом потребляемая насосом мощность Nдв2?
Трением и утечками в цилиндре пренебречь.
53
ЧАСТЬ 2. ГИДРАВЛИЧЕСКИЕ ПЕРЕДАЧИ
И ГИДРОПРИВОД
Объемные гидравлические машины и их выбор2
Объемные насосы и их выбор
Гидромашины являются силовыми элементами, от правильного
выбора которых во многом зависят экономические показатели гидропривода в целом.
Серийно выпускаемые объемные насосы характеризуются главными и основными параметрами. В качестве главного параметра принят
рабочий объем в см3/об, в качестве основных параметров приняты: номинальное давление рн, МПа; номинальная производительность Qн,
дм3/мин; номинальная частота вращения nн, об/мин.
Нормальный ряд рабочих объемов насосов и насос-моторов в см3/об:
1,6; 2,5; 4; 5; 6,3; 8; 10; 12,5; 16; 20; 25; 32; 40; 50; 63; 80; 100; 125; 160;
200; 250; 320; 400; 500; 630; 800.
Нормальный ряд давлений насосов и насос-моторов в МПa:
2,5; 6,3; 10; 12,5; 16; 20; 32; 50.
Насосы с указанными параметрами приведены в табл. П 2.2.
Параметры насосов, выпускаемых серийно, в настоящее время могут
не соответствовать параметрам нормального ряда. Значения параметров
тех насосов, которые еще не приведены в соответствие с ГОСТами,
оставлены без изменений.
В табл. П 2.3 приведены основные характеристики шестеренных и пластинчатых
насосов, производство которых начато до введения ГОСТ 13823–78 ("Насосы oбъемные и
моторы. Основные параметры"), 13824–80 ("Насосы объемные и моторы. Рабочие параметры"), 14057–68 ("Насосы шестеренные гидравлические. Основные параметры"), I4058–
68 ("Насосы шиберные. Основные параметры"), 14059–68 (Поршневые насосы гидравлические. Основные параметры").
Кроме пластинчатых насосов, указанных в табл. П 2.3, промышленностью выпускаются пластинчатые секционные (сдвоенные) насосы для двух независимых потоков. Секционные пластинчатые насосы комплектуются из одинарных насосов типа Г12.
Регулируемые аксиально-поршневые насосы по виду управления
выпускаются с ручным, следящим, электромагнитным и комбинированным управлениями, а также с управлением по давлению.
Серийно выпускаемым насосам присваивается шифр согласно «Единой системе шифровки гидравлического, пневматического и смазочного
оборудования общемашиностроительного применения».
Бутов А.И., Водяник Г.М., Карастан П.С. Объемный гидропривод. –
Новочеркасск: Изд-во Новочеркасского политехнического института, 1979.
2
54
За основу шифровки по «Единой системе шифровки» приняты рабочий объем и давление, например: насос аксиально-поршневой, регулируемый с креплением на фланце, с рабочим объемом 20 см 3/об и номинальным давлением 32 МПа шифруется НА-Ф 20/320. Насос шестеренный с фланцевым креплением, рабочим объемом 32 см3 и номинальным давлением 16 МПа шифруется НШ-Ф-32/160.
Изделиям, разработчиком которых является ЭНМИМС, присваивается шифр по системе шифровки, принятой в станкостроении. Изделиям, разработчиком которых является
Гипроуглемаш, присваивается шифр по системе Гипроуглемаша.
Примером шифровки по системе, принятой в станкостроении, могут служить обозначения, данные в табл. П 2.3. По этой системе шестеренным машинам присвоен шифр
Г11, пластинчатым – Г12, поршневым – Г13. Далее указывается цифрой исполнение насоса и цифрой с буквами или без них – производительность насоса, например: насос шестеренный на давление рн = 2,5 МПа, производительностью 12 л/мин, обозначается Г11-22А.
Насос пластинчатый на номинальное давление 6,3 МПа с металлокерамическим статором производительностью 5 л/мин обозначается Г12-31А.
Пользуясь таблицами П 2.2 и П 2.3, по производительности, рабочему объему и номинальному давлению можно определять шифр насоса.
Насосы для гидросистем выбираются по давлению и производительности. Давление насоса ориентировочно определяется по формуле
pн  pг 
 p ,
где рг – давление перед гидромотором.
При выборе насоса суммарные потери давления
 p
рекоменду-
ется предварительно принимать:
 p  0,20  0,30   p
г
.
Производительность насоса Qн c учетом утечек предварительно
принимается равной:
Qн  1,05  1,10   Qг ,
где Qг – расход рабочей жидкости, проходящей через гидромотор.
Полученные значения рн и Qн корректируются по техническим характеристикам. Насос выбирается по возможности с запасом производительности (3–6) л/мин. Может оказаться, что паспортные данные
насоса по давлению несколько не соответствуют выбранному давлению,
т.к. в паспортах (технических характеристиках) указывается производительность при максимальном паспортном давлении рп. Производительность насоса при рабочем давлении рр можно подсчитать по формуле
Qнр 
Qнп
он
 Qнп 
pр 1  он

.
pп он
Для питания двух гидродвигателей желательно принимать секционные пластинчатые насосы.
55
При пользовании табл. П 2.3 вначале необходимо ориентировочно
выбрать частоту вращения приводного двигателя и определить рабочий
объем насоса по формуле
qн 
Qн
.
nн
(1)
По рабочему объему насоса, давлению и частоте вращения выбирается тип насоса и уточняется его производительность с учетом действительного рабочего объема и объемного КПД насоса он:
Qнр  qн  nн  он .
(2)
КПД насосов ориентировочно принимают в зависимости от их типа.
Тип насоса
о
общ
Пластинчатый
0,7–0,9
0,6–0,75
Шестеренный
0,7–0,9
0,25–0,70
0,95–0,98
0,8–0,9
Поршневой
Если частота вращения вала насоса по технической характеристике
не совпадает с частотой вращения вала приводного двигателя, например
электродвигателя, то паспортная производительность насоса Qн корректируется по формуле
n
Qнр  Qн  эл .
nн
Пример выбора насоса. Необходимо выбрать нерегулируемый гидронасос производительностью 2,3 10-4 м3/с на давление 16 МПа.
Из табл. П 2.2 ориентировочно принимаем частоту вращения насоса nн = 1440 об/мин и определяем по (1) рабочий объем насоса:
qн 
2,3  10 4  10 6  60
 9,6 см 3 /об .
1440
Принимаем насос типа БГ12 с рабочим объемом 12,5 см3/об, номинальным давлением 16 МПа и номинальной частотой вращения
1440 мин-1. Уточняем производительность насоса по формуле (2), учитывая, что объемный КПД пластинчатых насосов находится на уровне
0,7–0,9:
Qн  12,5 1440  0,8  15000 см3/мин = 2,510-3 м3 /с .
Таким образом, действительная производительность насоса несколько больше заданной, что соответствует общепринятым рекомендациям.
56
Объемные гидромоторы и их выбор
В табл. П 2.4 приведены технические характеристики основных типов и типоразмеров гидромоторов, которые наиболее широко применяются в промышленности. КПД гидромоторов ориентировочно можно
принимать таким же, как и насосов соответствующей конструкции.
Исходными данными для выбора гидромоторов в основном является нагрузочный момент Мс и пределы изменения частоты вращения вала
гидромотора. В зависимости от заданных параметров и паспортных
данных (см. табл. П 2.4) выбирают тип гидромотора. Причем необходимо, чтобы момент Мг, развиваемый гидромотором, был больше нагрузочного момента примерно на 5–10%, а частота вращения вала гидромотора обеспечивала заданную. После выбора типоразмера гидромотора
по максимальной частоте вращения можно рассчитать расход рабочей
жидкости Qг, потребляемой гидромотором, по формуле
Qг  qг 
nг max
ог
,
(3)
где qг – рабочий объем гидромотора.
Перепад давления в гидромоторе при нагрузочном моменте Мc
определяется по формуле
2    M c  ог
.
(4)
pг 
qг  общ
Давление перед гидромотором можно представить в виде суммы
перепада давления на гидромоторе и потерь давления в сливной гидролинии:
(5)
pг  pг  pс .
Потери давления в сливной гидролинии рс обычно не превышают
0,2–0,3 МПа.
По полученным значениям Qг и рг выбирают гидромотор.
Пример выбора гидромотора. Исходные данные: нагрузочный момент на валу гидромотора Мс = 8000 Нм; частота вращения изменяется в
пределах nг = 10–80 мин-1.
Из табл. П 2.4 выбираем радиально-поршневой гидромотор типа
МР-6,3/10 с номинальным развиваемым моментом Мг = 9520 Нм, при
перепаде давления рг = 10 Мпa, с рабочим объемом qг = 6300 cм3/oб и
ог = 0,93.
Расход рабочей жидкости, потребляемой гидромотором, определяем по формуле (3)
Qг 
6300  80
 542000 см 3 /мин  9,02  10 -3 м 3 /с .
0,93
57
Перепад давления рг при Мс = 8000 Нм определяем по (4):
pг 
2  3,14  8000  0,93
 10 6  8,35  10 6 Н/м 2  8,35 МПа .
6300  0,89
Давление перед гидромотором, принимая давление на сливе
рс = 0,2 МПа, по формуле (5)
pг  8,35  0,2  8,55 МПа .
Таким образом, исходными данными для дальнейших расчетов являются расход гидромотора 9,02 10-3 м3/c и давление перед гидромотором рг = 8,55 МПа.
Гидроцилиндры и их выбор
В табл. П 2.5 приведены технические характеристики основных типов гидроцилиндров.
Серийно выпускаемые промышленностью гидроцилиндры подбираются по длине хода поршня L и рабочему давлению или диаметру D.
Длина хода штока должна быть равна длине хода рабочего органа, рабочее давление и диаметр должны обеспечить заданное усилие Rг.
Для определения геометрических размеров гидроцилиндра необходимо знать максимальное усилие на штоке.
При установившемся движении усилие сопротивления движению
поршня определяется по формуле
Rc  pг  F  Rг  Rтр  Rпр .
Величина противодавления Rпр определяется суммой гидравлических сопротивлений в сливной гидролинии.
Сила трения Rтр зависит от вида уплотнения. Для резинового
уплотнения сила трения определяется по фoрмуле
Rтр    D  h   , или
Rтр   d  h   ,
где   2,2  10 5 Нм, a h – ширина уплотнения, м.
По максимальному усилию Rc определяют диаметр поршня гидроцилиндра D.
Так как до выбора гидроцилиндра такой параметр, как диаметр
уплотняющей поверхности, неизвестен, то рекомендуется определять D
по заданному усилию на штоке Rг:
D
4  Rг
k ,
  pг
где k – коэффициент запаса, принимаемый равным 1,2–1,3.
58
(6)
Найденный диаметр округляют до ближайшего большего стандартного размера. Затем уточняют давление в гидроцилиндре при том же
усилии на штоке, считая, что противодавление отсутствует:
pг 
4  Rг
  D2
k .
(7)
Согласно ГОСТ 6540-68 внутренний диаметр цилиндра в мм следует выбирать из ряда: 10, 12, 16, 20, 25, 32, 36, 40, 45, 50, 56, 63, 70, 80,
90, 100, 110, 125, 140, 160, 180, 200, 220, 250, 280, 320, 360, 400, 450,
500, 560, 710, 800, 900, а ход поршня в мм – из следующего ряда: 4, 6, 8,
10, 12, 16, 20, 25, 32, 40, 50, 56, 63, 70, 80, 90, 100, 110, 125, 140, 160,
180, 200, 220, 250, 280, 320, 360, 400, 450, 500, 560, 630, 710, 800, 900,
1000, 1200, 1250, 1400, 1600, 1800, 2000, 2240, 2500, 2800, 3000, 3150,
3350, 3550, 3750, 4000, 4250, 4500, 4750, 5000, 5300, 5600, 6000, 6300,
6700, 7100, 7500, 8000, 8500, 9000, 9500, 10000 (размеры основного ряда
подчеркнуты).
После определения параметров гидроцилидра и выбора его по
табл. П 2.5 определяют максимальное усилие, причем Rc должно быть
больше заданного усилия Rг. Затем рассчитывают расход жидкости Q1,
необходимый для перемещения поршня с заданной скоростью V:
для поршневой полости
Q1 
для штоковой полости
Q1 
  D2
V ;
4   об
(8)
  D 2  d 2 
V .
4  об
Обычно диаметр штока d  0,3  0,45   D .
В гидроцилиндрах, поршни и штоки которых уплотнены манжетами и кольцами из резиновых смесей и пластмасс, утечки практически
отсутствуют, и для таких гидроцилиндров значения объемного КПД
равны единице.
Пример выбора гидроцилиндра. Исходные данные: усилие на штоке
Rг = 30000 Н, ход поршня L = 0,2 м, максимальная скорость перемещения поршня при рабочем ходе 0,4 м/мин; усилие при холостом ходе отсутствует.
1. Ориентировочно принимаем давление в системе рг = 10 МПа и
определяем диаметр поршня по формуле (6):
D
4  30000
 1,3  0,0705 м = 70,5 мм .
3,14  10  10 6
59
По длине хода и диаметру поршня принимаем гидроцилиндр типа
Д443-1003-00-2 с D = 80 мм, L = 275 мм и номинальным давлением
рг = 10 МПа (табл. П 2.5).
2. Уточняем давление в цилиндре по формуле (7):
pг 
4  30000
 1,3  7800000 Па = 7,8 МПа .
3,14  0,08 2
Расход жидкости через гидроцилиндр определяем по формуле (8):
Q1 
3,14  0,08 2
 0,4  2,01  10 3 м 3 /мин .
4  1,0
Исходными данными для дальнейших расчетов и выбора гидрооборудования являются давление рг = 7,8 МПа и расход Q1 = 2,0110-3 м3/мин.
Задачи
Задача 1. Подобрать регулируемый (+) / нерегулируемый (–) насос
производительностью Qн, создающий давление рн по исходным данным,
приведенным в таблице.
Вариант №
Qн104,
м3/с
р н,
МПа
Регулируемый
Вариант №
Qн104,
м3/с
р н,
МПа
Регулируемый
1
15
12
–
6
2,2
14
+
2
6
28
–
7
3,2
24
–
3
2
22
–
8
1,8
12
–
4
8
16
+
9
0,8
16
+
5
0,5
18
–
10
2,6
26
+
Задача 2. Нагрузочный момент на валу гидромотора Мс и частота
вращения nг (номинальная либо пределы ее изменения) приведены в
таблице. Подобрать для заданного варианта гидромотор и определить
его характеристики.
Частота вращения, мин-1
№
Мс,
Нм
номинальная
1
1000
100
2
6500
3
100
4
1800
5
800
пределы
20–120
1000
10–200
160
60
№
Мс,
Нм
Частота вращения, мин-1
6
1500
10–200
7
50
8
20
9
2800
10
500
номинальная
пределы
1000
400–800
10–250
180
Задача 3. Усилие на штоке Rг, ход поршня L, максимальная скорость перемещения поршня при рабочем ходе V; усилие при холостом
ходе отсутствует. Подобрать гидроцилиндр и определить расход жидкости через него и ее давление на входе.
Вариант №
Rг , Н
L, м
V, м/мин Вариант №
Rг , Н
L, м
V, м/мин
1
45000
0,4
0,6
6
20000
0,4
1,2
2
100000
0,5
0,25
7
5000
0,6
1,6
3
800000
0,2
0,5
8
12000
0,8
1,0
4
120000
0,45
0,3
9
100000
0,12
0,8
5
40000
0,6
1,2
10
30000
0,5
0,6
Мощность и тепловые потери гидропривода
Режим работы гидроприводов машин и механизмов может характеризоваться следующими величинами:
Кр – коэффициентом использования давления:
К р  p pн ,
где p – наибольшее давление, при котором работает гидропривод продолжительное время;
Кп – коэффициент продолжительности работы гидропривода под
нагрузкой:
К п  tp tз ,
где tp – время работы гидропривода в течение заданного периода
(например часа или смены); tз – полное заданное время;
Кн – коэффициент, учитывающий неустановившийся характер работы гидропривода:
К н  tн t у ,
где tн – время работы гидропривода при неустановившемся режиме; tу –
время работы гидропривода при установившемся режиме.
Мощность гидропривода в общем случае зависит от характера
нагрузки. С этой точки зрения гидроприводы можно разделить на три
группы:
 работающие с постоянной нагрузкой в течение длительного
времени;
 работающие с кратковременной нагрузкой, когда время остановки много больше времени работы гидропривода;
61
 с повторно-кратковременной нагрузкой, когда чередуются между
собой соизмеримые по времени периоды нагрузки и работы вхолостую.
К первой группе относятся гидроприводы с последовательно включенным дросселем и постоянной нагрузкой. Для этих гидроприводов
Кр = 1,0, а мощность определяется по формулам
N н  Qг  Q   pг  p , Вт ,
N г  Qг  pг , Вт.
(9)
Для гидроприводов, работающих кратковременно, целесообразно
выбирать мощность по фактическому, а не по номинальному давлению:
N н  К р  pн  Qн , Вт;
(10)
N г  К р  pг  Qг , Вт.
(11)
В формулах (10) и (11) давление, производительность и расход
принимают по паспортным данным гидромашины.
К гидроприводам с повторно-кратковременной нагрузкой можно
отнести все гидроприводы возвратно-поступательного движения с объемным регулированием скорости и с дросселем, включенным параллельно. Для этих условий тепловые потери при постоянной скорости
движения выходного звена исполнительного механизма пропорциональны нагрузке.
Мощность гидромашины (гидронасоса и гидродвигателя) определяется по ее средней величине:
N н(г)   N i 
ti
, Вт,
tц
(12)
где Ni – мощность на i-м участке нагрузочной диаграммы; ti – время, в
течение которого мощность равна Ni; tц – время цикла.
Мощность, подводимая к насосу, равна
N под 
К
н общ
 N н , Вт,
(13)
где К – допустимая перегрузка.
По расчетной мощности и частоте вращения вала насоса выбирают
приводной двигатель.
Все потери мощности в гидросистеме превращаются в тепло, которое способствует нагреву рабочей жидкости. С повышением температуры уменьшается вязкость жидкости, что приводит к увеличению утечек
через зазоры гидрооборудования.
Особенно интенсивно нагревается жидкость при отсутствии разгрузки, низком КПД насоса или гидродвигателя и при дроссельном ре62
гулировании гидропривода. Если отсутствует разгрузка насоса, то при
остановках гидродвигателя вся жидкость сливается через предохранительный гидроклапан и вся мощность переходит в тепло:
Q  N под  t , Дж.
При работе насоса на потребителя количество выделяемого тепла
определяется по формуле
Q  N под  1  с   t , Дж.
(14)
КПД системы c определяется как отношение мощности гидродвигателя к подводимой мощности насоса, c  N г N под .
Для поддержания температуры рабочей жидкости в допустимых
пределах применяют естественное и принудительное (с помощью теплообменников) охлаждение. Для естественного охлаждения большое
значение имеет правильный выбор емкости гидробака, в котором размещается рабочая жидкость. Полезную емкость гидробака обычно выбирают по ГОСТ I6770–7I, равную не менее трехминутной производительности насоса.
Ёмкость гидробака, необходимую для нормальной работы гидропривода, можно определить также по формуле
3


Q
3
W  0,001 
 ,м ,


4

T

T
0


(15)
где Q – количество тепла за 3600 c, кДж.
Рабочей температурой считается температура в пределах
Т = (323–333) К или (50–60)˚С.
При длительной работе гидропривода установившуюся температуру при известном количестве рабочей жидкости определяют по формуле
T  T0 
1,5  10 4  Q
3
W2
.
(16)
Когда расчетные размеры гидробака чрезмерно большие, необходимо применять теплообменники.
Пример расчета мощности и тепловых потерь привода.
Задано: расход гидродвигателя Qг = 1,6610-3 м3/с, общий КПД
насоса н общ = 0,93, общий КПД гидроцилиндра г общ = 0,96, потери
давления в гидролинии р = 0,1 МПа, потери давления в гидрораспределителе ргр = 0,2 МПа.
Режим работы – повторно-кратковременный: в течение t1 = 10 c
р1 = 10 МПа, в течение t2 = 5 c р2 = 2 МПа. Утечки в гидроаппаратуре
составляют 0,0110-3 м3/с.
63
Определяем:
1) суммарные потери в гидролинии и гидрораспределителе:
p  0,1106  0,2 106  0,3 106 Па ;
2) мощность на выходе из насоса по формуле (9)
при t1
при t2


 0,3  10   3840 Вт ;
Nн1  1,66  0,01 103  10 106  0,3 106  17200 Вт ;

Nн2  1,66  0,01 103  2 106
6
3) среднюю мощность на выходе гидронасоса по (12) при tц = 15 с:
10
5
 3840   12750 Вт ;
15
15
4) подводимую мощность к насосу по формуле (13) при К=1:
Nн  17200 
N под 
1
 12750  13710 Вт ;
0,93
5) КПД всей системы по формуле
c  н общ  г общ  г  0,93  0,96  0,96  0,86 ,
где
г  1 
p  Q
0,3  10 6  1,67  10 3
 1
 0,96 ;
N под
13710
6) количество выделяемого за 1 час тепла по формуле (14):
Q  13710 1  0,86  3600  6,91106 Дж = 6,91103 кДж ;
7) емкость гидробака по формуле (15):
3
 6,91  10 3 
3
W  0,001  
  0,255 м ;
 4  330  293  
Принимаем фактическую емкость бака W = 0,3 м3. Тогда установившаяся температура определится по формуле (16):
T  293 
1,5  10 4  1,67  10 3
3
0,3
2
 319 К или 46  С.
Расчет механических характеристик гидроприводов
Исходными данными для расчета характеристик гидропривода с
дроссельным регулированием являются: площадь поршня Sп, м2; производительность насоса Q м3/c; нагрузка на штоке гидроцилиндра Rг, Н;
давление настройки предохранительного гидроклапана Rн, Па.
64
Расчет ведется в такой последовательности. Определяют максимальное проходное сечение дросселя:
Q
S др 

2

, м2 ,
 pдр
рдр необходимо брать из технической характеристики. При отсутствии этого параметра в технической характеристике принимают его в
пределах (0,2–0,5) МПа.
Коэффициент расхода дросселя  для щелевых дросселей принимают равным 0,67–0,70, а для игольчатых – 0,75–0,80.
Скорость штока гидроцилиндра в зависимости от нагрузки для гидропривода с последовательным включением дросселя в напорной гидролинии:
V
1
2 
R 
    др  S др
  pн  г  , м/с ,
Sп
 
Sп 
(18)
где др – параметр регулирования дросселя.
Скорость штока гидроцилиндра в зависимости от нагрузки для
гидропривода с последовательным включением дросселя в сливной
гидролинии:
V
1
2 
S
R 
    др  S др
  p  п  г  , м/с ,
Sп
  н Sш Sш 
(19)
где Sп и Sш – площади поршня со стороны рабочей и штоковой полостей.
Скорость штока гидроцилиндра в зависимости от нагрузки для гидропривода с параллельным включением дросселя:
V

Qн
1
2  Rг
    S др   др 
 
 pc  , м/с .
Sп
Sп
  Sп

(20)
Частота вращения вала гидромотора для гидропривода с дросселем,
включенным параллельно,
nг 

Qг
1
2  Mc
    S др   др 
 
 pн  , об/с ,
qг
qг
  Kм

где
Kм 
qг
.
2 
65
(21)
Частота вращения вала гидромотора для гидропривода с дросселем,
включенным последовательно,
nг   
1
2
 S др   др 
qг


M 
  pн  c  , об/с .
Kм 

(22)
Подставляя в формулы (18 – 22) различные значения нагрузки и
изменяя величину параметра регулирования др, можно получить графические зависимости nг  f (M c ) и V    pг  при различных значениях др, которые являются механическими характеристиками гидропривода с дроссельным регулированием.
Немаловажным является установление пределов регулирования.
Утечки в гидромашинах можно найти из уравнений:
Qн  Qн  1  он , Qг  Qг  1  ог  .
(23)
Утечки в гидроаппаратуре определяются по техническим характеристикам. При практических расчетах утечками в гидроаппаратуре можно
пренебречь, т.к. они значительно меньше утечек в гидромашинах.
Минимальный параметр регулирования:
 др.мин 
Q
.
Qдр
(24)
Коэффициент диапазона регулирования:
K рег 
1
 др.мин
.
(25)
Минимальная скорость штока гидроцилиндра:
Vмин  V 
1
, м/с .
K рег
(26)
Минимальная частота вращения вала гидромотора:
nг мин  nг 
1
, об/с .
K рег
(27)
Исходными данными для расчета характеристик гидропривода с
объемным регулированием являются: момент на валу гидромотора
Мс, Нм; частота вращения вала гидромотора nг; объемный коэффициент полезного действия гидромотора ог; производительность насоса
Q, м3/с; частота вращения вала насоса nн, об/с; объемный КПД насоса
он; давление, развиваемое насосом, рн, Па; параметр регулирования
насоса н и гидромотора г.
66
В ходе расчета определяют следующие параметры:
коэффициент момента гидромотора:
Kг 
M гн 3
,м ;
pг
(28)
Qн 3
, м /с ;
nм
(29)
рабочий объем гидромотора:
qг 
теоретическую производительность насоса:
Qнт 
Qн
он
, м3 /с ;
(30)
утечки в насосе:
Qн  Qнт  1  он , м3 /с ;
(31)
утечки в гидромоторе:
Qг  Qг  1  ог , м3 /с .
(32)
Коэффициенты утечек насоса Qн и гидромотора Qг:
aн 
Qн
Qг 5
; aг 
, м /Н  с .
pн
pг
(33)
Общий коэффициент утечек:
a  aн  aг , м5 /Н  с .
(34)
Уравнение механической характеристики для гидропривода с регулируемым насосом и нерегулируемым гидромотором имеет вид
nг 
Qнт   н a  M c

, об/с .
qг
K г  qг
(35)
Уравнение механической характеристики для гидропривода с регулируемым гидромотором и нерегулируемым насосом имеет вид
nг 
a  Mc
Qнт

, об/с .
qг   г K г  qг   г
(36)
Уравнение механической характеристики для гидропривода с регулируемым насосом и регулируемым гидромотором имеет вид
nг 
a  Mc
Qнт   н

, об/с .
qг   г
K г  qг   г
67
(37)
Минимальный параметр регулирования насоса:
 н мин 
a  Mc
.
K г  Qнт
(38)
Коэффициент диапазона регулирования:
K рег 
1
 н мин
.
(39)
Минимальная частота вращения вала гидромотора:
nг мин  nг 
1
, об/с .
К рег
(40)
Максимальная частота вращения nг макс достигается при максимальном расходе и ограничивается конструктивными особенностями гидродвигателя.
Минимальная частота вращения при номинальной нагрузке может
достигать 0,67–0,75 об/с для гидросистем с замкнутой циркуляцией
жидкости и 0,05–0,067 об/с для гидросистем с разомкнутой циркуляцией жидкости.
Подставляя величину момента в формулы (35–37) в пределах от
нуля до заданного значения, получим зависимость частоты вращения в
функции момента нагрузки при различных параметрах регулирования
насоса и гидромотора.
Примечание. При расчете коэффициента Кг момента гидромотора в
уравнение (28) значения моментов Мг и рг можно подставлять из технической характеристики гидромотора при номинальном расходе. Общий
вид характеристик гидроприводов с дроссельным и объемным регулированием показан на рис. 1 и 2.
Рис. 1
68
Рис. 2
Пример расчета механических характеристик гидропривода с дроссельным регулированием для гидропривода типа «насос – гидроцилиндр».
Исходные данные для расчета: площадь поршня Sп = 510-3 м2; производительность насоса Qн = 0,9210-3 м3/с при номинальном давлении
рн = 6,3 МПа; он = 0,86; нагрузка на штоке гидроцилиндра Rг = 20000 Н.
В качестве регулирующего элемента применен дроссель типа Г77-34 с
номинальной пропускной способностью Qдр = 1,1710-3 м3/с.
Потери давления в дросселе при номинальном расходе составляют
рдр = 0,3 МПа. Плотность рабочей жидкости  = 900 кг/м3, коэффициент расхода  = 0,7.
В ходе расчета необходимо определить:
1) максимальное проходное сечение дросселя по формуле (17):
1,17  10 3
S др 
0,7 
2
 0,3  10 6
900
 6,5  10 5 м 2 .
2) скорость штока в зависимости от нагрузки по формуле (18):
V
1
2 
Rг 
 0,7   др  6,5  10 5 
  6,3  10 6 

3
900 
5  10
5  10 -3 
 6,1  103   др  3,15  104  Rг ;
Подставляя в это выражение различные значения нагрузки при различных значениях параметра регулирования дросселя, получим графики
семейства зависимости V  f Rг  .
69
Расчетные данные для построения графика
№ п/п
Расчетное значение скорости поршня при нагрузке R, кН
др
0
4
8
12
16
20
24
28
31,5
1
1,0
1,06
1,01
0,936
0,85
0,76
0,65
0,53
0,36
0
2
0,8
0,84
0,81
0,75
0,68
0,61
0,52
0,42
0,29
0
3
0,6
0,63
0,61
0,56
0,51
0,46
0,39
0,32
0,22
0
4
0,4
0,42
0,40
0,38
0,34
0,30
0,26
0,21
0,14
0
5
0,2
0,21
0,20
0,19
0,17
0,15
0,13
0,11
0,072
0
3) утечки в гидроприводе по формуле (23):
Qн  0,92 103  1  0,86  0,128 103 м3/с ;
4) минимальное значение параметра регулирования дросселя по (24):
 др мин 
0,128  10 3
 0,139 ;
0,92  10 3
5) дапазон регулирования, выраженный коэффициентом, по (25):
1
K рег 
 7, 2 ;
0,139
6) минимальную скорость штока гидроцилидра по формуле (27):
1
Vмин  0,65 
 0,09 м/с.
7, 2
Здесь взята максимальная скорость при нагрузке Rг = 20000 Н и
др = 1,0 V = 0,65.
Пример расчета механических характеристик гидропривода с объемным регулированием.
Исходные данные: насос регулируемый Qн = 2,510-3 м3/с, nн =
1470 об/мин, рн = 10 МПа, он = 0,88; гидромотор нерегулируемый
Мгн = 140 Нм, рг = 10 МПа, nг = 6,67 oб/c, ог = 0,9.
Необходимо определить:
1) коэффициент момента гидромотора по формуле (28):
140
Kг 
 1,4  10 5 м3 ;
10  10 6
2) рабочий объем гидромотора по формуле (29):
qг 
2,5  10 3
 0,375  10 3 м 3 /об ;
6,67
70
3) теоретическую производительность насоса по формуле (30):
Qнт 
6,25  10 3
 2,84  10 3 м 3 /с ;
0,88
4) утечки в насосе по формуле (31):
Qн  2,84 103  1  0,88  0,34 103 м3 /с ;
5) утечки в гидромоторе по формуле (32):
Qг  2,5 103  1  0,9  0,25 103 м3 /с ;
6) коэффициент утечек насоса и гидромотора по формуле (33):
aн 
0,34  10 3
 3,4  10 11 м 5 / Н  с  ;
10  10 6
0,25  10 3
 2,5  10 11 м 5 / Н  с  ;
10  10 6
7) суммарный коэффициент утечек по формуле (34):
aг 
a  3,4  1011  2,5 1011  5,9 1011 м5 /Н  с ;
8) уравнение механической характеристики по формуле (35):
nг 
5,9  10 11  M c
2,84  10 3
 н 
, об/с
3
0,375  10
1,4  10 5  0,375  10 3
или
nг  7,85   н  1,12  102  M c , об/с ;
подставляя значения Мс в пределах от нуля до Мг, можно получить
для любого заданного значения параметра регулирования насоса зависимость:
nг  f M c  ;
9) минимальный параметр регулирования по формуле (38):
 н мин 
5,9  10 11  140
 0,208 ;
1,4  10 5  2,84  10 3
10) коэффициент диапазона регулирования по формуле (39):
1
K рег 
 4,81 ;
0,208
11) минимальную частоту вращения вала гидромотора по формуле (40):
1
nг мин  6,01 
 1,25 об/с .
4,81
71
Расчет трубопроводов
При расчете трубопроводов гидросистемы необходимо выбрать
марку жидкости. При этом следует учитывать тип принятого гидрооборудования и температурный режим работы гидросистемы.
В гидравлических системах, предназначенных для работы в стабильных температурных условиях, рекомендуются жидкости с вязкостью (20–40)10-6 м2/с при давлении до 10 МПа; (40–60)10-5 м2/с – при
давлении до 20 МПа и (110–175)10-5 м2/с – при давлении 50–60 МПа.
Расчет трубопроводов включает в себя расчет геометрических размеров и расчет потерь давления. Расчет потерь в трубопроводах и соединениях проводится после определения длины трубопроводов гидросистемы.
Рекомендуемые размеры стальных труб, параметры рукавов, нормализованная арматура и соединительные части трубопроводов и рукавов приведены в табл. П 2.7–П 2.9.
Расчет внутреннего диаметра трубы ведется прежде всего из условия обеспечения допустимой скорости потока:
d в 
4 Q
 .
 V
(41)
Во всасывающем трубопроводе допускаемая скорость потока V
равна 0,5–2 м/с. Большее значение принимается в тех случаях, когда
высота всасывания мала и нет приемного фильтра.
В напорной гидролинии допускаются скорости 3 м/с при давлении
20 МПа и 5 м/с при давлении 10 МПа. На отдельных коротких участках
длиною менее 100dв скорость потока допускается до 7–10 м/с.
Внутренний диаметр трубы, исходя из условия ламинарного потока
в трубе (Re < 2300), определяется по формуле
4
Q
 ,
2300   
а исходя из допустимых потерь давления (р) в трубах:
d в 
d в  4
128     L  Q
.


p
(42)
(43)
Потери давления выбираются в пределах менее 0,2 МПа, но не более 0,1ри. Из трех значений, определенных по формулам (41–43), выбирают большее.
При расчете трубопроводов по формуле (42) кинематическая вязкость берется при температуре 323 К, а в формуле (43) – при температуре 293 К.
72
Потери давления в системе трубопровода слагаются из потерь по
длине трубопровода рL и местных потерь (колена, расширения, сужения и т.п.) рм:
(44)
 p  pL   pм .
Потери давления во всех элементах гидропривода определяют после размещения гидрооборудования на машине, для которой проектируют гидропривод. В этом случае практически известна длина трубопровода L, число соединений и их виды. По табл. П 2.10 определяют
коэффициенты местных сопротивлений . Общие потери давления (потери в трубопроводе и соединительной арматуре) по длине трубопровода определяются по формуле
128    L
(45)
p 
 Q, Па ,
  d в4
где  – динамический коэффициент вязкости ( =  , Пас).
Суммарная длина трубопровода складывается из длины L гидросистемы и эквивалентной длины Lэкв:
(46)
L  L  Lэкв .
Эквивалентная длина трубопровода характеризует величину местных потерь и определяется по формуле
Re
,
(47)
Lэка    d в 
64
где Re – критерий Рейнольдса:
V  dв
.
(48)
Re =


Пример расчета трубопровода.
Задано: расход в системе Q = 1,6710-3 м3/с; рабочее давление
рн = 10 МПа; масло "Индустриальное–30"; трубопровод имеет длину
L = 6 м, 6 соединительных штуцеров, 2 переходника, 4 поворота под
прямым углом и 1 соединение с резервуаром.
Определяем:
1) внутренний диаметр трубы при V = 5 м/с по формуле (41):
4  1,67  10 3
 0,021 м ;
 5
2) по табл. П 2–1 коэффициент кинематической вязкости масла
"Индустриальное–30": при Т = 323 K,  = 3,010-5 м2/с, при Т = 29З К,
 = 2010-5 м2/с;
3) внутренний диаметр трубы исходя из условия ламинарного потока в трубе по формуле (42):
d в 
d в 
4
1,67  10 3

 0,033 м ;
2300   3,0  10 5
73
4) внутренний диаметр трубы исходя из допустимых потерь меньше 0,2 МПа по формуле (43):
d в  4
128  900  20  10 5  6  1,67  10 3
 0,027 м .
  0,2  10 6
По таблицам П 2.7–П 2.9 находим, что ближайший больший внутренний диаметр dв = 0,034 м (34 мм) при толщине стенок 4 мм. Наружный диаметр трубы 42 мм.
5) критерий Рейнольдса по формуле (48):
Re =
1,84  0,034
 2085  2300 ,
3  10 5
где
V
4Q
4  1,67  10 3

 1,84 м/с ;
  d в2 3,14  0,034 2
6) суммарную величину коэффициентов местных сопротивлений
(см. табл. П 2.10):
   6  0,15  2  0,15  4 1,5  1  8,2 ;
7) эквивалентную длину трубопровода по формуле (47):
2085
 9м;
64
8) суммарную длину трубопровода по формуле (46):
Lэкв  8,2  0,034 
L  6  9  15 м ;
9) потери давления в трубопроводе по формуле (45):
p 
150  0,027  15
 1,67  10 3  24200 Па = 0,024 МПа ,
3,14  0,034 4
где      900  3 105  0,027, Па  с .
Гидродинамические передачи
Гидродинамической передачей называют машину, обеспечивающую передачу мощности с ведущего вала на ведомый без жестких связей за счет взаимодействия лопастных систем с рабочей жидкостью.
Этот тип передач используют с целью согласования работы двигателя,
рассчитанного на работу в определенном режиме, при котором его экономические показатели оптимальны, с исполнительным механизмом,
работающим при переменных нагрузках.
74
КПД гидропередачи:

N 2 M 2  n2

 k  i,
N1
M 1  n1
где N2 и N1 – мощности на выходном и входном валах гидропередачи,
соответственно; M2 и M1 – моменты на выходном и входном валах
гидропередачи; n2 и n1 – частота вращения ведомого и ведущего валов;
k  M 2 M1 – коэффициент трансформации крутящего момента;
i  n2 n1 – передаточное отношение.
В установившемся режиме работы условие равновесия может быть
представлено в следующем виде:
M1  M 2  M 3  0,
где M3 – момент, воспринимаемый внешними опорами.
В случае, если в гидропередаче отсутствует внешняя опора (М3=0),
ее называют гидромуфтой. Для гидромуфты справедливы следующие
соотношения:
M1  M 2 , k  1,   i.
Гидротрансформатор – это гидропередача, в которой с целью
трансформации (изменения) крутящего момента установлены внешние
опоры, способные воспринимать некоторую его долю.
Гидромуфта состоит из центробежного насоса (н) и центростремительной турбины (т) с предельно сближенными лопастными системами.
Интенсивность циркуляции жидкости в ней и, следовательно, величина
передаваемого момента определяются скольжением, которое вычисляют
по формуле
n  nт
s н
.
nн
Максимальный момент гидромуфта развивает в момент включения,
т.е. при nт = 0.
КПД гидромуфты и его связь со скольжением описывают следующими зависимостями:
  i, s  1  .
При проектировании гидромуфт используют обобщенные характеристики, полученные при исследовании моделей и уравнения мощности
и момента, найденные на основании теории подобия, а именно
N  NГ    n3  D5 , M  MГ    n2  D5 ,
где NГ – коэффициент мощности ( NГ  N (   n3  D5 ) );
MГ – коэффициент момента ( MГ  M (   n2  D5 ) ).
75
Внешней характеристикой гидромуфты называют зависимость крутящего момента, мощности и КПД от числа оборотов турбинного (ведомого) вала при постоянном числе оборотов вала насосного колеса
(ведущего вала).
Приведенной характеристикой называют зависимость коэффициента момента от скольжения, либо передаточного отношения.
Для построения графика совместной работы двигателя и гидромуфты необходимо располагать внешней характеристикой двигателя –
Mдв = f(nдв) и приведенной характеристикой гидромуфты.
Поскольку насосный вал гидромуфты жестко связан с валом двигателя, то nн = nдв.
Задаются значением передаточного отношения i и по приведенной
характеристике муфты находят соответствующее значение коэффициента момента MГ. Используя уравнение момента, строят кривую моментов насосного колеса от его оборотов – M = f(nн). Точка пересечения
этой кривой с характеристикой двигателя представляет собой точку
совместной работы. Построения повторяют для различных значений
передаточных отношений.
Гидромуфту можно считать приспособленной к двигателю, если
соблюдаются два условия:
 оптимальный режим (i = 0,97) муфты совпадает с оптимальным
режимом двигателя;
 при остановке турбинного вала из-за перегрузки двигатель развивает максимальный момент.
Задачи
Задача 1. Пользуясь характеристикой гидромуфты, определить
расчетный и максимальный моменты, передаваемые ею, а также передаточное отношение, коэффициент полезного действия и скольжение при
этих режимах, если активный диаметр гидромуфты D, частота вращения
ведущего вала n1, рабочая жидкость – трансформаторное масло. Как
изменятся передаваемый крутящий момент и мощность, если частоту
вращения ведущего вала увеличить в полтора раза?
Характеристика гидромуфты
i = n2/n1
0
0,2
0,4
0,6
0,8
0,9
1,0
110
60
56,5
51
43
32
24
0
7
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
D, мм
440
420
500
450
440
430
420
460
480
500
n1, об/мин
1500 2000 1500 1200 2200 1800 1400 1000 1300 1600
76
Задача 2. Пользуясь характеристикой, приведенной в задаче 7,
определить активный диаметр и построить внешнюю (моментную)
характеристику гидромуфты, предназначенной для работы с асинхронным электродвигателем, развивающим максимальный крутящий
момент Mдмакс при частоте вращения nд. Рабочая жидкость – минеральное масло.
Указание. Активный диаметр может быть определен по уравнению
моментов совмещением режимов гидромуфты при i = 0 и электродвигателя при М дмакс.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
М дмакс, Нм
300
350
250
400
300
350
250
400
270
280
nд, об/мин
2200 1100 1100 2200 1100 2200 2200 2200 1100 2200
Определение основных параметров гидротрансформатора
Определение основных параметров гидротрансформатора заключается в выборе типа, определении активного диаметра, проверке возможности совместной работы его с двигателем.
Расчет гидротрансформатора производят в следующем порядке:
1) подбирают прототип по существующим наиболее подходящим
внешним или безразмерным характеристикам;
2) производят построение безразмерной характеристики гидротрансформатора по внешней характеристике прототипа (если безразмерная характеристика прототипа отсутствует);
3) определяют активный диаметр проектируемого гидротрансформатора;
4) строят характеристику совместной работы гидротрансформатора
с двигателем и производят ее анализ;
5) строят выходную характеристику гидротрансформатора.
При выборе типа гидротрансформатора для установки на тяговую
машину необходимо исходить из типа двигателя, установленного на
машине, назначения машины и требуемых запасов мощности.
Гидротрансформатор с прозрачной характеристикой дает возможность получить при одной и той же частоте вращения коленчатого вала
двигателя большую, по сравнению с гидротрансформатором с непрозрачной характеристикой, частоту вращения турбинного колеса, а в месте с этим и большую скорость движения машины. При трогании машины с места с двигателя снимается больший крутящий момент, а при разгоне – увеличение частоты вращения двигателя позволяет получить
большие скорости движения машины. Гидротрансформаторы с боль77
шим коэффициентом прозрачности иногда называют транспортными и
устанавливают их на машинах, работающих длительное время в транспортном режиме.
На автомобилях, особенно с карбюраторными двигателями, чаще
всего находят применение гидротрансформаторы с прозрачной характеристикой. Коэффициент прозрачности у одноступенчатых гидротрансформаторов, установленных на автомобилях с карбюраторными двигателями, находится в пределах 1,5–2,0.
Гидротрансформаторы с непрозрачной характеристикой или с малой прозрачностью (П = 1,1–1,3) устанавливают на тяжелых грузовых и
лесовозных автомобилях, тракторах и дорожных машинах.
На грузовых автомобилях, тракторах и тягачах устанавливают гидротрансформаторы с коэффициентом трансформации 2,5–4,0.
На легковых автомобилях применяют гидротрансформаторы с коэффициентом трансформации 2–2,5 при высоком значении КПД в области больших величин передаточных отношений.
Для расширения рабочего участка внешней характеристики гидротрансформатора за счет повышения КПД в диапазоне, расположенном
правее точки k = 1 (Мт = Мн), применяют комплексные гидротрансформаторы с одним или двумя реактивными колесами.
На основании выбранного типа гидротрансформатора строится соответствующая безразмерная его характеристика.
При отсутствии безразмерной характеристики гидротрансформатора она может быть построена по данным пересчета внешней характеристики, полученной экспериментальным путем. Для пересчета значений
внешней характеристики необходимо знать активный диаметр выбранного гидротрансформатора и плотность рабочей жидкости.
Коэффициенты моментов насосного и турбинного колес рассчитывают по формуле
MГ  M (   n2  D5 )
для 5–7 значений моментов на насосном и турбинном колесах Мн и Мт,
находящихся в пределах от минимального до максимального их значений, для задаваемых величин частоты вращения турбинного колеса nт.
Эти же значения частоты вращения турбинного колеса используют для
нахождения соответствующих значений передаточных отношений. По
полученным расчетным данным и строят безразмерную характеристику.
Определение активного диаметра гидротрансформатора
Для вновь проектируемого гидротрансформатора активный диаметр рассчитывают по формуле


Da  5 M н н    nн2 .
78
В данном случае величину коэффициента момента насосного колеса определяют по безразмерной характеристике для случая максимального значения КПД.
Из формулы видно, что изменяя в определенных пределах значения
параметров Мн, н,  либо nн можно получить различные значения активного диаметра.
Изменение Мн и nн можно осуществить за счет установки редуктора
между двигателем и гидротрансформатором. Гидротрансформаторы с
одинаковым активным диаметром могут иметь различные коэффициенты момента н вследствие различных углов входа и выхода лопаток рабочего колеса.
Для более полного использования мощности двигателя при его работе с некомплексным гидротрансформатором обычно крутящий момент Ме и частоту вращения двигателя nе принимают соответствующими максимальной мощности двигателя, а значение величины коэффициента момента н – значению, соответствующему максимальному КПД
гидротрансформатора.
В том случае, когда проектирование гидротрансформатора осуществляется методом подобия и даны параметры исходного гидротрансформатора (Dмод, nмод, Ммод), то определение активного диаметра производится по формуле
Da  Dмод  5
2
M н  nмод
,
M мод  nн2
где Da – активный диаметр проектируемого гидротрансформатора, м;
Dмод – активный диаметр исходного гидротрансформатора (модели), м;
Мн – момент на насосном колесе проектируемого гидротрансформатора, Нм; Ммод – момент на насосном колесе исходного гидротрансформатора, Нм; nн – частота вращения насосного колеса проектируемого
гидротрансформатора, с-1; nмод – частота вращения насосного колеса
исходного гидротрансформатора, с-1.
Проверка возможности совместной работы
гидротрансформатора с двигателем
Совместная работа двигателя с гидротрансформатором должна
обеспечить:
1) использование номинальной мощности двигателя;
2) наилучшее использование приспособляемости двигателя;
3) возможность длительного движения машины в тяжелых условиях без перегрева рабочей жидкости в гидропередаче;
4) работу двигателя по возможности на экономичных режимах расхода топлива.
79
Для исследования совместной работы гидротрансформатора с двигателем строят характеристику их совместной работы.
Характеристика совместной работы двигателя с гидротрансформатором представляет собой кривые крутящего момента двигателя Ме,
крутящего момента на насосном колесе Мн при различных изменениях
передаточных отношений i в зависимости от частоты вращения насосного колеса. Для ее построения необходимо иметь внешнюю скоростную характеристику двигателя и безразмерную характеристику гидротрансформатора. Затем необходимо построить нагрузочную характеристику гидротрансформатора, которая показывает изменение крутящего
момента на насосном колесе при различных значениях передаточного
отношения в зависимости от его частоты вращения.
Для построения нагрузочной характеристики гидротрансформатора
определяют значения моментов на насосном колесе для различных передаточных отношений по формуле
M н  н    nн2  Da5 .
Значения коэффициентов момента берут из безразмерной характеристики гидротрансформатора выбранного типа для различных величин передаточных отношений. Полученные расчетные данные сводят в таблицу, с помощью которой строят нагрузочную характеристику (см. рис. 1).
i
н
Значения моментов для различной частоты вращения
nн1
nн2
nн3
...
nнi
0
н0
Мн1(i=0)
Мн2(i=0)
Мн3(i=0)
...
Мнi(i=0)
0,1
н1
Мн1(i=0,1)
Мн2(i=0,1)
Мн3(i=0,1)
...
Мнi(i=0,1)
0,2
н2
Мн1(i=0,2)
Мн2(i=0,2)
Мн3(i=0,2)
...
Мнi(i=0,2)
0,3
н3
Мн1(i=0,3)
Мн2(i=0,3)
Мн3(i=0,3)
...
Мнi(i=0,3)
и т.д.

После этого на кривые изменения момента нагрузочной характеристики гидротрансформатора наносят кривую скоростной характеристики двигателя, выполненную в том же масштабе (рис. 2), и проводят анализ полученной характеристики совместной работы.
Точки пересечения парабол M н  f (nн ) с кривой крутящего момента двигателя M e  f (ne ) и характеризуют режим совместной работы
гидротрансформатора с двигателем. Полученные точки должны распо80
лагаться в пределах рабочего диапазона двигателя, т.е. в пределах работы двигателя с частотой вращения nM max и nN max, соответствующей максимальному значению крутящего момента Me max и максимальной мощности двигателя Ne max.
Рис. 1. Нагрузочная
характеристика прозрачного
гидротрансформатора
Рис. 2. Характеристика
совместной работы двигателя
с гидротрансформатором
Из характеристики совместной работы двигателя с гидротрансформатором видно, что при трогании машины с места передаточное отношение равно нулю (i = 0) и двигатель работает на режиме, близком к
режиму Me max, а гидротрансформатор – на режиме максимального значения коэффициента трансформации момента К. Этим обеспечивается
максимальное значение момента на турбинном колесе и, следовательно,
высокая интенсивность разгона машины. По мере увеличения скорости
движения машины точка совместной работы перемещается вправо и
гидротрансформатор начинает работать в зоне характеристики, близкой
к Ne max, nNe max и max. Скорость движения машины при этом достигает
максимального значения. Из рассмотренного анализа видно, что полученная характеристика совместной работы двигателя с гидротрансформатором удовлетворяет требованиям, предъявляемым к динамическим
качествам тяговой машины.
В случае получения характеристики совместной работы двигателя с
гидротрансформатором со смещенным расположением пучка парабол
вправо или влево от оптимального диапазона частоты вращения двигателя необходимо внести соответствующие коррективы.
Изменяя активный диаметр гидротрансформатора и частоту вращения насосного колеса, можно осуществить смещение пучка парабол вправо или влево и тем самым улучшить характеристику совместной работы.
Изменение частоты вращения насосного колеса при расчетной мощности
или момента двигателя осуществляется установкой редуктора между двигателем и гидротрансформатором с передаточным числом ip.
81
Увеличение активного диаметра гидротрансформатора и уменьшение передаточного числа редуктора приводит к смещению пучка парабол влево и, наоборот, уменьшение активного диаметра и увеличение
передаточного числа редуктора приводит к смещению пучка парабол
вправо.
Анализ характеристики совместной работы двигателя с непрозрачным гидротрансформатором осуществляется в той же последовательности, но вместо пучка парабол на характеристике будет всего одна парабола с единственной точкой совместной работы двигателя с гидротрансформатором. Положение этой точки также зависит от величины активного диаметра и передаточного отношения редуктора. Режим совместной
работы для таких гидротрансформаторов выбирается в зоне максимальной эффективной мощности Ne max или в зоне минимального удельного
расхода топлива. Возможно и компромиссное решение, когда за счет незначительного снижения мощности повышают экономичность.
Построение выходной характеристики гидротрансформатора
Выходная характеристика гидротрансформатора представляет собой кривые изменения крутящего момента на валу турбины и КПД гидротрансформатора в зависимости от частоты вращения турбинного колеса. Зная изменение крутящих моментов на турбинном колесе в зависимости от частоты его вращения можно построить тяговую или динамическую характеристику машины.
Для построения выходной характеристики гидротрансформатора
необходимо воспользоваться построенной характеристикой совместной
работы двигателя с гидротрансформатором и безразмерной характеристикой гидротрансформатора выбранного типа.
При расчете следует иметь в виду, что
nн  ne i p и M н  M e  i p   p ,
где ip – передаточное число редуктора; p– механический КПД редуктора.
Для построения выходной характеристики составляют таблицу, в
которую заносят необходимые данные, получаемые из безразмерной
характеристики и характеристики совместной работы двигателя с гидротрансформатором, а также данные, полученные расчетным путем.
i
0
0,1
0,2
nн
nт
К
Мн
Мт

82
0,3
...
0,9
Заполнение граф таблицы осуществляют следующим образом. Значения коэффициентов трансформации К и КПД гидротрансформатора в
зависимости от передаточного отношения гидротрансформатора i берут
из его безразмерной характеристики. Значение частоты вращения nн и
крутящего момента Мн для различных значений передаточных отношений i берут непосредственно из характеристики совместной работы двигателя с гидротрансформатором. Точки пересечения парабол, характеризующие изменение крутящего момента Мн в зависимости от частоты
вращения вала насоса для заданных передаточных отношений i, с кривой изменения крутящего момента двигателя определяют оптимальные
значения nн и Мн.
После этого определяют расчетным путем частоту вращения
турбинного колеса и величину момента на турбинном колесе при
различных значениях передаточного отношения гидротрансформатора по формулам
nт  nн  i и M т  K  M н .
По данным таблицы строят выходную характеристику гидротрансформатора (рис. 3).
83
Рис. 3. Выходная характеристика
гидротрансформатора
ЧАСТЬ 3. ГАЗОВАЯ ДИНАМИКА
Основные газодинамические понятия и зависимости
Основными параметрами, отражающими состояние газа, являются
абсолютное давление p, Па; абсолютная температура T, К и плотность
, кг/м3. При нормальном атмосферном давлении на уровне моря
(1,013105 Па) и температуре 288 К плотность воздуха равна 1,23 кг/м3.
Давление, плотность и температура газа связаны между собой
уравнением состояния, которое для идеального газа имеет вид
p  R    T,
где R – газовая постоянная (для воздуха R = 287,1 Дж/(кгК)).
При отсутствии теплообмена с окружающей средой и необратимых
потерь механической энергии между параметрами газа существует соотношение, которое называют уравнением изоэнтропической адиабаты:
p  c  k ,
где с – постоянная, которая определяется по параметрам начального
состояния газа, k  c p cv – показатель изоэнтропической адиабаты,
ср – изобарная теплоемкость, Дж/(кг К); сv – изохорная теплоемкость,
Дж/(кгК). Для одноатомных газов показатель адиабаты равен 1,66;
для двухатомных, к которым относят и воздух, – 1,4; для многоатомных – 1,33.
Связь между основными параметрами в различных точках рассматриваемого процесса определяется следующими уравнениями:
k
p   
  ;
po   o 
k
p  T  k 1
  ;
po  To 
1
  T  k 1
  .
 o  To 
Характеристикой энергетического состояния газа является скорость
звука в нем. Под скоростью звука в газовой динамике понимают скорость распространения в газе слабых возмущений, и она может быть
вычислена по формуле
a
kp

 k  R T .
Зависимость скорости звука от высоты над уровнем моря в свободной атмосфере может быть определена по “стандартной атмосфере”
(см. табл. П 3.1).
84
Важнейшим газодинамическим параметром является число Маха –
отношение скорости движения газа к местной скорости звука в нем:
M
V
.
a
Конусом Маха (линией Маха в плоском течении) называют огибающую поверхность звуковых сферических волн. Угол наклона элемента
линии Маха  по отношению к вектору скорости потока в данной точке
называют углом Маха. Между углом Маха и числом Маха существует
следующее соотношение:
sin  
1
.
M
Параметры потока, соответствующие числу Маха, равному единице,
называют критическими и обозначают "*": a*, p*, *, T *, i * . Параметры неподвижного газа (заторможенного потока) обозначают индексом "о": Tо, pо, о, io.
При расчете одномерных адиабатических течений идеального газа
главную роль играет уравнение сохранения энергии (уравнение Бернулли):
V2
 i  io ,
2
где i – энтальпия газа, Дж/кг,
i
a2
k
p k  R T
.

 
k 1 k 1 
k 1
Уравнение энергии применяют в одной из следующих форм:
   
T
k 1 2
 1
 ;
To
k 1
k
p  k  1 2  k 1
   
 1 
  ;
po  k  1

1
  k  1 2  k 1
   
 1 
  ,
o  k  1 
где   V a – коэффициент скорости; (), () и ()
ческие функции (значения их приведены в табл. П 3.2).
85
– газодинами-
Коэффициент скорости и число Маха связаны между собой уравнениями
k 1
M2
2
 
;
k 1
2
1
M
2
2
2
M2 

.
k  1 1  k  1  2
k 1
2
Задачи
Задача 1. Определить газодинамические функции потока воздуха,
движущегося со скоростью V из бака, температура в котором Tо, давление – ро.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
V, м/с
200
300
400
500
200
300
400
500
200
500
Tо, К
300
350
400
300
350
400
300
350
400
300
ро, МПа
0,2
0,3
0,4
0,5
0,6
0,2
0,3
0,4
0,5
0,6
Задача 2. На высоте H самолет достиг скорости V. Какая это скорость, дозвуковая или сверхзвуковая?
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
Н, км
1
2
3
4
5
6
7
8
9
10
V, м/с
300
300
300
300
300
400
400
400
400
400
Задача 3. До и после изоэнтропического сжатия в некотором объеме воздуха произведены измерения скорости звука. Определить порядок
изменения плотности воздуха, если скорость звука возросла на х %.
Варианты
Величина
x,%
1
2
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
11
12
86
Задача 4. Звук работы двигателя зарегистрирован через с после
пролета самолета над пунктом регистрации. Определить скорость пролета, если высота H.
Варианты
Величина
, с
км
1
2
3
4
5
6
7
8
9
10
2,0
2,0
2,0
2,5
2,5
2,5
3,0
3,0
3,0
3,0
1
2
3
1
2
3
4
5
3
6
Задача 5. Определить максимальную скорость воздуха, при которой его можно рассматривать как несжимаемую жидкость, если допустимо пренебрегать изменениями плотности до x %. Параметры торможения – стандартные на уровне моря.
Варианты
Величина
x, %
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
1
2
3
4
5
Одномерное изоэнтропическое течение газа
Уравнение сохранения энергии может быть представлено в следующих формах:
V12
k
p V2
k
p

 1  2 
 2  const;
2 k  1 1
2 k  1 2
V12
k
V2
k

 R  T1  2 
 R  T2  const;
2 k 1
2 k 1
V12
a
V2
a
 1  2  2  const.
2 k 1 2 k 1
Связь между параметрами движущегося и заторможенного газа
осуществляется с помощью уравнений:
ao2
k 1
 1
M2 ;
2
a2
To
k 1
 1
M2 ;
T
2
87
1
o  k  1
 k 1
 1 
M2 ;
 
2

k
po  k  1
 k 1
 1 
M2 .
p 
2

Скорость газа, равную местной скорости звука, называют критической. Параметры потока в точках, где движение происходит с критической скоростью, также называют критическими.
Критические параметры могут быть определены через параметры
торможения, если учесть, что при V  a * M  1 :
1
a*

ao
k
 *  2  k 1

 ;
o  k  1 
2
T*
2
;

;
k  1 To
k 1
p *  2  k 1

 .
po  k  1 
Уравнение сохранения энергии применяют для определения параметров движущегося газа в различных сечениях. При истечении из бака,
внутри которого параметры газа равны р0, T0, a0, 0 скорость истечения
рассчитывают по формуле
k 1


2  k po   p  k 

 1  
.
k  1  o   po  


V
Максимальная скорость, которая может быть получена лишь при
истечении через сопло Лаваля, имеющего как сужающийся, так и расширяющийся участки, при противодавлении р, равном нулю, определяется по выражению
Vmax 
2  ao2
.
k 1
Задачи
Задача 1. В потоке воздуха без ударных волн махметр показывает в
одной точке угол Маха 1, в другой – 2. Каково соотношение между
статическими давлениями в этих точках?
Варианты
Величина
1
2
3
4
5
6
7
8
9
10

27,7
27,7
27,7
20
20
20
30
30
30
30

35
40
50
35
40
50
35
40
45
50
88
Задача 2. Какие параметры (p, t) должен иметь воздух в форкамере
сверхзвуковой трубы, чтобы при расчетном расширении он вытекал в
атмосферу со скоростью Vм/с при температуре –70˚С? Каково при
этом будет соотношение между плотностью воздуха в струе и плотностью воздуха при нормальных условиях?
Варианты
Величина
Vм/с
1
2
3
4
5
6
7
8
9
10
800
900
1000
950
850
750
700
650
600
1200
Задача 3. По теневому фотоснимку обтекания иглы сверхзвуковым
потоком воздуха измерен угол  между поверхностью слабой конической
волны и направлением невозмущенного потока. Термопара, открытая
навстречу потоку, показывает температуру Tо. Найти скорость потока.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
о
15
20
25
30
15
20
25
30
15
20
TоК
289
300
310
320
330
300
310
320
330
340
Задача 4. Найти скорость звука, критерий Маха, коэффициент скорости  и значение газодинамической функции  для струи воздуха, вытекающей из баллона со скоростью, равной половине максимальной
теоретической скорости истечения. Температура в баллоне Tо.
Варианты
Величина
TоК
1
2
3
4
5
6
400
500
600
700
800
900
7
8
9
10
1000 1100 1200 1300
Задача 5. Какую максимальную скорость воздуха можно получить
в сверхзвуковой трубе без подогрева, если учесть, что воздух сжижается при температуре T = 78 K, а истекает из баллона, температура в
котором Tо.
Варианты
Величина
TоК
1
2
3
4
5
6
7
8
9
10
293
300
320
340
360
380
400
420
440
460
89
Определение расхода газа через сопло
Практически важным примером движения газа, которое с хорошим
приближением можно считать одномерным и изоэнтропическим, является его истечение из резервуара через сопло, когда давление на его срезе равно давлению во внешней среде, внутри сопла нет скачков уплотнения и в минимальном сечении скорость газа равна скорости звука.
При подсчете секундного расхода газа через сопло удобно пользоваться
приведенным секундным расходом q:
q
 V
S*

,
 * a * S
где S* – площадь критического сечения сопла; S – площадь сечения, в
котором достигается скорость V.
Приведенный секундный расход является функцией числа Маха
(либо коэффициента скорости) и определяется по формулам
k 1
k 1

 k  1  2k 1
 k 1
 2k 1
qM   
 M  1 
M2

2
 2 


или
1
1
 k  1  k 1
 k  1 2  k 1
q   
  .
    1 
 2 
 k 1

Значения q(M) и q() приведены в табл. П 3.2.
Приведенный секундный расход можно также выразить через отношение давлений :
1
 k  1  k 1 k  1
q   
  k 
 
k 1
 2 
2
k 1
k
.
(1)
При истечении газа через сужающееся (конфузорное) сопло в случае, когда pa po  p * po , секундный весовой расход рассчитывают по
формуле
Gt  BG 
p 
 S  q a  ,
To
 po 
po
(2)
а когда pa po  p * po – по формуле
Gt  BG 
90
po
To
S .
(3)
Здесь ра – давление во внешней среде, Па; S – площадь выходного
сечения сопла, м2; постоянная BG  k  2 k  1k 1 k 1 R ; k – показатель адиабаты; R – газовая постоянная, Дж/(кг К). Для воздуха k = 1,4;
R = 287 Дж/(кг К); BG = 0,0405, сК1/2/м.
Эти формулы можно использовать и при расчете расхода газа через
сопло Лаваля. В этом случае S = Sвых (Sвых – площадь выходного сечения
сопла). Далее по дозвуковой части табл. П 3.2 определяют безразмерное
давление 1д, соответствующее величине Sмин Sвых данного сопла.
Если pa po   1д , то в формулу (2) необходимо подставить значение q  Sмин Sвых . Это равносильно применению формулы (3), в которой
S = Sмин. Данное условие означает, что в горле сопла скорость звуковая.
В случае, когда pa po   1д , величина q в формуле (2) должна
определяться не соотношением площадей S мин S вых , а рассчитываться
по формуле (1) в соответствии со значением   pa po .
В некоторых задачах весовой секундный расход вычисляют по
формуле
p
Gt  BG 
 S  y   ,
To
где y   q     – газодинамическая функция.
Скорость дозвукового потока определяют по уравнению
k 1
2  k  R  To
 1 k .
k 1
По данному уравнению можно рассчитать и скорость сверхзвукового потока газа, если известно изоэнтропическое давление торможения
сверхзвукового потока (например, давление в резервуаре, из которого
происходит истечение).
V
Задачи
Задача 1. Воздух истекает из баллона в атмосферу через конфузорное
сопло с диаметром выходного сечения d. Давление газа в баллоне ро и
температура – Tо. Найти массовый секундный расход воздуха через сопло.
Варианты
Величина
d, м
1
2
3
4
5
6
7
8
9
10
0,03
0,04
0,05
0,06
0,07
0,03
0,04
0,05
0,06
0,07
ро, ата
10
15
20
25
10
15
20
25
10
15
Tо, K
400
450
500
400
450
500
400
450
500
400
91
Задача 2. Найти площади входного и выходного сечений S1 и S2 дозвукового диффузора ВРД для полета при числе 1 на высоте H, если
максимальный секундный расход воздуха через диффузор Gt равен
200 кг/с; на выходе из диффузора 2 не должна превышать величины,
указанной в таблице. Потерями полного давления можно пренебречь.
Определить р1 и р2.
Варианты
Величина
1
км
2
1
2
3
4
5
6
7
8
9
10
0,8
0,7
0,6
0,5
0,9
0,8
0,7
0,6
0,7
0,6
2
3
4
5
2
3
4
5
2
3
0,2
0,15
0,1
0,1
0,3
0,2
0,15
0,1
0,15
0,2
Задача 3. Подобрать площадь критического сечения сверхзвукового сопла, обеспечивающую секундный расход воздуха Gt, если истечение расчетное, давление торможения ро = 5 ати, а температура торможения Tо = 288 К.
Варианты
Величина
Gt, кг/с
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
1
2
3
4
5
Задача 4. Задано соотношение площадей выходного и минимального сечений сопла S1/Sмин. При
каких соотношениях давлений рa/ро можно применить для расчета массового секундного расхода
воздуха через сопло формулу
Gt  0,0405 
To
 S мин ?
Варианты
Величина
S1/Sмин
po
1
2
3
4
5
6
7
8
9
10
2
3
4
2
3
4
2
3
4
2
Задача 5. В сечении 1 дозвуковой части идеального сопла Лаваля
известны: давление в потоке р1, температура торможения Tо1, приведен92
ная скорость 1. Требуется определить приведенную скорость 2 и давление воздуха в сечении 2, где T2 задана.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
р1
16
20
15
20
25
15
20
25
15
16
Tо1, K
400
450
500
400
450
500
400
450
600
500
1
0,6
0,7
0,5
0,6
0,7
0,8
0,5
0,6
0,7
0,6
T2, K
273
300
310
280
300
310
320
340
350
360
10-5, Па
Прямые скачки уплотнения
Торможение плоского сверхзвукового потока газа происходит посредством скачков уплотнения. Торможение на скачке является адиабатическим, но неизоэнтропическим процессом. На скачке скорость (V),
число Маха (M), коэффициент скорости ()  уменьшаются, а плотность (), абсолютное давление (р) и абсолютная температура (T)  увеличиваются.
Из параметров торможения не претерпевает разрыва на скачках
температура торможения (Tо) и связанные с нею Vmax, ао, а*, iо,
ро/оДавление торможения и плотность торможения уменьшаются на
скачках. Величина   po 2 po1   o 2  o1  коэффициент восстановления
полного давления, характеризует необратимые потери механической
энергии на скачке (индексом “1” отмечены параметры потока до скачка,
а индексом “2” – после скачка).
При переходе через прямой скачок направление потока газа не изменяется.
Основное соотношение, используемое при расчете изменений скорости в прямом скачке, имеет вид
V1  V2  a *2 или 1  2  1 .
Давления и плотности до и после скачка связаны зависимостью
k  1 p1

2
k  1 p2
.

1 k  1  p1  1
k  1 p2
93
Для чисел Маха имеем:
k 1
 M 12
2
.
M 
k 1
k  M 12 
2
Коэффициент восстановления давления торможения  определяется по числу Маха до скачка M1 на основании следующей зависимости:
1
2
2

2
k  1
 


2
k
 1


k

1

M
1


k
k 1
k 1
 2k

 M 12 

k

1
k
1


1
k 1
,
а при использовании в качестве аргумента коэффициента скорости 1
формула примет вид
1

k  1 2  k 1
 1 
1
 .
  12   k  1
1  k  1  1 
 k  1 12 
Коэффициент восстановления давления торможения может быть
найден и с помощью приведенного секундного расхода q():
 1 
q 

q1 
q1 
 

  2.

q2 
q

1
2
q 
 1 
Статические давления и плотности на скачке подчиняются соотношениям
p2 2  k
k 1

 M12 
,
p1 k  1
k 1
k 1
 M1
2
2

.
1 1  k  1  M 2
1
2
2
Отношение давления торможения после скачка к статическому
давлению до скачка определяют по формуле Релея:
k
po 2  k  1
k 1
 k 1  2  k

 M 12   
 M 12 

p1  2
k 1

 k 1
94

1
k 1
.
Формулу Релея применяют при расчете скорости сверхзвукового
потока. Соотношения между параметрами воздуха на прямом скачке
приведены в табл. П 3.3.
Задачи
Задача 1. Сравнить увеличение плотности:
 при ударном сжатии воздуха;
 при изоэнтропическом сжатии воздуха,
если в том и другом случаях давление возрастает в N раз. Объяснить
отличия результатов.
Варианты
Величина
N
1
2
3
4
5
6
7
8
9
10
5
10
15
15
10
5
5
10
15
20
Задача 2. Температура воздуха в форкамере сверхзвуковой трубы
Tо. Поток на срезе сопла трубы имеет скорость V1 и обтекает преграду с
образованием прямого скачка. Найти скорость воздуха после скачка V2.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
Tо, K
288
300
350
400
450
500
550
600
550
600
V1, м/с
530
550
600
550
600
500
550
600
650
700
Задача 3. Скорость воздуха, измеренная после прямого скачка V2. Термопара, размещенная в кожухе, показала
температуру Tо. Найти температуру потока до скачка T1.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
V2, м/с
280
300
350
250
280
300
350
250
280
300
Tо, K
350
400
350
300
400
450
300
350
400
450
95
Задача 4. Давление, измеренное в сверхзвуковом потоке трубкой полного напора, в X раз
больше давления, измеренного на щеке клина.
Найти коэффициент восстановления давления
торможения  в прямом скачке.
Варианты
Величина
X
1
2
3
4
5
6
7
8
9
10
10
12
15
13
20
10
12
15
13
20
Задача 5. Воздух истекает из баллона на расчетном режиме, где
он имеет температуру Tо, через сопло с отношением площадей
Sвых S*  4,23 . Найти скорость, которую поток будет иметь, пройдя
прямой скачок.
Варианты
Величина
Tо, K
1
2
3
4
5
6
7
8
9
10
290
300
310
320
330
340
350
360
370
380
Течение газа с учетом трения
Качественные выводы о влиянии трения и изменения сечения газохода на скорость одномерного потока газа могут быть сделаны на основании уравнения:
  1 d  1  kk  11    dSS  
2
2


тр

k
 2  dx ,
k 1
(1)
где , S и x – коэффициент скорости газа, площадь поперечного сечения
и координата данного сечения трубы, выраженная в калибрах трубы,
соответственно; тр – коэффициент сопротивления трубы.
Для адиабатического течения газа в цилиндрической трубе коэффициент скорости находят по уравнению
1
12

1
2
 ln
2
,
12
которое является интегралом уравнения (1) при dS = 0 и тр  const .
96
(2)
В уравнении (2)  – коэффициент скорости в начальном сечении
трубы,   тр  x  2  k k  1 – приведенная длина трубы.
Скорость газа на входе определяет величину
 max 
1

2
1
 1  ln
1
12
.
Предположим, что <1. Тогда, если
   max, то  = 1;
 <  max, то   1;
   max , то течение с числом 1 на входе невозможно.
При 1 > 1 возможны следующие варианты:
   max,   = 1;
 <  max,    1;
   max,  торможение посредством скачков уплотнения приведет к   1 на выходе.
Задачи
Задача 1. В трубу длиной x калибров воздух втекает с безразмерной скоростью 1. Приняв коэффициент трения тр  0,015 , определить
режим истечения из трубы (< 1, = 1, > 1).
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
x , калибров
100
110
120
100
110
120
130
100
110
120

0,4
0,5
0,6
0,3
0,4
0,5
0,6
0,6
0,5
0,4
Задача 2. Найти длину трубы, из которой воздух будет истекать со
скоростью звука, если на входе в трубу безразмерная скорость , коэффициент трения тр.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10

0,6
0,7
0,5
0,6
0,7
0,5
0,6
0,7
0,5
0,6
тр102
0,5
2
1
2
1,5
1,5
2,5
2
1,5
1
97
Задача 3. Поток воздуха входит в трубу длиной x калибров. Найти
минимальную сверхзвуковую скорость на входе, при которой в трубе
появится скачок уплотнения. Считать тр  0,015 .
Варианты
Величина
x , калибров
1
2
3
4
5
6
7
8
9
10
50
60
70
80
90
50
60
70
80
90
Задача 4. Воздух течет через сопло Лаваля с дозвуковой скоростью.
Площадь выходного сечения сопла S2 в n раз больше площади минимального сечения S1. Трубкой полного напора в выходном сечении
определено давление ро2 = 1,085 ата. В минимальном сечении через отверстие в стенке измерено давление р1 = 0,978 ата. Определить коэффициент восстановления давления торможения между минимальным и
выходным сечениями.
Варианты
Величина
n
1
2
3
4
5
6
7
8
9
10
1,7
1,8
1,9
2,0
1,9
1,8
1,7
1,6
1,5
2,0
Задача 5. Конический переходник 1–2 соединяет
трубы диаметром D1 и D2. В сечении 1 давление торможения ро1, а безразмерная скорость 1. Найти R – силу
воздействия на фундамент в сечении 1, возникающую за
счет течения воздуха по переходнику. Потери давления
торможения отразить, положив   po 2 po1  0,95
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
D1, мм
357
400
450
400
350
400
450
500
600
500
D2, мм
564
600
650
550
600
550
600
700
800
750
ро1, ата
3
3
4
3,5
3
3
3,5
3
3
3,5
0,8
0,8
0,7
0,75
0,7
0,8
0,7
0,75
0,7
0,8
1
98
Течение газа при наличии энергообмена
В практическом занятии рассматривается одномерное течение газа,
происходящее либо с добавлением энергии извне (подогрев, работа
компрессора), либо с отводом энергии во внешнюю среду. Качественная
сторона задач такого типа описывается уравнением
M
2
dS k  1
1
 dV


 dQ  dL ,
V
S
a
a
1
2
2
где dQ – теплота, сообщаемая газу или отнимаемая у него; dL – механическая работа, совершаемая газом (dL > 0), либо работа, совершаемая
над газом (dL < 0).
Для течений с подводом и отводом теплоты в цилиндрических трубах имеют место следующие зависимости:
уравнение неразрывности:
  V  const ;
уравнение сохранения полного импульса:
p    V 2  const
и их следствия:
p2 1  k  M 12

;
p1 1  k  M 22
2
T2  M 2 1  k  M 12 
 ;


T1  M 1 1  k  M 22 
2
 2  M 1  1  k  M 22
 
;

1  M 2  1  k  M 12
k 1
2 1
 M 22
To 2  M 2 1  k  M 12 
2
 
.


To1  M 1 1  k  M 22  1  k  1  M 2
1
2
Для определения результирующих сил, действующих на газопроводы, применяют теорему импульсов в векторной форме:
R  p1  S1  p2  S 2  Gt  V1  V2 ,
либо (для труб с прямолинейной осью) в одной из скалярных форм:
 k 1
  k 1

R
 a * Gt  z    
 a * Gt  z   ;
2

k
2

k

2 
1
99
R   po  S  f  2   po  S  f  1 ;
 p V   p V 
  
 ,
R  
 r    2  r   1
где f() и r() – газодинамические функции, содержащиеся в табл. П 3.2.
Если обозначить полный секундный импульс газа в данном сечении Gt  V  p  S  j , то формулы для определения функций z(), f() и
r() будут следующими:
z    2 
j
1
 ;
j*


1

j
 k  1 2  k 1
f   
 1  2  1 
  ;
po  S
 k 1

pS
r   

j
1
k 1 2

k 1
.
1  2
Задачи
Задача 1. Скорость газа, текущего по цилиндрической трубе, возрастает от V1 до V2 за счет подогрева. Найти величину понижения давления в газе, если плотность газа до подогрева 1.
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
V1, м/с
100
150
200
100
150
200
100
100
200
300
V2, м/с
300
350
400
250
300
350
300
400
400
400
1,
2,4
3,0
3,5
2,0
2,5
2,5
3,0
3,0
3,0
3,0
кг/м3
Задача 2. Поток воздуха нагревается в цилиндрической трубе за
счет теплоты сгорания топлива, расход которого составляет 5% от расхода воздуха. До подогрева скорость воздуха V1, давление р1, температура торможения Tо1. Найти скорость и давление газа в сечении трубы,
где температура торможения Tо2 = 1500 К.
Принять k = 1,33; R = 291 Дж/(кг К). Трением пренебречь.
100
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
V1, м/с
50
60
70
50
50
50
50
50
50
50
р1, МПа
1,0
1,2
1,0
1,0
1,0
1,0
1,5
1,5
1,5
2,0
Tо1, К
400
450
400
450
500
550
450
500
550
500
Задача 3. Найти реакцию потока газа на стенки канала ПВРД при
скорости полета V на высоте H. Площадь потока, захватываемого двигателем, S = 0,7 м2, показатель адиабаты k = 1,3, температура торможения
газов на выходе из двигателя 2000 К.
Принять вых = 0,98вх. Различие расхода газа на входе в двигатель
и выходе из него не учитывать.
Варианты
Величина
1
V, км/час
2
3
4
5
6
7
8
9
10
2000 2500 2700 3000 2000 2500 2700 3000 2000 2500
H, км
9
10
9
8
7
8
10
9
8
7
Задача 4. На входе в цилиндрическую трубу скорость потока воздуха V1 при значении числа Маха, равном M1. Поток в трубе ускоряется компрессором без теплообмена с окружающей средой. С какой скоростью
воздух истекает из трубы, если на выходе из нее число
Маха принимает значение М2?
Варианты
Величина
1
2
3
4
5
6
7
8
9
10
400
350
300
400
400
400
450
450
550
350
М1
1
0,7
0,6
1,2
1,3
1,4
1,3
1,5
1
1
М2
3
3
3
3,5
3,5
3,5
3
3
3
3
V1, м/с
Задача 5. В результате отвода теплоты от воздуха, движущегося по
цилиндрической трубе, давление, измеряемое на стенке трубы, уменьшилось на участке охлаждения в N раз. Найти число Маха потока в конце участка охлаждения, если в начале участка M = 2,16.
101
Варианты
Величина
N
1
2
3
4
5
6
7
8
9
10
1,8
2,0
2,2
1,8
2,0
2,2
2,4
1,8
2,0
2,2
Задача 6. Определить максимальное повышение температуры торможения воздуха при подогреве его в трубе без изменения параметров
потока в начальном сечении, если начальная температура торможения
To = 400 К, а начальная безразмерная скорость воздуха 1.
Варианты
Величина
1
1
2
3
4
5
6
7
8
9
10
0,3
0,4
0,5
0,2
0,3
0,4
0,5
0,2
0,3
0,3
Задача 7. На входе в цилиндрическую подогревательную трубу поток воздуха имеет температуру торможения To1 = 300 К и безразмерную
скорость 1 = 0,5. Найти температуру торможения To2 после подогрева,
обеспечивающую на выходе из трубы безразмерную скорость 2.
Варианты
Величина
2
1
2
3
4
5
6
7
8
9
10
0,9
0,8
0,7
0,9
0,9
0,8
0,7
0,9
0,8
0,7
102
ПРИЛОЖЕНИЕ 1
Таблица П 1.1
Плотность и вязкость некоторых жидкостей
t, оС
, кг/м3
, м2/с
20
751
0,0064
40
735
–
20
819
0,025
40
808
–
0
1267
–
20
1259
8,7
0
903
76
20
892,5
11,2
40
881
2,7
0
892,5
1,35
20
880,3
0,36
40
868,2
0,15
Масло турбинное
20
940–952
–
Нефть
20
850–950
–
20
878,7
0,08
40
865,4
0,046
Наименование
Бензин (Б–70)
Керосин (Т–1)
Глицерин
Масло М–20
Масло
трансформаторное
Топливо дизельное
Таблица П 1.2
Коэффициенты объемного сжатия воды
W  1010 , Па-1, при давлении, МПа
t, oC
0,5
1
2
3,9
7,8
0
5,4
5,37
5,31
5,23
5,15
5
5,29
5,23
5,18
5,08
4,93
10
5,23
5,18
5,08
4,98
4,81
15
5,18
5,1
5,03
4,88
4,7
20
5,15
5,05
4,95
4,81
4,6
103
Таблица П 1.3
Коэффициенты температурного расширения воды
 t  106 , К-1, при давлении, МПа
t, oC
0,1
10
20
50
90
1–10
14
43
72
149
229
10–20
150
165
183
236
289
40–50
422
422
426
429
437
60–70
556
548
539
523
514
90–100
719
704
–
661
621
Таблица П 1.4
Физические свойства воздуха
t, оС
, кг/м3
 , м2/с
t, оС
, кг/м3
 , м2/с
10
1,247
14,16
60
1,060
18,97
20
1,205
15,06
70
1,029
20,02
30
1,165
16,00
80
1,000
21,09
40
1,128
16,96
90
0,972
22,10
50
1,093
17,95
100
0,946
23,13
Таблица П 1.5
Физические свойства пресной воды
t, оС
, кг/м3
 , м2/с
 103, Н/м
ps, Па
1
2
3
4
5
0
999,87
1,789
75,65
613
10
999,73
1,306
74,22
1197
20
998,23
1,006
72,74
2385
30
995,68
0,805
71,20
4240
40
992,25
0,658
69,60
7360
104
Окончание табл. П 1.5
1
2
3
4
5
50
988,1
0,556
67,95
12320
60
983,2
0,478
66,24
19920
70
977,8
0,415
64,49
31160
80
971,8
0,366
62,68
47360
90
965,3
0,326
60,82
70110
100
958,4
0,294
58,92
101320
Таблица П 1.6
Положение центра тяжести плоских фигур
и формулы моментов инерции относительно оси,
проходящей через центр тяжести
Форма пластины
Центр тяжести
Момент инерции
xH 2
J 0  b  H 3 12
xD 2
J 0    D 4 64
xH 3
J 0  b  H 3 36
x
H 2b  a

3 ab
x  D 4,71
105
J0 

H 3  a2  4  a  b  b2
36  a  b 
J 0  D 4 145,4

Таблица П 1.7
Эквивалентная равномерно-зернистая шероховатость
Материал и вид трубы
Тянутые из цветных металлов
Бесшовные стальные
Стальные сварные
Оцинкованные железные
Чугунные
Асбоцементные
э, мм
Состояние трубы
Новые, технически гладкие
0–0,002
Новые и чистые
0,01–0,02
После эксплуатации
0,15–0,3
Новые и чистые
0,03–0,1
С незначительной коррозией
после очистки
0,1–0,2
Умеренно заржавевшие
0,3–0,7
Старые заржавевшие
0,8–1,5
Сильно заржавевшие
2–4
Новые чистые
0,1–0,2
После нескольких лет
эксплуатации
0,4–0,7
Новые асфальтированные
0–0,16
Новые без покрытия
0,2–0,5
Бывшие в употреблении
0,5–1,5
Новые
0,05–0,1
Таблица П 1.8
Коэффициент формы поперечного сечения
Форма поперечного сечения
dэ
А
а
57
Равносторонний треугольник со стороной а
0,58а
53
Кольцевой просвет шириной a  D  d  2
2а
96
2а
96
a b  0,25
1,6а
73
a b  0,5
1,3а
62
Квадрат со стороной а
Прямоугольник со сторонами a и b:
a b0
106
Таблица П 1.9
Коэффициент скорости возрастания шероховатости
Коррозионное
воздействие
, мм/год
Характеристика природных вод
Слабое
Слабоминерализованные некоррозионные воды;
0,005–0,055
воды с незначительным содержанием органических веществ и растворенного железа
Умеренное
Слабоминерализованные коррозионные воды;
воды, содержащие органические вещества и рас- 0,055–0,18
творенное железо в количестве меньше 3 мг/л
Значительное
Весьма коррозионные воды с содержанием железа более 30 мг/л, но с малым содержанием
хлоридов и сульфатов
0,18–0,40
Сильное
Коррозионные воды с большим содержанием
хлоридов и сульфатов (больше 500–700 мг/л);
необработанные воды с большим содержанием
органических веществ
0,40–0,60
Воды со значительной карбонатной и малой
постоянной жесткостью с плотным остатком
Очень сильное
более 2000 мг/л; сильно минерализованные и
коррозионные
От 0,6 до 1
и более
Таблица П 1.10
Значения параметра А и ς кв для некоторых местных сопротивлений
А
 кв
Кран пробочный
150
0,4
Вентиль обыкновенный
3000
6
Вентиль угловой
400
0,8
Клапан шаровой
Устройство
5000
45
Угольник
90о
400
1,4
Угольник
135о
600
0,4
30
1
Вход из бака в трубу
30
0,5
Тройник
150
0,3
Задвижка полностью открытая
75
0,15
Выход из трубы в бак
107
Таблица П 1.11
Коэффициенты истечения из насадков
П 1.12. Значения коэффициентов местных потерь давления
для наиболее характерных групп элементов
Вход потока в трубу
Потери давления при входе потока в трубу, помимо критерия Рейнольдса, существенно зависят от конструктивного и технологического оформления входа, а также угла  между осью трубы и стенкой (рис. П 1.1).
Рис. П 1.1. Вход потока в трубу
1. Прямой вход при наличии сужения (рис. П 1.1, а) без учета неравномерности профилей скорости:

    1 

108
S2 
.
S1 
Коэффициент  определяют по приближенной формуле
2

  180  300 


L 
    0,05  .
d2   d2

Потери давления рассчитывают по скорости V2 в выходном сечении.
2. Прямой вход при наличии коллектора радиусом R и торцевой
стенки (рис. П 1.1, б) (Reавт = 104).
R/d
0
0,02
0,08
0,16
0,20

0,5
0,36
0,15
0,06
0,03
3. Косой вход в трубу без скругления (рис. П 1.1, в) (Reавт = 104):
  0,5  0,3  cos  0,2  cos2 .
4. Прямой вход через конический коллектор (рис. П 1.1, г). При
 = 180˚ независимо от отношения h/D,  = 0,5. При  = 40–60˚ имеет
наименьшее значение:
h/D
0,025
0,05
0,075
0,15
0,60
min
0,4
0,3
0,23
0,15
0,11
Изменение площади поперечного сечения потока
без изменения направления течения
Различают внезапные и плавные изменения площадей сечений, характерные примеры которых показаны на рис. П 1.2.
Рис. П 1.2. Изменение площади сечения потока
без изменения направления
109
1. Внезапное расширение (рис. П 1.2, а). Коэффициент потери давления отнесен к скорости до расширения. Его значение при Re > 104, без
учета действительного профиля скорости определяют по формуле
2

 1  1 

S1 
 ,
S 2 
а при Re > 10
30
.
Re
2. Плавное расширение в диффузорах (рис. П 1.2, б). Коэффициент
потери давления в диффузоре приближенно оценивают в долях от коэффициента при внезапном расширении:
 1д  1д   1 ,
1 
где 1д – коэффициент смягчения “удара”.
У конических диффузоров при угле > 60˚ 1д = 1, т.е. потери такие же, как и при внезапном расширении. В диапазоне углов от 0˚ до 60˚
значения коэффициента смягчения “удара” берут из таблицы.

о
1д
10
20
30
40
50
0,2
0,5
0,7
0,85
0,95
3. Внезапное сужение (рис. П 1.2, в). Коэффициент потери давления
отнесен к скорости после сужения. Без учета действительного профиля
скоростей формула имеет вид

 2c  0,5  1 

S2 
.
S1 
4. Плавное сужение (конфузор) (рис. П 1.2, г). Коэффициент потери
давления в конфузоре приближенно оценивают в долях от коэффициента при внезапном сужении с одинаковым отношением площадей с помощью коэффициента смягчения сужения с:
 2к   c   2 д .
Для углов сужения конических диффузоров (40–80)˚ с = 0,1–0,2. Минимальными значениями коэффициента потери давления обладают конические конфузоры с углом при вершине 15–55˚; для них к = 0,04–0,05.
5. Выход потока из трубопровода (рис. П 1.2, д):
 вых  1,
где 1 – коэффициент неравномерности кинетической энергии (коэффициент Кориолиса) в трубопроводе.
110
Изменение направления потока
Изменение направления течения в трубопроводах осуществляется в
отводах и коленах (рис. П 1.3).
Рис. П 1.3. Изменение направления течения: а – отвод; б – колено
Колено – крутоизогнутый отвод – может быть составным и снабжено внутри лопатками. Коэффициент потери давления в отводах и коленах, помимо критерия Рейнольдса и шероховатости поверхности, зависит от угла поворота , а для отводов – от относительного радиуса
погиба R/d. В области автомодельности при Re > 2105 коэффициент
потери давления отвода отв (рис. П 1.3, а) рассчитывают по формуле
 R
d
 отв  0,73  f1    f 2  .
Значения f1() и f2(R/d) приведены в таблице.
, о
f1()
40
60
90
120
180
R/d
0,55 0,75 1,05 1,20 1,40 f2(R/d)
1
2
4
6
10
0,32
0,2
0,14
0,11
0,09
Для стандартных отводов постоянного сечения с углом  = 90˚ коэффициент потери давления можно принимать равным:
R/d
1
2
3
4
5
отв (гладкие)
0,29
0,23
0,23
0,26
0,29
отв (шероховатые)
0,54
0,38
0,34
0,36
0,38
111
Коэффициент потери давления в простом колене при Re > 2105
(рис. П 1.3, б) можно принимать равным нижеприведенным значениям в
зависимости от угла поворота.
, о
15
30
45
60
90
кол
0,06
0,17
0,32
0,68
1,26
Узлы деления и слияния потоков
В узлах деления потока потери давления распространяются по всем
направлениям. Потери давления в магистральном канале при проходе
узла называют потерями на проход, в ответвлениях – потерями на ответвление. В ветвях, сходящихся к узлу, средние скорости различны и
потери давления могут относиться к любой из них в зависимости от
удобства дальнейшего использования. Принятая индексация скоростей,
давлений, площадей для тройников при делении и слиянии потоков показана на рис. П 1.4.
Рис. П 1.4. Узлы деления и слияния потоков
Область автомодельности для тройников наступает при Re > 104.
Коэффициент потери давления на проход сп, отнесенный к скорости в магистральном канале до деления потока Vс, определяют приближенно по формуле
2
 сп
 V 
 0,4  1  п  .
 Vc 
Коэффициент потери давления на ответвление сб оценивают по
уравнению
 сб
  V 2

V 
 A  1   б   2   б   cos ,
  Vc 

 Vc 


где А = 1,0 при Vб/Vс < 0,8 и А = 0,9 при Vб/Vс > 0,8.
112
Коэффициент потерь давления на проход в магистральном канале
при слиянии потоков определяют из выражения
2
2
 Sc 
 Qб   S c 
 S c 







 .
 сп
    cos  1 


2

  
 S п 
 Sб 
 Qc   S п 
Коэффициент потерь давления потока, направленного из ответвления в магистральный канал, отнесенный к скорости в сечении после
слияния, определяют по формуле
Q 
 1  2   б 
 Qc 

 Qб 

 Qc 
2
 сб  kсб  1  

2
2
S 
Q 
  c   2   б 
S
 б
 Qc 
2
S 
 Q 
  c   cos  2  1  б 
S
 б
 Qc 
2
 S 
  c .
 S п 
Значения kсб находятся в пределах 0,6–1,0. Для прямых тройников
( = 90˚) kсб находят в зависимости от отношения площадей Sб/Sс.
Sб/Sс
0–0,2
0,3–0,4
0,6
0,8
1,0
kсб
1,0
0,75
0,70
0,65
0,60
Трубопроводная арматура
Задвижки с листовым шибером. При Re > 105 для круглого и прямоугольного сечений в зависимости от степени открытия (h/D или h/B)
коэффициент местных потерь давления имеет следующие значения:
h/D или h/B
0,4
0,6
0,8
1,0
кругл
4,0
1,0
0,2
0,01
прямоуг
8,0
2,0
0,4
0,015
Клапаны. В зависимости от условного диаметра Dу при Re>104 коэффициент местных потерь для полностью открытого клапана равен:
Dу, мм
20
40
80
100
150
200
авт
4,3
4,4
4,7
4,8
5,1
5,4
Краны. Для проходных фланцевых кранов при Re > 104 коэффициенты местных потерь давления для полностью открытых кранов приведены в таблице.
Dу, мм
20
32
40
50
70
80
авт
2,4
2,0
1,8
1,5
1,0
0,8
Сетки приемные. При Re > 2104 коэффициент местной потери давления находится в диапазоне 0,3–0,7.
113
ПРИЛОЖЕНИЕ 2
Таблица П 2.1
Характеристики масел для гидросистем
Название масла
Плотность кг/м3
Кинематическая вязкость, м2/с
при 293 К
при 323 К
610-5
Индустриальное 12
Индустриальное 20
876–891
881–901
1010-5
1,210-5
2,010
Индустриальное 30
886–916
2010-5
3,010-5
890–920
890–930
4810-5
4,510-5
Турбинное 22
900
810-5
5,810-5
2,1510-5
АМГ-10
850
210-5
0,7510-5
Индустриальное 45
Индустриальное 50
Таблица П 2.2
Характеристики серийно выпускаемых насосов
Характеристики
Частота вращения, мин-1
Номинальное давление, Мпа
Рабочий объем, см3/об
4
6,3
8
10
12,5
16
20
25
32
40
50
63
80
100
Шесте- Пла- Аксиально-пор- Аксиально-порренные стинча- шневые регули- шневые нерегуНШ-Ф тые БГ12 руемые НА
лируемые НА
1920
16
1440
16
+
+
1500
20
1500
32
+
+
+
1500
20
1500
32
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+ – исполнение предусмотрено.
114
+
+
+
+
+
+
+
+
+
Таблица П 2.3
Шестеренные и пластинчатые насосы
Шестеренные
Пластинчатые
Р, МПа
0,5
1,3
2,5
50
6,3
6,3
12,5
n, мин-1
1450
1450
1450
1450
950
950
950
Q, л/мин
обозначение / объемный КПД насоса
Г12-41Б / 0,64
3
5
Г11-11А / 0,70
Г12-41А / 0,7
Г12-21А / 0,62
Г12-31А / 0,62
БГ12-21А / 0,6
8
Г11-11 / 0,72
Г12-41 / 0,73
Г12-21 / 0,71
Г12-31 / 0,71
БГ12-21 / 0,65
Г12-42А / 0,8
Г12-22А / 0,77
Г12-32А / 0,77
БГ12-22А/0,72
Г12-32 / 0,79
БГ12-22 / 0,80
12
Г11-12А
Г11-22А / 0,76
18
Г11-12
Г11-22 / 0,78
Г12-22 / 0,79
25
Г11-13А
Г11-23А / 0,80
Г12-23А / 0,85
35
Г11-13
Г11-23 / 0,82
Г12-23 / 0,88
50
Г11-14А
Г11-24А / 0,84
Г12-24А / 0,85
БГ12-24А / 0,80
70
Г11-14
Г11-24 / 0,88
Г12-24 / 0,86
БГ12-24 / 0,86
100
Г11-15А
Г11-25 / 0,92
Г12-25А / 0,88
140
Г12-25 / 0,90
Г12-33А / 0,85 БГ12-23А / 0,74
Г12-33 / 0,88
БГ12-23 / 0,78
Таблица П 2.4
Технические характеристики гидромоторов
Тип
гидромотора
1
Номинальный
крутящий момент, Нм
Частота вращения, мин-1
Номинальная
Пределы
4
Рабочий объем,
см3/об
Объемный
КПД
Номинальное
давление, МПа
2
3
5
6
7
МР–0,16/10
240
240
160
0.91
10
МР–0,25/10
380
240
250
0,94
10
МР–0,4/10
570
192
400
0,94
10
МР–0,63/10
900
150
630
0,95
10
МР–1/10
1480
120
1000
0,94
10
МР–1,6/10
2390
96
1600
0,95
10
МР–2,5/10
3540
96
2500
0,94
10
МР–4/10
5700
96
4000
0,94
10
МР–6,3/10
9520
60
6300
0,93
10
МР–10/10
15120
37,8
10000
0,96
10
МР–16/10
22960
24
16000
0,95
10
МР–25/10
37500
9,6
25000
0,95
10
МР–450
1340
130
451
–
21
1,5–400
Окончание табл. П 2.4
2
3
4
5
6
7
МР–700
1
2110
120
1–340
707
–
21
МР–1100
3380
100
1–280
1126
–
21
МР–1800
5440
80
1–220
1809
–
21
МР–1800
8370
60
1–170
2780
–
21
МР–4500
13550
40
1–120
4503
–
21
Г16–11
5,0
1000
300–2500
8
0,70
6,3
Г16–12
11,5
1000
300–2500
18
0,73
6,3
Г16–13
23,7
1000
300–2200
36
0,75
6,3
Г16–14
48,5
1000
300–1800
71
0,80
6,3
Г16–15А
70,4
1000
300–1800
100
0,85
6,3
Г16–15
101,8
1000
300–1500
140
0,88
6,3
Г16–16А
155,2
1000
300–1500
200
0,90
6,3
Г15–21
6
1000
40–2400
11,2
–
6,3
Г15–22
12,5
1000
30–2100
20
–
6,3
Г15–23
25
1000
20–1800
40
–
6,3
Г15–24
50
1000
20–1500
80
–
6,3
Г15–25
100
1000
20–1300
160
–
6,3
Г15–26
200
1000
10–1000
320
–
6,3
Таблица П 2.5
Гидроцилиндры
Тип
гидроцилиндра
Диаметр
поршня, мм
Номинальное
давление, МПа
Ход
поршня, мм
Вес, кг
1
73.001
ПГУ–61
ПГУ–3Б
3А1 0–II–001
3А151–II–001
3AI6I–II–001
БУ–0600–00
ЗА423–II–001
3AI64–II–001
3AI64–II–001
3BI64Б–II–001
БУ55–0600–00–1
Д443–I003–00–2
Д535–04–00
Д443А–0604–00–4
Ц60,8/80–630/
Ц80,4/80–800/
Ц80,8/80–8000/
Ц100,4/80–1000/
Ц125,4/100–1250/
Ц125,8/100–1250/
Ц160,4/125–1600/
Ц160,8/125–1600/
Ц200,4/200–2000/
Ц60,7/80–630/
Ц80,3/80–800/
Ц80,7/80–800/
Ц100,3/80–1000/
Ц100,7/80–1000/
Ц125,3/100–1250/
Ц125,7/100–1250/
Ц160,3/125–1600/
Ц160,7/125–1600/
2
40
65
65
70
80
80
90
90
110
110
110
80
80
80
80
60
80
80
100
125
125
160
160
200
60
80
80
100
100
125
125
160
160
3
16
10
10
1,б
1,6
1,6
10
1,6
1,б
1,6
1,6
10
10
10
10
16
10
16
10
10
16
10
16
10
16
10
16
10
16
10
16
10
16
4
720
850
850
685
650
920
650
1600
1820
2520
1270
635
275
635
275
80–630
80–800
80–800
80–1000
100–1250
100–1250
125–1600
125–1600
200–2000
80–630
80–800
80–800
80–1000
80–1000
100–1250
100–1250
125–1600
125–1600
5
18,0
12,5
12,5
23,2
30,0
34,2
44,7
73,5
148,0
168,0
132,0
40,7
28,6
38,8
50,0
7,7–18,86
15,74–37,48
16,76–41,74
28,38–63,44
39,48–111,37
40,29–125,87
69,38–190,2
74,58–224,49
131,5–339,0
6,9–18,06
13,23–34,98
14,29–39,22
24,45–59,10
26,64–67,74
36,27–108,13
37,19–122,54
64,01–172,49
71,67–233,68
118
Окончание табл. П 2.5
1
Ц200,3/200–2000/
Ц60,5/80–630/
Ц80,1/80–800/
Ц80,5/80–800/
Ц100,1/80–1000/
Ц100,5/80–1000/
Ц125,1/100–1250/
Ц125,5/100–1250/
Ц160,5/125–1600/
Ц200,1/200–2000/
Д230–14сб
Д183Б–14сб
М6–0204–00
М6–0205–00
4009–4635010
4000М–4630010–Б
404БЛ–4630010
4046–4614011
4008–4632010
ГПIУ–9.01
ГПIУ3
МК1.20.03.000
ОМКТ1–1–31К
ДСШ14.56.001
9ЭА–8603010–13
220В–8600015
60.04.04.00СА
БКГМ–020Е
Ц60,6/80–630/
Ц80,2/80–800/
Ц100,2/80–1000/
Ц100,6/80–1000/
Ц125,2/100–1250/
Ц125,6/100–1250/
Ц160,2/125–1600/
Ц160,6/125–1600/
Ц200,2/200–2000/
2
200
60
80
80
100
100
125
125
160
200
180
180
180
180
70
120
120
120
145
90
90
125
100
36
145
220
70
70
60
80
100
100
125
125
160
160
200
3
10
16
10
16
10
16
10
16
16
10
3
3
4
4
10
12
10
10
8
7
7
15
20
7
10
5
10
10
16
10
10
16
10
16
10
16
10
119
4
200–2000
80–630
80–800
80–800
80–1000
80–1000
100–1250
100–1250
125–1600
200–2000
718
752
520
520
140
400
360
130
565
295
700
675
900
250
505
785
82
841
80–630
80–800
80–1000
80–1000
100–1250
100–1250
125–1600
125–1600
200–2000
5
120,8–328,0
7,08–18,24
14,11–25,62
15,11–49,85
25,41–60,47
26,3–68,4
22,18–116,12
22,71–130,09
82,24–224,25
131,1–339,34
98,3
97,4
90,0
90,0
–
–
–
–
–
29,0
47,0
119,8
191,0
4,5
38,6
–
4,6
26,7
8,39–19,5
11,39–22,2
26,38–61,44
27,39–69,50
41,85–113,74
45,99–131,14
74,24–207,22
89,71–251,72
42,26–341,6
Таблица П 2.6
Гидроаппаратура гидроприводов
Гидроаппаратура
1
Обратные клапаны
Предохранительные
клапаны
Напорные клапаны
Последние цифры в обозначении гидроаппаратуры при расходе, л/мин
Давление,
МПа
Обозначение
2
3
3–20
Г51
5
Г52
5–20
БГ52
13
5–20
1СКП52
13
5–20
1КРМ
15
5–20
1КР
15
5–20
2БГ52
13
2,5
Г54
12
22
23
5,0
Г54
12
22
23
10,0
Г54
12
22
23
1,5
3
5
8
12
18
25
35
50
4
5
6
7
8
9
10
11
12
21
22
23
12
13
Продолжение табл. П 2.6
1
Регуляторы потока
с электрогидравлическим
управлением
Фильтры
2
3
4
5
6
7
8
9
10
6,4
Г55
12,5
Г55
12,5
ДГ–73
20
Г63
13
20
Г64
23
6,3
0,08Г41
6,3
0,12Г41
–
С41
0,6
0,05С42
0,6
0,08С42
0,6
21
31В
31Б
31А
11
31
12
11
32А
32
13
12
12
13
23
33
14
13
11
11
11
14
12
12
13
14
11
12
13
14
0,15С42
11
12
13
0,63
ФМ
1
0,63
ФМС
12
2
3
12
13
Окончание табл. П 2.6
1
Регуляторы потока
2
3
12,5
Г55
12,5
Г55
12,5
Г55
20
Г55
4
61В
5
6
61Б
7
61А
8
61
9
10
11
12
42А
42
43
62А
62
63
22
32
62
72
12Б5
Г77
20
Г77
12
Г57
20
РКР
ручным управлением
8,0
Г74
гидравлич. управлением
5,0
Г72
электрич. управлением
5,0
Г73
Дроссели
Редукционные клапаны
31В
31Б
31А
31
32А
32
33
12
13
13
Распределители с:
21
12
13
22
33
13А
Таблица П 2.7
Рекомендуемые размеры стальных труб в зависимости от расхода
Внутренний диаметр трубы, мм
Расход, л/мин
Трубопроводы нагнетательные и сливные
Трубопроводы всасывающие
до 5
8
23
5–10
12
28
10–30
16
30
30–60
20
34
60–100
23
40
100–140
25
44
140–200
28
48
Таблица П 2.8
Рекомендуемые размеры стальных труб для гидросистем
Рабочее давление, МПа
Наружный
диаметр
трубы, мм
25
100
200
320
dвн, мм
, мм
dвн, мм
, мм
dвн, мм
, мм
dвн, мм
, мм
14
8
3,0
8
3,0
7
3,5
7
3,5
18
12
3,0
11
3,5
9
4,5
9
4,5
22
–
–
14
3,5
12
5,0
12
5,0
25
19
3,0
–
–
–
–
–
–
28
–
–
20
4,0
16
6,0
16
6,0
32
25
3,5
–
–
–
–
–
–
Таблица П 2.9
Сортамент стальных бесшовных труб
Внешний
диаметр
трубы, мм
Толщина стенки, мм
от
до
Внешний
диаметр
трубы, мм
4
0,2
1,2
5
0,2
1,6
6
0,2
7
0,2
8
0,2
9
0,2
10
0,2
11
0,2
12
0,2
13
0,2
33
Толщина стенки, мм
от
до
Внешний
диаметр
трубы, мм
14
0,2
4,0
/15/
0,2
2,0
16
2,5
/17/
2,5
2,8
3,5
3,5
4,0
4,0
0,4
9,0
40
0,4
42
1,0
45
1,0
48
1,0
50
1,0
Толщина стенки, мм
от
до
/24/
0,4
7,0
5,0
25
0,4
7,0
0,2
5,0
/26/
0,4
7,0
0,2
5,0
/27/
0,4
7,0
18
0,2
5,0
28
0,4
7,0
/19/
0,2
6,0
30
0,4
8,0
20
0,2
6,0
32
0,4
8,0
/21/
0,4
6,0
34
0,4
8,0
22
0,4
6,0
/35/
0,4
8,0
/23/
0,4
6,0
36
0,4
8,0
/51/
1,0
12
63
1,0
12
9,0
53
1,0
12
65
1,0
12
9,0
/54/
1,0
12
/68/
1,0
12
10
56
1,0
12
70
1,0
12
10
/57
1,0
12
/73/
1,0
12
12
60
1,0
12
75
1,0
12
Таблица П 2.10
Коэффициенты местных потерь
Для гидрораспределителей золотникового типа в зависимости от характера движения и количества поворотов
потока жидкости
2–4
Для гидродвигателей и обратных (запорных) гидроклапанов клапанного типа
2–3
Для самозапирающихся соединений (муфт)
1–1,5
Для штуцеров, присоединяющих трубы к гидроклапанам, и переходников, соединяющих отрезки труб
0,1–0,15
Для плавных колен (отводов) трубопроводов под углом 90° (радиус изгиба равен (3 – 5) диаметрам трубы)
0,12–0,15
Для угольников с поворотом под прямым углом
1,5–2
Для прямоугольных тройников с разделением и соединением потоков:
отвод части потока под углом 90˚
0,9–1,2
транзитный поток
0,1–0,2
разделение потока
1–1,5
ПРИЛОЖЕНИЕ 3
Таблица П 3.1
Таблица стандартной атмосферы
H, м
PH, мм рт. ст.
ToH, К

H104, м2/с
аH, м/с
0
760,0
288,0
1,000
0,144
340,2
500
716,0
284,75
0,953
0,150
338,3
1000
674,1
281,5
0,907
0,155
336,4
1500
634,2
278,25
0,864
0,161
334,4
2000
596,2
275,0
0,822
0,168
332,5
2500
560,1
271,75
0,781
0,175
330,5
3000
525,8
268,5
0,742
0,182
328,5
3500
493,2
265,25
0,705
0,189
326,5
4000
462,2
262,0
0,669
0,197
324,5
4500
432,9
258,75
0,634
0,206
322,5
5000
405,1
255,5
0,601
0,214
320,5
5500
378,7
252,25
0,569
0,224
318,4
6000
353,8
249,0
0,538
0,234
316,3
6500
330,2
245,75
0,509
0,244
314,3
7000
307,8
242,5
0,481
0,255
312,2
7500
286,8
239,25
0,454
0,267
310,1
8000
266,9
236,0
0,429
0,280
308,0
8500
248,1
232,75
0,404
0,293
305,9
9000
230,5
229,5
0,381
0,307
303,7
9500
213,8
226,25
0,358
0,323
301,6
10000
198,2
223,0
0,337
0,339
299,4
Принятые обозначения: H – высота над уровнем моря; РH – давление воздуха на соответствующей высоте; TоH – температура торможения
на высоте H;   относительная плотность воздуха при параметрах
торможения; H  коэффициент кинематической вязкости воздуха; аH –
скорость звука в воздухе.
127
Таблица П 3.2
Газодинамические функции




q
y
f
r
M
1
2
3
4
5
6
7
8
9
0,00
1,0000
1,0000
1,0000
0,0000
0,0000
1,0000
1,0000
0,0000
0,05
0,9996
0,9986
0,9990
0,0788
0,0789
1,0015
0,9971
0,0457
0,10
0,9983
0,9942
0,9959
0,1571
0,1580
1,0058
0,9885
0,0914
0,15
0,9963
0,9870
0,9907
0,2344
0,2375
1,0129
0,9744
0,1372
0,20
0,9933
0,9768
0,9834
0,3102
0,3176
1,0227
0,9551
0,1830
0,25
0,9896
0,9640
0,9742
0,3842
0,3985
1,0350
0,9314
0,2290
0,30
0,9850
0,9485
0,9630
0,4557
0,4804
1,0496
0,9037
0,2760
0,35
0,9796
0,9303
0,9497
0,5243
0,5636
1,0661
0,8727
0,3228
0,40
0,9733
0,9097
0,9346
0,5897
0,6482
1,0842
0,8391
0,3701
0,45
0,9663
0,8868
0,9178
0,6515
0,7346
1,1036
0,8035
0,4179
0,50
0,9583
0,8616
0,8991
0,7091
0,8230
1,1239
0,7666
0,4663
0,55
0,9496
0,8344
0,8787
0,7623
0,9136
1,1445
0,7290
0,5152
0,60
0,9400
0,8053
0,8567
0,8109
1,0069
1,1651
0,6912
0,5649
0,65
0,9296
0,7745
0,8332
0,8543
1,1030
1,1852
0,6535
0,6154
0,70
0,9183
0,7422
0,8082
0,8924
1,2024
1,2042
0,6163
0,6668
0,75
0,9063
0,7086
0,7819
0,9250
1,3054
1,2216
0,5800
0,7192
0,80
0,8933
0,6738
0,7543
0,9518
1,4126
1,2370
0,5447
0,7727
0,85
0,8796
0,6382
0,7256
0,9729
1,5243
1,2498
0,5107
0,8274
0,90
0,8650
0,6019
0,6959
0,9879
1,6412
1,2595
0,4779
0,8833
0,95
0,8496
0,5653
0,6653
0,9970
1,7638
1,2658
0,4466
0,9409
1,00
0,8333
0,5283
0,6340
1,0000
1,8929
1,2679
0,4167
1,0000
1,05
0,8163
0,4913
0,6019
0,9969
2,0291
1,2655
0,3882
1,0609
1,10
0,7983
0,4546
0,5694
0,9880
2,1734
1,2584
0,3613
1,1239
1,15
0,7796
0,4184
0,5366
0,9735
2,3269
1,2463
0,3357
1,1890
1,20
0,7600
0,3827
0,5035
0,9531
2,4906
1,2286
0,3115
1,2566
1,25
0,7396
0,3479
0,4704
0,9275
2,6660
1,2054
0,2886
1,3268
1,30
0,7183
0,3142
0,4374
0,8969
2,8547
1,1765
0,2670
1,4002
1,35
0,6962
0,2816
0,4045
0,8614
3,0586
1,1417
0,2467
1,4769
128
Окончание табл. П 3.2
1
2
3
4
5
6
7
8
9
1,40
0,6733
0,2505
0,3720
0,8216
3,2798
1,1012
0,2275
1,5575
1,45
0,6496
0,2209
0,3401
0,7778
3,5211
1,0551
0,2094
1,6423
1,50
0,6250
0,1930
0,3088
0,7307
3,7858
1,0037
0,1923
1,7321
1,55
0,5996
0,1669
0,2784
0,6807
4,0778
0,9472
0,1762
1,8273
1,60
0,5733
0,1427
0,2489
0,6282
4,4020
0,8861
0,1611
1,9290
1,65
0,5463
0,1205
0,2205
0,5740
4,7647
0,8210
0,1467
2,0380
1,70
0,5183
0,1003
0,1934
0,5187
5,1735
0,7524
0,1333
2,1555
1,75
0,4896
0,0821
0,1677
0,4630
5,6383
0,6813
0,1205
2,2831
1,80
0,4600
0,0660
0,1435
0,4075
6,1723
0,6085
0,1085
2,4227
1,85
0,4296
0,0520
0,1210
0,3530
6,7934
0,5349
0,0971
2,5766
1,90
0,3983
0,0399
0,1002
0,3002
7,5243
0,4617
0,0864
2,7481
1,95
0,3662
0,0297
0,0812
0,2497
8,3985
0,3899
0,0763
2,9414
2,00
0,3333
0,0214
0,0642
0,2024
9,4640
0,3203
0,0668
3,1622
2,05
0,2996
0,0147
0,0491
0,1588
10,794
0,2556
0,0576
3,4190
2,10
0,2650
0,0096
0,0361
0,1198
12,500
0,1956
0,0490
3,7240
2,15
0,2296
0,0058
0,0253
0,0857
14,772
0,1420
0,0408
4,0961
2,20
0,1933
0,0032
0,0164
0,0570
17,949
0,0960
0,0331
4,5674
2,25
0,1563
0,00151 0,00966 0,0343
22,712
0,0585
0,0269
5,1958
2,30
0,1183
0,00057 0,00482 0,0175
30,658
0,0302
0,0189
6,1033
2,35
0,0796
0,00014 0,00170 0,0063
46,593
0,0111
0,0122
7,6053
2,40
0,0400 0,000128 0,00032 0,0012
94,703
0,0022
0,0059
10,957

0
0

2,449
0
0
0
0
Принятые обозначения:
k
T
k 1 2
p  k  1 2  k 1
   1
 ;  
 1 
   ; k  1,4;
To
k 1
po  k  1

1
1
  k  1 2  k 1
S
 V
 k  1  k 1

 1 
  ; q 
   
      ;
0  k  1 
S
 a  2 
1
const
q 

f  const  q      ; r 
; y
.
1
 






y       


129
Таблица П 3.3
Соотношения между параметрами потока воздуха
на прямом скачке
М1
М2
p2/p1
σ
М1
М2
p2/p1
σ
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,0000
0,9531
0,9118
0,8750
0,8422
0,8126
0,7860
0,7618
0,7397
0,7196
1,000
1,120
1,245
1,376
1,513
1,656
1,805
1,960
2,120
2,286
1,0000
0,9999
0,9989
0,9967
0,9928
0,9871
0,9794
0,9697
0,9582
0,9448
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
2,95
3,00
0,5083
0,5039
0,4996
0,4956
0,4918
0,4882
0,4847
0,4814
0,4782
0,4752
7,420
7,720
8,026
8,338
8,656
8,980
9,310
9,645
9,986
10,333
0,4793
0,4601
0,4416
0,4236
0,4062
0,3895
0,3733
0,3577
0,3428
0,3283
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,05
2,10
0,7011
0,6841
0,6684
0,6540
0,6405
0,6281
0,6165
0,6057
0,5956
0,5862
0,5774
0,5691
0,5613
2,458
2,636
2,820
3,010
3,205
3,406
3,613
3,826
4,045
4,270
4,500
4,736
4,978
0,9298
0,9132
0,8952
0,8760
0,8557
0,8346
0,8127
0,7902
0,7674
0,7442
0,7209
0,6975
0,6742
3,05
3,10
3,15
3,20
3,25
3,30
3,35
3,40
3,45
3,50
3,55
3,60
3,65
0,4723
0,4695
0,4669
0,4643
0,4619
0,4596
0,4573
0,4552
0,4531
0,4512
0,4492
0,4474
0,4456
10,686
11,045
11,410
11,780
12,156
12,538
12,926
13,320
13,720
14,125
14,536
14,953
15,376
0,3145
0,3012
0,2885
0,2762
0,2645
0,2533
0,2425
0,2322
0,2224
0,2129
0,2039
0,1953
0,1871
2,15
2,20
2,25
2,30
2,35
2,40
2,45
2,50
0,5540
0,5471
0,5406
0,5344
0,5286
0,5231
0,5179
0,5130
5,226
5,480
5,740
6,005
6,276
6,553
6,836
7,125
0,6511
0,6281
0,6055
0,5833
0,5615
0,5401
0,5193
0,4990
3,70
3,75
3,80
3,85
3,90
3,95
4,00
0,4439
0,4423
0,4407
0,4392
0,4377
0,4363
0,4350
15,805
16,240
16,680
17,126
17,578
18,036
18,500
0,1792
0,1717
0,1645
0,1576
0,1510
0,1448
0,1388
130
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ....................................................................................................1
ЧАСТЬ 1 ГИДРАВЛИКА И ГИДРАВЛИЧЕСКИЕ СИСТЕМЫ ..............4
СВОЙСТВА ЖИДКОСТЕЙ .............................................................................4
ГИДРАВЛИЧЕСКИЙ УДАР ............................................................................6
ГИДРОСТАТИКА..........................................................................................9
ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ ....................................................... 13
ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ ...................................16
РАСПЫЛИВАНИЕ ТОПЛИВА В ДИЗЕЛЯХ .................................................... 20
ОСНОВЫ ГИДРАВЛИЧЕСКИХ РАСЧЕТОВ СИСТЕМ .....................................25
Потери напора на трение ............................................................... 25
Местные потери давления в трубах .............................................. 27
ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ И НАСАДКОВ ............................. 34
Истечение из малых отверстий в тонкой стенке сосуда ........... 34
Истечение из насадков и коротких труб ......................................35
Истечение при переменном напоре ................................................ 35
НАСОСЫ И ИХ РАБОТА НА СЕТЬ ............................................................... 39
Центробежные насосы ...................................................................39
Насосы объемного типа ..................................................................44
ГИДРОДВИГАТЕЛИ ................................................................................... 50
ЧАСТЬ 2. ГИДРАВЛИЧЕСКИЕ ПЕРЕДАЧИ И ГИДРОПРИВОД ......... 54
ОБЪЕМНЫЕ ГИДРАВЛИЧЕСКИЕ МАШИНЫ И ИХ ВЫБОР ............................ 54
Объемные насосы и их выбор .......................................................... 54
Объемные гидромоторы и их выбор .............................................. 57
Гидроцилиндры и их выбор .............................................................. 58
МОЩНОСТЬ И ТЕПЛОВЫЕ ПОТЕРИ ГИДРОПРИВОДА .................................61
РАСЧЕТ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ГИДРОПРИВОДОВ ................. 64
РАСЧЕТ ТРУБОПРОВОДОВ......................................................................... 72
ГИДРОДИНАМИЧЕСКИЕ ПЕРЕДАЧИ .......................................................... 74
Определение основных параметров гидротрансформатора ......77
ЧАСТЬ 3. ГАЗОВАЯ ДИНАМИКА ........................................................... 84
ОСНОВНЫЕ ГАЗОДИНАМИЧЕСКИЕ ПОНЯТИЯ И ЗАВИСИМОСТИ ............... 84
ОДНОМЕРНОЕ ИЗОЭНТРОПИЧЕСКОЕ ТЕЧЕНИЕ ГАЗА ................................ 87
ОПРЕДЕЛЕНИЕ РАСХОДА ГАЗА ЧЕРЕЗ СОПЛО ........................................... 90
ПРЯМЫЕ СКАЧКИ УПЛОТНЕНИЯ............................................................... 93
ТЕЧЕНИЕ ГАЗА С УЧЕТОМ ТРЕНИЯ ........................................................... 96
ТЕЧЕНИЕ ГАЗА ПРИ НАЛИЧИИ ЭНЕРГООБМЕНА........................................ 99
ПРИЛОЖЕНИЕ 1 ...................................................................................... 103
ПРИЛОЖЕНИЕ 2 ...................................................................................... 114
ПРИЛОЖЕНИЕ 3 ...................................................................................... 127
Учебное издание
Остренко Сергей Александрович
Пермяков Владимир Васильевич
ГИДРАВЛИКА,
ГИДРАВЛИЧЕСКИЙ ПРИВОД
И ГАЗОВАЯ ДИНАМИКА
Учебное пособие
Редактор Т.Э. Заворотная
Корректор Л.З. Анипко
Компьютерная верстка С.Ю. Заворотной
Лицензия на издательскую деятельность ИД № 03816 от 22.01.2001
Подписано в печать 11.07.2003. Формат 6084/16.
Бумага писчая. Печать офсетная. Усл. печ. л. 8,83.
Уч.-изд. л. 8,0. Тираж 300 экз. Заказ
________________________________________________________
Издательство Владивостокского государственного университета
экономики и сервиса
690600, Владивосток, ул. Гоголя, 41
Отпечатано в типографии ВГУЭС
690600, Владивосток, ул. Державина, 57