Лабораторная работа № 5 RC Цель работы
реклама

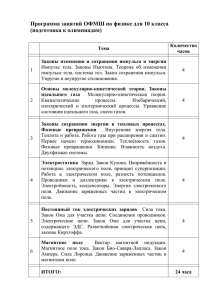
Лабораторная работа № 5 ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ RC-ЦЕПИ Цель работы. Анализ переходных процессов в простейших RC-цепях, а также условий дифференцирования и интегрирования сигналов с помощью этих цепей. Изучение методов расчета и анализа данных цепей. В радиоэлектронных устройствах различного назначения широко используются сигналы сложной формы. С целью получения таких сигналов могут применяться различные формирующие цепи. К их числу относятся простейшие RC-цепи, на выходе которых форма сигнала приближенно соответствует производной или интегралу от напряжения, поданного на их вход. В общем виде дифференцирующую и интегрирующую цепи можно представить как линейные четырехполюсники (рис. 5.1, а, б). В явном виде для R и C элементов дифференцирующая цепь показана на рис. 5.2, а, а интегрирующая – на рис. 5.2, б. Ниже показано, что, используя такие цепи и варьируя величиной постоянной времени = RC, можно реализовать операции дифференцирования, интегрирования или получить переходную цепь. d U1 U2 U1 dt U2 Рис. 5.1 R C U1 U2 R U1 а U2 C б Рис. 5.2 Для выяснения физических процессов, протекающих в таких цепях, рассмотрим переходные процессы, возникающие при заряде и разряде конденсатора в цепи, состоящей из активного сопротивления и емкости. Пусть в момент времени t01 = 0, напряжение Uc = 0 (рис. 5.3), RC-цепь подклю25 чается к источнику постоянного напряжения, и в ней появляется ток заряда конденсатора. Тогда, пренебрегая внутренним сопротивлением источника сигнала, согласно второму закону Кирхгофа, для этой цепи можно записать UС + UR = E . (5.1) Но dU C dU . iз С C и U R iз R RС (5.2) dt dt Подставляя значение UR из соотношения (5.2) в выражение (5.1), после очевидных преобразований имеем dUС 1 1 (5.3) UC E. dt RC RC Уравнение (5.3) является линейным дифференциальным уравнением, и его решение можно записать в виде U С E 1 e t , (5.4) где = RC – постоянная времени цепи. Продифференцировав уравнение (5.4) по времени, с учетом выражения (5.2), получим dU С CE t iз C e dt E e t . R Тогда напряжение UR будет равно U R Riз Ee t . 1 K 2 (5.5) Iз С UС Iр (5.6) + Выражения (5.4)–(5.6) показывают, E R UR что напряжение на емкости в процессе заряда возрастает, а ток через сопротивление и напряжение на нем убывает по экспоненциальному закону. Скорость Рис. 5.3 этих процессов определяется постоянной времени цепи : чем больше величина емкости и активного сопротивления, тем медленнее растет напряжение UС и медленнее спадает напряжение UR. Зависимости изменения тока заряда и напряжений на емкости и сопротивлении показаны на рис. 5.4, а. 26 –Iр U0С R Iз E R t01 t02 t UС UС E U0С t01 t t02 t t –UR UR E U0С t01 t02 t а t б Рис. 5.4 Если в момент времени t02 замкнуть заряженный конденсатор С на активное сопротивление R, то в нем потечет разрядный ток, и тогда можно записать UС U R 0 , (5.7) где U R iр R, а iр С dU С . dt (5.8) С учетом выражения (5.8), соотношение (5.7) принимает вид U C RС dU С 0 . dt (5.9) Решением дифференциального уравнения (3.9) является выражение U C U 0С e t , (5.10) где U0С – начальное напряжение на конденсаторе в момент времени t02. Подстановка в выражение (5.8) значения UС из зависимости (5.10) позволяет записать для величины тока разряда 27 iр С dU С U U C 0С e t 0С e t dt R . (5.11) Аналогично с течением времени изменяется и напряжение на активном сопротивлении (5.12) U R i p R U 0С et . Появление знака «минус» в выражениях (5.11) и (5.12) объясняется выбором направления обхода контура при записи уравнения (5.7). Осциллограммы изменения тока разряда и напряжений на емкости С и сопротивлении R представлены на рис. 5.4, б. Теоретически переходные процессы длятся бесконечно долго. Однако процесс принято считать установившимся (оконченным), если разность между изменяющейся величиной и ее предельным значением составляет 5 %. Поэтому при определении времени переходного процесса выражение (5.4) можно переписать в виде 0,95E U С t tпер E 1 e tпер , где tпер – время переходного процесса, откуда следует, что t e пер 0,05. Прологарифмировав равенство (5.13), получим tпер 3 . (5.13) (5.14) Для выяснения физического смысла величины определим разность между пределом, к которому стремится экспонента, и любыми двумя мгновенными значениями ее, разделенными временем, равным : UС t t1 t 1 E 1 e , U С t t1 t 1 E 1 e . (5.15) t t 1 1 E E 1 e Ee , (5.16) Тогда указанные разности запишутся E U С t t 1 t t1 1 E E 1 e Ee , E U С t t1 а их отношение будет равно E UС E UС 28 t t1 t t1 e. (5.17) Таким образом, постоянная численно равна промежутку времени, в течение которого разность между экспоненциально изменяющейся величиной и ее пределом уменьшается в 2,71 раза. Очевидно, что рассмотренный случай заряда и разряда конденсатора аналогичен ситуации, когда на вход RC-цепи подается одиночный прямоугольный импульс и выполняется условие tи. На рис. 5.5 приведены UС 1 1 временные диаграммы 2 2 3 напряжений UС (t) и UR (t) 4 3 для различных отношений 4 между постоянной времени tи t цепи и длительностью UR входного импульса tи. Из 4 1 < 2 < 3 < 4 3 рисунка видно, что при ма2 лом по сравнению с tи зна1 чении форма напряжения на емкости UС (t) оказываt ется близкой к форме входного импульса Uвх(t), обо 1 2 3 4 значенного на рис. 5.5 пунктиром. С увеличением Рис. 5.5 отношения / tи длительность фронта UС (t) растет, а его амплитуда уменьшается. Как следует также из рис. 5.5, при больших значениях величины / tи форма напряжения на резисторе UR (t) оказывается близкой к форме Uвх(t). При этом наблюдается завал вершины импульса напряжения UR (t), а также отрицательный выброс после его окончания. Величины завала и отрицательного выброса уменьшаются при увеличении отношения / tи. При достаточно малых значениях / tи форма напряжения на сопротивлении представляет собой два импульса остроконечной формы. 1 Дифференцирующие цепи С помощью RC-цепи можно проводить дифференцирование импульса. Пусть на вход RC-цепи (рис. 5.6) подан сигнал Uвх. Тогда UС UR Uвх , 1 но UС idt , а UR = Ri и, следовательно, C 1 U вх idt Ri . (5.18) C 29 Умножая числитель и знаменатель первого слагаемого в правой части уравнения (5.18) на R и учитывая, что напряжение на выходе Uвых = UR, получим 1 U вх U вых dt U вых . (5.19) RC Дифференцируя обе части уравнения (5.19) по времени t, приходим к выражению dU вх 1 dU вых . U вых (5.20) dt dt При условии и что dU вых dt 1 U вых , что справедливо, когда достаточно мала tи, на основании равенства (5.20) будем иметь dU U вых вх , (5.21) dt откуда следует, что выходное напряжение пропорционально производной от входного, т. е. имеет место процесс дифференцирования сигнала. 1 Если положить, что очень велика ( tи), и значением U вых по dU вых сравнению с С можно пренебречь, то на основании соотношения dt dU вх dU вых (5.20) получим , откуда Uвых = Uвх и RC-цепь в этих усло dt dt виях становится переходной, т. е. такой цепью, проходя через которую, выходной сигнал повторяет входной. Эта цепь может использоваться, например, для связи между отдельными каскадами многокаскадного усилителя. Из сказанного выше следует, что дифференцирование будет тем точнее, чем меньше постоянная времени цепи = RC. Дифференцирующую цепь называют также обостряющей или С укорачивающей, так как длительность выходных импульсов меньше длительности входных, а их вершина является острой. Uвх Uвых R В случае tи при определении длительности продифференцированных импульсов появляется некоторая неопредеРис. 5.6 ленность. Если же величину длительности импульса определять на уровне 0,5Um, где Um – его амплитуда, то то30 гда 0,5U m U m e t и 0,5 , откуда ln 0,5 tи0,5 , и тогда длительность импульса по уровню 0,5 будет равна tи 0 ,5 0,7. (5.22) Формула (3.22) может быть использована при экспериментальном определении постоянной времени цепи. Интегрирующие цепи Рассмотрим схему, изображенную на рис. 5.7. В данном случае выходной сигнал снимается с емкости и уравнение, описывающее рассматриваемую цепь Uвх = Ri + Uвых, можно представить в виде dU U вх вых U вых . (5.23) dt Пусть в выражении (5.23) велика так, что иметь U вх dU вых dt U вых , тогда будем dU вых , откуда dt 1 U вх dt , (5.24) т. е. выходное напряжение пропорционально интегралу от входного, и поэтому с помощью данной цепи выполняется операция интегрирования. Если же в равенстве (5.23) положить, что мала и выполняется соотU вых ношение dU вых dt U вых , то можем записать U вых U вх . (5.25) В этих условиях цепь называется переходной, т. к. выходной сигнал повторяет входной. Интегрирование происходит тем точR нее, чем больше постоянная времени . Но увеличение величины , как следует из выUвх Uвых С ражения (5.24), ведет к уменьшению величины выходного напряжения, поэтому идеально точное интегрирование с помощью рассмотренной выше цепи невозможно. Рис. 5.7 Условием приближенного интегрирования импульса является неравенство tи . 31 Аналогичные результаты по дифференцированию и интегрированию сигналов могут быть получены и с помощью RL-цепей, имеющих постоянную времени L / R. Расчетное задание 1. Рассчитать форму импульсов на выходе дифференцирующей цепи при действии на ее входе прямоугольного импульса длительностью tи, которая задана согласно варианту таблицы. Расчет производить по формуле (5.6) для значений 1 = 0,033tи и 2 = 0,33tи. Величину Е принять равной единице. 2. Зарисовать форму рассчитанных импульсов и оцифровать графики. 3. Рассчитать величины R и С для дифференцирующих и интегрирующих цепей при значениях 1 = 0,033tи, 2 = 0,33tи, 3 = tи, 4 = 3,3tи. Вариант f, кГц tи=Т/2, мкс 1 1,0 500 2 1,2 417 3 1,4 357 4 1,6 278 5 1,8 250 6 2,0 227 7 2,2 208 8 2,4 192 9 2,6 179 Лабораторное задание и методические указания 1. Собрать на стенде дифференцирующую цепь (1 = 0,033tи). 2. Подать с генератора импульсы прямоугольной формы с частотой следования f и длительностью tи = T / 2 (меандр). 3. Подключить осциллограф к выходу дифференцирующей цепи и зарисовать форму напряжения на выходе. При оцифровке графиков учесть, что все мгновенные значения напряжения импульса необходимо разделить на величину амплитуды входного импульса, т. е. провести нормировку, что облегчит сравнение расчетных и экспериментальных данных. Амплитуду входного импульса следует определять для каждого случая подключения RC-цепочки. Опред елить экспериментально по длительности продифференцированного импульса на уровне 0,5 постоянную времени дифференцирующей цепи. Полученные данные сравнить с расчетными. 4. Изменяя постоянную времени цепи = RC согласно теоретическому заданию, произвести измерения аналогично п. 3. 5. Поочередно собрать на стенде интегрирующие цепи с постоянной времени цепи согласно расчетному заданию. Подать на вход исследуемых схем прямоугольные импульсы длительностью tи и зарисовать осциллограмму выходного напряжения. Полученные рисунки оцифровать. 32 6. Сравнить расчетные и экспериментальные данные, объяснить возможные расхождения. 7. Используя программу Electronics Workbench, собрать схему дифференцирующей цепи соответственно рис. 5.8. Изменяя постоянную времени цепи согласно теоретическому заданию, произвести измерения аналогично п. 3. 8. В среде Electronics Workbench поочередно собрать интегрирующие цепи с постоянной времени цепи согласно расчетному заданию. Подать на вход исследуемых схем прямоугольные импульсы длительностью tи и зарисовать осциллограмму выходного напряжения. Полученные рисунки оцифровать. Исследуемая цепь Рис. 5.8 Контрольные вопросы 1. Какие физические процессы протекают в цепи при подключении к источнику тока последовательно включенных сопротивления R и емкости C? 2. Какие физические процессы протекают в цепи, если к заряженному конденсатору подключить сопротивление? 3. Каков физический смысл постоянной времени цепи ? 4. Если сигнал снимается с сопротивления R, почему цепь называют обостряющей или дифференцирующей, а если с емкости С, то интегрирующей? 5. Как меняется спектр сигнала дифференцирующей цепью? 6. Как меняется спектр сигнала интегрирующей цепью? 33 Лабораторная работа № 6 ПОСЛЕДОВАТЕЛЬНЫЙ И ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ Цель работы. Исследование резонансных свойств последовательного и параллельного колебательных контуров. В различных радиотехнических устройствах, в частности, в радиоприемных, одной из важнейших операций является выделение полезного сигнала из всевозможных побочных сигналов и помех. Эти функции выполняются электрическими колебательными системами, основной элемент которых – колебательный контур. При изучении свойств колебательного контура главное внимание обращается на его резонансные свойства, которые и определяют его частотную избирательность. В зависимости от способа включения элементов колебательного контура индуктивности L и емкости С по отношению к внешнему источнику возбуждения различают последовательный и параллельный колебательные контуры. Свободные колебания в контуре При отсутствии внешнего возбуждения в колебательном контуре с первоначально запасенной энергией электрического поля в конденсаторе или магнитного поля в индуктивности возникают свободные колебания. Рассмотрим переходные процессы в цепи, состоящей из индуктивности L, емкости C и активного сопротивления R (рис. 3.1). Если предварительно зарядить конденсатор C, а затем в начальный момент времени t = 0 замкнуть его на цепь, состоящую из последовательно включенных элементов L и R, то в таком контуре будет идти процесс периодического преобразования электрической энергии в магнитную, и наоборот. В этом случае функция, описыK вающая внешнее воздействие при любых t ≥ 0, равна нулю и уравнение Кирхгофа для R такой цепи имеет вид + L C di 1 Ri L idt 0 . (6.1) dt C После дифференцирования обеих частей соотношения (6.1) по времени и деления на Рис. 6.1 L приходим к следующему дифференциаль34 ному уравнению для тока в контуре d 2i R di 1 i 0. 2 L dt LC dt Введем следующие параметры: 1 R 1 , 0 или f 0 . 2L LC 2 LC Тогда с учетом соотношения (6.1) уравнение (6.2) принимает вид d 2i di 2 2i 0 . 0 dt dt 2 (6.2) (6.3) (6.4) Решение этого дифференциального уравнения будем искать в виде (6.5) I t Ze t , где Z – некоторая новая переменная. Подстановка решения (6.5) в уравнение (6.4) приводит к d 2Z (6.6) 0 2 2 Z 0 . 2 dt Обозначим 2 (6.7) 0 2 . С учетом обозначения (6.7) дифференциальное уравнение (6.6) принимает вид d 2Z 2 Z 0. 2 dt (6.8) Как известно, решением колебательного уравнения (6.8) является функция вида Z I m cos t . (6.9) После подстановки этого решения в выражение (6.5) для тока І получим окончательно I t I met cos t . (6.10) Из уравнения (6.10) следует, что ток в колебательном контуре изменяется по гармоническому закону, причем его амплитуда с течением времени непрерывно уменьшается. Затухание амплитуды тока аналитически описывается множителем e–t. Скорость затухания собственных колебаний в контуре можно охарактеризовать отношением амплитуд тока в некоторые моменты времени t1 и t1 + T, отстоящих друг от друга на период колебаний Т (рис. 6.2). С учетом формулы (6.10), находим это отношение 35 Ime–t I I(t) t1 I(t + T) t1 +T t Рис. 6.2 i t1 et1 e T . (6.11) i t1 T e t1 T Натуральный логарифм выражения (6.11) носит название логарифмического декремента затухания контура, и для контура с малыми потерями будет иметь вид Т R R , LC (6.12) где L C – волновое или характеристическое сопротивление контура. На практике вместо логарифмического декремента затухания (6.12) часто используется пропорциональная ему величина – затухание d: d R 1 , Q (6.13) Q=/R, (6.14) где параметр Q, равный называется добротностью контура. С энергетической точки зрения добротность контура характеризует отношение запасенной электромагнитной энергии контура при резонансе к средней энергии, теряемой в этом режиме на активном сопротивлении контура за один период изменения тока. Добротность Q контура с малым затуханием можно оценить путем подсчета по осциллограмме числа периодов свободных колебаний в контуре m за интервал времени, в течение которого амплитуда собственных колебаний контура уменьшается, например, в два раза. Тогда согласно e t соотношению (6.12) t mT 2, или emТ= 2, откуда mТ = ln 3. При e этом логарифмический декремент затухания на основании формулы 1 1 36 (6.12) будет равен = T = ln 2/m, а затухание d выразится как d = / = ln 2/m. Отсюда добротность контура будет равна Q 1 m 4,53m . d ln 2 (6.15) Последовательный колебательный контур Последовательный колебательный контур (рис. 6.3) образуется при последовательном включении емкости C, индуктивности L и генератора ЭДС e(t). Для учета всех активных потерь в контуре L на схемах включают эквивалентное сопротивление R. R Будем считать в дальнейшем ЭДС гармонической, а C e(t) внутреннее сопротивление генератора Ri = 0. В этом случае все частотные характеристики контура называются предельными. Для цепи, изображенной на рис. 6.3, можно запиРис. 6.3 сать уравнение Кирхгофа в комплексном виде 1 E IR IjL I , jC (6.16) j t j t E Eme jt , I I m e I I me jt . Здесь Em и Im – амгде E E m e плитуды, E m и Im – комплексные амплитуды соответственно ЭДС и тока. Тогда, согласно методу комплексных амплитуд, на основании (6.16) получим Im E m 1 R j L C E m Z j . (6.17) В выражении (6.17) 1 Z j R j L R jX C (6.18) называют комплексным входным сопротивлением, в котором величина X L 1 C (6.19) является его реактивной составляющей. ФЧХ контура при этом определяется зависимостью arctg X arctg R L R 1 C . (6.20) 37 Рассмотрим зависимость входного сопротивления последовательного колебательного контура Z j от частоты генератора. На рис. 6.4 построены зависимости ХL = L и –ХC = –1 / C, а также X = XL + (–XC) как функции частоты генератора . Как видно из рисунка, характер сопротивления контура определяется соотношением между ХL и ХC. Так, для частот < 0 выполняется неравенство XL < XC, и характер сопротивления контура емкостный, а при > 0 – неравенство ХL > ХC, и характер сопротивления контура индуктивный. С практической точки зрения случай = 0, когда XL = XC, представляет наибольший интерес, поскольку соответствует условию резонанса. XL, XC, XL + XC ХL = L XL + XC о XC = 1 C Рис. 6.4 1 1 Итак, при резонансе Х = 0 или 0 L C 0, отсюда 0 . АмLC 0 плитуда тока при резонансе достигает максимума и равна I0 = Em / R. Напряжения на реактивных элементах L и C соответственно имеют значения U L j рез Em E 1 0 L jEm jQEm и U Cрез m jEm jQEm , R R R j0C R т. е. напряжения на индуктивности и емкости при резонансе в последовательном колебательном контуре равны по модулю, сдвинуты по фазе на и в Q раз больше, чем ЭДС источника. Параллельный колебательный контур Параллельным колебательным контуром называется цепь, состоящая из параллельно включенных индуктивности L, емкости C и генератора ЭДС. Если заменить индуктивность L и емкость C соответствующими эквивалентными элементами, состоящими из включенных последовательно L и rL для индуктивности и C и rC для конденсатора, то приходим к схеме параллельного контура, представленной на рис. 6.5. Рассмотрим предварительно предельные характеристики такого параллельного кон38 тура. Они реализуются, если к контуру подключить источник тока с внутренним сопротивлением Ri . Ri e(t) L С rL rC IC IL I Рис. 6.5 Для входного сопротивления контура запишем очевидное равенство 1 L rС rL rC rL rC jC C Z пар j 2 1 1 2 rL rС j L C rL rC L C jL rL rL 1 1 L 1 rС2L rL2 L LrC L C C C C C j 2 2 1 1 2 2 r r L r r L L C L C C C . (6.21) Резонансную частоту можно найти, если приравнять к нулю мнимую часть выражения (6.21), а именно ее числитель 2 rC p L rL 2 1 L 1 p L 0. p C C p C (6.22) Тогда решение уравнения (6.22) относительно p дает 2 p С учетом того, что rL С L 2 rC C 2 L L2 C 1 LC 1 LC rL2 C 1 L . rС2 C 1 L (6.23) 0 , а L , соотношение (6.23) принимает C р 0 2 rL2 . 2 r C2 вид (6.24) Простейший анализ выражения (6.24) приводит к следующим выводам. 39 1. Если r L = r C = 0 или rL = rC 0, то р = 0, т. е. резонансная частота параллельного контура совпадает с резонансной частотой последовательного контура, состоящего из идентичных параллельному элементов. 2. Если rL > rC или rC = 0, то р < 0, а при rL < rC или rL = 0, р > 0. Таким образом, р в зависимости от соотношения между rL и rC может быть как больше, так и меньше 0. Расчетное задание Последовательный контур: 1. Определить по формуле (6.3) частоту f0 для последовательных контуров рис. 6.3, у которых L = 0,97 мГн, а С берется согласно заданному варианту из таблицы. Вариант C, нФ R, Ом 1 2,7 18 2 3,0 9,1 3 3,3 15 4 3,6 16 5 3,9 10 6 4,3 12 7 4,7 10 8 5,1 8,2 9 5,6 13 10 6,2 6,2 2. Определить с помощью соотношений (6.14) величины добротности Q1 и Q2 контуров у которых: а) RГ = 8,2 Ом, RL = 2,7 Ом, C берется согласно варианту из таблицы, L = 0,97 мГн (рис. 6.6, а); б) RГ = 8,2 Ом, RL = 2,7 Ом, C и R берутся согласно варианту из таблицы, L = 0,97 мГн (рис. 6.6, б). RL – активное сопротивление катушки индуктивности. На схемах рис. 6.6 оно не показано. Параллельный контур: 1. Определить по формуле (6.24) частоту fp параллельного контура (рис. 6.7). Считать при этом, что все активное сопротивление контура RL = 2,7 Ом сосредоточено в его индуктивной ветви. L Uвх L С Uвых Uвх RГ а С RГ б Рис. 6.6 40 R Uвых С1 Uвх С L Uвых Рис. 6.7 Лабораторное задание и методические указания 1. На монтажной плате стенда собрать поочередно последовательные контуры, изображенные на рис. 6.6. Элементы контуров взять согласно расчетному заданию. 2. Собрать схему для исследования последовательного контура. Для этого на вход собранного контура подключить генератор, а к выходу контура подключить осциллограф либо вольтметр переменных напряжений. 3. Снять необходимые данные и построить графики резонансных кривых для контуров рис. 6.6. С этой целью сначала следует по осциллографу или вольтметру настроиться на резонансную частоту (по максимуму показания прибора). Затем, задавая расстройку (например, через 1кГц) при постоянном напряжении, подаваемом с генератора, получить данные для построения резонансной кривой. 4. По полученным данным построить графики резонансных кривых. 5. Для схемы рис. 6.7 провести измерения, аналогичные п. 3. 6. Определить добротность контура методом ударного возбуждения. С этой целью подать от генератора на вход контура последовательность импульсов прямоугольной формы. Подобрать их частоту так, чтобы на экране осциллографа получилось изображение, аналогичное рис. 6.2. По полученной осциллограмме определить число m периодов колебаний, на протяжении которых амплитуда собственных колебаний контура уменьшается в 2 раза. Рассчитать по формуле (6.15) добротность контура. 7. Используя программу Electronics Workbench, собрать изображенную на рис. 6.8 схему. 8. Снять и построить АЧХ последовательного колебательного контура. Для построения АЧХ (включена кнопка Magnitude) установить на измерителе АЧХ линейную (кнопка Lin) шкалу по вертикали и линейную (кнопка Lin) – по горизонтали. Минимальную (кнопка I) и макси41 мальную (кнопка F) частоты задавать в зависимости от резонансной частоты колебательного контура в пределах ±10 кГц. При необходимости произвести корректировку установленных значений частоты. В блоке Vertical задать изменение коэффициента передачи в пределах 0 100. При необходимости произвести корректировку установленных значений коэффициента передачи. Номинальное значение емкости С взять из табл. 6.1, а величину резистора R изменять от 6,2 Ом до 18 Ом. Снять и зарисовать пять АЧХ колебательного контура при различных значениях резистора R. По полученным АЧХ определить полосу пропускания контура и рассчитать его добротность для каждого случая. Для расчета добротf ности использовать выражение Qэксп 0 , где f – полоса пропуска2f ния контура, определяемая на уровне 0,7 от максимального значения коэффициента передачи, а f 0 – его резонансная частота. Колебательный контур Рис. 6.8 5. Пользуясь выражением Qрасч , где L , рассчитать велиC R чину добротности для каждого случая и сравнить с полученной экспериментально. Полученные данные свести в таблицу, в которой указать величины R, L, C, f , Qэксп и Qрасч . Контрольные вопросы 1. Какими параметрами характеризуется колебательный контур? 2. Какие электромагнитные колебания в контуре называются собственными; вынужденными? 3. Чем определяется частота свободных колебаний в контуре? 42