Решение задач типа А3 ОГЭ по информатике
реклама
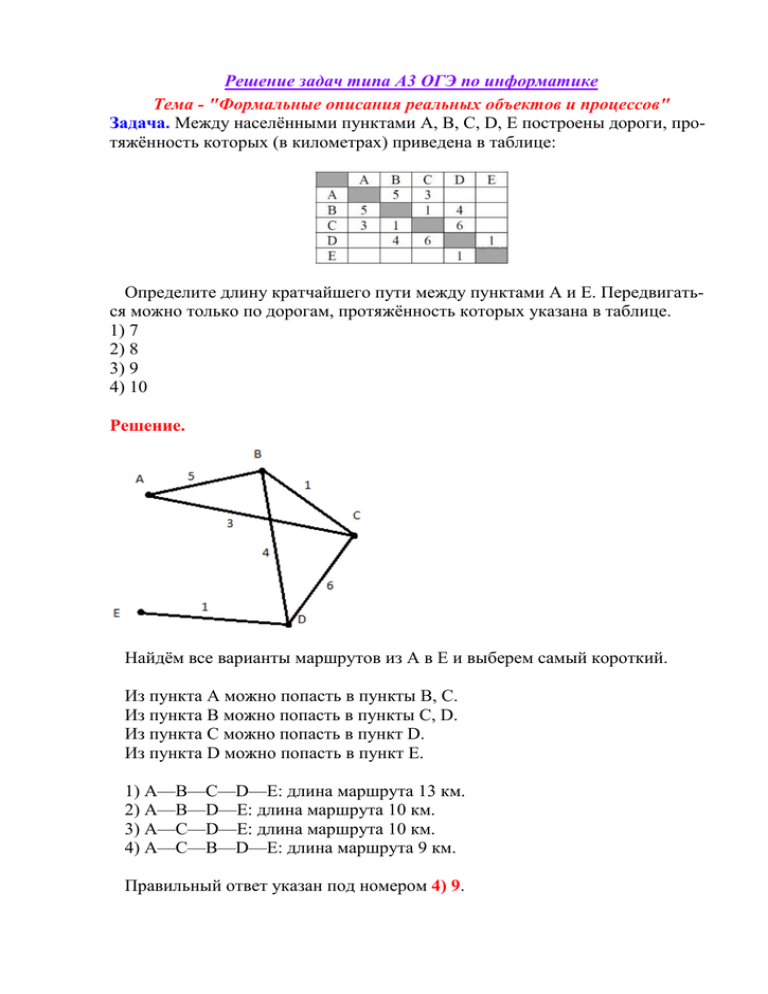
Решение задач типа А3 ОГЭ по информатике Тема - "Формальные описания реальных объектов и процессов" Задача. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице: Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. 1) 7 2) 8 3) 9 4) 10 Решение. Найдём все варианты маршрутов из A в E и выберем самый короткий. Из пункта A можно попасть в пункты B, С. Из пункта B можно попасть в пункты C, D. Из пункта C можно попасть в пункт D. Из пункта D можно попасть в пункт E. 1) A—B—C—D—E: длина маршрута 13 км. 2) A—B—D—E: длина маршрута 10 км. 3) A—C—D—E: длина маршрута 10 км. 4) A—C—B—D—E: длина маршрута 9 км. Правильный ответ указан под номером 4) 9. Задача. Иван-Царевич спешит выручить Марью-Царевну из плена Кощея. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого длинного участка кратчайшего пути от Ивана-Царевича до Марьи Царевны (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице: 1) 1 2) 2 3) 4 4) 6 Решение. Найдём все варианты маршрутов из И в М и выберем самый короткий. Из пункта И можно попасть в пункты А, Б, Г, М. Из пункта Г можно попасть в пункты И, М. Из пункта В можно попасть в пункты А, Б. Из пункта Б можно попасть в пункты В, И, М. И—А—В—Б—М: длина маршрута 7 км. И—Б—М: длина маршрута 4 км. И—Г—М: длина маршрута 7 км. И—М: длина маршрута 8 км. Самый короткий путь: И—Б—М; Длина маршрута 4 км, самый длинный участок этого пути равен 3) 4. Задача. У Пети Иванова родственники живут в 5 разных городах России. Расстояния между городами внесены в таблицу: Петя перерисовал её в блокнот в виде графа. Считая, что мальчик не ошибся при копировании, укажите, какой граф у Пети в тетради. 1) 2) 3) 4) Решение. Проверим последовательно каждый граф. 1) Не соответствует таблице, поскольку согласно графу не существует прямой дороги из пункта A в пункт D. 2) Не соответствует таблице, поскольку согласно графу расстояние между пунктами D и B равно 3. 3) Граф соответствует таблице. 4) Не соответствует таблице, поскольку согласно графу не существует прямой дороги из пункта D в пункт C. Правильный ответ указан под номером 3. Задача. Водитель автомобиля должен добраться из пункта А в пункт D за 5 часов. Из представленных таблиц выберите такую, согласно которой водитель сможет доехать из пункта А в пункт D за это время. В ячейках таблицы указано время (в часах), которое занимает дорога из одного пункта в другой. Передвигаться можно только по дорогам, указанным в таблицах. 1) 1 2) 2 3) 3 4) 4 Решение. Найдём кратчайшие маршруты из A в D для каждой таблицы. Исходя из первой таблицы, кратчайший маршрут из A в D: A—C—B—D, его можно преодолеть за 6 часов. Кратчайший маршрут из A в D для второй таблицы: A—B—D, его можно преодолеть за 5 часов. Для третьей таблицы кратчайшая дорога: A—C—B—D, она занимает 6 часов. Для четвёртой таблицы кратчайший маршрут: A—D, его можно преодолеть за 6 часов. Правильный ответ указан под номером 2) 2. Задача. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице. A A B C D E F B C D E F 3 5 15 3 3 5 3 5 2 5 3 2 7 15 3 7 Определите длину кратчайшего пути между пунктами A и F. Передвигаться можно только по дорогам, указанным в таблице. 1) 9 2) 11 3) 13 4) 15 Решение. Для удобства отобразим табличные данные в виде графа Решение задачи 2 ГИА по информатике Теперь переберем все возможные пути из A в F: A-B-C-E-F = 3+3+2+7 = 15 A-B-C-D-F = 3+3+5+3 = 14 A-C-E-F = 5+2+7 = 14 A-C-D-F = 5+5+3 = 13 ну и A-F = 15 Как видно, кратчайший вариант A-C-D-F = 13км. Правильный ответ 3. Задача. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице. A B C D E A 2 5 1 B 2 1 C 5 1 3 2 D 1 3 E 2 Определите длину кратчайшего пути между пунктами A и Е. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. 1) 4 2) 5 3) 6 4) 7 Решение. Для удобства предлагаю поступить так же, как и при решении задачи ГИА 2013 года и отобразить таблицу в виде графа. Для этого на листе расставляем точки — населенные пункты. В соответствии с таблицей соединяем их и подписываем расстояния. Осталось рассмотреть все возможные маршруты из A в E и найти кратчайший из них. При этом обращаем внимание на то, что в пункт E мы можем попасть только из пункта C. A-B-C-E = 2+1+2 = 5 A-C-E = 5+2 = 7 A-D-C-E = 1+3+2 = 6 Как видим, минимальное расстояние — 5 километров (маршрут A-B-CE). Правильный ответ 2. Задача. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице. Определите длину кратчайшего пути между пунктами A и B (при условии, что передвигаться можно только по построенным дорогам). 1) 11 2) 12 3) 13 4) 14 Решение. Преобразуем таблицу в граф для удобства. Осталось перебрать все маршруты из A в B и посмотреть их длину: A-C-D-B = 8+1+4 = 13 A-C-E-B = 8+3+1 = 12 A-D-B = 10+4 = 14 A-D-C-E-B = 10+1+3+1 = 15 Как видим, минимальный по длине маршрут A-C-E-B, который составляет 12 километров. Правильный ответ 2. Задача. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице: Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. 1) 5 2) 6 3) 7 4) 8 Решение. Найдём все варианты маршрутов из A в E и выберем самый короткий. Из пункта A можно попасть в пункт B. Из пункта B можно попасть в пункты C, D, E. Из пункта C можно попасть в пункт E. Из пункта D можно попасть в пункт E. A—B: длина маршрута 1 км. A—B—C—E: длина маршрута 6 км. A—B—D—E: длина маршрута 7 км. A—B—E: длина маршрута 8 км. Правильный ответ 2.





