Правила преобразования уравнений
реклама
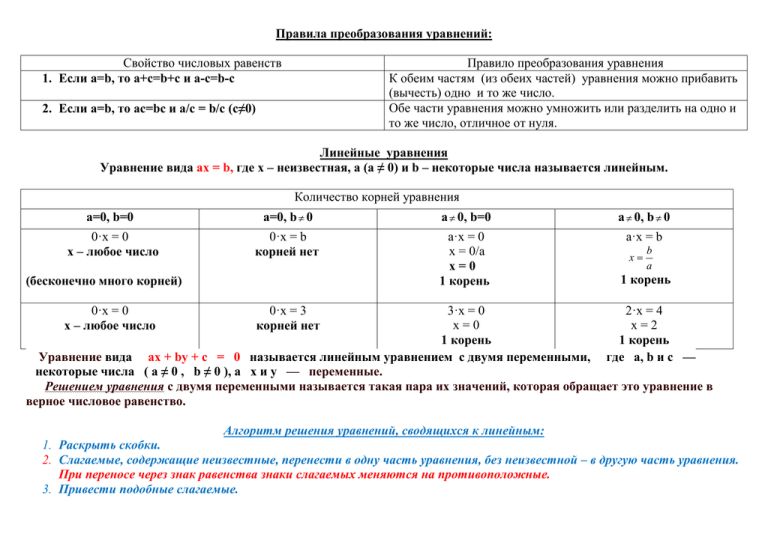
Правила преобразования уравнений: Свойство числовых равенств 1. Если а=b, то a+c=b+с и a-c=b-c Правило преобразования уравнения К обеим частям (из обеих частей) уравнения можно прибавить (вычесть) одно и то же число. Обе части уравнения можно умножить или разделить на одно и то же число, отличное от нуля. 2. Если a=b, то ac=bc и a/c = b/c (c≠0) Линейные уравнения Уравнение вида ax = b, где x – неизвестная, a (а ≠ 0) и b – некоторые числа называется линейным. Количество корней уравнения a=0, b=0 a=0, b 0 a 0, b=0 a 0, b 0 0·x = 0 x – любое число 0·x = b корней нет a·x = 0 x = 0/а x=0 1 корень a·x = b (бесконечно много корней) 0·x = 0 x – любое число x b a 1 корень 0·x = 3 корней нет 3·x = 0 2·x = 4 x=0 x=2 1 корень 1 корень Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными, где a, b и c — некоторые числа ( a ≠ 0 , b ≠ 0 ), а х и у — переменные. Решением уравнения с двумя переменными называется такая пара их значений, которая обращает это уравнение в верное числовое равенство. Алгоритм решения уравнений, сводящихся к линейным: 1. Раскрыть скобки. 2. Слагаемые, содержащие неизвестные, перенести в одну часть уравнения, без неизвестной – в другую часть уравнения. При переносе через знак равенства знаки слагаемых меняются на противоположные. 3. Привести подобные слагаемые. 4. Найти неизвестный множитель (решить уравнение вида ax = b, x = b , где a≠0). a Чтобы выяснить, является уравнение линейным надо привести его к стандартному виду. ax + by + c = 0 либо y = kx + m, где k = – a/b, а m=-c/b График линейного уравнения с двумя переменными Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения. Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными. Алгоритм построения графика линейного уравнения с двумя переменным. 1. Начертить координатные оси, подписать их и отметить единичный масштаб. 2. В линейном уравнении положить х = 0, и решить полученное уравнение относительно у. Отметить полученную точку на графике. 3. В линейном уравнении в качестве у взять число 0, и решить полученное уравнение относительно х. Отметить полученную точку на графике 4. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую. (Для построения прямой достаточно указать две её точки) Пример: Построить график уравнения 3x – 2y =6; Если х=0, тогда – 2y =6; y= -3; Если y=0, тогда 3x = 6; x=2; Записать можно и в виде таблицы: х у 0 -3 2 0 Отмечаем полученные точки (0;-3) и (2;0) на графике, проводим через них прямую и подписываем её.
