домашняя контрольная работа по дисциплине Техническая

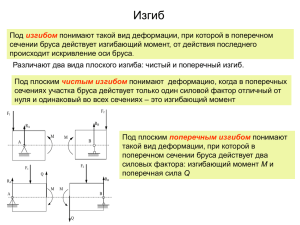
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Дисциплина «Техническая механика» для строительных специальностей включает
в себя три раздела: теоретическую механику, сопротивление материалов и статику
сооружений.
В результате освоения дисциплины обучающийся должен уметь:
 выполнять основные расчеты по теоретической механике, сопротивлению
материалов и статике сооружений;
В результате освоения дисциплины обучающийся должен знать:
 основные понятия и аксиомы теоретической механики;
 законы равновесия и перемещения тел;
 основные расчеты статически определимых плоских систем;
 методы расчета элементов конструкций на прочность, жесткость и устойчивость
Предлагаемое учебное пособие подготовлено в соответствии с государственным
стандартом по этой дисциплине. Предназначаемые студентам методические
рекомендации дают возможность целенаправленно ориентировать их в основных
вопросах программы. В методических рекомендациях указана основная литература. При
написании домашней контрольных работ студенты могут использовать предлагаемую
литературу, а также использовать другую литературу по дисциплине.
В процессе изучения курса студенту необходимо выполнить 1 домашнюю
контрольную работу. Выполнение данной работы определяется степень усвоения
студентами изученного материала и умение применять полученные знания при решении
практических задач.
Каждый студент должен выполнить 4 задания различного уровня сложности. В
каждом задание по 9 вариантов. Вариант контрольной работы определяется по двум
последним цифрам шифра. Если последние цифры больше 9, то их необходимо сложить
и по сумме определить номер варианта. Например, студент, имеющий шифр 11 - 03,
выполняет вариант 3, имеющий шифр 11 – 14, выполняет вариант 5 (1+4=5).
При выполнении домашней контрольной работы студент должен соблюдать
следующие требования:
1. К выполнению контрольной работы следует приступать лишь после того, как
весь учебный материал задания будет тщательно и глубоко изучен;
2. Контрольная работа должна представляться в сроки указанные в учебном
графике;
3. Работа должна быть выполнена аккуратно, разборчивым почерком;
4. В контрольную работу записывается условия задач;
5. Решение задач следует сопровождать пояснениями;
6. Вычислениям должны предшествовать исходные формулы;
7. Для всех исходных и вычислительных физических величин должны указываться
размерности;
8. Приводятся необходимые эскизы, схемы;
1
9. На каждой странице оставляются поля шириной 3 – 4 см, для замечаний
проверяющего работу;
10. Контрольная работа должна быть правильно оформлена. Образец титульного
листа выдается на заочном отделении. Обратите внимание на правильное
название дисциплины (по учебному плану) в конце работы следует указать
список учебной литературы, используемой при написании данной контрольной
работы (не менее 4 – 5 источников), фамилию автора, название книги и год
издания. Работу необходимо подписать и поставить дату ее выполнения;
11. При получении проверенной работы студент должен внимательно прочитать
замечания преподавателя, выполнить все его рекомендации и советы по
устранению недоработок и ошибок. Рецензирование контрольных работ имеет
целью дать студенту правильную направленность в самостоятельной работе над
учебным материалом, проверить качество работы студента по данному предмету
и умение применять теоретические знания при решении практических вопросов,
отметить положительные стороны в его работе, указать на имеющиеся ошибки,
рекомендовать пути их исправления;
6. Зачтенная контрольная работа предъявляется преподавателю на экзамене;
7. Контрольная работа не принимается на рецензию и возвращается студенту с
указанием причин в следующих случаях:
 если студент выполнил не свой вариант контрольной работы;
 если работа выполнена небрежно, неразборчивым почерком;
 если контрольная работа выполнена не в полном объеме.
В методических указаниях приведены примеры решения и оформления задач.
2
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ
ЗАДАНИЕ 1. Определить реакции в двухопроных балках
Таблица 1 – Схемы задач
Основные формулы и предпосылки расчета
1. Виды опор балок и их реакции
2. Момент силы относительно точки
3. Правило знаков момента сил относительно точки
Если сила относительно точки вращается по часовой стрелке, то момент
положительный. Если сила относительно точки вращается против часовой стрелки, то
момент отрицательный.
4. Условия равновесия


П
 FКХ  0 ;
П
 FКУ  0 ;
0
0
П
П
 FКХ  0 ;
0
 m КА  0 Проверка:
 m КА  0 ;
0
П
0
П
m
КВ
 0.
0
П
 m КВ  0 . Проверка:
0
П
F
КУ
 0.
0
3
Пример решения задач
Определить реакции опор в двухопорной балке.
Решение
1. Освобождаем балку от связей, действие которых заменяем их реакциями:
вертикальными RВУ, RАУ и вертикальной RАХ. Равномерно распределенную нагрузку
заменяем ее равнодействующей Fq, которая определяется как
Fq  q  2
Линия действия равнодействующей проходит через середину участка, на котором
расположена равномерно распределенная нагрузка.
2. Составляем уравнения равновесия.
 mA  0; F  3  m  q  2  2  R BY  4  0 (1)
m  0; - F 1  m  q  2  2  R
(3)
 X  0; R  0
B
AY
4  0
(2)
AX
3. Решаем систему уравнений
Из уравнения (1) находим:
R BY 
F  3  m  q  2  2 25  3  20  30  2  2

 53,75 кН.
4
4
Из уравнения (2) находим:
R AY 
F 1  m  q  2  2 25 1  20  30  2  2

 31,25 кН
4
4
4. Выполнить проверку:
Y  0;
R BY  q  2  F  R AY  0
53,75  30  2  25  31,25  0
Следовательно, реакции опор найдены, верно.
4
ЗАДАНИЕ 2. Определить положение центра тяжести в сечении, состоящего из простых
геометрических фигур
Таблица 1 – Схемы задач
Основные формулы и предпосылки расчета
1. Центры тяжести плоских фигур.
2. Координаты центров тяжести сложных и составных сечений.
n
XC 
 AK  XK
n
A
K
 УK
;
;
УC 
A
A
где АК – площади частей сечения;
ХК, УК – координаты центра тяжести частей сечений;
0
0
П
А – суммарная площадь сечения; А   А К .
0
3. Порядок решения задач:
5






Разбить конструкцию на простые фигуры;
Отметить центры тяжести каждой отдельной фигуры;
Отметить центр тяжести всей конструкции;
Провести оси координат;
Определить площади сечений каждой фигуры;
Определить координаты расположения каждого центра тяжести в
плоскости;
 Определить центр тяжести всей конструкции.
Пример решения задач
Определить положение центра тяжести в сечении, состоящего из простых
геометрических фигур.
Решение
1. Разбиваем сечение на три части:
1 – прямоугольник;
2 – трапеция;
3 – прямоугольник.
2. Отмечаем центры тяжести каждой отдельной части. Проводим оси координат.
3.Определяем координаты центра тяжести сечения С (хС, уС). составное сечение
симметрично, поэтому центр тяжести находится на оси симметрии и координата х С = 0,
то есть С (0, уС).
 А Н  У Н  А1  У1  А 2  У 2  А 3  У 3
УС 
А1  А 2  А 3
 АН
 вычисляем площадь отдельных фигур
А1  2  7  14 м2.
ав
73
А2 
h 
 2  10 м2
2
2
2
А 3  4  3  12 м
 определяем координаты центров тяжести отдельных фигур:
2
У1  8   7 м
2
7  3 2 2
У2  6 
  5,13 м
73 3
4
У3   2 м
2
14  7  10  5,13  12  2
УС 
 4,81 м
14  10  12
6
ЗАДАНИЕ 3. Для ступенчатого стального бруса требуется:
 определить значение продольной силы и нормального напряжения по длине
бруса;
 построить эпюры  и ;
 определить абсолютное удлинение (укорочение) бруса.
Модуль продольной упругости Е  2  105 МПа.
Таблица 1 – Схемы задач
Таблица 2 – Исходные данные
№ схемы
F1, м2
F2, м2
1
0,001
0,002
3
0,0055
0,0017
5
0,0012
0,0024
7
0,0035
0,0015
9
0,005
0,0025
№ схемы
F1, кН
2
26
4
17
6
10
8
40
P1, кН
20
90
15
60
70
F2, кН
20
13
12
55
P2, кН
30
40
25
20
30
F3, кН
10
8
13
24
l1 , м
1,2
2,5
2,5
1,4
2
l2 , м
1,5
0,7
2
0,8
1,3
A1, см2
4,6
2
0,9
2,8
l3 , м
1,8
1,9
1,4
1,7
1,1
l4 , м
1,3
0,5
2
A2, см
2,4
2,5
0,7
3,4
Необходимые формулы
1. Продольная сила
N   Fi
2. Правило знаков
7
3. Нормальное напряжение
Ν
σ ,
Α
где  - продольная сила;
А – площадь поперечного сечения.
4. Удлинение (укорочение) бруса
Δl 
N l
σ l
или Δl 
,
A E
E
где Е – модуль упругости;
l – начальная длина стержня.
Последовательность решения задач:
1. Разбиваем брус на участки, начинают свободного конца. Границами участков
являются: начало и конец бруса, границы сечений, точки приложения сил.
2. Определить по методу сечений продольную силу для каждого участка и
построить эпюру продольных сил . Проведя параллельно оси бруса базовую
(нулевую) линию эпюры, отложить перпендикулярно ей в произвольном
масштабе получаемые значения. Штриховку каждого участка производить
четкими перпендикулярными линиями относительно нулевой линии.
3. Для построения эпюр нормальных напряжений определяем напряжения в
поперечных сечениях каждого из участков. В пределах каждого участка
напряжения постоянны, то есть эпюра на данном участке изображается прямой,
параллельной оси бруса.
4. Перемещение свободного конца бруса определяется как сумму удлинений
(укорочений) участков бруса, вычисленных по формуле Гука.
Пример решения задач
Для ступенчатого стального бруса требуется:
 определить значение продольной силы и нормального напряжения по длине
бруса;
 построить эпюры  и ;
 определить абсолютное удлинение (укорочение) бруса.
Модуль продольной упругости Е  2  105 МПа.
Решение
1. Разбиваем брус на участки.
2. Определяем продольную силу на каждом участке
8
1 = 0
2 = F1 = 50 кН
3 = F1 + F2 = 50 + 21 = 71 кН
4 = F1 + F2 + F3 = 50 + 21 + 5 = 76 кН
3. По найденным значениям строим эпюру продольных сил.
4. Определяем нормальное напряжение на каждом участке
Ν
σ1  1  0
Α1
Ν2 50  103
σ2 

 36 МПа
Α1 14  10 2
Ν3 71  103
σ3 

 55 МПа
Α2 13  10 2
σ4 
Ν4 76  103

 63 МПа
Α3 12  10 2
5. По найденным значениям строим эпюру нормальных напряжений.
6. Определяем перемещение свободного конца
lОБЩ = l1 + l2 + l3 + l4
Δl1 
N1  l1
0
E  A1
Δl 2 
N 2  l2
50 103  400

 0,71 мм
E  A1 2 105 14 10 2
Δl 3 
N 3  l3
71103  500

0,13 мм
E  A2 2 105 13 10 2
N 4  l4
76 103  400
Δl 4 

 0,13 мм
E  A3 2 105 12 10 2
lОБЩ = 0 + 0,71 + 0,13 + 0,13 = 0,97 мм.
9
ЗАДАНИЕ 4. Для консольной балки построить эпюры поперечных сил и изгибающих
моментов. Проверить выполнения условия прочности при изгибе. Размеры сечения даны
в мм.
Таблица 1 – Схемы задач
Таблица 2 – Исходные данные
№ схемы
F, кН
1
2
2
5
3
8
4
2
5
8
6
15
7
2
8
8
9
5
q, кН/м
0,5
10
4
4
2
12
10
4
2
a1 , м
0,8
0,5
0,8
1
0,2
0,5
1
0,5
1
a2, м
1,2
1
0,7
1
0,7
1
0,5
1
0,8
a3, м
0,5
0,5
0,7
Основные положения и расчетные формулы при изгибе
1. Изгибающий момент в сечении:
П
М И   mi
0
2. Поперечная сила в сечении:
П
Q   FiY
0
3. Правило знаков:
 Поперечных сил
 Изгибающих моментов
4. Правила построения эпюр.
10
 Для эпюр поперечных сил:
1. На участке, нагруженном равномерно распределительной нагрузкой, эпюра
изображается прямой, наклонной к оси балки.
2. На участке, свободном от распределенной нагрузки, эпюра изображается прямой,
параллельной оси балки.
3. В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не
изменяет своего значения.
4. В сечении, где приложенная сила, эпюра поперечных сил меняется на значение,
равное приложенной силе.
5. В концевом сечении балки поперечная сила численно равна сосредоточенной
силе, приложенной в этом сечении. Если в концевом сечении балки не приложена
сосредоточенная сила, то поперечная сила в этом сечении равна нулю.
 Для эпюр изгибающих моментов:
1. На участке, нагруженном равномерно распределенной нагрузкой, эпюра
моментов изображается параболой.
2. На участке, свободном от равномерно распределенной нагрузки, эпюра моментов
изображается прямой линией.
3. В сечении балки, где приложена сосредоточенная пара сил (момент), изгибающий
момент меняется скачкообразно на значение, равное моменту приложенной пары.
4. Изгибающий момент в концевом сечении балки равен нулю, если в нем не
приложена сосредоточенная пара сил (момент). Если же в концевом сечении
приложен момент, то изгибающий момент в этом сечении равен внешнему
моменту.
5. На участке, где поперечная сила равна нулю, балка испытывает изгиб, и эпюра
изгибающих моментов изображается прямой, параллельной оси балки.
Для построения эпюр проводят нулевую линию под изображением балки. При
построении эпюры поперечных сил положительные значения откладывают вверх от
нулевой линии, а отрицательные – вниз. При построении эпюры изгибающих моментов
положительные значения откладываются вниз от нулевой линии, а отрицательные –
вверх.
6.Условие прочности
М
σ
 [σ ]
WХ
7. Единицы переводов
1 кН = 103Н
1 м = 103 мм
1 МПа = 1 Н/мм2
1 Па = 1 Н/м2
8. Моменты сопротивления:
 для круга
WX  0,1 d 3
 для кольца
WX  0,1d 3H  (1  α4 ) ,
11
dH
d ВН
 для прямоугольника
где α 
bh 2
hb 2
, WY 
WX 
6
6
 для квадрата
WX  WY 
a3
6
Пример решения задач
Для консольной балки построить эпюры поперечных сил и изгибающих моментов.
Проверить выполнения условия прочности при изгибе. Размеры сечения даны в мм.
Решение
1. Определяем поперечную силу на каждом участке.
Q1Н  0
Q1К  q  3  2  3  6 кН
Q 2  q  3 - F  2  3  4  2 кН.
2. По найденным значениям строим эпюру поперечных сил (Q).
3. Определяем изгибающий момент в каждой точке приложения внешних сил.
МИА = 0
М ИС  q  3 1,5  2  3 1,5  9 кНм
М ИС  q  3  4,5  F  3  2  3  4,5  4  3  15 кНм
4. По найденным значениям строим эпюру изгибающих моментов (МИ).
5. Проверяем выполнения условия прочности при изгибе:
М
σ  ИMAX  σ ,
WX
так как сечение прямоугольное, то момент сопротивления определяем по формуле:
b  h 2 50  150 2
WX 

 187500 мм.
6
6
15  10 3  10 3
σ
 80 МПа < 160 МПа
187500
условие прочности выполняется.
12
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
Михайлов А.М. «Сопротивление материалов», М: Высшая школа, 1989.
Мухин Н.В. «Статика сооружений в примерах», М: Высшая школа, 1987.
Мухин Н.В. «Статика сооружений», М: Высшая школа, 1987.
Портаев Л.П., Петраков А.А., Портаев В.Л. «Техническая механика», М:
Стройиздат, 1987.
5. Сетков В.И. «Сборник задач по технической механике», М: Издательский центр
«Академия», 2003.
1.
2.
3.
4.
13